Skip to main content
SpringerLink
Log in

Dynamical analysis of a fractional-order predator–prey model incorporating a constant prey refuge and nonlinear incident rate

  • Original Article
  • Published:
Modeling Earth Systems and Environment Aims and scope Submit manuscript

Abstract

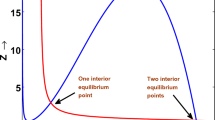
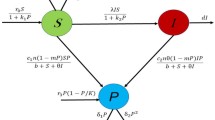
In this work, we have formulated and analyzed a fractional-order predator–prey model with an asymptotic incidence rate and constant prey refuge. Due to vulnerability, it is assumed that predator consumes only infected prey. Our mathematical formulation of the non-integer-order initial value problem has been developed on the famous fractional-order Caputo derivative. The main objective of this work is to investigate the influence of fractional-order derivatives on the system over the classical integer-order model. We have discussed the existence of non-negative solution, uniqueness and boundedness of our considered model. Analysis of local stability and Hopf bifurcation are performed both analytically and numerically. Sufficient conditions are established to guarantee the global stability of the interior equilibrium point by constructing a suitable Lyapunov function. Finally, some numerical simulations are provided to validate our results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Abbas S, Mahto L, Favini A, Hafayed M (2016) Dynamical study of fractional model of allelopathic stimulatory phytoplankton species. Differ Equ Dyn Syst 24:267–280

    Google Scholar 

  • Abdelouahab MS, Hamri N, Wang J (2012) Hopf bifurcation and chaos in fractional-order modified hybrid optical system. Nonlinear Dyn 69:275–284

    Google Scholar 

  • Ahmed E, El-Sayed AMA, El-Saka HAA (2006) On some Routh-Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rossler, Chua and Chen systems. Phys Lett A 358:1–4

    Google Scholar 

  • Ahmed E, El-Sayed AMA, El-Saka HAA (2007) Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models. J Math Anal Appl 325:542–553

    Google Scholar 

  • Assaleh K, Ahmad WM (2007) Modelling of speech signals using fractional calculus. In: 9th International Symposium on signal processing and its applications (ISSPA 2007)

  • Bera SP, Maiti A, Samanta GP (2015) A prey-predator model with infection in both prey and predator. Filomat 29(8):1753–1767. https://doi.org/10.2298/FIL1508753B

    Article  Google Scholar 

  • Choi SK, Kang B, Koo N (2014) Stability for Caputo fractional differential systems. Abstr Appl Anal 2014:1–6

    Google Scholar 

  • Cole KS (1993) Electric conductance of biological systems. In: Cold Spring Harbor Symposium on quantitative biology, pp 107–116

  • Das S, Mahato P, Mahato SK (2020) Disease control prey-predator model incorporating prey refuge under fuzzy uncertainty. Model Earth Syst Environ. https://doi.org/10.1007/s40808-020-00892-w

    Article  Google Scholar 

  • Debnath L (2003) Recent applications of fractional calculus to science and engineering. Int J Math Math Sci 54:3413–3442

    Google Scholar 

  • Diethem K, Ford NJ, Freed AD (2002) A predictor corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn 29:23–22

    Google Scholar 

  • Elsadany AA, Matouk AE (2015) Dynamical behaviors of fractional-order Lotka-Volterra predator-prey model and its discretization. J Appl Math Comput 49:269–283

    Google Scholar 

  • El-Sayed S (1998) Nonlinear functional differential equations of arbitrary orders. Nonlinear Anal Theory Methods Appl 33(2):181–186

    Google Scholar 

  • El-Sayed A, El-Mesiry A, EL-Saka H (2007) On the fractional order logistic equation. Appl Math Lett 20(7):817–823

    Google Scholar 

  • Fedri Y (2012) Some applications of fractional order calculus to design digital filters for biomedical signal processing. J Mech Med Biol 12(2):13

    Google Scholar 

  • Ghaziani R, Alidousti J, Eshkaftaki AB (2016) Stability and dynamics of a fractional order Leslie- Gower prey-predator model. Appl Math Model 40:2075–2086

    Google Scholar 

  • Gonzalez-Olivares E, Ramos-Jiliberto R (2003) Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecol Model 166:135–146

    Google Scholar 

  • Hadeler KP, Freedman HI (1989) Predator-prey populations with parasitic infection. J Math Biol 27:609–631

    Google Scholar 

  • Haque M, Venturino E (2009) Modelling disease spreading in symbiotic communities. Wildlife: destruction, conservation and biodiversity. Nova Science Publishers

  • Hethcote H, Wang W, Han L, Ma Z (2004) A predator-prey model with infected prey. Theor Popul Biol 66:259–268

    Google Scholar 

  • Holt RD, Roy M (2007) Predation can increase the prevalence of infectious disease. Am Nat 169:690–699

    Google Scholar 

  • Hsieh YH, Hsiao CK (2008) Predator-prey model with disease infection in both populations. Math Med Biol 25:247–266

    Google Scholar 

  • Huang Y, Chen F, Zhong L (2006) Stability analysis of a prey-predator model with Holling type III response function incorporating a prey refuge. Appl Math Comput 182:672–683

    Google Scholar 

  • Hudson PJ, Dobson AP, Newborn D (1992) Do parasite make prey vulnerable to predation Red grouse and parasite. J Anim Ecol 61:681–692

    Google Scholar 

  • Huo J, Zhao H, Zhu L (2015) The effect of vaccines on backward bifurcation in a fractional order HIV model. Nonlinear Anal 26:289–305

    Google Scholar 

  • Jana D, Ray S (2016) Impact of physical and behavioral prey refuge on the stability and bifurcation of Gause type Filippov prey-predator system. Model Earth Syst Environ. https://doi.org/10.1007/s40808-016-0077-y

    Article  Google Scholar 

  • Javidi M, Nyamoradi N (2013) Dynamic analysis of a fractional order prey-predator interaction with harvesting. Appl Math Model 37:8946–8956

    Google Scholar 

  • Ji G, Ge Q, Xu J (2016) Dynamic behaviors of a fractional order two-species cooperative systems with harvesting. Chaos Solitons Fract 92:51–55

    Google Scholar 

  • Kar TK (2006) Modelling and analysis of a harvested prey-predator system incorporating a prey refuge. J Comput Appl Math 185:19–33

    Google Scholar 

  • Kermack W, McKendrick A (1927) A contribution to the mathematical theory of epidemics. Proc R Soc A 115:700–721

    Google Scholar 

  • Krivan V (1998) Effects of optimal anti predator behavior of prey on predator-prey dynamics: the role of refuges. Theor Popul Biol 53:131–142

    Google Scholar 

  • Krivan V (2011) On the Gause predator-prey model with a refuge: A fresh look at the history. J Theoret Biol 274:67–73

    Google Scholar 

  • Li C, Tao C (2009) On the fractional Adams method. Comput Math Appl 58(8):1573–1588

    Google Scholar 

  • Li HL, Long Z, Cheng H, Yao-Lin J, Zhidong T (2016) Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J Appl Math Comput 54:435–449

    Google Scholar 

  • Machado JAT (2010) Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn 62(1–2):371–378

    Google Scholar 

  • Machado JAT, Galhano AMSF (2012) Fractional order inductive phenomenona based on the skin effect. Nonlinear Dyn 68(1–2):107–115

    Google Scholar 

  • Maji C, Kesh D, Mukherjee D (2019) Bifurcation and global stability in an eco-epidemic model with refuge. Energ Ecol Environ 4:103–115

    Google Scholar 

  • Maji C, Mukherjee D, Kesh D (2020) Study of a fractional-order model of chronic wasting disease. Math Methods App Sci 43(7):4669–4682

    Google Scholar 

  • Mandal M, Jana S, Nandi SK et al (2020) Modeling and analysis of a fractional-order prey-predator system incorporating harvesting. Model Earth Syst Environ. https://doi.org/10.1007/s40808-020-00970-z

    Article  Google Scholar 

  • Matouk AE, Elsadany AA (2016) Dynamical analysis, stabilization and discretization of a chaotic fractional-order GLV model. Nonlinear Dyn 85:1597–1612

    Google Scholar 

  • Matouk AE, Elsadany AA, Ahmed E, Agiza H (2015) Dynamical behavior of fractional-order Hastings-Powell food chain model and its discretization. Commun Nonlinear Sci Numer Simul 27:153–167

    Google Scholar 

  • Matignon D (1996) Stability results in fractional differential equation with applications to control processing. In: Proceedings of the Multiconference on computational engineering in systems and application IMICS.IEEE-SMC. Life, France. 2: 963–968

  • Moustafa M, Mohd MH, Ismail AI, Abdullah FA (2019) Stage structure and refuge effects in the dynamical analysis of a fractional order Rosenzweig-MacArthur prey-predator model. Prog Fract Differ Appl 5:1–16

    Google Scholar 

  • Mukherjee D (2014) The effect of prey refuges on a three species food chain model. Differ Equ Dyn Syst 22:413–426

    Google Scholar 

  • Mukherjee D (2016) The effect of refuge and immigration in a predator-prey systems in the presence of a competitor for the prey. Nonlinear Anal Real World Appl 31:277–287

    Google Scholar 

  • Nosrati K, Shafiee M (2017) Dynamic analysis of fractional-order singular holling type-ii predator-prey system. Appl Math Comput 313:159–179

    Google Scholar 

  • Packer C, Holt RD, Hudson PJ, Lafferty KD, Dobson AP (2003) Keeping the herds healthy and alert: implications of predator control for infectious disease. Ecol Lett 6:797–802

    Google Scholar 

  • Rihan FA, Abdelrahman DH (2013) Delay differential model for tumor-immune dynamics with HIV infection of CD$^+$ T-cells. Int J Comput Math 90(3):594–614

    Google Scholar 

  • Ruxton GD (1995) Short term refuge use and stability of predator-prey models. Theor Popul Biol 47(1):1–17

    Google Scholar 

  • Samanta GP, Maiti A, Das M (2018) Stability analysis of a prey-predator fractional order model incorporating prey refuge. Ecol Genet Gener 7:33–46

    Google Scholar 

  • Sharma S, Samanta GP (2015) A Leslie-Gower predator-prey model with disease in prey incorporating a prey refuge. Chaos Solitons Fract 70:69–84

    Google Scholar 

  • Shi XY, Cui J, Zhou XY (2011) Stability and Hopf bifurcation analysis of an eco-epidemic model with a stage structure. Nonlinear Anal 74:1088–106

    Google Scholar 

  • Sih A (1987) Prey refuges and predator-prey stability. Theoret Popul Biol 31:1–12

    Google Scholar 

  • Singh H, Dhar J, Bhatti HS (2016) Dynamics of a prey-generalized predator system with disease in prey and gestation delay for predator. Model Earth Syst Environ. https://doi.org/10.1007/s40808-016-0096-8

    Article  Google Scholar 

  • Venturino E (1994) The influence of diseases on Lotka-Volterra systems. Rocky Mt J Math 24:381–402

    Google Scholar 

  • Wang S, Ma Z (2012) Analysis of an ecoepidemiological model with prey refuges. J Appl Math. https://doi.org/10.1155/2012/371685

    Article  Google Scholar 

  • Wei Z, Li Q, Che J (2010) Initial value problems for fractional differential equations involving Riemann-Liouville sequential derivative. J Math Appl 367:260–72

    Google Scholar 

  • Xiao YN, Chen LS (2001) Analysis of a three species eco-epidemiological model. J Math Anal Appl 258(2):733–754

    Google Scholar 

  • Zhang JF, Li WT, Yan XP (2008) Hopf bifurcation and stability of periodic solutions in a delayed eco-epidemiological system. Appl Math Comput 198:865–76

    Google Scholar 

  • Zhou XY, Shi XY, Song XY (2009) Analysis of a delay prey-predator model with disease in the prey species only. J Korean Math Soc 46(4):713–731

    Google Scholar 

  • Zhou X, Cui J (2010) Stability and Hopf bifurcation analysis of an eco-epidemiological model with delay. J Frank Inst 347:1654–80

    Google Scholar 

Download references

Acknowledgements

The authors are grateful to the Editor and anonymous reviewers for their helpful comments and suggestions for improving the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Vivekananda College, Thakurpukur, Kolkata, 700063, India

    Chandan Maji

Authors
  1. Chandan Maji
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chandan Maji.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publishing of the paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maji, C. Dynamical analysis of a fractional-order predator–prey model incorporating a constant prey refuge and nonlinear incident rate. Model. Earth Syst. Environ. 8, 47–57 (2022). https://doi.org/10.1007/s40808-020-01061-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40808-020-01061-9

Keywords

Search

Navigation