1 Introduction

With the rapid development of computer technology and network communication technology, more and more functionalities and facilities have been brought to us by the network. However, at the same time, there is a dramatic increase in computer viruses, which has brought about huge financial losses and social panic [1–3]. Consequently, it is quite urgent to understand the spread law of computer viruses over the network.

To this end, and based on the fact that the propagation of computer viruses among computers resembles that of biological viruses among a population, dynamical modeling is one of the most effective approaches. Since the pioneering work of Kephart and White [4, 5], many dynamical models describing the propagation of computer viruses in the network have been established by appropriately modifying epidemic models, such as SIR [6, 7], SIRS [8–11], SEIR [12], SEIRS [13, 14], SLBS [15–17], SLBQRS [18], SEVIR [19] models and so on. All the computer virus models above neglect the fact that computer viruses possess a paroxysmal nature in common and computer viruses have the possibility of an outbreak absence of aura. Namely, they assume that once a susceptible computer in the network is infected, it is in its latency. In addition, antivirus techniques always lag behind virus techniques. Thus, computers in the network are susceptible to the attack during the period that the anti-virus software aims to conquer the new viruses. Based on this, Xu and Ren [20] proposed the following SEIR computer virus spreading model in the network with limited anti-virus ability:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt}=b-\beta S(t)I(t)-\varrho S(t), \\ \frac{dE(t)}{dt}=(1-p)\beta S(t)I(t)-\gamma E(t)+\varepsilon I(t)- \varrho E(t), \\ \frac{dI(t)}{dt}=p\beta S(t)I(t)+\gamma E(t)-\varepsilon I(t)- \alpha I(t)-\varrho I(t), \\ \frac{dR(t)}{dt}=\alpha I(t)-\varrho R(t), \end{cases} $$
(1)

where \(S(t)\), \(E(t)\), \(I(t)\) and \(R(t)\) denote the numbers of the susceptible computers, the exposed computers where computer viruses are latent, the infected computers where computer viruses are breaking out and the recovered computers that have been equipped with anti-virus software at time t, respectively. β is the transmission rate of the infected computers; p is the rate at which a susceptible computer breaks out suddenly due to its connection with infected computers; \(1-p\) is the rate at which a susceptible computer is latent due to its connection with infected computers; ϱ is the death rate of computers in the network; γ, ε and α are the state transition rates. Xu and Ren [20] studied stabilities of virus-free equilibrium and virus equilibrium.

However, it should be pointed out that system (1) neglects the time delay due to the latent period of computer viruses in the exposed computers and the time delay due to the period that anti-virus software uses to clean the viruses in the infected computers. As is known, in order to reflect the dynamical behaviors of a dynamical model depending on the past history of the system, it is often necessary to incorporate time delays into the model. Dynamical models with time delay have been investigated extensively by scholars at home and abroad in recent years, especially predator-prey models [21–26], epidemic models [27–29] and computer virus models [9–11, 30, 31]. Motivated by the work above, we consider the following computer virus model with delays:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = b-\beta S(t)I(t)-\varrho S(t), \\ \frac{dE(t)}{dt} = (1-p)\beta S(t)I(t)-\gamma E(t-\tau_{1})+\varepsilon I(t)-\varrho E(t), \\ \frac{dI(t)}{dt} = p\beta S(t)I(t)+\gamma E(t-\tau_{1})-\varepsilon I(t)-\alpha I(t-\tau_{2})-\varrho I(t), \\ \frac{dR(t)}{dt} = \alpha I(t-\tau_{2})-\varrho R(t), \end{cases} $$
(2)

where \(\tau_{1}\) is the time delay due to the latent period of computer viruses in the exposed computers and \(\tau_{2}\) is the time delay due to the period that anti-virus software uses to clean the viruses in the infected computers. For convenience, throughout this paper, we assume that \(\tau_{1}=\tau_{2}\). Then system (2) becomes

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = b-\beta S(t)I(t)-\varrho S(t), \\ \frac{dE(t)}{dt} = (1-p)\beta S(t)I(t)-\gamma E(t-\tau )+\varepsilon I(t)-\varrho E(t), \\ \frac{dI(t)}{dt} = p\beta S(t)I(t)+\gamma E(t-\tau )-\varepsilon I(t)- \alpha I(t-\tau )-\varrho I(t), \\ \frac{dR(t)}{dt} = \alpha I(t-\tau )-\varrho R(t). \end{cases} $$
(3)

The remainder of this paper is organized in the following pattern. In Section 2, local stability of the viral equilibrium and the existence of a Hopf bifurcation are examined. In Section 3, the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions are investigated. In order to illustrate the validity of the theoretical analysis, a numerical example is presented in Section 4. Some main conclusions are drawn in Section 5.

2 Stability of the viral equilibrium and existence of Hopf bifurcation

Solving the algebraic system

$$ \textstyle\begin{cases} b-\beta SI-\varrho S=0, \\ (1-p)\beta SI-\gamma E+\varepsilon I-\varrho E=0, \\ p\beta SI+\gamma E-(\varepsilon +\alpha +\varrho )I=0, \\ \alpha I-\varrho R=0, \end{cases} $$
(4)

we can get the unique viral equilibrium \(P_{*}(S_{*}, E_{*}, I_{*}, R _{*})\) of system (3) if \(b\beta \gamma +pb\beta \varrho +\gamma \varrho \varepsilon >\varrho (\gamma +\varrho )(\varepsilon + \alpha +\varrho )\) and \(\varepsilon +\alpha +\varrho >\frac{pb\beta }{ \varrho +\beta I_{*}}\), where

$$\begin{aligned}& S_{*} = \frac{b}{\varrho +\beta I_{*}}, \qquad E_{*}=\frac{I_{*}}{\gamma } \biggl(\varepsilon +\alpha +\varrho -\frac{pb\beta }{\varrho +\beta I _{*}} \biggr), \\& I_{*} = \frac{b\beta \gamma +pb\beta \varrho +\gamma \varrho \varepsilon -\varrho (\gamma +\varrho )(\varepsilon +\alpha +\varrho )}{\beta \gamma (\alpha +\varrho )+\beta \varrho (\varepsilon +\alpha +\varrho )}, \\& R_{*}=\frac{\alpha }{\varrho }I_{*}. \end{aligned}$$

In what follows, we can get the characteristic equation of system (3) at \(P_{*}(S_{*}, E_{*}, I_{*}, R_{*})\)

$$\begin{aligned}& \lambda^{4}+\alpha_{3}\lambda^{3}+\alpha_{2}\lambda^{2}+ \alpha_{1} \lambda +\alpha_{0} \\& \quad {}+ \bigl(\beta_{3}\lambda^{3}+\beta_{2} \lambda^{2}+\beta_{1}\lambda +\beta _{0} \bigr)e^{-\lambda \tau } \\& \quad {} + \bigl(\gamma_{2}\lambda^{2}+\gamma_{1} \lambda +\gamma_{0} \bigr)e^{-2\lambda \tau }=0, \end{aligned}$$
(5)

where

$$\begin{aligned}& \alpha_{0} = \alpha_{22}\alpha_{44}( \alpha_{11}\alpha_{33}-\alpha_{13} \alpha_{31}), \\& \alpha_{1} = \alpha_{13}\alpha_{31}( \alpha_{22}+\alpha_{44})-\alpha _{11} \alpha_{22}(\alpha_{33}+\alpha_{44})- \alpha_{33}\alpha_{44}( \alpha_{11}+ \alpha_{22}), \\& \alpha_{2} = \alpha_{11}\alpha_{22}+ \alpha_{33}\alpha_{44}-\alpha_{13} \alpha_{31}+(\alpha_{11}+\alpha_{22}) ( \alpha_{33}+\alpha_{44}), \\& \alpha_{3} = -(\alpha_{11}+\alpha_{22}+ \alpha_{33}+\alpha_{44}), \\& \beta_{0} = \alpha_{11}\alpha_{44}( \alpha_{22}\beta_{33}+\alpha_{33} \beta_{22})-\alpha_{44}\beta_{32}( \alpha_{11}\alpha_{23}-\alpha_{13} \alpha_{21})-\alpha_{13}\alpha_{31} \alpha_{44}\beta_{32}, \\& \beta_{1} = \beta_{32}(\alpha_{11} \alpha_{23}-\alpha_{13}\alpha_{21})+ \alpha_{23}\alpha_{44}\beta_{32}- \beta_{22} \bigl(\alpha_{11}\alpha_{33}+ \alpha_{44}(\alpha_{11}+\alpha_{33}) \bigr) \\& \hphantom{\beta_{1} = }{} +\alpha_{13}\alpha_{31}- \beta_{13} \bigl(\alpha_{11}\alpha_{22}+\alpha _{44}(\alpha_{11}+\alpha_{22}) \bigr), \\& \beta_{2} = \beta_{22}(\alpha_{11}+ \alpha_{33}+\alpha_{44})+\beta_{33}( \alpha_{11}+\alpha_{22}+\alpha_{44})- \alpha_{23}\beta_{32}, \\& \beta_{3} = -(\beta_{22}+\beta_{33}), \\& \gamma_{0} = \alpha_{11}\alpha_{44} \beta_{22}\beta_{33}, \\& \gamma_{1}=- \beta_{22}\beta_{33}( \alpha_{11}+\alpha_{44}), \\& \gamma_{3}=\beta_{22} \beta_{33}, \end{aligned}$$

with

$$\begin{aligned}& \alpha_{11} = -(\beta I_{*}+\varrho ), \qquad \alpha_{13}=-\beta S_{*}, \\& \alpha_{21}=(1-p)\beta I_{*}, \qquad \alpha_{22}=- \varrho ,\qquad \alpha_{23} = (1-p)\beta S_{*}+\varepsilon , \\& \alpha_{31}=p\beta I_{*},\qquad\alpha_{33}=p\beta S_{*}-\varepsilon -\varrho , \\& \alpha_{44} = -\varrho , \\& \beta_{22}=-\gamma , \qquad \beta_{32}=\gamma , \\& \beta_{33}=-\alpha , \qquad \beta_{43}=\alpha . \end{aligned}$$

Multiplying \(e^{\lambda \tau }\) on both sides of Eq. (5), Eq. (5) equals

$$\begin{aligned}& \beta_{3}\lambda^{3}+\beta_{2} \lambda^{2} + \beta_{1}\lambda +\beta _{0} \\& \quad {} + \bigl(\lambda^{4}+\alpha_{3}\lambda^{3}+ \alpha_{2}\lambda^{2}+\alpha _{1}\lambda + \alpha_{0} \bigr)e^{\lambda \tau } \\& \quad {} + \bigl(\gamma_{2}\lambda^{2}+\gamma_{1} \lambda +\gamma_{0} \bigr)e^{-\lambda \tau }=0. \end{aligned}$$
(6)

When \(\tau =0\), then Eq. (6) reduces to

$$\begin{aligned} \lambda^{4}+\alpha_{03}\lambda^{3}+ \alpha_{02}\lambda^{2}+\alpha_{01} \lambda + \alpha_{00}=0, \end{aligned}$$
(7)

where

$$\begin{aligned}& \alpha_{00}=\alpha_{0}+\beta_{0}+ \gamma_{0},\qquad \alpha_{01}=\alpha_{1}+ \beta_{1}+\gamma_{1}, \\& \alpha_{02}=\alpha_{2}+\beta_{2}+ \gamma_{2},\qquad \alpha_{03}=\alpha_{3}+ \beta_{3}. \end{aligned}$$

Thus, according to the Routh-Hurwitz criterion, the real parts of all roots of Eq. (7) are negative if and only if \(\alpha_{00}>0\), \(\alpha_{03}>0\), \(\alpha_{02}\alpha_{03}>\alpha_{01}\) and \(\alpha_{01}\alpha_{02}\alpha_{03}>\alpha_{00}\alpha_{03}^{2}+ \alpha_{01}^{2}\).

Let \(\lambda =i\omega\) (\(\omega >0\)) be the root of Eq. (6), then

$$ \textstyle\begin{cases} (\omega^{4}-(\alpha_{2}+\gamma_{2})\omega^{2}+\alpha_{0}+\gamma_{0}) \cos \tau \omega -((\alpha_{1}-\gamma_{1})\omega -\alpha_{3}\omega ^{3})\sin \tau \omega =\beta_{2}\omega^{2}-\beta_{0}, \\ (\omega^{4}-(\alpha_{2}-\gamma_{2})\omega^{2}+\alpha_{0}-\gamma_{0}) \sin \tau \omega +((\alpha_{1}+\gamma_{1})\omega -\alpha_{3}\omega ^{3})\cos \tau \omega =\beta_{3}\omega^{3}-\beta_{1}\omega , \end{cases} $$

from which we obtain

$$\begin{aligned}& \cos \tau \omega =\frac{f_{6}\omega^{6}+f_{4}\omega^{4}+f_{2}\omega ^{2}+f_{0}}{\omega^{8}+e_{3}\omega^{6}+e_{2}\omega^{4}+e_{1}\omega ^{2}+e_{0}}, \\& \sin \tau \omega =\frac{f_{7}\omega^{6}+f_{5}\omega^{4}+f_{3}\omega ^{2}+f_{1}\omega }{\omega^{8}+e_{3}\omega^{6}+e_{2}\omega^{4}+e_{1} \omega^{2}+e_{0}}, \end{aligned}$$

with

$$\begin{aligned}& e_{0} = \alpha_{0}^{2}-\gamma_{0}^{2}, \\& e_{1}=2\gamma_{0}\gamma_{2}- \gamma_{1}^{2}+\alpha_{1}^{2}-2 \alpha_{0}\alpha_{2}, \\& e_{2} = \alpha_{2}^{2}+2\alpha_{0}- \gamma_{2}^{2}-2\alpha_{1}\alpha _{2}, \\& e_{3}=\alpha_{3}^{2}-2\alpha_{2}, \\& f_{0} = \beta_{0}(\gamma_{0}- \alpha_{0}), \\& f_{1}=\beta_{0}(\alpha_{1}+ \gamma_{1})-\beta_{1}(\alpha_{0}+ \gamma_{0}), \\& f_{2} = \beta_{0}(\alpha_{2}- \gamma_{2})+\beta_{2}(\alpha_{0}-\gamma _{0})+\beta_{1}(\gamma_{1}-\alpha_{1}), \\& f_{3} = \beta_{1}(\alpha_{2}+ \gamma_{2})+\beta_{3}(\alpha_{0}+\gamma _{0})-\beta_{2}(\alpha_{1}+\gamma_{1})- \alpha_{3}\beta_{0}, \\& f_{4} = \alpha_{1}\beta_{3}+\alpha_{3} \beta_{1}-\beta_{3}\gamma_{1}- \beta_{0}-\beta_{2}(\alpha_{2}- \gamma_{2}), \\& f_{5} = \alpha_{3}\beta_{2}-\beta_{1}- \beta_{3}(\alpha_{2}+\gamma_{2}), \\& f_{6}=\beta_{2}, \\& f_{7}=\beta_{3}. \end{aligned}$$

Then we can get the equation with respect to ω of the following form:

$$ \cos^{2}\tau \omega +\sin^{2}\tau \omega =1. $$
(8)

Next, we give the following assumption. \((H_{1})\): Eq. (8) has at least one positive root \(\omega_{0}\). For \(\omega_{0}\), we have

$$ \tau_{0}=\frac{1}{\omega_{0}}\times \arccos { \biggl\{ \frac{f_{6}\omega _{0}^{6}+f_{4}\omega_{0}^{4}+f_{2}\omega_{0}^{2}+f_{0}}{\omega_{0} ^{8}+e_{3}\omega_{0}^{6}+e_{2}\omega_{0}^{4}+e_{1}\omega_{0}^{2}+e _{0}}} \biggr\} . $$

Differentiating Eq. (6) with respect to τ, we have

$$ \biggl[\frac{d\lambda }{d\tau } \biggr]^{-1}=\frac{G(\lambda )}{H(\lambda )}- \frac{\tau }{\lambda }, $$

with

$$\begin{aligned}& G(\lambda ) = 3\beta_{3}\lambda^{2}+2\beta_{2} \lambda +\beta_{1}+ \bigl(4 \lambda^{3}+3\alpha_{3} \lambda^{2}+2\alpha_{2}\lambda +\alpha_{1} \bigr)e ^{\lambda \tau }+(2\gamma_{2}\lambda +\gamma_{1})e^{-\lambda \tau }, \\& H(\lambda ) = \lambda \bigl(\gamma_{2}\lambda^{2}+ \gamma_{1}\lambda +\gamma _{0} \bigr)e^{-\lambda \tau }-\lambda \bigl(\lambda^{4}+\alpha_{3}\lambda^{3}+ \alpha_{2}\lambda^{2}+\alpha_{1}\lambda + \alpha_{0} \bigr). \end{aligned}$$

Then

$$ \operatorname{Re} \biggl[\frac{d\lambda }{d\tau } \biggr]_{\lambda =i\omega_{0}} ^{-1}=\frac{G_{1R}\times G_{2R}+G_{1I}\times G_{2I}}{G_{2R}^{2}+G_{2I} ^{2}}, $$

where

$$\begin{aligned}& G_{1R} = \bigl(\alpha_{1}+\gamma_{1}-3 \alpha_{3}\omega_{0}^{2} \bigr)\cos \tau _{0}\omega_{0}- \bigl(2(\alpha_{2}- \gamma_{2})\omega_{0}-4\omega_{0}^{3} \bigr)\sin \tau_{0} \omega_{0}+\beta_{1}-3 \beta_{3}\omega_{0}^{2}, \\& G_{1I} = \bigl(\alpha_{1}-\gamma_{1}-3 \alpha_{3}\omega_{0}^{2} \bigr)\sin \tau _{0}\omega_{0} + \bigl(2(\alpha_{2}+ \gamma_{2})\omega_{0}-4\omega_{0}^{3} \bigr)\cos \tau_{0} \omega_{0}+2\beta_{2} \omega_{0}, \\& G_{2R} = \bigl(\gamma_{0}\omega_{0}- \gamma_{2}\omega_{0}^{3} \bigr)\sin \tau_{0} \omega_{0}-\gamma_{1} \omega_{0}^{2}\cos \tau_{0}\omega_{0}- \alpha_{3} \omega_{0}^{4}+\alpha_{1} \omega_{0}^{2}, \\& G_{2I} = \bigl(\gamma_{0}\omega_{0}- \gamma_{2}\omega_{0}^{3} \bigr)\cos \tau_{0} \omega_{0}+\gamma_{1} \omega_{0}^{2}\sin \tau_{0}\omega_{0}- \omega_{0} ^{5}+\alpha_{2}\omega_{0}^{3}. \end{aligned}$$

To establish a Hopf bifurcation at \(\tau =\tau_{0}\), we make the following assumption. \((H_{2})\): \(G_{1R}\times G_{2R}+G_{1I}\times G _{2I}\neq 0\).

Summarizing the above analysis, and based on the Hopf bifurcation theorem in [32], we have the following.

Theorem 1

Suppose that conditions \((H_{1})\)-\((H_{2})\) hold for system (3). \(P_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) is locally asymptotically stable when \(\tau \in [0, \tau_{0})\); a Hopf bifurcation occurs at \(P_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) when \(\tau =\tau_{0}\) and a family of periodic solutions bifurcate from \(P_{*}(S_{*}, E_{*}, I _{*}, R_{*})\).

3 Direction of the Hopf bifurcation and stability of the bifurcating periodic solutions

In this section, we will employ the algorithm of Hassard et al. in [32] to analyze the direction of the Hopf bifurcation and the stability of bifurcating periodic solutions from the viral equilibrium \(P_{*}(S _{*}, E_{*}, I_{*}, R_{*})\) of system (3) at \(\tau =\tau _{0}\). Let \(u_{1}(t)=S(t)-S_{*}\), \(u_{2}(t)=E(t)-E_{*}\), \(u_{3}(t)=I(t)-I _{*}\), \(u_{4}(t)=R(t)-R_{*}\), and rescale the delay by \(t\rightarrow (t/\tau )\). Let \(\tau =\tau_{0}+\mu \), \(\mu \in R\). Then system (3) can be transformed into the following form:

$$ \dot{u}(t)=L_{\mu }u_{t}+F(\mu , u_{t}), $$
(9)

in the phase space \(C=C([-1, 0], R^{4})\), where \(u_{t}=(u_{1}(t), u _{2}(t), u_{3}(t), u_{4}(t))^{T}=(S, E, I, R)^{T} \in R^{4}\), \(u_{t}(\theta )=u(t+\theta )\in C\) and \(L_{\mu }\): \(C\rightarrow R ^{4}\), \(F(\mu , u_{t})\rightarrow R^{4}\) are given as follows:

$$ L_{\mu }\phi =(\tau_{0}+\mu ) \bigl(A_{\mathrm{trix}}\phi (0)+B_{\mathrm{trix}}\phi (-1) \bigr) $$
(10)

and

$$ F(\mu ,\phi )=(\tau_{0}+\mu )\left ( \textstyle\begin{array}{@{}c@{}} -\beta \phi_{1}(0)\phi_{3}(0) \\ (1-p)\beta \phi_{1}(0)\phi_{3}(0) \\ p\beta \phi_{1}(0)\phi_{3}(0) \\ {0} \end{array}\displaystyle \right ) , $$
(11)

with

$$ A_{\mathrm{trix}}=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{11} &{0} &\alpha_{13} &{0} \\ \alpha_{21} &\alpha_{22} &\alpha_{23} &{0} \\ \alpha_{31} &{0} &\alpha_{33} &{0} \\ {0} &{0} &a_{43} &\alpha_{44} \end{array}\displaystyle \right ) ,\qquad B_{\mathrm{trix}}= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} {0} &{0} &{0} &{0} \\ {0} &\beta_{22} &{0} &{0} \\ {0} &\beta_{32} &\beta_{33} &{0} \\ {0} &{0} &\beta_{43} &{0} \end{array}\displaystyle \right ) . $$

Based on the Riesz representation theorem, there is a matrix whose components are bounded variation functions \(\eta (\theta , \mu )\) in \(\theta \in [-1, 0]\) such that

$$ L_{\mu }\phi = \int_{-1}^{0}\,d\eta (\theta , \mu )\phi (\theta ) $$
(12)

for \(\phi \in C\). In fact, we choose

$$ \eta (\theta ,\mu )=(\tau_{0}+\mu ) \bigl(A_{\mathrm{trix}} \delta (\theta )+B_{\mathrm{trix}} \delta (\theta +1) \bigr), $$
(13)

with \(\delta (\theta )\) is the Dirac delta function.

For \(\phi \in C([-1,0], R^{4})\), define

$$ A(\mu )\phi = \textstyle\begin{cases} \frac{d\phi (\theta )}{d\theta },& -1\leq \theta < 0, \\ \int_{-1}^{0}\,d\eta (\theta ,\mu )\phi (\theta ),& \theta =0, \end{cases} $$
(14)

and

$$ R(\mu )\phi =\left \{ \textstyle\begin{array}{l@{\quad}l} 0,&-1\leq \theta < 0, \\ F(\mu ,\phi ),& \theta =0. \end{array}\displaystyle \right . $$
(15)

Then system (9) is equivalent to

$$ \dot{u}(t)=A(\mu )u_{t}+R(\mu )u_{t}. $$
(16)

For \(\varphi \in C^{1}([0, 1], (R^{4})^{*})\), the adjoint operator \(A^{*}\) of \(A(0)\) (the linear operator of Eq. (16)) is defined as follows:

$$\begin{aligned}& A^{*}(\varphi )=\left \{ \textstyle\begin{array}{l@{\quad}l} -\frac{d\varphi (s)}{ds},& 0< s\leq 1, \\ \int_{-1}^{0}d{\eta }^{T}(s,0)\varphi (-s),& s=0, \end{array}\displaystyle \right . \end{aligned}$$
(17)
$$\begin{aligned}& \bigl\langle \varphi (s),\phi (\theta ) \bigr\rangle =\bar{\varphi }(0)\phi (0)- \int_{\theta =-1}^{0} \int_{\xi =0}^{\theta }\bar{\varphi }(\xi - \theta )\,d\eta ( \theta )\phi (\xi )\,d\xi , \end{aligned}$$
(18)

where \(\eta (\theta )=\eta (\theta , 0)\).

Suppose that \(q(\theta )=(1, q_{2}, q_{3}, q_{4})^{T}e^{i\omega_{0} \tau_{0}\theta }\) is the eigenvector of \(A(0)\) associated with \(+i\omega_{0}\tau_{0}\) and \(q^{*}(s)=D(1, q_{2}^{*}, q_{3}^{*}, q_{4} ^{*})^{T}e^{i\omega_{0}\tau_{0}s}\) is the eigenvector of \(A^{*}\) associated with \(-i\omega_{0}\tau_{0}\). Then one can obtain

$$\begin{aligned}& A(0)q(\theta )=i\omega_{0}\tau_{0}q(\theta ), \end{aligned}$$
(19)
$$\begin{aligned}& A^{*}q^{*T}(\theta )=-i\omega_{0} \tau_{0}q^{*T}(\theta ). \end{aligned}$$
(20)

Then, by the definitions of \(A(0)\) and \(A^{*}\), we have

$$\begin{aligned}& A(0)q(\theta )=\frac{dq(\theta )}{d\theta }, \end{aligned}$$
(21)
$$\begin{aligned}& A^{*}q^{*T}(s)=-\frac{dq(\theta )}{d\theta }. \end{aligned}$$
(22)

Therefore,

$$ q(\theta )=q(0)e^{i\omega_{0}\tau_{0}\theta } $$
(23)

and

$$ q^{*}(s)=q^{*}(0)e^{i\omega_{0}\tau_{0}s}. $$
(24)

In addition,

$$\begin{aligned}& \int_{-1}^{0}\,d\eta (\theta )q(\theta )=A_{\mathrm{trix}}q(0)+B_{\mathrm{trix}}q(-1)=A(0)q(0)=i \omega_{0}q(0) \end{aligned}$$
(25)

and

$$\begin{aligned}& \int_{-1}^{0}\,d\eta (\theta )q^{*}(-s)=A_{\mathrm{trix}}^{T}q^{*T}(0)+B_{\mathrm{trix}} ^{T}q^{*T}(-1)=A^{*}q^{*T}(0)=-i \omega_{0}q^{*T}(0). \end{aligned}$$
(26)

Thus, we can get the expressions of \(q_{2}\), \(q_{3}\), \(q_{4}\) and \(q_{2}^{*}\), \(q_{3}^{*}\), \(q_{4}^{*}\) as follows:

$$\begin{aligned}& q_{2} = \frac{\alpha_{21}+\alpha_{23}q_{3}}{i\omega_{0}-\alpha_{22}- \beta_{22}e^{-i\tau_{0}\omega_{0}}},\qquad q_{3}=\frac{i\omega_{0}-\alpha _{11}}{\alpha_{13}}, \qquad q_{4} = \frac{\beta_{43}e^{-i\tau_{0}\omega_{0}}}{i\omega_{0}-\alpha _{44}}, \\& q_{2}^{*} = -\frac{(i\omega_{0}+\alpha_{11})\beta_{32}e^{i\tau_{0} \omega_{0}}}{\alpha_{21}\beta_{32}e^{i\tau_{0}\omega_{0}}-\alpha_{31}(i \omega_{0}+\alpha_{22}+\beta_{22}e^{i\tau_{0}\omega_{0}})}, \\& q_{3}^{*} = -\frac{(i\omega_{0}+\alpha_{22}+\beta_{22}e^{i\tau_{0} \omega_{0}})q_{2}}{\beta_{32}e^{i\tau_{0}\omega_{0}}}, \\& q_{4} = -\frac{(i\omega_{0}+\alpha_{33}+\beta_{33}e^{i\tau_{0}\omega _{0}})q_{3}+\alpha_{13}+\alpha_{23}q_{2}}{\beta_{43}e^{i\tau_{0}\omega _{0}}}. \end{aligned}$$

In order to assure \(\langle q^{*}, q\rangle =1\), we need to calculate the expression of D. From Eq. (18), we have

$$\begin{aligned}& \bigl\langle q^{*}(s), q(\theta ) \bigr\rangle \\& \quad = \bar{q}^{*}(0)q(0)- \int_{\theta =-1}^{0} \int_{\xi =0}^{\theta }\bar{q}^{*T}(\xi -\theta )\,d \eta (\theta )\phi (\xi )\,d\xi \\& \quad = \bar{D} \biggl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*}+q_{4}\bar{q} _{4}^{*} \\& \quad \quad {} - \int_{\theta =-1}^{0} \int_{\xi =0}^{\theta }\tau_{0} \bigl(1, \bar{q}_{2} ^{*}, \bar{q}_{3}^{*}, \bar{q}_{4}^{*} \bigr) \bigl(A_{\mathrm{trix}}\delta ( \theta )+B _{\mathrm{trix}}\delta (\theta +1) \bigr) (1, q_{2}, q_{3}, q_{4})^{T}e^{i\tau_{0} \omega_{0}\theta }\,d\xi d\theta \biggr] \\& \quad = \bar{D} \bigl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*}+q_{4}\bar{q} _{4}^{*}+ \tau_{0}e^{-i\tau_{0}\omega_{0}} \bigl(q_{2} \bigl( \beta_{22} \bar{q}_{2} ^{*}+\beta_{32} \bar{q}_{3}^{*} \bigr)+q_{3} \bigl( \beta_{33}\bar{q}_{3}^{*}+ \beta _{43} \bar{q}_{4}^{*} \bigr) \bigr) \bigr]. \end{aligned}$$

Thus,

$$ \bar{D}= \bigl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*}+q_{4}\bar{q}_{4} ^{*}+\tau_{0}e^{-i\tau_{0}\omega_{0}} \bigl(q_{2} \bigl( \beta_{22}\bar{q}_{2}^{*}+ \beta_{32} \bar{q}_{3}^{*} \bigr)+q_{3} \bigl( \beta_{33}\bar{q}_{3}^{*}+\beta_{43} \bar{q}_{4}^{*} \bigr) \bigr) \bigr]^{-1}. $$
(27)

On the other hand, according to \(\langle \varphi , A\phi \rangle = \langle A^{*}\varphi , \phi \rangle \), we obtain

$$ -i\omega_{0}\tau_{0} \bigl\langle q^{*}, \bar{q} \bigr\rangle = \bigl\langle q^{*}, A \bar{q} \bigr\rangle = \bigl\langle A^{*}q^{*} , \bar{q} \bigr\rangle \bigl\langle -i\omega _{0}\tau_{0}q^{*}, \bar{q} \bigr\rangle =i \omega_{0}\tau_{0} \bigl\langle q^{*}, \bar{q} \bigr\rangle . $$
(28)

Obviously, \(\langle q^{*}, \bar{q}\rangle =0\).

Next, we compute the coordinates to describe the center manifold \(C_{0}\) at \(\mu =0\). Let \(u_{t}\) be the solution of Eq. (16) when \(\mu =0\). Define

$$ z(t)= \bigl\langle q^{*}, u_{t} \bigr\rangle ,\qquad W(t, \theta )=u_{t}(\theta )-2 \operatorname{Re} \bigl\{ z(t)q( \theta ) \bigr\} $$
(29)

on the center manifold \(C_{0}\), then we have

$$ W(t, \theta )=W \bigl(z(t), \bar{z}(t), \theta \bigr), $$
(30)

where

$$ W \bigl(z(t), \bar{z}(t), \theta \bigr)=W(z, \bar{z})=W_{02} \frac{z^{2}}{2}+W _{11}z \bar{z}+W_{02}\frac{\bar{z}^{2}}{2}+ \cdots $$
(31)

and z and z̄ are local coordinates for the center manifold \(C_{0}\) in the direction of \(q^{*}\) and \(\bar{q}^{*}\). Here, we only deal with real solutions, which gives

$$ \dot{z}=i\omega_{0}\tau_{0}z+ \bar{q}^{*}F \bigl(0, W(z, \bar{z}, 0)+2 \operatorname{Re} \bigl\{ zq( \theta ) \bigr\} \bigr)=i\omega_{0}\tau_{0}z+g(z, \bar{z}), $$
(32)

where

$$\begin{aligned} g(z, \bar{z}) &=\bar{q}^{*}(0)F_{0}(z, \bar{z})=g_{20}\frac{z^{2}}{2}+g _{11}z \bar{z}+g_{02}\frac{\bar{z}^{2}}{2}+g_{21} \frac{z^{2}\bar{z}}{2}+ \cdots . \end{aligned}$$
(33)

Thus,

$$ g(z, \bar{z})=\bar{D} \bigl(1, \bar{q}_{2}^{*}, \bar{q}_{3}^{*}, \bar{q} _{4}^{*} \bigr) \bigl(F_{1}(0, u_{t}), F_{2}(0, u_{t}), F_{3}(0, u_{t}), 0 \bigr)^{T}, $$
(34)

where

$$\begin{aligned}& F_{1}(0, u_{t}) = -\beta \tau_{0} \bigl[ \phi_{1}(0)\phi_{3}(0) \bigr], \\& F_{2}(0, u_{t}) = (1-p)\beta \tau_{0} \bigl[ \phi_{1}(0)\phi_{3}(0) \bigr], \\& F_{3}(0, u_{t}) = p\beta \bigl[\phi_{1}(0) \phi_{3}(0) \bigr]. \end{aligned}$$

Since

$$\begin{aligned}& u_{t}=W(z, \bar{z}, \theta )+zq(\theta )+\bar{z} \bar{q}(\theta ),\quad q( \theta )=(1, q_{2}, q_{3}, q_{4})^{T}e^{i\omega_{0}\tau_{0}\theta }, \end{aligned}$$
(35)

we have

$$\begin{aligned}& u_{t}=\left [ \textstyle\begin{array}{c} W^{(1)}(t+\theta ) \\ W^{(2)}(t+\theta ) \\ W^{(3)}(t+\theta ) \\ {0} \end{array}\displaystyle \right ] +z\left [ \textstyle\begin{array}{c} {1} \\ q_{2} \\ q_{3} \\ q_{4} \end{array}\displaystyle \right ] e^{i\omega_{0}\tau_{0}\theta }+\bar{z}\left [ \textstyle\begin{array}{c} {1} \\ \bar{q}_{2} \\ \bar{q}_{3} \\ \bar{q}_{4} \end{array}\displaystyle \right ] e^{-i\omega_{0}\tau_{0}\theta }, \\& \phi_{1}(0) = z+\bar{z}+W_{20}^{(1)}(0) \frac{z^{2}}{2}+W_{11}^{(1)}(0)z \bar{z}+W_{02}^{(1)} \frac{\bar{z}^{2}}{2}+\cdots , \\& \phi_{2}(0) = zq_{2}+\bar{z}\bar{q}_{2}+W_{20}^{(2)}(0) \frac{z^{2}}{2}+W_{11}^{(2)}(0)z\bar{z}+W_{02}^{(2)} \frac{\bar{z}^{2}}{2}+\cdots , \\& \phi_{3}(0) = zq_{3}+\bar{z}\bar{q}_{3}+W_{20}^{(3)}(0) \frac{z^{2}}{2}+W_{11}^{(3)}(0)z\bar{z}+W_{02}^{(3)} \frac{\bar{z}^{2}}{2}+\cdots , \\& \phi_{4}(0) = zq_{4}+\bar{z}\bar{q}_{4}+W_{20}^{(4)}(0) \frac{z^{2}}{2}+W_{11}^{(4)}(0)z\bar{z}+W_{02}^{(4)} \frac{\bar{z}^{2}}{2}+\cdots . \end{aligned}$$
(36)

Based on Eq. (31)-Eq. (35), one can obtain

$$\begin{aligned} g(z, \bar{z})=\bar{D} \bigl(1, \bar{q}_{2}^{*}, \bar{q}_{3}^{*}, \bar{q} _{4}^{*} \bigr) \times \left [ \textstyle\begin{array}{c} L_{11}z^{2}+L_{12}z\bar{z}+L_{13}\bar{z}^{2}+L_{14}z^{2}\bar{z} \\ L_{21}z^{2}+L_{22}z\bar{z}+L_{23}\bar{z}^{2}+L_{24}z^{2}\bar{z} \\ L_{31}z^{2}+L_{32}z\bar{z}+L_{33}\bar{z}^{2}+L_{34}z^{2}\bar{z} \\ {0} \end{array}\displaystyle \right ] +\cdots , \end{aligned}$$
(37)

with

$$\begin{aligned} L_{11} =&-\beta q_{3},\qquad L_{12}=-\beta (q_{3}+\bar{q}_{3}),\qquad L_{13}=- \beta \bar{q}_{3}, \\ L_{14} =&-\beta \biggl(W_{11}^{(1)}(0)q_{3}+ \frac{1}{2}W_{20}^{(1)}(0) \bar{q}_{3}+W_{11}^{(3)}(0)+ \frac{1}{2}W_{20}^{(3)}(0) \biggr), \\ L_{21} =&(1-p)\beta q_{3}, \qquad L_{22}=(1-p) \beta (q_{3}+\bar{q}_{3}),\qquad L _{23}=(1-p)\beta \bar{q}_{3}, \\ L_{24} =&\beta \biggl(W_{11}^{(1)}(0)q_{3}+ \frac{1}{2}W_{20}^{(1)}(0) \bar{q}_{3}+W_{11}^{(3)}(0)+ \frac{1}{2}W_{20}^{(3)}(0) \biggr), \\ L_{31} =&\beta q_{3}, \qquad L_{32}=\beta (q_{3}+\bar{q}_{3}),\qquad L_{33}=\beta \bar{q}_{3}, \\ L_{34} =&\beta \biggl(W_{11}^{(1)}(0)q_{3}+ \frac{1}{2}W_{20}^{(1)}(0) \bar{q}_{3}+W_{11}^{(3)}(0)+ \frac{1}{2}W_{20}^{(3)}(0) \biggr). \end{aligned}$$

Therefore,

$$\begin{aligned} g(z, \bar{z}) &=\bar{D} \bigl[ \bigl(L_{11}+ \bar{q}_{2}^{*}L_{21}+\bar{q}_{3}^{*}L _{31} \bigr)z^{2}+ \bigl(L_{12}+ \bar{q}_{2}^{*}L_{22}+ \bar{q}_{3}^{*}L_{32} \bigr)z \bar{z} \\ &\quad {}+ \bigl(L_{13}+\bar{q}_{2}^{*}L_{23}+ \bar{q}_{3}^{*}L_{33} \bigr)\bar{z}^{2}+ \bigl(L _{14}+\bar{q}_{2}^{*}L_{24}+ \bar{q}_{3}^{*}L_{34} \bigr)z^{2}\bar{z} \bigr]+ \cdots . \end{aligned}$$
(38)

Thus, from Eq. (33) and Eq. (38), we have

$$\begin{aligned}& g_{20} = 2\beta \tau_{0}\bar{D}q_{3} \bigl((1-p) \bar{q}_{2}^{*}+p\bar{q} _{3}^{*}-1 \bigr), \\& g_{11} = \operatorname{Re}\{q_{3}\}\beta \tau_{0} \bar{D} \bigl((1-p)\bar{q}_{2}^{*}+p \bar{q}_{3}^{*}-1 \bigr), \\& g_{02} = 2\beta \tau_{0}\bar{D}\bar{q}_{3} \bigl((1-p)\bar{q}_{2}^{*}+p \bar{q}_{3}^{*}-1 \bigr), \\& g_{21} = 2\beta \tau_{0}\bar{D} \bigl((1-p) \bar{q}_{2}^{*}+p\bar{q}_{3}^{*}-1 \bigr) \biggl(W _{11}^{(1)}(0)q_{3}+ \frac{1}{2}W_{20}^{(1)}(0) \bar{q}_{3}+W_{11}^{(3)}(0)+ \frac{1}{2}W_{20}^{(3)}(0) \biggr). \end{aligned}$$

Next, we need to obtain the expressions of \(W_{20}\) and \(W_{11}\). From Eq. (29)-Eq. (33), we have

$$ \dot{W}= \textstyle\begin{cases} AW-2\operatorname{Re}\{\bar{q}^{*}(0)F_{0}q(\theta )\},& -1\leq \theta < 0, \\ AW-2\operatorname{Re}\{\bar{q}^{*}(0)F_{0}q(\theta )\}+F_{0},& \theta =0, \end{cases}\displaystyle =AW+H(z, \bar{z}, \theta ), $$
(39)

where

$$ H(z, \bar{z}, \theta )=H_{20}(\theta ) \frac{z^{2}}{2}+H_{11}(\theta )\frac{z \bar{z}}{2}+H_{02}( \theta )\frac{\bar{z}^{2}}{2}+\cdots . $$
(40)

From Eq. (30), Eq. (31), Eq. (39) and Eq. (40), we have

$$\begin{aligned}& (2i\omega_{0}\tau_{0}-A)W_{20}( \theta )=H_{20}(\theta ) \end{aligned}$$
(41)

and

$$\begin{aligned}& AW_{11}(\theta )=-H_{11}(\theta ). \end{aligned}$$
(42)

Now, for \(\theta \in [-1, 0)\),

$$\begin{aligned} H(z, \bar{z}, \theta ) &=-2\operatorname{Re} \bigl\{ \bar{q}^{*}(0)F_{0}q(\theta ) \bigr\} \\ &=- \bigl(g_{20}q(\theta )+\bar{g}_{11}\bar{q}(\theta ) \bigr) \frac{z^{2}}{2}- \bigl(g _{11}q(\theta )+\bar{g}_{02} \bar{q}(\theta ) \bigr)z\bar{z}+\cdots . \end{aligned}$$
(43)

Comparing the coefficients of Eq. (40) and Eq. (43), the following two equations can be obtained:

$$\begin{aligned}& H_{20}(\theta )=-g_{20}q(\theta )- \bar{g}_{02}\bar{q}(\theta ), \end{aligned}$$
(44)
$$\begin{aligned}& H_{11}(\theta )=-g_{11}q(\theta )- \bar{g}_{11}\bar{q}(\theta ). \end{aligned}$$
(45)

Then we have

$$\begin{aligned}& \dot{W}_{20}(\theta )=2i\omega_{0} \tau_{0}W_{20}(\theta )+g_{20}q( \theta )+ \bar{g}_{02}\bar{q}(\theta ), \end{aligned}$$
(46)
$$\begin{aligned}& \dot{W}_{11}(\theta )=g_{11}q(\theta )+ \bar{g}_{11}\bar{q}(\theta ). \end{aligned}$$
(47)

Therefore,

$$\begin{aligned}& W_{20}(\theta )=\frac{ig_{20}q(0)}{\tau_{0}\omega_{0}}e^{i\tau_{0} \omega_{0}\theta }+ \frac{i\bar{g}_{02}\bar{q}(0)}{3\tau_{0}\omega_{0}}e^{-i\tau_{0}\omega _{0}\theta }+E_{1}e^{2i\tau_{0}\omega_{0}\theta }, \end{aligned}$$
(48)
$$\begin{aligned}& W_{11}(\theta )=-\frac{ig_{11}q(0)}{\tau_{0}\omega_{0}}e^{i\tau_{0} \omega_{0}\theta }+ \frac{i\bar{g}_{11}\bar{q}(0)}{\tau_{0}\omega_{0}}e ^{-i\tau_{0}\omega_{0}\theta }+E_{2}, \end{aligned}$$
(49)

where \(E_{1}\) and \(E_{2}\) are constant vectors to be determined. It follows from Eq. (44) and Eq. (45) that

$$\begin{aligned}& \int_{-1}^{0}\,d\eta (\theta )W_{20}( \theta )=2i\omega_{0}\tau_{0}W_{20}(0)-H _{20}(0), \end{aligned}$$
(50)
$$\begin{aligned}& \int_{-1}^{0}\,d\eta (\theta )W_{11}( \theta )=-H_{11}(0), \end{aligned}$$
(51)

where \(\eta (\theta )=\eta (0, \theta )\). From Eq. (41) and Eq. (42), one has

$$\begin{aligned}& H_{20}(0)=-g_{20}q(\theta )- \bar{g}_{02}\bar{q}(0)+(L_{11}, L_{21}, L _{31}, 0)^{T}, \end{aligned}$$
(52)
$$\begin{aligned}& H_{11}(0)=-g_{11}q(\theta )- \bar{g}_{11}\bar{q}(0)+(L_{12}, L_{22}, L _{32}, 0)^{T}. \end{aligned}$$
(53)

Noticing that

$$\begin{aligned}& \biggl(i\omega_{0}\tau_{0}I- \int_{-1}^{0}d\eta (\theta )e^{i\omega_{0} \tau_{0}} \biggr)q(0)=0, \end{aligned}$$
(54)
$$\begin{aligned}& \biggl(-i\omega_{0}\tau_{0}I- \int_{-1}^{0}d\eta (\theta )e^{-i\omega _{0}\tau_{0}} \biggr) \bar{q}(0)=0, \end{aligned}$$
(55)

and substituting Eq. (48) and Eq. (52) into Eq. (50), we obtain

$$ \biggl(2i\omega_{0}\tau_{0}I- \int_{-1}^{0}\,d\eta (\theta )e^{2i\omega _{0}\tau_{0}\theta } \biggr)E_{1}=\left ( \textstyle\begin{array}{c} -\beta q_{3} \\ (1-p)\beta q_{3} \\ \beta q_{3} \\ {0} \end{array}\displaystyle \right ) . $$
(56)

Thus,

$$ E_{1}=2\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{11*} &{0} &-\alpha_{13} &{0} \\ -\alpha_{21} &\alpha_{22*} &-\alpha_{23} &{0} \\ -\alpha_{31} &\alpha_{32*} &a_{33*} &{0} \\ {0} &{0} &\alpha_{43*} &a_{44*} \end{array}\displaystyle \right ) ^{-1}\times \left ( \textstyle\begin{array}{@{}c@{}} -\beta q_{3} \\ (1-p)\beta q_{3} \\ {p\beta q_{3}} \\ {0} \end{array}\displaystyle \right ). $$
(57)

Similarly, we have

$$ E_{2}=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \alpha_{11} &{0} &\alpha_{13} &{0} \\ \alpha_{21} &\alpha_{22}+\beta_{22} &\alpha_{23} &{0} \\ \alpha_{31} &a_{32}+\beta_{32} &\alpha_{33}+\beta_{33} &{0} \\ {0} &{0} &\alpha_{43}+\beta_{43} &\alpha_{44} \end{array}\displaystyle \right ) ^{-1}\times \left ( \textstyle\begin{array}{@{}c@{}} -\beta \operatorname{Re}\{q_{3}\} \\ (1-p)\beta \operatorname{Re}\{q_{3}\} \\ {p\beta \operatorname{Re}\{q_{3}\}} \\ {0} \end{array}\displaystyle \right ) , $$
(58)

with

$$\begin{aligned}& \alpha_{11*} = 2i\omega_{0}-\alpha_{11}, \\& \alpha_{22*} = 2i\omega_{0}-\alpha_{22}- \beta_{22}e^{-2i\tau_{0}\omega _{0}}, \\& \alpha_{32*} = -a_{32}-\beta_{32}e^{-2i\tau_{0}\omega_{0}}, \\& \alpha_{33*} = 2i\omega_{0}-\alpha_{33}- \beta_{33}e^{-2i\tau_{0}\omega _{0}}, \\& \alpha_{43*} = -\alpha_{43}-\beta_{43}e^{-2i\tau_{0}\omega_{0}}, \\& \alpha_{44*} = 2i\omega_{0}-\alpha_{44}. \end{aligned}$$

Therefore, one can compute the following parameters:

$$\begin{aligned}& C_{1}(0) = \frac{i}{2\tau_{0}\omega_{0}} \biggl(g_{11}g_{20}-2 \vert g_{11} \vert ^{2}-\frac{\vert g_{02} \vert ^{2}}{3} \biggr)+ \frac{g_{21}}{2}, \end{aligned}$$
(59)
$$\begin{aligned}& \mu_{2} = -\frac{\operatorname{Re}\{C_{1}(0)\}}{\operatorname{Re}\{\lambda '(\tau_{0}) \}}, \end{aligned}$$
(60)
$$\begin{aligned}& \beta_{2} = 2{\operatorname{Re} \bigl\{ C_{1}(0) \bigr\} }, \end{aligned}$$
(61)
$$\begin{aligned}& T_{2} = -\frac{\operatorname{Im}\{C_{1}(0)\}+\mu_{2}\operatorname{Im}\{\lambda '(\tau _{0})\}}{\tau_{0}\omega_{0}}. \end{aligned}$$
(62)

In conclusion, we have the following for system (3) based on the results in [32].

Theorem 2

If \(\mu_{2}>0\) (\(\mu_{2}<0\)), then the Hopf bifurcation is supercritical (subcritical); if \(\beta_{2}<0\) (\(\beta_{2}>0\)), then the bifurcating periodic solutions are stable (unstable); if \(T_{2}>0\) (\(T_{2}<0\)), then the period of the bifurcating periodic solutions increases (decreases).

4 Numerical example

In this section, we present a numerical simulation to justify the obtained theoretical results in Section 2 and Section 3. Choosing \(b=5\), \(\beta =0.075\), \(\varrho =0.06\), \(p=0.9\), \(\gamma =0.5\), \(\varepsilon =0.2\) and \(\alpha =0.1\), we consider the following special case of system (3):

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = 5-0.075 S(t)I(t)-0.06 S(t), \\ \frac{dE(t)}{dt} = 0.0075 S(t)I(t)-0.5 E(t-\tau )+0.2 I(t)-0.06 E(t), \\ \frac{dI(t)}{dt} = 0.0675 S(t)I(t)+0.5 E(t-\tau )-0.2 I(t)-0.1 I(t- \tau )-0.06 I(t), \\ \frac{dR(t)}{dt} = 0.1 I(t-\tau )-0.06 R(t), \end{cases} $$
(63)

from which we get \(b\beta \gamma +pb\beta \varrho +\gamma \varrho \varepsilon =0.2138\), \(\varrho (\gamma +\varrho )(\varepsilon +\alpha +\varrho )=0.0121\). Then we obtain \(I_{*}=26.4638\). Further, \(\varepsilon +\alpha +\varrho =0.36\), \(\frac{pb\beta }{\varrho + \beta I_{*}}=0.1651\), and we obtain the unique viral equilibrium \(P_{*}(2.4452, 10.3180, 26.4638, 44.1063)\) of system (63). Thus, we have \(\omega_{0}=0.3907\), \(\tau_{0}=5.0895\) and \(\lambda^{\prime }(\tau_{0})=0.4743-2.8554i\).

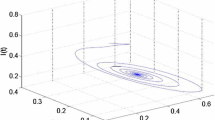
Let \(\tau =4.250\in (0, \tau_{0})\), \(P_{*}(2.4452, 10.3180, 26.4638, 44.1063)\) is asymptotically stable according to Theorem 1 and the dynamic behavior of system (63) is as shown in Figure 1. However, once the value of the time delay τ passes through the critical value \(\tau_{0}=5.0895\), for example, \(\tau =5.375\), \(P_{*}(2.4452, 10.3180, 26.4638, 44.1063)\) will lose its stability and a Hopf bifurcation occurs, and a family of periodic solutions bifurcate from \(P_{*}(2.4452, 10.3180, 26.4638, 44.1063)\). This can be depicted by Figure 2. The bifurcation phenomenon can be also illustrated by the bifurcation diagram in Figure 3.

Figure 1
figure 1

Dynamic behavior of system ( 63 ): projection on S-E-R with \(\pmb{\tau=4.250}\) .

Full size image
Figure 2
figure 2

Dynamic behavior of system ( 63 ): projection on S-E-R with \(\pmb{\tau=5.375}\) .

Full size image
Figure 3
figure 3

Bifurcation diagram with respect to τ .

Full size image

In addition, we obtain \(C_{1}(0)=-1.9265-0.3022i\) by some complex computation with the help of Matlab software package. Thus, based on Eq. (59)-Eq. (62), we get \(\mu_{2}=4.0681>0\), \(\beta_{2}=-3.8530<0\) and \(T_{2}=5.9846>0\). Then, based on Theorem 2, it can be concluded that the Hopf bifurcation at \(\tau_{0}=5.0895\) is supercritical, the bifurcating periodic solutions are stable and the period of the bifurcating periodic solutions increases.

5 Conclusions

By incorporating the time delay due to the latent period of computer viruses in the exposed computers and the time delay due to the period that anti-virus software uses to clean the viruses in the infected computers into the model proposed in the literature [20], a delayed computer virus spreading model is considered in the present paper. Compared with the work in the literature [20], the model considered in this paper is more general, and we mainly investigate the effects of delay on the proposed model.

It has been proved that there exists a stability switch in the delayed computer virus spreading model by taking the delay as the bifurcation parameter. The model is asymptotically stable when the value of the delay is below the critical value, and the viruses can be controlled easily in this case. However, the viruses will be out of control when the delay passes through the critical value. Based on the simulation results, we can conclude that the computer viruses can be controlled by shortening the latent period of the viruses and the period that the anti-virus software uses to clean the viruses.

However, it should be pointed out that our paper focuses on analyzing the effect of the time delay. Other impact factors such as network topology [33] and network eigenvalue [34] to computer virus propagation will be left for our future research. In addition, it is an interesting problem to take both time delay and other key parameter as the bifurcation parameter and investigate the codimension-two bifurcation, such as Hopf-Pitchfork bifurcation [35] of the proposed computer virus model. This is another interesting future research direction for us.