Dispersion relation and growth rate in thermal plasma-loaded traveling wave tube with corrugated waveguide hollow electron beam

Abstract

A theory of relativistic traveling wave tube with magnetized thermal plasma-filled corrugated waveguide with annular electron beam is given. The dispersion relation is obtained by linear fluid theory. The characteristic of the dispersion relation is obtained by numerical solutions. The effect of plasma density, corrugated period, waveguide radius and plasma thermal effect on the dispersion relation and growth rate are analyzed. Some useful results are given.

Introduction

Relativistic traveling wave tube (RTWT) is an important high-power microwave (HPM) apparatus which has been developed in the past 20 years [1–3]. Most of the TWT mathematical analysis has been done by John Robinson Pierce and his colleagues at Bell Labs [4–6] and then has been developed by Chu et al. [7–9]. In TWT, sinusoidal corrugated slow wave structure (SWS) is used to reduce the phase velocity of the electromagnetic wave to synchronize it with the electron beam velocity, so that a strong interaction between the two can take place [10, 11]. TWT is extensively applied in satellite and airborne communications, radar, particle accelerators, cyclotron resonance and electronic warfare system. The plasma injection to TWT has been studied recently which can increase the growth rate and improve the quality of transmission of electron beam. We investigate the effect of thermal plasma and electron beam on the growth rate [12–17].

The use of plasmas for generating high-power microwaves is studied for more than 50 years. During the 1990s plasma-assisted slow-wave oscillators (SWO) were invented and actively developed at Hughes Research Lab (HRL) [22–27].

An analytical and numerical study is made on the dispersion properties of a cylindrical waveguide filled with plasma. An electron beam and static external magnetic field are considered as the mechanisms for controlling the field attenuation and possible stability of the waveguide [24–29].

In this paper, a RTWT with magnetized thermal plasma-filled corrugated waveguide with annular electron beam is studied. The dispersion relation of corrugated waveguide is derived from a solution of the field equations. By numerical computation, the dispersion characteristics of the RTWT are analyzed in detail in different cases of various geometric parameters of slow-wave structure.

In Sect. 2, the physical model of the RTWT filled with thermal plasma is established in an infinite longitudinal magnetic field. In Sect. 3, the dispersion relation of the RTWT is derived. In Sect. 4, the dispersion characteristics of the RTWT are analyzed by numerical computation.

Physical model

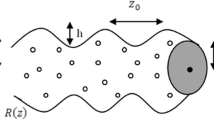
The analysis presented in this paper is based on the SWS shown in Fig. 1. The SWS of the system is the corrugated waveguide that reduce the speed of wave. Wave after collision with waveguide its speed is reduced and reaches to speed of the electron beam (synchronism), so the wave is amplified.

$$ R\left( z \right) = R_{0} + h\;\cos (\kappa_{0} z), $$

(1)

$$ K_{n} = k_{z} + n\kappa_{0} , $$

(2)

$$ \kappa_{0} = \frac{2\pi }{{z_{0} }}, $$

(3)

Fig. 1

Slow-wave structure and annular electron beam model of a plasma-filled relativistic traveling wave tube

Cylindrical waveguide, whose wall radius $R\left( z \right),$ varies sinusoidal according to the relation (1), h is the corrugation amplitude, $\kappa_{0} = 2\pi \;z_{0}$ is the corrugation wave number, and $z_{0}$ is the length of the corrugation period, $R_{0 }$ is the waveguide radius and $k_{z}$ is the axial wave number.

A finite annular relativistic electron beam with density $n_{\text{b}}$ and radius $R_{\text{b}}$ goes through the cylindrical waveguide, which is loaded completely with a thermal, uniform and collision less plasma of density $n_{\text{p}}$.The entire system is immersed in a strong, longitudinal magnetic field, which magnetizes both the beam and the plasma. Because dielectric constant is an anisotropic so it will be a tensor. In the beam–plasma case in a linearized scheme, the dielectric tensor, in cylindrical coordinates, may be given by:

$$ \sigma = \left[ {\begin{array}{*{20}c} {\frac{i\omega }{{\omega^{2} - \omega_{c}^{2} }}} & {\frac{{ - \omega_{c} }}{{\omega^{2} - \omega_{c}^{2} }}} & 0 \\ {\frac{{\omega_{c} }}{{\omega^{2} - \omega_{c}^{2} }}} & {\frac{i\omega }{{\omega^{2} - \omega_{c}^{2} }}} & 0 \\ 0 & 0 & {\frac{1}{{ - i\omega + \frac{{ik_{n}^{2} \gamma P_{0} }}{mn\omega }}}} \\ \end{array} } \right] $$

(4)

$$ \varepsilon = \varepsilon { \cdot }\left( {1 + \frac{i\sigma }{{\varepsilon { \cdot }\omega }}} \right) $$

(5)

$$ [ \in ] = \varepsilon_{0} \left[ {\begin{array}{*{20}c} {1 - \frac{{\omega_{p}^{2} }}{{\omega^{2} - \omega_{c}^{2} }}} & { - \frac{{{\text{i}}\omega_{p}^{2} \omega_{c} }}{{\omega (\omega^{2} - \omega_{c}^{2} )}}} & 0 \\ {\frac{{{\text{i}}\omega_{p}^{2} \omega_{c} }}{{\omega (\omega^{2} - \omega_{c}^{2} )}}} & {1 - \frac{{\omega_{p}^{2} }}{{\omega^{2} - \omega_{c}^{2} }}} & 0 \\ 0 & 0 & {1 - \frac{{\omega_{p}^{2} }}{{\omega^{2} - \frac{{k_{n}^{2} \gamma P_{0} }}{mn}}}} \\ \end{array} } \right] = 0 $$

(6)

$$ [ \in ] = \varepsilon_{0} \left[ {\begin{array}{*{20}c} {\varepsilon_{1} } & {\varepsilon_{2} } & 0 \\ { - \varepsilon_{2} } & {\varepsilon_{1} } & 0 \\ 0 & 0 & {\varepsilon_{3} } \\ \end{array} } \right] = 0 $$

(7)

We assume that $B_{0}$ is very strong that $\varepsilon_{1} = 1$ and $|\varepsilon_{2} |$ is negligibly small.

$$ \left[ \in \right] = \varepsilon_{0} \times \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} v} \right)^{2} - 3K_{n}^{2} {\text{v}}_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \\ \end{array} } \right], $$

(8)

$$ \varepsilon_{3} = 1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} {\text{v}}} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2 } }} $$

(9)

Here, $\omega_{\text{p}} = (\frac{{n_{\text{p}} e^{2} }}{{m\varepsilon_{0} }})^{1/2}$ is the plasma frequency, $\omega_{\text{b}} = (\frac{{n_{\text{b}} e^{2} }}{{m\varepsilon_{0} }})^{1/2}$ is the beam frequency, ω is the angular frequency of the electromagnetic wave, $\gamma$ is the relativistic factor, $v_{{{\text{th}}_{\text{p}} }} = \sqrt {\frac{{KT_{\text{p}} }}{m}}$ is the thermal velocity of the plasma, $v_{{{\text{th}}_{\text{b}} }} = \sqrt {\frac{{KT_{\text{b}} }}{m}}$ is the thermal velocity of the beam, $v$ is the velocity of the beam, $T_{\text{b}}$ is the beam temperature, $T_{\text{p}}$ is the plasma temperature and $K$ is the Boltzmann constant.

Dispersion equation

In the above physical model, its Maxwell equations can be written as:

$$ \nabla \times B = \frac{ - i\omega }{c} \varepsilon { \cdot }E, $$

(10)

$$ \nabla \times E = \frac{i\omega }{c} B, $$

(11)

$$ \nabla { \cdot }B = 0, $$

(12)

$$ \nabla { \cdot }D = 0. $$

(13)

Suppose that every variable can be regarded as:

$$ A = A{\text{e}}^{{i(K_{n} z - \omega t)}} . $$

(14)

From Eqs. (10) and (11) we can obtain:

$$ \nabla \nabla \;{ \cdot }E - \nabla^{2} E = \frac{{\omega^{2} }}{{c^{2} }} \varepsilon \;{ \cdot }E, $$

(15)

$$ \nabla^{2} E_{z} - [\nabla \left( {\nabla { \cdot }E} \right)]_{z} + \frac{{\omega^{2} }}{{c^{2} }}\varepsilon_{3} E_{z} = 0, $$

(16)

Now Substituting Eq. (9) into Eq. (16), we have:

$$ \nabla^{2} E_{z} - [\nabla \left( {\nabla \;{ \cdot }E} \right)]_{z} + \frac{{\omega^{2} }}{{c^{2} }}\times \left( {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} v} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right)E_{z} = 0. $$

(17)

From Eq. (13), we have:

$$ \nabla { \cdot }\varepsilon_{3} E_{z} = 0. $$

(18)

Substituting Eq. (9) into Eq. (18), we obtain:

$$ \nabla \;{ \cdot }E_{z} = \frac{\partial }{\partial z}E_{z} \left[ {\frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} v} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} + \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right]. $$

(19)

From Eqs. (16) and (19), the wave equation is obtained in the area of plasma-beam as follows:

$$ \left[ {\nabla_{ \bot }^{2} + \left( {\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} } \right)\left( {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} } \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right)} \right]E_{z} , $$

(20)

$$ \nabla_{ \bot }^{2} = \nabla^{2} - \frac{{\partial^{2} }}{{\partial z^{2 } }} $$

(21)

$$ E_{z} \left( {r,z} \right) = E_{zn} \left( r \right){\text{e}}^{{i\left( {K_{n} z - \omega t} \right)}} , $$

(22)

$$ E_{r} \left( {r,z} \right) = \frac{{iK_{n} }}{{\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} }}{\text{e}}^{{i(K_{n} z - \omega t)}} \frac{{{\text{d}}E_{zn} }}{{{\text{d}}r}}. $$

(23)

We investigated ground state (n = 0) in solving the equation, substituting Eq. (21) into Eq. (20), we have:

$$ \begin{gathered} A_{0} J_{0} \left( {T_{1} r} \right)\,\,\,0 \le r \le R_{{{\text{b}} }} ; \hfill \\ E_{zn} = \left\{ {\begin{array}{*{20}c} {B_{0} J_{0} \left( {T_{2} r} \right) + C_{0} N_{0} \left( {T_{2} r} \right)R_{{{\text{b}} }} \le r \le R_{c } ;} \\ {D_{0} J_{0} \left( {T_{1} r} \right) + F_{0} N_{0} \left( {T_{1} r} \right)R_{ c} \le r \le R(z);} \\ \end{array} } \right. \hfill \\ \end{gathered} $$

(24)

According to Fig. 1, in the area of $0 \le r \le R_{\text{b}}$, there is Plasma only, and in the area of $R_{{{\text{b}} }} \le r \le R_{c }$, there are plasma + beam, and in the area of $R_{c } \le r \le Rz$, there is plasma only.

$$ T_{1}^{2} = \left( {\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} } \right)\left( {1 - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right), $$

(25)

$$ T_{2}^{2} = \left( {\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} } \right)\left( {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} v} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right). $$

(26)

The field components must satisfy the following continuity equations (first boundary condition):

$$ E_{z} \left( {r = R_{\text{b }}^{ - } } \right) = E_{z} \left( {r = R_{{{\text{b}} }}^{ + } } \right), $$

(27)

$$ E_{z} \left( {r = R_{c }^{ - } } \right) = E_{z} (r = R_{c }^{ + } ) $$

(28)

$$ E_{r} \left( {r = R_{{{\text{b}} }}^{ - } } \right) = E_{r} (r = R_{{{\text{b}} }}^{ + } ) $$

(29)

$$ E_{r} \left( {r = R_{c }^{ - } } \right) = E_{r} (r = R_{c }^{ + } ) $$

(30)

As a result, the field components are obtained as follows:

$$ B_{0} = - \frac{\pi }{2}R_{{{\text{b}} }} s_{0} A_{0} $$

(31)

$$ C_{0} = - \frac{\pi }{2}R_{\text{b }} l_{0} A_{0} $$

(32)

$$ F_{0} = \frac{{\pi^{2} }}{4}R_{{{\text{b}} }} R_{c } U_{0} A_{0} $$

(33)

$$ D_{0} = \frac{{\pi^{2} }}{4}R_{{{\text{b}} }} R_{c } H_{0} A_{0} $$

(34)

where

$$ s_{0} = T_{2} J_{0} \left( {T_{1} R_{\text{b }} } \right)N_{1} \left( {T_{2} R_{{{\text{b}} }} } \right){-}T_{1} J_{1} \left( {T_{1} R_{{{\text{b}} }} } \right) N_{0} \left( {T_{2} R_{{{\text{b}} }} } \right) $$

(35)

$$ l_{0} = T_{1} J_{1} \left( {T_{1} R_{{{\text{b}} }} } \right)J_{0} \left( {T_{2} R_{{{\text{b}} }} } \right) {-}T_{2} J_{0} \left( {T_{1} R_{{{\text{b}} }} } \right)J_{1} \left( {T_{2} R_{{{\text{b}} }} } \right) $$

(36)

$$ H_{0} = s_{0} \left( {T_{1} J_{0} \left( {T_{2} R_{c } } \right)N_{1} \left( {T_{1} R_{c } } \right){-}T_{1} J_{1} \left( {T_{2} R_{c } } \right)N_{0} \left( {T_{1} R_{c } } \right)} \right) + l_{0} \left( {T_{1} N_{0} \left( {T_{2} R_{c } } \right)N_{1} \left( {T_{1} R_{c } } \right){-}T_{2} N_{1} \left( {T_{2} R_{c } } \right)N_{0} \left( {T_{1} R_{c } } \right)} \right) $$

(37)

$$ U_{0} = s_{0} \left( {T_{2} J_{1} \left( {T_{2} R_{c } } \right)J_{0} \left( {T_{1} R_{c } } \right){-}T_{1} J_{1} \left( {T_{1} R_{c } } \right)J_{0} \left( {T_{2} R_{c } } \right)} \right) + l_{0} \left( {T_{2} N_{1} \left( {T_{2} R_{c } } \right)J_{0} \left( {T_{1} R_{c } } \right){-}T_{1} N_{0} \left( {T_{2} R_{c } } \right)J_{1} \left( {T_{1} R_{c } } \right)} \right) $$

(38)

At the perfectly conducting corrugated waveguide surface (second boundary condition), the tangential electric field must be zero,

$$ E_{z} \left( {r = R\left( z \right)} \right) + E_{r} \left( {r = R\left( z \right)} \right)\frac{{{\text{d}}R\left( z \right)}}{{{\text{d}}z}} = 0 . $$

(39)

Substituting Eqs. (22)–(24) into Eq. (39), we investigate second boundary condition in ground state (n = 0) to achieve the dispersion equation.

$$ D_{0} J_{0} \left( {T_{1} R\left( z \right)} \right) + F_{0} N_{0} \left( {T_{1} R\left( z \right)} \right){\text{e}}^{{i\left( {k_{0} z - \omega t} \right)}} + \frac{{ik_{0} }}{{\frac{{\omega^{2} }}{{c^{2} }} - k_{0}^{2} }}{\text{e}}^{{i\left( {k_{0} z - \omega t} \right)}} \times \frac{\text{d}}{{{\text{d}}R\left( z \right)}}\left[ {D_{0} J_{0} \left( {T_{1} R\left( z \right)} \right) + F_{0} N_{0} \left( {T_{1} R\left( z \right)} \right){\text{e}}^{{i\left( {k_{0} z - \omega t} \right)}} } \right]\frac{{{\text{d}}R\left( z \right)}}{{{\text{d}}z}} = 0 $$

(40)

Using the factorization of Eq. (40) and substituting $B_{0}$ and $C_{0}$, we obtain:

$$ - {\text{e}}^{{i\left( {k_{0} z - \omega t} \right)}} \frac{\pi }{2}R_{{{\text{b}} }} A_{0} \left( {1 + \frac{{ik_{0} }}{{\frac{{\omega^{2} }}{{c^{2} }} - k_{0}^{2} }}\frac{\text{d}}{{{\text{d}}z}}} \right) \times \left[ {H_{0} J_{0} \left( {T_{1} R\left( z \right)} \right) + U_{0} N_{0} \left( {T_{1} R\left( z \right)} \right)} \right] = 0 $$

(41)

$$ D{ \cdot }A = D_{n} A_{n} = D_{0} A_{0} = 0, $$

(42)

“A” is a vector with element $A_{0}$ and “D” is a matrix with element $D_{0}$. With the help of derivative of Bessel functions and substituting Eq. (1), the dispersion relation can be obtained and written as [18–22],

$$ D_{0} = \left( {1 + \frac{{ik_{0} }}{{\frac{{\omega^{2} }}{{c^{2} }} - k_{0}^{2} }}} \right) \times [T_{1} h\kappa_{0} \left( {H_{0} J_{1} \sin (\kappa_{0} z} \right) + U_{0} N_{1} \sin (\kappa_{0} z))] $$

(43)

Numerical result and discussion

The analysis of the dispersion relation is obtained by Eq. 40. First, we consider the dispersion analysis in the absence of the electron beam.

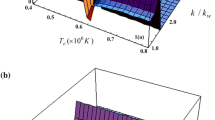
In Fig. 2, the chosen parameters are as follows: $n_{\text{p}} = 3 \times 10^{11} {\text{cm}}^{ - 3}$, R ₀ = 1.60 cm, h = 0.7 cm, R _b = 0.7 cm, z = 0.33 cm and $T_{\text{p}} = 30 \times 10^{8} \;{^\circ }{\text{K}}$, Fig. 2 shows the variation of normalized frequency $\text{Re} (\frac{\omega }{{c\kappa_{0} }} )$ versus wave number ($\frac{{k_{\text{z}} }}{{\kappa_{0} }}$) for several values of the corrugation periods ($z_{0}$). As seen in this figure the effect of $z_{0}$ increases the frequency.

Fig. 2

Dispersion relation ${\text{Re}}\left( \omega \right)$–$k_{z}$ for various corrugation periods

The effect of the plasma temperature on the frequency of the system as a function of $k_{z}$ is shown in Fig. 3. The chosen parameters are as follows: n _p = 3 × 10¹¹ cm⁻³, R ₀ = 1.60 cm, h = 0.7 cm, R _b = 0.7 cm, z = 0.33 cm and z ₀ = 0.66 cm. Figure 3 shows that the effect of plasma temperature increases the frequency. This effect is in good agreement with the thermal plasma dispersion relation $\omega^{2} = \omega_{\text{p}}^{2} + 3k_{z}^{2} v_{\text{th}}^{2}$ .

Fig. 3

Dispersion relation ${\text{Re}}(\omega )$–$k_{z}$ for various plasma temperatures

The effect of waveguide radius on the frequency of the wave as a function of $k_{z}$ is shown in Fig. 4. The chosen parameters are as follows:$n_{\text{p}} = 3 \times 10^{11} {\text{cm}}^{ - 3} ,$ h = 0.7 cm, R _b = 0.7 cm, z = 0.33 cm, $T_{\text{p}} = 30 \times 10^{8} \;{^\circ }{\text{K}}$ and z ₀ = 0.66 cm. As illustrated in this figure, the frequency decreases with increase in the waveguide radius.

Fig. 4

Dispersion relation ${\text{Re}}(\omega )$–$k_{z}$ for various waveguideradiuses

The variations of the frequency as a function of the wave number for different values of the plasma density are shown in Fig. 5. The chosen parameters are as follows: R ₀ = 1.60 cm, h = 0.7 cm, R _b = 0.7 cm, z = 0.33 cm, z ₀ = 0.66 cm and $T_{\text{p}} = 30 \times 10^{8} \;{^\circ }{\text{K}}$. It is clear that from the figure, the effect of plasma considerably increases the frequency. This effect is in good agreement with the simple relation of the plasma ($\omega^{2} = \omega_{\text{p}}^{2} + 3k_{z}^{2} v_{\text{th}}^{2}$).

Fig. 5

Dispersion ration ${\text{Re}}(\omega )$–$k_{z}$ for various plasma densities

Now, we consider the analysis of the growth rate in the presence of the electron beam.

Figure 6, shows the effect of corrugation period on the normalized growth rate Im ($\frac{\omega }{{c\kappa_{0} }}$) as a function of the normalized wave number ($\frac{{k_{z} }}{{\kappa_{0} }}$). The chosen parameters are as follows: γ = 1.001, h = 0.7 cm, R ₀ = 1.6 cm, R _b = 0.7 cm, z = 0.33 cm, n _b = 10 × 10¹¹ cm⁻³, n _p = 3 × 10¹¹ cm⁻³, T _p = 30 × 10⁸ °K and T _b = 20 × 10⁷ °K. It is clear that from Fig. 6, the growth rate increases by increasing the corrugation period.

Fig. 6

Growth rate for various corrugation periods

The effect of electron beam internal radius on the growth rate on the frequency of the wave as a function of $k_{z}$ is shown in Fig. 7. The chosen parameters are as follows n _p = 3 × 10¹¹ cm⁻³, R ₀ = 1.6 cm, z ₀ = 0.66 cm, γ = 1.001, z = 0.33 cm, h = 0.7 cm, n _b = 10 × 10¹¹ cm⁻³, T _p = 30 × 10⁸ °K and T _b = 20 × 10⁷ °K. As illustrated in this figure, the frequency decreases by increasing the electron beam internal radius.

Fig. 7

Growth rate for various electron beam internal radius

Figure 8, shows the effect of waveguide radius on the growth rate as a function of wave number for several values of waveguide radius. The chosen parameters are as follows: n _p = 3 × 10¹¹ cm⁻³, h = 0.7 cm, T _p = 30 × 10⁸ °K, R _b = 0.7 cm, z = 0.33 cm, γ = 1.001, z ₀ = 0.66 cm, n _b = 10 × 10¹¹ cm⁻³ and T _b = 20 × 10 °K. As seen in this figure, the growth rate decreases by increasing the R ₀.

Fig. 8

Growth rate for various waveguide radiuses

The effect of the plasma density on the growth rate of the system as a function of the wave number is shown in Fig. 9. It is clear that in this frequency range the effect of plasma density decreases the growth rate of the system. The chosen parameters are as follows: R₀ = 1.6 cm, h = 0.7 cm, T _p = 30 × 10⁸ °K, R _b = 0.7 cm, z = 0.33 cm, γ = 1.001, z ₀ = 0.66 cm, n _b = 10 × 10¹¹ cm⁻³ and T _b = 20 × 10⁷ °K. Figure 10 illustrates the variation of the growth rate for several values of the electron beam density. It is clear that from the figure, because of bunching effect, the increasing e-beam density increases the growth rate. The chosen parameters are as follows: $R_{0} = 1.6 cm , h = 0.7 cm , T_{p} = 30 \times 10^{8} \;{^\circ }{\text{K}}, \;R_{\text{b}} = 0.7 {\text{cm }}, z = 0.33 \;{\text{cm}}, \gamma = 1.001,\;z_{0} = 0.66\; {\text{cm}},\; n_{\text{p}} = 3 \times 10^{11} \;{\text{cm}}^{ - 3} , {\text{and}}\;T_{\text{b}} = 20 \times 10^{7} \;{^\circ }{\text{K}}.$

Fig. 9

Growth rate for various plasma densities

Fig. 10

Growth rate for various electron beam densities

Figure 11 shows the variation of the growth rate as a function of the wave number for several values of the electron beam energy. The chosen parameters are as follows: R ₀ = 1.6 cm, h = 0.7 cm, z ₀ = 0.66 cm, R _b = 0.7 cm, z = 0.33 cm, n _b = 10 × 10¹¹ cm⁻³, T _p = 30 × 10⁸ °K, n _p = 3 × 10¹¹ cm⁻³ and T _b = 20 × 10⁷ °K. As seen this figure because of the synchronism condition, the effect of γ decreases the growth rate.

Fig. 11

Growth rate for various electron beam energies

The plasma temperature effect on the growth rate as a function of the normalized wave number is given in Fig. 12. The figure shows, the plasma temperature considerably increases the growth rate. The chosen parameters are as follows: n _p = 3 × 10¹¹ cm⁻³, h = 0.7 cm, R ₀ = 1.6 cm, R _b = 0.7 cm, z = 0.33 cm, γ = 1.001, z ₀ = 0.66 cm, n _b = 0

Fig. 12

Growth rate for various plasma temperatures with $T_{b} = 0$

The plasma temperature effect on the growth rate with constant value $T_{\text{b}} = 50 \times 10^{8} \;{^\circ }{\text{K}},$ is given in Fig. 13. The figure shows, the plasma temperature at first decrease to the point $T_{\text{p}} = 55 \times 10^{8} \;{^\circ }{\text{K}}$, and then the graph increases. The chosen parameters are as follows: $n_{p} = 3 \times 10^{11} {\text{cm}}^{ - 3} , h = 0.7 {\text{cm}},\; R_{0} = 1.6 \;{\text{cm}},\; R_{b} = 0.7 {\text{cm}}, z = 0.33 \,{\text{cm}}, \gamma = 1.001,\;\;z_{0} = 0.66 \;{\text{cm}}, n_{\text{b}} = 10 \times 10^{11} {\text{cm}}^{ - 3} \;{\text{and}} \;T_{\text{b}} = 50 \times 10^{8} \;{^\circ }{\text{K}}.$

Fig. 13

Growth rate for various plasma temperatures with $T_{b} = 50 \times 10^{8} \;{^\circ }{\text{K}}$

The beam temperature effect on e growth rate as a function of the normalized wave number is given in Fig. 14. It is clear that from the figure, the beam temperature considerably increases the growth rate. The chosen parameters are as follows: $h = 0.7\;{\text{cm}}, \;R_{0} = 1.6\; {\text{cm}}, R_{\text{b}} = 0.7\;{\text{cm}}, \;z = 0.33\; {\text{cm}}, \gamma = 1.001,\;z_{0} = 0.66 \;{\text{cm}}, n_{\text{b}} = 10{ \times }10^{11} \;{\text{cm}}^{{\text{ - } 3}} ,\;T_{\text{p}} = 0.$

Fig. 14

Growth rate for various beam temperatures with $T_{p} = 0$

The beam temperature effect on the growth rate as a function of the normalized wave number is given in Fig. 15. It is clear from the figure that the beam temperature at first increase but from point $T_{\text{b}} = 32 \times 10^{8} \;{^\circ }{\text{K}}$ the graph decreases. The chosen parameters are as follows: $h = 0.7\;{\text{cm}}, \;R_{0} = 1.6\; {\text{cm}},\;R_{\text{b}} = 0.7\;{\text{cm}}, z = 0.33\;{\text{cm}},\;\gamma = 1.001,\;z_{0} = 0.66\;{\text{cm}},\;n_{\text{b}} = 10{ \times }10^{11} \;{\text{cm}}^{{\text{ - } 3}}$, $T_{\text{p}} = 12 \times 10^{9} \;{^\circ }{\text{K}}$, $n_{\text{p}} = 3 \times 10^{11} \;{\text{cm}}^{ - 3} .$

Fig. 15

Growth rate for various beam temperatures with $T_{p} = 12 \times 10^{9} \;{^\circ }{\text{K}}$

Conclusions

In this paper, useful results are obtained as:

• 1. In the absence of the electron beam, the frequency increases by increasing the length of the corrugation period, plasma temperature and plasma density.

• 2. The frequency decreases by increasing the waveguide radius in the absence of the electron beam.

• 3. In the presence of the electron beam, the growth rate increases by increasing the corrugation period and e-beam density.

• 4. The growth rate decreases by increasing the waveguide radius, plasma density and e-beam energy in the presence of the electron beam.