Dispersion characteristics of plasma-filled cylindrical waveguide

Abstract

An analytical and numerical study is made on the dispersion properties of a cylindrical waveguide filled with plasma. An electron beam and static external magnetic field are considered as the mechanisms for controlling the field attenuation and possible stability of the waveguide. The effects of plasma warmness and inhomogeneity are also considered. Dispersion relations in ω describing different physical situations that govern the mode propagation in the waveguide are obtained. The plasma dielectric tensors and the dispersion relations which describe E and H waves and, hence, the damping rate of these waves are calculated and studied. The necessary conditions for the field stability in the waveguide and amplification coefficients for these waves are also obtained. H-wave modes are always attenuated by collisional effect. The growth of the excited E wave is calculated in the resonance case, and the stability condition for the E wave is obtained. E waves are found to be more stable in warm plasma compared to cold plasma. The results obtained here are of great interest and may be used to analyze how the plasma affects the electromagnetic properties of the cavity of the 1–2 MW 140–170 GHz continuous-wave gyrotron (for W7-X stellarator and ITER), for MW gyrotron development for fusion plasma applications, and for second harmonic generation in a plasma-filled parallel plane waveguide.

Introduction

There has been growing interest in the plasma-filled cylindrical waveguides in recent years [1–4]. A considerable number of microwave sources employ cylindrical waveguides, containing axis encircling electron beams. In these devices the annular plasma column interacts with the modes of empty waveguides, in which case they have been referred to as large-orbit gyrotrons, or with the azimuthally periodic wiggler magnetic field where they are called circular geometry free electron lasers. In either case, frequencies of the generated electromagnetic–electrostatic waves have been shown to have a strong dependence on the radii of coaxial waveguide and on relative positions of the inner and outer radii of the beam [5]. Analysis of the plasma waveguide requires knowledge of its eigenmodes. High-frequency eigenmodes of a magnetized plasma waveguide are characterized in four families, EH and HE waveguide modes, cyclotron modes, and space-charge modes.

Besides, a lot of effort has been taken to study the physical and geometrical parameters which cause attenuation of waves (signals) through the waveguides. Interest in studying plasma-filled waveguides has been growing with the development of high-frequency electronics with the objective of creating powerful microwave generators. A great interest and importance have been shown in the past [6–8] and in recent years [9–12] on wave propagation in plasma-filled waveguides. This subject is currently of considerable interest for optical systems and in the development of high-power millimeter wave amplifiers and its application via high-resolution and imaging radar, high information density communication, NDT, RF sources for the next generation of particle accelerators and fusion experiments.

In some experiments, when considering the physical properties of the inner medium of the waveguide, it is found that the average transferred energy increases with the increase of the gas pressure, evacuating it or by replacing it by a highly ionized gas. The results of these experiments concluded the following explanation: the propagated electromagnetic waves in the waveguide ionize the air inside it under average pressure and temperature, forming a plasma which absorbs the wave energy and consequently causes field attenuation.

A promising mechanism to conserve field stability and to control field attenuation in a waveguide is to inject into the plasma a fast electron beam to excite the natural oscillations of the plasma and additional electromagnetic modes which compensates the losses in the original field.

Many theoretical investigations have been performed to describe the fundamental principles of electromagnetic wave excitation by an electron beam in a partially dielectric-filled waveguide [13–18].

In this work, we investigate the electromagnetic wave propagation in a plasma-filled cylindrical waveguide. Analytical calculations are performed to find the plasma dielectric tensor. By applying the boundary conditions at the plasma–conductor interface, we find the dispersion equations which describe the wave modes (E- and H- waves) propagated inside the waveguide and their physical properties. It is of interest to investigate also the effect of a relativistic electron beam on the field stability and minimize the energy losses in the waveguide. Also, the cases of warm and magnetized plasma are considered.

The conductivity of the metal conductor is assumed to be infinite, and the interior is filled with plasma.

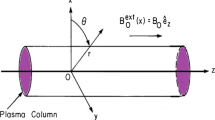
Let Fig. 1 represent a section of cylindrical waveguide with the z-axis parallel to the axis of the tube.

Fig. 1

Cylindrical waveguide

Waveguide filled with warm plasma and a relativistic electron beam (REB)

Currents in plasma

Now, we consider the wave propagation in a cylindrical waveguide filled with collisional, warm plasma and a relativistic electron beam. We use the hydrodynamic model for the warm plasma in which the essential equations are the continuity equation, equation of motion and Maxwell’s equations. We take into consideration that the plasma is quasineutral and that the plasma electrons have a finite temperature, whereas the beam electrons are cold but move at a velocity comparable to light velocity.

The initial equations which describe the system are continuity equation, equation of motion and Maxwell’s equations:

$$\frac{\mathit{\partial }{N}_{\mathit{\alpha }}}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}·(N_{\mathit{\alpha }}{\overrightarrow{V}}_{\mathit{\alpha }})=0,$$

(1)

$$\frac{d}{dt}\frac{{\overrightarrow{V}}_{\mathit{\alpha }}}{\sqrt{1-\frac{V_{\mathit{\alpha }}^2}{c^2}}}=\frac{e_{\mathit{\alpha }}}{m_{\mathit{\alpha }}}\left[\overrightarrow{E}+\frac{1}{c}{\overrightarrow{V}}_{\mathit{\alpha }}\times (\overrightarrow{H}+{\overrightarrow{H}}_{ext.})\right]-{\mathit{\nu }}_{\mathit{\alpha }}{\overrightarrow{V}}_{\mathit{\alpha }}-\frac{1}{N_{\mathit{\alpha }}{m}_{\mathit{\alpha }}}\overrightarrow{\mathrm{\nabla }}P,$$

(2)

$$\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{E}=-\frac{1}{c}\frac{\mathit{\partial }\overrightarrow{H}}{\mathit{\partial }t},$$

(3-a)

$$\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{H}=\frac{1}{c}\frac{\mathit{\partial }\overrightarrow{D}}{\mathit{\partial }t}=\frac{4\mathit{\pi }}{c}\overrightarrow{J}+\frac{1}{c}\frac{\mathit{\partial }\overrightarrow{E}}{\mathit{\partial }t},$$

(3-b)

where N _α and ${\overrightarrow{V}}_{\mathit{\alpha }}$ are the density and the mean velocity of α-type particles (plasma and beam electrons and plasma ions), ν _α is the electron–electron collision frequency and all other terms have their usual meaning. Besides, we considered the effect of static external magnetic field along the axis of the guide, i.e., ${\overrightarrow{H}}_{\text{ext}}={\overrightarrow{e}}_z{H}_{\text{ext}}$

The current density $\overrightarrow{J}$ is defined through the plasma quantities as:

$$\overrightarrow{J}=\sum _{\mathit{\alpha }}{e}_{\mathit{\alpha }}{N}_{\mathit{\alpha }}{\overrightarrow{V}}_{\mathit{\alpha }},$$

(4)

The interaction of the electromagnetic waves with the plasma will disturb the equilibrium density and velocity of the latter. It is convenient to expand N _α and ${\overrightarrow{V}}_{\mathit{\alpha }}$ in the form:

$$N_{\mathit{\alpha }}=n_{0_{\mathit{\alpha }}}+n_{\mathit{\alpha }};{\overrightarrow{V}}_{\mathit{\alpha }}={\overrightarrow{V}}_{0_{\mathit{\alpha }}}+{\overrightarrow{V}}_{\mathit{\alpha }};{\overrightarrow{V}}_{0_{\mathit{\alpha }}}={\overrightarrow{e}}_z{V}_{0_{\mathit{\alpha }}}$$

The previous set of equations gives a remarkably accurate description of the small-amplitude perturbations. We linearize the above system of equations by considering small deviations from the equilibrium state ($n_{\mathit{\alpha }}<<n_{0_{\mathit{\alpha }}};\left|V_{\mathit{\alpha }}\right|<<\left|V_{0_{\mathit{\alpha }}}\right|$).

All perturbations are described by the ansatz $F(\mathit{\rho },\mathit{\phi },z,t)\approx f(\mathit{\rho })·e^{i(kz+\ell \mathit{\phi }-\mathit{\omega }t)}.$

The perturbed density will have the form:

$$n_{\mathit{\alpha }}=-\frac{i{n}_{\circ \mathit{\alpha }}}{\tilde{\mathit{\omega }}}\left[\frac{1}{\mathit{\rho }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}(\mathit{\rho }{V}_{\mathit{\rho }})+\frac{i\ell }{\mathit{\rho }}{V}_{\mathit{\phi }}+ik{V}_z\right],$$

(5)

where, $\tilde{\mathit{\omega }}=\mathit{\omega }{a}_{\mathit{\alpha }},a_{\mathit{\alpha }}=1-n{\mathit{\beta }}_{\circ \mathit{\alpha }},{\mathit{\beta }}_{\circ \mathit{\alpha }}=\frac{V_{\circ \mathit{\alpha }}}{c},n=\frac{kc}{\mathit{\omega }}.$

From (2), the velocity components read:

$$\begin{array}{c}{V}_{\mathit{\rho }}=\frac{i{e}_{\mathit{\alpha }}}{m_{\mathit{\alpha }}}\frac{1}{W_{\mathit{\alpha }}}\left[(E_{\mathit{\rho }}-{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\phi }})+\frac{i{\mathit{\omega }}_{c\mathit{\alpha }}}{{\mathit{\gamma }}_{\mathit{\alpha }}\tilde{\mathit{\omega }}+i{\mathit{\nu }}_{\mathit{\alpha }}}(E_{\mathit{\phi }}+{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\rho }})\right],\\ V_{\mathit{\phi }}=\frac{i{e}_{\mathit{\alpha }}}{m_{\mathit{\alpha }}}\frac{1}{W_{\mathit{\alpha }}}\left[(E_{\mathit{\phi }}+{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\rho }})-\frac{i{\mathit{\omega }}_{c\mathit{\alpha }}}{{\mathit{\gamma }}_{\mathit{\alpha }}\tilde{\mathit{\omega }}+i{\mathit{\nu }}_{\mathit{\alpha }}}(E_{\mathit{\rho }}-{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\phi }})\right],\\ V_z=\frac{i{e}_{\mathit{\alpha }}}{m_{\mathit{\alpha }}}\frac{1}{W_{T\mathit{\alpha }}}{E}_z,\end{array}$$

(6)

where,

$$\begin{array}{c}{\mathit{\gamma }}_{\mathit{\alpha }}=\frac{1}{\sqrt{1-{\mathit{\beta }}_{{}_{\circ \mathit{\alpha }}}^2}},W_{\mathit{\alpha }}=\frac{{({\mathit{\gamma }}_{\mathit{\alpha }}\tilde{\mathit{\omega }}+i{\mathit{\nu }}_{\mathit{\alpha }})}^2-{\mathit{\omega }}_{c\mathit{\alpha }}^2}{{\mathit{\gamma }}_{\mathit{\alpha }}\tilde{\mathit{\omega }}+i{\mathit{\nu }}_{\mathit{\alpha }}},W_{T\mathit{\alpha }}={\mathit{\gamma }}_{\mathit{\alpha }}^3\tilde{\mathit{\omega }}+i{\mathit{\nu }}_{\mathit{\alpha }}-\frac{3k^2{V}_{T\mathit{\alpha }}^2}{\tilde{\mathit{\omega }}},\\ {\mathit{\omega }}_{c\mathit{\alpha }}=\frac{e_{\mathit{\alpha }}{H}_{\circ }}{m_{\mathit{\alpha }}c},V_{T\mathit{\alpha }}=\sqrt{\frac{K{T}_{\mathit{\alpha }}}{m_{\mathit{\alpha }}}},K=\text{Boltmann's Constant}\end{array}$$

Using (1)–(6), we can derive the following expressions for the current density components:

$$\begin{array}{c}\frac{4\mathit{\pi }}{c}{J}_{\mathit{\rho }}=\sum _{\mathit{\alpha }}\frac{i{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}\left[(E_{\mathit{\rho }}-{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\phi }})+W_{c\mathit{\alpha }}(E_{\mathit{\phi }}+{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\rho }})\right],\\ \frac{4\mathit{\pi }}{c}{J}_{\mathit{\phi }}=\sum _{\mathit{\alpha }}\frac{i{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}\left[(E_{\mathit{\phi }}+{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\rho }})-W_{c\mathit{\alpha }}(E_{\mathit{\rho }}-{\mathit{\beta }}_{\circ \mathit{\alpha }}{H}_{\mathit{\phi }})\right],\\ \frac{4\mathit{\pi }}{c}{J}_z=\sum _{\mathit{\alpha }}\frac{i{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{T\mathit{\alpha }}}\left(1+\frac{k{V}_{\circ \mathit{\alpha }}}{\tilde{\mathit{\omega }}}\right)E_z,\end{array}$$

(7)

where, $W_{c\mathit{\alpha }}=\frac{i{\mathit{\omega }}_{c\mathit{\alpha }}}{{\mathit{\gamma }}_{\mathit{\alpha }}\tilde{\mathit{\omega }}+i{v}_{\mathit{\alpha }}}$, and ${\mathit{\Omega }}_{\mathit{\alpha }}=\sqrt{\frac{4\mathit{\pi }{e}_{\mathit{\alpha }}^2{n}_o{}_{\mathit{\alpha }}}{m_{\mathit{\alpha }}}}$

W _cα is the effect of external magnetic field. In relations (7) we took into consideration that when an electron beam is injected into a dense plasma, an inverse current is induced in the plasma, compensating the current and the corresponding magnetic field of the beam [19, 20], i.e.,

$$J_{0z}=\sum _{\mathit{\alpha }}{e}_{\mathit{\alpha }}{n}_{0_{\mathit{\alpha }}}{V}_{0_{\mathit{\alpha }}}=0.$$

The non-axisymmetric permittivity tensor (l ≠ 0)

From Maxwell’s equations, the following set of relations are obtained

$$\begin{array}{c}{H}_{\mathit{\rho }}=\frac{lc}{\mathit{\rho }\mathit{\omega }}{E}_z-n{E}_{\mathit{\phi }},\\ H_{\mathit{\phi }}=\frac{ic}{\mathit{\omega }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}{E}_z+n{E}_{\mathit{\rho }},\\ H_z=-\frac{ic}{\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\mathit{\rho }{E}_{\mathit{\phi }}-\frac{lc}{\mathit{\rho }\mathit{\omega }}{E}_{\mathit{\rho }},\end{array}$$

(8)

and

$$\begin{array}{c}\sum _{\mathit{\alpha }}\left\{\left(k-\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}{\mathit{\beta }}_{\circ \mathit{\alpha }}\right)H_{\mathit{\rho }}-\left(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}{\mathit{\beta }}_{\circ \mathit{\alpha }}{W}_{c\mathit{\alpha }}\right)H_{\mathit{\varphi }}+i\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}{H}_Z\right\}\\ =\sum _{\mathit{\alpha }}\left\{\left(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}{W}_{c\mathit{\alpha }}\right)E_{\mathit{\rho }}+\left(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}-\frac{\mathit{\omega }}{c}\right)E_{\mathit{\phi }}\right\}-\frac{l}{\mathit{\rho }}{H}_{\mathit{\rho }}-\frac{i}{\mathit{\rho }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\mathit{\rho }{H}_{\mathit{\phi }}=\sum _{\mathit{\alpha }}\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{T\mathit{\alpha }}}\left(1+\frac{k{V}_{\circ \mathit{\alpha }}}{\tilde{\mathit{\omega }}}\right)-\frac{\mathit{\omega }}{c}{E}_z,\end{array}$$

(9)

$$\begin{array}{c}\sum _{\mathit{\alpha }}\left\{\left(-\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}{\mathit{\beta }}_{\circ \mathit{\alpha }}{W}_{c\mathit{\alpha }}\right)H_{\mathit{\rho }}+\left(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}{\mathit{\beta }}_{\circ \mathit{\alpha }}-k\right)H_{\mathit{\phi }}+\frac{l}{\mathit{\rho }}{H}_Z\right\}\\ =\sum _{\mathit{\alpha }}\left\{\left(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}-\frac{\mathit{\omega }}{c}\right)E_{\mathit{\rho }}+\left(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}}{W}_{c\mathit{\alpha }}\right)E_{\mathit{\phi }}\right\},\end{array}$$

(10)

The permittivity tensor operator ${\widehat{\mathit{\epsilon }}}_{ij}$ which describes the wave propagation in the waveguide is determined according to the relation:

$$D_i\equiv {\widehat{\mathit{\epsilon }}}_{ij}{\overrightarrow{E}}_j={\overrightarrow{E}}_i+\frac{4\mathit{\pi }i}{\mathit{\omega }}{\overrightarrow{J}}_i,$$

(11)

Inserting (8) and (9) into (10), ${\widehat{\mathit{\epsilon }}}_{ij}$ reads:

$${\widehat{\mathit{\epsilon }}}_{ij}=\left(\begin{array}{ccc}1+\frac{ic}{\mathit{\omega }}\sum _{\mathit{\alpha }}{A}_{1\mathit{\alpha }}(1-n{\mathit{\beta }}_{\circ \mathit{\alpha }})& \frac{ic}{\mathit{\omega }}\sum _{\mathit{\alpha }}{A}_{2\mathit{\alpha }}(1-n{\mathit{\beta }}_{\circ \mathit{\alpha }})& \frac{i{c}^2}{{\mathit{\omega }}^2}\sum _{\mathit{\alpha }}{\mathit{\beta }}_{\circ \mathit{\alpha }}\left(\frac{l}{\mathit{\rho }}{A}_{2\mathit{\alpha }}-i{A}_{1\mathit{\alpha }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)\\ -\frac{ic}{\mathit{\omega }}\sum _{\mathit{\alpha }}{A}_{2\mathit{\alpha }}(1-n{\mathit{\beta }}_{\circ \mathit{\alpha }})& 1+\frac{ic}{\mathit{\omega }}\sum _{\mathit{\alpha }}{A}_{1\mathit{\alpha }}(1-n{\mathit{\beta }}_{\circ \mathit{\alpha }})& \frac{i{c}^2}{{\mathit{\omega }}^2}\sum _{\mathit{\alpha }}{\mathit{\beta }}_{\circ \mathit{\alpha }}\left(\frac{l}{\mathit{\rho }}{A}_{1\mathit{\alpha }}+i{A}_{2\mathit{\alpha }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)\\ 0& 0& 1+\frac{ic}{\mathit{\omega }}\sum _{\mathit{\alpha }}{A}_{3\mathit{\alpha }}\left(1+\frac{k{V}_{\circ \mathit{\alpha }}}{\tilde{\mathit{\omega }}}\right)\\ \end{array}\right)$$

(12)

where, $A_{1\mathit{\alpha }}=\frac{i{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{\mathit{\alpha }}},A_{2\mathit{\alpha }}=A_{1\mathit{\alpha }}{W}_{c\mathit{\alpha }},A_{1\mathit{\alpha }}=\frac{i{\mathit{\Omega }}_{\mathit{\alpha }}^2}{c{W}_{T\mathit{\alpha }}}.$

Electromagnetic field components

From Maxwell’s equations, and using (5)–(7), we can obtain the following expressions for the electric and magnetic field components E _ρ , E _φ , H _ρ , H _φ in terms of the z-components H _z and E _z :

$$E_{\mathit{\rho }}=\frac{1}{{\mathit{\beta }}^2}\left[\frac{l}{\mathit{\rho }}{M}_1{E}_z+M_2\frac{\mathit{\partial }{E}_z}{\mathit{\partial }\mathit{\rho }}+\frac{l}{\mathit{\rho }}{M}_3{H}_z+M_4\frac{\mathit{\partial }{H}_z}{\mathit{\partial }\mathit{\rho }}\right],$$

(13)

$$E_{\mathit{\phi }}=\frac{1}{{\mathit{\beta }}^2}\left[i\frac{l}{\mathit{\rho }}{M}_2{E}_z+i{M}_1\frac{\mathit{\partial }{E}_z}{\mathit{\partial }\mathit{\rho }}+i\frac{l}{\mathit{\rho }}{M}_4{H}_z+i{M}_3\frac{\mathit{\partial }{H}_z}{\mathit{\partial }\mathit{\rho }}\right],$$

(14)

$$H_{\mathit{\rho }}=\frac{c}{\mathit{\omega }}\frac{l}{\mathit{\rho }}\left(1-i\frac{k}{{\mathit{\beta }}^2}{M}_2\right)E_z-i\frac{c}{\mathit{\omega }}\frac{k}{{\mathit{\beta }}^2}\left(M_1\frac{\mathit{\partial }{E}_z}{\mathit{\partial }\mathit{\rho }}+\frac{l}{\mathit{\rho }}{M}_4{H}_z+M_3\frac{\mathit{\partial }{H}_z}{\mathit{\partial }\mathit{\rho }}\right),$$

(15)

$$H_{\mathit{\phi }}=\frac{c}{\mathit{\omega }}\frac{k}{{\mathit{\beta }}^2}\left(\frac{l}{\mathit{\rho }}{M}_1{E}_z+\frac{l}{\mathit{\rho }}{M}_3{H}_z+M_4\frac{\mathit{\partial }{H}_z}{\mathit{\partial }\mathit{\rho }}\right)-\frac{c}{\mathit{\omega }}\left(1-\frac{k}{{\mathit{\beta }}^2}{M}_2\right)\frac{\mathit{\partial }{E}_z}{\mathit{\partial }\mathit{\rho }},$$

(16)

where

$$\begin{array}{c}{M}_1={\mathit{\beta }}_1{\mathit{\beta }}_3+{\mathit{\beta }}_2{\mathit{\beta }}_4,M_2=i[({\mathit{\beta }}_2-k{\mathit{\beta }}_1){\mathit{\beta }}_1-({\mathit{\beta }}_3-k{\mathit{\beta }}_4){\mathit{\beta }}_4],M_3=({\mathit{\beta }}_2-k{\mathit{\beta }}_1),M_4=i({\mathit{\beta }}_3-k{\mathit{\beta }}_4),\\ \mathit{\beta }=\frac{V}{c},{\mathit{\beta }}_1=n-\sum _{\mathit{\alpha }}\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{\mathit{\omega }}\frac{{\mathit{\beta }}_{\circ \mathit{\alpha }}}{W_{\mathit{\alpha }}},{\mathit{\beta }}_2=\frac{\mathit{\omega }}{c}\left(1-\sum _{\mathit{\alpha }}\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{\mathit{\omega }{W}_{\mathit{\alpha }}}\right),{\mathit{\beta }}_3=\sum _{\mathit{\alpha }}\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{\mathit{\omega }}\frac{W_{C\mathit{\alpha }}}{W_{\mathit{\alpha }}},{\mathit{\beta }}_4=\sum _{\mathit{\alpha }}\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{\mathit{\omega }}\frac{W_{C\mathit{\alpha }}{\mathit{\beta }}_{\circ \mathit{\alpha }}}{W_{\mathit{\alpha }}}.\end{array}$$

To find the final picture of the electric and magnetic components (13)–(16), we have to solve the following differential equations, which describe different wave modes in waveguides filled with warm-magnetized plasma:

$$\frac{1}{\mathit{\rho }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\left(\mathit{\rho }\frac{\mathit{\partial }{H}_z}{\mathit{\partial }\mathit{\rho }}\right)+\left(Q_{}^2-\frac{l^2}{{\mathit{\rho }}^2}\right)H_z=F(E_z),$$

(17)

$$\frac{1}{\mathit{\rho }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\left(\mathit{\rho }\frac{\mathit{\partial }{E}_z}{\mathit{\partial }\mathit{\rho }}\right)+\left(q_{}^2-\frac{l^2}{{\mathit{\rho }}^2}\right)E_z=F(H_z),$$

(18)

where,

$$\begin{array}{c}{Q}^2=\frac{\mathit{\omega }}{c}\frac{{\mathit{\beta }}^2}{(k{\mathit{\beta }}_1-{\mathit{\beta }}_2)},q^2=i\frac{\mathit{\eta }}{{\mathit{\eta }}^{\prime }}\frac{{\mathit{\omega }}^2}{c^2},\\ \mathit{\eta }=i\sum _{\mathit{\alpha }}\left[\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{\mathit{\omega }{\mathit{\Delta }}_{\mathit{\alpha }T}}\left(1+\frac{k{V}_{\circ \mathit{\alpha }}}{\tilde{\mathit{\omega }}}-1\right)\right],{\mathit{\eta }}^{\prime }=1-i\frac{k}{{\mathit{\beta }}^2}{M}_2,\\ F(E_z)=-\left[\frac{1}{\mathit{\rho }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\left(\mathit{\rho }\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)-\frac{l^2}{{\mathit{\rho }}^2}\right]E_z,\\ F(H_z)=\frac{i}{{\mathit{\eta }}^{\prime }}\frac{k{M}_4}{{\mathit{\beta }}^2}\left[\frac{1}{\mathit{\rho }}\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\left(\mathit{\rho }\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)-\frac{l^2}{{\mathit{\rho }}^2}\right]H_z.\end{array}$$

Equations (17) and (18) represent two linearly independent equations for the two basic types of electromagnetic waves which can propagate in a cylindrical waveguide filled with warm-magnetized plasma. The solution for (17) gives the TE or H wave with an entirely transverse electric field (E _z  = 0) and the axial component H _z of the magnetic field. The solution of (18) gives the TM or E wave with H _z  = 0. The general solution of the equations with E _z  ≠ 0 and H _z  ≠ 0 will be a linear combination of the two types (TEM).

Magnetic wave mode (H wave)

Equation (17) has the following solutions:

$$\begin{array}{c}{E}_z=0,\\ H_z=H_{\circ }{J}_l(Q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\\ E_{\mathit{\rho }}=\frac{1}{{\mathit{\beta }}^2}{H}_{\circ }\left(\frac{l}{\mathit{\rho }}{M}_3+M_4\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)J_l(Q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\\ E_{\mathit{\phi }}=\frac{i}{{\mathit{\beta }}^2}{H}_{\circ }\left(\frac{l}{\mathit{\rho }}{M}_4+M_3\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)J_l(Q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\\ H_{\mathit{\rho }}=-n{E}_{\mathit{\phi }},H_{\mathit{\phi }}=n{E}_{\mathit{\rho }},\end{array}$$

(19)

where J _l (Qρ) is the Bessel function of order l.

As we have seen, the warm plasma can be described as an equivalent dielectric medium obeying Maxwell’s equations. The boundary conditions at the interface between the plasma and a conductor are thus the classical (usual) conditions of electromagnetic theory, since the plasma behaves simply as a polarizable medium with strongly frequency-dependent tonsorial permittivity.

Accordingly, we can still use the boundary condition;

$$E_{\mathit{\phi }}\to 0\text{at}\mathit{\rho }={\mathit{\rho }}_0,$$

$$J_l^{\prime }=(Q{\mathit{\rho }}_0)=0.$$

(20)

Equation (20) has an infinite number of real roots which define correspondingly an infinite number of modes propagating in the waveguide. Let these roots be defined by χ_ℓ,m, where ℓ, m = 0, 1, 2, 3,… Accordingly, if the waveguide is filled with warm-magnetized plasma, the propagation wave number k is determined by:

$$Q=\frac{{\mathit{\chi }}_{\ell ,m}}{{\mathit{\rho }}_0}.$$

(21)

Equation (21) represents the dispersion relation for the H wave.

Electric wave mode (E wave)

We derive from Eq. (18) the following solutions for the E mode:

$$\begin{array}{c}{H}_z=0,\\ E_z=E_0{J}_l(q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\\ E_{\mathit{\rho }}=\frac{E_0}{{\mathit{\beta }}^2}\left(\frac{l}{\mathit{\rho }}{M}_1+M_2\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)J_l(q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\\ E_{\mathit{\phi }}=\frac{E_0}{{\mathit{\beta }}^2}\left(\frac{l}{\mathit{\rho }}{M}_1^{\prime }+M_2^{\prime }\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right)J_l(q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\\ H_{\mathit{\rho }}=\frac{c}{\mathit{\omega }}{E}_0\left[\frac{l}{\mathit{\rho }}\left(1-\frac{k}{{\mathit{\beta }}^2}{M}_1^{\prime }\right)-\frac{k}{{\mathit{\beta }}^2}{M}_2^{\prime }\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right]J_l(q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\\ H_{\mathit{\phi }}=\frac{c}{\mathit{\omega }}{E}_0\left[\frac{k}{{\mathit{\beta }}^2}{M}_1-\left(1-\frac{k}{{\mathit{\beta }}^2}{M}_2\right)\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\right]J_l(q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)},\end{array}$$

(22)

and the propagation wave number q is determined by the dispersion relation:

$$q=\frac{x_{\ell ,m}^{\prime }}{{\mathit{\rho }}_0}.$$

(23)

x ^′_ℓ,m are the roots when considering the boundary condition E _z  → 0 at ρ = ρ₀, then J _l (qρ_∘) = 0.

Figures 2 and 3 show the magnetic ρ and electric E _z modes propagating in a waveguide filled with warm-magnetized plasma for different numbers (ℓ, m = 0, 1, 2, 3, …..).

Fig. 2

Magnetic modes H _z for different numbers (ℓ, m = 0, 1, 2, 3, …)

Fig. 3

Electric modes E _z for different numbers (ℓ, m = 0, 1, 2, 3, …)

Power flow in waveguide

Homogeneous, collisionless, unmagnetized cold plasma

When considering a metallic cylindrical waveguide completely filled with a homogenous, unmagentized, collisionless cold plasma, the dielectric constant is simply given by the well-known form

$${\mathit{\epsilon }}_p=1-{\left(\frac{{\mathit{\Omega }}_p}{\mathit{\omega }}\right)}^2,$$

where ${\mathit{\Omega }}_p=\sqrt{\frac{4\mathit{\pi }{e}^2{n}_{0e}}{m_e}}$ is the Langmuir electron frequency.

To get the average power flux S_l,m we use the well-known Poynting formula:

$${\overrightarrow{S}}_{\ell ,m}=\frac{c}{8\mathit{\pi }}\text{Re}(\overrightarrow{E}\times {\overrightarrow{H}}^{\ast }).$$

Accordingly, it is easy to compare the average rate of power transmitted in the empty waveguide S ⁽⁰⁾_ℓ,m with that in the waveguide filled with plasma S ^(P)_ℓ,m .

For H wave, it is easy to check that

$$\frac{S_{\ell ,m}^{(P)}}{S_{\ell ,m}^{(0)}}=\frac{{\mathit{\epsilon }}_P-N_{\ell ,m}^2}{1-N_{\ell ,m}^2}<1,N_{\ell ,m}=\frac{c}{\mathit{\omega }}\frac{x_{\ell ,m}}{{\mathit{\rho }}_0},$$

(24)

and for E wave,

$$\frac{S_{\ell ,m}^{(P)}}{S_{\ell ,m}^{(0)}}={\mathit{\epsilon }}_p\sqrt{\frac{{\mathit{\epsilon }}_P-N_{\ell ,m}^{{}^{\prime }2}}{1-N_{\ell ,m}^{{}^{\prime }2}}}<1,N_{\ell ,m}^{\prime }=\frac{c}{\mathit{\omega }}\frac{{\mathit{\chi }}_{\ell ,m}^{\prime }}{{\mathit{\rho }}_{\circ }}.$$

(25)

Relations (24) and (25) show that, for a given frequency, the average rate of energy flow in a waveguide filled with plasma is lower than the flow in the empty waveguide.

For H wave, the propagation number k is determined from (21) as:

$$k=\frac{\mathit{\omega }}{c}\sqrt{1-{\left(\frac{{\mathit{\omega }}_{cr}^{(P)}}{\mathit{\omega }}\right)}^2}$$

(26)

where ω ^(p) _cr is the critical frequency for H_l,m modes in the presence of plasma

$${\mathit{\omega }}_{cr}^{(p)}=\sqrt{{\mathit{\Omega }}_p^2+\left(\frac{c{\mathit{\chi }}_{\ell m}}{{\mathit{\rho }}_0}\right)},$$

(27)

It is clear that the cutoff frequency for a given mode in a waveguide filled with plasma ω ^(p) _cr differs from that for an empty (evacuated) waveguide ω ⁽⁰⁾ _cr [18], where

$${\mathit{\omega }}_{cr}^{(0)}=c\frac{R_{lm}}{{\mathit{\rho }}_{\circ }}\sqrt{\mathit{\epsilon }},$$

Here, R _lm are the roots of J ^′ _l (κρ_∘) = 0 and ${\mathit{\kappa }}^2=\frac{{\mathit{\omega }}^2}{c^2}(\mathit{\epsilon }-n^2),n=\frac{kc}{\mathit{\omega }},\mathit{\epsilon }\ne {\mathit{\epsilon }}_p.$

This difference is a measure of phase shift Δω = ω ^(p) _cr  − ω ⁽⁰⁾ _cr for the wave modes H_ℓ,m and usually used to determined the plasma density inside the waveguide (Δω is proportional to Ω _p ).

Relations (24) and (25) are also valid for E_ℓ,m wave modes. This could be checked and achieved by replacing χ_ℓ,m by χ^′_ℓ,m.

Different plasmas

Homogeneous cold-magnetized plasma

When considering a waveguide filled with a cold-magnetized plasma, the average power flux ${\overrightarrow{s}}_H$ for the H wave is given by:

$${\overrightarrow{s}}_H=\frac{c}{8\mathit{\pi }}\frac{1}{{\mathit{\beta }}^2}{H}_0^2\left[\left(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{{\mathit{\omega }}_{\mathit{\alpha }}^2-{\mathit{\omega }}_{c\mathit{\alpha }}^2}\frac{{\mathit{\omega }}_{c\mathit{\alpha }}}{\mathit{\omega }}\right)\right.J_l(Q\mathit{\rho })+\left.\frac{n}{{\mathit{\beta }}^2}{\left({(\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{{\mathit{\omega }}_{\mathit{\alpha }}^2-{\mathit{\omega }}_{c\mathit{\alpha }}^2}\frac{{\mathit{\omega }}_{c\mathit{\alpha }}}{\mathit{\omega }})}^2+\frac{\mathit{\omega }}{c}(n^2-\mathit{\epsilon })\right)}^2{J}_l^{\prime }(Q\mathit{\rho })\right]J_l^{\prime }(Q\mathit{\rho }),$$

(28)

while for the E wave ${\overrightarrow{S}}_E$ is given by:

$$\begin{array}{c}{\overrightarrow{S}}_E=\frac{c}{8\mathit{\pi }}\frac{E_0^2}{\mathit{\omega }{\mathit{\beta }}^2}\frac{{\mathit{\Omega }}_{\mathit{\alpha }}^2}{{\mathit{\omega }}_{\mathit{\alpha }}^2-{\mathit{\omega }}_{c\mathit{\alpha }}^2}\frac{{\mathit{\omega }}_{c\mathit{\alpha }}^{}}{\mathit{\omega }}n\stackrel{}{}\times \\ \stackrel{}{}\stackrel{}{}\stackrel{}{}\left[(1-\mathit{\epsilon }-n^2)J_l(q\mathit{\rho })+\frac{k}{{\mathit{\beta }}^2}\left({\frac{k}{n}}^2(n^2-\mathit{\epsilon })\frac{{\mathit{\omega }}_{\mathit{\alpha }}^2-{\mathit{\omega }}_{c\mathit{\alpha }}^2}{{\mathit{\Omega }}_{\mathit{\alpha }}^2}\frac{\mathit{\omega }}{{\mathit{\omega }}_c}+\frac{{\mathit{\omega }}_{c\mathit{\alpha }}}{\mathit{\omega }}\right)J_l^{\prime }(q\mathit{\rho })\right]J_l^{\prime }(q\mathit{\rho }),\end{array}$$

(29)

Figures 4 and 5 show the dispersion relations for H wave and E waves in a waveguide filled with magnetized, cold plasma for different numbers (ℓ, m = 0, 1, 2, 3,…), while Fig. 6 shows the power flux flow for H wave, E wave and a comparison with unmagnetized cold plasma.

Fig. 4

Dispersion relation for H wave in magnetized, cold plasma

Fig. 5

Dispersion relation for E wave in magnetized, cold plasma

Fig. 6

Power flux flow a for H wave (pink line) in magnetized, cold plasma, b for E wave (blue line) in magnetized, cold plasma, c for E wave (blue line) in magnetized, and unmagnetized (red line) cold plasma

Homogeneous warm unmagnetized plasma

When considering a waveguide filled with a warm unmagnetized plasma, the average power flux ${\overrightarrow{s}}_H$ for the H wave is given by:

$${\overrightarrow{s}}_H=\frac{c}{8\mathit{\pi }}\frac{1}{{\mathit{\beta }}^2}{H}_{\circ }^2\mathit{\epsilon }\left[\left(\frac{l^2}{{\mathit{\rho }}^2}-1\right)k+\frac{l}{\mathit{\rho }}\right]J_l^2(Q\mathit{\rho }),$$

(30)

while for the E wave, ${\overrightarrow{S}}_E$ is given by

$${\overrightarrow{S}}_E=\frac{c^2}{8\mathit{\pi }}{E}_0^2\frac{1}{\mathit{\omega }}\left[J_l(\mathit{\rho }q)J_l^{\prime }(\mathit{\rho }q)+\frac{l}{\mathit{\rho }}{J}_l^2(\mathit{\rho }q)-\frac{k^2}{{\mathit{\beta }}^4}{(\mathit{\epsilon }-n^2)}^2{J}_l^{{}^{\prime }2}(\mathit{\rho }q)+\frac{l^2}{{\mathit{\rho }}^2}\frac{k}{{\mathit{\beta }}^2}(\mathit{\epsilon }-n^2)J_l^2(\mathit{\rho }q)\right],$$

(31)

Figures 7 and 8 show the dispersion relations for H wave and E waves in a waveguide filled with unmagnetized, warm plasma for different numbers (ℓ, m = 0, 1, 2, 3, …..), while Fig. 9 shows the power flux flow for H wave, E wave and a comparison with unmagnetized cold plasma.

Fig. 7

Dispersion relation for H wave in unmagnetized, warm plasma

Fig. 8

Dispersion relation for E wave in unmagnetized, warm plasma

Fig. 9

Power flux flow a for H wave (pink line) in un-magnetized, warm plasma, b for E wave (red line) in un-magnetized, warm plasma, c for E wave in un-magnetized cold (blue line), and warm (red line) plasmas

Inhomogeneous cold unmagnetized plasma

We consider plasma inhomogeneity along the waveguide axis. Starting from the equations of motion and continuity equations for inhomogeneous cold unmagnetized plasma, we obtain the following solutions for H and E waves:

H wave

$$E_{\mathit{\rho }}=-\frac{c}{\mathit{\omega }}\frac{1}{\mathit{\epsilon }-n^2}\frac{l}{\mathit{\rho }}{H}_{\circ }{J}_l(Q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)}$$

$$E_{\mathit{\phi }}=i\frac{c}{\mathit{\omega }}\frac{1}{\mathit{\epsilon }-n^2}H{}_{\circ }(\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}+\frac{1}{\mathit{\rho }})J_l(Q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)}$$

$$H_{\mathit{\rho }}=n{E}_{\mathit{\phi }}$$

$$H_{\mathit{\phi }}=n{E}_{\mathit{\rho }}$$

E wave

$$E_{\mathit{\rho }}=i\frac{c}{\mathit{\omega }}\frac{1}{\mathit{\epsilon }-n^2}\frac{1}{n\mathit{\rho }}{E}_0\left(\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\rho }}\mathit{\rho }\right)J_l(q\mathit{\rho })e^{i(kz+l\mathit{\phi }-\mathit{\omega }t)}$$

$$ E_{\varphi } = \frac{c}{\omega }\frac{1}{{\varepsilon - n^{2} }}\frac{nl}{\rho }E_{0} \left( {\frac{\partial }{\partial \rho }\rho } \right)J_{l} (q\rho )e^{i(kz + l\varphi - \omega t)} $$

$$H_{\mathit{\rho }}=-\frac{\mathit{\epsilon }}{n}{E}_{\mathit{\phi }}$$

$$H_{\mathit{\phi }}=-\mathit{\epsilon }n{E}_{\mathit{\rho }}$$

Using Poynting formula, the average power flux ${\overrightarrow{s}}_H$ for the H wave is given by:

$${\overrightarrow{S}}_H=\frac{c}{8\mathit{\pi }}\frac{c^2}{{\mathit{\omega }}^2}\frac{1}{{(\mathit{\epsilon }-n^2)}^2}{H}_0^2\left[J_l^2(\mathit{\rho }Q)-n{\left(\frac{l}{\mathit{\rho }}\right)}^2{J}_l^2(\mathit{\rho }Q)-\frac{2}{\mathit{\rho }}{J}_l(\mathit{\rho }Q)J_l^{\prime }(\mathit{\rho }Q)-\frac{1}{{\mathit{\rho }}^2}{J}_l^2(\mathit{\rho }Q)\right],$$

(32)

while for the E wave, ${\overrightarrow{S}}_E$ is given by

$${\overrightarrow{S}}_E=\frac{1}{8\mathit{\pi }}\frac{c^2}{\mathit{\omega }}\frac{1}{{(\mathit{\epsilon }-n^2)}^2}{E}_0^2\mathit{\epsilon }\left[\frac{1}{n}{J}_l^{{}^{\prime }2}(\mathit{\rho }q)+l^{2}n{J}_l^{{}^{\prime }2}(\mathit{\rho }q)-\frac{1}{\mathit{\epsilon }-n^2}l{J}_l^2(\mathit{\rho }q)\right],$$

(33)

Figures 10 and 11 show the dispersion relations for H wave and E waves in a waveguide filled with an inhomogeneous unmagnetized, cold plasma for different numbers (l, m = 0, 1, 2, 3, …), while Fig. 12 shows the power flux flow for H wave, E wave and a comparison with unmagnetized cold plasma.

Fig. 10

Dispersion relation for H wave in an inhomogeneous plasma

Fig. 11

Dispersion relation for E wave in an inhomogeneous plasma

Fig. 12

Power flux flow a for H-Wave (pink line) in an inhomogeneous plasma, b for E-Wave (light blue line) in an inhomogeneous plasma, c for E-Wave in an inhomogeneous (dark blue line) and homogeneous (red line) plasmas

Collisional plasma

In the previous section, collisions have been neglected. Let us now consider the case when electrons collision frequency is small compared to field frequency, i.e., ν _e  < < ω.

Accordingly, we can rewrite the plasma dielectric tensor as:

$${\mathit{\epsilon }}_p=1-{\left(\frac{{\mathit{\Omega }}_p}{\mathit{\omega }}\right)}^2\left(1-i\frac{{\mathit{\nu }}_e}{\mathit{\omega }}\right),$$

Using (29) and (30) we can write the refractive index in the form:

$$n=n_{\text{real}}+i{n}_{\text{imag}},$$

$$n_{\text{real}}=\sqrt{1-{\left(\frac{{\mathit{\omega }}_{cr}^{(p)}}{\mathit{\omega }}\right)}^2},$$

(34)

$$k_i=\frac{\mathit{\omega }}{c}{n}_{\text{imag}}=\frac{1}{2}\frac{\mathit{\omega }}{c}\frac{1}{n_{\text{real}}}\left(\frac{{\mathit{\nu }}_e}{\mathit{\omega }}\right){\left(\frac{{\mathit{\Omega }}_p}{\mathit{\omega }}\right)}^2.$$

(35)

From (35) it is clear that the wave number k _i has a complex form. The presence of the imaginary part leads to the damping of the wave, and accordingly the average rate of energy flow in the filled waveguide decreases exponentially as e^−ξ·z, where the attenuation coefficient is given by:

$$\mathit{\zeta }=\frac{v_e}{c}\frac{1}{n_{\text{real}}}{\left(\frac{{\mathit{\Omega }}_p}{\mathit{\omega }}\right)}^2,$$

(36)

We should mention here that high field attenuation occurs when: (1) the plasma is sufficiently dense or (2) plasma is strongly collisional.

Excitation of waves by a relativistic cold electron beam

In the previous sections, we could get the spectra of E and H waves propagating in a waveguide filled with warm plasma or cold plasma placed in a static magnetic field. We now consider the problem of the excitation of these waves by a relativistic electron beam. The calculation will be simpler for the case of unmagnetized plasma.

A cold electron beam passing along the axis of a plasma waveguide will interact strongly with a plasma wave and excite it. This interaction takes place under the resonance (Cherenkov) condition, such that the longitudinal phase velocity of the wave equals to the beam velocity, i.e., under the condition ω = kV_0b, which is necessary but not sufficient for wave excitation. In addition to this condition, the existence of fields which are growing in amplitude requires certain limits to be imposed on the plasma and the beam parameters. These limits (conditions) could be obtained from the dispersion equation which describes the beam–plasma system.

In our case, it is convenient to consider that the beam density n _b is much smaller than the electron plasma density n _P (i.e., n _b  < < n _p ). This assumption enables us to continue considering small oscillations and applying the linear approximation.

We shall discuss here the case of waveguide filled with a warm, homogeneous unmagnetized plasma. The summations over α include both the plasma and beam electrons. As we consider a case of high-frequency waves, the oscillations of the ions are neglected.

From Eq. (7) we have the following expressions for the warm plasma and the cold beam:

$$\begin{array}{c}{a}_P=1(V_{0P}=0);a_b=1-n{\mathit{\beta }}_0\left({\mathit{\beta }}_0=\frac{V_{0b}}{c}\right)\\ b_P=1-W_T^2\left(W_T^2=\frac{3k^2{V}_{T_e}^2}{{\mathit{\omega }}^2}\right),b_b=1(\text{cold}\text{beam})\\ {\mathit{\Delta }}_P=1,{\mathit{\Delta }}_b=\mathit{\gamma }(1-n{\mathit{\beta }}_0)=\mathit{\gamma }{a}_b,{\tilde{\mathit{\Delta }}}_P=1,{\tilde{\mathit{\Delta }}}_b={\mathit{\gamma }}^3{a}_b,\end{array}$$

$$\mathit{\gamma }=\frac{1}{\sqrt{1-{\mathit{\beta }}_0^2}},$$

(37)

and the dielectric components read now as:

$$\begin{array}{c}{\mathit{\epsilon }}_1={\mathit{\epsilon }}_P-\frac{W_b^2}{\mathit{\gamma }},\left(W_b^2=\frac{{\mathit{\Omega }}_b^2}{{\mathit{\omega }}^2},{\mathit{\Omega }}_b=\sqrt{\frac{4\mathit{\pi }{e}^2{n}_{0b}}{m_e}}\right)\\ {\mathit{\epsilon }}_2={\mathit{\epsilon }}_P-\frac{W_b^2}{{\mathit{\Delta }}_b},{\mathit{\epsilon }}_3={\mathit{\epsilon }}_P-W_P^2{W}_T^2-\frac{W_b^2}{{\mathit{\gamma }}^3{a}_b^2}=1-\frac{W_P^2}{1-W_T^2}-\frac{W_b^2}{{\mathit{\gamma }}^3{a}_b^2},W_T^2<<1.\end{array}$$

(38)

H wave

Taking into account the beam contribution in the dispersion relation (21), we get:

$$n^2=1-{\left(\frac{{\mathit{\Omega }}_p}{\mathit{\omega }}\right)}^2-\frac{1}{\mathit{\gamma }}{\left(\frac{{\mathit{\Omega }}_b}{\mathit{\omega }}\right)}^2-{\left(\frac{c{\mathit{\chi }}_{l,m}}{\mathit{\omega }{\mathit{\rho }}_{\circ }}\right)}^2,$$

(39)

In zero approximation, i.e., in case of no beam, we obtain the following expression for the phase velocity:

$$V_{ph.}=\frac{c}{\sqrt{1-{\left(\frac{{\mathit{\omega }}_{cr}^P}{\mathit{\omega }}\right)}^2}}>c.$$

(40)

Relations (39) and (40) show that the phase velocity of H waves always exceeds the velocity of light, i.e., the Cherenkov condition cannot be fulfilled.

Therefore, the relativistic electron beam will not be able to interact with the wave modes H _l,m . These modes are always attenuated by the collisional effect.

E- Wave

The corresponding dispersion relation will have the form:

$${\left(\frac{c}{\mathit{\omega }}\frac{{\mathit{\chi }}_{l,m}^{{}^{\prime }}}{{\mathit{\rho }}_0}\right)}^2[(n_{}^2-{\mathit{\epsilon }}_1){\mathit{\epsilon }}_3+{\mathit{\epsilon }}_2^2]=n^2({\mathit{\epsilon }}_1-n^2){\mathit{\epsilon }}_4,$$

(41)

Here, the dielectrics ɛ₁, ɛ₂, ɛ₃ read as:

$$\begin{array}{c}{\mathit{\epsilon }}_1-{\mathit{\epsilon }}_P=-\frac{1}{\mathit{\gamma }}\frac{{\mathit{\Omega }}_b^2}{{\mathit{\omega }}^2}\\ {\mathit{\epsilon }}_2-{\mathit{\epsilon }}_P=\frac{1}{1-n{\mathit{\beta }}_0}({\mathit{\epsilon }}_1-{\mathit{\epsilon }}_P)\\ {\mathit{\epsilon }}_3-{\mathit{\epsilon }}_P=\frac{1}{{\left(1-n{\mathit{\beta }}_0\right)}^2}({\mathit{\epsilon }}_1-{\mathit{\epsilon }}_P)\\ {\mathit{\epsilon }}_4-{\mathit{\epsilon }}_P=\frac{1}{{\left[\mathit{\gamma }\left(1-n{\mathit{\beta }}_0\right)\right]}^2}({\mathit{\epsilon }}_1-{\mathit{\epsilon }}_P),\end{array}$$

In the absence of electron beamΩ _b  = 0, as for the case of H wave, we find the threshold frequency by setting in (41) Ω _b  = 0, and with n = n ₀ we get:

$$\left(1-\frac{W_P^2}{1-W_T^2}\right)(n_0^2-{\mathit{\epsilon }}_P)+{\mathit{\epsilon }}_P{\left(\frac{c}{\mathit{\omega }}\frac{{\mathit{\chi }}_{l.m}^{{}^{\prime }}}{{\mathit{\rho }}_0}\right)}^2=0.$$

(42)

It is easy to check that the refractive index is given by:

$$n_0=\frac{k_{0}c}{\mathit{\omega }}=\sqrt{{\mathit{\epsilon }}_P-{\left(\frac{c}{\mathit{\omega }}\frac{{\mathit{\chi }}_{l.m}^{{}^{\prime }}}{{\mathit{\rho }}_0}\right)}^2},$$

(43)

while for the relation between natural plasma frequency Ω _P and E wave, an oscillation frequency ω is given by:

$$\mathit{\omega }=\sqrt{{(k_{0}c)}^2+{\mathit{\Omega }}_p^2+{\left(\frac{c}{\mathit{\omega }}\frac{{\mathit{\chi }}_{l.m}^{{}^{\prime }}}{{\mathit{\rho }}_0}\right)}^2}.$$

(44)

In the presence of electron beam, Ω _b  ≠ 0, E wave and H wave coupling modes exist and the electron beam changes the refractive index n_∘ by a small addition:

$$n=n_{\circ }+\mathit{\delta }n;\mathit{\delta }n<<n_{\circ }$$

with δn representing the growth of the excited E wave in the presence of REB.

The dispersion relation (35) reads:

$$2n_0{\mathit{\epsilon }}_P\mathit{\delta }n-\frac{{\mathit{\Omega }}_b^2{\mathit{\Omega }}_P^2}{{\mathit{\omega }}^4}\frac{{\mathit{\beta }}_0^2}{\mathit{\gamma }{\left(1-n_0{\mathit{\beta }}_0\right)}^2}{\left(\frac{c{x}_{l,m}^{\prime }}{\mathit{\omega }{\mathit{\rho }}_0}\right)}^3=0$$

(45)

At resonance, δn = 1 − n_∘β_∘ = (δn)_real + i(δn)_imag, (45) reads:

$$\mathit{\delta }n=\sqrt[3]{1}·\left(\frac{c{\mathit{\chi }}_{l,m}^{\prime }}{{\mathit{\rho }}_{\circ }\mathit{\omega }}\right){\left(\frac{{\mathit{\Omega }}_b^2{\mathit{\Omega }}_p^2}{2\mathit{\gamma }{\mathit{\epsilon }}_p{\mathit{\omega }}^4}\right)}^{1/3}{\mathit{\beta }}_{\circ }$$

(46)

Since

$$\sqrt[3]{1}=1-\frac{-1\pm i\sqrt{3}}{2},$$

it follows from (45), and under the condition (δn)_imag < 0, the wave number (δn)_real corresponding to (46) is given by:

$$k_i^{{}^{\prime }}=k_{\circ }-\frac{\sqrt{3}}{2}\frac{\mathit{\omega }}{c}{\left(\frac{{\mathit{\Omega }}_b^2{\mathit{\Omega }}_p^2}{2\mathit{\gamma }{\mathit{\epsilon }}_p{\mathit{\omega }}^4}{\left(\frac{c{\mathit{\chi }}_{l,m}^{\prime }}{{\mathit{\rho }}_{\circ }\mathit{\omega }}\right)}^2\right)}^{1/3}.$$

(47)

Equating (47) and (35), i.e., k _i  = k ^′ _i , we get the following condition for the stability of the propagating E wave through the waveguide filled with plasma:

$$\frac{k_{\circ }c}{\mathit{\omega }}=\frac{\sqrt{3}}{2}{\left(\frac{{\mathit{\Omega }}_b^2{\mathit{\Omega }}_p^2}{2{\mathit{\epsilon }}_p{\mathit{\omega }}^4}{(\frac{c{\mathit{\chi }}_{l,m}^{\prime }}{{\mathit{\rho }}_{\circ }\mathit{\omega }})}^2\frac{1}{\mathit{\gamma }}\right)}^{1/3}+\frac{1}{2n_{real}}\left(\frac{{\mathit{\nu }}_e}{\mathit{\omega }}\right){\left(\frac{{\mathit{\Omega }}_p}{\mathit{\omega }}\right)}^2,$$

(48)

Let us now investigate two cases:

• 1. Cold plasma

In this case W _T  = 0, and equation (42) reduces to

$${\mathit{\epsilon }}_P\left[n_0^2-{\mathit{\epsilon }}_P+{\left(\frac{c{\mathit{\chi }}_{l,m}}{\mathit{\omega }}\right)}^2\right]=0,$$

(49)

Accordingly, we have two types of waves with frequencies:

$$\mathit{\omega }={\mathit{\Omega }}_P,$$

(50-a)

which represents the plasma oscillations, and

$$\mathit{\omega }={[{\mathit{\Omega }}_P^2+(k_0^2+{\mathit{\chi }}_{l,m}^2)c^2]}^{1/2}={\mathit{\omega }}_{\text{cold}},$$

(50-b)

which represents the electromagnetic modes included in the dispersion relation (41).

When Ω _b  ≠ 0, and for cold plasma, by setting relation (45) into the dispersion relation (41), we can derive the following expression for δn:

$$\mathit{\delta }n={\left[\frac{W_b^2{W}_{P_{}}^2}{2{\mathit{\epsilon }}_P}{\left(\frac{c{\mathit{\chi }}_{l,m}}{\mathit{\omega }}\right)}^2\frac{1}{\mathit{\gamma }}\right]}^{1/3}{\mathit{\beta }}_0,$$

(51)

To derive (51) we considered the resonance case when From (51) with combination of (41), the axial wave number gets the form:

$$k=k_0-i\frac{\sqrt{3}}{2}\frac{\mathit{\omega }}{c}{\left[\frac{W_b^2{W}_{P_{}}^2}{2{\mathit{\epsilon }}_P}{\left(\frac{c{\mathit{\chi }}_{l,m}}{\mathit{\omega }}\right)}^2\frac{1}{\mathit{\gamma }}\right]}^{1/3}.$$

(52)

and the condition for the E wave stabilization reads:

$$\frac{\mathit{\nu }}{\mathit{\omega }}=\sqrt{3}{\mathit{\beta }}_0{\left[{\left(\frac{c{\mathit{\chi }}_{l,m}}{\mathit{\omega }}\right)}^2\frac{W_b^2}{{\mathit{\epsilon }}_P{W}_{P_{}}^4}\right]}^{1/3}{\left[{\mathit{\epsilon }}_P-{\left(\frac{c{\mathit{\chi }}_{l,m}}{\mathit{\omega }}\right)}^2\right]}^{1/2}.$$

(53)

In this case the imaginary part of k (due to collisions) which is presented by Eq. (52) compensates that due to beam excitation.

• 2. Warm plasmaInstead of Eq. (43), the E wave frequency is now given by:

$$\mathit{\omega }={\mathit{\omega }}_{\text{warm}}={\left(\frac{1}{2}\sqrt{{\mathit{\omega }}_{\text{cold}}^2+\sqrt{{\mathit{\omega }}_{\text{cold}}^4-4{\mathit{\Omega }}_T^2{\mathit{\chi }}_{l,m}^2{c}^2}}\right)}^{1/2},$$

(54)

where ω_cold is given by relation (50-b) and Ω _P  > > Ω _T , Ω _T  = ωW _T .

When Ω _b  ≠ 0, we get, from (41), the following expression for the growth rate of E waves in warm plasma in the presence of the REB:

$$\mathit{\delta }n={\left[\frac{W_b^2{W}_{P_{}}^2}{2{\mathit{\epsilon }}_P{\mathit{\epsilon }}_T}{\left(\frac{c{\mathit{\chi }}_{l,m}}{\mathit{\omega }}\right)}^2\frac{1}{\mathit{\gamma }}\right]}^{1/3}{\mathit{\beta }}_0,$$

(55)

with ɛ _T  = 1 − W ² _T .

On comparing (51) and (55), we get

$$\frac{{(\mathit{\delta }n)}_{\text{cold}}}{{(\mathit{\delta }n)}_{\text{warm}}}\approx {({\mathit{\epsilon }}_T)}^{1/3}<1.$$

(56)

The axial wave number will have the same form as (52), but with ε _P ε _T in the denominator instead of ε _P .

The condition for E wave stabilization in a waveguide filled with warm plasma is given by

$$ \left( {\frac{\nu }{\omega }} \right)_{\text{warm}} = \varepsilon_{T}^{ - 1/3} \left( {\frac{\nu }{\omega }} \right)_{\text{cold}} . $$

(57)

Relation (57) shows that the E wave is more stable in warm plasma.

Results and conclusions

This work is mainly devoted to conserve the field stability using an REB. We demonstrated the case of electromagnetic wave propagation and excitation in a cylindrical waveguide filled with warm (magnetized/non magnetized) plasma. Dispersion relations in ω describing different physical situations that govern the mode propagation in the waveguide are obtained ((21), (23), (35), (41) and (43)). In addition, an attempt is made to examine the effect of density inhomogeneity on the energy gain acquired by the relativistic electron beam bunching when it is injected in the waveguide along the direction of mode propagation.

The expressions for currents, dielectric tensor and electromagnetic field components are obtained. Two modes of waves are found, E and H waves, and the corresponding dispersion equation of each type are derived and solved.

In case of waveguide filled with unmagnetized warm nonmoving plasma, the two wave modes have different dispersion relations, which agree for the thermal parameter Ω _T  → 0. The spectrum of each mode is obtained and compared with that for the empty waveguide (relations (18)–(20)). The case of magneto-active moving plasma will be investigated in due course.

In case of collisionless plasma, it is found that the cutoff frequency for a given mode ω ^(P) _cr differs from that for an empty waveguide ω ⁽⁰⁾ _cr . This difference is a measure of the phase shift and could be used via plasma diagnostics to determine the plasma density inside the waveguide. It is also found that, for a given frequency, the average rate of energy flow in plasma-filled waveguide is smaller than that of an empty waveguide. This lets us suggest that the power could be increased through the waveguide by avoiding the formation of a plasma in the waveguide by operating it with increased air pressure (or vacuum). Generally speaking, to obtain a high power transition in a waveguide, the formation of a plasma should be avoided, not only because the propagation of energy is hindered by the plasma, but also by the large absorption by collisional damping, especially in a waveguide filled with high-pressure gases (plasmas).

When we reconsider the collisions in the plasma, the average rate of energy flow in the waveguide is decreased exponentially with attenuation factor proportional to the collision frequency ν. High attenuation occurs when the plasma is sufficiently dense to attenuate the field, but not yet dense enough to exclude it.

Wave propagation in waveguide filled with magnetized, cold, nonmoving homogeneous plasma is also studied. We obtained analytical expressions for wave modes, their dispersion relations, cutoff frequencies, and average power fluxes in rarefied weakly magnetized plasma.

The effect of a relativistic electron beam on the wave propagation in plasma-filled waveguide is also investigated. It is found that the phase velocity of the H wave always exceeds the velocity of light and, due to the Cerenkov condition, the REB will not be able to interact with the H wave. These waves are always attenuated by collisions.

The growth of the excited E wave is calculated in the resonance case, and the stability condition for the E wave is obtained. E waves are found to be more stable in warm plasma compared to cold plasma.

The dispersion relation (41) for unmagnetized, collisionless, cold plasma has been reduced to the results similarly obtained in earlier works [18]. The results obtained here are also in agreement with special cases of unmagnetized warm plasm [19] by same author (IEEE Transactions on Plasma Science, 1(1983)PS-11).

Recently, waveguides filled with plasma represent a great interest through reconfigurable plasma antenna [20], propagation of high-power microwave and its interaction with a plasma in a metallic waveguide [21], and waveguide resonators with combined Bragg reflectors [22].

The results obtained are of great interest and may be used to analyze how the plasma affects the electromagnetic properties of the cavity of the 1–2 MW 140–170 GHz continuous-wave gyrotron (for W7-X stellarator and ITER) [23–25], for MW gyrotron development for fusion plasma applications [26] and second harmonic generation in a plasma-filled parallel plane waveguide [27].

Parallel works on dispersion characteristics of the cylindrical waveguide filled by magnetoactive plasma [28] have been considered for different conditions from ours (i.e., cold, collisionless, symmetric plasma). The authors have also not considered minimizing the energy losses in the waveguide.