Theoretical analysis of a thermal plasma-loaded relativistic traveling wave tube having corrugated slow wave structure with solid electron beam

Abstract

A relativistic traveling wave tube with thermal plasma-filled corrugated waveguide is driven by a finite solid electron beam with the entire system immersed in a strong longitudinal magnetic field that magnetized plasma and electron beam. The dispersion relation for the relativistic traveling wave tube is obtained by linear fluid theory. The numerical results show that the growth rate decreases by increasing plasma temperature, waveguide radius, plasma density and electron beam energy. As show in this paper the effect of electron beam density and corrugation period is to increase growth rate.

Introduction

Relativistic traveling wave tube (RTWT) is an important high-power microwave (HPM) apparatus which has been developed in the past 20 years [1–3]. Most of the TWT mathematical analysis has been done by John Robinson Pierce and his colleagues at Bell Labs [4–6] and then have been developed by Chu, Jackson and Freund [7–9]. In TWT, sinusoidal corrugated slow wave structure (SWS) is used to reduce the phase velocity of the electromagnetic wave to synchronize it with the electron beam velocity, so that a strong interaction between the two can take place [10, 11]. TWT is extensively applied in satellite and airborne communications, radar, particle accelerators, cyclotron resonance and electronic warfare system. The plasma injection to TWT has been studied recently which can increase the growth rate and improve the quality of transmission of electron beam. We investigate the effect of thermal plasma and electron beam on the growth rate [12–17].

In this paper, RTWT with magnetized thermal plasma-filled corrugated waveguide with solid electron beam is studied. The dispersion relation of corrugated waveguide is derived from a solution of the field equations. By numerical computation, the dispersion characteristics of RTWT are analyzed in detail with different cases of various geometric parameters of slow wave structure.

In “Physical model”, the physical model of RTWT filled with thermal plasma is established in an infinite longitudinal magnetic field. In “Dispersion equation”, the dispersion relation of RTWT is derived. In “Numerical result and discussion”, the dispersion characteristics of the RTWT are analyzed by numerical computation.

Physical model

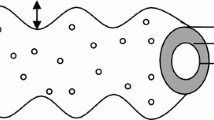
The analysis presented in this paper is based on the SWS shown in Fig. 1. The SWS is a sinusoidal cylindrical waveguide that consists of an axially symmetric.

$$ R\left( z \right) = R_{0} + h\;\cos (\kappa_{0} {\text{z}}), $$

(1)

$$ K_{n} = k_{z} + n\kappa_{0} , $$

(2)

$$ \kappa_{0} = \frac{2\pi }{{z_{0} }}, $$

(3)

Fig. 1

Slow wave structure model of a plasma-filled relativistic traveling wave tube

Cylindrical waveguide, whose wall radius $R\left( z \right),$ varies sinusoidal according to the relation (1), h is the corrugation amplitude, $\kappa_{0} = 2\pi /z_{0}$ is the corrugation wave number, and $z_{0}$ is the length of the corrugation period, $R_{0 }$ is the waveguide radius and $k_{z}$ is the axial number wave.

A finite solid relativistic electron beam with density $n_{\text{b}}$ and radius $R_{\text{b}}$ goes through the cylindrical waveguide, which is loaded completely with thermal, uniform and collisionless plasma of density $n_{\text{p}}$. The entire system is immersed in a strong, longitudinal magnetic field, which magnetizes both the beam and the plasma. Because of being anisotropic of dielectric constant it will be a tensor. In the beam-plasma case in a linearized scheme, the dielectric tensor in cylindrical coordinates may be given by:

$$ \left[ \varepsilon \right] = \varepsilon_{0} \left[ {\begin{array}{*{20}c} {\varepsilon_{1} } & {\varepsilon_{2} } & 0 \\ { - \varepsilon_{2} } & {\varepsilon_{1} } & 0 \\ 0 & 0 & {\varepsilon_{3} } \\ \end{array} } \right], $$

(4)

We assume that $B_{0}$ is very strong that $\varepsilon_{1} = 1$ and $\left| {\varepsilon_{2} } \right|$ is negligibly small.

$$ \left[ \varepsilon \right] = \varepsilon_{0} \times \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} v} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{p}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \\ \end{array} } \right], $$

(5)

$$ \varepsilon_{3} = 1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} {\text{v}}} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2 } }} $$

(6)

Here, $\omega_{\text{p}} = ( \frac{{n_{\text{p}} e^{2} }}{{m\varepsilon_{0} }})^{1/2}$ is the plasma frequency, $\omega_{\text{b}} = ( \frac{{n_{\text{b}} e^{2} }}{{m\varepsilon_{0} }})^{1/2}$ is the beam frequency, $\omega$ is the angular frequency of the electromagnetic wave, $\gamma$ is the electron beam energy, $v_{{{\text{th}}_{\text{p}} }} = \sqrt {\frac{{KT_{\text{p}} }}{m}}$ is the thermal velocity of the plasma, $v_{{{\text{th}}_{\text{b}} }} = \sqrt {\frac{{KT_{\text{b}} }}{m}}$ is the thermal velocity of the beam, $v$ is the velocity of the beam, $T_{\text{b}}$ is the beam temperature, $T_{\text{p}}$ is the plasma temperature and $K$ is the Boltzmann constant.

Dispersion equation

In the above physical model, its Maxwell equations can be written as:

$$ \nabla \times B \, = \,\frac{ - i\omega }{c} \varepsilon .E, $$

(7)

$$ \nabla \times E \, = \,\frac{ i\omega }{c} B, $$

(8)

$$ \nabla \;\cdot\;B = 0, $$

(9)

$$ \nabla \;\cdot\;D = 0. $$

(10)

Suppose that every variable can be regarded as:

$$ A = A{\text{e}}^{{i(K_{n} z - \omega t)}} . $$

(11)

From Eqs. (7) and (8), we can obtain:

$$ \nabla \nabla \;\cdot\;E - \nabla^{2} E = \,\frac{{\omega^{2} }}{{c^{2} }} \varepsilon \cdot\;E $$

(12)

$$ \nabla^{2} E_{z} - [\nabla \left( {\nabla \;\cdot\;E} \right)]_{z} + \frac{{\omega^{2} }}{{c^{2} }}\varepsilon_{3} E_{z} = 0, $$

(13)

Now Substituting Eq. (6) into Eq. (13), we have:

$$ \nabla^{2} E_{z} - [\nabla \left( {\nabla \;\cdot\;E} \right)]_{z} + \frac{{\omega^{2} }}{{c^{2} }}\left( {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} v} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right)E_{z} = 0 $$

(14)

From Eq. (10), we have:

$$ \nabla \cdot\varepsilon_{3} E_{z} = 0 . $$

(15)

Substituting Eq. (6) into Eq. (15), we obtain:

$$ \nabla \cdot E_{z} = \frac{\partial }{\partial z}E_{z} \left[ {\frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} v} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} + \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right]. $$

(16)

From Eqs. (13) and (16), the wave equation is obtained in the area of plasma beam as follows:

$$ \left[ {\nabla_{ \bot }^{2} + \left( {\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} } \right)\times\left( {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} } \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right)} \right]E_{z } , $$

(17)

$$ \nabla_{ \bot }^{2} = \nabla^{2} - \frac{{\partial^{2} }}{{\partial z^{2 } }}. $$

(18)

$$ E_{z} \left( {r,z} \right) = E_{zn} \left( r \right){\text{e}}^{{i\left( {K_{n} z - \omega t} \right)}} , $$

(19)

$$ E_{r} \left( {r,z} \right) = \frac{{iK_{n} }}{{\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} }}{\text{e}}^{{i(K_{n} z - \omega t)}} \frac{{{\text{d}}E_{zn} }}{{{\text{d}}r}} . $$

(20)

We investigate a ground state (n = 0) to solve the equation. With substituting Eq. (19) into Eq. (17), we have:

$$ E_{zn} = \left\{ {\begin{array}{*{20}l} {A_{0} J_{0} \left( {T_{1} r} \right)} \hfill & {\quad 0 \le r \le R_{\text{b}} ;} \hfill \\ {B_{0} J_{0} \left( {T_{2} r} \right) + C_{0} N_{0} \left( {T_{2} r} \right) } \hfill & {\quad R_{{{\text{b}} }} \le r \le R\left( z \right);} \hfill \\ \end{array} } \right. $$

(21)

$$ T_{1}^{2} = \left( {\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} } \right)\times\left( {1 - \frac{{\omega_{\text{b}}^{2} }}{{\gamma^{3} \left( {\omega - K_{n} {\text{v}}} \right)^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{b}} }}^{2} }} - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right), $$

(22)

$$ T_{2}^{2} = \left( {\frac{{\omega^{2} }}{{c^{2} }} - K_{n}^{2} } \right)\left( {1 - \frac{{\omega_{\text{p}}^{2} }}{{\omega^{2} - 3K_{n}^{2} v_{{{\text{th}}_{\text{p}} }}^{2} }}} \right). $$

(23)

The field components must satisfy the following continuity equations (first boundary condition):

$$ E_{z} \left( {r = R_{{{\text{b}} }}^{ - } } \right) = E_{z} \left( {r = R_{{{\text{b}} }}^{ + } } \right), $$

(24)

$$ E_{r} \left( {r = R_{{{\text{b}} }}^{ - } } \right) = E_{r} (r = R_{{{\text{b}} }}^{ + } ). $$

(25)

As a result, the field components are obtained as follows:

$$ B_{0} = - \frac{\pi }{2}R_{{{\text{b}} }} s_{0} A_{0} , $$

(26)

$$ C_{0} = - \frac{\pi }{2}R_{{{\text{b}} }} l_{0} A_{0} , $$

(27)

where

$$ s_{0} = T_{2} J_{0} ({T_{1} R_{\rm b}})N_{1} ({T_{2} R_{\rm b}}) - T_{1} J_{1} ({T_{1} R_{\rm b}}) N_{0} ({T_{2} R_{\rm b}}), $$

(28)

$$ l_{0} = T_{1} J_{0} ({T_{2} R_{\rm b}})J_{1} ({T_{1} R_{\rm b}}) - T_{2} J_{0} ({T_{1} R_{\rm b}})J_{1} ({T_{2} R_{\rm b}}). $$

(29)

At the perfectly conducting corrugated waveguide surface (Second boundary condition), the tangential electric field must be zero,

$$ E_{z} \left( {r = R\left( z \right)} \right) + E_{r} \left( {r = R\left( z \right)} \right)\frac{{{\text{d}}R\left( z \right)}}{{{\text{d}}z}} = 0 . $$

(30)

With substituting Eqs. (19), (20) and (21) into Eq. (30), we investigate second boundary condition in ground state (n = 0) to achieve the dispersion equation.

$$ B_{0} J_{0} \left( {T_{2} R\left( z \right)} \right) + C_{0} N_{0} \left( {T_{2} R\left( z \right)} \right){\text{e}}^{{i\left( {K_{0} z - \omega t} \right)}} + \frac{{iK_{0} }}{{\frac{{\omega^{2} }}{{c^{2} }} - K_{0}^{2} }}{\text{e}}^{{i\left( {K_{0} z - \omega t} \right)}} \times \frac{\text{d}}{{{\text{d}}R\left( z \right)}}\left[ {B_{0} J_{0} \left( {T_{2} R\left( z \right)} \right) + C_{0} N_{0} \left( {T_{2} R\left( z \right)} \right){\text{e}}^{{i\left( {K_{0} z - \omega t} \right)}} } \right]\frac{{{\text{d}}R\left( z \right)}}{{{\text{d}}z}} = 0 , $$

(31)

Using the factorization of Eq. (31) and substituting $B_{0}$ and $C_{0}$, we obtain:

$$ - {\text{e}}^{{i\left( {K_{0} z - \omega t} \right)}} \frac{\pi }{2}R_{{{\text{b}} }} A_{0} \left( {1 + \frac{{iK_{0} }}{{\frac{{\omega^{2} }}{{c^{2} }} - K_{0}^{2} }}\frac{\text{d}}{{{\text{d}}z}}} \right) \times \left[ {s_{0} J_{0} \left( {T_{2} R\left( z \right)} \right) + l_{0} N_{0} \left( {T_{2} R\left( z \right)} \right)} \right] = 0 . $$

(32)

$$ D { \cdot }A = D_{n} A_{n} = D_{0} A_{0} = 0 , $$

(33)

“A” is a vector with element $A_{0}$ and “D” is a matrix with element $D_{0}$. With the help of derivative of Bessel functions, the dispersion relation can be obtained as, [18–22]

$$ D_{0} = \left( {1 + \frac{{iK_{0} }}{{\frac{{\omega^{2} }}{{c^{2} }} - K_{0}^{2} }}} \right) \times [T_{2} h\kappa_{0} \left( {s_{0} J_{1} \sin (\kappa_{0} z} \right) + l_{0} N_{1} \sin (\kappa_{0} z))] $$

(34)

Numerical result and discussion

The analysis of the dispersion relation is obtained by Eq. 34. First, we consider the dispersion analysis in the absence of the electron beam.

Figure 2 shows the variation of normalized frequency ${\text{Re }}\left( {\frac{\omega }{{c\kappa_{0} }}} \right)$ versus wave number $\left( { \frac{{k_{z} }}{{\kappa_{0} }}} \right)$ for several values of the corrugation period $\left( {z_{0} } \right)$. As seen in this figure the effect of $z_{0}$ is to increase the frequency.

Fig. 2

Variation of normalized frequency ${\text{Re }}\left( {\frac{\omega }{{ c\kappa_{0} }}} \right)$ with normalized wave number $\left( { \frac{{k_{z} }}{{\kappa_{0} }} } \right)$ for several values of the corrugation period. The chosen parameters are as follows: $n_{\text{p}} = 3 \times 10^{11} , \,\,R_{0} = 1. 60,\,\,h = 0. 7$ and $T_{\text{p}} = 30 \times 10^{8}$

The effect of the plasma temperature on the frequency of the system as a function of $k_{z}$ is shown in Fig. 3. This figure shows that the effect of plasma temperature increases the frequency. This effect is in good agreement with the thermal plasma dispersion relation $\omega^{2} = \omega_{\text{p}}^{2} + 3k_{z}^{2} v_{\text{th}}^{2}$.

Fig. 3

Variation of normalized frequency ${\text{Re}} \left( {\frac{\omega }{{ c\kappa_{0} }} } \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{ \kappa_{0} }}} \right)$ for several values of the plasma temperature. The chosen parameters are as follows: $n_{\text{p}} = 3 \times 10^{11} , R_{0} = { 1}. 60, \, h \, = 0. 7,\,\,R_{\text{b}} = 0.7,\,z = 0.33$ and $z_{0} = 0.66$

The effect of waveguide radius on the frequency of the wave as a function of $k_{z}$ is shown in Fig. 4. As illustrated in this figure, the frequency decreases with increase in the waveguide radius. The phase velocity of the system decreases by increasing the radius. It may be cause to the wave exit from the resonant condition.

Fig. 4

Variation of normalized frequency ${\text{Re }}\left( {\frac{\omega }{{ c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{\kappa_{0} }}} \right)$ for several values of the waveguide radius. The chosen parameters are as follows: $n_{\text{p}} = 3 \times 10^{11} , \;h \, = 0. 7,\,\,R_{\text{b}} = 0.7, z = 0.33, T_{\text{p}} = 30 \times 10^{8}$ and $z_{0} = 0.66$

Variations of the frequency as a function of the wave number for different values of the plasma density are shown in Fig. 5. It is clear that from the Fig. 5, the effect of plasma considerably increases the frequency. This effect is in good agreement with the simple relation of the plasma ($\omega^{2} = \omega_{\text{p}}^{2} + 3k_{z}^{2} v_{\text{th}}^{2}$).

Fig. 5

Variation of normalized frequency ${\text{Re }}\left( {\frac{\omega }{{ c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{ \kappa_{0} }}} \right)$ for several values of the plasma density. The chosen parameters are as follows: $R_{0} = 1.60,\,\,h \, = 0. 7, R_{\text{b}} = 0.7, z = 0.33, \,\,z_{0} = 0.66$ and $T_{\text{p}} = 30 \times 10^{8}$

Now, we consider the analysis of the growth rate in the presence of the electron beam.

It is clear that from Fig. 6, the growth rate increases by increasing the corrugation period. The increase in the corrugation period helps the wave to be included in the resonant condition and finally increases the growth rate.

Fig. 6

Variation of the normalized growth rate $\text{Im} \left( {\frac{\omega }{{c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{ \kappa_{0} }}} \right)$ for several values of the corrugation period. The chosen parameters are as follows: $\gamma = 1.001, h = 0.7, R_{0} = 1.6 , R_{\text{b}} = 0.7,\,\,z = 0.33 , n_{\text{b}} = 10 \times 10^{11} , n_{\text{p}} = 3 \times 10^{11} , T_{\text{p}} = 30 \times 10^{8}$ and $T_{\text{b}} = 20 \times 10^{7}$

It is clear that from Fig. 7, the plasma temperature considerably decreases the growth rate. By increasing the plasma temperature, the electrons exit from the resonant condition and finally decrease the growth rate.

Fig. 7

Variation of the normalized growth rate $\text{Im} \left( {\frac{\omega }{{ c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{\kappa_{0} }}} \right)$ for several values of the plasma temperature. The chosen parameters are as follows: $n_{\text{p}} = 3 \times 10^{11} , h = 0.7 , R_{0} = 1.6 ,\,\,z = 0.33 , \,\,\gamma = 1.001, z_{0} = 0.66, n_{\text{b}} = 10 \times 10^{11}$ and $T_{\text{b}} = 20 \times 10^{7}$

As seen in Fig. 8, the growth rate decreases by increasing the $R_{0}$. The waveguide radius has the important role in the determination of wave phase velocity. According to the Fig. 4, the phase velocity decreases by increasing the radius, and as seen in Fig. 8 the growth rate decreases by increasing the radius. By decreasing the phase velocity the wave exits from resonant condition.

Fig. 8

Variation of the normalized growth rate $\text{Im} \left( {\frac{\omega }{{c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{\kappa_{0} }}} \right)$ for several values of the waveguide radius. The chosen parameters are as follows: $n_{\text{p}} = 3 \times 10^{11} , h = 0.7, \;T_{\text{p}} = 30 \times 10^{8} , R_{\text{b}} = 0.7 , z = 0.33 , \gamma = 1.001 , z_{0} = 0.66, n_{\text{b}} = 10 \times 10^{11}$ and $T_{\text{b}} = 20 \times 10^{7}$

The effect of the plasma density on the growth rate of the system as a function of the wave number is shown in Fig. 9. It is clear that in this frequency range the effect of plasma density is to decrease the growth rate of the system. According to the Fig. 5, the phase velocity increases by increasing the plasma density. By increasing the plasma density the wave exit from the resonant condition and finally the growth rate decreases.

Fig. 9

Variation of the normalized growth rate $\text{Im} \left( {\frac{\omega }{{c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{ \kappa_{0} }}} \right)$ for several values of the plasma density. The chosen parameters are as follows: $R_{0} = 1.6, h = 0.7, T_{\text{p}} = 30 \times 10^{8} , R_{\text{b}} = 0.7 , z = 0.33 , \gamma = 1.001, z_{0} = 0.66, n_{\text{b}} = 10 \times 10^{11}\,\, {\text{and }}T_{\text{b}} = 20 \times 10^{7}$

It is clear that from Fig. 10, because of bunching effect, the increasing e-beam density increases the growth rate. As seen from Fig. 11, because of the synchronism condition, the effect of electron beam energy is to decrease the growth rate.

Fig. 10

Variation of the normalized growth rate $\text{Im} \left( {\frac{\omega }{{c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{ \kappa_{0} }}} \right)$ for several values of the electron beam density. The chosen parameters are as follows: $R_{0} = 1.6, h = 0.7, z = 0.33,\,R_{\text{b}} = 0.7 , \gamma = 1.001, z_{0} = 0.66 , n_{\text{p}} = 3 \times 10^{11} , T_{\text{b}} = 20 \times 10^{7}\, {\text{and }}T_{\text{p}} = 30 \times 10^{8}$

Fig. 11

Variation of the normalized growth rate $\text{Im} \left( {\frac{\omega }{{ c\kappa_{0} }}} \right)$ with normalized wave number $\left( {\frac{{k_{z} }}{{\kappa_{0} }}} \right)$ for several values of the electron beam energy. The chosen parameters are as follows: $R_{0} = 1.6, h = 0.7, z_{0} = 0.66, \,R_{\text{b}} = 0.7 , \;z = 0.33 , \;n_{\text{b}} = 10 \times 10^{11} , \;T_{\text{p}} = 30 \times 10^{8} , \;n_{\text{p}} = 3 \times 10^{11} {\text{and }}T_{\text{b}} = 20 \times 10^{7}$

Conclusions

In this paper, useful results are obtained as:

• 1. In the absence of the electron beam, the frequency increases by increasing the length of the corrugation period, plasma temperature and plasma density.

• 2. The frequency decreases by increasing the waveguide radius in the absence of the electron beam.

• 3. In the presence of the electron beam, the increase in the corrugation period and e-beam density help the wave to be included in the resonant condition and finally increase the growth rate.

• 4. The growth rate decreases by increasing the plasma temperature, waveguide radius, plasma density and e-beam energy and decreases the phase velocity. By decreasing the phase velocity the wave exits from resonant condition.