The effect of beam and plasma parameters on the four modes of plasma-loaded traveling-wave tube with tape helix

Saviz, S.

doi:10.1007/s40094-014-0135-7

The effect of beam and plasma parameters on the four modes of plasma-loaded traveling-wave tube with tape helix

Research
Open access
Published: 02 July 2014

Volume 8, article number 135, (2014)
Cite this article

Download PDF

You have full access to this open access article

Journal of Theoretical and Applied Physics

The effect of beam and plasma parameters on the four modes of plasma-loaded traveling-wave tube with tape helix

Download PDF

S. Saviz¹

1422 Accesses
3 Citations
Explore all metrics

Abstract

Field theory is applied to analyze the behavior of the electromagnetic wave in the presence of a solid electron beam and magnetized plasma-loaded tape helix traveling-wave tube. The obtained dispersion relation implicitly includes azimuthal variations and all spatial harmonics of the tape helix. Results indicate that the frequency and the phase velocity of (X_bp − X_p) and (O_bp − X_p) modes increase with cyclotron frequency and for (O_bp − O_p) and (X_bp − O_p) modes decrease. In the strong magnetic field limit, the maximum growth rate and frequency of all modes are constant at different values of cyclotron frequency and beam energy. If the plasma density increases, the frequency and phase velocity of four modes will increase. The maximum growth rates of the four modes in the lower plasma density are equal and for higher values of plasma density the (O_bp − X_p) mode has greatest value. The phase velocity and the frequency of (X_bp − X_p) with (X_bp − O_p) modes and (O_bp − O_p) with (O_bp − X_p) modes are coinciding with each other and for first case increase with beam density, but for latter decrease. The maximum growth rate of (O_bp − O_p) mode and the maximum frequency of (X_bp − X_p) mode have highest values as a function of the electron beam density.

Dielectric-Loaded Plasma Filled Helix Traveling Wave Tube Analysis Based on the Linearized Field Theory

Article 30 December 2015

Designing a Beam-Plasma Traveling Wave Tube

Article 01 May 2019

Dispersion relation and growth rate in thermal plasma-loaded traveling wave tube with corrugated waveguide hollow electron beam

Article Open access 10 February 2015

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Introduction

In recent years, there has been increasing interest in high-power and high-frequency microwave devices for generating radiation at millimeter and sub-millimeter wavelengths. The relativistic traveling-wave tube (TWT) is an important high-power microwave apparatus, developed over the last several decades [1–5]. One of the common features of a TWT is a slow-wave structure (SWS) such as a dielectric material, disk-loaded waveguide, or a helix [6–10]. The physical mechanism of operation is that the SWS reduces the phase velocity of the electromagnetic wave to synchronize it with the electron beam velocity so that a strong interaction between the two can take place.

Pierce and his co-workers [11–13] employed the coupled-wave analysis in their pioneering work, and the analysis of TWT improved using linear theories based on the Maxwell’s equations in a sheath helix [14, 15]. The coupled-wave Pierce theory recovers the near-resonant limit. Both coupled-wave and field theories of TWT have discussed in [16] and [17]. Freund and co-workers developed the field theories of beam-loaded helix TWTs for tape helix model [18]. Freund and co-workers [19] described the numerical comparison between the complete dispersion equation and the Pierce model in helix TWT and shown that the coupled-wave theory breaks down for sufficiently high currents. The complete field theory is more exact than the coupled-wave theory.

The Experimental results show that the presence of plasma considerably enhances the interaction gain and the output power in comparison with vacuum. The plasma-assisted tubes can improve the transportation of larger beam current and also guide the beam without requiring a very strong guide field [20, 21]. For high-power devices driven by intense electron beams, neutralizing plasma can shield the beam space-charge effects. Experimental investigation for the electromagnetic properties of corrugated and smooth waveguide filled with inhomogeneous plasma done with Shkvarunets [22]. Nusinovich et al. [23] shows that in the case of operating at frequencies between the plasma frequency and the upper-hybrid frequency, the space-charge forces can significantly enhance the efficiency.

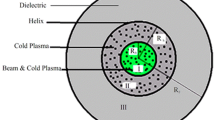
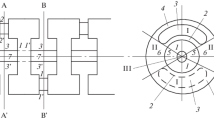
The purpose of the present paper is investigating the effects of plasma density, axial guide magnetic field, and beam energy and density on the growth rate and phase velocity of the system. The schematic illustrations of boundaries shown in Fig. 1 include three regions: (1) inside the beam that includes the electron beam and plasma (2) between the beam and helix that includes plasma (3) between the helix and the wall, which is a vacuum. We are investigating these effects on the four modes: (1) The coupling of the beam–plasma extraordinary mode and the plasma extraordinary mode in regions I and II, respectively (X_bp − X_p), (2) the coupling of the beam–plasma ordinary mode and plasma ordinary mode in regions I and II, respectively (O_bp − O_p), (3) The coupling of the beam–plasma extraordinary mode and plasma ordinary mode in region I, II, respectively (X_bp − O_p), (4) The coupling of the beam–plasma ordinary mode and plasma extraordinary mode in region I and II, respectively (O_bp − X_p). It is important to note that this nomenclature is only for convenience. More accurately, the O- and X-modes characterize modes propagating perpendicular to the ambient magnetic field in an infinite homogeneous plasma, while we are perceive with the modes propagating parallel to the ambient magnetic field in a bounded beam and/or plasma enclosed by both a tape helix and a conducting wall. We expand to a complete self-consistent and relativistic field theory of the plasma-loaded helix TWT by solution of the relativistic fluid equation and Maxwell’s equations. The dispersion relation implicitly contains space-charge effects without recourse to a heuristic model of the space-charge field.

The organization of the paper is as follows. Section 2 is devoted to the derivation of the perturbed transverse fields in regions 1 and 2. The dispersion relation is determined in Sect. 3 through application of the appropriate boundary conditions upon the solution of Maxwell’s equations. In Sect. 4, we deal with numerical results and conclusion.

Perturbed transfer fields

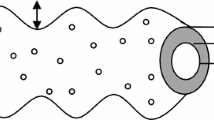
We used the equilibrium model of a solid electron beam that propagates through a plasma-filled tape helix in the presence of a uniform axial magnetic field $B_{0} = B_{0} {\hat{e}}_{z}$ . The azimuthally symmetric charge density described by

n_{0} (r) = n_{b} H (R_{b} - r)

where n_b is the ambient beam density, R_b is the beam radius, and H is the Heaviside function. Figure 1 shows the schematic cross-section of the system. It supposes that the beam propagates uniformly along the symmetry axis of the system, and the equilibrium velocity is $v_{0} = v_{0} {\hat{e}}_{z}$ .

Here, the employed helix is thin enough such that a conducting cylindrical sheet of radius R_h, width ς, and pitch angle φ can model it. The unit vector describing the pitch of the helix is [18]

{\hat{e}}_{φ} = {\hat{e}}_{θ} cos φ + {\hat{e}}_{z} sin φ .

We found the perturbed current density and the beam velocity in regions (I) and (II) by small perturbations about the equilibrium state in which n_e = n_0e + δn_e and $v_{e} = v_{0 e} + δ v_{e}$ for electron beam, and n_p = n_0p + δn_p and $v_{p} = δ v_{p}$ for cold plasma. Here, we neglected the nonlinear effects. The linearized continuity and momentum transfer equations for electron beam and cold plasma are as follows:

For electron beam

[\frac{\partial}{\partial t} + v_{0 e} \frac{\partial}{\partial z}] δ n_{e} + n_{0 e} \nabla . δ v_{e} = 0,

(1)

[\frac{\partial}{\partial t} + v_{0 e} \frac{\partial}{\partial z}] δ v_{e} = Ω_{c e} {\hat{e}}_{z} \times δ v_{e} - \frac{e}{γ_{0 e} m_{e}} [(I - β_{0 e}^{2} {\hat{e}}_{z} {\hat{e}}_{z}) . δ E + β_{0 e} {\hat{e}}_{z} \times δ B] .

(2)

For cold plasma

\frac{\partial δ n_{p}}{\partial t} + n_{0 p} \nabla . δ v_{p} = 0,

(3)

\frac{\partial δ v_{p}}{\partial t} = - \frac{e}{m_{e}} δ E + γ_{0 e} Ω_{c e} {\hat{e}}_{z} \times δ v_{p} .

(4)

here, e and m_e are charge and rest mass of the electron, respectively. β_0e = v_0e/c is the normalized axial velocity of the electron beam, γ_0e = 1/(1 − β ²_0e )^1/2 and ${\hat{Ω}}_{c e} = e B_{0} / γ_{0 e} m_{e} c = Ω_{c e} / γ_{0 e}$ stand for relativistic factor and the electron cyclotron frequency. Fluctuating electric and magnetic fields are designated by δE and δB and I is the unit dyadic.

To determine the periodicity of the steady state, Floquet’s theorem requires that all perturbed quantities have the following complex Fourier series representation [18]:

δ f (x, t) = \sum_{l, m = - \infty}^{\infty} δ \hat{f} (r) exp [i k_{m} z + i l θ - i ω t] .

(5)

Here, k_m = k + mk_h denotes the wave number and ω is the angular frequency. Inserting an Eq. (5) into Eqs. (1)–(4) yields the following equations for electron beam and cold plasma.

For electron beam

δ {\hat{n}}_{e l, m} = \frac{n_{0 e}}{Δ ω_{m}} [k_{m} ({\hat{e}}_{z} . δ {\hat{v}}_{e l, m}) - i \nabla_{⊥} . δ {\hat{v}}_{e l, m}]

(6)

δ {\hat{v}}_{e l, m} = δ {\hat{v}}_{e r l, m} {\hat{e}}_{r} + δ {\hat{v}}_{e θ l, m} {\hat{e}}_{θ} + δ {\hat{v}}_{e z l, m} {\hat{e}}_{z} = - \frac{i e}{γ_{0 e} m_{e}} \{\frac{i Ω_{c e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [- (δ {\hat{E}}_{θ l, m} + β_{0 e} δ B_{r l, m}) {\hat{e}}_{r} + (δ {\hat{E}}_{r l, m} - β_{0 e} δ {\hat{B}}_{l, m}) {\hat{e}}_{θ}] + \frac{Δ ω_{m}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [(δ {\hat{E}}_{r l, m} - β_{0 e} δ {\hat{B}}_{θ l, m}) {\hat{e}}_{r} + (δ {\hat{E}}_{θ l, m} + β_{0 e} δ {\hat{B}}_{r l, m}) {\hat{e}}_{θ}] \frac{1}{Δ ω_{m} γ_{0 e}^{2}} δ {\hat{E}}_{z l, m} {\hat{e}}_{z}\} = - \frac{i e}{γ_{0 e} m_{e}} \{\frac{1}{Δ ω_{m} γ_{0 e}^{2}} ({\hat{e}}_{z} . δ {\hat{E}}_{l, m}) {\hat{e}}_{z} + \frac{i Ω_{c e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} ({\hat{e}}_{z} \times δ {\hat{E}}_{⊥ l, m} - β_{0 e} δ {\hat{B}}_{⊥ l, m}) + \frac{Δ ω_{m}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} (δ {\hat{E}}_{⊥ l, m} + β_{0 e} {\hat{e}}_{z} \times δ {\hat{B}}_{⊥ l, m})\}

(7)

Here, Δω_m = ω − k_mv_0e.

For cold plasma

δ {\hat{n}}_{p l, m} = \frac{n_{0 p}}{ω} [k_{m} ({\hat{e}}_{z} . δ {\hat{v}}_{p l, m}) - i \nabla_{⊥} . δ {\hat{v}}_{p l, m}],

(8)

\begin{matrix} δ {\hat{v}}_{p l, m} = δ {\hat{v}}_{p r l, m} {\hat{e}}_{r} + δ {\hat{v}}_{p θ l, m} {\hat{e}}_{θ} + δ {\hat{v}}_{p z l, m} {\hat{e}}_{z} = - \frac{i e}{m_{e}} \{\frac{i Ω_{c e} γ_{0 e}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} [- δ {\hat{E}}_{θ l, m} {\hat{e}}_{r} + δ {\hat{E}}_{r l, m} {\hat{e}}_{θ}] + \frac{ω}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} [δ {\hat{E}}_{r l, m} {\hat{e}}_{r} + δ {\hat{E}}_{θ l, m} {\hat{e}}_{θ}] + \frac{1}{ω} δ {\hat{E}}_{z l, m} {\hat{e}}_{z}\} = - \frac{i e}{m_{e}} \{\frac{1}{ω} ({\hat{e}}_{z} . δ {\hat{E}}_{l, m}) {\hat{e}}_{z} + \frac{i Ω_{c e} γ_{0 e}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} ({\hat{e}}_{z} \times δ {\hat{E}}_{⊥ l, m}) + \frac{ω}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} δ {\hat{E}}_{⊥ l, m}\} \end{matrix}

(9)

The perturbed current density in the region (I) is given by

δ {\hat{J}}_{I l, m} = - e (n_{0 e} δ {\hat{v}}_{e l, m} + n_{0 p} δ {\hat{v}}_{p l, m} + δ {\hat{n}}_{e l, m} v_{0 e}),

(10)

And in region (II), the perturbed current density is

δ {\hat{J}}_{I I l, m} = - e n_{0 p} δ {\hat{v}}_{p l, m} .

(11)

Substituting Eqs. (6)–(9) into the Eq. (10) yields the perturbed current density in the region (I) as

δ {\hat{J}}_{I l, m} = \frac{i ω_{b}^{2}}{4 π Δ ω_{m}} \{\frac{ω}{Δ ω_{m} γ_{0 e}^{2}} ({\hat{e}}_{z} . δ {\hat{E}}_{l, m}) {\hat{e}}_{z} + \frac{i Ω_{c e} Δ ω_{m}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} ({\hat{e}}_{z} \times δ {\hat{E}}_{⊥ l, m} - β_{0 e}^{} δ {\hat{B}}_{⊥ l, m}) + \frac{Δ ω_{m}^{2}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} (δ {\hat{E}}_{⊥ l, m} + β_{0 e}^{} {\hat{e}}_{z} \times δ {\hat{B}}_{⊥ l, m}) - \frac{i v_{0 e} Δ ω_{m}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [{\hat{e}}_{z} \nabla_{⊥} . δ {\hat{E}}_{⊥ l, m} - β_{0 e}^{} \nabla_{⊥} δ {\hat{B}}_{⊥ l, m}] - \frac{v_{0 e} Ω_{c e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [{\hat{e}}_{z} ({\hat{e}}_{z} . \nabla_{⊥} \times δ {\hat{E}}_{⊥ l, m}) + β_{0 e}^{} {\hat{e}}_{z} \nabla_{⊥} . δ {\hat{B}}_{⊥ l, m}]\} + \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω} \{({\hat{e}}_{z} . δ {\hat{E}}_{z l, m}) {\hat{e}}_{z} + \frac{i Ω_{c e} γ_{0 e} ω}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} ({\hat{e}}_{z} \times δ {\hat{E}}_{⊥ l, m}) + \frac{ω^{2}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} δ {\hat{E}}_{⊥ l, m}\}

(12)

where ${\hat{ω}}_{b} = {(4 n_{e} e^{2} / γ_{0 e} m_{e})}^{1 / 2} = ω_{b} / γ_{0 e}^{1 / 2}$ and ${\hat{ω}}_{p} = {(4 n_{p} e^{2} / γ_{0 e} m_{e})}^{1 / 2} = ω_{p} / γ_{0 e}^{1 / 2}$ are the beam and the plasma-region plasma frequencies, respectively.

The perturbed current density in the region (II) obtained by substituting Eqs. (8) and (9) into the Eq. (11), the result is:

δ {\hat{J}}_{I I l, m} = \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω} \{({\hat{e}}_{z} . δ {\hat{E}}_{l, m}) {\hat{e}}_{z} + \frac{i Ω_{c e} γ_{0 e} ω}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} ({\hat{e}}_{z} \times δ {\hat{E}}_{⊥ l, m}) + \frac{ω^{2}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} δ {\hat{E}}_{⊥ l, m}\} .

(13)

Similarly, the perturbed charge density for electron beam and plasma is as:

δ {\hat{ρ}}_{e l, m} = \frac{i ω_{b}^{2}}{4 π Δ ω_{m}^{2}} \{\frac{k_{m}}{γ_{0 e}^{2}} ({\hat{e}}_{z} . δ {\hat{E}}_{l, m}) - \frac{i Δ ω_{m}^{2}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [\nabla_{⊥} . δ {\hat{E}}_{l, m} - β_{0 e}^{} {\hat{e}}_{z} . \nabla_{⊥} \times δ {\hat{B}}_{⊥ l, m}] - \frac{Δ ω_{m} Ω_{c e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [{\hat{e}}_{z} . \nabla_{⊥} \times δ {\hat{E}}_{⊥ l, m} + β_{0 e}^{} \nabla_{⊥} . δ {\hat{B}}_{⊥ l, m}]\}

(14)

δ ρ_{p l, m} = \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω^{2}} \{k_{m} ({\hat{e}}_{z} . δ {\hat{E}}_{l, m}) - {\frac{i ω^{2}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})}}_{} \nabla_{⊥} . δ {\hat{E}}_{⊥ l, m} - \frac{ω Ω_{c e} γ_{0 e}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} {\hat{e}}_{z} . \nabla_{⊥} \times δ {\hat{E}}_{⊥ l, m}\} .

(15)

The fluctuating transverse fields are derived by employing Maxwell’s equations together with Floquet’s theorem. The results in region (I) and (II) are as

Region I

δ E_{⊥, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \nabla_{⊥} δ {\hat{E}}_{z, l, m} - \frac{ω}{c} {\hat{e}}_{z} \times \nabla_{⊥} δ {\hat{B}}_{z, l, m} - \frac{4 π ω}{c^{2}} δ {\hat{J}}_{⊥, I l, m}],

(16)

δ {\hat{B}}_{⊥, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \nabla_{⊥} δ {\hat{B}}_{z, l, m} + \frac{ω}{c} {\hat{e}}_{z} \times \nabla_{⊥} δ {\hat{E}}_{z, l, m} - \frac{4 π k_{m}}{c} {\hat{e}}_{z} \times δ J_{⊥, I l, m}],

(17)

where $χ_{m}^{2} = ω^{2} / c^{2} - k_{m}^{2} .$ Region II

δ {\hat{E}}_{⊥, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \nabla_{⊥} δ {\hat{E}}_{z, l, m} - \frac{ω}{c} {\hat{e}}_{z} \times \nabla_{⊥} δ {\hat{B}}_{z, l, m} - \frac{4 π ω}{c^{2}} δ {\hat{J}}_{⊥ I I l, m}]

(18)

δ {\hat{B}}_{⊥, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \nabla_{⊥} δ {\hat{B}}_{z, l, m} + \frac{ω}{c} {\hat{e}}_{z} \times \nabla_{⊥} δ E_{z, l, m} - \frac{4 π k_{m}}{c} {\hat{e}}_{z} \times δ J_{, I I l, m}] .

(19)

The transverse source current is obtained from Eqs. (12) and (13) and (16)–(19) in terms of the axial components of electric and magnetic fields in regions I and II as follow:

Region I

δ {\hat{J}}_{⊥, I l, m} = - \frac{c}{4 π} \frac{1}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} \{[A_{b} (ω, k_{m}) + A_{p} (ω, k_{m}) + A_{b p} (ω, k_{m})] \nabla_{⊥} δ {\hat{E}}_{z, l, m} + [B_{b} (ω, k_{m}) + B_{p} (ω, k_{m}) + B_{b p} (ω, k_{m})] {\hat{e}}_{z} \times \nabla_{⊥} δ {\hat{B}}_{z, l, m} + [D_{b} (, k_{m}) + D_{p} (, k_{m}) + D_{b p} (, k_{m})] {\hat{e}}_{z} \times \nabla_{⊥} δ {\hat{E}}_{z, l, m} + [E_{b} (ω, k_{m}) + E_{p} (ω, k_{m})] \nabla_{⊥} δ {\hat{B}}_{z, l, m}\},

(20)

where

\begin{matrix} A_{b} (ω, k_{m}) = α_{b} (ω, k_{m}) [\frac{c k_{m} - ω β_{0 e}^{}}{Δ ω_{m}} Λ_{0 b} (ω, k_{m})], A_{p} (ω, k_{m}) = α_{p} (ω, k_{m}) [\frac{c k_{m}}{ω_{}} Λ_{0 p} (ω, k_{m})], A_{b p} (ω, k_{m}) = - α_{p} (ω, k_{m}) α_{b} (ω, k_{m}) \{(c k_{m} - ω β_{0 e}^{}) (\frac{1}{Δ ω_{m}} - \frac{Ω_{c e}^{2} γ_{0 e}}{ω Δ ω_{m}^{2}}) + c k_{m} (\frac{1}{ω} - \frac{Ω_{c e}^{2} γ_{0 e}}{ω^{2} Δ ω_{m}})\}, B_{b} (ω, k_{m}) = - α_{b} (ω, k_{m}) Λ_{0 b} (ω, k_{m}), B_{p} (ω, k_{m}) = - α_{p} (ω, k_{m}) Λ_{0 p} (ω, k_{m}), B_{b p} (ω, k_{m}) = - α_{p} (ω, k_{m}) α_{b} (ω, k_{m}) 2 (\frac{Ω_{c e}^{2} γ_{0 e}}{ω Δ ω_{m}} - 1) D_{b} (ω, k_{m}) = α_{b} (ω, k_{m}) [\frac{i Ω_{c e}}{Δ ω_{m}^{2}} (c k_{m} - ω β_{0 e}^{})], D_{p} (ω, k_{m}) = α_{p} (ω, k_{m}) [\frac{i Ω_{c e} γ_{0 e}}{ω^{2}} (c k_{m})], D_{b p} (ω, k_{m}) = - i α_{b} (ω, k_{m}) α_{p} (ω, k_{m}) \{(c k_{m} - ω β_{0 e}^{}) (\frac{Ω_{c e}}{Δ ω_{m}^{2}} - \frac{Ω_{c e} γ_{0 e}}{ω Δ ω_{m}}) + c k_{m} (\frac{Ω_{c e} γ_{0 e}}{ω^{2}} - \frac{Ω_{c e}}{ω Δ ω_{m}})\}, E_{b} (ω, k_{m}) = α_{b} (ω, k_{m}) [\frac{i Ω_{c e}}{Δ ω_{m}}], E_{p} (ω, k_{m}) = α_{p} (ω, k_{m}) [\frac{i Ω_{c e} γ_{0 e}}{ω}], Λ_{+ b p} (ω, k_{m}) = [1 - \frac{ω_{b}^{2} Δ ω_{m}}{c^{2} χ_{m}^{2} (Δ ω_{m} - Ω_{c e})} - \frac{ω_{p}^{2} γ_{0 e} ω}{c^{2} χ_{m}^{2} (ω - Ω_{c e} γ_{0 e})}], Λ_{- b p} (ω, k_{m}) = [1 - \frac{ω_{b}^{2} Δ ω_{m}}{c^{2} χ_{m}^{2} (Δ ω_{m} + Ω_{c e})} - \frac{ω_{p}^{2} γ_{0 e} ω}{c^{2} χ_{m}^{2} (ω + Ω_{c e} γ_{0 e})}], α_{b} (ω, k_{m}) = \frac{ω_{b}^{2} Δ ω_{m}^{2}}{c^{2} χ_{m}^{2} (Δ ω_{m}^{2} - Ω_{c e}^{2})}, α_{p} (ω, k_{m}) = \frac{γ_{0 e} ω_{p}^{2} ω^{2}}{c^{2} χ_{m}^{2} (ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})} Λ_{0 b} (ω, k_{m}) = 1 - \frac{ω_{b}^{2}}{c^{2} χ_{m}^{2}}, Λ_{0 p} (ω, k_{m}) = 1 - \frac{ω_{p}^{2} γ_{0 e}}{c^{2} χ_{m}^{2}} . \end{matrix}

Region II:

δ {\hat{J}}_{⊥, I I, l, m} = - \frac{c}{4 π} \frac{α_{p} (ω, k_{m}) Λ_{0 p} (ω, k_{m})}{Λ_{+ p} (ω, k_{m}) Λ_{- p} (ω, k_{m})} \{\frac{c k_{m}}{ω} \nabla_{⊥} δ {\hat{E}}_{z, l, m} - {\hat{e}}_{z} \times \nabla_{⊥} δ {\hat{B}}_{z, l, m} + i [\frac{c k_{m}}{ω} {\hat{e}}_{z} \times \nabla_{⊥} δ {\hat{E}}_{z, l, m} + \nabla_{⊥} δ {\hat{B}}_{z, l, m}]\},

(21)

the transverse components of the fluctuating electric and magnetic fields are obtained by substitution of Eqs. (20) and (21) into (16)–(19).

Region I:

δ {\hat{E}}_{r, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} + \frac{i l}{c r} δ {\hat{B}}_{z, l, m} + \frac{ω}{c} \frac{1}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} \{[A_{b} (ω, k_{m}) + A_{p} (ω, k_{m}) + A_{b p} (ω, k_{m})] \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} - [B_{b} (ω, k_{m}) + B_{p} (ω, k_{m}) + B_{b p} (ω, k_{m})] \frac{i l}{r} δ {\hat{B}}_{z, l, m} - [D_{b} (ω, k_{m}) + D_{p} (ω, k_{m}) + D_{b p} (ω, k_{m})] \frac{i l}{r} δ {\hat{E}}_{z, l, m} + [E_{b} (ω, k_{m}) + E_{p} (ω, k_{m})] \frac{\partial δ {\hat{B}}_{z, l, m}}{\partial r}\}]

(22)

δ {\hat{E}}_{θ, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \frac{i l}{r} δ {\hat{E}}_{z, l, m} - \frac{ω}{c} \frac{\partial δ {\hat{B}}_{z, l, m}}{\partial r} + \frac{ω}{c} \frac{1}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} \{[A_{b} (ω, k_{m}) + A_{p} (ω, k_{m}) + A_{b p} (ω, k_{m})] \frac{i l}{r} δ {\hat{E}}_{z, l, m} + [B_{b} (ω, k_{m}) + B_{p} (ω, k_{m}) + B_{b p} (ω, k_{m})] \frac{\partial δ {\hat{B}}_{z, l, m}}{\partial r} + [D_{b} (ω, k_{m}) + D_{p} (ω, k_{m}) + D_{b p} (ω, k_{m})] \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} + [E_{b} (ω, k_{m}) + E_{p} (ω, k_{m})] \frac{i l}{r} δ {\hat{B}}_{z, l, m}\}]

(23)

δ {\hat{B}}_{r, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \frac{\partial δ {\hat{B}}_{z, l, m}}{\partial r} - \frac{i l ω}{c r} δ {\hat{E}}_{z, l, m} + \frac{k_{m}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} \{- [A_{b} (ω, k_{m}) + A_{p} (ω, k_{m}) + A_{b p} (ω, k_{m})] \frac{i l}{r} δ {\hat{E}}_{z, l, m} - [B_{b} (ω, k_{m}) + B_{p} (ω, k_{m}) + B_{b p} (ω, k_{m})] \frac{\partial δ {\hat{B}}_{z, l, m}}{\partial r} - [D_{b} (ω, k_{m}) + D_{p} (ω, k_{m}) + D_{b p} (ω, k_{m})] \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} - [E_{b} (ω, k_{m}) + E_{p} (ω, k_{m})] \frac{i l}{r} δ {\hat{B}}_{z, l, m}\}]

(24)

δ {\hat{B}}_{θ, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \frac{i l}{r} δ {\hat{B}}_{z, l, m} + \frac{ω}{c} \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} + \frac{k_{m}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} \{[A_{b} (ω, k_{m}) + A_{p} (ω, k_{m}) + A_{b p} (ω, k_{m})] \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} - [B_{b} (ω, k_{m}) + B_{p} (ω, k_{m}) + B_{b p} (ω, k_{m})] \frac{i l}{r} δ {\hat{B}}_{z, l, m} - [D_{b} (ω, k_{m}) + D_{p} (ω, k_{m}) + D_{b p} (ω, k_{m})] \frac{i l}{r} δ {\hat{E}}_{z, l, m} + [E_{b} (ω, k_{m}) + E_{p} (ω, k_{m})] \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r}\}]

(25)

Region II:

δ {\hat{E}}_{r, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} + \frac{i l ω}{c r} δ {\hat{B}}_{z, l, m} + \frac{ω}{c} R_{p} (ω, k_{m}) (\frac{\partial}{\partial r} + \frac{l}{r}) [\frac{c k_{m}}{ω} δ {\hat{E}}_{z, l, m} + i δ {\hat{B}}_{z, l, m}]]

(26)

δ {\hat{E}}_{θ, l, m} = \frac{i}{χ_{m}^{2}} [i k_{m} \frac{l}{r} δ {\hat{E}}_{z, l, m} - \frac{ω}{c} \frac{\partial δ {\hat{B}}_{z, l, m}}{\partial r} + i \frac{ω}{c} R_{p} (ω, k_{m}) (\frac{\partial}{\partial r} + \frac{l}{r}) [\frac{c k_{m}}{ω} δ {\hat{E}}_{z, l, m} + i δ {\hat{B}}_{z, l, m}]]

(27)

δ {\hat{B}}_{r, l, m} = \frac{i}{χ_{m}^{2}} [k_{m} \frac{\partial δ {\hat{B}}_{z, l, m}}{\partial r} - \frac{i l ω}{c r} δ {\hat{E}}_{z, l, m} - i k_{m} R_{p} (ω, k_{m}) (\frac{\partial}{\partial r} + \frac{l}{r}) [\frac{c k_{m}}{ω} δ {\hat{E}}_{z, l, m} + i δ {\hat{B}}_{z, l, m}]]

(28)

δ {\hat{B}}_{θ, l, m} = \frac{i}{χ_{m}^{2}} [i k_{m} \frac{l}{r} δ {\hat{B}}_{z, l, m} + \frac{ω}{c} \frac{\partial δ {\hat{E}}_{z, l, m}}{\partial r} + k_{m} R_{p} (ω, k_{m}) (\frac{\partial}{\partial R} + \frac{l}{r}) [\frac{c k_{m}}{ω} δ {\hat{E}}_{z, l, m} + i δ {\hat{B}}_{z, l, m}]]

(29)

where

R_{p} (ω, k_{m}) = \frac{α_{p} (ω, k_{m}) Λ_{0 p} (ω, k_{m})}{Λ_{+ p} (ω, k_{m}) Λ_{- p} (ω, k_{m})}

(30)

Λ_{+ p} (ω, k_{m}) = 1 - \frac{ω_{p}^{2} γ_{0 e} ω}{c^{2} χ_{m}^{2} (ω - Ω_{c e} γ_{0 e})}

(31)

Λ_{- p} (ω, k_{m}) = 1 - \frac{ω_{p}^{2} γ_{0 e} ω}{c^{2} χ_{m}^{2} (ω + Ω_{c e} γ_{0 e})}

(32)

To obtain the conductivity tensor, we first substitute the magnetic field in the following Maxwell’s equation

\frac{ω}{c} δ B_{l, m} = k_{m} {\hat{e}}_{z} \times δ E_{⊥, l, m} + i {\hat{e}}_{z} \times \nabla_{⊥} δ E_{z, l, m},

(33)

Into the Eq. (12) to obtain the source current, in cylindrical coordinate, as a function of electric field in regions I and II:

Region I:

δ {\hat{J}}_{r, I, l, m} = [\frac{i ω_{b}^{2} Δ ω_{m}^{2}}{4 π ω (Δ ω_{m}^{2} - Ω_{c e}^{2})} + \frac{i ω_{p}^{2} γ_{0 e} ω}{4 π (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})}] δ {\hat{E}}_{r, l, m} + [\frac{ω_{b}^{2} Δ ω_{m} Ω_{c e}}{4 π ω (Δ ω_{m}^{2} - Ω_{c e}^{2})} + \frac{ω_{p}^{2} γ_{0 e}^{2} Ω_{c e}}{4 (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})}] δ E_{θ, l, m} + [- i v_{0 e} \frac{\partial}{\partial r} - \frac{Ω_{c e} v_{0 e}}{Δ ω_{m} r} \frac{\partial}{\partial θ}] δ {\hat{E}}_{z, l, m}

(34)

δ {\hat{J}}_{θ, I, l, m} = [\frac{i ω_{b}^{2} Δ ω_{m}^{2}}{4 π ω (Δ ω_{m}^{2} - Ω_{c e}^{2})} + \frac{i ω_{p}^{2} γ_{0 e} ω}{4 π (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})}] δ {\hat{E}}_{θ, l, m} - [\frac{ω_{b}^{2} Δ ω_{m} Ω_{c e}}{4 π ω (Δ ω_{m}^{2} - Ω_{c e}^{2})} + \frac{ω_{p}^{2} γ_{0 e}^{2} Ω_{c e}}{4 π (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})}] δ {\hat{E}}_{r, l, m} + [- i v_{0 e} \frac{\partial}{\partial θ} + \frac{Ω_{c e} v_{0 e}}{Δ ω_{m}} \frac{\partial}{\partial r}] δ {\hat{E}}_{z, l, m}

(35)

\begin{matrix} δ {\hat{J}}_{z, I, l, m} = [\frac{i ω_{b}^{2}}{4 π ω Δ ω_{m}^{2}} \{\frac{ω^{2}}{γ_{0 e}^{2}} - \frac{Δ ω_{m}^{2} v_{0 e}^{2}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} \nabla_{⊥}^{2}\} + \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω}] δ {\hat{E}}_{z, l, m} - \frac{i ω_{b}^{2}}{4 π ω} \frac{v_{0 e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} \{[i \frac{Δ ω_{m}}{r} + i Δ ω_{m} \frac{\partial}{\partial r} - \frac{Ω_{c e}}{r} \frac{\partial}{\partial θ}] δ {\hat{E}}_{r, l, m} + [i \frac{Δ ω_{m}}{r} \frac{\partial}{\partial θ} + Ω_{c e} \frac{\partial}{\partial r} + \frac{Ω_{c e}}{r}] δ {\hat{E}}_{θ, l, m}\} \end{matrix}

(36)

Region II

δ {\hat{J}}_{r, I I, l, m} = \frac{i ω_{p}^{2} γ_{0 e} ω}{4 π (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})} δ {\hat{E}}_{r, l, m} + \frac{ω_{p}^{2} γ_{0 e}^{2} Ω_{c e}}{4 π (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})} δ E_{θ, l, m},

(37)

δ {\hat{J}}_{θ, I I, l, m} = \frac{i ω_{p}^{2} γ_{0 e} ω}{4 π (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})} δ {\hat{E}}_{θ, l, m} - \frac{ω_{p}^{2} γ_{0 e}^{2} Ω_{c e}}{4 π (ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})} δ {\hat{E}}_{r, l, m},

(38)

δ {\hat{J}}_{z, I I, l, m} = \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω} δ {\hat{E}}_{z, l, m} .

(39)

Then, substituting Eqs. (36) and (39) into the following electric displacement,

δ {\hat{D}}_{l, m} = ε_{l, m} . δ {\hat{E}}_{l, m} = (I + \frac{4 π i}{ω} σ_{l, m}) . δ {\hat{E}}_{l, m},

(40)

where $σ_{l, m}$ is the conductivity tensor. The components of the dielectric tensor in regions (I) and (II) are:

Region I

ε_{r r, I} = ε_{θ θ, I} = 1 - \frac{ω_{b}^{2}}{ω^{2}} \frac{Δ ω_{m}^{2}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} - \frac{ω_{p}^{2} γ_{0 e}}{(ω^{2} - {(ω_{c e} γ_{0 e})}^{2})},

(41)

ε_{r θ, I} = - ε_{θ r, I} = \frac{i ω_{b}^{2}}{ω^{2}} \frac{Δ ω_{m} Ω_{c e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} + \frac{i ω_{p}^{2} γ_{0 e}}{ω} \frac{Ω_{c e} γ_{0 e}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})}

(42)

ε_{r z, I} = \frac{i ω_{b}^{2}}{ω^{2}} \frac{v_{0 e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [Δ ω_{m} \frac{\partial}{\partial r} + \frac{Ω_{c e} l}{r}],

(43)

ε_{z r, I} = \frac{i ω_{b}^{2}}{ω^{2}} \frac{v_{0 e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [Δ ω_{m} (\frac{\partial}{\partial r} + \frac{1}{r}) - \frac{Ω_{c e} l}{r}],

(44)

ε_{θ z, I} = - \frac{ω_{b}^{2}}{ω^{2}} \frac{v_{0 e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [Ω_{c e} \frac{\partial}{\partial r} + \frac{Δ ω_{m} l}{r}],

(45)

ε_{z θ, I} = \frac{ω_{b}^{2}}{ω^{2}} \frac{v_{0 e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} [Ω_{c e} (\frac{\partial}{\partial r} + \frac{l}{r}) - \frac{Δ ω_{m} l}{r}],

(46)

ε_{z z, I} = 1 - \frac{ω_{b}^{2}}{γ_{0 e}^{2} Δ ω_{m}^{2}} + \frac{ω_{b}^{2}}{ω^{2}} \frac{v_{0 e}^{2}}{(Δ ω_{m}^{2} - Ω_{c e}^{2})} \nabla_{⊥}^{2} - \frac{ω_{p}^{2} γ_{0 e}}{ω^{2}},

(47)

Region II

ε_{r r, I I} = ε_{θ θ, I I} = 1 - \frac{ω_{p}^{2} γ_{0 e}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})},

(48)

ε_{r θ, I I} = - ε_{θ r, I I} = \frac{i ω_{p}^{2} γ_{0 e}}{ω} \frac{Ω_{c e} γ_{0 e}}{(ω^{2} - {(Ω_{c e} γ_{0 e})}^{2})},

(49)

ε_{r z, I I} = 0, ε_{z r, I I} = 0, ε_{θ z, I I} = 0, ε_{z θ, I I} = 0,

(50)

ε_{z z, I I} = 1 - \frac{ω_{p}^{2} γ_{0 e}}{ω^{2}} .

(51)

The dispersion relation

The governing Maxwell’s equations for the fluctuating axial electric and magnetic fields in regions I and II are of the form:

Region I

[\nabla_{⊥}^{2} + χ_{m}^{2}] δ {\hat{E}}_{z, l, m} = 4 π i [k (δ {\hat{ρ}}_{e, I, l, m} + δ {\hat{ρ}}_{p, I, l, m}) - \frac{ω}{c^{2}} δ {\hat{J}}_{z, I, l, m}],

(52)

[\nabla_{⊥}^{2} + χ_{m}^{2}] δ {\hat{B}}_{z, l, m} = - \frac{4 π}{c} ({\hat{e}}_{z} . \nabla_{⊥} \times δ {\hat{J}}_{⊥, I, l, m}),

(53)

Region II

[\nabla_{⊥}^{2} + χ_{m}^{2}] δ {\hat{E}}_{z, l, m} = 4 π i [k δ {\hat{ρ}}_{p, I I, l, m} - \frac{ω}{c^{2}} δ {\hat{J}}_{z, I I, l, m}],

(54)

[\nabla_{⊥}^{2} + χ_{m}^{2}] δ {\hat{B}}_{z, l, m} = - \frac{4 π}{c} ({\hat{e}}_{z} . \nabla_{⊥} \times δ {\hat{J}}_{⊥, I I, l, m}),

(55)

where $δ {\hat{ρ}}_{e, I, l, m}$ and $δ {\hat{ρ}}_{p, I, l, m}$ denote the electron beam and plasma charge densities in region I, and $δ {\hat{ρ}}_{p, I I, l, m}$ is the charge density of the plasma in region II.

The source charge and current density in region I, Eqs. (12), (14)–(15), and in region II, Eqs. (13) and (15), must be expressed in terms of axial components of electric and magnetic fields. The source charge and current densities are obtained by the Eqs. (16)–(21):

Region I

δ {\hat{J}}_{z, I, l, m} = [\frac{i ω_{b}^{2}}{4 π Δ ω_{m}^{2}} \frac{ω}{γ_{0 e}^{2}} + \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω}] δ {\hat{E}}_{z, l, m} + \frac{i ω_{b}^{2}}{4 π Δ ω_{m}^{2}} \frac{Δ ω_{m}^{2} β_{0 e}}{(Δ ω_{m}^{2} - Ω_{c e}^{2}) χ_{m}^{2}} [{\bar{A}}_{e, I, 1} \nabla_{⊥}^{2} δ {\hat{E}}_{z, l, m} + {\bar{A}}_{e, I, 2} \nabla_{⊥}^{2} δ {\hat{B}}_{z, l, m}]

(56)

δ {\hat{ρ}}_{e, I, l, m} = \frac{i ω_{b}^{2}}{4 π Δ ω_{m}^{2}} [\frac{k_{m}}{γ_{0 e}^{2}} δ {\hat{E}}_{z, l, m} + \frac{Δ ω_{m}^{2}}{(Δ ω_{m}^{2} - Ω_{c e}^{2}) c χ_{m}^{2}} [{\bar{A}}_{e, I, 1} \nabla_{⊥}^{2} δ {\hat{E}}_{z, l, m} + {\bar{A}}_{e, I, 2} \nabla_{⊥}^{2} δ {\hat{B}}_{z, l, m}]]

(57)

δ ρ_{p, I, l, m} = \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω^{2}} [k_{m} δ {\hat{E}}_{z, l, m} + \frac{ω^{2}}{(ω^{2} - {(γ_{0 e} Ω_{c e})}^{2}) c χ_{m}^{2}} [{\bar{A}}_{p, I, 1} \nabla_{⊥}^{2} δ {\hat{E}}_{z, l, m} + {\bar{A}}_{p, I, 2} \nabla_{⊥}^{2} δ {\hat{E}}_{z, l, m}]],

(58)

where

\begin{matrix} {\bar{A}}_{e, I, 1} = (k_{m} c - ω β_{0 e}) [1 + \frac{α_{b} (ω, k_{m})}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} (Λ_{0 b} (ω, k_{m}) + \frac{Ω_{c e}^{2}}{Δ ω_{m}^{2}})] + \frac{Δ ω_{m}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [(A_{p} (ω, k_{m}) + A_{b p} (ω, k_{m}))] - \frac{i Ω_{c e}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [(D_{p} (ω, k_{m}) + D_{b p} (ω, k_{m})] \end{matrix}

(59)

\begin{matrix} {\bar{A}}_{e, I, 2} = i Ω_{c e} [1 + \frac{α_{b} (ω, k_{m})}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} (1 + Λ_{0 b} (ω, k_{m}))] + \frac{Δ ω_{m}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} (E_{p} (ω, k_{m})) - \frac{i Ω_{c e}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [B_{p} (ω, k_{m}) + B_{b p} (ω, k_{m})] \end{matrix}

(60)

\begin{matrix} {\bar{A}}_{p, I, 1} = k_{m} c + \frac{α_{b} (ω, k_{m}) (k_{m} c - ω γ_{0 e})}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [\frac{ω}{Δ ω_{m}} Λ_{0 b} (ω, k_{m}) + \frac{Ω_{c e}^{2} γ_{0 e}}{Δ ω_{m}^{2}})] + \frac{ω}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [(A_{p} (ω, k_{m}) + A_{b p} (ω, k_{m})] - \frac{i Ω_{c e} γ_{0 e}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [(D_{p} (ω, k_{m}) + D_{b p} (ω, k_{m})] \end{matrix}

(61)

\begin{matrix} {\bar{A}}_{p, I, 2} = i Ω_{c e} γ_{0 e} \{1 + \frac{α_{b} (ω, k_{m})}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [\frac{ω}{Δ ω_{m} γ_{0 e}} + Λ_{0 b} (ω, k_{m})]\} + \frac{ω}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} (E_{p} (ω, k_{m})) - \frac{i Ω_{c e} γ_{0 e}}{Λ_{+ b p} (ω, k_{m}) Λ_{- b p} (ω, k_{m})} [B_{p} (ω, k_{m}) + B_{b p} (ω, k_{m})] \end{matrix}

(62)

Region II

δ {\hat{J}}_{z, I I, l, m} = \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω} δ {\hat{E}}_{z, l, m},

(63)

δ {\hat{ρ}}_{p, I I, l, m} = \frac{i ω_{p}^{2} γ_{0 e}}{4 π ω^{2}} [k_{m} δ {\hat{E}}_{z, l, m} + \frac{ω^{2}}{(ω^{2} - {(γ_{0 e} Ω_{c e})}^{2}) c χ_{m}^{2}} [{\bar{B}}_{p, I I, 1} \nabla_{⊥}^{2} δ {\hat{E}}_{z, l, m} + i {\bar{B}}_{p, I I, 2} \nabla_{⊥}^{2} δ B_{z, l, m}]]

(64)

where

{\bar{B}}_{p, I I, 1} = c k_{m} [1 + \frac{α_{p} (ω, k_{m})}{Λ_{+ p} (ω, k_{m}) Λ_{- p} (ω, k_{m})} [Λ_{0 p} (ω, k_{m}) + \frac{{(Ω_{c e} γ_{0 e})}^{2}}{ω^{2}}]],

(65)

B_{p, I I, 2} = Ω_{c e} γ_{0 e} [1 + \frac{α_{p} (ω, k_{m})}{Λ_{+ p} (ω, k_{m}) Λ_{- p} (ω, k_{m})} [1 + Λ_{0 p} (ω, k_{m})]] .

(66)

Substitution of Eqs. (56)–(66) into Eqs. (52)–(55) yields the following fourth-order differential equations for the electric and magnetic fields in the two regions:

Region I

(\nabla_{⊥}^{2} + χ_{+, I, bp, m}^{2}) (\nabla_{⊥}^{2} + χ_{-, bp, m}^{2}) δ {\hat{E}}_{z, l, m} = 0,

(67)

(\nabla_{⊥}^{2} + χ_{+, I, bp, m}^{2}) (\nabla_{⊥}^{2} + χ_{-, bp, m}^{2}) δ {\hat{B}}_{z, l, m} = 0,

(68)

Region II

(\nabla_{⊥}^{2} + χ_{+, I I, p, m}^{2}) (\nabla_{⊥}^{2} + χ_{-, p, m}^{2}) δ {\hat{E}}_{z, l, m} = 0,

(69)

(\nabla_{⊥}^{2} + χ_{+, I I, p, m}^{2}) (\nabla_{⊥}^{2} + χ_{-, p, m}^{2}) δ {\hat{B}}_{z, l, m} = 0,

(70)

where

χ_{\pm, I, b p, m} = \frac{1}{2 [1 - \frac{ω_{b}^{2}}{γ_{0 e}^{2} (Δ ω_{m}^{2} - Ω_{c e}^{2})} + Λ_{+ b p} Λ_{- b p} Y 3]} \{\{[1 - \frac{ω_{b}^{2}}{γ_{0 e}^{2} (Δ ω_{m}^{2} - Ω_{c e}^{2})} + Λ_{s c} (1 - 2 α_{b})] χ_{m}^{2} + Λ_{+ b p} Λ_{- b p} Y 1\} \mp {\{{[1 - \frac{ω_{b}^{2}}{γ_{0 e}^{2} (Δ ω_{m}^{2} - Ω_{c e}^{2})} + Λ_{s c} (1 - 2 α_{b})]}^{2} χ_{m}^{4} + {(Λ_{+ b p} Λ_{- b p} Y 1)}^{2} + 2 Λ_{+ b p} Λ_{- b p} Y 1 χ_{m}^{2} [1 - \frac{ω_{b}^{2}}{λ_{0 e}^{2} (Δ ω_{m}^{2} - Ω_{c e}^{2})} + Λ_{s c} (1 - 2 α_{b})] - 4 Λ_{s c} Λ_{+ b p} Λ_{- b p} χ_{m}^{4} (1 - \frac{ω_{b}^{2}}{γ_{0 e}^{2} (Δ ω_{m}^{2} - Ω_{c e}^{2})}) - 4 Y 4 {(Λ_{+ b p} Λ_{- b p})}^{2}\}}^{1 / 2}\}

(71)

χ_{\pm, I I, p, m} = \frac{χ_{m}^{2}}{2 [1 - \frac{ω_{p}^{2} γ_{0 e}}{(ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})}]} [1 - \frac{ω_{p}^{2} γ_{0 e}}{(ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})} + Λ_{s c p} (1 - 2 α_{p})] \mp {\{{[1 - \frac{ω_{p}^{2} γ_{0 e}}{(ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})} + Λ_{s c p} (1 - 2 α_{p})]}^{2} - 4 Λ_{s c p} Λ_{+ p} Λ_{- p} (1 - \frac{ω_{p}^{2} γ_{0 e}}{(ω^{2} - {(γ_{0 e} Ω_{c e})}^{2})})\}}^{1 / 2}

(72)

\begin{matrix} Λ_{s c} = 1 - \frac{ω_{b}^{2}}{Δ ω_{m}^{2} γ_{0 e}^{2}}, Λ_{s c p} = 1 - \frac{ω_{p}^{2} γ_{0 e}}{ω^{2}}, Y 1 = - \frac{χ_{m}^{2} Λ_{s c} (B_{p} + B_{bp})}{Λ_{+ bp} (ω, k_{m}) Λ_{- bp} (ω, k_{m})} - (1 + \frac{α_{b} Λ_{0 b}}{Λ_{+ bp} Λ_{- bp}}) (\frac{χ_{m}^{2} ω_{p}^{2} γ_{0 e}}{ω^{2}}) + (\frac{χ_{m}^{2} ω_{p}^{2} γ_{0 e}}{ω^{2}}) (\frac{(B_{p} + B_{bp})}{Λ_{+ bp} Λ_{- bp}}) + \frac{(c k_{m} - ω β_{0 e}) χ_{m}^{2} α_{b}}{Δ ω_{m}^{2}} \{\frac{Δ ω_{m}}{Λ_{+ bp} Λ_{- bp}} (A_{p} + A_{bp}) - \frac{i Ω_{c e}}{Λ_{+ bp} Λ_{- bp}} (D_{p} + D_{bp})\} + \frac{χ_{m}^{2} α_{p} (k_{m} c)}{ω^{2}} {\bar{A}}_{p, I, 1} \end{matrix}

(73)

\begin{matrix} Y 3 = - \{1 + \frac{α_{b} {(c k_{m} - ω β_{0 e})}^{2} [1 + \frac{α_{b}}{Λ_{+ b p} Λ_{- b p}} (Λ_{0 b} + \frac{Ω_{c e}^{2}}{Δ ω_{m}^{2}})]}{Δ ω_{m}^{2}}\} (\frac{B_{p} + B_{b p}}{Λ_{+ b p} Λ_{- b p}}) + (1 + \frac{α_{b} Λ_{0 b}}{Λ_{+ b p} Λ_{- b p}}) \{\frac{(c k_{m} - ω β_{0 e}) α_{b}}{Δ ω_{m}^{2}} \{\frac{Δ ω_{m}}{Λ_{+ b p} Λ_{- b p}} (A_{p} + A_{b p}) - \frac{i Ω_{c e}}{Λ_{+ b p} Λ_{- b p}} (D_{p} + D_{b p})\} + \frac{α_{p} (k_{m} c)}{ω^{2}} {\bar{A}}_{p, I, 1}\} + (\frac{B_{p} + B_{b p}}{Λ_{+ b p} Λ_{- b p}}) \{\frac{(c k_{m} - ω β_{0 e}) α_{b}}{Δ ω_{m}^{2}} \{\frac{Δ ω_{m}}{Λ_{+ b p} Λ_{- b p}} (A_{p} + A_{b p}) - \frac{i Ω_{c e}}{Λ_{+ b p} Λ_{- b p}} (D_{p} + D_{b p})\} + \frac{α_{p} (k_{m} c)}{ω^{2}} {\bar{A}}_{p, I, 1}\} + \frac{i α_{b} Ω_{c e} (c k_{m} - ω β_{0 e})}{Δ ω_{m}^{2}} [1 + \frac{α_{b}}{Λ_{+ b p} Λ_{- b p}} (1 + Λ_{0 b})] [\frac{D_{p} + D_{b p}}{Λ_{+ b p} Λ_{- b p}}] + \{[\frac{α_{b} (c k_{m} - ω β_{0 e})}{Δ ω_{m}^{2}}] [\frac{Δ ω_{m}}{Λ_{+ b p} Λ_{- b p}} E_{p} - \frac{i Ω_{c e}}{Λ_{+ b p} Λ_{- b p}} (B_{p} + B_{b p})] + \frac{α_{p} (k_{m} c)}{ω^{2}} {\bar{A}}_{p, I, 2}\} \{\frac{i α_{b} Ω_{c e}}{Λ_{+ b p} Λ_{- b p}} \frac{(c k_{m} - ω β_{0 e})}{Δ ω_{m}^{2}}\} + [\frac{D_{p} + D_{b p}}{Λ_{+ b p} Λ_{- b p}}] \{[\frac{α_{b} (c k_{m} - ω β_{0 e})}{Δ ω_{m}^{2}}] [\frac{Δ ω_{m}}{Λ_{+ b p} Λ_{- b p}} E_{p} - \frac{i Ω_{c e}}{Λ_{+ b p} Λ_{- b p}} (B_{p} + B_{b p})] + \frac{α_{p} (k_{m} c)}{ω^{2}} {\bar{A}}_{p, I, 2}\} \end{matrix}

(74)

\begin{matrix} Y 4 = Y 3 [χ_{m}^{4} Λ_{s c} - χ_{m}^{4} \frac{ω_{p}^{2} γ_{0 e}}{ω^{2}}] - χ_{m}^{4} \frac{ω_{p}^{2} γ_{0 e}}{ω^{2}} [(1 + \frac{α_{b} Λ_{0 b}}{Λ_{+ b p} Λ_{- b p}}) \{1 + \frac{α_{b} {(c k_{m} - ω β_{0 e})}^{2} [1 + \frac{α_{b}}{Λ_{+ b p} Λ_{- b p}} (Λ_{0 b} + \frac{Ω_{c e}^{2}}{Δ ω_{m}^{2}})]}{Δ ω_{m}^{2}}\} - \frac{α_{b}^{2} Ω_{c e}^{2} {(c k_{m} - ω β_{0 e})}^{2}}{Δ ω_{m}^{4} Λ_{+ b p} Λ_{- b p}} \{1 + \frac{α_{b}}{Λ_{+ b p} Λ_{- b p}} (1 + Λ_{0 b})\}] \end{matrix}

(75)

We can obtain the dispersion relation by solutions of Eqs. (67)–(70) with appropriate boundary conditions. For one of the two appropriate modes in each region, these equations reduce to:

Region I

(\nabla_{⊥}^{2} + χ_{\pm, I, b p, m}^{2}) δ {\hat{E}}_{z, l, m} = 0

(76)

(\nabla_{⊥}^{2} + χ_{\pm, I, b p, m}^{2}) δ {\hat{B}}_{z, l, m} = 0

(77)

Region II

(\nabla_{⊥}^{2} + χ_{\pm, I I, p, m}^{2}) δ {\hat{E}}_{z, l, m} = 0

(78)

(\nabla_{⊥}^{2} + χ_{\pm, I I, p, m}^{2}) δ {\hat{B}}_{z, l, m} = 0

(79)

The solutions of Eqs. (76)–(79) in the three regions are as follows:

δ {\hat{E}}_{z, l, m} = \{\begin{matrix} A_{l, m} J_{l} (χ_{\pm, I, b p, m} r), 0 \leq r \leq R_{b} \\ B_{l, m} J_{l} (χ_{\pm, I I, p, m} r) + C_{l, m} Y_{l} (χ_{\pm, I I, p, m} r), R_{b} < r \leq R_{h} \\ D_{l, m} J_{l} (χ_{m} r) + E_{l, m} Y_{l} (χ_{m} r), R_{h} < r \leq R_{g} \end{matrix}

(80)

δ {\hat{B}}_{z, l, m} = \{\begin{matrix} F_{l, m} J_{l} (χ_{\pm, I, b p, m} r), 0 \leq r \leq R_{b} \\ G_{l, m} J_{l} (χ_{\pm, I I, p, m} r) + H_{l, m} Y_{l} (χ_{\pm, I I, p, m} r), R_{b} < r \leq R_{h} \\ K_{l, m} J_{l} (χ_{m} r) + L_{l, m} Y_{l} (χ_{m} r), R_{h} < r \leq R_{g} . \end{matrix}

(81)

Having applied the boundary condition of the waveguide wall, the solution in R_h < r ≤ R_g is:

δ {\hat{E}}_{z, l, m} = D_{l, m} W_{l} (χ_{m} R_{g}, χ_{m} r), R_{h} < r \leq R_{g},

(82)

δ {\hat{B}}_{z, l, m} = K_{l, m} W_{l}^{'} (χ_{m} R_{g}, χ_{m} r), R_{h} < r \leq R_{g},

(83)

where

W_{l} (χ_{m} R_{g}, χ_{m} r) = Y_{l} (χ_{m} R_{g}) J_{l} (χ_{m} r) - J_{l} (χ_{m} R_{g}) Y_{l} (χ_{m} r),

(84)

W_{l}^{'} (χ_{m} R_{g}, χ_{m} r) = Y_{l}^{'} (χ_{m} R_{g}) J_{l} (χ_{m} r) - J_{l}^{'} (χ_{m} R_{g}) Y_{l} (χ_{m} r) .

(85)

The boundary conditions at the edge of the beam and the interface of the regions I and II require

1.
$δ {\hat{E}}_{z, l, m} (R_{b} - ε) = δ {\hat{E}}_{z, l, m} (R_{b} + ε)$
2.
$δ {\hat{E}}_{θ, l, m} (R_{b} - ε) = δ {\hat{E}}_{θ, l, m} (R_{b} + ε)$
3.
$\begin{matrix} δ {\hat{E}}_{r, l, m} (R_{b} - ε) + ε_{r θ, I} δ {\hat{E}}_{θ, l, m} (R_{b} - ε) + ε_{r z, I} δ {\hat{E}}_{z, l, m} (R_{b} - ε) = ε_{r r, I I} δ {\hat{E}}_{r, l, m} (R_{b} + ε) + ε_{r θ, I I} δ {\hat{E}}_{θ, l, m} (R_{b} + ε) + ε_{r z, I I} δ {\hat{E}}_{z, l, m} (R_{b} + ε) \end{matrix}$
4.
$δ {\hat{B}}_{z, l, m} (R_{b} - ε) = δ {\hat{B}}_{z, l, m} (R_{b} + ε)$

By applying the boundary conditions, we obtain the following four equations:

A_{l, m} J_{l} (χ_{\pm, I, b p, m} R_{b}) = B_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b}) + C_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}),

(86)

i P_{l, m} A_{l, m} + Q_{l, m} F_{l, m} = \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [G_{l, m} Θ 1_{l, m} + H_{l, m} Θ 2_{l, m} + i B_{l, m} Θ 3_{l, m} + i C_{l, m} Θ 4_{l, m}],

(87)

S_{l, m} A_{l, m} + i T_{l, m} F_{l, m} = \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [i G_{l, m} Θ 5_{l, m} + i H_{l, m} Θ 6_{l, m} + B_{l, m} Θ 7_{l, m} + C_{l, m} Θ 8_{l, m}],

(88)

F_{l, m} J_{l} (χ_{\pm, I, b p, m} R_{b}) = G_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b}) + H_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) .

(89)

Where P_{l, m}, Q_{l, m}, S_{l, m}and T_{l, m} are:

P_{l, m} = \frac{1}{Λ_{+ b p} Λ_{- b p}} [α_{b} Λ_{0 b} \frac{(c k_{m} - ω β_{0 e})}{Δ ω_{m}} + α_{p} Λ_{0 p} \frac{c k_{m}}{ω}] J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) - α_{b} α_{p} \{J_{l}^{'} (χ_{\pm, I, b p, m} R_{b}) \{(c k_{m} - ω β_{0 e}) [\frac{1}{Δ ω_{m}^{2}} + \frac{Ω_{c e} β_{0 e}}{ω Δ ω_{m}^{2}} + \frac{Ω_{c e}}{Δ ω_{m}^{2}} - \frac{Ω_{c e} β_{0 e}}{ω Δ ω_{m}}] + c k_{m} [\frac{1}{ω^{2}} + \frac{Ω_{c e}}{Δ ω_{m} ω^{2}} + \frac{Ω_{c e} β_{0 e}}{ω^{2}} - \frac{Ω_{c e}}{ω Δ ω_{m}}]\} + \frac{l}{R_{b} χ_{\pm, I, b p, m}} J_{l} (χ_{\pm, I, b p, m} R_{b}) \{(c k_{m} - ω β_{0 e}) [\frac{1}{Δ ω_{m}} - \frac{Ω_{c e}^{2} γ_{0 e}}{ω Δ ω_{m}^{2}}] + c k_{m} [\frac{1}{ω} - \frac{Ω_{c e}^{2} γ_{0 e}}{Δ ω_{m} ω^{2}}]\}\}

(90)

Q_{l, m} = \{- J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) + \frac{1}{Λ_{+ b p} Λ_{- b p}} \{- [α_{b} Λ_{0 b} + α_{p} Λ_{0 p}] J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) + Λ_{b p} \{J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) \{- \frac{2 Ω_{c e}^{2} γ_{0 e}}{ω Δ ω_{m}} + 2\} + \frac{l}{R_{b} χ_{\pm, I, b p, m}} J_{l} (χ_{\pm, I, b p, m} R_{b}) \{\frac{1}{Δ ω_{m}} + \frac{Ω_{c e} β_{0 e}}{ω Δ ω_{m}} + \frac{1}{ω} + \frac{Ω_{c e}}{Δ ω_{m}}\}\}\}\}

(91)

Θ 1_{l, m} = - J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{b}) - R_{p} (ω, k_{m}) J_{l - 1} (χ_{\pm, I I, p, m} R_{b}),

(92)

Θ 2_{l, m} = Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{b}) - R_{p} (ω, k_{m}) Y_{l - 1} (χ_{\pm, I I, p, m} R_{b}),

(93)

Θ 3_{l, m} = \frac{k_{m} c R_{p} (ω, k_{m})}{ω} J_{l - 1} (χ_{\pm, I I, p, m} R_{b}),

(94)

Θ 4_{l, m} = \frac{k_{m} c R_{p} (ω, k_{m})}{ω} Y_{l - 1} (χ_{\pm, I I, p, m} R_{b}),

(95)

Θ 5_{l, m} = \frac{ω}{2 c k_{m}} [(ε_{+ p} + 2 R_{p} (ω, k_{m}) ε_{+ p} - 1) J_{l - 1} (χ_{\pm, I I, p, m} R_{b}) + (ε_{- p} - 1) J_{l + 1} (χ_{\pm, I I, p, m} R_{b})],

(96)

Θ 6_{l, m} = \frac{ω}{2 c k_{m}} [(ε_{+ p} + 2 R_{p} (, k_{m}) ε_{+ p} - 1) Y_{l - 1} (χ_{\pm, I I, p, m} R_{b}) + (ε_{- p} - 1) Y_{l + 1} (χ_{\pm, I I, p, m} R_{b})],

(97)

Θ 7_{l, m} = J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{b}) + \frac{1}{2} [(ε_{+ p} + 2 R_{p} (ω, k_{m}) ε_{+ p} - 1) J_{l - 1} (χ_{\pm, I I, p, m} R_{b}) - (ε_{- p} - 1) J_{l + 1} (χ_{\pm, I I, p, m} R_{b})],

(98)

Θ 8_{l, m} = Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{b}) + \frac{1}{2} [(ε_{+ p} + 2 R_{p} (ω, k_{m}) ε_{+ p} - 1) Y_{l - 1} (χ_{\pm, I I, p, m} R_{b}) - (ε_{- p} - 1) Y_{l + 1} (χ_{\pm, I I, p, m} R_{b})],

(99)

\begin{matrix} S_{l, m} = J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) + \frac{ω}{2 c k_{m}} \frac{(c k_{m} - ω β_{0 e})}{Δ ω_{m}} [ε_{+ b} + \frac{2 α_{b} Λ_{0 b}}{Λ_{+ b p} Λ_{- b p}} ε_{+ b} - 1] J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) - \frac{1}{2} (ε_{- b} - 1) J_{l + 1} (χ_{\pm, I, b p, m} R_{b}) + \frac{1}{2} \{[ε_{+ p} + \frac{2 α_{p} Λ_{0 p}}{Λ_{+ b p} Λ_{- b p}} ε_{+ p} - 1] J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) - (ε_{- p} - 1) J_{l + 1} (χ_{\pm, I, b p, m} R_{b})\} + F F 1, \end{matrix}

(100)

\begin{matrix} T_{l, m} = \frac{ω}{2 c k_{m}} [(ε_{+ b} + \frac{2 α_{b} Λ_{0 b}}{Λ_{+ b p} Λ_{- b p}} ε_{+ b} - 1) J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) + (ε_{- b} - 1) J_{l + 1} (χ_{\pm, I, b p, m} R_{b})] + \frac{ω}{2 c k_{m}} [(ε_{+ p} + \frac{2 α_{p} Λ_{0 p}}{Λ_{+ b p} Λ_{- b p}} ε_{+ p} - 1) J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) + (ε_{- p} - 1) J_{l + 1} (χ_{\pm, I, b p, m} R_{b})] + F F 2, \end{matrix}

(101)

\begin{matrix} F F 1 = \frac{ω}{c k_{m}} \frac{1}{Λ_{+ b p} Λ_{- b p}} \{- \frac{ω_{b}^{2}}{ω^{2}} \frac{Δ ω_{m} α_{p} Λ_{0 p}}{(Δ ω_{m} - Ω_{c e})} \frac{c k_{m}}{ω} \frac{ω_{p}^{2} γ_{0 e}}{ω} \frac{α_{b} Λ_{0 b}}{(ω - γ_{0 e} Ω_{c e})} \frac{(c k_{m} - ω β_{0 e})}{Δ ω_{m}}\} J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) + \frac{ω}{c k_{m}} (ε_{r r, I} R 1 + i_{r θ, I} R 2), \end{matrix}

(102)

F F 2 = \frac{ω}{c k_{m}} \frac{1}{Λ_{+ b p} Λ_{- b p}} \{- \frac{ω_{b}^{2}}{ω^{2}} \frac{Δ ω_{m} α_{p} Λ_{0 p}}{(Δ ω_{m} - Ω_{c e})} \frac{ω_{p}^{2} γ_{0 e} α_{b} Λ_{0 b}}{ω (ω - γ_{0 e} Ω_{c e})}\} J_{l - 1} (χ_{\pm, I, b p, m} R_{b}) + \frac{ω}{c k_{m}} (ε_{r r, I} R 3 + i ε_{r θ, I} R 4),

(103)

R 1 = \frac{1}{Λ_{+ b p} Λ_{- b p}} \{J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) A_{b p} (ω, k_{m}) + \frac{i l D_{b p} (ω, k_{m})}{χ_{\pm, I, b p, m} R_{b}} J_{l} (_{\pm, I, b p, m} R_{b}) + \frac{l α_{b} α_{p}}{χ_{\pm, I, b p, m} R_{b}} J_{l} (χ_{\pm, I, b p, m} R_{b}) \{(c k_{m} - ω β_{0 e}) [\frac{1}{Δ ω_{m}^{2}} + \frac{γ_{0 e} Ω_{c e}}{ω Δ ω_{m}^{2}}] + c k_{m} [\frac{1}{ω^{2}} + \frac{Ω_{c e}}{ω^{2} Δ ω_{m}}]\}\},

(104)

R 2 = \frac{1}{Λ_{+ b p} Λ_{- b p}} \{- i J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) D_{b p} (ω, k_{m}) + \frac{l A_{b p} (ω, k_{m})}{χ_{\pm, I, b p, m} R_{b}} J_{l} (χ_{\pm, I, b p, m} R_{b}) - α_{b} α_{p} J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) \{(c k_{m} - ω β_{0 e}) [\frac{1}{Δ ω_{m}^{2}} + \frac{γ_{0 e} Ω_{c e}}{ω Δ ω_{m}^{2}}] + c k_{m} [\frac{1}{ω^{2}} + \frac{Ω_{c e}}{ω^{2} Δ ω_{m}}]\}\},

(105a)

R 3 = \frac{1}{Λ_{+ b p} Λ_{- b p}} \{- \frac{l B_{b p} (ω, k_{m})}{χ_{\pm, I, b p, m} R_{b}} J_{l} (χ_{\pm, I, b p, m} R_{b}) - α_{b} α_{p} J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) [\frac{1}{Δ ω_{m}} + \frac{γ_{0 e} Ω_{c e}}{ω Δ ω_{m}} + \frac{1}{ω} + \frac{Ω_{c e}}{ω Δ ω_{m}}]\},

(105b)

R 4 = \frac{1}{Λ_{+ b p} Λ_{- b p}} \{- B_{b p} (ω, k_{m}) J_{l}^{^{'}} (χ_{\pm, I, b p, m} R_{b}) - α_{b} α_{p} \frac{l}{χ_{\pm, I, b p, m} R_{b}} J_{l} (χ_{\pm, I, b p, m} R_{b}) [\frac{1}{Δ ω_{m}} + \frac{γ_{0 e} Ω_{c e}}{ω Δ ω_{m}} + \frac{1}{ω} + \frac{Ω_{c e}}{ω Δ ω_{m}}]\},

(106)

ε_{\pm b} = 1 - \frac{ω_{b}^{2}}{ω^{2}} \frac{Δ ω_{m}}{(Δ ω_{m} \mp Ω_{c e})},

(107)

ε_{\pm p} = 1 - \frac{ω_{p}^{2} γ_{0 e}}{ω (ω \mp Ω_{c e} γ_{0 e})},

(108)

Equations (86)–(89) include six unknown coefficients and allow us to find the solutions in terms of the two unknown coefficients. After some straightforward algebra, the axial electric and magnetic fields are written as follows:

δ {\hat{E}}_{z, l, m} = \{\begin{matrix} A_{l, m} J_{l} (χ_{\pm, I, b p, m} r), 0 \leq r \leq R_{b} \\ A_{l, m} [a_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} r) + a_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} r)] \\ + i F_{l, m} [c_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} r) + c_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} r)], R_{b} < r \leq R_{h} \\ D_{l, m} W_{l} (χ_{m} R_{g}, χ_{m} r), R_{h} < r \leq R_{g} \end{matrix}

(109)

δ {\hat{B}}_{z, l, m} = \{\begin{matrix} F_{l, m} J_{l} (χ_{\pm, I, b p, m} r), 0 \leq r \leq R_{b} \\ F_{l, m} [b_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} r) + b_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} r)] \\ + i A_{l, m} [d_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} r) + d_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} r)], R_{b} < r \leq R_{h} \\ K_{l, m} W_{l}^{^{'}} (χ_{m} R_{g}, χ_{m} r), R_{h} < r \leq R_{g} \end{matrix}

(110)

where a ⁽¹⁾_{l, m} , a ⁽²⁾_{l, m} , b ⁽¹⁾_{l, m} , b ⁽²⁾_{l, m} c ⁽¹⁾_{l, m} , c ⁽²⁾_{l, m} , d ⁽¹⁾_{l, m} and d ⁽²⁾_{l, m} are as follows:

a_{l, m}^{(1)} = \frac{1}{G_{l, m}^{(2)}} [- J_{l} (χ_{\pm, I, b p, m} R_{b}) ς_{14} + Y_{l} (χ_{\pm, I I, p, m} R_{b}) ς_{12}],

(111)

a_{l, m}^{(2)} = \frac{1}{G_{l, m}^{(2)}} [J_{l} (χ_{\pm, I, b p, m} R_{b}) ς_{13} - J_{l} (χ_{\pm, I I, p, m} R_{b}) ς_{12}],

(112)

c_{l, m}^{(1)} = - \frac{1}{G_{l, m}^{(2)}} [Y_{l} (χ_{\pm, I I, p, m} R_{b}) ς_{11}], c_{l, m}^{(2)} = \frac{1}{G_{l, m}^{(2)}} [J_{l} (χ_{\pm, I I, p, m} R_{b}) ς_{11}],

(113)

b_{l, m}^{(1)} = \frac{1}{G_{l, m}^{(1)}} [- J_{l} (χ_{\pm, I, b p, m} R_{b}) ϑ_{14} + Y_{l} (χ_{\pm, I I, p, m} R_{b}) ϑ_{12}],

(114)

b_{l, m}^{(2)} = \frac{1}{G_{l, m}^{(1)}} [- J_{l} (χ_{\pm, I, b p, m} R_{b}) ϑ_{13} - J_{l} (χ_{\pm, I I, p, m} R_{b}) ϑ_{12}],

(115)

d_{l, m}^{(1)} = \frac{1}{G_{l, m}^{(1)}} [Y_{l} (χ_{\pm, I I, p, m} R_{b}) ϑ_{11}], d_{l, m}^{(2)} = - \frac{1}{G_{l, m}^{(1)}} [J_{l} (χ_{\pm, I I, p, m} R_{b}) ϑ_{11}],

(116)

G_{l, m}^{(1)} = [Y_{l} (χ_{\pm, I I, p, m} R_{b}) ϑ_{13} - J_{l} (χ_{\pm, I I, p, m} R_{b}) ϑ_{14}],

(117)

G_{l, m}^{(2)} = [Y_{l} {(χ_{\pm, I I, p, m} R_{b})}_{13} - J_{l} (χ_{\pm, I I, p, m} R_{b}) ϑ_{14}],

(118)

\begin{matrix} ϑ_{11} = \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [Θ 7_{l, m} \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} J_{l} (χ_{\pm, I, b p, m} R_{b}) - S_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 4_{l, m} Θ 7_{l, m} - Θ 3_{l, m} Θ 8_{l, m}] - \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [Θ 7_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 8_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [P_{l, m} Θ 7_{l, m} - S_{l, m} Θ 3_{l, m}] \end{matrix}

(119)

\begin{matrix} ϑ_{12} = \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [T_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 4_{l, m} Θ 7_{l, m} - Θ 3_{l, m} Θ 8_{l, m}] - [Q_{l, m} Θ 7_{l, m} + T_{l, m} Θ 3_{l, m}] \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [Θ 7_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 8_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] \end{matrix}

(120)

\begin{matrix} ϑ_{13} = {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 4_{l, m} Θ 7_{l, m} - Θ 3_{l, m} Θ 8_{l, m}] [Θ 5_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] - {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 7_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 8_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 7_{l, m} Θ 1_{l, m} + Θ 5_{l, m} Θ 3_{l, m}] \end{matrix}

(121)

\begin{matrix} ϑ_{14} = {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 6_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 4_{l, m} Θ 7_{l, m} - Θ 3_{l, m} Θ 8_{l, m}] - {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 7_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 8_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 2_{l, m} Θ 7_{l, m} + Θ 6_{l, m} Θ 3_{l, m}] \end{matrix}

(122)

\begin{matrix} ς_{11} = \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [Θ 5_{l, m} \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} J_{l} (χ_{\pm, I, b p, m} R_{b}) - T_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 2_{l, m} Θ 5_{l, m} - Θ 1_{l, m} Θ 6_{l, m}] - \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [Θ 5_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 6_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Q_{l, m} Θ 5_{l, m} - T_{l, m} Θ 1_{l, m}] \end{matrix}

(123)

\begin{matrix} ς_{12} = \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [S_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 2_{l, m} Θ 5_{l, m} - Θ 1_{l, m} Θ 6_{l, m}] - [P_{l, m} Θ 5_{l, m} + S_{l, m} Θ 1_{l, m}] \frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}} [Θ 5_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 6_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] \end{matrix}

(124)

\begin{matrix} ς_{13} = {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 2_{l, m} Θ 5_{l, m} - Θ 1_{l, m} Θ 6_{l, m}] [Θ 7_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] - {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 5_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 6_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 3_{l, m} Θ 5_{l, m} + Θ 7_{l, m} Θ 1_{l, m}] \end{matrix}

(125)

\begin{matrix} ς_{14} = {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 8_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 2_{l, m} Θ 5_{l, m} - Θ 1_{l, m} Θ 6_{l, m}] - {(\frac{χ_{\pm, I I, p, m}}{χ_{\pm, I, b p, m}})}^{2} [Θ 5_{l, m} Y_{l} (χ_{\pm, I I, p, m} R_{b}) - Θ 6_{l, m} J_{l} (χ_{\pm, I I, p, m} R_{b})] [Θ 4_{l, m} Θ 5_{l, m} + Θ 1_{l, m} Θ 8_{l, m}] \end{matrix}

(126)

By imposing the following conditions at the helix

1 δ {\hat{E}}_{z, l, m} (R_{h} - ε) = δ {\hat{E}}_{z, l, m} (R_{h} + ε)

(127)

2 δ {\hat{E}}_{θ, l, m} (R_{h} - ε) = δ {\hat{E}}_{θ, l, m} (R_{h} + ε)

(128)

D_{l, m} and K_{l, m} are given by

D_{l, m} = \frac{1}{W_{l} (χ_{m} R_{g}, χ_{m} R_{h})} \{A_{l, m} [a_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} R_{h}) + a_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} R_{h})] + i F_{l, m} [c_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} R_{h}) + c_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} R_{h})]\}

(129)

K_{l, m} = \frac{χ_{\pm, I I, p, m}}{χ_{m} W_{l}^{^{''}} (χ_{m} R_{g}, χ_{m} R_{h})} [F_{l, m} ϕ_{l, m}^{(1)} + i A_{l, m} ϕ_{l, m}^{(2)}],

(130)

where

\begin{matrix} ϕ_{l, m}^{(1)} = [b_{l, m}^{(1)} J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + b_{l, m}^{(2)} Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + \frac{c k_{m} R_{p} (ω, k_{m})}{ω} [c_{l, m}^{(1)} J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + c_{l, m}^{(2)} Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + \frac{l}{χ_{\pm, I I, p, m} R_{h}} \frac{c k_{m}}{ω} R_{p} (ω, k_{m}) [c_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} R_{h}) + c_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} R_{h})] + R_{p} (ω, k_{m}) [b_{l, m}^{(1)} J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + b_{l, m}^{(2)} Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + \frac{l}{χ_{\pm, I I, p, m} R_{h}} R_{p} (ω, k_{m}) [b_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} R_{h}) + b_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} R_{h})] \end{matrix}

(131)

\begin{matrix} ϕ_{l, m}^{(2)} = [d_{l, m}^{(1)} J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + d_{l, m}^{(2)} Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] - \frac{c k_{m} R_{p} (ω, k_{m})}{ω} [a_{l, m}^{(1)} J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + a_{l, m}^{(2)} Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] - \frac{l}{χ_{\pm, I I, p, m} R_{h}} \frac{c k_{m}}{ω} R_{p} (ω, k_{m}) [a_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} R_{h}) + a_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} R_{h})] + R_{p} (ω, k_{m}) [d_{l, m}^{(1)} J_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + d_{l, m}^{(2)} Y_{l}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + \frac{l}{χ_{\pm, I I, p, m} R_{h}} R_{p} (ω, k_{m}) [d_{l, m}^{(1)} J_{l} (χ_{\pm, I I, p, m} R_{h}) + d_{l, m}^{(2)} Y_{l} (χ_{\pm, I I, p, m} R_{h})] \end{matrix}

(132)

To obtain the final dispersion relation, we must employ the discontinuity conditions in the axial and azimuthal magnetic fields due to the helix current sheet as follows:

1 δ {\hat{B}}_{z, l, m} (R_{h} - ε) - δ {\hat{B}}_{z, l, m} (R_{h} + ε) = \frac{4 π}{c} δ {\hat{J}}_{‖} Δ R_{h} cos φ,

(133)

2 δ B_{θ, l, m} (R_{h} + ε) - δ B_{θ, l, m} (R_{h} - ε) = \frac{4 π}{c} δ J_{‖} Δ R_{h} sin φ,

(134)

where, δJ_∥ is the surface current density parallel to the helix [18].

The only non-vanishing terms in the decomposition of the helix current are those for l = −m [18].

By employing Eqs. (129)–(134) and onerous manipulations, we get:

A_{- m, m} = \frac{4 δ {\hat{J}}_{l l} Δ R_{h}}{c} [\frac{- i W_{- m}^{^{''}} (χ_{m} R_{g}, χ_{m} R_{h}) cos φ T_{3} - i χ_{m}^{2} sin φ T_{1}}{T_{1} T_{4} + T_{3} T_{2}}],

(135)

F_{- m, m} = \frac{4 π δ J_{l l} Δ R_{h}}{c} [\frac{W_{- m}^{^{''}} (χ_{m} R_{g}, χ_{m} R_{h}) cos φ T_{4} - χ_{m}^{2} sin φ T_{2}}{T_{1} T_{4} + T_{3} T_{2}}],

(136)

where T₁, T₂, T₃, T₄ are:

\begin{matrix} T_{1} = [b_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + b_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] W_{- m}^{^{''}} (χ_{m} R_{g}, χ_{m} R_{h}) - \frac{χ_{\pm, I I, p, m}}{χ_{m}} W_{- m}^{^{'}} (χ_{m} R_{g}, χ_{m} R_{h}) ϕ_{- m, m}^{(1)} \end{matrix}

(137)

\begin{matrix} T_{2} = [d_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + b_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] W_{- m}^{^{''}} (χ_{m} R_{g}, χ_{m} R_{h}) - \frac{χ_{\pm, I I, p, m}}{χ_{m}} W_{- m}^{^{'}} (χ_{m} R_{g}, χ_{m} R_{h}) ϕ_{- m, m}^{(2)} \end{matrix}

(138)

\begin{matrix} T_{3} = - \frac{m k_{m}}{R_{h}} \frac{χ_{\pm, I I, p, m}}{χ_{m}} \frac{W_{- m}^{^{'}} (χ_{m} R_{g}, χ_{m} R_{h})}{W_{- m}^{^{''}} (χ_{m} R_{g}, χ_{m} R_{h})} ϕ_{- m, m}^{(1)} + \frac{χ_{m}}{c W_{- m} (χ_{m} R_{g}, χ_{m} R_{h})} [Y_{- m} (χ_{m} R_{g}) J_{- m}^{^{'}} (χ_{m} R_{h}) - J_{- m} (χ_{m} R_{g}) Y_{- m}^{^{'}} (χ_{m} R_{h})] [c_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + c_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] + \frac{m k_{m}}{R_{h}} [b_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + b_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] - [\frac{χ_{\pm, I I, p, m}}{c} + k_{m} R_{p} (ω, k_{m}) \frac{c k_{m}}{ω} χ_{\pm, I I, p, m}] [c_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + c_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + k_{m} R_{p} (ω, k_{m}) \frac{c k_{m}}{ω} \frac{m}{R_{h}} [c_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + c_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] - k_{m} R_{p} (ω, k_{m}) χ_{\pm, I I, p, m} [b_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + b_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + k_{m} R_{p} (ω, k_{m}) \frac{m}{R_{h}} [b_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + b_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] \end{matrix}

(139)

\begin{matrix} T_{4} = \frac{m k_{m}}{R_{h}} \frac{χ_{\pm, I I, p, m}}{χ_{m}} \frac{W_{- m}^{^{'}} (χ_{m} R_{g}, χ_{m} R_{h})}{W_{- m}^{^{''}} (χ_{m} R_{g}, χ_{m} R_{h})} ϕ_{- m, m}^{(2)} + \frac{χ_{m} ω}{c W_{- m} (χ_{m} R_{g}, χ_{m} R_{h})} [Y_{- m} (χ_{m} R_{g}) J_{- m}^{^{'}} (χ_{m} R_{h}) - J_{- m} (χ_{m} R_{g}) Y_{- m}^{^{'}} (χ_{m} R_{h})] [a_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + a_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] - \frac{m k_{m}}{R_{h}} [d_{- m, m}^{(1)} J_{- m} (_{\pm, I I, p, m} R_{h}) + d_{- m, m}^{(2)} Y_{- m} (_{\pm, I I, p, m} R_{h})] - [\frac{χ_{\pm, I I, p, m} ω}{c} + k_{m} R_{p} (ω, k_{m}) \frac{c k_{m}}{ω} χ_{\pm, I I, p, m}] [a_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + a_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + k_{m} R_{p} (ω, k_{m}) \frac{c k_{m}}{ω} \frac{m}{R_{h}} [a_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + a_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] + k_{m} R_{p} (ω, k_{m}) χ_{\pm, I I, p, m} [d_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + d_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] - k_{m} R_{p} (ω, k_{m}) \frac{m}{R_{h}} [d_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + d_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] \end{matrix}

(140)

The final condition is that the electric field parallel to the helix must be zero,

\sum_{m = - \infty}^{\infty} exp [i k_{m} z - i m θ] [δ E_{z, - m, m} sin φ + δ E_{z, - m, m} cos φ] = 0,

(141)

The dispersion relation obtained by employing Eqs. (135) and (136) as follows:

\sum_{m = - \infty}^{m = \infty} exp [i k_{m} z - i m θ] \{Ψ_{m}^{(1)} + Ψ_{m}^{(2)}\} = 0,

(142)

where

Ψ_{m}^{(1)} = \frac{4 π δ {\hat{J}}_{‖} Δ R_{h}}{c} [\frac{- i W_{- m}^{″} (χ_{m} R_{g}, χ_{m} R_{h}) c o s φ T_{3} - i χ_{m}^{2} s i n φ T_{1}}{T_{1} T_{4} + T_{3} T_{2}}] [[a_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + a_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] (sin φ + \frac{m k_{m}}{χ_{m}^{2} R_{h}} cos φ [1 + R_{p} (ω, k_{m})]) + [d_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + d_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] (\frac{ω χ_{\pm, I I, p, m}}{c χ_{m}^{2}} cos φ [1 + R_{p} (ω, k_{m})]) - \frac{k_{m} χ_{\pm, I I, p, m}}{χ_{m}^{2}} R_{p} (ω, k_{m}) cos φ [a_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + a_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] - \frac{m ω}{c R_{h} χ_{m}^{2}} R_{p} (ω, k_{m}) cos φ [d_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + d_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})]],

(143)

And

ψ_{m}^{(2)} = \frac{i 4 π δ {\hat{J}}_{‖} Δ R_{h}}{c} [\frac{W_{- m}^{″} (χ_{m} R_{g}, χ_{m} R_{h}) cos φ T_{4} - χ_{m}^{2} sin φ T_{2}}{T_{1} T_{4} + T_{3} T_{2}}] [[c_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + c_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})] (sin φ + \frac{m k_{m}}{χ_{m}^{2} R_{h}} cos φ [1 + R_{p} (ω, k_{m})]) - [b_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + b_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] (\frac{ω χ_{\pm, I I, p, m}}{c_{m}^{2}} cos φ [1 + R_{p} (ω, k_{m})]) - \frac{k_{m} χ_{\pm, I I, p, m}}{χ_{m}^{2}} R_{p} (ω, k_{m}) cos φ [c_{- m, m}^{(1)} J_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h}) + c_{- m, m}^{(2)} Y_{- m}^{^{'}} (χ_{\pm, I I, p, m} R_{h})] + \frac{m ω}{c R_{h} χ_{m}^{2}} R_{p} (ω, k_{m}) cos φ [b_{- m, m}^{(1)} J_{- m} (χ_{\pm, I I, p, m} R_{h}) + b_{- m, m}^{(2)} Y_{- m} (χ_{\pm, I I, p, m} R_{h})]] .

(144)

Numerical results and conclusions

Cold helix analysis

We analyze the dispersion characteristic of the slow-wave structure from the numerical computation of the dispersion equation (142). The nominal parameters of this system correspond to a helix with a period $λ_{h} = 1.966 cm$ , a width $ς_{h} = 0.764 cm$ and a radius of $R_{h} = 1.4 cm$ enclosed within a wall of radius $R_{w} = 3.63 cm$ .

Figure 2a–d shows the plot of the frequency versus wave number of four modes for several values of cyclotron frequency. It is clear that in these figures for wave number approximately greater than 0.45, the frequency for (X_bp − X_p) and (O_bp − X_p) modes increases with cyclotron frequency, while decreases for (O_bp − O_p) and (X_bp − O_p) modes.

Figure 3a–d illustrates the phase velocity as a function of frequency for different values of cyclotron frequency. Figure 3a and d indicates that for (X_bp − X_p) and (O_bp − X_p) modes, for f < 1.5 GHz the phase velocity decreases with cyclotron frequency and for f > 1.5 GHz increases. Figure 3b and c shows that for (O_bp − O_p) and (X_bp − O_p) modes, for f < 1.4 GHz phase velocity increases with cyclotron frequency and for f > 1.4 GHz decreases.

Figure 4a–d illustrates the frequency as a function of wave number for different values of the plasma density. As seen in these figures, the frequencies of all modes increase with plasma frequency for 0.5 < k < 0.8.

Figure 5a–d illustrates the phase velocity as a function of frequency for different values of the plasma density. From the mentioned figures, it is clear that the phase velocity of four modes increases with the plasma density for 1.3 GHz < f < 2.4 GHz.

Hot helix analysis

Considering the hot helix analysis of the system for a beam voltage $V_{b} = 16 kv$ , beam current $I_{b} = 1.25 A$ and beam radius $R_{b} = 1 cm$ .

Figure 6 shows the frequency versus cyclotron frequency for $\hat{k} = k / k_{h} = 0.5$ . As seen in this figure, the frequency of all modes decreases with cyclotron frequency for 0.0 < Ω_ce < 0.03. It is clear from Fig. 6 that the frequency of (X_bp − X_p) and (O_bp − X_p) modes increases with cyclotron frequency and the (O_bp − O_p) and (X_bp − O_p) modes decreases, for 0.04 < Ω_ce < 0.12. The order of frequency for four modes is ω_X–X > ω_X–O > ω_O–X > ω_O–O.

Figure 7a–d illustrates the phase velocity as a function of frequency for different values of cyclotron frequency. From Fig. 7a and d, the phase velocity of (X_bp − X_p) and (O_bp − X_p) modes increases with the cyclotron frequency for 0.8 GHz < f < 2.8 GHz and Fig. 7b and c shows that the phase velocity of (O_bp − O_p) and (X_bp − O_p) modes decreases with the cyclotron frequency, for 1.9 GHz < f < 2.3 GHz.

The plot of the normalized frequency at $\hat{k} = 0.605$ as a function of plasma frequency is shown in Fig. 8. The frequencies of all modes increase with plasma frequency and the order of these frequencies is ω_X-X > ω_X-O > ω_O-X > ω_O–O.

Figure 9a–d illustrates the phase velocity as a function of frequency for different values of plasma frequency. The phase velocity of all modes increases with plasma frequency.

The phase velocity as a function of plasma frequency at f = 2.305 GHz is shown in Fig. 10. As shown in Fig. 10, the order of the phase velocity is v_phOX > v_phO > v_phX > v_phXO. This figure has good agreement with the simple dispersion relation of electromagnetic wave propagation inside the plasma that is, ω² = k²c² + ω ²_p . According to this relation, the phase velocity of electromagnetic wave inside the plasma is proportional to plasma frequency and the plasma frequency increases the phase velocity.

The plot of the normalized frequency as a function of beam–plasma frequency at $\hat{k} = 0.605$ is shown in Fig. 11. As seen in this figure, the frequency of (O_bp − O_p) mode with (O_bp − X_p) mode and (X_bp − X_p) mode with (X_bp − O_p) mode approximately coincides with each other and decreases and increases with beam density, respectively. The order of the normalized frequency is ω_X-X > ω_X-O > ω_O-X > ω_O–O.

The plot of the normalized phase velocity corresponding to f = 2.34 GHz as a function of beam density is illustrated in Fig. 12. The phase velocity of (X_bp − X_p) with (X_bp − O_p) modes and (O_bp − O_p) with (O_bp − X_p) modes approximately coincides with each other. As shown in Fig. 12, the order of the phase velocity is v_phXX > v_phXO > v_phOX > v_phOO.

The plot of the normalized frequency corresponding to $\hat{k} = 0.605$ as a function of beam energy (γ) is shown in Fig. 13a and b. As seen in Fig. 13a, for 1.005 < γ < 1.03, the frequency of the (O_bp − O_p) and (O_bp − X_p) modes decreases with beam energy and for 1.03 < γ < 1.1 increases. Also from Fig. 13b, for 1.005 < γ < 1.06, the frequency of the (X_bp − X_p) and (X_bp − O_p) modes increases with beam energy and for 1.08 < γ < 1.1 decreases. As shown in Fig. 13a and b, the orders of the normalized frequency are: ω_X-X > ω_X-O > ω_O-X > ω_O–O.

The plot of the normalized phase velocity corresponding to f = 2.34 GHz as a function of beam energy is illustrated in the Fig. 14. Figure 14 shows that, the phase velocity is a increasing function of the beam energy and remains constant after γ > 1.05. The order of the phase velocity is v_phXX > v_phOX > v_phXO > v_phOO for γ > 1.05.

Dispersion relation analysis

Figure 15 shows the plot of the growth rate as a function of frequency for all of the modes. As seen in the figure, the growth rate and the frequency bandwidth of the (X_bp − O_p) mode are greater than the other modes.

The variation in the normalized maximum growth rate ( ${(Im \hat{k})}_{Max}$ ) and frequency of maximum growth rate (f_Max) with the cyclotron frequency for four modes are shown in Figs. 16, 17, 18 and 19. It is clear from the Fig. 16 that, for the (X_bp − X_p) mode the ${(Im \hat{k})}_{Max}$ and f_Max increase with cyclotron frequency up to Ω_ce = 0.02 and remain relatively constant thereafter. It is clear that at sufficiently strong magnetic field, the electron motion will be effectively one dimensional since the transverse motion of the electron beam in the combined axial magnetic field and the RF fields of the helix will be suppressed. It is noteworthy that using plasma in the helix, not only the maximum growth rate will increase, but also the frequency increases as well. As seen in Fig. 17, for the (O_bp − O_p) mode the ${(Im \hat{k})}_{Max}$ and f_Max reach their highest value at Ω_ce = 0.05. The maximum growth rate and the frequency decrease with increasing the cyclotron frequency and remain approximately constant after Ω_ce = 0.07. Figure 18 shows that for (X_bp − O_p) mode the maximum growth rate and the frequency are increasing function of Ω_ce and remain relatively constant after Ω_ce = 0.09. Figure 19 illustrates that for (O_bp − X_p) mode the maximum growth rate and the respected maximum frequency have opposite behavior. It is clear from this figure that maximum gain and frequency are constant for Ω_ce > 0.11. From Figs. 16, 17, 18, and 19, one can conclude that the point where the maximum growth rate and frequency becomes constant is different for every mode. The angular rotation velocity for infinitely long non-neutral plasma column confined radially by a uniform magnetic field given by [4, 24] $ω_{r e}^{\pm} = Ω_{c e} / 2 γ \{1 \pm {(1 - 2 ω_{b}^{2} / Ω_{c e}^{2})}^{1 / 2}\}$ . In the presence of plasma or some positive ions laminar rotation frequency expressed by: $ω_{r e}^{\pm} = Ω_{c e} / 2 γ \{1 \pm {(1 - 2 ω_{b}^{2} / Ω_{c e}^{2} (1 - f - β_{b}^{2}))}^{1 / 2}\}$ . Here, $f$ is the fractional charge neutralization. The Brillouin flow in the case of propagation in vacuum corresponds to $Ω_{c e} \geq \sqrt{2} ω_{b} / γ^{3 / 2}$ and in the presence of plasma; we should be rewriting the right-hand side of the above equation as $2 ω_{b}^{2} (1 - f - β_{b}^{2}) / γ$ . In this case, there is no variation in the axial velocity across the beam. There is a maximum possible radial variation in the axial velocity of the beam as the axial magnetic field increases, $Ω_{c e} γ^{\frac{3}{2}} / \sqrt{2} ω_{b} \to \infty$ . This radial variation depends on the parameters of the beam and plasma. According to the above equation, the angular rotation frequency goes to zero as the magnetic field goes to infinity.

The variation in the ${(Im \hat{k})}_{Max}$ and f_Max with the plasma frequency for the four modes is shown in Figs. (20)-(23). Figure 20 shows that for (X_bp − X_p) mode for ω_p < 0.04, the maximum growth rate increases with plasma frequency and the frequency of the maximum growth rate decreases with plasma frequency. It is clear from the Fig. 20 that, for ω_p > 0.07, the maximum growth rate increases with increasing plasma frequency and the frequency of the maximum growth rate remains relatively constant.

Figure 21 shows that for (O_bp − O_p) mode, for ω_p < 0.04, the maximum growth rate increases with plasma frequency and the frequency of the maximum growth rate decreases. It is clear from Fig. 21 that for ω_p > 0.1, the maximum growth rate increases with plasma frequency and the frequency of the maximum growth rate remains relatively constant.

Figure 22 shows that for (X_bp − O_p) mode for ω_p > 0.1, the maximum growth rate increases with the increasing plasma frequency and the frequency of maximum growth rate remains relatively constant. Figure 23 shows that for (O_bp − X_p) mode the behaviors of the variation of the ${(Im \hat{k})}_{Max}$ and f_Max with increasing plasma frequency are the same as each other. The highest values of the growth rate and the frequency are at ω_p = 0.06. The presence of plasma strongly increases the growth rate. The presence of plasma should increase the growth rate of the electromagnetic wave. The growth rate is proportional to the Pierce gain parameter known in the theory of TWTs $C = {(Z I_{b} / 4 V_{b})}^{1 / 3}$ . Where, I_b is the electron beam current and Z is the coupling impedance of electrons to the wave, which depends on the transverse structure of the wave in the beam region. The coupling impedance of solid electron beam in the presence of plasma can be much larger than the vacuum case [25]. On the other hand, presence of plasma leads to higher field concentration inside the helix than outside.

Figure 24a shows the comparison between the maximum growth rates of the four modes as a function of the plasma frequency. It is clear that the behaviors of the (X_bp − X_p) with (X_bp − O_p) modes and (O_bp − O_p) with (O_bp − X_p) modes approximately have similar behavior. As seen in this figure, for ω_p < 0.02, all the modes approximately have an equal maximum growth rate. It is clear that for ω_p > 0.04, the maximum growth rate of (O_bp − X_p) mode is greater than the others.

Figure 24b shows the comparison between the maximum frequencies of the four modes as a function of the plasma frequency. It is clear that the behaviors of the (X_bp − X_p) with (X_bp − O_p) modes and (O_bp − O_p) with (O_bp − X_p) modes approximately have similar behavior. The variation in the normalized growth rate and the frequency of the maximum growth rate with the beam–plasma frequency for the all modes are shown in Figs. 25, 26, 27, and 28. Figure 25 shows that for (X_bp − X_p) mode, for ω_b < 0.0125, the maximum growth rate increases with beam density and the frequency of the maximum growth rate remains relatively constant. It is clear from the figure that for ω_b > 0.0225, the maximum growth rate and the maximum frequency have the opposite behavior.

Figure 26 shows that for (O_bp − O_p) mode, the maximum growth rate has a maximum value at ω_b = 0.025. As seen in this figure for ω_b > 0.025, the maximum growth rate decreases and the maximum frequency remains relatively constant.

Figure 27 shows that for (X_bp − O_p) mode for ω_b < 0.0225, the maximum growth rate increases and the maximum frequency decreases as the ω_b increases. As seen in this figure for ω_b > 0.03, the maximum growth rate and the maximum frequency remain relatively constant.

Figure 28 shows that for (O_bp − X_p) mode, for ω_b > 0.015, the maximum growth rate increases and the maximum frequency remains approximately constant. The efficiency of a plasma-filled device estimated in the same way as for vacuum Cherenkov device [26]. The electron efficiency is $η ≅ (γ + 1) / 2 \sqrt{(γ^{2} - 1)} C$ , and for low-voltage devices described by $η ≅ {(\sqrt{V_{b}} Z I_{b})}^{1 / 3}$ . The effect of beam energy and current is to increase the efficiency of device.

Figure 29 shows the comparison between the maximum growth rate of the four modes as a function of ω_b. It is clear that the behaviors of the (X_bp − X_p) and (X_bp − O_p) modes as a function of ω_b are the same as well as the behavior of the (O_bp − O_p) and (O_bp − X_p) modes. As seen in Fig. 29 for ω_b > 0.0125, the maximum growth rate of (O_bp − O_p) mode is higher than the others. Figure 30 shows the comparison between the maximum frequency of the four modes as a function of the ω_b. It is clear that the behaviors of the (X_bp − X_p) and (X_bp − O_p) modes as a function of ω_b are the same as well as the behavior of the (O_bp − O_p) and (O_bp − X_p) modes. As seen in Fig. 30 the maximum frequency of (X_bp − X_p) mode is higher than the others.

The variation in the normalized maximum growth rate and frequency of maximum growth rate with the beam energy effect for the four modes are shown in Figs. 31, 32, 33, and 34. As seen in Fig. 31, the maximum frequency remains relatively constant as the beam energy increases. Figure 31 shows that the highest value of the maximum growth rate occurs at a special value of beam energy. Figs. 32, 33 and 34 show that the maximum growth rate and frequency are constant for γ > 1.03, γ > 1.01 and γ > 1.015, respectively. It is consistent with Fig. 14 where the phase velocities of all modes are constant as the beam energy increases.

Conclusions

Now, we can summarize the specific results of this project as follows.

1.
In cold helix analysis, increasing in cyclotron frequency values, increases the normalized oscillation frequency ( $\hat{ω}$ ) and normalized phase velocity ( ${\hat{v}}_{ph}$ ) for (X_bp − X_p) and (O_bp − X_p) modes while decreases $\hat{ω}$ and ${\hat{v}}_{p h}$ for (O_bp − O_p) and (X_bp − O_p) modes.
2.
In cold helix analysis, increasing in plasma frequency values, increases the normalized oscillation frequency ( $\hat{ω}$ ) and normalized phase velocity ( ${\hat{v}}_{ph}$ ) for all of the four modes.
3.
In hot helix analysis, in special value of $\hat{k}$ the normalized frequency of all four modes for 0.0 < Ω_ce < 0.03 decreases and for higher values of Ω_ce the (X_bp − X_p) and (O_bp − X_p) modes are increase and (O_bp − O_p) and (X_bp − O_p) modes decrease. Increasing in the cyclotron frequency increases the phase velocity of (X_bp − X_p) and (O_bp − X_p) modes and decreases the phase velocity of (O_bp − O_p) and (X_bp − O_p) modes.
4.
In hot helix analysis, all of the four modes increase as the plasma frequency increases. As seen in these figures, the phase velocity is a decreasing function of frequency. The order of the phase velocity as a function of plasma frequency is v_phOX > v_phO > v_phX > v_phXO.
5.
In hot helix analysis, the normalized phase velocity of the (X_bp − X_p) and (X_bp − O_p) modes approximately coincides and increases as the ω_b increases, while the modes (O_bp − O_p) and (O_bp − X_p) coincide with each other and approximately stay constant as the ω_b increases.
6.
The phase velocity of all four modes in f = 2.34 GHz is increasing function of the beam energy and remains constant after γ > 1.05. The order of the phase velocity is v_phXX > v_phOX > v_phXO > v_phOO for γ > 1.05.
7.
One can conclude that the cyclotron frequency where the maximum growth rate and frequency becomes constant is different for every mode.
8.
The comparison between the maximum growth rates of the four modes as a function of the plasma frequency, ω_p shows that the behaviors of the (X_bp − X_p) and (X_bp − O_p) modes approximately are the same and the (O_bp − O_p) and (O_bp − X_p) modes have similar behavior. As seen in this figure, for ω_p < 0.02, all the modes approximately have an equal maximum growth rate.
9.
The comparison between the maximum growth rate of the four modes as a function of ω_b shows that the behaviors of the (X_bp − X_p) and (X_bp − O_p) modes as a function of ω_b are the same as well as the behavior of the (O_bp − O_p) and (O_bp − X_p) modes.
10.
The maximum growth rate and frequency are constant for, γ > 1.03, γ > 1.01 and γ > 1.015, respectively.

References

Shiffler, D., Nation, J.A., Graham, S.K.: A high-power, traveling wave tube amplifier. IEEE Trans. Plas. Sci. 18, 546 (1990)
Article Google Scholar
Sawhney, R., Maheshwari, K.P., Choyal, Y.: Effect of plasma on efficiency enhancement in a high power relativistic backward wave oscillator. IEEE Trans. Plas. Sci. 21, 609 (1993)
Article Google Scholar
Zavjalov, M.A., Mitin, L.A., Perevodchikov, V.I., Tskhai, V.N., Shapiro, A.L.: Powerful wideband amplifier based on hybrid plasma-cavity slow-wave structure. IEEE Trans. Plas. Sci. 22, 600 (1994)
Article Google Scholar
Nusinovich, G.S., Carmel, Y., Jr. Antonsen, T.M.: Recent progress in the development of plasma-filled traveling-wave tubes and backward-wave oscillators. IEEE Trans. Plasm. Sci.,26, 628 (1998)
Kobayashi Jr, S., Antonsen, T.M., Nusinovich, G.S.: Linear theory of a plasma loaded, helix type, slow wave amplifier. IEEE Trans. Plas. Sci. 26, 669 (1998)
Article Google Scholar
Pierce, J.R.: Travelling-Wave Tubes. New York: Van Nostrand Reinhold, ch. 3 (1950)
Hutter, R.G.: Beam and Wave Electronics in Microwave Tubes. New York: Van Nostrand, ch. 7 (1960)
Watkins, D.A.: Topics in Electromagnetic Theory. New York: Wiley, ch. 3 (1958)
Uhm, H.S., Choe, J.Y.: Properties of the electromagnetic wave propagation in a helix loaded waveguide. J. App. Phys. 53, 8483 (1982)
XiaoFang, Z., ZhongHai, Y., Bin, L.: Modeling of T- shaped vane loaded helical slow-wave structures. IEEE Trans. Plasma. Sci. 34, 563–571 (2006)
Article Google Scholar
Pierce, J.R., Field, L.M.: Traveling-wave tubes. Proc. IRE 35, 108 (1947)
Article Google Scholar
Chu, L.J., Jackson, J.D.: Field theory of traveling-wave tubes. Proc. IRE 36, 853–863 (1945)
Article Google Scholar
Yan-Yu, W., Wen-Xiang, W., Jia-Hong, S., Sheng-Gang, L., Jia, B.F., Park, G.S.: Dielectric effect on the rf characteristics of a helical groove travelling wave tube. Chin. Phys. B.11, 277–281 (2002)
Rydbeck, O.E.H.: Theory of the traveling wave tube. Ericsson Techn. 46, 3 (1948)
Google Scholar
Chodorow, M., Nalos, N.J.: The design of high-power traveling-wave tubes. Proc. IRE. 44, 649–659 (1956)
Article Google Scholar
Beck, A.H.W.: Space-Charge Waves. Pergamon, New York (1958)
MATH Google Scholar
Hutter, R.G.E.: Beam and Wave Electronics in Microwave Tubes. VanNostrand, New York (1960)
MATH Google Scholar
Freund, H.P., Vanderplaats, N.R., Kodis, M.A.: Field Theory of a Traveling Wave Tube Amplifier with a Tape Helix. IEEE Trans. Plasma Sci.21, 654–668 (1993)
Freund, H.P., Kodis, M.A., Vanderplaats, N.R.: Self-consistent field theory of a helix traveling wave tube amplifier. IEEE Trans. Plasma Sci. 20, 543–553 (1992)
Article Google Scholar
Kumar, M., Bhasin, L., Tripathi, V.K.: Plasma effects in a travelling wave tube. Phys. Scr.81, 025502 (1–6) (2010)
Pu-Kun, L., Hong-Quan, X.: Theoretical analysis of a relativistic travelling wave tube filled with plasma. Chin. Phy. B. 16, 766–771 (2007)
Article Google Scholar
Shkvarunets, A.G., Kobayashi, S., Weaver, J., Carmel, Y.. Rodgers, J., Antonsen, T.M., Granatstein, V.L., Destler, W.W.: Electromagnetic properties of corrugated and smooth waveguides filled with radially inhomogeneous plasma. IEEE Tran. Plasma. Sci.24(3), 905 (1996)
Nusinovich, G.S., et al.: Linear theory of a plasma loaded, helix type, slow wave amplifier , IEEE Trans. Plasm. Sci.26(3), 669(1998)
Davidson, RC.: Physics of Non-neutral Plasmas, Addison-wesley, New Jersey (1990)
Nusinovich, G.S., Mitin, L.A., Vlasov, A.N.: Space charge effects in plasma-filled traveling-wave tubes. Phys. Plasma 4, 4394 (1997)
Article Google Scholar
Gaponov- Grekhov, A.V., Granatstein, V.L.: Applications of High-Power Microwave, Eds. Boston, MA: Artech House, ch. 2 (1994)

Download references

Author information

Authors and Affiliations

Plasma Physics Research Center, Science and Research Branch, Islamic Azad University, Tehran, Iran
S. Saviz

Authors

S. Saviz
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Saviz.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.

Reprints and permissions

About this article

Cite this article

Saviz, S. The effect of beam and plasma parameters on the four modes of plasma-loaded traveling-wave tube with tape helix. J Theor Appl Phys 8, 135 (2014). https://doi.org/10.1007/s40094-014-0135-7

Download citation

Received: 07 April 2014
Accepted: 01 June 2014
Published: 02 July 2014
DOI: https://doi.org/10.1007/s40094-014-0135-7

Keywords

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

The effect of beam and plasma parameters on the four modes of plasma-loaded traveling-wave tube with tape helix

Abstract

Similar content being viewed by others

Dielectric-Loaded Plasma Filled Helix Traveling Wave Tube Analysis Based on the Linearized Field Theory

Designing a Beam-Plasma Traveling Wave Tube

Dispersion relation and growth rate in thermal plasma-loaded traveling wave tube with corrugated waveguide hollow electron beam

Introduction

Perturbed transfer fields

The dispersion relation