Introduction

In the recent years, the free-electron laser (FEL) in the presence of the plasma has been widely discussed. Pei et al. [1] have proposed and examined cold plasma-loaded FEL. They have shown that the efficiency of the FEL considerably enhanced in the presence of the dense plasma. Pant et al. [2] illustrated that in the whistler mode FEL the growth rate considerably enhanced in the presence of the plasma. Serbto et al. [3], by making use of the collective description derived by Bonifacio et al. [4], discussed the characteristic of a gas-filled FEL and shown that the efficiency and power enhanced considerably. Zongjon Shi [5] investigated the cylindrical waveguide with a cold plasma-loaded FEL and shown that growth rate is enhanced at low frequency and it is decreased at high frequency. The electron trajectories and gain in the whistler mode FEL were investigated by Jafari et al. [6, 7]. The effects of the two-stream instability on the linear gain and growth rate of the two-stream FEL in different configuration were investigated by Saviz et al. [8–10]. They discussed the gain in two-stream FEL with planar wiggler and ion-channel guiding. Especially it is necessary to study the thermal plasma-loaded FEL with helical wiggler.

In the present paper, we investigated the effect of plasma density and temperature on the electrostatic and electromagnetic mode of the two-stream FEL. The research is not done until now. We show that the effect of growth rate occurs at the special range of the plasma temperature and plasma density. Moreover, we show that because of the presence of the two-stream instability, the growth rate of the electrostatic mode is two times greater than that of the electromagnetic mode.

The configuration of the present paper is as follows: The physical model is given in “Physical model”. In “The general dispersion equation”, we obtain the general dispersion equation using linear fluid theory. The numerical results and discussion are given in “The characteristic of dispersion equation” and conclusions are given in “Conclusion”.

Physical model

The considered physical configuration is the idealized one-dimensional limit in which the two-stream relativistic electron beams are passing through the thermal plasma-loaded helical wiggler. We consider that the two-electron beams are moving along the z direction. The idealized helical wiggler magnetic field is described by the vector potential as follows:

$$ A_{\text{w}} (z) = - A_{\text{w}} [\hat{e}_{x} \cos (k_{\text{w}} z) + \hat{e}_{y} \sin (k_{\text{w}} z)], $$
(1)

where, A w = B w/k w, λ w = 2π/k w and λ w is the wiggler period, k w is the wiggler wave number, and B w denotes the amplitude of wiggler field. The vector potential of optical field is given as follows:

$$ A_{\text{s}} (z,t) = (B_{\text{s}} /k_{\text{s}} )[\hat{e}_{x} \cos (k_{\text{s}} z - w_{\text{s}} t + \varphi_{\text{s}} (t)) - \hat{e}_{y} \sin (k_{\text{s}} z - w_{\text{s}} t + \varphi_{\text{s}} (t))], $$
(2)

where, k s is optical wave number, B s is the field strength and φ s(t) is initial of optical phase, which is usually looked as zero. The interaction among electron beams, background thermal plasma and optical field is described by the wave equation as follows:

$$ \left( {{{\partial^{2} } \mathord{\left/ {\vphantom {{\partial^{2} } {\partial z^{2} }}} \right. \kern-0pt} {\partial z^{2} }} - (1/c^{2} ){{\partial^{2} } \mathord{\left/ {\vphantom {{\partial^{2} } {\partial t^{2} }}} \right. \kern-0pt} {\partial t^{2} }}} \right)\vec{A}_{ \, } = - (4\pi /c)\vec{J}_{ \bot } , $$
(3)

where the transverse current is as follows:

$$ J_{ \bot } = - \frac{{en_{0p} }}{m}\delta P_{p \bot } - \frac{{en_{0b1} }}{{\gamma_{01} m}}\delta P_{b \bot 1} - \frac{{en_{0b2} }}{{\gamma_{02}^{{}} m}}\delta P_{b \bot 2} - \frac{{eP_{0b \bot 1} }}{{\gamma_{01} m}}\delta_{nb1} - \frac{{eP_{0b \bot 2} }}{{\gamma_{02} m}}\delta_{nb2} , $$
(4)

In Eq. (3b), n 0p and n 0b are the plasma and electron beams density, respectively. The P 0b⊥1 and P 0b⊥2 are the two-beam transverse momentum, and γ 01 and γ 02 are relativistic factor for two beams. The electrostatic field is as follows:

$$ \vec{E}_{z} (t) = \hat{e}_{z} E_{z} \sin [ - k_{1} z + w_{1} t + \theta ] = \hat{e}_{z} E_{z} \sin (\varPsi + \delta ) $$
(5)

where Ψ = −k 1 z + w 1 t is the pondermotive wave phase, and δ is the mismatch phase of a three-wave interaction. The phase-matching condition is given by w 1 = −w s and k 1 = −(k s  + k w ). In Eq. (5), E z is the total longitudinal electric field produced by perturbed density of two-electron beams and background thermal plasma given by Poisson Equation:

$$ {{\partial E_{z} } \mathord{\left/ {\vphantom {{\partial E_{z} } {\partial z}}} \right. \kern-0pt} {\partial z}} = - 4\pi e(\delta n_{b1} + \delta n_{b2} + \delta n_{p} ). $$
(6)

The general dispersion equation

The momentum transfer equation for the electron beams and plasma is obtained as follows:

$$ d\vec{P}_{\text{b}} /dt = - e\left[ {\vec{E}_{z} + \vec{E}_{\text{s}} + V_{\text{b}} /c \times (\vec{B}_{\text{w}} + \vec{B}_{\text{s}} )} \right], $$
(7)

By linearizing the Eq. (8) with P b1,2 = P 01,2 + δP b1,2 and n b1,2 = n 01,2 + δn b1,2, the equilibrium and perturbed momentum of electron beam are obtained as follows:

$$ P_{01,2} = e/(cA_{\text{w}} ) + \gamma_{01,2} mv_{01,2} ,\;\delta P_{b1,2} = (e/c)A_{s} . $$
(8)

Using the momentum equation, the following equations are obtained for the plasma:

$$ d(m\delta \vec{v}_{{{\text{p}} \bot }} )/dt = (e/c)\partial /\partial t\vec{A}_{\text{s}} - (e/c)\delta \vec{v}_{\text{pz}} \times \vec{B}_{\text{w}} , $$
(9)
$$ d(m\delta \vec{v}_{\text{pz}} )/dt = - eE_{\text{z}} - (e/c)\delta \vec{v}_{{{\text{p}} \bot }} \times \vec{B}_{\text{w}} - (3k_{b} T_{e} /n_{{ 0 {\text{p}}}} m_{\text{e}} )(\partial \delta n_{\text{p}} /\partial z), $$
(10)

where T e is the plasma electron temperature and k b is the Boltzman constant.

After some straightforward algebra, the dispersion relation is obtained by Eqs. (3)–(10) as follows:

$$ \begin{gathered} (w_{\text{s}}^{2} - c^{2} k_{\text{s}}^{2} - \omega_{\text{p}}^{ 2} - (\omega_{\text{b1}}^{2} /\gamma_{01} ) - (\omega_{\text{b2}}^{2} /\gamma_{02} ))\{ [(w_{1} - k_{1} v_{1} )^{2} (w_{1} - k_{1} v_{2} )^{2} - (\omega_{\text{b1}}^{2} /\gamma_{01}^{3} )(w_{1} - k_{1} v_{2} )^{2} - (\omega_{\text{b2}}^{2} /\gamma_{02}^{3} )(w_{1} - k_{1} v_{1} )^{2} ](w_{1}^{2} - \omega_{\text{ce}}^{2} /2 - \omega_{\text{T}}^{2} - \omega_{\text{p}}^{2} ) \hfill \\ - \omega_{\text{p}}^{2} (w_{\text{s}}^{2} - c^{2} k_{\text{s}}^{2} - \omega_{\text{p}}^{2} - (\omega_{{{\text{b}}1}}^{2} /\gamma_{01} ) - (\omega_{\text{b2}}^{2} /\gamma_{02} )) \hfill \\ \{ [(w_{1} - k_{1} v_{1} )^{2} (w_{1} - k_{1} v_{2} )^{2} - (\omega_{\text{b1}}^{ 2} /\gamma_{01}^{3} )(w_{1} - k_{1} v_{2} )^{2} - (\omega_{\text{b2}}^{2} /\gamma_{02}^{3} )(w_{1} - k_{1} v_{1} )^{2} ](w_{1}^{2} - \omega_{\text{ce}}^{ 2} /2 - \omega_{\text{T}}^{2} \hfill \\ - \omega_{\text{p}}^{ 2} ) - \omega_{\text{p}}^{2} - 2k_{1} (\omega_{\text{p}}^{2} \omega_{\text{b1}}^{2} /\gamma_{01}^{4} k_{\text{w}} )(w_{1} - k_{1} v_{2} )^{2} - 2k_{1} \omega_{\text{p}}^{2} \omega_{\text{b2}}^{2} /(k_{\text{w}} \gamma_{02}^{4} )(w_{1} - k_{1} v_{1} )^{2} + \omega_{\text{p}}^{2} [(w_{1} - k_{1} v_{1} )^{2} \hfill \\ (w_{1} - k_{1} v_{2} )^{2} - (\omega_{\text{b1}}^{ 2} /\gamma_{01}^{3} )(w_{1} - k_{1} v_{2} )^{2} - (\omega_{\text{b2}}^{ 2} /\gamma_{02}^{3} )(w_{1} - k_{1} v_{1} )^{2} ] + 2(\omega_{\text{b1}}^{ 2} /\gamma_{01}^{4} )(\omega_{\text{b2}}^{2} /\gamma_{01}^{4} )(k_{1} /k_{\text{w}} )^{2} \hfill \\ (w_{1}^{2} - \omega_{\text{ce}}^{2} /2 - \omega_{\text{T}}^{ 2} ) - (k_{1} /k_{\text{w}} )^{2} (w_{1}^{2} - \omega_{\text{ce}}^{ 2} /2 - \omega_{\text{T}}^{2} )[\omega_{\text{b1}}^{2} \omega_{\text{b2}}^{2} /(\gamma_{01}^{5} \gamma_{02}^{3} ) + \omega_{\text{b1}}^{ 2} \omega_{\text{b2}}^{2} /(\gamma_{02}^{5} \gamma_{01}^{3} )]] = 0 \hfill \\ \end{gathered} $$
(11)

where ω 2p  = 4πn 0p e 2/m e, ω 2b1,2  = 4πn 0b1,2 e 2/m e, ω 2T  = 3k b T e k 2/m e, w 1 = w s and k 1 = k w + k s.

The characteristic of dispersion equation

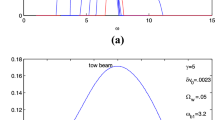
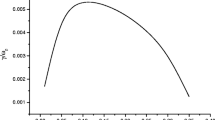
In this section, we focus on the characteristic of the dispersion equation, Eq. (11), through the numerical analysis. In the numerical calculation, we have found two unstable growing roots: one for electrostatic wave and the other for electromagnetic wave. In the presence of the thermal plasma, we have illustrated the growth rate as a function of normalized wave number (k/k w) and plasma electron temperature (T e). Figure 1a shows the growth rate (Imω/(ck w)) of the electrostatic mode with respect to the plasma temperature, T e (in the region 0.4 × 107 K < T e < 0.6 × 107 K). In this figure, the parameters used are chosen to be γ 1 = 1.25, γ 2 = 1.232, B w  = 2000G, n p  = 2.5 × 1011/cm 3 and n b1,2 = 4 × 108/cm 3. As shown in this figure, the growth rate rapidly increases with plasma temperature and reaches the maximum near the plasma optimum temperature, and decreases when the plasma temperature was above the optimum value. These interesting phenomena come from the interaction of two-stream instability coupling FEL instability. Figure 1b shows the growth rate (Imω/(ck w)) of the electromagnetic mode with respect to the plasma temperature, T e (in the region 0.4 × 107 K < T e < 0.6 × 107 K). As seen in Fig. 1b, the maximum values of wave number occur in the special range of plasma temperature (nearly 0.5 × 107 K < T e < 0.57 × 107 K). The effect of plasma density on the growth rate of electrostatic and electromagnetic modes, for specified values of parameters and range of normalized k(k/k w), is given in Fig. 2a, b, respectively. The chosen parameters are as: γ 1 = 1.25, γ 2 = 1.232, B w = 2000G, T e = 5 × 106 K and n b1,2 = 4 × 108/cm3. Figure 2a shows that at fixed values of wave number there is the critical plasma density after which the growth rate decreases gradually with plasma density. This phenomenon is because of the fact that the synchronism condition of electron beam and optical wave is destroyed at higher plasma density. The plasma effect on the electromagnetic mode is given in Fig. 2b. Figure 2b shows that increase in the plasma temperature causes the shift of wave number to the lower values. This figure also shows that the maximum growth rate of this instability occurs in the special range of plasma density corresponding to the given range of wave number. The growth rate of the electrostatic mode is two times greater than that of the electromagnetic mode. This difference is because of the fact that the two-stream instability affects the electrostatic mode and this difference is because of the two-stream instability. The growth rate as a function of the plasma density at k/k w = 1.0 is shown in Fig. 3 which is the 2D plot of Fig. 2a and is for clarity.

Fig. 1
figure 1

The normalized growth rate Im(ω/ck w) of the electrostatic wave as a function of k/k w and plasma electron temperature T e a for the electrostatic mode, and b for the electromagnetic mode

Full size image
Fig. 2
figure 2

The normalized growth rate Im(ω/ck w) of the electrostatic wave as a function of k/k w and plasma density n p a for the electrostatic mode, and b for the electromagnetic mode

Full size image
Fig. 3
figure 3

The normalized growth rate Im(ω/ck w) of the electrostatic wave versus plasma density n p for k/k w = 1.0

Full size image

Conclusion

In this work, we have investigated the instability of two-stream FELs that contain thermal plasma. The dispersion relation is obtained by employing the linear fluid theory and calculated numerically. The results show that the growth rate depends on the plasma temperature and plasma density. It was found that the growth rate in the special values of the plasma temperature enhances considerably and the growth rate after critical plasma density gradually decreases. In the plasma-loaded FEL [1–5], all authors use the single-electron beam but in the present work we use the two-electron beams. In the single electron beam case there is only the electromagnetic mode but as seen the results there is the new electrostatic mode that is two times stronger than electromagnetic mode. The electrostatic mode does not appear in single-stream FEL.