Introduction

Water quality is controlled by many factors including climate, soil topography, and water rock interaction (Farnham et al. 2003; Love et al. 2004; Li et al. 2016a, b). These factors lead to a variation in hydrogeochemical process of groundwater using statistical techniques. Detailed hydrochemical research is needed to evaluate the different processes and mechanisms involved in polluting water (Helena et al. 1999). Earlier studies have been focused in hydrogeochemical process of groundwater using statistical analysis (Ashley and Llyod 1978; Reghunath et al. 2002; Liu et al 2003; Monjerezi et al. 2008; Nagaraju et al. 2014a, b; Wu et al. 2014; Li et al. 2016a, b). These techniques constitute a useful tool for groundwater quality characterization for identification of the regional groundwater flow pattern and investigation of groundwater contamination like trace elements (Voudouris et al. 1997; Cloutier et al. 2008; Belkhiri et al. 2010; Kumar et al. 2013). The multivariate statistical analysis methods have the advantage of explaining complex water quality monitoring data. Earlier workers have been successfully applied to a number of hydrogeochemical studies (Singh et al. 2005; Kowalkowskia et al. 2006; Boyacioglu 2008; Wu et al. 2014; Nagaraju et al. 2016a, b). Further, these studies have shown that multivariate statistical analysis can help to interpret the complex datasets, and it is useful in verifying temporal and spatial variations caused by natural and anthropogenic factors. Surface water, groundwater quality assessment, and environmental research employing multi-component techniques are well described in the literature (Praus 2005). Multivariate statistical approaches allow deriving hidden information from the dataset about the possible influences of the environment on water quality (Spanos et al. 2003).

This multivariate method was used here to obtain information about the most relevant characteristics of the physico-chemical variables with a minimal loss of original data (De Bartolomeo et al. 2004; Altun et al. 2008; Kazi et al. 2009), to create an entirely new set of factors much smaller in number when compared to the original dataset of variables focused on reducing the contribution of the less significant variables to simplify even more the data structure coming from the principal component analysis (İşçen et al. 2008).

Factor analysis attempts to explain the correlations between the observations in terms of the underlying factors, which are not directly observable (Yu et al. 2003). There are three stages in factor analysis (Gupta et al. 2005): for all the variables a correlation matrix is generated, factors are extracted from the correlation matrix based on the correlation coefficients of the variables, and to maximize the relationship between some of the factors and variables, the factors are rotated. Cluster Analysis was used to explore the similarities between water samples (Kotti et al. 2005) and grouping the sites according to the similarity of contaminants. Hierarchical agglomerative CA was performed on the normalized dataset using squared Euclidean distances as a measure of similarity. The CA technique is a classification procedure that involves measuring either the distance or the similarity between the objects to be clustered.

Therefore, the main objectives of the present study are the following: (i) to assess the status of water quality in relation to physico-chemical parameters; (ii) to assess the correlations between the different water quality parameters (iii) to find out the similarities and dissimilarities among the different sampling sites, and (iv) to ascertain the influence of the pollution sources on the water quality variables.

Area of study

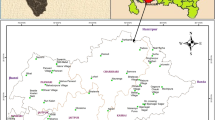
This study area is about 40 sq.km and is located in the Rapur Taluk of Nellore District, Andhra Pradesh. It forms part of the Survey of India toposheet No. 57 N/11 and lies between 14°16′ 30′′ forms and 14°19′N latitude and 79°38′ and 79°41′ east longitude (Fig. 1). The area is accessible by the Nellore Rapur road which passes through North–Western portion of the area. The area is characterized by hot and sub-humid climate and is in the tropical region. In general, the climate is good and is not subjected to sudden variations in temperature. The maximum, average, and minimum temperatures are 44, 31, and 18 °C respectively. They receive rainfall during the months of July, August, September, and October with maximum precipitation in October. The heavy rainfall is limited to a few days in a year due to depressions in Bay of Bengal which leads to flash floods of high discharge. The annual normal rainfall of this area is about 1084 mm. The dry climate, the atmospheric dust, and low intensity of precipitation affect the quality of precipitation water.

Fig. 1
figure 1

Map of the study area depicting sample locations

Full size image

Hydrogeological setting

This area lies in the semi-arid region of Andhra Pradesh and is susceptible to various threats such as growing urban areas as well as developing agricultural areas. This area is underlain by variety of geological formations comprising from the oldest archaeans to recent alluvium. Hydrogeologically, these formations are classified as consolidated (hard), semi-consolidated (soft), and unconsolidated (soft) formations. The consolidated formations include mainly migmatized high grade metamorphics (essentially garnetiferous amphibolites and pelitic schist), low grade metamorphics (essentially amphibolites and pelitic schists) of Nellore schist belt, and granitic gneiss and Cuddapahs (quartzites and shales) of Pre-cambrian period.

Ground water occurs in almost all geological formations, and its potential depends upon the nature of geological formations, geographical set up, incidence of rainfall, recharge, and other hydrogeological characters of the aquifer. Among the consolidated formations, gneisses are relatively good aquifers. Schistose formations also form potential aquifers when the wells tapping the contact zones with intrusives. Quartzites and shales of Cuddapah group are of little significance from the ground water point of view as they are restricted to the hilly terrain in the western margin of the district. In the consolidated formations, ground water occurs under unconfined to semiconfined conditions. Ground water is developed in these formations by dug wells, dug cum bore wells, and bore wells tapping weathered and fractured zones. The yield of the dug wells is in the range of 15–35 m3/day and reduces considerably during peak summer periods. The occurrence of fractures in these formations is limited to 40–60 m bgl and occasionally extends down to 70–80 m bgl. The bore wells in these formations generally tap the weathered and fractured zones.

Materials and methods

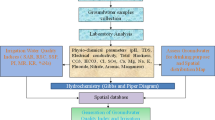
Groundwater samples were collected from 30 locations from Rapur area during April 2014 (Fig. 1). The collected water samples were transferred into precleaned polythene container for analysis of chemical characters. Samples were analyzed in the laboratory for the physico-chemical attributes like pH, electrical conductivity (EC), total hardness (TH), total dissolved solids (TDS), dissolved silica, and major ions (Ca2+, Mg2+, Na+, Cl–, CO3 2–, HCO3 –, and SO4 2–). All parameters were analyzed by following the standard methods (APHA 2005). The pH and conductivity were measured using Systronics micro pH meter model 361 and Deluxe conductivity meter model 601. Total hardness (TH), Ca2+, Mg2+, Cl–, CO3 2–, and HCO3 – were determined by titration. Na+ and K+ were measured by Flame photometry, SO42– by Lovibond spectrophotometer.

Statistical analysis

The descriptive statistics (minimum, maximum, mean, standard deviation, standard error, skewness, and kurtosis) were calculated for the physico-chemical variables in water samples. The Pearson correlation coefficient was obtained to describe the degree of association between two variables under study. Factor analysis was employed to establish the possible relationships between the physico-chemical variables of the sites sampled. Cluster analysis and principal component analysis (PCA) were applied to determine water quality. SPSS 16.0 version statistical program was used for descriptive statistics and multivariate data analysis.

Results and discussion

The descriptive statistics concerning quality of water from 30 stations are presented (Table 1). The range, mean, the standard error, and the standard deviation were shown for all studied parameters as well as other statistical parameters (skewness and kurtosis). From Table 1, it is clear that the 15 analyzed parameter values and standard deviation value range varies considerably. The analyzed parameter values and standard deviation value range vary considerably (Table 1; Fig. 2). From this, it is clear that there is a wide variation of studied parameters in the water. Skewness values of Ca, K, CO3, and hardness are bigger than the unit which means these parameters positively skewed toward lower concentrations, as can also be confirmed by the fact that their median concentrations are lower than their mean concentrations. Generally, the skewness and kurtosis values should be in the range of ±2, otherwise it is considered as extreme (Reimann et al. 2008). In the studied area, the K (skewness 2.539 and kurtosis 5.431), CO3 (skewness 2.062 and kurtosis 4.605), and hardness (skewness 1.645 and kurtosis 2.838) are considered to be extreme. This is due to the presence of outliers, which correspond to samples with elevated values of these concentrations.

Table 1 Descriptive statistics of the water quality parameters
Full size table
Fig. 2
figure 2

Frequency curves of water quality parameters

Full size image

Further, the Pearsons correlation coefficients for physico-chemical parameters of water in the study area are presented in Table 2. A significantly positive correlation at P < 0.01 was found between the elemental pairs EC–Mg (0.592), EC–Na + K (0.733), EC–K (0.548), EC–HCO3 (0.542), EC–Cl (0.810), EC–TDS (0.935), EC–hardness (0.588), and EC–alkalinity (0.542). The vide variety of EC concentrations, reflecting dissolved solutes, is related to lithology, land use, and human activity in the Rapur area (Rezaei and Sayadi 2015). It is obvious that pH and Si have relatively poor correlations with the other studied parameters except Si-alkalinity (0.489). Ca is also significantly positively correlated with hardness (0.552) (Wu et al. 2014) and negatively correlated with Na (−0.551) at P < 0.01 (Li et al. 2013a). Mg is also significantly positively correlated with HCO3, Cl, TDS, hardness, and alkalinity at P < 0.01. Na has relatively strong correlations (P < 0.01) with Na + K (0.572), Cl (0.546). A high positive correlation between Cl and Na concentrations has been reported (Giridharan et al. 2009; Li et al. 2013b, 2014).

Table 2 Pearson correlation coefficient of physico-chemical parameters of water
Full size table

Hierarchical cluster analysis (HCA)

The HCA is a data classification technique. There are different clustering techniques, but the hierarchical clustering is the one most widely applied in Earth sciences (Davis 1986), and often used in the classification of hydrogeochemical data (Steinhorst and Williams 1985; Schot and van der Wal 1992; Ribeiro and Macedo 1995; Güler et al. 2002). Cluster analysis was carried out to investigate the relationship among water quality parameters which play significant role in groundwater studies. Cluster analysis is also useful to handle large water quality datasets and identify the dominant mechanisms and factors which control the groundwater chemistry (Kouping et al. 2006). In the present study, the cluster analysis has provided sampled groups of similar stations and created a dendrogram (Fig. 3). This has resulted into four statistically significant clusters from 30 sampling stations of Rapur area. Further, the phenon line was drawn across the dendrogram and are scaled at a distance of cluster combination of about 8. Thus, this position of the phenon line allows a division of the dendrogram into 4 clusters of water samples. The first cluster consists of 6 locations (1, 2, 11, 12, 13, and 21), the second cluster is composed of samples from 5 locations (4, 5, 6, 7, and 24), the third one consists only two samples (23 and 28), and the rest samples form the last cluster.

Fig. 3
figure 3

Hierarchical cluster results of dendogram of sampling sites

Full size image

In the present study, Fig. 4 shows that the monitoring data obtained at 30 stations were classified and have produced a dendrogram. The clustering procedure generated two very convincing groups from the data. Cluster 1 consists of pH, Si, CO3, Mg, SO4, Ca, K, HCO3, alkalinity, Na, Na + K, Cl, and hardness, which may be representative of overall effects of water–rock interactions and rock weathering on general groundwater quality, as this cluster includes almost every cation and anion of groundwater. Cluster 2 has two contributive parameters: EC and TDS. These two parameters represent the salinity of groundwater. Thus, cluster 2 can be regarded as a salinity factor. It may represent the overall effects of climatic factors, especially the evaporation, on groundwater salinity. As the groundwater salinity is also influenced by human activities in this area, the values of EC and TDS variation at the stations were greatly shaped by human activities such as industrial and municipal and agricultural activities, in addition to the factor of climate change mentioned above (Sayadi et al. 2014).

Fig. 4
figure 4

Dendrogram of water quality parameters

Full size image

Principal component analysis (PCA)

The application of different multivariate statistical techniques, such as principal component analysis (PCA) assists in the interpretation of complex data matrices for a better understanding of water quality of a study area. A matter in the water quality monitoring is the complexity related with analyzing a large number of measured variables. The correlation matrix of variables was generated and factors were extracted by the centroid method, rotated by Varimax. From the results of Table 3, the first five eigenvalues were found to be bigger than 1 (Fig. 5).

Table 3 Extracted values of various factor analysis parameters along with total variance
Full size table
Fig. 5
figure 5

Screen plot of the eigenvalue and component number

Full size image

From Tables 3 and 4, it is clear that the first factor (factor 1), accounted for 36.218 of the total variance, had high positive loading in EC, Mg, Cl, TDS and Hardness which were 0.730, 0.900, 0.783, 0.769 and 0.909, respectively. This factor (factor 1) represents the contribution of EC to this factor, which can be considered a result of action-exchange processes in soil–water interface (Guo and Wang 2004). This factor also represents the contribution of point pollution and the physico-chemistry of the stream. The point pollution is from domestic wastewater, nonpoint pollution is from agricultural and livestock farms. Mg is a basic metal which increases Hardness of water (Razmkhah et al. 2010). Factor 2 explains 17.742% of the total variance and is positively correlated with K, Na + K, and HCO3 which were 0.931, 0.788 and 0.584, respectively. This factor may also be due to anthropogenic activities such as domestic waste water or influents. The loading for factor 3 was 11.470% for Ca and Na which is correlated at −0.788 and 0.902, respectively. Thus, this factor contains hydrogeochemical variable Ca, originating, at a first glance, from mineralization of the geological components of soils. The contribution of Ca to this factor can be considered a result of action-exchange processes in soil–water interface (Guo and Wang 2004).

Table 4 Rotated component loading matrix (loadings of 15 experimental variables)
Full size table

Factor 4 explains 10.565% of the total variance and is positively correlated with pH, Si, CO3 and alkalinity which were 0.605, 0.657, 0.666, and 0.706, respectively. This factor contains hydrogeochemical variable pH, Si, CO3, originating, at a first glance, from mineralization of the geological components of soils. The loading for factor 5 was 7.916% for SO4 which is correlated at 0.916. The sources of dissolved SO4 in natural waters may include dissolution of sedimentary sulfates, oxidation of both sulfide minerals and organic materials, and anthropogenic inputs.

Piper diagram

Piper (1944) based on the concentration of dominant cations and anions have proposed a trilinear diagram to show the percentages at mill equivalents per liter of cations and anions in water samples. The Piper diagram was modified by Davis and Dewiest (1967). This is useful to understand the total chemical character of water samples in terms of cation–anion pairs. The Piper diagram reveals similarities and differences among groundwater samples because those with similar qualities will tend to plot together as groups (Todd 2001). This diagram is very useful in bringing out chemical relationships among groundwater in more definite terms (Walton 1970). The Piper diagram consists of two triangular and one intervening diamond-shaped field (Fig. 6). The percentage reacting values at the three cation groups—Ca, Mg, and (Na + K)—are plotted as a single point in the left triangular field and the three anion groups—(HCO3 + CO3), SO4, and Cl—similarly on the right triangular field. The plots suggest that among cations Ca2+ do not have a clear dominance, and the other two major cations (Mg2+ and Na+) have greater dominance than Ca2+. Among anions Cl− dominate in the groundwater samples. From Fig. 6, it is clear that the rate of increase in the concentration of Cl− ions is more than SO4 2+ ions. It may be due to dissolution of evaporate minerals such as gypsum and halite (Sappa et al. 2014).

Fig. 6
figure 6

Piper diagram for representing the analysis of ground water

Full size image

Conclusions

Water quality monitoring programs generate complex dataset that needs multivariate statistical methods for interpretation of the underlying information. The present work applied multivariate statistical techniques to study the source/genesis of chemical parameters in groundwaters of the Rapur area of Andhra Pradesh including cluster analysis, and factor analysis. The factor analysis (FA) identified five factors responsible for data structure explaining 83.91% of total variance. The cluster analysis classified the locations into 5 clusters which possess different groundwater quality characteristics. It also yielded 2 clusters regarding water quality parameters. This study shows that multivariate analysis is a useful method that could assist decision makers in determining the source and extent of pollution.