Optical solitons for dispersive concatenation model with power-law of self-phase modulation: a sub-ODE approach

Abstract

This work retrieves a plethora of optical soliton solutions to the dispersive concatenation model with power-law of self-phase modulation. The implementation of the sub-ODE method and its variations and versions yielded such soliton solutions. The intermediary functions were Weierstrass’ elliptic functions as well as Jacobi’s elliptic functions. Their special cases gave way to soliton solutions. In particular, for Jacobi’s elliptic functions, when the modulus of ellipticity approached unity, the soliton solutions have naturally emerged.

Introduction

A decade ago, the concept of the concatenation model had surfaced [1,2,3,4,5]. This is an unique and novel concept of conjoining three pre-existing nonlinear evolution equations that govern the propagation of solitons through optical fibers into a single equation [6,7,8,9,10]. This is the combination of the nonlinear Schrödinger’s equation (NLSE), Lakshmanan–Porsezian–Daniel (LPD) model and the Sasa–Satsuma equation [11,12,13,14,15]. Subsequently during the same year, a different form of concatenation model, with dispersive components included, gave way to the dispersive concatenation model [16,17,18,19,20]. This model is the combination of the Schrödinger–Hirota equation (SHE), LPD model and the fifth-order NLSE [21,22,23,24,25]. Thus, there are two sources of dispersion embedded in this model, namely, the SHE and the fifth-order dispersion in the dispersive NLSE component [26,27,28,29,30]. This makes the newly structured concatenation model true to its name [1,2,3,4,5]. This dispersive concatenation model has been extensively studied with various characteristic features, namely, the retrieval of optical soliton solutions with the usage of the method of undetermined coefficients as well as additional integration tools and also addressing the model in the absence of self-phase modulation (SPM) [31,32,33,34,35,36,37]. Later, the model was also studied with nonlinear form of chromatic dispersion (CD) and quiescent optical solitons were recovered in this context [6,7,8].

The current paper will carry out further studies with the model. First, the SPM will be generalized from Kerr law to power-law. Subsequently, the sub ordinary differential equation (ODE) (AKA sub-ODE) approach together with its variations and versions will recover a full spectrum of soliton solutions along with a plethora of additional forms of soliton solutions that are being reported in this paper for the first time. The pathway to the retrieval of optical soliton solutions to the model is through the intermediary Weierstrass’ and Jacobi’s elliptic functions. The special cases of Weierstrass’s elliptic functions will yield soliton solutions. On the other hand, for Jacobi’s elliptic functions, when the modulus of ellipticity approached unity, the doubly periodic functions migrate to soliton solutions. The spectrum of results are enumerated and exhibited in details after a re-visitation to the model and recapitulating the applied integration algorithms. The details follow through in the subsequent sections and subsections.

The shift from Kerr law to power-law may have limitations and may not universally apply. The assumption of a power-law behavior requires careful justification. The accuracy of the sub-ODE approach relies on valid assumptions. The use of Weierstrass’ and Jacobi’s elliptic functions introduces mathematical complexity. The conditions under which special cases yield soliton solutions are clearly defined.

Governing model

The dimensionless form of the generalized concatenation model with power-law of SPM:

$$\begin{aligned}{} & {} iq_{t}+aq_{xx} + b\left| q\right| ^{2n}q - i\delta _{1}\left[ \sigma _{1}q_{xxx} + \sigma _{2}\left| q\right| ^{2n}q_{x}\right] \nonumber \\{} & {} \qquad + \delta _{2} \left[ \sigma _{3}q_{xxxx} + \sigma _{4}\left| q\right| ^{2n}q_{xx} + \sigma _{5}\left| q\right| ^{2n+2}q \right. \nonumber \\{} & {} \qquad \left. + \sigma _{6}\left| q_{x}\right| ^{2}q + \sigma _{7}q_{x}^{2}q^{*}+ \sigma _{8}q_{xx}^{*}q^{2} \right] \nonumber \\{} & {} \qquad - i\delta _{3} \left[ \sigma _{9}q_{xxxxx} + \sigma _{10}\left| q\right| ^{2n}q_{xxx} + \sigma _{11}\left| q\right| ^{2n+2}q_{x} \right. \nonumber \\{} & {} \qquad \left. + \sigma _{12}qq_{x}q_{xx}^{*} + \sigma _{13}q^{*}q_{x}q_{xx} + \sigma _{14}qq_{x}^{*}q_{xx} + \sigma _{15}q_{x}^{2}q_{x}^{*} \right] = 0, \end{aligned}$$

(1)

where q(x, t) is a complex valued function that represents the wave amplitude and $q^{*}(x,t)$ is its complex-conjugate while $i=\sqrt{-1}.$ The first term represents the linear temporal evolution. The constants a and b are coefficients of CD and the power-law of SPM terms respectively. The parameters $\sigma _{j}$, for $1 \le j \le 15$ are all real–valued constants. If $\delta _{1} = \delta _{2} = \delta _{3}=0,$ Eq.(1) reduces to the standard NLSE which describes the propagation of pulses through optical fibers. If $\delta _{1}\ne 0,\delta _{2}=\delta _{3}=0,$ Eq.(1) reduces to SHE. If $\delta _{1}=\delta _{3}=0,\delta _{2}\ne 0,$ Eq.(1) reduces to the LPD model. If $\delta _{1}=\delta _{2}=0,\delta _{3}\ne 0,$ Eq.(1) reduces to quintic NLSE that introduces dispersive effects. Finally, n signifies the arbitrary intensity parameter.

This work is organized. In Section–2, the governing model is displayed. In Section–3, the mathematical analysis is introduced. In Section–4, the model is analyzed using the integration technology and the recovered solutions are enumerated. Finally, in Section–5, a few words of Conclusions are jotted.

Mathematical preliminaries

In order to solve Eq.(1), setting:

$$\begin{aligned} q(x,t)=\phi (\xi )\exp [i\theta (x,t)],\ \ \theta (x,t)=-\kappa x+wt+\theta _{0},{ \ \ }\xi =x-Vt, \end{aligned}$$

(2)

where $\kappa$ is the soliton frequency, w is the wave number, $\theta _{0}$ is the phase constant and V is the velocity of the soliton. Finally $\phi \$is a real function which represents amplitude of wave transformation. Exchanging (2) into Eq. (1) and separating the real and imaginary parts, we get the real part is given by:

$$\begin{aligned}{} & {} \Delta _{1}\phi ^{\left( 4\right) }\left( \xi \right) +\Delta _{2}\phi ^{2n}\left( \xi \right) \phi ^{\prime \prime }\left( \xi \right) \nonumber \\{} & {} \qquad +\Delta _{3}\phi ^{2}\left( \xi \right) \phi ^{\prime \prime }\left( \xi \right) +\Delta _{4}\phi \left( \xi \right) \phi ^{\prime 2}\left( \xi \right) \nonumber \\{} & {} \qquad +\Delta _{5}\phi ^{\prime \prime }\left( \xi \right) +\Delta _{6}\phi \left( \xi \right) +\Delta _{7}\phi ^{3}\left( \xi \right) \nonumber \\{} & {} \qquad +\Delta _{8}\phi ^{2n+1}\left( \xi \right) +\Delta _{9}\phi ^{2n+3}\left( \xi \right) =0, \end{aligned}$$

(3)

where

$$\begin{aligned} \begin{aligned}&\Delta _{1}=\delta _{2}\sigma _{3}-5\delta _{3}\sigma _{9}\kappa , \\&\Delta _{2}=-3\delta _{3}\sigma _{10}\kappa +\delta _{2}\sigma _{4}, \\&\Delta _{3}=\delta _{2}\sigma _{8}-\delta _{3}\sigma _{12}\kappa -\delta _{3}\sigma _{13}\kappa +\delta _{3}\sigma _{14}\kappa ^{2}, \\&\Delta _{4}=2\delta _{3}\sigma _{12}\kappa -2\delta _{3}\sigma _{13}\kappa -2\delta _{3}\sigma _{14}\kappa -\delta _{3}\sigma _{15}\kappa +\delta _{2}\sigma _{6}+\delta _{2}\sigma _{7},\ \\&\Delta _{5}=10\delta _{3}\sigma _{9}\kappa ^{3}-6\delta _{2}\sigma _{3}\kappa ^{2}-3\delta _{1}\sigma _{1}\kappa +a, \\&\Delta _{6}=-w-a\kappa ^{2}+\delta _{1}\sigma _{1}\kappa ^{3}+\delta _{2}\sigma _{3}\kappa ^{4}-\delta _{3}\sigma _{9}\kappa ^{5}, \\&\Delta _{7}=\delta _{3}\sigma _{12}\kappa ^{3}+\delta _{3}\sigma _{13}\kappa ^{3}-\delta _{3}\sigma _{14}\kappa ^{3}-\delta _{3}\sigma _{15}\kappa ^{3}\\&\qquad +\delta _{2}\sigma _{6}\kappa ^{2}-\delta _{2}\sigma _{7}\kappa ^{2}-\delta _{2}\sigma _{8}\kappa ^{2}, \\&\Delta _{8}=b-\delta _{1}\sigma _{2}\kappa -\delta _{2}\sigma _{4}\kappa ^{2}+\delta _{3}\sigma _{10}\kappa ^{3}, \\&\Delta _{9}=\delta _{2}\sigma _{5}-\delta _{3}\sigma _{11}\kappa , \end{aligned} \end{aligned}$$

(4)

while the imaginary part is:

$$\begin{aligned}{} & {} \phi ^{\left( 5\right) }\left( \xi \right) +A_{1}\phi ^{2}\left( \xi \right) \phi ^{\prime \prime \prime }\left( \xi \right) +A_{2}\phi ^{2}\left( \xi \right) \phi ^{\prime }\left( \xi \right) \nonumber \\{} & {} \qquad +A_{3}\phi ^{2n}\left( \xi \right) \phi ^{\prime }\left( \xi \right) +A_{4}\phi \left( \xi \right) \phi ^{\prime }\left( \xi \right) \phi ^{\prime \prime }\left( \xi \right) \nonumber \\{} & {} \qquad +A_{5}\phi ^{^{\prime \prime \prime }}\left( \xi \right) +A_{6}\phi ^{\prime 3}\left( \xi \right) +A_{7}\phi ^{2n+2}\left( \xi \right) \phi ^{\prime }\left( \xi \right) +A_{8}\phi ^{\prime }\left( \xi \right) =0, \end{aligned}$$

(5)

where

$$\begin{aligned} \begin{array}{l} A_{1}=\frac{\sigma _{10}}{\sigma _{9}}, \\ A_{2}=\frac{1}{\delta _{3}\sigma _{9}}\left[ 2\delta _{2}\kappa (\sigma _{7}+\sigma _{8})+\delta _{3}\kappa ^{2}(\sigma _{12}-3\sigma _{13}+\sigma _{14}+\sigma _{15})\right] , \\ A_{3}=\frac{1}{\delta _{3}\sigma _{9}}\left[ \delta _{1}\sigma _{2}+2\delta _{2}\sigma _{4}\kappa -3\delta _{3}\sigma _{10}\kappa ^{2}\right] , \\ A_{4}=\frac{1}{\sigma _{9}}(\sigma _{12}+\sigma _{13}+\sigma _{14}),\ \\ A_{5}=\frac{1}{\delta _{3}\sigma _{9}}\left[ \delta _{1}\sigma _{1}+4\delta _{2}\sigma _{3}\kappa +10\delta _{3}\sigma _{9}\kappa ^{2}\right] , \\ A_{6}=\frac{\sigma _{15}}{\sigma _{9}}, \\ A_{7}=\frac{\sigma _{11}}{\sigma _{9}}, \\ A_{8}=\frac{1}{\delta _{3}\sigma _{9}}\left[ V-3\delta _{1}\sigma _{1}\kappa ^{2}-4\delta _{2}\sigma _{3}\kappa ^{3}+5\delta _{3}\sigma _{9}\kappa ^{4}+2a\kappa \right] , \end{array} \end{aligned}$$

(6)

provided $\delta _{3}\ne 0,\sigma _{9}\ne 0$. Applying the linearly independent in Eq.(3) gives the frequency

$$\begin{aligned} \kappa= & {} \frac{\delta _{2}\sigma _{3}}{5\delta _{3}\sigma _{9}}=\frac{\delta _{2}\sigma _{4}}{3\delta _{3}\sigma _{10}}=\frac{\delta _{2}\sigma _{5}}{ \delta _{3}\sigma _{11}}=-\tfrac{\delta _{2}(\sigma _{6}+\sigma _{7})}{ \delta _{3}(2\sigma _{12}-2\sigma _{13}-2\sigma _{14}-\sigma _{15})}\\= & {} -\tfrac{ \delta _{2}(\sigma _{6}-\sigma _{7}-\sigma _{8})}{\delta _{3}(\sigma _{12}+\sigma _{13}-\sigma _{14}-\sigma _{15})}, \end{aligned}$$

and the wave number,

$$\begin{aligned} w=\kappa ^{2}\left( -a+\delta _{1}\sigma _{1}\kappa +\delta _{2}\sigma _{3}\kappa ^{2}-\delta _{3}\sigma _{9}\kappa ^{3}\right) , \end{aligned}$$

as well as the constraint condition

$$\begin{aligned} \begin{array}{l} \delta _{2}\sigma _{8}+\delta _{3}\kappa (-\sigma _{12}-\sigma _{13}+\sigma _{14}\kappa )=0, \\ a+10\delta _{3}\sigma _{9}\kappa ^{3}-6\delta _{2}\sigma _{3}\kappa ^{2}-3\delta _{1}\sigma _{1}\kappa =0, \\ b-\kappa \left( \delta _{1}\sigma _{2}+\delta _{2}\sigma _{4}\kappa -\delta _{3}\sigma _{10}\kappa ^{2}\right) =0. \end{array} \end{aligned}$$

(7)

Let us now solve Eq.(5) using the following method.

Enhanced sub-ODE approach

Zi Liang-Li [12] proposed a generalized version of sub-ODE method, while Zayed and Alngar [13] introduced the modified Sub-ODE method, Recently, Zayed et al. [14] have suggested the addendum to modified sub-ODE method which will be applied here to solve Eq.(5). The current paper refers to the addendum as the enhanced version of the sub-ODE approach. To accomplish this, we assume that the solution of Eq.(5) is equivalent to the solution of the auxiliary equation:

$$\begin{aligned} H^{\prime 2}(\xi )= & {} A\ H^{2-2p}(\xi )+B\ H^{2-p}(\xi )+C\ H^{2}(\xi )\nonumber \\{} & {} +D\ H^{2+p}(\xi )+E\ H^{2+2p}(\xi ), \end{aligned}$$

(8)

where A, B, C, D and E are constants, while p is a positive integer.

It is well known [12,13,14] that Eq.(8) has many particular solutions which will be used throughout this section to find the optical soliton solutions of Eq.(1). Let us now study the following sets:

Set-1 Inserting $A=B=D=0$ in Eq.(8) we have:

$$\begin{aligned} H^{\prime 2}(\xi )=C\ H^{2}(\xi )+E\ H^{2+2p}(\xi ). \end{aligned}$$

(9)

substituting (9) into Eq.(5) we get

$$\begin{aligned}{} & {} C^{2}+CE(1+p)(1+2p)[1+(1+2p)^{2}]H^{2p}(\xi )\nonumber \\{} & {} \qquad +2pE^{2}(1+p)(1+2p)(1+4p)H^{4p}(\xi ) \nonumber \\{} & {} \qquad +(1+p)^{2}(1+2p)(1+3p)(1+4p)E^{2}H^{4p}(\xi )+A_{1}CH^{2n}(\xi )\nonumber \\{} & {} \qquad +A_{1}E(1+p)(1+2p)H^{2n+2p}(\xi ) \nonumber \\{} & {} \qquad +A_{2}H^{2}(\xi )+A_{3}H^{2n}(\xi )+A_{4}CH^{2}(\xi )+A_{4}EH^{2P+2}(\xi )\nonumber \\{} & {} \qquad +A_{5}C+A_{5}E(1+p)(1+2p)H^{2p}(\xi ) \nonumber \\{} & {} \qquad +A_{6}CH^{2}(\xi )+A_{6}EH^{2+2p}(\xi )+A_{7}H^{2n+2}(\xi )+A_{8}=0. \end{aligned}$$

(10)

Comparing the exponent $2n+2p$ with 4p we get $p=n.$ Then, Eq.(10) gives

$$\begin{aligned}{} & {} \left[ CE(1+n)(1+2n)+CE(1+n)(1+2n)^{3}+A_{3}\right. \nonumber \\{} & {} \qquad \left. +A_{1}C+A_{5}E(1+n)(1+2n)\right] H^{2n}(\xi ) \nonumber \\{} & {} \qquad +\left[ (1+n)^{2}(1+2n)(1+3n)(1+4n)E^{2}\right. \nonumber \\{} & {} \qquad \left. +A_{1}E(1+n)(1+2n)\right] H^{4n}(\xi ) \nonumber \\{} & {} \qquad +\left[ A_{2}+C(A_{4}+A_{6})\right] H^{2}(\xi )+\left[ A_{7}+E(A_{4}+A_{6}) \right] \nonumber \\{} & {} \qquad H^{2n+2}(\xi )+C^{2}+CA_{5}+A_{8}=0. \end{aligned}$$

(11)

From Eq.(11) we have the algebraic equations:

$$\begin{aligned}{} & {} CE(1+n)(1+2n)+CE(1+n)(1+2n)^{3}+A_{3}\nonumber \\{} & {} \qquad +A_{1}C+A_{5}E(1+n)(1+2n)=0, \nonumber \\{} & {} \qquad (1+n)^{2}(1+2n)(1+3n)(1+4n)E^{2}\nonumber \\{} & {} \qquad +A_{1}E(1+n)(1+2n)=0,\nonumber \\{} & {} \qquad A_{2}+C(A_{4}+A_{6})=0, \nonumber \\{} & {} \qquad A_{7}+E(A_{4}+A_{6})=0, \nonumber \\{} & {} \qquad C^{2}+CA_{5}+A_{8}=0. \end{aligned}$$

(12)

On solving the above algebraic Eq. (12) with C, E, which are non-zero constants, we have:

$$\begin{aligned} C=-\frac{A_{2}}{A_{4}+A_{6}},\ \ \ E=-\frac{A_{7}}{A_{4}+A_{6}}\ , \end{aligned}$$

(13)

along with the conditions

$$\begin{aligned} \left. \begin{array}{l} n=n,{ \ }A_{1}=\frac{(1+n)(1+3n)(1+4n)A_{7}}{A_{4}+A_{6}}, \\ \\ A_{5}=\frac{A_{3}(A_{4}+A_{6})^{2}+(1+2n)(4n^{3}+8n^{2}+2n+1)A_{2}A_{7}}{ (1+n)(1+2n)A_{7}(A_{4}+A_{6})}, \\ \\ A_{8}=\frac{A_{2}A_{3}(A_{4}+A_{6})^{2}+n(1+2n)(4n^{2}+8n+1)A_{2}^{2}A_{7}}{ (1+n)(1+2n)A_{7}(A_{4}+A_{6})^{2}}, \end{array} \right. \end{aligned}$$

(14)

where $A_{2},A_{4},A_{7}$ are non-zero constants.

It is well known [1,2,3] that, when $E<0\$and $C>0$, Eq.(1) has the bright soliton solution:

$$\begin{aligned} q(x,t)= & {} \left\{ \varepsilon \sqrt{-\frac{A_{2}}{A_{7}}}\text{ sech }{}\left[ n(x-Vt)\sqrt{-\frac{A_{2}}{A_{4}+A_{6}}}\ \right] \right\} ^{\frac{1}{n} }\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(15)

provided $A_{2}A_{7}<0,A_{2}(A_{4}+A_{6})<0,\varepsilon =\pm 1.$ The above solution (15) is obtained under the restriction (14).

Set-2 Inserting $A=B=0$, in Eq.(8) we have:

$$\begin{aligned} H^{\prime 2}(\xi )=C\ H^{2}(\xi )+D\ H^{2+p}(\xi )+E\ H^{2+2p}(\xi ). \end{aligned}$$

(16)

Substituting (16) into Eq. (5) we get

$$\begin{aligned}{} & {} C^{2}+\frac{1}{2}CD(1+p)(2+p)(2+2p+p^{2})H^{p}(\xi )\nonumber \\{} & {} \qquad +(1+p)(2+p)\left[ \frac{1 }{4}(2+p)^{2}D^{2}+2Ep(1+2p)\right. \nonumber \\{} & {} \qquad \left. +CE(2+2p)\right] H^{2p}(\xi ) \nonumber \\{} & {} \qquad +\frac{1}{2}ED(1+p)(1+3p)(2+p)(7p^{2}+11p+6)H^{3p}(\xi )\nonumber \\{} & {} \qquad +(1+p)(1+2p)(1+3p)(1+4p)E^{2}H^{4p}(\xi )+A_{1}CH^{2n}(\xi ) \nonumber \\{} & {} \qquad +\frac{1}{2}A_{1}D(1+p)(2+p)H^{2n+p}(\xi )\nonumber \\{} & {} \qquad +A_{1}(1+p)(1+2p)H^{2n+2p}(\xi )\nonumber \\{} & {} \qquad +A_{2}H^{2}(\xi )+A_{3}H^{2n}(\xi )+A_{4}CH^{2}(\xi ) \nonumber \\{} & {} \qquad +\frac{1}{2}A_{4}(2+p)DH^{P+2}(\xi )+A_{4}(1+p)EH^{2P+2}(\xi )\nonumber \\{} & {} \qquad +CA_{5}+\frac{1 }{2}A_{5}D(1+p)(2+p)H^{p}(\xi )+A_{5}E(1+p)(1+2p)H^{2p}(\xi ) \nonumber \\{} & {} \qquad +A_{6}CH^{2}(\xi )+A_{6}DH^{2+p}(\xi )+A_{6}EH^{2+2p}(\xi )\nonumber \\{} & {} \qquad +A_{7}H^{2n+2}(\xi )+A_{8}=0. \end{aligned}$$

(17)

Comparing the exponent $2p+2n$ with 4p we get $p=n$, or $2p+2n$ with 3p we get $p=2n$. Let us now discuss the case $p=n$ (similarly $p=2n$). Then, Eq.(17) reduces to

$$\begin{aligned}{} & {} \left\{ (1+n)(2+n)\left[ \frac{1}{4}(2+n)^{2}D^{2}+2En(1+2n)\right. \right. \nonumber \\{} & {} \qquad \left. \left. +CE(2+2n)+A_{5}E \right] +A_{1}C+A_{3}\right\} H^{2n}(\xi ) \nonumber \\{} & {} \qquad +\left[ \frac{1}{2}ED(1+n)(1+3n)(2+n)(7n^{2}+11n+6)\right. \nonumber \\{} & {} \qquad \left. +\frac{1}{2} A_{1}D(1+n)(2+n)\right] H^{3n}(\xi ) \nonumber \\{} & {} \qquad +\left[ (1+n)(1+2n)(1+3n)(1+4n)E^{2}\right. \nonumber \\{} & {} \qquad \left. +A_{1}(1+n)(1+2n)\right] H^{4n}(\xi ) \nonumber \\{} & {} \qquad +\left[ \frac{1}{2}CD(1+n)(2+n)(2+2n+n^{2})\right. \nonumber \\{} & {} \qquad \left. +\frac{1}{2}A_{5}D(1+n)(2+n) \right] H^{n}(\xi ) \nonumber \\{} & {} \qquad +\left[ A_{7}+E(1+n)A_{4}+EA_{6}\right] H^{2n+2}(\xi )\nonumber \\{} & {} \qquad +\left[ A_{2}+C(A_{4}+A_{6})\right] H^{2}(\xi ) \nonumber \\{} & {} \qquad +\left[ \frac{A_{4}}{2}(2+n)D+A_{6}D\right] H^{2+n}(\xi )+C^{2}+CA_{5}+A_{8}=0. \end{aligned}$$

(18)

From Eq.(18) we have the algebraic equations:

$$\begin{aligned}{} & {} (1+n)(2+n)\left[ \frac{1}{4}(2+n)^{2}D^{2}+2En(1+2n)\right. \nonumber \\{} & {} \qquad \left. +CE(2+2n)+A_{5}E\right] +A_{1}C+A_{3}=0, \nonumber \\{} & {} \qquad \frac{1}{2}ED(1+n)(1+3n)(2+n)(7n^{2}+11n+6)\nonumber \\{} & {} \qquad +\frac{1}{2}A_{1}D(1+n)(2+n)=0, \nonumber \\{} & {} \qquad (1+n)(1+2n)(1+3n)(1+4n)E^{2}+A_{1}(1+n)(1+2n)=0, \nonumber \\{} & {} \qquad \frac{1}{2}CD(1+n)(2+n)(2+2n+n^{2})+\frac{1}{2}A_{5}D(1+n)(2+n)=0, \nonumber \\{} & {} \qquad A_{7}+E(1+n)A_{4}+EA_{6}=0, \nonumber \\{} & {} \qquad A_{2}+C(A_{4}+A_{6})=0, \nonumber \\{} & {} \qquad \frac{A_{4}}{2}(2+n)D+A_{6}D=0, \nonumber \\{} & {} \qquad C^{2}+CA_{5}+A_{8}=0. \end{aligned}$$

(19)

On solving the above algebraic equations (19) with C, D, E, which are non-zero constants, we have the results:

$$\begin{aligned} \left\{ \begin{array}{c} C=\frac{2A_{2}}{nA_{4}},\ \ {\ \ }\ E=\frac{-2A_{7}}{nA_{4}}, \\ \\ D^{2}=-\tfrac{4E}{(2+n)^{2}}\left[ 2n(1+2n)+4C(1+n)+A_{5}\right] -\tfrac{ 4(A_{1}C+A_{3})}{(1+n)(2+n)^{3}}\text { }, \\ \end{array} \right. \end{aligned}$$

(20)

along with conditions,

$$\begin{aligned} \left. \begin{array}{c} n=n,{ \ \ }A_{1}=-\frac{(1+3n)(6+11n+7n^{2})^{2}}{(1+4n)},{ \ \ } A_{5}=-\frac{2A_{2}(2+2n+n^{2})}{nA_{4}},{ \ \ } \\ A_{7}=-\frac{n(6+11n+7n^{2})A_{4}}{2(1+4n)},{ \ \ }A_{6}=-\frac{ (2+n)A_{4}}{2},{ \ \ \ \ }A_{8}=\frac{4A_{2}^{2}(1+2n+n^{2})}{ n^{2}A_{4}^{2}}, \end{array} \right. \end{aligned}$$

(21)

where $A_{2}$ and $A_{4}$ are non-zero constants. With the aid of [1,2,3], Eq.(1) has the following solutions:

(a) The soliton solutions:

$$\begin{aligned} q(x,t)= & {} \left[ -\frac{\frac{2A_{2}D}{nA_{4}}\text{ sech}^{2}\sqrt{\frac{nA_{2} }{2A_{4}}}\ (x-Vt)}{D^{2}-\frac{4A_{2}(6+11n+7n^{2})}{nA_{4}(1+4n)}\left[ 1+\varepsilon \tanh \sqrt{\frac{nA_{2}}{2A_{4}}}\ (x-Vt)\right] ^{2}}\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(22)

$$\begin{aligned} q(x,t)= & {} \left[ \frac{\frac{2A_{2}D}{nA_{4}}\text{ csch}^{2}\sqrt{\frac{nA_{2}}{ 2A_{4}}}\ (x-Vt)}{D^{2}-\frac{4A_{2}(6+11n+7n^{2})}{nA_{4}(1+4n)}\left[ 1+\varepsilon \coth \sqrt{\frac{nA_{2}}{2A_{4}}}\ (x-Vt)\right] ^{2}}\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(23)

$$\begin{aligned} q(x,t)= & {} \left[ -\frac{\frac{2A_{2}}{nA_{4}}\text{ sech}^{2}\sqrt{\frac{nA_{2}}{ 2A_{4}}}\ (x-Vt)}{D+2\varepsilon \sqrt{\frac{4A_{2}(6+11n+7n^{2})}{ nA_{4}(1+4n)}}\tanh \sqrt{\frac{nA_{2}}{2A_{4}}}\ (x-Vt)}\right] ^{\frac{1}{n }}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(24)

$$\begin{aligned} q(x,t)= & {} \left[ \frac{\frac{2A_{2}}{nA_{4}}\text{ csch}^{2}\sqrt{\frac{nA_{2}}{ 2A_{4}}}\ (x-Vt)}{D+2\varepsilon \sqrt{\frac{4A_{2}(6+11n+7n^{2})}{ nA_{4}(1+4n)}}\coth \sqrt{\frac{nA_{2}}{2A_{4}}}\ (x-Vt)}\right] ^{\frac{1}{n }}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(25)

provided $A_{2}A_{4}$ $>0,\varepsilon =\pm 1.$

(b) The singular soliton solution:

$$\begin{aligned} q(x,t)= & {} \left[ -\frac{2A_{2}}{nA_{4}D}\left\{ 1+\varepsilon \coth \sqrt{\frac{ nA_{2}}{2A_{4}}}\ (x-Vt)\right\} \right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(26)

provided $A_{2}A_{4}$ $>0,$ $D^{2}+\frac{16A_{2}A_{7}}{n^{2}A_{4}^{2}}=0,$ $\varepsilon =\pm 1.$

(c) The bright soliton solution:

$$\begin{aligned} q(x,t)= & {} \left[ \frac{\frac{4A_{2}}{nA_{4}}}{\varepsilon \sqrt{D^{2}+\frac{ 16A_{2}A_{7}}{n^{2}A_{4}^{2}}}\cosh \sqrt{\frac{nA_{2}}{2A_{4}}}\ (x-Vt)-D} \right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(27)

provided $A_{2}A_{4}$ $>0,$ $D^{2}+\frac{16A_{2}A_{7}}{n^{2}A_{4}^{2}}>0,$ $\varepsilon =\pm 1.$

(d) The singular soliton solution:

$$\begin{aligned} q(x,t)= & {} \left[ \frac{\frac{4A_{2}}{nA_{4}}}{\varepsilon \sqrt{-\left( D^{2}+ \frac{16A_{2}A_{7}}{n^{2}A_{4}^{2}}\right) }\sinh \sqrt{\frac{nA_{2}}{2A_{4}} }\ (x-Vt)-D}\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(28)

provided $A_{2}A_{4}$ $>0,$ $D^{2}+\frac{16A_{2}A_{7}}{n^{2}A_{4}^{2}}<0,$ $\varepsilon =\pm 1.$ All the solutions (22–28) are existed under the restriction (21).

Set-3 Inserting $A=B=E=0$ in Eq.(8) we have:

$$\begin{aligned} H^{\prime 2}(\xi )=C\ H^{2}(\xi )+D\ H^{2+p}(\xi ). \end{aligned}$$

(29)

Substituting (29) into Eq.(5) we get

$$\begin{aligned}{} & {} C^{2}+\frac{1}{2}CD(1+p)(1+2p)(2+2p+p^{2})H^{p}(\xi )\nonumber \\{} & {} \qquad +\frac{1}{4} D^{2}(1+p)(1+2p)(2+p)(3p+2)H^{2p}(\xi ) \nonumber \\{} & {} \qquad +A_{1}CH^{2n}(\xi )+\frac{1}{2}A_{1}D(1+p)(2+p)H^{2n+p}(\xi )\nonumber \\{} & {} \qquad +A_{2}H^{2}(\xi )+A_{3}H^{2n}(\xi )+A_{4}CH^{2}(\xi )+ \nonumber \\{} & {} \qquad \frac{1}{2}(2+p)DA_{4}H^{P+2}(\xi )+CA_{5}+\frac{1}{2}A_{5}D(1+p)(2+p)\nonumber \\{} & {} \qquad H^{p}(\xi )+A_{6}CH^{2}(\xi )+A_{6}DH^{2+p}(\xi ) \nonumber \\{} & {} \qquad +A_{7}H^{2n+2}(\xi )+A_{8}=0. \end{aligned}$$

(30)

Comparing the exponent $2n+2$ with $p+2$ or $2n+p$ with 2p we get $p=2n.$ Then, Eq.(30) reduces to

$$\begin{aligned}{} & {} C^{2}+A_{8}+CA_{5} \nonumber \\{} & {} \qquad +\left[ \frac{1}{2}CD(1+2n)(1+4n)(2+4n+4n^{2})+A_{1}C+A_{3}\right. \nonumber \\{} & {} \qquad \left. +\frac{1}{2} A_{5}D(1+2n)(2+2n)\right] H^{2n}(\xi ) \nonumber \\{} & {} \qquad +\left[ \frac{1}{4}D^{2}(1+2n)(1+4n)(2+2n)(6n+2)\right. \nonumber \\{} & {} \qquad \left. +\frac{1}{2}A_{1}D(1+n)(2+2n) \right] H^{4n}(\xi ) \nonumber \\{} & {} \qquad +\left[ A_{2}+A_{4}C+A_{6}C\right] H^{2}(\xi )+\left[ A_{6}D\right. \nonumber \\{} & {} \qquad \left. +\frac{1}{2} (2+2n)DA_{4}+A_{7}\right] H^{2n+2}(\xi )=0. \end{aligned}$$

(31)

From Eq.(31) we have the algebraic equations:

$$\begin{aligned}{} & {} C^{2}+A_{8}+CA_{5}=0, \nonumber \\{} & {} \qquad CD(1+2n)(1+4n)(1+2n+2n^{2})+A_{1}C\nonumber \\{} & {} \qquad +A_{3}+A_{5}D(1+2n)(1+n)=0, \nonumber \\{} & {} \qquad D^{2}(1+n)(1+2n)(1+3n)(1+4n)\nonumber \\{} & {} \qquad +A_{1}D(1+2n)(1+n)=0, \nonumber \\{} & {} \qquad A_{2}+A_{4}C+A_{6}C=0, \nonumber \\{} & {} \qquad A_{6}D+(1+n)DA_{4}+A_{7}=0. \end{aligned}$$

(32)

On solving the above algebraic equations (32) with C, D, which are non-zero constant, we have:

$$\begin{aligned} C=-\frac{A_{2}}{A_{4}+A_{6}},\ \ \ D=-\frac{A_{7}}{(1+n)A_{4}+A_{6}}\ , \end{aligned}$$

(33)

along with the conditions

$$\begin{aligned} \left. \begin{array}{l} n=n,{ \ }A_{1}{\ }=\frac{A_{7}(1+3n)(1+4n)}{(1+n)A_{4}+A_{6}}, \\ \\ A_{5}=\frac{A_{3}\left[ (1+n)A_{4}+A_{6}\right] }{A_{7}(1+n)(1+2n)}+\frac{ A_{2}(1+4n)\left[ (1+2n)(1+2n+2n^{2})-(1+3n)\right] }{(1+n)(A_{4}+A_{6})}, \\ \\ A_{8}=-\frac{A_{2}A_{3}\left[ (1+n)A_{4}+A_{6}\right] }{ A_{7}(1+n)(1+2n)(A_{4}+A_{6})}-\frac{A_{2}^{2}(1+4n)(1+2n)\left[ 2n^{2}+2n-1 \right] }{(1+n)(A_{4}+A_{6})^{2}}, \end{array} \right. \end{aligned}$$

(34)

where $A_{2},A_{3},A_{4},A_{6}$ and $A_{7}$ are non-zero constants.

It is well known [12,13,14] that, when $D<0\$and $C>0$, Eq.(1) has the bright soliton solution:

$$\begin{aligned} q(x,t)= & {} \left\{ -\frac{A_{2}\left[ (1+n)A_{4}+A_{6}\right] }{ A_{7}(A_{4}+A_{6})}\text{ sech}^{2}{}\right. \nonumber \\{} & {} \left. \sqrt{-\frac{n^{2}A_{2}}{A_{4}+A_{6}}}\ (x-Vt)\right\} ^{\frac{1}{2n}}e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(35)

provided $A_{2}(A_{4}+A_{6})<0,$ $A_{7}\left[ (1+n)A_{4}+A_{6}\right] >0.$ The above solution (35) is obtained under the restriction (34).

Set-4 Inserting $B=D=0$ into Eq.(8), we have:

$$\begin{aligned} H^{\prime 2}(\xi )=A\ H^{2-2p}(\xi )+C\ H^{2}(\xi )+E\ H^{2+2p}(\xi ). \end{aligned}$$

(36)

Substituting (36) into Eq.(5) we get

$$\begin{aligned}{} & {} A^{2}(1-p)(1-2p)(1-3p)(1-4p)H^{-4p}(\xi )\nonumber \\{} & {} \qquad +C^{2}+2AE+2AC(1-p)(1-2p)(1-2p+p^{2})H^{-2p}(\xi ) \nonumber \\{} & {} \qquad +E^{2}(1+p)(1+2p)(1+3p)(1+4p)H^{4p}(\xi )\nonumber \\{} & {} \qquad +2EC(1+p)(1+2p)(1+2p+2p^{2})E^{2}H^{2p}(\xi ) \nonumber \\{} & {} \qquad +A_{1}A(1-p)(1-2p)H^{2n-2p}(\xi )+A_{1}CH^{2n}(\xi )\nonumber \\{} & {} \qquad +A_{1}E(1+p)(1+2p)H^{2n+2p}(\xi )+A_{2}H^{2}(\xi ) \nonumber \\{} & {} \qquad +A_{3}H^{2n}(\xi )+A_{4}A(1-p)H^{2-2p}(\xi )+A_{4}CH^{2}(\xi )\nonumber \\{} & {} \qquad +A_{4}E(1+p)H^{2P+2}(\xi )+CA_{5} \nonumber \\{} & {} \qquad +A_{5}A(1-p)(1-2p)H^{-2p}(\xi )+A_{5}E(1+p)(1+2p)H^{2p}(\xi )\nonumber \\{} & {} \qquad +A_{6}AH^{2-2p}(\xi ) \nonumber \\{} & {} \qquad +A_{6}CH^{2}(\xi )+A_{6}EH^{2+2p}(\xi )+A_{7}H^{2n+2}(\xi )+A_{8}=0. \end{aligned}$$

(37)

Comparing the exponent $2n+2p$ with 4p we get $p=n.$ Then, Eq.(37) is reduced to

$$\begin{aligned}{} & {} \left[ A^{2}(1-n)(1-2n)(1-3n)(1-4n)\right] H^{-4n}(\xi ) \nonumber \\{} & {} \qquad +\left[ 2AC(1-n)(1-2n)(1-2n+n^{2})+A_{5}A(1-n)\right. \nonumber \\{} & {} \qquad \left. (1-2n)\right] H^{-2n}(\xi ) \nonumber \\{} & {} \qquad +\left[ E^{2}(1+n)(1+2n)(1+3n)(1+4n)+EA_{1}(1+n)\right. \nonumber \\{} & {} \qquad \left. (1+2n)\right] H^{4n}(\xi ) \nonumber \\{} & {} \qquad +\left[ 2CE(1+n)(1+2n)(1+2n+2n^{2})+A_{1}C+A_{3}\right. \nonumber \\{} & {} \qquad \left. +A_{5}E(1+n)(1+2n)\right] H^{2n}(\xi ) \nonumber \\{} & {} \qquad \left[ A_{6}A+A_{4}A(1-n)\right] H^{2-2n}(\xi )+\left[ A_{4}E(1+n)\right. \nonumber \\{} & {} \qquad \left. +A_{6}E+A_{7}\right] H^{2+2n}(\xi )+\left[ A_{2}+C(A_{4}+A_{6}) \right] H^{2}(\xi ) \nonumber \\{} & {} \qquad +2AE+C^{2}+CA_{5}+A_{8}+A_{1}A(1-n)(1-2n)=0. \end{aligned}$$

(38)

From (38) we get the algebraic equations:

$$\begin{aligned}{} & {} A^{2}(1-n)(1-2n)(1-3n)(1-4n)=0, \nonumber \\{} & {} 2AC(1-n)(1-2n)(1-2n+n^{2})+A_{5}A(1-n)(1-2n)=0, \nonumber \\{} & {} E^{2}(1+n)(1+2n)(1+3n)(1+4n)+EA_{1}(1+n)(1+2n)=0, \nonumber \\{} & {} 2CE(1+n)(1+2n)(1+2n+2n^{2})+A_{1}C+A_{3}\nonumber \\{} & {} \qquad +A_{5}E(1+n)(1+2n)=0, \nonumber \\{} & {} A_{6}A+A_{4}A(1-n)=0, \nonumber \\{} & {} A_{4}E(1+n)+A_{6}E+A_{7}=0, \nonumber \\{} & {} A_{2}+C(A_{4}+A_{6})=0, \nonumber \\{} & {} 2AE+C^{2}+CA_{5}+A_{8}+A_{1}A(1-n)(1-2n)=0. \end{aligned}$$

(39)

On solving Eq.(39) with A, C, E, which are non-zero constants, we have the results:

$$\begin{aligned} C=-\frac{A_{2}}{nA_{4}},\ \ \ E=-\frac{A_{7}}{2nA_{4}}\ , \end{aligned}$$

(40)

along with the conditions:

$$\begin{aligned} \left. \begin{array}{l} \text { }n=1,\frac{1}{2},\frac{1}{3},\frac{1}{4},{ \ } \\ \\ A_{1}=\frac{(1+3n)(1+4n)A_{7}}{2nA_{4}},{ \ \ \ }A_{3}=\frac{ (-8n^{4}-20n^{3}-5n^{2}+n-3)A_{2}A_{7}}{2n^{2}A_{4}^{2}}, \\ \\ A_{5}=\frac{2A_{2}(1-n)^{2}}{nA_{4}},{ \ \ \ }A_{6}=-(1-n)A_{4}, \\ \\ A_{8}=\frac{A_{2}^{2}(1-4n+2n^{2})}{n^{2}A_{4}^{2}}-\frac{ AA_{7}[-2+(1-n)(1-2n)(1+3n)(1+4n)]}{2nA_{4}}, \end{array} \right. \end{aligned}$$

(41)

where $A_{2},A_{4},A_{7}$ are non-zero constants. Let us discuss the following cases:

Case-1 If $A>0$, then with reference to [1,2,3], Eq.(1) has the Weierstrass elliptic function solutions:

(a) If $g_{2}=\frac{4A_{2}^{2}}{3n^{2}A_{4}^{2}}+2AA_{7}$, $g_{3}=\frac{ 4A_{2}^{2}}{27n^{2}A_{4}^{2}}\left[ \frac{2A_{2}^{2}}{nA_{4}}+\frac{9}{2} AA_{7}\right]$ we have

$$\begin{aligned} q(x,t)= & {} \left\{ -\frac{2nA_{4}}{A_{7}}\wp \left( n(x-Vt),g_{2},g_{3}\right) - \frac{2A_{2}}{3A_{7}}\right\} ^{\frac{1}{2n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0} \text { })},\ \end{aligned}$$

(42)

and

$$\begin{aligned} q(x,t)=\left\{ \frac{3A}{3\wp \left( n(x-Vt),g_{2},g_{3}\right) +\frac{A_{2} }{nA_{4}}}\right\} ^{\frac{1}{2n}}e^{i(-\kappa x+wt+\theta _{0}\text { })},\ \end{aligned}$$

(43)

provided $A_{2}A_{7}<0$, $A_{4}A_{7}$ $<0$ and $A_{2}A_{4}$ $>0$.

(b) If $g_{2}=\frac{1}{nA_{4}}\left[ \frac{A_{2}^{2}}{12nA_{4}}-AA_{7}\right]$, $g_{3}=\frac{A_{2}}{216n^{2}A_{4}^{2}}\left[ \frac{A_{2}^{2}}{nA_{4}} +18AA_{7}\right]$ we have

$$\begin{aligned} q(x,t)= & {} \left\{ \frac{6\sqrt{A}\wp \left( n(x-Vt),g_{2},g_{3}\right) -\frac{ \sqrt{A}A_{2}}{nA_{4}}}{3\wp ^{\prime }\left( n(x-Vt),g_{2},g_{3}\right) } \right\} ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })},\ \end{aligned}$$

(44)

and

$$\begin{aligned} q(x,t)= & {} \left\{ \frac{3\sqrt{-\frac{2nA_{4}}{A7}}\wp ^{\prime }\left( n(x-Vt),g_{2},g_{3}\right) }{6\wp \left( n(x-Vt),g_{2},g_{3}\right) -\frac{ A_{2}}{nA_{4}}}\right\} ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { } )},\ \end{aligned}$$

(45)

provided $A_{2}A_{4}<0$ and $A_{4}A_{7}<0$, where $\wp ^{\prime }\left( p\xi ,g_{2},g_{3}\right) =\frac{d\wp \left( p\xi ,g_{2},g_{3}\right) }{d\xi }.$

Case-2 If $A=\frac{5C^{2}}{36E},\$then with reference to [1,2,3], Eq.(1) has the Weierstrass elliptic function solution:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \sqrt{-\frac{5A_{2}^{2}}{18nA_{4}A_{7}}}\dfrac{ 6\wp \left[ \left( x-Vt\right) ,g_{2},g_{3}\right] -\frac{A_{2}}{nA_{4}}}{ \text { }3\wp ^{\prime }\left[ \left( x-Vt\right) ,g_{2},g_{3}\right] } \right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(46)

provided $A_{4}A_{7}<0$ and $A_{2}A_{4}$ $<0$, where the invariants $g_{2},g_{3}$ of the Weierstrass elliptic function solution (46) are given by

$$\begin{aligned} g_{2}=\frac{2A_{2}^{2}}{9n^{2}A_{4}^{2}}\ \text { and }\ g_{3}=-\frac{ A_{2}^{3}}{54n^{3}A_{4}^{3}}. \end{aligned}$$

(47)

The solutions (42–46) are obtained under the restriction (41).

Case-3 With references [1,2,3], Eq.(1) has three Jacobian elliptic function solutions as:

(I) If $C>0,A=\frac{C^{2}m^{2}(m^{2}-1)}{E(2m^{2}-1)^{2}},0<m<1,$

$$\begin{aligned} q(x,t)= & {} \left\{ \varepsilon \sqrt{-\frac{2A_{2}m^{2}}{A_{7}(2m^{2}-1)}} \text{ cn }\left( n(x-Vt)\right. \right. \nonumber \\{} & {} \left. \left. \sqrt{-\frac{A_{2}}{nA_{4}(2m^{2}-1)}}\right) \right\} ^{\frac{1}{n}}e^{i(-\kappa x+wt+\theta _{0}\text { })},\ \end{aligned}$$

(48)

provided $A_{2}A_{7}(2\,m^{2}-1)<0,A_{2}A_{4}(2\,m^{2}-1)<0, \varepsilon =\pm 1.$

(II) If $C>0,A=\frac{C^{2}(1-m^{2})}{E(2-m^{2})^{2}},0<m<1,$

$$\begin{aligned} q(x,t)= & {} \left\{ \varepsilon \sqrt{-\frac{2A_{2}}{A_{7}(2-m^{2})}}\text{ dn } \left( n(x-Vt)\right. \right. \nonumber \\{} & {} \left. \left. \sqrt{-\frac{A_{2}}{nA_{4}(2-m^{2})}}\right) \right\} ^{\frac{1 }{n}}e^{i(-\kappa x+wt+\theta _{0}\text { })},\ \end{aligned}$$

(49)

provided $A_{2}A_{7}<0,A_{2}A_{4}<0,\varepsilon =\pm 1.$ The above solutions (48), (49) are valid under the restriction (41).

In particular, when $m\rightarrow 1^{-}$in (48) and (49), we have $A=0$ and then Eq.(1) has the bright soliton solution:

$$\begin{aligned} q(x,t)=\left\{ \varepsilon \sqrt{-\frac{2A_{2}}{A_{7}}}\text{ sech }{}\left[ n(x-Vt)\sqrt{-\frac{A_{2}}{nA_{4}}}\ \right] \right\} ^{\frac{1}{n} }e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(50)

(III) If $C<0,A=\frac{C^{2}m^{2}}{E(m^{2}+1)^{2}},0<m<1,$

$$\begin{aligned} q(x,t)= & {} \left\{ \varepsilon \sqrt{-\frac{2A_{2}m^{2}}{A_{7}(m^{2}+1)}} \text{ sn }\left( n(x-Vt)\sqrt{\frac{A_{2}}{nA_{4}(m^{2}+1)}}\right) \right\} ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })},\ \end{aligned}$$

(51)

provided $A_{2}A_{7}<0,A_{2}A_{4}>0,\varepsilon =\pm 1.$

Additional results

It is well known that Weierstrass elliptic function $\wp \left( \xi ;g_{2},g_{3}\right)$ can be written in the form:

$$\begin{aligned} \left. \begin{array}{c} \wp \left( \xi ;g_{2},g_{3}\right) =l_{2}-(l_{2}-l_{3})\text{ cn }{}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) , \\ \\ \wp \left( \xi ;g_{2},g_{3}\right) =l_{3}+(l_{1}-l_{3})\text{ ns }{}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) , \end{array} \right\} \end{aligned}$$

(52)

in terms of the Jacobian elliptic functions where $m=\sqrt{\tfrac{l_{2}-l_{3} }{l_{1}-l_{3}}}$ is the modulus of the Jacobian elliptic function; $l_{j}(j=1,2,3)$, $l_{1}\ge l_{2}$ $\ge l_{3}$ are the three roots of the cubic equation $4y^{3}-g_{2}y-g_{3}=0$.

Substituting (52) into (42) we have Jacobi elliptic function solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ -\frac{2nA_{4}}{A_{7}}\text { }\left[ l_{2}-(l_{2}-l_{3})\text{ cn }{}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] \right. \nonumber \\{} & {} \left. -\frac{2A_{2}}{3A_{7}}\right] ^{\frac{1}{2n}}e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(53)

and

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ -\frac{2nA_{4}}{A_{7}}\text { }\left[ l_{3}+(l_{1}-l_{3})\text{ ns }{}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] \right. \nonumber \\{} & {} \left. -\frac{2A_{2}}{3A_{7}}\right] ^{\frac{1}{2n}}e^{i(-\kappa x+wt+\theta _{0}\text { })}. \end{aligned}$$

(54)

In particular, if $m\rightarrow 1^-$, then $l_{1}\rightarrow l_{2}$ and we have $\text{ cn }(\xi ,1)\rightarrow \text{ sech }(\xi )$ and $\text{ ns }(\xi ,1)\rightarrow \coth (\xi )$. Now, we have the bright soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ -\frac{2nA_{4}}{A_{7}}\text { }\left[ l_{2}-(l_{2}-l_{3})\text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] \right. \nonumber \\{} & {} \left. -\frac{2A_{2}}{3A_{7}}\right] ^{\frac{1}{2n}}e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(55)

and the singular soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ -\frac{2nA_{4}}{A_{7}}\text { }\left[ l_{3}+(l_{2}-l_{3})\text{ coth }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] \right. \nonumber \\{} & {} \left. -\frac{2A_{2}}{3A_{7}}\right] ^{\frac{1}{2n}}e^{i(-\kappa x+wt+\theta _{0}\text { })}. \end{aligned}$$

(56)

Substituting (52) into (44) we have Jacobi elliptic solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \dfrac{A}{\text { }l_{2}-(l_{2}-l_{3})\text{ cn } {}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) +\frac{A_{2}}{3nA_{4}}}\right] ^{\frac{1}{2n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(57)

and

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \dfrac{A}{\text { }l_{3}+(l_{1}-l_{3})\text{ ns } {}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) +\frac{A_{2}}{3nA_{4}}}\right] ^{\frac{1}{2n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}. \end{aligned}$$

(58)

In particular, if $m\rightarrow 1^-$, we have the singular soliton solution:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \dfrac{A}{\text { }l_{2}-(l_{2}-l_{3})\text{ sech } {}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) +\frac{A_{2}}{3nA_{4}}}\right] ^{ \frac{1}{2n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}. \end{aligned}$$

(59)

Substituting (52) into (45) we have Jacobi elliptic solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \left[ \tfrac{\sqrt{A}\left[ l_{2}-(l_{2}-l_{3}) \text{ cn }{}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] -\frac{\sqrt{A} A_{2}}{6nA_{4}}}{\sqrt{l_{1}-l_{3}}(l_{2}-l_{3})\text{ cn }{}\left( \sqrt{ l_{1}-l_{3}}\xi ;m\right) \text{ sn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ dn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) }\right] ^{\frac{1}{n} }\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(60)

and

$$\begin{aligned}{} & {} q(x,t)=\varepsilon \ \nonumber \\{} & {} \qquad \left[ -\tfrac{6\sqrt{A}\left[ l_{3}+(l_{1}-l_{3})\text{ ns }{}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] -\frac{\sqrt{A}A_{2}}{nA_{4}}}{2\sqrt{l_{1}-l_{3}}\text { } (l_{1}-l_{3})\text{ cn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ dn } {}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ ns}^{3}{}\left( \sqrt{ l_{1}-l_{3}}\xi ;m\right) }\right] ^{\frac{1}{n}}\text { }\nonumber \\{} & {} \qquad e^{i(-\kappa x+wt+\theta _{0}\text { })}. \end{aligned}$$

(61)

In particular, if $m\rightarrow 1^-$, we have the straddled bright–singular soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \tfrac{\sqrt{A}\left[ l_{2}-(l_{2}-l_{3}) \text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] -\frac{\sqrt{A} A_{2}}{6nA_{4}}}{\sqrt{l_{2}-l_{3}}(l_{2}-l_{3})\text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \text{ tanh }{}\left( \sqrt{l_{2}-l_{3}}\xi \right) }\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { } )}, \end{aligned}$$

(62)

and the straddled singular–singular soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \left[ -\tfrac{6\sqrt{A}\left[ l_{3}+(l_{2}-l_{3}) \text{ coth }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] -\frac{\sqrt{A} A_{2}}{nA_{4}}}{2\sqrt{l_{2}-l_{3}}(l_{2}-l_{3}){}\text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \text{ coth}^{3}{}\left( \sqrt{l_{2}-l_{3}}\xi \right) }\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { } )}, \end{aligned}$$

(63)

provided $A>0,\varepsilon =\pm 1.$

Substituting (54) into (46) we have Jacobi elliptic solutions:

$$\begin{aligned}{} & {} q(x,t)=\varepsilon \ \nonumber \\{} & {} \qquad \left[ \tfrac{\sqrt{-\frac{2nA_{2}}{A_{7}}}\sqrt{ l_{1}-l_{3}}(l_{2}-l_{3})\text{ cn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ sn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ dn }{}\left( \sqrt{ l_{1}-l_{3}}\xi ;m\right) }{\text { }\left[ l_{2}-(l_{2}-l_{3})\text{ cn } {}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] -\frac{A_{2}}{6nA_{4}}} \right] ^{\frac{1}{n}}\nonumber \\{} & {} \qquad e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(64)

and

$$\begin{aligned}{} & {} q(x,t)=\varepsilon \ \nonumber \\{} & {} \qquad \left[ -\tfrac{\sqrt{-\frac{2nA_{2}}{A_{7}}} \sqrt{l_{1}-l_{3}}(l_{1}-l_{3})\text{ cn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ dn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ ns } ^{3}{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) }{\text { }\left[ l_{3}+(l_{1}-l_{3})\text{ ns }{}^{2}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] -\frac{A_{2}}{6nA_{4}}}\right] ^{\frac{1}{n}}\text { }\nonumber \\{} & {} \qquad e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(65)

provided $A_{2}A_{7}<0,\varepsilon =\pm 1.$

In particular, if $m\rightarrow 1^-$, we have the straddled bright–singular soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \tfrac{\sqrt{-\frac{2nA_{2}}{A_{7}}}\sqrt{ l_{2}-l_{3}}(l_{2}-l_{3})\text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \text{ tanh }{}\left( \sqrt{l_{2}-l_{3}}\xi \right) }{\text { }\left[ l_{2}-(l_{2}-l_{3})\text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] -\frac{A_{2}}{6nA_{4}}}\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(66)

and the straddled bright–singular soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ -\tfrac{\sqrt{-\frac{2nA_{2}}{A_{7}}} \sqrt{l_{2}-l_{3}}(l_{2}-l_{3})\text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \text{ coth }{}^{3}\left( \sqrt{l_{2}-l_{3}}\xi \right) }{\text { } \left[ l_{2}-(l_{2}-l_{3})\text{ coth }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] -\frac{A_{2}}{6nA_{4}}}\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}. \end{aligned}$$

(67)

Substituting (54) into (47) we have Jacobi elliptic solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \tfrac{2\sqrt{-\frac{5A_{2}^{2}}{18nA_{4}A_{7}}} \text { }\left[ l_{2}-(l_{2}-l_{3})\text{ cn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] -\frac{A_{2}}{6nA_{4}}}{\text { }\sqrt{l_{1}-l_{3}} (l_{2}-l_{3})\text{ cn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ sn } {}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ dn }{}\left( \sqrt{l_{1}-l_{3}} \xi ;m\right) }\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(68)

and

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ -\tfrac{2\sqrt{-\frac{5A_{2}^{2}}{18nA_{4}A_{7}}} \text { }\left[ l_{3}+(l_{1}-l_{3})\text{ ns }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \right] -\frac{A_{2}}{6nA_{4}}}{\sqrt{l_{1}-l_{3}}(l_{1}-l_{3}) \text{ cn }{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) \text{ dn }{}\left( \sqrt{ l_{1}-l_{3}}\xi ;m\right) \text{ ns}^{3}{}\left( \sqrt{l_{1}-l_{3}}\xi ;m\right) }\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(69)

provided $A_{2}A_{7}<0,\varepsilon =\pm 1.$

In particular, if $m\rightarrow 1^-$, we have the straddled bright–singular soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ \tfrac{2\sqrt{-\frac{5A_{2}^{2}}{18nA_{4}A_{7}}} \text { }\left[ l_{2}-(l_{2}-l_{3})\text{ sech }{}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] -\frac{A_{2}}{6nA_{4}}}{\text { }\sqrt{l_{2}-l_{3}} (l_{2}-l_{3})\text{ sech }{}^{2}\left( \sqrt{l_{2}-l_{3}}\xi \right) \text{ tanh }{}\left( \sqrt{l_{2}-l_{3}}\xi \right) }\right] ^{\frac{1}{n} }\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}, \end{aligned}$$

(70)

and the straddled singular-singular soliton solutions:

$$\begin{aligned} q(x,t)= & {} \varepsilon \ \left[ -\tfrac{2\sqrt{-\frac{5A_{2}^{2}}{18nA_{4}A_{7}}} \text { }\left[ l_{3}+(l_{2}-l_{3})\text{ coth }{}\left( \sqrt{l_{2}-l_{3}}\xi \right) \right] -\frac{A_{2}}{6nA_{4}}}{\sqrt{l_{2}-l_{3}}(l_{2}-l_{3}) \text{ sech}^{2}{}\left( \sqrt{l_{2}-l_{3}}\xi \right) \text{ coth } ^{3}{}\left( \sqrt{l_{2}-l_{3}}\xi \right) }\right] ^{\frac{1}{n}}\nonumber \\{} & {} e^{i(-\kappa x+wt+\theta _{0}\text { })}. \end{aligned}$$

(71)

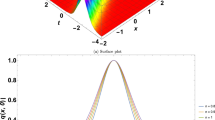
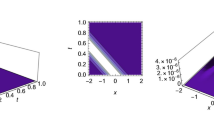
Fig. 1 illustrates the 2D and surface plots of a bright optical soliton (15), showcasing the results under the following parameter settings: $\varepsilon =1$, $V=1$, $\sigma _{11}=1$, $\sigma _{12}=1$, $\sigma _{13}=1$, $\sigma _{14}=1$, $\sigma _{15}=1$, $\delta _{2}=1$, $\delta _{3}=-1$, $\sigma _{3}=1$, $\sigma _{7}=1$, $\sigma _{8}=1$, and $\sigma _{9}=-1$.

Fig. 1

Analysis of the individual properties showcased by a bright optical soliton

Conclusions

The current paper addressed the dispersive concatenation model with power-law of SPM by the aid of sub-ODE and its variants to recover a spectrum of optical solitons. In addition, versions of the algorithm also yielded a wider spectrum of soliton solutions to the model that are being reported for the first time in this work. While a full spectrum of solitons are enumerated and exhibited, it is proved that dark 1-solitons exist only for Kerr law of nonlinear refractive index change [38]. These results are important in the optoelectronics area and will be of great advantage to carry out further research related investigations with the model. Thus, the future holds strong for its research activities. Later, the model will be addressed with differential group delay and also for dispersion–flattened fibers. The application to other optoelectronic devices with this model is also awaited. These include optical metamaterials, optical couplers, gap solitons, quiescent optical solitons and several others. The results of such research activities will be reported after the recovered results are aligned with the pre-existing ones [9,10,11,12,13,14,15].