Introduction

The dispersive concatenation model is an extension of the regular concatenation model that was first proposed a decade ago [1,2,3,4,5,6]. Subsequently the dispersive concatenation model came to light that contains dispersive effects [7,8,9,10,11,12]. This model is a conjunction of the Schrodinger-Hirota equation (SHE), Lakshmanan-Porsezian-Daniel (LPD) model along with the fifth-order nonlinear Schrodinger’s equation (NLSE) [13,14,15,16,17,18]. The dispersive effect for this model stems from the third-order dispersion in SHE, fourth-order dispersion in LPD and fifth-order dispersion in dispersive NLSE [19,20,21,22,23,24]. This model was extensively studied in the scalar case as well as in polarization-preserving fibers [25,26,27,28,29,30]. The quiescent optical solitons for the model with nonlinear chromatic dispersion have also been recovered [31,32,33,34,35,36]. The model with the presence of white noise has been addressed in the past [37,38,39,40,41,42].

The current work studies the model numerically with the aid of Laplace-Adomian decomposition scheme. The bright soliton solutions are recovered, and the results are compared with almost perfect accuracy with the ones that are recovered analytically [43,44,45,46,47,48,49]. The dark soliton solutions are skipped in the current work since this was covered in the earlier paper that was addressed with Kerr law of self-phase modulation (SPM). It has been proved that dark solitons for power law of SPM would exist provided this power-law collapses to Kerr law of SPM [7]. A few specific values of the power-law parameter are chosen that lies within the regime to avoid the effect of self-focusing singularity. The numerical results are exhibited in details after an illustrative introduction to the model. These are detailed in the subsequent sections.

Dispersive concatenation model with power-law of self-phase modulation

The dimensionless form of the system under consideration in this paper is denoted as:

$$\begin{aligned}&i q_t + aq_{xx} + b \left| q \right| ^{2n} q-i\delta _{1}\big (\sigma _{1}q_{xxx}+\sigma _{2}\vert q\vert ^{2n}q_{x}\big )\nonumber \\&+ \delta _{2} \left[ \sigma _{3} q_{xxxx} + \sigma _{4} \vert q \vert ^{2n}q_{xx}+\sigma _{5} \vert q \vert ^{2n+2}q+ \sigma _{6} \left| q_x \right| ^{2} q\right. \nonumber \\&\left. +\sigma _{7}(q_{x})^{2}q^{*}+\sigma _{8}q^{*}_{xx}q^{2} \right] - i \delta _{3}\left[ \sigma _{9} q_{xxxxx} + \sigma _{10} \left| q \right| ^{2n} q_{xxx}\right. \nonumber \\&\left. + \sigma _{11} \vert q \vert ^{2n+2}q_{x} +\sigma _{12}qq_{x}q^{*}_{xx}+\sigma _{13}q^{*}q_{x}q_{xx}\right. \nonumber \\&\left. +\sigma _{14}qq^{*}_{x}q_{xx}+\sigma _{15}(q_x)^{2}q^{*}_{x}\right] =0. \end{aligned}$$
(1)

Equation (1) is the dispersive concatenation model with power-law of SPM, q is a complex-valued function representing the wave profile, while \(q^{*}\) is its complex conjugate and \(i^2=-1\) moreover a and b are the coefficients of CD and SPM respectively. The coefficients \(\sigma _j\) with \(j=1,2,\ldots ,15\) and \(\delta _s\) with \(s=1,2,3\), are all real constants. In particular, the coefficient of \(\delta _{1}\) contains the remaining terms of the SHE that is recoverable from the standard NLSE via Lie transform. In addition, the coefficients of \(\delta _{2}\) and \(\delta _{3}\) are from LPD and SHE respectively.

Equation (1) represents a real combination of established models that describe the trans-continental and trans-oceanic dynamics of soliton transmission. The Adomian decomposition approach, together with the well recognized Laplace transform, will be utilized to introduce optical solitons for model (1) for the first time. The establishment of various forms of constraint requirements for the system’s structure can also ensure the occurrence of solitons. In the following sections, specific details are enumerated and presented.

Bright optical solitons for the governing model

The 1-bright soliton solution to (1), which was recently investigated using the indeterminate coefficients method in [7], is provided by

$$\begin{aligned} q(x,t) = A\; \text{ sech}^{\frac{1}{n}}[B(x-vt)] e^{i \left( -\kappa x + \omega t + \theta _0 \right) }, \end{aligned}$$
(2)

where the bright soliton’s velocity v is computed as

$$\begin{aligned} sss = -2\kappa \left( a+4\kappa ^{2}\delta _{2}\sigma _{3} \right) . \end{aligned}$$
(3)

The angular velocity \(\omega \) is also calculated from the system coefficients, as

$$\begin{aligned} \omega =\frac{\delta _{2}\sigma _{3}(Z_{5}^{2}-3\kappa ^{4}(Z_{1}+Z_{3})^2 )-Z_{2}Z_{5}(Z_{1}+Z_{3})-a\kappa ^{2}(Z_{1}+Z_{3})^2}{(Z_{1}+Z_{3})^2}. \end{aligned}$$
(4)

The width of the soliton as a function of n and some coefficients of the model is obtained as follows

$$\begin{aligned} B=\sqrt{-\frac{n^2 Z_{5}}{Z_{1}+Z_{3}}}, \end{aligned}$$
(5)

where the restriction must be imposed:

$$\begin{aligned} Z_{5}(Z_{1}+Z_{3})<0. \end{aligned}$$
(6)

The amplitude of the soliton can be obtained by

$$\begin{aligned} A=\root 2n \of {-\frac{Z_{5}(Z_{1}+(n+1)Z_{3})}{\delta _{2}\sigma _{5}(Z_{1}+Z_{3})}}, \end{aligned}$$
(7)

Thus, the subsequent restriction was imposed:

$$\begin{aligned} \delta _{2}\sigma _{5}(Z_{1}+(n+1)Z_{3})>0. \end{aligned}$$
(8)

The preceding assertion remains valid when considering the subsequent solvability conditions:

$$\begin{aligned}{} & {} (Z_{1}+(n+1)Z_{3})\sigma _{4}-(2n+1)(3n+1)\delta _{2}\sigma _{3}\sigma _{5}=0,\end{aligned}$$
(9)
$$\begin{aligned}{} & {} [Z_{1}+(n+1)Z_{3}](n^{2}Z_{4}+\delta _{2}\sigma _{4}B^{2})\nonumber \\{} & {} =(n+1)\delta _{2}\sigma _{5}[n^{2}Z_{2}+2\sigma _{3}\delta _{2}(1+2n(n+1))B^{2}]. \end{aligned}$$
(10)

Brief overview of methodology

This section will present a succinct explanation of the often employed Adomian decomposition method and its improved version obtained by combining the approach with the Laplace transform [8, 9]. The proposed methodology will be employed to acquire bright solitons for the novel concatenation model with power-law of self-phase modulation (1).

In general, using operators we can write Eq. (1) as

$$\begin{aligned} D_{t}q(x,t)+Lq(x,t)+Nq(x,t)=0 \end{aligned}$$
(11)

subject to an initial condition

$$\begin{aligned} q(x,0)=f(x). \end{aligned}$$
(12)

Within the framework of the operational Eq. (11), the operators apply their effects on a function q that possesses complex values in the following manner:

$$\begin{aligned} D_{t}q=iq_{t},\end{aligned}$$
(13)
$$\begin{aligned}{} & {} Lq(x,t)=aq_{xx}-i\delta _{1}\sigma _{1} q_{xxx}+\delta _{2}\sigma _{3}q_{xxxx}-i\delta _{3}\sigma _{9}q_{xxxxx},\end{aligned}$$
(14)
$$\begin{aligned} Nq(x,t)= & {} b \left| q \right| ^{2n} q-i\delta _{1}\sigma _{2}\vert q\vert ^{2n}q_{x} + \delta _{2} \left[ \sigma _{4} \vert q \vert ^{2n}q_{xx}\right. \nonumber \\{} & {} \left. +\sigma _{5} \vert q \vert ^{2n+2}q+ \sigma _{6} \left| q_x \right| ^{2} q +\sigma _{7}(q_{x})^{2}q^{*}+\sigma _{8}q^{*}_{xx}q^{2} \right] \nonumber \\{} & {} - i \delta _{3}\left[ \sigma _{10} \left| q \right| ^{2n} q_{xxx} + \sigma _{11} \vert q \vert ^{2n+2}q_{x} +\sigma _{12}qq_{x}q^{*}_{xx}\right. \nonumber \\{} & {} \left. +\sigma _{13}q^{*}q_{x}q_{xx}+\sigma _{14}qq^{*}_{x}q_{xx}+\sigma _{15}(q_x)^{2}q^{*}_{x}\right] \end{aligned}$$
(15)

The nonlinearity of the operator N is easy to see. As a result, the Adomian decomposition approach permits its decomposition into the following series:

$$\begin{aligned} Nq(x,t)=\sum _{k=0}^{\infty }M_{k}(q_{0},\ldots ,q_{k}), \end{aligned}$$
(16)

where each of the \(M_n\) is an Adomian polynomial [10]. Also, by the Adomian decomposition method we have

$$\begin{aligned} q(x,t)=\sum _{k=0}^{\infty }q_{k}(x,t). \end{aligned}$$
(17)

To conveniently represent the nonlinear operator denoted by (16), we may write it as

$$\begin{aligned} Nq(x,t)=\sum _{l=1}^{13}N_{l}q(x,t), \end{aligned}$$
(18)

where

$$\begin{aligned} N_{1}q= & {} b\vert q\vert ^{2n} q,\quad N_{2}q=-i\delta _{1}\sigma _{2}\vert q\vert ^{2n}q_{x}, \quad N_{3}q= \delta _{2}\sigma _{4} \vert q \vert ^{2n}q_{xx}, \nonumber \\ \quad N_{4}q= & {} \delta _{2}\sigma _{5} \vert q \vert ^{2n+2}q,\quad N_{5}q=\delta _{2}\sigma _{6} \left| q_x \right| ^{2} q,\nonumber \\ N_{6}q= & {} \delta _{2}\sigma _{7}(q_{x})^{2}q^{*},\quad N_{7}q=\delta _{2}\sigma _{8}q^{*}_{xx}q^{2},\nonumber \\ \quad N_{8}q= & {} -i\delta _{3}\sigma _{10} \left| q \right| ^{2n} q_{xxx},\quad N_{9}q=-i\delta _{3}\sigma _{11} \vert q \vert ^{2n+2}q_{x},\end{aligned}$$
(19)
$$\begin{aligned} N_{10}q= & {} -i\delta _{3}\sigma _{12}qq_{x}q^{*}_{xx},\quad N_{11}q=-i\delta _{3}\sigma _{13}q^{*}q_{x}q_{xx}, \nonumber \\ \quad N_{12}q= & {} -i\delta _{3}\sigma _{14}qq^{*}_{x}q_{xx},\quad N_{13}q=-i\delta _{3}\sigma _{15}(q_x)^{2}q^{*}_{x}, \end{aligned}$$
(20)

and all nonlinear components \(N_{1},\ldots , N_{13}\) can be decomposed into infinite series of Adomian polynomials given by:

$$\begin{aligned} N_{l}q=\sum _{k=0}^{\infty }M_{k}^{l}(q_{0},q_{1},\ldots , q_k),\quad l=1,2,\ldots ,13. \end{aligned}$$
(21)

\(M_{k}^{l}\) represents the Adomian polynomials for each \(l=1,2,\ldots , 13\) in Eq. (21), which can be calculated using the formulas established in [11], i.e.

$$\begin{aligned}{} & {} M_{k}^{l}(q_{0},q_{1},\ldots , q_n)\nonumber \\{} & {} = \left\{ \begin{array}{ll} N_l(q_0), &{} k=0 \\ \frac{1}{k}\sum _{i=0}^{k-1}(i+1)q_{i+1}\frac{\partial }{\partial q_{0}}M_{n-1-i}^{l}, &{} k=1,2,3,\ldots \end{array} \right. \end{aligned}$$
(22)

In this context, the symbol \(\mathscr {L}\) will be used to represent the Laplace transform, while \(\mathscr {L}^{-1}\) will represent its inverse operator. Next, we apply the Laplace transform \(\mathscr {L}\) to both sides of the operational Eq. (11) to obtain

$$\begin{aligned} \mathscr {L}\{D_{t}q(x,t)+Lq(x,t)+Nq(x,t)\}=0. \end{aligned}$$
(23)

By utilizing the initial condition, which is obtained from the initial profiles of the solitons f, we acquire

$$\begin{aligned} \mathscr {L}\{q(x,t)\}=\frac{1}{s}f(x)-\frac{1}{s}\big (\mathscr {L}\{Lq(x,t)\}+\mathscr {L}\{N q(x,t)\}\big ). \end{aligned}$$
(24)

By substituting the Eqs. (16), (17) and (21) into Eq. (24), we get

$$\begin{aligned} \mathscr {L}\big \{\sum _{k=0}^{\infty }q_{k}(x,t)\big \}= & {} \frac{1}{s}f(x)-\frac{1}{s}\Big (\mathscr {L}\big \{L\big (\sum _{k=0}^{\infty }q_{k}(x,t)\big )\big \}\nonumber \\{} & {} \quad +\mathscr {L}\big \{\sum _{j=1}^{8}\sum _{k=0}^{\infty }M_{k}^{j}(q_{0},\ldots , q_{k})\big \}\Big ). \end{aligned}$$
(25)

By equating both sides of Eq. (25), we can calculate the Laplace transform of each individual component of the solution, that is

$$\begin{aligned} \mathscr {L}\{q_{0}(x,t)\}=\frac{1}{s}f(x) \end{aligned}$$
(26)

The recursive relations can be written as follows for all values of m that are greater than one:

$$\begin{aligned} \mathscr {L}\{q_{m}(x,t)\}= & {} -\frac{1}{s}\Big (\mathscr {L}\{Lq_{m-1}(x,t)\}\nonumber \\{} & {} \quad +\mathscr {L}\big \{\sum _{j=1}^{8}\sum _{m=0}^{\infty }M_{m-1}^{j}(q_{0},\ldots , q_{m-1})\big \}\Big ). \end{aligned}$$
(27)

In order to calculate Adomian polynomials, we will focus on the nonlinear operators \(N_j\) acting on the function q described in Eq. (19). By applying the formula (22), for example, for \(n=1\), we may get the following results:

$$\begin{aligned} M_{0}^{1}&=bq_{0}^{2}q^{*}_{0},\\ M_{1}^{1}&=b(q^{*}_{1}q_{0}^{2}+2q^{*}_{0}q_{1}q_{0}), \\ M_{2}^{1}&= b(q^{*}_{2}q_{0}^{2}+q^{*}_{0}q_{1}^{2}+2q^{*}_{0}q_{2}q_{0}+2q^{*}_{1}q_{1}q_{0}),\\ M_{3}^{1}&= b(q^{*}_{3}q_{0}^{2} +q^{*}_{1}q_{1}^{2}+2q^{*}_{2}q_{1}q_{0}+2q^{*}_{1}q_{2}q_{0}\\&\quad +2q^{*}_{0}q_{3}q_{0}+2q^{*}_{0}q_{1}q_{2}),\\ M_{4}^{1}&= b(q^{*}_{4}q_{0}^{2}+q^{*}_{2}q_{1}^{2}+q^{*}_{0}q_{2}^{2}+2q^{*}_{3}q_{1}q_{0}+2q^{*}_{2}q_{2}q_{0}\\&\quad +2q^{*}_{1}q_{3}q_{0}+2q^{*}_{0}q_{4}q_{0}+2q^{*}_{1}q_{1}q_{2}+2q^{*}_{0}q_{1}q_{3}), \end{aligned}$$
$$\begin{aligned} M_{0}^{2}&=-i\delta _{1}\sigma _{2}q_{0}q^{*}_{0}q_{0x}, \\ M_{1}^{2}&=-i\delta _{1}\sigma _{2}(q_{1}q^{*}_{0}q_{0x}+q_{0}q^{*}_{1}q_{0x}+q_{0}q^{*}_{0}q_{1x}), \\ M_{2}^{2}&=-i\delta _{1}\sigma _{2}(q_{2}q^{*}_{0}q_{0x}+q_{1}q^{*}_{1}q_{0x}+q_{0}q^{*}_{2}q_{0x}\\&\quad +q_{1}q^{*}_{0}q_{1x}+q_{0}q^{*}_{1}q_{1x}+q_{0}q^{*}_{0}q_{2x}), \\ M_{3}^{2}&=-i\delta _{1}\sigma _{2}(q_{3}q^{*}_{0}q_{0x}+q_{2}q^{*}_{1}q_{0x}+q_{1}q^{*}_{2}q_{0x}\\&\quad +q_{0}q^{*}_{3}q_{0x} +q_{2}q^{*}_{0}q_{1x}+q_{1}q^{*}_{1}q_{1x}+q_{0}q^{*}_{2}q_{1x}\\&\quad +q_{1}q^{*}_{0}q_{2x}+q_{0}q^{*}_{1}q_{2x}+q_{0}q^{*}_{0}q_{3x}),\\ M_{4}^{2}&=-i\delta _{1}\sigma _{2}(q_{4}q^{*}_{0}q_{0x}+q_{3}q^{*}_{1}q_{0x}+q_{2}q^{*}_{2}q_{0x}+q_{1}q^{*}_{3}q_{0x}\\&\quad +q_{0}q^{*}_{4}q_{0x}+q_{3}q^{*}_{0}q_{1x} +q_{2}q^{*}_{1}q_{1x}+q_{1}q^{*}_{2}q_{1x}\\&\quad +q_{0}q^{*}_{3}q_{1x}+q_{2}q^{*}_{0}q_{2x}+q_{1}q^{*}_{1}q_{2x}+q_{0}q^{*}_{2}q_{2x}\\&\quad +q_{1}q^{*}_{0}q_{3x}+q_{0}q^{*}_{1}q_{3x}+q_{0}q^{*}_{0}q_{4x}), \end{aligned}$$
$$\begin{aligned} M_{0}^{3}&= \delta _{2}\sigma _{4}q^{*}_{0}q_{0}q_{0 xx},\\ M_{1}^{3}&=\delta _{2}\sigma _{4}(q^{*}_{1}q_{0}q_{0 xx}+q^{*}_{0}q_{1}q_{0 xx}+q^{*}_{0}q_{0}q_{1 xx}),\\ M_{2}^{3}&=\delta _{2}\sigma _{4}(q^{*}_{2}q_{0}q_{0 xx}+q^{*}_{1}q_{1}q_{0 xx}+q^{*}_{0}q_{2}q_{0 xx}\\&\quad +q^{*}_{1}q_{0}q_{1 xx}+q^{*}_{0}q_{1}q_{1 xx}+q^{*}_{0}q_{0}q_{2 xx}),\\ M_{3}^{3}&=\delta _{2}\sigma _{4}(q^{*}_{3}q_{0}q_{0 xx}+q^{*}_{2}q_{1}q_{0 xx}+q^{*}_{1}q_{2}q_{0 xx}\\&\quad +q^{*}_{0}q_{3}q_{0 xx}+q^{*}_{2}q_{0}q_{1 xx}+q^{*}_{1}q_{1}q_{1 xx}\\&\quad +q^{*}_{0}q_{2}q_{1 xx}+q^{*}_{1}q_{0}q_{2 xx}\\&\quad +q^{*}_{0}q_{1}q_{2 xx}+q^{*}_{0}q_{0}q_{3 xx}),\\ M_{4}^{3}&=\delta _{2}\sigma _{4}(q^{*}_{4}q_{0}q_{0 xx}+q^{*}_{3}q_{1}q_{0 xx}+q^{*}_{2}q_{2}q_{0 xx}+q^{*}_{1}q_{3}q_{0 xx}\\&\quad +q^{*}_{0}q_{4}q_{0 xx}+q^{*}_{3}q_{0}q_{1 xx}+q^{*}_{2}q_{1}q_{1 xx}+q^{*}_{1}q_{2}q_{1 xx}\\&\quad +q^{*}_{0}q_{3}q_{1 xx} +q^{*}_{2}q_{0}q_{2xx} +q^{*}_{1}q_{1}q_{2 xx}+q^{*}_{0}q_{2}q_{2 xx}\\&\quad +q^{*}_{1}q_{0}q_{3 xx} +q^{*}_{0}q_{1}q_{3 xx}+q^{*}_{0}q_{0}q_{4 xx}), \end{aligned}$$
$$\begin{aligned} M_{0}^{4}&= \delta _{2}\sigma _{5}q^{*2}_{0}q_{0}^3,\\ M_{1}^{4}&= \delta _{2}\sigma _{5}(2q^{*}_{0}q^{*}_{1}q_{0}^3+3q^{*2}_{0}q_{1}q_{0}^2),\\ M_{2}^{4}&= \delta _{2}\sigma _{5}(q^{*2}_{1}q_{0}^3+2q^{*}_{0}q^{*}_{2}q_{0}^3+6q^{*}_{0}q^{*}_{1}q_{1}q_{0}^2+3q^{*2}_{0}q_{2}q_{0}^2\\&\quad +3q^{*2}_{0}q_{1}^2q_{0}),\\ M_{3}^{4}&= \delta _{2}\sigma _{5}(2q^{*}_{1}q^{*}_{2}q_{0}^3+2q^{*}_{0}q^{*}_{3}q_{0}^3 +3q^{*2}_{1}q_{1}q_{0}^2\\&\quad +6q^{*}_{0}q^{*}_{2}q_{1}q_{0}^2+6q^{*}_{0}q^{*}_{1}q_{2}q_{0}^2+3q^{*2}_{0}q_{3}q_{0}^2\\&\quad +6q^{*}_{0}q^{*}_{1}q_{1}^2q_{0}+6q^{*2}_{0}q_{1}q_{2}q_{0}+q^{*2}_{0}q_{1}^3),\\ M_{4}^{4}&= \delta _{2}\sigma _{5}(q^{*2}_{2}q_{0}^3+2q^{*}_{1}q^{*}_{3}q_{0}^3+2q^{*}_{0}q^{*}_{4}q_{0}^3 +6q^{*}_{1}q^{*}_{2}q_{1}q_{0}^2\\&\quad +6q^{*}_{0}q^{*}_{3}q_{1}q_{0}^2+3q^{*2}_{1}q_{2}q_{0}^2 +6q^{*}_{0}q^{*}_{2}q_{2}q_{0}^2+6q^{*}_{0}q^{*}_{1}q_{3}q_{0}^2\\&\quad +3q^{*2}_{0}q_{4}q_{0}^2+3q^{*2}_{1}q_{1}^2q_{0}+6q^{*}_{0}q^{*}_{2}q_{1}^2q_{0}+3q^{*2}_{0}q_{2}^{2}q_{0}\\&\quad +12q^{*}_{0}q^{*}_{1}q_{1}q_{2}q_{0}+6q^{*2}_{0}q_{1}q_{3}q_{0}+2q^{*}_{0}q^{*}_{1}q_{1}^3+3q^{*2}_{0}q_{1}^2q_{2}), \end{aligned}$$
$$\begin{aligned} M_{0}^{5}&=\delta _{2}\sigma _{6}q_{0}q^{*}_{0x}q_{0x},\\ M_{1}^{5}&=\delta _{2}\sigma _{6}(q_{0}q^{*}_{0x}q_{1x}+q_{0}q^{*}_{1x}q_{0x}+q_{1}q^{*}_{0x}q_{0x}),\\ M_{2}^{5}&=\delta _{2}\sigma _{6}(q_{0}q^{*}_{0x}q_{2x}+q_{0}q^{*}_{1x}q_{1x}+q_{0}q^{*}_{2x}q_{0x}+q_{1}q^{*}_{0x}q_{1x}\\&\quad +q_{1}q^{*}_{1x}q_{0x}+q_{2}q^{*}_{0x}q_{0x}),\\ M_{3}^{5}&=\delta _{2}\sigma _{6}(q_{0}q^{*}_{0x}q_{3x}+q_{0}q^{*}_{1x}q_{2x}\\&\quad +q_{0}q^{*}_{2x}q_{1x}+q_{0}q^{*}_{3x}q_{0x}+q_{1}q^{*}_{0x}q_{2x}+q_{1}q^{*}_{1x}q_{1x}\\&\quad +q_{1}q^{*}_{2x}q_{0x}+q_{2}q^{*}_{0x}q_{1x}+q_{2}q^{*}_{1x}q_{0x}+q_{3}q^{*}_{0x}q_{0x}),\\ M_{4}^{5}&=\delta _{2}\sigma _{6}(q_{0}q^{*}_{0x}q_{4x}+q_{0}q^{*}_{1x}q_{3x}+q_{0}q^{*}_{2x}q_{2x}+q_{0}q^{*}_{3x}q_{1x}\\&\quad +q_{0}q^{*}_{4x}q_{0x}+q_{1}q^{*}_{0x}q_{3x}+q_{1}q^{*}_{1x}q_{2x}\\&\quad +q_{1}q^{*}_{2x}q_{1x}+q_{1}q^{*}_{3x}q_{0x}+q_{2}q^{*}_{0x}q_{2x}+q_{2}q^{*}_{1x}q_{1x}\\&\quad +q_{2}q^{*}_{2x}q_{0x}+q_{3}q^{*}_{0x}q_{1x}+q_{3}q^{*}_{1x}q_{0x}+q_{4}q^{*}_{0x}q_{0x}), \end{aligned}$$
$$\begin{aligned} M_{0}^{6}&=\delta _{2}\sigma _{7}q_{0x}^{2}q^{*}_{0},\\ M_{1}^{6}&=\delta _{2}\sigma _{7}(q^{*}_{1}q_{0x}^{2}+2q^{*}_{0}q_{1x}q_{0x}), \\ M_{2}^{6}&= \delta _{2}\sigma _{7}(q^{*}_{2}q_{0x}^{2}+q^{*}_{0}q_{1x}^{2}+2q^{*}_{0}q_{2x}q_{0x}+2q^{*}_{1}q_{1x}q_{0x}),\\ M_{3}^{6}&= \delta _{2}\sigma _{7}(q^{*}_{3}q_{0x}^{2} +q^{*}_{1}q_{1x}^{2}+2q^{*}_{2}q_{1x}q_{0x}+2q^{*}_{1}q_{2x}q_{0x}\\&\quad +2q^{*}_{0}q_{3x}q_{0x}+2q^{*}_{0}q_{1x}q_{2x}),\\ M_{4}^{6}&= \delta _{2}\sigma _{7}(q^{*}_{4}q_{0x}^{2}+q^{*}_{2}q_{1x}^{2}+q^{*}_{0}q_{2x}^{2}+2q^{*}_{3}q_{1x}q_{0x}\\&\quad +2q^{*}_{2}q_{2x}q_{0x}+2q^{*}_{1}q_{3x}q_{0x}+2q^{*}_{0}q_{4x}q_{0x}\\&\quad +2q^{*}_{1}q_{1x}q_{2x}+2q^{*}_{0}q_{1x}q_{3x}), \end{aligned}$$
$$\begin{aligned} M_{0}^{7}&=\delta _{2}\sigma _{8}q_{0}^{2}q^{*}_{0xx},\\ M_{1}^{7}&=\delta _{2}\sigma _{8}(q_{0}^{2}q^{*}_{1xx}+2q_{0}q_{1}q^{*}_{0xx}),\\ M_{2}^{7}&=\delta _{2}\sigma _{8}(q_{1}^{2}q^{*}_{0xx}+2q_{0}q_{2}q^{*}_{0xx}+2q_{0}q_{1}q^{*}_{1xx}+q_{0}^{2}q^{*}_{2xx}),\\ M_{3}^{7}&=\delta _{2}\sigma _{8}(q_{1}^{2}q^{*}_{1xx}+2q_{1}q_{2}q^{*}_{0xx}+2q_{0}q_{3}q^{*}_{0xx}\\&\quad +2q_{0}q_{2}q^{*}_{1xx}+2q_{0}q_{1}q^{*}_{2xx}+q_{0}^{2}q^{*}_{3xx}),\\ M_{4}^{7}&=\delta _{2}\sigma _{8}(q_{1}^{2}q^{*}_{2xx}+2q_{1}q_{2}q^{*}_{1xx}+q_{2}^{2}q^{*}_{0xx}+2q_{1}q_{3}q^{*}_{0xx}\\&\quad +2q_{0}q_{4}q^{*}_{0xx}+2q_{0}q_{3}q^{*}_{1xx}+2q_{0}q_{2}q^{*}_{2xx}\\&\quad +2q_{0}q_{1}q^{*}_{3xx}+q_{0}^{2}q^{*}_{4xx}), \end{aligned}$$
$$\begin{aligned} M_{0}^{8}&=-i\delta _{3}\sigma _{10}q_{0}q^{*}_{0}q_{0xxx},\\ M_{1}^{8}&=-i\delta _{3}\sigma _{10}(q_{0}q^{*}_{0}q_{1xxx}+q_{0}q^{*}_{1}q_{0xxx}+q_{1}q^{*}_{0}q_{0xxx}),\\ M_{2}^{8}&=-i\delta _{3}\sigma _{10}(q_{0}q^{*}_{0}q_{2xxx}+q_{0}q^{*}_{1}q_{1xxx}+q_{0}q^{*}_{2}q_{0xxx}\\&\quad +q_{1}q^{*}_{0}q_{1xxx}+q_{1}q^{*}_{1}q_{0xxx}+q_{2}q^{*}_{0}q_{0xxx}),\\ M_{3}^{8}&=-i\delta _{3}\sigma _{10}(q_{0}q^{*}_{0}q_{3xxx}+q_{0}q^{*}_{1}q_{2xxx}+q_{0}q^{*}_{2}q_{1xxx}\\&\quad +q_{0}q^{*}_{3}q_{0xxx}+q_{1}q^{*}_{0}q_{2xxx}+q_{1}q^{*}_{1}q_{1xxx}\\ {}&+q_{1}q^{*}_{2}q_{0xxx}+q_{2}q^{*}_{0}q_{1xxx}+q_{2}q^{*}_{1}q_{0xxx}+q_{3}q^{*}_{0}q_{0xxx}),\\ M_{4}^{8}&=-i\delta _{3}\sigma _{10}(q_{0}q^{*}_{0}q_{4xxx}+q_{0}q^{*}_{1}q_{3xxx}+q_{0}q^{*}_{2}q_{2xxx}\\&\quad +q_{0}q^{*}_{3}q_{1xxx}+q_{0}q^{*}_{4}q_{0xxx}+q_{1}q^{*}_{0}q_{3xxx}+q_{1}q^{*}_{1}q_{2xxx}\\&\quad +q_{1}q^{*}_{2}q_{1xxx}+q_{1}q^{*}_{3}q_{0xxx}+q_{2}q^{*}_{0}q_{2xxx}+q_{2}q^{*}_{1}q_{1xxx}\\&\quad +q_{2}q^{*}_{2}q_{0xxx}+q_{3}q^{*}_{0}q_{1xxx}+q_{3}q^{*}_{1}q_{0xxx}+q_{4}q^{*}_{0}q_{0xxx}), \end{aligned}$$
$$\begin{aligned} M_{0}^{9}&=-i\delta _{3}\sigma _{11}q_{0}^{2}q^{*2}_{0}q_{0x}, \\ M_{1}^{9}&=-i\delta _{3}\sigma _{11}(q_{1}^{2}q^{*2}_{0}q_{0x}+q_{0}^{2}q^{*2}_{1}q_{0x}+q_{0}^{2}q^{*2}_{0}q_{1x}), \\ M_{2}^{9}&=-i\delta _{3}\sigma _{11}(q_{2}^{2}q^{*2}_{0}q_{0x}+q_{1}^{2}q^{*2}_{1}q_{0x}\\&\quad +q_{0}^{2}q^{*2}_{2}q_{0x}+q_{1}^{2}q^{*2}_{0}q_{1x}+q_{0}^{2}q^{*2}_{1}q_{1x}+q_{0}^{2}q^{*2}_{0}q_{2x}), \\ M_{3}^{9}&=-i\delta _{3}\sigma _{11}(q_{3}^{2}q^{*2}_{0}q_{0x}+q_{2}^{2}q^{*2}_{1}q_{0x}\\&\quad +q_{1}^{2}q^{*2}_{2}q_{0x}+q_{0}^{2}q^{*2}_{3}q_{0x}+q_{2}^{2}q^{*2}_{0}q_{1x}+q_{1}^{2}q^{*2}_{1}q_{1x}\\&\quad +q_{0}^{2}q^{*2}_{2}q_{1x}+q_{1}^{2}q^{*2}_{0}q_{2x}+q_{0}^{2}q^{*2}_{1}q_{2x}+q_{0}^{2}q^{*2}_{0}q_{3x}),\\ M_{4}^{9}&=-i\delta _{3}\sigma _{11}(q_{4}^{2}q^{*2}_{0}q_{0x}+q_{3}^{2}q^{*2}_{1}q_{0x} +q_{2}^{2}q^{*2}_{2}q_{0x}\\&\quad +q_{1}^{2}q^{*2}_{3}q_{0x}+q_{0}^{2}q^{*2}_{4}q_{0x}+q_{3}^{2}q^{*2}_{0}q_{1x} +q_{2}^{2}q^{*2}_{1}q_{1x}\\&\quad +q_{1}^{2}q^{*2}_{2}q_{1x}+q_{0}^{2}q^{*2}_{3}q_{1x}+q_{2}^{2}q^{*2}_{0}q_{2x} +q_{1}^{2}q^{*2}_{1}q_{2x}\\&\quad +q_{0}^{2}q^{*2}_{2}q_{2x}+q_{1}^{2}q^{*2}_{0}q_{3x}+q_{0}^{2}q^{*2}_{1}q_{3x}+q_{0}^{2}q^{*2}_{0}q_{4x}), \end{aligned}$$
$$\begin{aligned} M_{0}^{10}&=-i\delta _{3}\sigma _{12}q_{0}q^{*}_{0xx}q_{0x},\\ M_{1}^{10}&=-i\delta _{3}\sigma _{12}(q_{0}q^{*}_{0xx}q_{1x}+q_{0}q^{*}_{1xx}q_{0x}+q_{1}q^{*}_{0xx}q_{0x}),\\ M_{2}^{10}&=-i\delta _{3}\sigma _{12}(q_{0}q^{*}_{0xx}q_{2x}+q_{0}q^{*}_{1xx}q_{1x}+q_{0}q^{*}_{2xx}q_{0x}\\&\quad +q_{1}q^{*}_{0xx}q_{1x}+q_{1}q^{*}_{1xx}q_{0x}+q_{2}q^{*}_{0xx}q_{0x}),\\ M_{3}^{10}&=-i\delta _{3}\sigma _{12}(q_{0}q^{*}_{0xx}q_{3x}+q_{0}q^{*}_{1xx}q_{2x}+q_{0}q^{*}_{2xx}q_{1x}\\&\quad +q_{0}q^{*}_{3xx}q_{0x}+q_{1}q^{*}_{0xx}q_{2x}+q_{1}q^{*}_{1xx}q_{1x}+q_{1}q^{*}_{2xx}q_{0x}\\&\quad +q_{2}q^{*}_{0x}q_{1xx}+q_{2}q^{*}_{1xx}q_{0x}+q_{3}q^{*}_{0xx}q_{0x}),\\ M_{4}^{10}&=-i\delta _{3}\sigma _{12}(q_{0}q^{*}_{0xx}q_{4x}+q_{0}q^{*}_{1xx}q_{3x}+q_{0}q^{*}_{2xx}q_{2x}\\&\quad +q_{0}q^{*}_{3xx}q_{1x}+q_{0}q^{*}_{4xx}q_{0x}+q_{1}q^{*}_{0xx}q_{3x}+q_{1}q^{*}_{1xx}q_{2x}\\&\quad +q_{1}q^{*}_{2xx}q_{1x}+q_{1}q^{*}_{3xx}q_{0x}+q_{2}q^{*}_{0xx}q_{2x}+q_{2}q^{*}_{1xx}q_{1x}\\&\quad +q_{2}q^{*}_{2xx}q_{0x}+q_{3}q^{*}_{0xx}q_{1x}+q_{3}q^{*}_{1xx}q_{0x}+q_{4}q^{*}_{0xx}q_{0x}), \end{aligned}$$
$$\begin{aligned} M_{0}^{11}&= -i\delta _{3}\sigma _{13}q^{*}_{0}q_{0 x}q_{0 xx},\\ M_{1}^{11}&=-i\delta _{3}\sigma _{13}(q^{*}_{1}q_{0 x}q_{0 xx}+q^{*}_{0}q_{1 x}q_{0 xx}+q^{*}_{0}q_{0 x}q_{1 xx}),\\ M_{2}^{11}&=-i\delta _{3}\sigma _{13}(q^{*}_{2}q_{0 x}q_{0 xx}+q^{*}_{1}q_{1 x}q_{0 xx}+q^{*}_{0}q_{2 x}q_{0 xx}\\&\quad +q^{*}_{1}q_{0 x}q_{1 xx}+q^{*}_{0}q_{1 x}q_{1 xx}+q^{*}_{0}q_{0 x}q_{2 xx}),\\ M_{3}^{11}&=-i\delta _{3}\sigma _{13}(q^{*}_{3}q_{0 x}q_{0 xx}+q^{*}_{2}q_{1 x}q_{0 xx}+q^{*}_{1}q_{2 x}q_{0 xx}\\&\quad +q^{*}_{0}q_{3 x}q_{0 xx}+q^{*}_{2}q_{0 x}q_{1 xx}+q^{*}_{1}q_{1 x}q_{1 xx}+q^{*}_{0}q_{2 x}q_{1 xx}\\&\quad +q^{*}_{1}q_{0 x}q_{2 xx}+q^{*}_{0}q_{1 x}q_{2 xx}+q^{*}_{0}q_{0 x}q_{3 xx}),\\ M_{4}^{11}&=-\delta _{3}\sigma _{13}(q^{*}_{4}q_{0x}q_{0 xx}+q^{*}_{3}q_{1x}q_{0 xx}+q^{*}_{2}q_{2x}q_{0 xx}\\&\quad +q^{*}_{1}q_{3x}q_{0 xx}+q^{*}_{0}q_{4x}q_{0 xx}+q^{*}_{3}q_{0x}q_{1 xx}+q^{*}_{2}q_{1x}q_{1 xx}\\&\quad +q^{*}_{1}q_{2x}q_{1 xx}+q^{*}_{0}q_{3x}q_{1 xx} +q^{*}_{2}q_{0x}q_{2xx}+q^{*}_{1}q_{1x}q_{2 xx}\\&\quad +q^{*}_{0}q_{2x}q_{2 xx}+q^{*}_{1}q_{0x}q_{3 xx}+q^{*}_{0}q_{1x}q_{3 xx}+q^{*}_{0}q_{0x}q_{4 xx}), \end{aligned}$$
$$\begin{aligned} M_{0}^{12}&= -i\delta _{3}\sigma _{14}q^{*}_{0x}q_{0 }q_{0 xx},\\ M_{1}^{12}&=-i\delta _{3}\sigma _{14}(q^{*}_{1x}q_{0}q_{0 xx}+q^{*}_{0x}q_{1}q_{0 xx}+q^{*}_{0x}q_{0}q_{1 xx}),\\ M_{2}^{12}&=-i\delta _{3}\sigma _{14}(q^{*}_{2x}q_{0}q_{0 xx}+q^{*}_{1x}q_{1}q_{0 xx}+q^{*}_{0x}q_{2}q_{0 xx}\\&\quad +q^{*}_{1x}q_{0 }q_{1 xx}+q^{*}_{0x}q_{1 }q_{1 xx}+q^{*}_{0x}q_{0 }q_{2 xx}),\\ M_{3}^{12}&=-i\delta _{3}\sigma _{14}(q^{*}_{3x}q_{0}q_{0 xx}+q^{*}_{2x}q_{1}q_{0 xx}+q^{*}_{1x}q_{2}q_{0 xx}\\&\quad +q^{*}_{0x}q_{3 }q_{0 xx}+q^{*}_{2x}q_{0}q_{1 xx}+q^{*}_{1x}q_{1}q_{1 xx}+q^{*}_{0x}q_{2}q_{1 xx}\\&\quad +q^{*}_{1x}q_{0}q_{2 xx}+q^{*}_{0x}q_{1}q_{2 xx}+q^{*}_{0x}q_{0}q_{3 xx}),\\ M_{4}^{12}&=-\delta _{3}\sigma _{14}(q^{*}_{4x}q_{0}q_{0 xx}+q^{*}_{3x}q_{1}q_{0 xx}+q^{*}_{2x}q_{2}q_{0 xx}\\&\quad +q^{*}_{1x}q_{3}q_{0 xx}+q^{*}_{0x}q_{4}q_{0 xx}+q^{*}_{3x}q_{0}q_{1 xx}+q^{*}_{2x}q_{1}q_{1 xx}\\&\quad +q^{*}_{1x}q_{2}q_{1 xx}+q^{*}_{0x}q_{3}q_{1 xx} +q^{*}_{2x}q_{0}q_{2xx} +q^{*}_{1x}q_{1}q_{2 xx}\\&\quad +q^{*}_{0x}q_{2}q_{2 xx} +q^{*}_{1x}q_{0}q_{3 xx}+q^{*}_{0x}q_{1}q_{3 xx}+q^{*}_{0x}q_{0}q_{4 xx}), \end{aligned}$$
$$\begin{aligned} M_{0}^{13}&=-i\delta _{3}\sigma _{15}q_{0x}^{2}q^{*}_{0x},\\ M_{1}^{13}&=-i\delta _{3}\sigma _{15}(q^{*}_{1x}q_{0x}^{2}+2q^{*}_{0x}q_{1x}q_{0x}), \\ M_{2}^{13}&= -i\delta _{3}\sigma _{15}(q^{*}_{2x}q_{0x}^{2}+q^{*}_{0x}q_{1x}^{2}+2q^{*}_{0x}q_{2x}q_{0x}+2q^{*}_{1x}q_{1x}q_{0x}),\\ M_{3}^{13}&= -i\delta _{3}\sigma _{15}(q^{*}_{3x}q_{0x}^{2}+q^{*}_{1x}q_{1x}^{2}+2q^{*}_{2x}q_{1x}q_{0x}+2q^{*}_{1x}q_{2x}q_{0x}\\&\quad +2q^{*}_{0x}q_{3x}q_{0x}+2q^{*}_{0x}q_{1x}q_{2x}),\\ M_{4}^{13}&= -i\delta _{3}\sigma _{15}(q^{*}_{4x}q_{0x}^{2}+q^{*}_{2x}q_{1x}^{2}+q^{*}_{0x}q_{2x}^{2}+2q^{*}_{3x}q_{1x}q_{0x}\\&\quad +2q^{*}_{2x}q_{2x}q_{0x}+2q^{*}_{1x}q_{3x}q_{0x}+2q^{*}_{0x}q_{4x}q_{0x}\\&\quad +2q^{*}_{1x}q_{1x}q_{2x}+2q^{*}_{0x}q_{1x}q_{3x}), \end{aligned}$$

and similarly for a variety of other Adomian polynomials.

Eventually, when contemplating the inverse Laplace transform \(\mathscr {L}^{-1}\), the components \(q_0\), \(q_1\), \(q_2\), and so forth, are subsequently ascertained through an iterative procedure, which is given as:

$$\begin{aligned} \left\{ \begin{array}{lllll} q_{0}(x,t)=f(x),\\ q_{1}(x,t)=-\mathscr {L}^{-1}\big (\frac{1}{s}\mathscr {L}\{Rq_{0}(x,t)\}+\frac{1}{s}\big [\mathscr {L}\big \{\sum _{j=1}^{13}P_{0}^{j}(q_{0})\big \}\big ]\big ),\\ q_{2}(x,t)=-\mathscr {L}^{-1}\big (\frac{1}{s}\mathscr {L}\{Rq_{1}(x,t)\}+\frac{1}{s}\big [\mathscr {L}\big \{\sum _{j=1}^{13}P_{1}^{j}(q_{0}, q_{1})\big \}\big ]\big ),\\ q_{m}(x,t)=-\mathscr {L}^{-1}\big (\frac{1}{s}\mathscr {L}\{Rq_{m-1}(x,t)\}+\frac{1}{s}\big [\mathscr {L}\big \{\sum _{j=1}^{13}P_{m-1}^{j}(q_{0},\ldots , q_{m-1})\big \}\big ]\big ),\quad m\ge 1. \end{array} \right. \end{aligned}$$
(28)

where \(q_0\) is referred to as the zero-th component, which is taken as the initial condition in this method.

Within the context of the Laplace-Adomian decomposition approach, the solution functions q are generated as

$$\begin{aligned} q(x,t)=\sum _{k=0}^{\infty }q_{k}(x,t). \end{aligned}$$
(29)

Numerical simulations and graphical results

The usefulness, utility, and precision of LADM in solving directly applicable mathematical models will be demonstrated by using an approximation level of N steps to generate solutions for system (1) with different parameter sets and beginning conditions. The value of the n index is obtained from the power law governing self-phase modulation (SPM). To prevent wave collapse [12], it is important that the value of n falls within the range of \(0< n < 2\).

Example 1

In this particular case, the simulation will be performed by considering equation (1) with a value of \(n=\frac{1}{4}\), and then collecting the coefficients that follow.:

$$\begin{aligned} \left\{ \begin{array}{lll} a=0.5,\; b=0.6,\; \delta _{1}=-0.4,\; \delta _{2}=6.1,\; \delta _{3}=0.1,\; \sigma _{1}=0.3,\; \sigma _{2}=2.1,\; \sigma _{3}=6.2,\; \sigma _{4}=2.0, \\ \; \sigma _{5}=0.1,\; \sigma _{6}=4.2,\; \sigma _{7}=-0.3,\; \sigma _{8}=1.1,\; \sigma _{9}=3.9,\; \sigma _{10}=2.6, \sigma _{11}=0.3,\; \sigma _{12}=4.3,\\ \sigma _{13}=0.5,\; \sigma _{14}=-3.3,\; \sigma _{15}=6.3 \end{array} \right. \end{aligned}$$
(30)

and with initial condition:

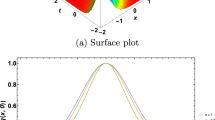
$$\begin{aligned}f(x)=6.2{\text {sech}}^{4}(1.55x) e^{i[-3.56x+2.33 ]}.\end{aligned}$$

Figure 1 illustrates the error committed in this numerical simulation, the two-dimensional density plot, and the graphical achievements of the three-dimensional profile evolution for \(\vert q\vert ^2\) in a number of \(N=15\) steps.

Example 2

In this particular case, the simulation will be performed by considering equation (1) with a value of \(n=\frac{1}{2}\), and then collecting the coefficients that follow.:

$$\begin{aligned} \left\{ \begin{array}{lll} a=5.2,\; b=0.7,\; \delta _{1}=4.5,\; \delta _{2}=0.3,\; \delta _{3}=2.2,\; \sigma _{1}=4.3,\; \sigma _{2}=1.8,\; \sigma _{3}=3.9,\; \sigma _{4}=5.5, \\ \; \sigma _{5}=0.5,\; \sigma _{6}=0.6,\; \sigma _{7}=8.8,\; \sigma _{8}=4.7,\; \sigma _{9}=0.8,\; \sigma _{10}=-1.3, \sigma _{11}=6.8,\; \sigma _{12}=0.7,\\ \sigma _{13}=9.2,\; \sigma _{14}=6.5,\; \sigma _{15}=0.5 \end{array} \right. \end{aligned}$$
(31)

and with initial condition:

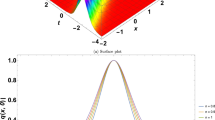
$$\begin{aligned}f(x)=5.8{\text {sech}}^{2}(1.31x) e^{i[-2.09x-5,25 ]}. \end{aligned}$$

Figure 1 illustrates the error committed in this numerical simulation, the two-dimensional density plot, and the graphical achievements of the three-dimensional profile evolution for \(\vert q\vert ^2\) in a number of \(N=15\) steps.

Example 3

In this particular case, the simulation will be performed by considering equation (1) with a value of \(n=\frac{5}{4}\), and then collecting the coefficients that follow.:

$$\begin{aligned} \left\{ \begin{array}{lll} a=1.5,\; b=0.8,\; \delta _{1}=0.2,\; \delta _{2}=0.5,\; \delta _{3}=0.4,\; \sigma _{1}=0.3,\; \sigma _{2}=8.5,\; \sigma _{3}=0.9,\; \sigma _{4}=6.7, \\ \; \sigma _{5}=3.0,\; \sigma _{6}=4.3,\; \sigma _{7}=0.7,\; \sigma _{8}=0.4,\; \sigma _{9}=2.8,\; \sigma _{10}=8.3, \sigma _{11}=2.1,\; \sigma _{12}=-8.2,\\ \sigma _{13}=1.1,\; \sigma _{14}=0.2,\; \sigma _{15}=3.2 \end{array} \right. \end{aligned}$$
(32)

and with initial condition:

$$\begin{aligned}f(x)=4.2{\text {sech}}^{4/5}(3.65x) e^{i[-3.23x+1.12 ]}. \end{aligned}$$

Figure 1 illustrates the error committed in this numerical simulation, the two-dimensional density plot, and the graphical achievements of the three-dimensional profile evolution for \(\vert q\vert ^2\) in a number of \(N=15\) steps.

Example 4

In this particular case, the simulation will be performed by considering equation (1) with a value of \(n=\frac{3}{2}\), and then collecting the coefficients that follow.:

$$\begin{aligned} \left\{ \begin{array}{lll} a=0.2,\; b=3.3,\; \delta _{1}=3.6,\; \delta _{2}=2.0,\; \delta _{3}=0.9,\; \sigma _{1}=3.4,\; \sigma _{2}=5.5,\; \sigma _{3}=3.8,\; \sigma _{4}=0.8, \\ \; \sigma _{5}=2.2,\; \sigma _{6}=7.2,\; \sigma _{7}=3.7,\; \sigma _{8}=2.2,\; \sigma _{9}=4.4,\; \sigma _{10}=3.5, \sigma _{11}=1.1,\; \sigma _{12}=0.3,\\ \sigma _{13}=4.4,\; \sigma _{14}=3.8,\; \sigma _{15}=0.1 \end{array} \right. \end{aligned}$$
(33)

and with initial condition:

$$\begin{aligned} f(x)=10.9{\text {sech}}^{2/3}(6.65x) e^{i[-3.23x+1.12 ]}. \end{aligned}$$

Figure 1 illustrates the error committed in this numerical simulation, the two-dimensional density plot, and the graphical achievements of the three-dimensional profile evolution for \(\vert q\vert ^2\) in a number of \(N=15\) steps (Figs. 2, 3, 4).

Fig. 1
figure 1

(left) 3D optical bright soliton solution of Eq. (1). (center) 2D density graphs represent bright soliton evolution. (right) The absolute error in the simulation for a total of \(N=15\) steps, using the parameter values presented in example 1

Full size image
Fig. 2
figure 2

(left) 3D optical bright soliton solution of Eq. (1). (center) 2D density graphs represent bright soliton evolution. (right) The absolute error in the simulation for a total of \(N=15\) steps, using the parameter values presented in example 2

Full size image
Fig. 3
figure 3

(left) 3D optical bright soliton solution of Eq. (1). (center) 2D density graphs represent bright soliton evolution. (right) The absolute error in the simulation for a total of \(N=15\) steps, using the parameter values presented in example 3

Full size image
Fig. 4
figure 4

(left) 3D optical bright soliton solution of Eq. (1). (center) 2D density graphs represent bright soliton evolution. (right) The absolute error in the simulation for a total of \(N=15\) steps, using the parameter values presented in example 4

Full size image

Conclusions

The current paper recovered bright optical solitons for the dispersive concatenation model with a few specific values of the power-law parameter n so that the regime of self-focusing singularity is avoided. The numerical algorithm is the LADM that has made this retrieval possible. The results are encouraging and will lead to promising research activities in the future. Later this model will be taken up with differential group delay and further down the road the results will be extended to dispersion-flattened fibers. The results of those research activities will be disseminated in future all across the board.