Introduction

The concatenation model made its first debut during 2014, a decade ago by conjoining three models, namely the nonlinear Schrödinger’s equation (NLSE), the Lakshmanan–Porsezian–Daniel (LPD) model and the Sasa–Satsuma equation (SSE) [1, 2]. This model was later extensively studied to extract its additional features in addition to the retrieval of its soliton solutions. These include the location of the conserved quantities, numerical analysis of the model with the usage of the Laplace–Adomian decomposition (LADM) scheme, addressing the model with polarization-mode dispersion and locating its corresponding soliton solutions as well as complexiton solutions. The quiescent optical solitons for the model with nonlinear chromatic dispersion (CD) were also recovered using Lie symmetry analysis, as well as additional approaches. Later, the bifurcation analysis of the model was also carried out. Finally, this model was applied to magneto-optic waveguides in addition to optical fibers.

The model was later studied with power law form of self-phase modulation (SPM). In this context too, the conservation laws were retrieved, the model was addressed by the aid of the complete discriminant approach, the numerical analysis was also presented by the LADM scheme. The effect of Internet bottleneck mitigation was also proposed by introducing the spatio-temporal dispersion in addition to the pre-existing CD. The bifurcation analysis was also conducted, and the quiescent optical solitons were also recovered for nonlinear CD with the usage of Lie symmetry. Subsequently, these models with Kerr law and power law of SPM were also addressed with the presence of white noise. Finally, these models were studied with the absence of SPM and the corresponding quiescent optical solitons were located.

Thereafter, during 2014 and 2015 another form of the concatenation model was proposed and this is being referred to as the dispersive concatenation model [3,4,5]. This one is a combination of the Schrödinger–Hirota equation (SHE), LPD and the fifth-order NLSE that produces the effect of dispersion, hence the name dispersive concatenation model. This model was also studied along with the recovery of its preliminary features both for the scalar version of the model and with differential group delay. The soliton solutions were located using a few approaches including the complete discriminant approach.

One of the common grounds that ties up the study of these models is their integration scheme. The method of undetermined coefficients has successfully recovered the 1-soliton solutions to these models, namely the concatenation model with Kerr law and power law of SPM; dispersive concatenation model with Kerr law. Thereafter, this methodology also successfully retrieved the 1-soliton solutions to the model in birefringent fibers [6,7,8,9]. It is now time to turn the page and move over. The current work recovers 1-soliton solution to the dispersive concatenation model with power law of SPM by the aid of undetermined coefficients. It must be noted that even though this integration algorithm had been successfully applied and soliton solutions have been recovered for this model, as well as for several other models, there are a couple of inherent shortcomings to this approach:

  1. 1.

    The scheme is only applicable to recover 1-soliton solution to the model. It fails to retrieve N-soliton solutions to the models for \(N>1\), unlike inverse scattering transform or the Hirota’s bilinear approach.

  2. 2.

    The scheme is also unable to recover soliton radiation unlike the inverse scattering transform approach or the variational principle.

Nevertheless, this algorithm points out to the fact that for power law of SPM, dark solitons cease to exist. It is only when the power law collapses to Kerr of SPM, dark solitons can be recovered. This is one of the hidden advantages of this approach that has been experimentally verified several decades ago. It must be noted that none of the plethora of modern approaches to integration of the models can elucidate this important observation and save undetermined coefficients. The current paper details the recovery of 1-soliton solutions to the dispersive concatenation model after its succinct introduction and its mathematical start-up.

Governing model

The dimensionless form of the system to be studied herein is given by [10, 11]:

$$\begin{aligned}{} & {} iq_t + a q_{xx} + b\left| q \right| ^{2n} q - i \delta _1 \left[ \sigma _1 q_{xxx} + \sigma _2 \left| q \right| ^{2n} q_x \right] \nonumber \\{} & {} \quad + \delta _2 \left[ \sigma _3 q_{xxxx} + \sigma _4 \left| q \right| ^{2n} q_{xx} + \sigma _5 \left| q \right| ^{2n+2} q \right. \nonumber \\{} & {} \quad \left. + \sigma _6 \left| q_x \right| ^2 q + \sigma _7 q_x^2 q^{*} + \sigma _8 q_{xx}^{*} q^2 \right] \nonumber \\{} & {} \quad - i\delta _3 \left[ \sigma _9 q_{xxxxx} + \sigma _{10} \left| q \right| ^{2n} q_{xxx} + \sigma _{11} \left| q \right| ^{2n+2} q_x \right. \nonumber \\{} & {} \quad \left. + \sigma _{12} q q_x q_{xx}^{*} + \sigma _{13} q^{*} q_x q_{xx} + \sigma _{14} q q_x^{*} q_{xx} + \sigma _{15} q_x^{2} q_x^{*} \right] = 0. \end{aligned}$$
(1)

Equation (1) is the dispersive concatenation model with power law of SPM. The dependent variable is q(x, t) that represents the soliton amplitude. The independent variables x and t are from the spatial and temporal coordinates, respectively. In Eq. (1), \(i = \sqrt{-1}\) while a and b are the coefficients of CD and SPM, respectively. The coefficient of \(\delta _1\) contains the remaining terms of the SHE that is recoverable from the standard NLSE via Lie transform. Next, the coefficients of \(\delta _2\) and \(\delta _3\) are from LPD and SHE, respectively.

In order to integrate dispersive concatenation model (1), the following hypothesis is applied [12,13,14,15,16,17,18,19,20]:

$$\begin{aligned} q(x,t) = P(x,t) e^{i \left( - \kappa x + \omega t + \Theta \right) }. \end{aligned}$$
(2)

On the proposed hypothesis the term \(\; P(x,t) \;\) represents the waveform, which is unique for each type of soliton, \(\; \kappa \;\) denotes the soliton frequency, \(\; \omega \;\) represents the wave number, and \(\; \Theta \;\) portrays a phase constant [21,22,23,24,25,26,27,28,29]. Inserting these hypotheses into system (1) splits the last in two parts, the real part being

$$\begin{aligned} \left. \begin{aligned}&\left[ \delta _2 \left( \sigma _6+\sigma _7 \right) +\kappa \delta _3 \left\{ (2\sigma _{12} -2 \left( \sigma _{13}+\sigma _{14} \right) -\sigma _{15} \right\} \right] P\left( \frac{\partial P}{\partial x} \right) ^2 \\&\quad + \left[ a-3\kappa (\delta _1\sigma _1 +2\kappa \delta _2\sigma _3)+10\kappa ^3\delta _3\sigma _9 \right] \\&\quad \frac{\partial ^2 P}{\partial x^2} + \left( \sigma _3\delta _2-5\kappa \sigma _9 \delta _3 \right) \frac{\partial ^4 P}{\partial x^4} \\&\quad + \left[ \delta _2 \sigma _{8} -\kappa \delta _3 \left( \sigma _{12} +\sigma _{13} - \sigma _{14} \right) \right] \\&\quad P^2 \frac{\partial ^2 P}{\partial x^2} +(\delta _2\sigma _4 -3\kappa \delta _3\sigma _{10}) P^{2n} \frac{\partial ^2 P}{\partial x^2} \\&\quad + (\delta _2\sigma _5-\kappa \delta _3 \sigma _{11}) P^{2n+3} \\&\quad + (b - \kappa \delta _1 \sigma _2 -\kappa ^2 \delta _2\sigma _4 +\kappa ^3\delta _3 \sigma _{10}) P^{2n+1} \\&\quad + \kappa ^2 \left[ \delta _2(\sigma _6-\sigma _7-\sigma _8) + \kappa \delta _3(\sigma _{12}\right. \\&\quad \left. + \sigma _{13} -\sigma _{14} - \sigma _{15} ) \right] P^3 \\&\quad + \left( \sigma _1\delta _1\kappa ^3 +\sigma _3\delta _2\kappa ^4 - \sigma _9\delta _3\kappa ^5-\omega - a\kappa ^2 \right) P = 0 \,, \end{aligned} \right\} \end{aligned}$$
(3)

and the resulting imaginary counterpart,

$$\begin{aligned} \left. \begin{aligned}&\frac{\partial P}{\partial t} -\kappa \left( 2a - 3\kappa \sigma _1\delta _1 -4\sigma _3\delta _2\kappa ^2 +5\kappa ^3 \sigma _9 \delta _3 \right) \frac{\partial P}{\partial x}\\&\quad - \left[ \sigma _1 \delta _1 +2\kappa \left( 2\sigma _3\delta _2 - 5 \kappa \sigma _9\delta _3 \right) \right] \frac{\partial ^3 P}{\partial x^3}-\sigma _9 \delta _3 \frac{\partial ^5 P}{\partial x^5} \\&\quad - \kappa \left[ 2\delta _2(\sigma _7-\sigma _8) +\kappa \delta _3(\sigma _{12} -3\sigma _{13} +\sigma _{14}\right. \\&\quad \left. + \sigma _{15} ) \right] P^2\frac{\partial P}{\partial x} - [ \delta _1\sigma _2 + \kappa (2\delta _2\sigma _4 - 3\kappa \delta _3 \sigma _{10}) ] P^{2n} \frac{\partial P}{\partial x} \\&\quad - \sigma _{10}\delta _3 P^{2n}\frac{\partial ^3 P}{\partial x^3} - \sigma _{11}\delta _3 P^{2n+2} \frac{\partial P}{\partial x} - \sigma _{15}\delta _3 \left( \frac{\partial P}{\partial x} \right) ^3\\&\quad -\delta _3 \left( \sigma _{12}+\sigma _{13}+\sigma _{14} \right) \\&\quad P\left( \frac{\partial P}{\partial x}\right) \left( \frac{\partial ^2 P}{\partial x^2}\right) = 0. \end{aligned} \right\} \end{aligned}$$
(4)

In fact, one can compute the soliton speed from (4), which in this case gives,

$$\begin{aligned} v = -2\kappa ( a+4\kappa ^2\delta _2\sigma _3 ) \end{aligned}$$
(5)

as long as the conditions

$$\begin{aligned}{} & {} \sigma _9 = \sigma _{10} = \sigma _{11} = \sigma _{15} = 0 \,, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \sigma _1\delta _{1} + 4\kappa \sigma _3\delta _2 = 0 \,, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \sigma _{12}+\sigma _{13}+\sigma _{14} = 0 \,, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \delta _2(\sigma _7-\sigma _8) -2\kappa \delta _3 \sigma _{13} = 0, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \delta _1\sigma _2 +2\kappa \delta _2\sigma _4 = 0 \end{aligned}$$
(10)

are secured. In view of the above conditions, real part equation (3) reduces to

$$\begin{aligned} \left. \begin{aligned}&\left[ \delta _2 \left( \sigma _6+\sigma _7 \right) +4\kappa \delta _3 \sigma _{12} \right] P\left( \frac{\partial P}{\partial x} \right) ^2 + \left( a-18\kappa ^2\delta _2\sigma _3 \right) \frac{\partial ^2 P}{\partial x^2} + \sigma _3\delta _2 \frac{\partial ^4 P}{\partial x^4} \\&\quad + \left( \delta _2 \sigma _{8} +2\kappa \delta _3 \sigma _{14} \right) P^2 \frac{\partial ^2 P}{\partial x^2} +\delta _2\sigma _4 P^{2n} \frac{\partial ^2 P}{\partial x^2} + \delta _2\sigma _5 P^{2n+3} + (b + \kappa ^2 \delta _2 \sigma _4 ) P^{2n+1} \\&\quad + \kappa ^2 \left[ \delta _2(\sigma _6-\sigma _7-\sigma _8) -2\kappa \delta _3\sigma _{14} \right] P^3 - \left( \omega +a\kappa ^2 +3\kappa ^4 \delta _2\sigma _3 \right) P = 0 \,. \end{aligned} \right\} \end{aligned}$$
(11)

The last equation will be key to construct four different types of optical soliton solutions from dispersive concatenation model (1).

Soliton solutions

We now proceed to construct optical soliton solutions for the dispersive concatenation model. Four different solitons are explored throughout the next four subsections by studying the integrability of real part Eq. (11) according to the corresponding waveform \(\,P(x,t)\).

Bright solitons

The first type of waveform to be studied is the bright soliton, whose waveform has typically a structure of the form [30,31,32,33,34,35],

$$\begin{aligned} P(x,t) = A\, {{\,\textrm{sech}\,}}^{p} \tau , \qquad \tau = B(x-vt), \end{aligned}$$
(12)

where A is the soliton amplitude with their width being B. The unknown exponent p will fall out by the aid of balancing principle. Substituting (12) into real part (11) transforms the last into

$$\begin{aligned} \left. \begin{aligned}&\left[ p^2Z_2B^2-\left( \omega +a\kappa ^2 +3\kappa ^4 \delta _2\sigma _3 \right) +p^4\delta _2\sigma _3B^4 \right] {{\,\textrm{sech}\,}}^p \tau \\&\quad + \left[ Z_5 + p^2(Z_1+Z_3)B^2 \right] A^2 {{\,\textrm{sech}\,}}^{3p} \tau + \delta _2\sigma _5 A^{2n+3}{{\,\textrm{sech}\,}}^{(2n+3)p} \tau \\&\quad - p(1+p)[ Z_2+2(2+p(2+p))\delta _2\sigma _3 B^2 ] B^2 {{\,\textrm{sech}\,}}^{p+2} \tau \\&\quad + p(1+p)(2+p)(3+p) \delta _2 \sigma _3 B^4 {{\,\textrm{sech}\,}}^{p+4} \tau \\&\quad - p \left[ pZ_1 + \left( 1+p \right) Z_3 \right] A^2B^2 {{\,\textrm{sech}\,}}^{3p+2} \tau \\&\quad + (Z_4+p^2\delta _2\sigma _4B^2)A^{2n} {{\,\textrm{sech}\,}}^{(2n+1)p} \tau \\&\quad - p(1+p) \delta _2\sigma _4B^2 A^{2n} {{\,\textrm{sech}\,}}^{2+(2n+1)p}\tau = 0. \end{aligned} \right\} \end{aligned}$$
(13)

On the above we have labeled the coefficients of real part equation (11) as

$$\begin{aligned} Z_1= & {} \delta _2 \left( \sigma _6+\sigma _7 \right) +4\kappa \delta _3 \sigma _{12}, \end{aligned}$$
(14)
$$\begin{aligned} Z_2= & {} a-18\kappa ^2\delta _2\sigma _3, \end{aligned}$$
(15)
$$\begin{aligned} Z_3= & {} \delta _2 \sigma _{8} +2\kappa \delta _3 \sigma _{14}, \end{aligned}$$
(16)
$$\begin{aligned} Z_4= & {} b + \kappa ^2 \delta _2 \sigma _4, \end{aligned}$$
(17)
$$\begin{aligned} Z_5= & {} \kappa ^2 \left[ \delta _2(\sigma _6-\sigma _7-\sigma _8) -2\kappa \delta _3\sigma _{14} \right] \end{aligned}$$
(18)

for the reader’s convenience. The balancing principle allows to compare the exponents \(\;(2n+1)p\;\) and \(\; p+2.\;\) it follows that

$$\begin{aligned} p=\frac{1}{n}. \end{aligned}$$
(19)

Upon substituting (19) on identity (13), and setting to zero the coefficients of the resulting linearly independent functions, one gets the wave number

$$\begin{aligned} \omega = \frac{\delta _2\sigma _3(Z^{2}_{5} -3\kappa ^4(Z_1+Z_3)^2) -Z_2Z_5(Z_1+Z_3) -a\kappa ^2(Z_1+Z_3)^2 }{(Z_1+Z_3)^2}, \end{aligned}$$
(20)

in view of the resulting width

$$\begin{aligned} B = \sqrt{-\frac{n^2Z_5}{Z_1+Z_3}} \end{aligned}$$
(21)

subject to

$$\begin{aligned} Z_5(Z_1+Z_3)< 0. \end{aligned}$$
(22)

After simplification, the amplitude results to be

$$\begin{aligned} A= \left[ - \frac{Z_5(Z_1+(n+1)Z_3)}{\delta _2\sigma _5(Z_1+Z_3)} \right] ^{\frac{1}{2n}} \end{aligned}$$
(23)

constrained to (22),

$$\begin{aligned} \delta _2\sigma _5(Z_1+(n+1)Z_3) > 0, \end{aligned}$$
(24)

and the solvability condition

$$\begin{aligned}{}[Z_1+(n+1)Z_3]\sigma _4-(2n+1)(3n+1)\delta _2\sigma _3\sigma _5 =0. \end{aligned}$$
(25)

The above are true whenever the solvability condition

$$\begin{aligned}{}[Z_1+(n+1)Z_3](n^2Z_4+\delta _2\sigma _4B^2) =(n+1)\delta _2 \sigma _5 [n^2Z_2+2\sigma _3\delta _2 (1+2n(n+1)) B^2] \end{aligned}$$
(26)

holds. Therefore, the bright 1-soliton solution for dispersive concatenation system (1) is given by

$$\begin{aligned} q(x,t) = A {{\,\textrm{sech}\,}}^{\frac{1}{n}} [B(x-vt)] e^{i \left( - \kappa x + \omega t + \Theta \right) }, \end{aligned}$$
(27)

where the amplitude is provided in (23), the width in (21), and the wave number is given by (20). The existence of the soliton solution is secured when solvability conditions (22), (24), (25) and (26) hold. The speed of the soliton was obtained earlier on (5). It is imperative to point out that the bright soliton solution is valid if in addition constraints (6)–(10) are satisfied.

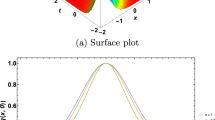
The graphs in Fig. 1 depict both 2D and surface plots of bright optical soliton (27), and the corresponding parameter values are \(v=1\), \(\kappa =1\), \(\delta _{2}=1\), \(\delta _{3}=1\), \(\sigma _{5}=1\), \(\sigma _{6}=1\), \(\sigma _{7}=1\), \(\sigma _{8}=1\), \(\sigma _{12}=1\), and \(\sigma _{14}=1\).

Fig. 1
figure 1

Profile of a bright optical soliton

Full size image

Dark solitons

In this subsection we aim to construct a single dark soliton solution supported by system (1). We start by assuming the waveform [36,37,38,39,40,41]

$$\begin{aligned} P(x,t) = A\, \tanh ^{p} \tau , \qquad \tau = B(x-vt). \end{aligned}$$
(28)

Here, v represents the soliton speed, while A and B are free parameters. The parameter \(\, p \,\) will be calculated according to the balancing principle. Upon substituting (28) into (11), it would lead to the simplified expression

$$\begin{aligned} \left. \begin{aligned}&-[(\omega + a\kappa ^2+3\kappa ^4\delta _2\sigma _3) \\&\quad +2p^2(Z_2-(5+3p^2)\delta _2\sigma _3B^2 )B^2] \tanh ^{p} \tau \\&\quad + [Z_5-p^2(Z_1+Z_3)B^2 ] A^2 \tanh ^{3p} \tau \\&\quad + p(1+p)[Z_2-4(2+p(2+p))\delta _2\sigma _3 B^2 ] B^2 \tanh ^{p+2}\\&\quad \tau + p(1+p)(2+p)(3+p)\delta _2\sigma _3B^4 \tanh ^{p+4} \tau \\&\quad + p[pZ_1+(1+p)Z_3]A^2B^2 \tanh ^{3p+2} \tau \\&\quad + p(p-1)[ Z_2 -4(2+p(p-2) )\delta _2\sigma _3 B^2] B^2 \tanh ^{p-2} \tau \\&\quad + p(p-1)(p-2)(p-3)\delta _2\sigma _3 B^4 \tanh ^{p-4} \tau \\&\quad + p[pZ_1 +(p-1)Z_3]A^2B^2 \tanh ^{3p-2} \tau \\&\quad +p(p-1)\delta _2\sigma _4 A^{2n}B^2 \tanh ^{(2n+1)p-2} \tau \\&\quad +p(1+p) \delta _2\sigma _4 A^{2n}B^2 \tanh ^{(2n+1)p+2} \tau \\&\quad +(Z_4-2p^2\delta _2\sigma _4B^2 )A^{2n} \tanh ^{(2n+1)p} \tau \\&\quad +\delta _2\sigma _5 A^{2n+2} \tanh ^{(2n+3)p} \tau = 0. \end{aligned} \right\} \end{aligned}$$
(29)

Notice we have adopted same notations (14)–(18) as we did for bright soliton. In this case the balance between nonlinearity and dispersion leads also to the value of p as in (19). However, from the coefficients of the stand-alone elements \(\, \tanh ^{p-2} \tau \,\) and \(\, \tanh ^{p-4} \tau \,\) we get \(p=1,\,\) implying \(n=1\). Thus, the power law nonlinearity collapses to Kerr law. Next, by substituting the resulting value of p into (29), and setting to zero the coefficients of the resulting independent functions we get in terms of the free parameter B the wave number

$$\begin{aligned} \omega = \frac{ [Z_4+Z_5-2(Z_1+Z_3+\delta _2\sigma _4)B^2 ] [\delta _2\sigma _3(16B^4-3\kappa ^4)-a\kappa ^2-2Z_2B^2 ] -2Z_1(Z_2-20\delta _2\sigma _3B^2)B^4 }{Z_4+Z_5-2(Z_1+Z_3+\delta _2\sigma _4)B^2}, \end{aligned}$$
(30)

where clearly,

$$\begin{aligned} Z_4+Z_5 \ne 2(Z_1+Z_3+\delta _2\sigma _4)B^2, \end{aligned}$$
(31)

and the parameter A,

$$\begin{aligned} A = \sqrt{- \frac{2(Z_2-20\delta _2\sigma _3B^2 )B^2}{[Z_4+Z_5-2(Z_1+Z_3+\delta _2\sigma _4)B^2 ]}} \end{aligned}$$
(32)

restricted to

$$\begin{aligned} (Z_2-20\delta _2\sigma _3B^2 ) \times \left[ Z_4+Z_5-2(Z_1+Z_3+\delta _2\sigma _4)B^2 \right] < 0. \end{aligned}$$
(33)

Here, the resulting parameter B is given by

$$\begin{aligned} B= & {} \left\{ \frac{ -Z^{2}_{1}Z_2 +4\delta _2\sigma _3(Z_4+Z_5)(Z_3+\delta _2\sigma _4) + 2Z_2[20\sigma _3\sigma _5\delta ^{2}_{2} -(Z_3+\delta _2\sigma _4)^2] }{8\delta _2\sigma _3[Z^{2}_{1} -3Z_1(Z_3+\delta _2\sigma _4) -4(Z_3+\delta _2\sigma _4)^2 +100\delta ^{2}_{2} \sigma _3 \sigma _5 ] } \right. \nonumber \\{} & {} \left. + \frac{ Z_1 [ 14(Z_4+Z_5)\delta _2\sigma _3-3Z_2(Z_3+\delta _2\sigma _4) ] }{8\delta _2\sigma _3[Z^{2}_{1} -3Z_1(Z_3+\delta _2\sigma _4) -4(Z_3+\delta _2\sigma _4)^2 +100\delta ^{2}_{2} \sigma _3 \sigma _5 ] } \right. \nonumber \\{} & {} \left. \pm \frac{\sqrt{[-10\delta _2\sigma _3(Z_4+Z_5) +Z_2(Z_1+Z_3+\delta _2\sigma _4) ]^2 [ (Z_1+2Z_3+2\delta _2\sigma _4)^2 -96\delta ^{2}_{2}\sigma _3\sigma _5 ] }}{8\delta _2\sigma _3[Z^{2}_{1} -3Z_1(Z_3+\delta _2\sigma _4) -4(Z_3+\delta _2\sigma _4)^2 +100\delta ^{2}_{2} \sigma _3 \sigma _5 ] } \right\} ^{\frac{1}{2}}, \end{aligned}$$
(34)

where corresponding constraints are assumed to be valid. Thus, the single dark soliton solution for concatenation model (1) is

$$\begin{aligned} q(x,t) = A \tanh [B(x-vt)] e^{i \left( - \kappa x + \omega t + \Theta \right) }, \end{aligned}$$
(35)

where the free parameter A on (32), and the wave number \(\omega\) on (30) are expressed in terms of the free parameter B, given in a simplified form on (34). The speed was retrieved on (5). For dark soliton solution, as for bright soliton, solvability conditions (6)–(9) along with (33) and resulting constraints from (34) must be satisfied in order for the soliton to evolve on time.

Figure 2 displays the 2D and surface plots associated with dark optical soliton (35). Notably, the parameter values utilized for this representation include \(a=1\), \(b=1\), \(v=1\), \(\kappa =1\), \(n=1\), \(\delta _{2}=1\), \(\delta _{3}=1\), \(\sigma _{3}=1\), \(\sigma _{4}=1\), \(\sigma _{5}=1\), \(\sigma _{6}=1\), \(\sigma _{7}=1\), \(\sigma _{8}=1\), \(\sigma _{12}=1\), and \(\sigma _{14}=1\).

Fig. 2
figure 2

Profile of a dark optical soliton

Full size image

Singular solitons (type-I)

In this subsection we explore the first type of singular soliton solution [42,43,44,45,46], whose waveform assumption is

$$\begin{aligned} P(x,t) = A\, {{\,\textrm{csch}\,}}^{p} \tau , \qquad \tau = B(x-vt), \end{aligned}$$
(36)

where A and B are set as free parameters. This assumption, when inserted into (11), would give:

$$\begin{aligned} \left. \begin{aligned}&\left[ p^2Z_2B^2-\left( \omega +a\kappa ^2 +3\kappa ^4 \delta _2\sigma _3 \right) +p^4\delta _2\sigma _3B^4 \right] {{\,\textrm{csch}\,}}^p \tau \\&\quad + \left[ Z_5 + p^2(Z_1+Z_3)B^2 \right] A^2 {{\,\textrm{csch}\,}}^{3p} \tau + \delta _2\sigma _5 A^{2n+3}{{\,\textrm{csch}\,}}^{(2n+3)p} \tau \\&\quad + p(1+p)[ Z_2+2(2+p(2+p))\delta _2\sigma _3 B^2 ] B^2 {{\,\textrm{csch}\,}}^{p+2} \tau \\&\quad + p(1+p)(2+p)(3+p) \delta _2 \sigma _3 B^4 {{\,\textrm{csch}\,}}^{p+4} \tau \\&\quad + p \left[ pZ_1 + \left( 1+p \right) Z_3 \right] A^2B^2 {{\,\textrm{csch}\,}}^{3p+2} \tau \\&\quad + (Z_4+p^2\delta _2\sigma _4B^2)A^{2n} {{\,\textrm{csch}\,}}^{(2n+1)p} \tau \\&\quad + p(1+p) \delta _2\sigma _4B^2 A^{2n} {{\,\textrm{csch}\,}}^{2+(2n+1)p} \tau = 0, \end{aligned} \right\} \end{aligned}$$
(37)

where notations (6)–(10) have been adopted for simplicity. Notice the balancing principle leads again to \(\; p=1/n. \;\) Thus, upon substituting such value into (37), and setting to zero the coefficients of the resulting linearly independent functions, wave number (20) and the parameter B in (21) are retrieved. Thus, constraint (22) is also required in this case. For type-1 soliton supported by system (1), the resulting parameter A is

$$\begin{aligned} A= \left[ \frac{Z_5(Z_1+(n+1)Z_3)}{\delta _2\sigma _5(Z_1+Z_3)} \right] ^{\frac{1}{2n}}, \end{aligned}$$
(38)

which is valid as long as

$$\begin{aligned} \delta _2\sigma _5(Z_1+(n+1)Z_3) < 0. \end{aligned}$$
(39)

The parameter A provided in (38) is valid as long as the condition

$$\begin{aligned} (2n+1)(3n+1)\delta _2\sigma _3\sigma _5 = \sigma _4[Z_1 +(n+1)Z_3] \end{aligned}$$
(40)

is satisfied. In addition, the following identity

$$\begin{aligned}{} & {} \sigma _4(Z_1+Z_3)Z_4Z_5[Z_1+(n+1)Z_3] \nonumber \\{} & {} \quad - (n+1)n^2\sigma _5[Z_2(Z_1+Z_3) -2(1+2n(1+n)) \delta _2\sigma _3Z_5] =0 \end{aligned}$$
(41)

must hold for the solution to exist. Therefore, the type-I singular soliton solution for the considered concatenation system resulted to be

$$\begin{aligned} q(x,t) = A {{\,\textrm{csch}\,}}^{\frac{1}{n}}[B(x-vt)] e^{i \left( - \kappa x + \omega t + \Theta \right) }, \end{aligned}$$
(42)

where the parameter A is given in (38), while the wave number and the parameter B are the same as in bright 1-soliton given on (20) and (21), respectively, along with their corresponding solvability constraints.

Singular solitons (type-II)

The last type of soliton to be studied in this manuscript is the type-II singular soliton [47,48,49,50], whose assumption for the waveform portion, P(x, t), is

$$\begin{aligned} P(x,t) = A\, \coth ^{p} \tau , \qquad \tau = B(x-vt). \end{aligned}$$
(43)

Here too, A and B are free parameters. Upon substituting into (11), it would lead to the identity

$$\begin{aligned} \left. \begin{aligned}&-[(\omega + a\kappa ^2+3\kappa ^4\delta _2\sigma _3) \\&\quad +2p^2(Z_2-(5+3p^2)\delta _2\sigma _3B^2 )B^2] \coth ^{p} \tau \\&\quad + [Z_5-p^2(Z_1+Z_3)B^2 ] A^2 \coth ^{3p} \tau \\&\quad + p(1+p)[Z_2-4(2+p(2+p))\delta _2\sigma _3 B^2 ] B^2 \coth ^{p+2}\\&\quad \tau + p(1+p)(2+p)(3+p)\delta _2\sigma _3B^4 \coth ^{p+4} \tau \\&\quad + p[pZ_1+(1+p)Z_3]A^2B^2 \coth ^{3p+2} \tau \\&\quad + p(p-1)[ Z_2 -4(2+p(p-2) )\delta _2\sigma _3 B^2] B^2 \coth ^{p-2} \tau \\&\quad + p(p-1)(p-2)(p-3)\delta _2\sigma _3 B^4 \coth ^{p-4} \tau \\&\quad + p[pZ_1 +(p-1)Z_3]A^2B^2 \coth ^{3p-2} \tau \\&\quad +p(p-1)\delta _2\sigma _4 A^{2n}B^2 \coth ^{(2n+1)p-2} \tau \\&\quad +p(1+p) \delta _2\sigma _4 A^{2n}B^2 \coth ^{(2n+1)p+2} \tau \\&\quad +(Z_4-2p^2\delta _2\sigma _4B^2 )A^{2n} \coth ^{(2n+1)p} \tau \\&\quad +\delta _2\sigma _5 A^{2n+2} \coth ^{(2n+3)p} \tau = 0. \end{aligned} \right\} \end{aligned}$$
(44)

Again, balancing principle between nonlinearity and dispersion leads to the same value of p as in the previous three cases, e.g., \(\;p=1/n.\;\) the coefficients of the stand-alone elements \(\; \coth ^{p-4} \tau \;\) and \(\; \coth ^{p-2}\tau \;\) dictate that \(p=1\), implying \(n=1,\) thus, in this case also the power law reduces to Kerr law nonlinearity. As usual, substituting the resulting value of p into Eq. (11) leads to exactly the same results as in the above case for dark solitons (30)–(34) with corresponding solvability conditions. Finally, the second type of the singular soliton solutions for system (1) is

$$\begin{aligned} q(x,t) = A \coth [B(x-vt)] e^{i \left( - \kappa x + \omega t + \Theta \right) }, \end{aligned}$$
(45)

where the parameters along with the corresponding solvability constraints resulted to be the same as for dark solitons.

Conclusions

This paper recovered the bright, dark and singular 1-soliton solutions to the dispersive concatenation model that was considered with power law of SPM. It has been proved that the dark solitons will exist for the model provided the power law collapses to Kerr law. This is a fact for various other models in optoelectronics too. This was experimentally verified decades ago [10, 11], but it is only the method of undetermined coefficients that can analytically prove it. The parameter constraints that naturally emerged from the integration scheme are also exhibited.

The results carry a lot of encouraging future aspect with this model and beyond. Later, the model will be taken up to address additional optoelectronic devices such as magneto–optic waveguides, optical couplers, optical metamaterials and metasurfaces and others. This model will be subsequently studied in dispersion-flattened fibers as well. The results are currently awaited but will be disseminated across various journals after they are aligned with the pre-existing results in the literature [10,11,12,13,14,15,16,17,18,19,20].