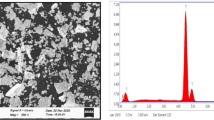
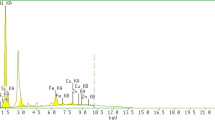
Abstract
The current study used the ARB method to fabricate multilayer Al/Cu/Brass composites. For this purpose, the ARB process was performed at six passes at room temperature without inter-passes heat treatment. X-ray diffraction (XRD) analysis showed that the intermetallic phase was not formed during rolling. Microstructural examination showed that the brass and Cu layers are fractured in the Al matrix after the second cycle. Mechanical tests such as tensile tests in RD and TD directions, microhardness, wear tests under three loads (10, 20, and 30 N), TOEFL, and impedance corrosion tests have been performed. The results revealed that increasing the ARB cycles increases the samples’ ultimate tensile strength and hardness. The related maximum values were obtained for the 6th cycle, equal to 288 MPa and 260 HV, respectively. The wear test results illustrated that the wear rate decreases significantly by increasing the ARB cycles and reaches a minimum in the 6th cycle, signifying that the wear resistance of the Al/Cu/Brass composite has increased significantly compared to the Al alloys. The worn surfaces were studied under a scanning electron microscope (SEM). The dominant wear mechanisms were delamination and oxidation. The corrosion test results indicated that increasing the ARB cycles up to the 5th cycle increases the corrosion resistance and then decreases.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Materials with multiple properties are needed in many industrial applications, which has led to the growth and development of composite production [1]. For example, in the automotive industry, due to the high stress applied to the parts, there is a need for materials with high mechanical properties and high wear resistance [2,3,4]. In the aerospace industry, materials with high strength-to-weight ratios, thermal stability, and corrosion resistance are needed [3, 5, 6]. Also, materials with electrical/thermal conductivity, low contact resistance, and corrosion resistance are needed in electrical and electronic industries [7, 8]. Generally, materials suitable for different industries are high strength, wear resistance and corrosion resistance, high thermal conductivity, and high strength-to-weight ratio [9,10,11]. These properties can be achieved by making an aluminum, copper, and brass composite. However, a suitable production method is needed to combine the properties of each metal without reducing the properties of other metals.
One way to increase materials’ mechanical properties is grain refinement. Metal matrix composite with ultra-fine grains can be produced by methods like powder metallurgy, mechanical alloying, and casting [12,13,14,15]. The ARB method does not have the disadvantages of the above methods, such as agglomeration during the distribution of reinforcement particles, the entry of impurities into the composition of the composite, and the creation of cracks and cavities during production. These defects in the composite structure cause the non-uniformity of the microstructure and the reduction of the mechanical properties of the produced material [16,17,18]. Also, with the grain refinement that is created during the ARB process, there is no need for a secondary process, such as extrusion etc., to achieve high-density production.
The ARB process is one of the most straightforward and economical processes compared to other methods, which has been considered for the forming of metals (especially sheets) and the production of layered composites [19, 20]. By performing the ARB process, the ARB samples can be prepared to achieve specific goals, such as increased mechanical and corrosion properties [21, 22].
In the ARB process, plastic instability occurs earlier in one of the layers than in the others, taking into account the differences in the mechanical properties of the layers when deforming different metals [23, 24]. With an increasing number of ARB cycles, the hardest layer is necked earlier than the rest and eventually breaks down in the matrix, resulting in improved mechanical properties of the material. In the production of composite materials by the ARB method, increasing the number of cycles increases the dislocation density, resulting in ultrafine-grained materials. By increasing the number of ARB cycles, a uniform distribution of the reinforcement within the matrix is achieved, improving the mechanical properties of the composite. During each ARB cycle, the density of dislocations is significantly increased, resulting in the rearrangement or removal of dislocations, which contributes to such phenomena as recovery or dynamic recrystallization in the microstructure of the composite material. The occurrence of such phenomena will have a significant impact on the microstructure, mechanical properties, wear behavior, and corrosion of the composite material [19, 20].
Talachi et al. [25] studied the wear behavior of pure Al over eight cycles of the ARB process. They concluded that the wear rate of ARBed Al is greater than that of non-ARBed Al. One of the reasons for the increased wear rate of ARBed Al is the presence of unbalanced and unstable grain boundaries with high energy. In fact, wear resistance is reduced due to mismatched strains between recrystallized grains (in the wear surface) and ultrafine grains (induced by the ARB process). Jamaati et al. [26] investigated the wear behavior of the Al-based composites reinforced with alumina. They concluded that the wear resistance of composites decreased with increasing number of ARB cycles. This results from delamination and spalling mechanisms such that these mechanisms destroy the role of both reinforcement and grain size reduction in increasing wear resistance. Darmiani et al. [27] studied the wear behavior of his SiC-reinforced Al-based composites during the ARB process. They concluded that the wear resistance of composites increased as the number of ARB cycles increased. This is because the SiC particles act as a solid lubricant, thereby improving the wear resistance of the composite.
Severe plastic deformation methods such as the ARB process have a positive effect on the corrosion behavior of MMC in such a manner that by increasing the number of ARB cycles many defects such as dislocations and sub-boundaries are created, increasing the internal stresses in the microstructure [28, 29]. Finally, these factors cause the creation of an ultra-fine-grained structure. All the mentioned factors will significantly affect the formation of the oxide layer on the matrix so that the tribofilm will be prone to nucleation in surface defects such as grain boundaries and dislocations. The ARB process leads to grain modification and crystal defects with high internal energy, such as high-angle grain boundaries and dislocations. These high-energy crystalline defects induce more nucleation sites for passive film formation in ultrafine-grained materials. Therefore, after placing the ultrafine grain materials in an aqueous solution, the passive film formation reaction occurs faster and more intensely, and a larger volume of oxide film defects is formed on the surface of ultrafine grain materials. The faster and more intense form of the passive film with a high defect volume is the reason for the increased corrosion resistance of the Al composite during the ARB process [30,31,32].
Nikfahm et al. [33] studied the results of grain size variation on the corrosion resistance of copper (Cu) subjected to the ARB process (for eight cycles). They concluded that the corrosion resistance of Cu is reduced until the second cycle of the ARB process, yet after the fourth cycle, the corrosion resistance rises due to the ultra-fine-grained microstructure. Additionally, the microstructure of the corroded samples shows that the type of corrosion changes with an increase in the number of ARB cycles. In other words, during the initial cycles, intergranular corrosion occurs, yet by raising the number of ARB cycles the microstructure becomes more uniform and fine-grained, leading to uniform corrosion. Fattah-alhosseini et al. [34] studied the electrochemical behavior of pure Cu during the ARB process in the borax solution. They reached the conclusion that by increasing the number of cycles of the ARB process, the conditions for the formation of the passive layer are improved and hence the corrosion resistance is elevated. Fattah-alhosseini et al. [30] investigated the passive behavior of the 1050 nanostructured Al by the ARB process in a borate buffer solution. The results show that by increasing the number of ARB cycles, the formation conditions of the passive layer are improved. Therefore, the corrosion resistance of ARB Al compared with annealed Al sheet is increased. Anne et al. [31] evaluated the corrosion behavior of the Mg-2%Zn/Al7075 layered composite during the ARB process. The results showed that with the progress of the ARB process, the cathodic kinetics are decreased, thereby increasing the corrosion resistance of the layered Mg-2%Zn/Al7075 composite. In addition, due to the ultrafine graining of the composite structure, the growth of the passive layer on the surface of the composite becomes better and more intense, increasing the composite corrosion resistance.
Overall, it can be stated that controlling the microstructure to achieve the optimal mechanical properties and favorable wear and corrosion behavior is highly complicated in ARB-layered composites. Therefore, choosing the type of matrix and reinforcement is highly crucial in preparing this type of composite. In the current study, with the progress of the ARB process, the brass and Cu layers in the Al matrix are torn and finally, a uniform distribution of the layers is developed in the Al matrix as a result of which the mechanical properties are improved.
To the authors’ best knowledge, no study has been conducted on the Al/Cu/Brass three-layered composite using the ARB method. Therefore, in this study, the Al/Cu/Brass composite has been produced by the ARB method, and its mechanical properties, corrosion, and wear behavior have been investigated.
2 Materials and Methods
2.1 Material
Al, Cu, and brass metal sheets with the chemical analysis given in Table 1 were used as raw materials. Before the rolling, the Al sheet, the Cu sheet, and the brass sheets were heat treated at 400 °C for 1 h, 500 °C for one h, and 600 °C for 2 h, respectively. The hardness, yield strength, UTS, and strain hardening exponent of the Al, Cu, and brass metal sheets have been presented in Table 2.
2.2 ARB
The Al /Cu/Brass multilayered composite was prepared in two stages. First, the stage was to do with the sandwich preparation (better known as the first cycle in the manuscript) and the second one had to do with performing the ARB process. In the first stage, in order to remove any dirt and grease and create a strong bond between the layers, the Al, Cu, and brass sheets were degreased with acetone, and then all the sheets were brushed with a wire brush. After the surface treatment, the layers were placed on one another based on Fig. 1 and rolled. After preparing the sandwich cycle, the sandwich panel is divided into two equal parts from the center and the surface treatment is performed on these two cut sheets, which are then re-rolled up. The thickness reduction was made by 50% at ambient temperature without lubrication.
2.3 Mechanical Tests
The tensile test was performed by the Hounsfield machine model H25KS with a strain rate of 0.001 s−1. The sub-size tensile test samples were prepared according to the ASTM-E8M standard. The micro-hardness test was carried out by the Leitz machine using the micro-Vickers method with a load of 10 g and for 15 s. The dry wear test was conducted by the pin-on-disk configuration at ambient temperature under loads of 10, 20, and 30 N, a constant speed of 0.5 m/s with a sliding distance of 1000 m. A 52,100 steel pin was used as an abrasive. To check the wear rate, Eq. (1) was used.
where V: wear volume, N: applied load, L: sliding distance, K: wear coefficient, and H: hardness of the wear surface.
2.4 Corrosion Test
The corrosion test was performed in a sodium chloride solution (3.5%) at room temperature, electrochemical impedance spectroscopy (EIS). A PARSTAT model 2273 potentiostat/galvanostat with three electrodes was used, a saturated calomel electrode (SCE) as the reference electrode, a platinum electrode as the auxiliary electrode and the test sample as the working electrode. The polarization curves were prepared from − 250 to 2000 mV with a scan rate of 1 mV/s.
2.5 Characterizations
To investigate the microstructure of the multilayered composite, the ARB samples were mounted and polished from the cross section. Then, the microstructure was examined by an Olympus optical microscope and a scanning electron microscope (SEM, model VEGA\TESCAN-LMU) equipped with the X-ray energy diffraction spectroscopy (EDS) elemental analysis. The X-ray diffraction test was performed using a Philips PW1800 X-ray machine with a voltage of 30 kV and 40 mA. In all the tests, a single-wavelength CuKα X-ray diffractometer (XRD) with a wavelength of 1.5405 Å, a scan rate of 0.05°/s and a scan step size of 0.05° was used.
3 Results and Discussion
3.1 Microstructure
Figure 2 shows the optical micrographs of the cross-sections of the samples after various passes. Figure 2a shows the optical micrograph of the Al/Cu/Brass multi-layer composites after the first cycle of the ARB process. Since the continuity of the reinforcing layers significantly affects the microstructure and mechanical properties of the Al/Cu/Brass composites, this factor was first investigated .As shown in the figure, there is no necking and fracture Phenomena observed at the Al and Cu.and Brass layers, and the layers are placed smoothly and continuously next to each other. Also, there is no gap between the interfaces of the layers and thus a strong bonding has been created at interface of the layers. Furthermore, during the 2nd cycle (Fig. 2b), due to the difference in the mechanical properties of the layers, plastic instability was occurred at the interface of the layers, resulting in occurrence of the localized flow and creation of the shear bands at the interfaces of the Al matrix/reinforcement’s layers. In general, shear bands are formed in metals that have been undergone severe strains and non-uniform deformation, and usually have an angle of 45o in relation to the rolling direction [35, 36].
However, as a result of the work hardening of the layers and the creation of shear bands in the microstructure of the Al/Cu/Brass composite, necking and fragmentation phenomena have occurred at the Cu and Brass layers, respectively. Generally, the occurrence of the necking phenomenon, which ultimately leads to fragmentation, depends on various factors such as ultimate tensile strength, hardness, elongation, tensile strength coefficient, work hardening exponent, and initial thickness ratio of the layers. Table 2 shows the mechanical properties of pure and annealed Al, Cu, and brass sheets. The work hardening exponent of the brass layer is higher than that of the Al and Cu layers (see Table 2), so the necking and fragmentation phenomena in the brass layer occurred earlier than the others. Similarly, the low elongation of the brass layer, among others, also contributes to the earlier occurrence of its necking and fragmentation phenomena. However, due to severe necking in the Cu layer and the presence of shear bands at the interfaces of the layers, island-like areas have been created in the composite microstructure. Similar conditions are evident in the third pass in Fig. 2c. Figure 2d, e show the optical micrographs of the multi-layer composites during the fourth and sixth cycles, respectively. As it is known, as the number of cycles of the ARB has increased due to the formation of multiple shear bands, severe necking and fragmentation occur at the Cu and brass reinforcing layers, creating many island-like areas in the Al matrix. Also, during the last cycle of the ARB process, due to strain induced by the ARB process, the mechanical properties of the layers in the composite got closer to each other. As a result, a more uniform distribution of reinforcing layers is seen in the Al matrix. Also, during the final cycles of the ARB process, the number of the interfaces of the layersincreases (based on the 2n − 1 formula) while decreasing their thickness.
Figure 3 shows the SEM micrographs of the interface of the layers. In all the passes of ARB, a proper connection has been established between the layers and the interface is free of cracks, cavities, and separation. In Fig. 3, the reduction of the layers thickness due to an increase in the ARB passes can be clearly observed. It is also obvious in the figure that with the increase of ARB passes severe necking and fracture occur in the Cu and Brass layers, respectively. the formation of island-like regions in the sample structure, which is caused by the creation of unequal, incompatible, and inhomogeneous strains between the hard and soft phases [37]. According to the image and XRD in Fig. 4, it is clear that the intermetallic phase is not formed during ARB and the interface between the layers is free of intermetallic compound, which is caused by the low deformation temperature.
Figure 5 exhibits the measured and calculated average thicknesses of the Al, brass, and Cu layers after different ARB cycles. The average thickness of each layer had been measured at equal intervals by Image J software and calculated by the formula in the previous research [38]. It can be observed that the thickness of the layers in the initial passes has experienced a significant reduction due to the acumulative deformation resulting from the ARB process. As discussed before, the thickness and hardness ratio and different flow properties of the layers are effective in the co-deformation of the layers. However, at the subsequent passes, the fracture of the layers also affects the layer thickness. As can be seen for both calculated and measured values, there exists reasonable compatibility, yet due to the distinctive properties and materials behavior, there exist certain differences. As can be seen from the first to the third cycle, the calculated value for Al thickness is noticeably greater than the measured one. Besides, for the three layers the measured values are more than the calculated ones. This can be due to both the difficult distinguishing of the layers boundaries by software and the layers behaviors. However, there are fewer differences between the values after the third cycle. As to the Al layers, the thickness reduction is continued until the last cycle, which is reasonable as the Al is regarded as a softer and thicker layer in the composite. On the contrary, the brass and Cu layers behave differently. As discussed before, these two layers are fractured in the early cycles, showing that their behavior is partly distinct from Al. It has been reported that once the hard layers fracture occurs, the hard layers thickness will level off when subjected to further ARB deformation [39]. The changes in the thickness of the Cu and brass layers are almost close to each other, yet those related to the Al layers are more noticeable than those pertinent to the Cu and brass layers. This arises from various factors such as the non-uniform strain and the difference in plastic instability, which leads to a fracture in brass and Cu layers.
3.2 Hardness
Figure 6 depicts the variation of microhardness with the number of ARB cycles. This reveals that with the increase of ARB passes the microhardness of the three layers increases. From the first to sixth cycle, the amounts of microhardness of Al, Cu, and brass increase slowly from 50, 140, and 210 Vickers to 70, 160, and 260 Vickers. The reason for the increase in microhardness during the early stages of the ARB process is the strain hardening and grain refinement at higher cycles, as shown in previous studies [38, 40]. Recent studies show that reducing grain size has less effect on increasing hardness [41]. As can be seen, the increasing rate of the brass layer microhardness is more than that of the other two layers. This can result from the difference in the SFE of the three metals. Low SFE lengthens the distance between the dislocations, which in turn lengthens the combination of cross slip and dislocations [42]. The samples’ temperature rises during the ARB process as a result of plastic deformation. Due to the different CTE of the layers, thermal stresses are produced at the layer interface when the samples are cooled after ARB. New dislocations are produced as a result of this process, which also makes the layers’ hardness higher.
3.3 Tensile
Figure 7 shows the stress-strain curves of the Al /Cu/Brass composites under different ARB cycles in transverse direction (TD) and rolling direction (RD). The yield stress, ultimate tensile strength, and total elongation obtained from the curves are summarized in Fig. 8 as a function of ARB cycle number. From the first to sixth cycle in both TD and RD directions, there has occurred an increase of 25% and 29% (from well under 255 and 288 MPa to just over 320 and 360 MPa) compared to the first pass, respectively. In the SPD method, strain-hardening plays a key role in increasing strength in the early stages, and in the final stages, grain refinement serves as a factor in controlling strength. Also, in layered composites, the layer boundaries act as a barrier against the movement of dislocations, which is another strengthening factor [43]. UTS in the RD is more than that in the TD, originating from the following reasons. First, the shape, size, and distribution of the broken layers play an influential role in strengthening. This is the reason for the difference between the increase in strength in TD and RD directions. Due to the fact that the applied strain in the rolling direction causes texture in the structure, more strength is obtained in the structure. On the other hand, more strain causes more layers to break and a more homogeneous distribution in the matrix, which results in a greater increase in strength. In fact, during ARB, the thickness of the metal layers decreases due to the applied non-uniform strain, which causes the layers to break and distribute the layer between the Al matrix. It can be said that incompatible strains between metal layers, activation of more slip systems at the interface between layers, and the difference between CTE between layers cause an increase in the density of dislocations during ARB, which It increases the strength of the composite.
A characteristic feature in Fig. 7b is the formation of a double stress peak. During the sixth ARB pass, there is a noticeable difference in the elongation between the aluminum and brass layers due to the high work hardening of the brass layer (reinforcement layer). Load transfer theory states that during a tensile test, the load is transferred from the aluminum layer to the brass layer, causing the brass layer to bear the load. As a result, at the maximum stress, brittle failure occurs in the reinforcement at once – However, cavitation and coalescence of cavities in the matrix have not reached a critical level–, and the applied load falls on the matrix. Therefore, the matrix must bear the applied load. As a result, it causes a step-like drop in the maximum stress, which causes a double stress peak in the stress-strain diagram. Even though in the lower ARB passes, the elongation of the reinforcement is such that cavities are formed/coalescence in the matrix. With the reinforcement’s fracture, the matrix cannot bear the load and causes the continuity of the strain stress diagram.
By examining the elongation of the samples in different passes, it is clear that a uniform decrease in elongation is observed with the increase of ARB passes, which can be seen in both TD and RD directions. Various parameters are effective in the elongation of samples in different passes, such as strain hardening, the type of interface, bond strength of the layerss, and the distribution of layers in the matrix. Strain hardening accumulates dislocations and internal stresses, forming cracks and voids and reducing elongation [44, 45]. By comparing the samples in RD and TD, it is clear that in all passes, the elongation of the samples in RD is more significant in TD. During the ARB process, in the rolling direction, the grains are elongated and compressed perpendicular to the rolling direction. Considering that the crack grows perpendicular to the loading direction, the bonding layer was likely to experience fractures during the tensile deformation in TD, and the laminated composites suffered damage and delamination cracking very soon. As a result, laminated composites had less elongation and deformation in the TD than in the RD [46]. On the other hand, increasing the bonding at the interface between layers suppresses cracking at the interface and increases elongation. More strain causes more layers to break and a more homogeneous distribution in the matrix, resulting in a considerable elongation increase. Furthermore, grains in the Al, Cu, and brass layers orient in the rolling direction. The microhardness of the Al layer in the composite was lower than that of other layers leading to significant plastic strain and apparent strain hardening during the tensile test in the rolling direction due to the high plasticity of the Al layer. The grains also adopt a particular orientation to create a wire or sheet texture, which can affect aterial’s mechanical qualities [46].
3.4 Fracture Surface
Figure 9 shows the fracture surface of samples at different passes. Based on the figure, it is clear that in the low cycles, a small number of dimples are observed in the Al layer, and that the fracture surface of the Cu and brass layers is brittle, which results from the smooth surface of the layers (Fig. 9a and b). In the higher magnification figure, there is no obvious debonding between the layers, which indicates a strong bond between the layers at the second pass (Fig. 9c). With the increase of ARB cycles, the presence of fine dimples in the Al layer becomes evident (Fig. 9d, e, and f). Yet the Cu layer still shows a brittle fracture surface (Fig. 9f). The dimples creation is due to the nucleation, growth, and coalescence of micro-voids [47,48,49]. With the increase of passes, the dimples depth are decreased, indicating the elongation reduction due to the work hardening of the layers [50]. Additionally, the dimples elongated, grow shallower, and exhibit ductile shear fractures (Fig. 9e). Following the initial pass, the dimples’ form and direction reveal, respectively, the type and direction of loading [51]. The non-uniform plastic strain creates the shear pressure that stretches the dimples in the upper cycle of the ARB process. The failure occurs resulting from the internal fracture resulting from microcavities coalescence and depressions in the shear stress [52]. Small, elongated shallow dimples that are in the shear direction can be noticed near the conclusion of the fourth cycle (Fgiure 9f). This rupture method also involves internal cavity cutting [53]. With the increase of passes the separation between the layers takes place (Fig. 9g, h, and i). Such phenomena have also been reported in other multilayer systems processed by ARB [45], originating from different work-hardening behaviors and tensile stresses created during the tensile test and leading to the separation of the layer interface [50].
3.5 Wear Behaviour
Figure 10 shows the weight loss, wear rate and specific wear rate of ARB treated composites at different cycles under different loads. According to Fig. 10a, the weight loss in all applied loads has decreased with the increase of ARB cycles. The samples are easily abraded at the lower passes and cause wear debris. The strength of the produced composites rises by increasing the ARB cycles, leading to a reduction in wear weight loss. Brass and Cu metals have a higher wear strength than Al. By increasing the ARB cycles and increasing the uniformity of the layer distribution, the wear rate is reduced [32].
The variations of the wear rate versus the number of cycles under different loads have been given in Fig. 10b. According to the figure, as expected, the wear rate has increased by raising the applied load, and the difference between the wear rate in different loads has decreased by increasing the cycles. Hence, from the fifth to the sixth pass the wear rate has remained virtually constant under loads of 10 to 30 N. A more uniform distribution of layers within the composite matrix improves microstructural refinement and increases the sub-boundaries, resulting in increased material strength and reduced wear rate [54].
Based on Eq. (1) and according to the experimental findings illustrated in Fig. 10, the wear rate increases as the applied weight increases. Weight loss with increasing hardness can also be described by an equation. Therefore, it can be said that the wear rate of the Al/Cu/Brass composite produced by the ARB method is greatly influenced by hardness and grain refinement [54, 55]. At early cycles, increasing hardness is the main reason for reduced wear rate, while at higher cycles, grain refinement is the main mechanism. In general, three main mechanisms are known for sliding wear: abrasion, adhesion and surface fatigue. The sliding wear can also be influenced by a variety of parameters, including crystal structure, hardness, work hardening, yield strength, and resistance to crack nucleation. According to the dislocation theory, plastic deformation and crack nucleation in the subsurface explain the formation of wear debris [56, 57].
Figure 11 illustrates the friction coefficient of samples under different loads at different passes. It is clear that with the increase of ARB cycles, the friction coefficient is decreased, and that the range of changes becomes more consistent. The critical point is to achieve the stability of the friction coefficient. By increasing the number of ARB cycles the friction coefficient reaches stability within a shorter distance. Losing the upper layer and reaching the lower layer lead to extreme changes in the friction coefficient in the initial wear distance [25, 58]. By increasing the applied load to 20 N, it is evident that the range of friction coefficient fluctuations is increased. It is also clear that reaching stability occurs within shorter distances. In the applied load of 30 N, it is obvious that the range of the friction coefficient changes is increased. However, from the second pass onward, the average friction coefficient becomes the same, which is caused by the higher plastic deformation rate of the surface due to the higher load.
The worn surface of the samples was studied by SEM to determine the dominant wear mechanisms. Figure 12 shows the worn surface of the samples under 10 N. As it is clear in the low magnification micrograph, by increasing the ARB cycles the range of the plastic deformation zone initiated from the wear of the samples becomes narrower in view of the fact that the composites strength is augmented by increasing the ARB cycles. In this figure, the deep grooves and the material flow reveal the abrasive and adhesion mechanism. The abrasive wear is caused by the deformation of the wear surface and damages due to the deep scratches created in the wear path [59]. It is also evident in the higher magnification micrographs that delamination has occurred for entire samples.
Delamination is a wear mechanism in which surface damage is created by the forces of a surface moving in thin sheets in a sliding [60]. In fact, at first, plastic deformation occurs on the surface, and then the crack nucleates on the lower surface. As the sliding continues, the cracks grow and conjoin, which causes the top layer to be separated from the worn surface. During delamination, the direct surface is affected by the applied stresses. In these circumstances, significant plastic flow occurs. Based on this theory of plastic deformation, shearing, crack nucleation, and/or propagation in the surface’s shallow depth, leads to a layer-to-layer separation. As the sliding distance increases, the dislocations assemble near the surface, and therefore the microcavities are created. Over time, the pores combine under applied stresses. Under these conditions, there occurs a significant plastic flow, creating cracks along the surface. Depending on the material properties, when the fracture crack reaches a critical value, the material begins to layer by layer detach from the surface. The high shear stresses on the sliding surface induces fatigue load in the creation of propagated cracks on the lower surface, resulting in the material being lost from the worn surface as wear debris [26]. The surface material flows significantly toward the slip on the surface and causes the delamination of the worn surface material and the trapping of small oxide particles.
From the first to the third cycle, the level of delamination decreases, in spite of the fact that in the subsequent third cycle, the intensity of delamination is reduced further and the oxidized areas are observed on the worn surface. Figure 13 shows the elemental map analysis of the worn surface of the sample in the second pass, which indicates extensive oxidation in the Al layer and the creation of scratches in the Al layer. The dominant mechanisms in low and high ARB cycles are delamination and oxidation, respectively.
Figure 14 illustrates the SEM micrographs of the worn surface of the samples under a 20 N load. As can be seen, severe oxidation has occurred on the worn surface. Furthermore, after the wear test, material transfer is seen. The EDS examination of the worn surface revealed iron, which suggests that iron was adherently transferred from the steel pin. Besides, oxygen in the atmosphere indicates that the wear mode can be oxidation as well. It can be stated that there is a combination of abrasion, adhesion, and delamination mechanisms at 20 N. Delamination is the primary wear process in high ARB cycles. The ARB process creates a hardened layer and increases the surface roughness. At the beginning of the ARB process, the brittle layer and the pre-formed oxide layer are fractured. Then, greater contact between the surfaces of the raw materials is formed where the surface expansion is somewhat bigger to generate a metal bond [61]. Therefore, in the wear test this created layer is separated in the higher cycles, and the dominant mechanism is delamination.
Figure 15 shows the SEM micrographs of the worn surface of the samples under 30 N. According to the figure, it is clear that oxidation has occurred in a large area on the worn surface. Based on the considerable cracks and dimples caused by large deformation, it is clear that delamination is the dominant wear mechanism. As a result, there is a significant degree of wear in this sample. Furthermore, scratches and grooves can be visible, indicating abrasive and adhesive wear mechanisms. However, compared to delamination, the wear rate caused on by these mechanisms is lower. With the increase of ARB passes the worn surfaces become similar to the first passes in all of the cycles, with the only difference that in the latest cycle, the delamination mechanism’s intensity has decreased. In general, it can be said a combination of oxidation and adhesion is the predominant mechanism in the last cycle (Figs. 15 and 16). Increasing the number of ARB cycles increases the number of layers and interfaces. Additionally, because the ARB technique creates unstable grain boundaries, grain coarsening, and recrystallization may take place, increasing wear resistance [62]. A previous study shows that these two factors reduce the wear rate in high cycles. As a hard layer, brass supports the Al layer, which, in addition to reducing the wear rate, causes the wear mechanism to transform from delamination to oxidation. This accomplishment can be put to use as an achievable solution to increase wear resistance.
3.6 Corrosion
Figure 17 shows the Nyquist (− Z” vs. Z’) curves associated with the samples studied. In general, each Nyquist curve consists of semicircles or semicircles sunk into each other, the diameters of which are the totality of these semicircles that can represent the system resistance against corrosion [63]. According to Fig. 17, among the investigated samples, the diameter of the semicircle of the samples of the second and third cycles is significantly more than that of the other samples, which indicates the higher corrosion resistance of these samples. After these samples lie sample 5. The smallest semicircle diameter and the lowest corrosion resistance belong to sample 1. The Bode curves are pertinent to the EIS test and provide useful data for system analysis. One side of these curves is the impedance coefficient (√(Z’2 + Z"2)), or |Z|, which is plotted as the logarithm of frequency, and the other side is the phase angle relationship ( Arc tan (Z” /Z’)) is plotted as the logarithm of frequency. The advantage of this representation over the Nyquist plot is that the frequency values are known from the plot. The curves of the Bode modulus impedance and Bode phase angle of the samples are shown in Fig. 18.
The impedance at the lowest frequency in Bode-module impedance curves has been shown to be representative of the overall system resistance [64]. This change in value indicates that the overall system resistance is higher in the second and third cycle samples than in the other samples. The presence of two peaks in the Bode-phase angle curves indicates that these curves have two time constants, which helps to select the appropriate equivalent circuit to model the results of this experiment. The use of the equivalent circuit for the analysis of impedance tests as a well-known method for studying corrosion mechanisms has been accepted [65]. Figure 17 shows the equivalent circuit used for the electrochemical model of this test result.In this circuit, Rs represents the solution resistance, and Rf and CPEf are the resistance and capacitance, respectively, of the top layer stationary phase element at the electrode surface. Rct and CPEdl are the resistance of charge transfer from the double layer and the capacitance of the double layer stationary phase element, respectively. This circuit uses fixed phase elements instead of ideal capacitors. Fixed phase elements are used instead of ideal capacitors because the planes of the double layer formed between the electrode surface and the electrolyte are not perfectly parallel and the electrode surfaces are rough and uneven [66]. The difference between these two is expressed in the impedance formula. The impedance of the capacitor is equal to Z = 1/jωC and this value for CPE is Z = 1/(Y0jω)n, where C represents the capacitance of the capacitor, ω represents the phase, Y0 represents conductivity and j is the imaginary term √(− 1).
Clearly, the only difference between these two values is as it were within the power of n, which may be a numerical esteem between 0 and 1. A value of 0 represents an ideal resistor and a value of 1 represents an ideal capacitor. Equivalence of the samples was measured by an electrochemical equivalent circuit run using ZsimpWin software. The results of the fit of this equivalent circuit have been shown on Bud and Nyquist diagrams in Figs. 17 and 18. The related images reveal that the electrochemical model results are in good agreement with the impedance test results. Table 3 shows the parameter values obtained from this equation. In this table, the power n is related to the constant phase element impedance formula described above. Here, as n approaches one, the surface uniformity increases and the constant phase element approaches an ideal capacitor. As n approaches one, the surface becomes more uneven and its uniformity decreases. Overall resistance, which is inversely proportional to corrosion rate, is found to be derived from the sum of load transfer resistance and surface resistance [67]. Therefore, in Table 3 the overall resistance of the samples was given using the parameter Rt. According to these results, the 2nd and 3rd cycle samples had the highest corrosion resistance among all the other samples, followed by the 5th cycle sample, and then the 6th cycle sample with the highest overall resistance. In addition, the first and fourth cycle samples have the lowest corrosion resistance, respectively.
The polarization diagrams (DC) of the samples are shown in Fig. 19. For a closer look at the polarization curves of the TOEFL region, these curves are extrapolated and the results are reported in Table 4. In this table, the slopes of the anodic and cathodic branches are βa and βc, respectively. Corrosion potential and corrosion current density are Ecorr and icorr, respectively. To find the polarization resistance (Rp), the Stern-Grey relationship (Eq. 2) was used [68].
Based on the results shown in Table 4, it is clear that the polarization resistance of the 2nd cycle sample, followed by the 3rd and 5th cycle samples is higher than the rest of the samples. It is also clear that the lowest values of polarization resistance are related to the samples of the first and fourth cycles, which also confirms the impedance test results.
Two factors contribute to the corrosion resistance of the produced composites: the structure homogeneity and the amount of plastic deformation. In the first cycles, the structure homogeneity and layer bond strength layers are the least. By increasing the process the homogeneity is increased, and the amount of plastic deformation is also increased. Increasing the plastic deformation results in raising the defects in the structure, thereby decreasing the corrosion resistance. Therefore, in the middle cycles (2, 3, and 5) the corrosion resistance is high.
4 Conclusions
In this study, the mechanical and corrosion behaviors of Cu/brass/Al composites fabricated by ARB method were investigated. The results are derived as follows:
-
1.
The microstructure investigations by optical and SEM showed that fracture occurred in the brass layers from the second cycle onwards which is caused by the accumulation of plastic strain in the samples during the ARB cycles.
-
2.
With the increase in the ARB cycles, the yield stress and ultimate tensile stress increased, and the highest ultimat tensile stress of 288 MPa (in the RD) was achieved in the sixth cycle, which is almost three times the ultimat tensile stress of Al. On the contrary, with the increase in the number of cycles, the elongation decreased. Besides, the UTS in the RD was more than that in the TD.
-
3.
The results showed that the wear rate decreased as the number of ARB cycles increased. Wear resistance is caused by the main mechanism change from delamination to oxidation.
-
4.
Clearly, as the ARB cycle increases, the coefficient of friction decreases and the change is smoothed. Increasing the number of ARB cycles stabilized the friction coefficient at shorter distances.
-
5.
Examining the fracture surfaces show that in low ARB passes, ductile fracture with the presence of shallow dimples was observed in the aluminum layer, brittle fracture was observed in the copper and brass layers, and in high ARB passes, shear fracture along with separation between the layers was evident.
-
6.
Corrosion behavior of samples in the TOEFL and impedance test shows the highest corrosion resistance relative to the sample after the fifth pass and the lowest corrosion resistance related to the pass firstly.
References
N. Chawla, K.K. Chawla, Metal Matrix Composites, 2nd edn. (Springer, New York, 2013). https://doi.org/10.1007/978-1-4614-9548-2
G.N.M. Rao, V.R.M. Kumar, A review on recent advances in accumulative roll bonding of similar, dissimilar and metal matrix composites. Mater. Today Proc. 56, A13–A18 (2022). https://doi.org/10.1016/j.matpr.2021.11.608
L. Song, H. Gao, L. Bhatt, C. Kong, H. Yu, Microstructure and mechanical properties of AA1050/AA6061 multilayer composites via accumulative roll bonding and cryorolling and subsequent aging. Mater. Sci. Eng. A 874, 145069 (2023). https://doi.org/10.1016/j.msea.2023.145069
D. Kumar, L. Thakur, Investigation on mechanical and wear performance of Ultrasonic-assisted stir cast AZ91D/Al2O3 magnesium matrix composites. Met. Mater. Int. 29, 2767–2781 (2023). https://doi.org/10.1007/s12540-023-01395-w
L. Wang, T. Wu, D. Wang, Z. Liang, X. Yang, Z. Peng, Y. Liu, Y. Liang, Z. Zeng, J.P. Oliveira, A novel heterogeneous multi-wire indirect arc directed energy deposition for in-situ synthesis Al–Zn–Mg–Cu alloy: process, microstructure and mechanical properties. Addit. Manuf. 72, 103639 (2023). https://doi.org/10.1016/j.addma.2023.103639
M. Qiu, W. Hu, H. Liu, Y. Pang, X. Du, Mechanical properties of (ce + yb) modified in situ TiB2/Al-Si Matrix composites enhanced via Thermal deformation combined with Heat Treatment. Met. Mater. Int. 29, 3078–3092 (2023). https://doi.org/10.1007/s12540-023-01425-7
D. Zhao, C. Jiang, K. Zhao, Ultrasonic welding of AZ31B magnesium alloy and pure copper: microstructure, mechanical properties and finite element analysis. J. Mater. Res. Technol. 23, 1273–1284 (2023). https://doi.org/10.1016/j.jmrt.2023.01.095
M.M. Sadawy, S.M. Fayed, M. Tayea, I.G. El-Batanony, Microstructure, corrosion and electrochemical properties of Cu/SiC composites in 3.5 wt% NaCl solution. Met. Mater. Int. (2023). https://doi.org/10.1007/s12540-023-01521-8
H.I. Kurt, M. Oduncuoglu, R. Asmatulu, Wear behavior of aluminum matrix hybrid composites fabricated through friction stir welding process. J. Iron Steel Res. Int. 23, 1119–1126 (2016). https://doi.org/10.1016/S1006-706X(16)30165-0
A.M. Rajesh, M. Kaleemulla, Experimental investigations on mechanical behavior of aluminium metal matrix composites. IOP Conf. Ser. Mater. Sci. Eng. 149, 012121 (2016). https://doi.org/10.1088/1757-899X/149/1/012121
C. Velmurugan, R. Subramanian, S. Thirugnanam, B. Anandavel, Investigation of friction and wear behavior of hybrid aluminium composites. Ind. Lubr. Tribol. 64, 152–163 (2012). https://doi.org/10.1108/00368791211218687
A.M. Sankhla, K.M. Patel, M.A. Makhesana, K. Giasin, D.Y. Pimenov, S. Wojciechowski, N. Khanna, Effect of mixing method and particle size on hardness and compressive strength of aluminium based metal matrix composite prepared through powder metallurgy route. J. Mater. Res. Technol. 18, 282–292 (2022). https://doi.org/10.1016/j.jmrt.2022.02.094
N. Panwar, A. Chauhan, Fabrication methods of particulate reinforced Aluminium metal matrix composite: a review. Mater. Today Proc. 5, 5933–5939 (2018). https://doi.org/10.1016/j.matpr.2017.12.194
U.K.G.B. Annigeri Veeresh Kumar, Method of stir casting of aluminum metal matrix composites: a review. Mater. Today Proc. 4, 1140–1146 (2017). https://doi.org/10.1016/j.matpr.2017.01.130
Y. Zhao, J. Jing, L. Chen, F. Xu, H. Hou, Current research status of interface of ceramic-metal laminated composite material for armor protection. Acta Met. Sin. 57, 1107–1125 (2021). https://doi.org/10.11900/0412.1961.2021.00051
F. Ferreira, I. Ferreira, E. Camacho, F. Lopes, A.C. Marques, A. Velhinho, Graphene oxide-reinforced aluminium-matrix nanostructured composites fabricated by accumulative roll bonding. Compos. Part B Eng. 164, 265–271 (2019). https://doi.org/10.1016/j.compositesb.2018.11.075
R.H. Gao, F. Li, W.T. Niu, P.D. Huo, Response mechanism of mechanical behavior with mg plate microstructure evolution during Al/Mg/Al composite plate rolled by hard plate. Met. Mater. Int. 29, 2004–2016 (2023). https://doi.org/10.1007/s12540-022-01348-9
C. Lin, S. Wang, H. Yan, Y. Han, J. Zhu, H. Shi, Optimization mechanisms of microstructure and mechanical properties of SiC fiber reinforced Ti/Al3Ti laminated composite synthesized using titanium barrier. Met. Mater. Int. 27, 306–318 (2021). https://doi.org/10.1007/s12540-020-00724-7
L. Ghalandari, M.M. Mahdavian, M. Reihanian, M. Mahmoudiniya, Production of Al/Sn multilayer composite by accumulative roll bonding (ARB): a study of microstructure and mechanical properties. Mater. Sci. Eng. A 661, 179–186 (2016). https://doi.org/10.1016/j.msea.2016.02.070
R.N. Dehsorkhi, F. Qods, M. Tajally, Investigation on microstructure and mechanical properties of Al–Zn composite during accumulative roll bonding (ARB) process. Mater. Sci. Eng. A 530, 63–72 (2011). https://doi.org/10.1016/j.msea.2011.09.040
M. Tayyebi, M. Alizadeh, Structural, mechanical, and corrosion evaluations of Cu/Zn/Al multilayered composites subjected to CARB process. J. Alloys Compd. 867, 158973 (2021). https://doi.org/10.1016/j.jallcom.2021.158973
J. Luo, M. Yarigarravesh, A.H. Assari, N.H. Amin, M. Tayyebi, M. Paidar, Investigating the solid-state diffusion at the interface of Ni/Ti laminated composite. J. Manuf. Process. 75, 670–681 (2022). https://doi.org/10.1016/j.jmapro.2022.01.042
Y. Wang, M. Tayyebi, M. Tayebi, M. Yarigarravesh, S. Liu, H. Zhang, Effect of whisker alignment on microstructure, mechanical and thermal properties of Mg–SiCw/Cu composite fabricated by a combination of casting and severe plastic deformation (SPD). J. Magnes Alloy. 11, 966–980 (2023). https://doi.org/10.1016/j.jma.2022.11.004
Y. Wang, P. Huang, S. Liu, M. Tayyebi, M. Tayebi, Microstructural evolution, shielding effectiveness, and the ballistic response of Mg/Al7075/B4C/Pb composite produced by combination of coating and severe plastic deformation (SPD) processes. J. Manuf. Process. 84, 977–985 (2022). https://doi.org/10.1016/j.jmapro.2022.10.062
A.K. Talachi, M. Eizadjou, H.D. Manesh, K. Janghorban, Wear characteristics of severely deformed aluminum sheets by accumulative roll bonding (ARB) process. Mater. Charact. 62, 12–21 (2011). https://doi.org/10.1016/j.matchar.2010.10.003
R. Jamaati, M. Naseri, M.R. Toroghinejad, Wear behavior of nanostructured Al/Al2O3 composite fabricated via accumulative roll bonding (ARB) process. Mater. Des. 59, 540–549 (2014). https://doi.org/10.1016/j.matdes.2014.03.027
E. Darmiani, I. Danaee, M.A. Golozar, M.R. Toroghinejad, A. Ashrafi, A. Ahmadi, Reciprocating wear resistance of Al–SiC nano-composite fabricated by accumulative roll bonding process. Mater. Des. 50, 497–502 (2013). https://doi.org/10.1016/j.matdes.2013.03.047
M. Tayyebi, M. Alizadeh, A novel two-step method for producing Al/Cu functionally graded metal matrix composite. J. Alloys Compd. 911, 165078 (2022). https://doi.org/10.1016/j.jallcom.2022.165078
Y. Wang, M. Tayyebi, A. Assari, Fracture toughness, wear, and microstructure properties of aluminum/titanium/steel multi-laminated composites produced by cross-accumulative roll-bonding process. Arch. Civ. Mech. Eng. 22, 49 (2022). https://doi.org/10.1007/s43452-021-00355-8
A. Fattah-alhosseini, S.O. Gashti, Passive behavior of ultra-fine-grained 1050 aluminum alloy produced by accumulative roll bonding in a borate buffer solution. Acta Metall. Sin. 28, 1222–1229 (2015). https://doi.org/10.1007/s40195-015-0316-7
G. Anne, M.R. Ramesh, H. Shivananda Nayaka, S.B. Arya, S. Sahu, Microstructure evolution and mechanical and corrosion behavior of accumulative roll bonded Mg-2%Zn/Al-7075 multilayered composite. J. Mater. Eng. Perform. 26, 1726–1734 (2017). https://doi.org/10.1007/s11665-017-2576-z
M. Kadkhodaee, M. Babaiee, H.D. Manesh, M. Pakshir, B. Hashemi, Evaluation of corrosion properties of Al/nanosilica nanocomposite sheet produced by accumulative roll bonding (ARB) process. J. Alloys Compd. 576, 66–71 (2013). https://doi.org/10.1016/j.jallcom.2013.04.090
M.R.T.A. Nikfahm, I. Danaee, A. Ashraf, Effect of grain size changes on corrosion behavior of copper produced by accumulative roll bonding process. Mater. Res. 16, 1379–1386 (2013). https://doi.org/10.1590/S1516-14392013005000135
A. Fattah-alhosseini, O. Imantalab, Effect of accumulative roll bonding process on the electrochemical behavior of pure copper. J. Alloys Compd. 632, 48–52 (2015). https://doi.org/10.1016/j.jallcom.2015.01.208
M.M. Mahdavian, L. Ghalandari, M. Reihanian, Accumulative roll bonding of multilayered Cu/Zn/Al: an evaluation of microstructure and mechanical properties. Mater. Sci. Eng. A 579, 99–107 (2013). https://doi.org/10.1016/j.msea.2013.05.002
L. Ghalandari, M.M. Mahdavian, M. Reihanian, Microstructure evolution and mechanical properties of Cu/Zn multilayer processed by accumulative roll bonding (ARB). Mater. Sci. Eng. A 593, 145–152 (2014). https://doi.org/10.1016/j.msea.2013.11.026
A. Shabani, M.R. Toroghinejad, A. Shafyei, Fabrication of Al/Ni/Cu composite by accumulative roll bonding and electroplating processes and investigation of its microstructure and mechanical properties. Mater. Sci. Eng. A 558, 386–393 (2012). https://doi.org/10.1016/j.msea.2012.08.017
L. Ghalandari, M.M. Moshksar, High-strength and high-conductive Cu/Ag multilayer produced by ARB. J. Alloys Compd. 506, 172–178 (2010). https://doi.org/10.1016/j.jallcom.2010.06.172
L. Su, C. Lu, A.K. Tieu, G. Deng, X. Sun, Ultrafine grained AA1050/AA6061 composite produced by accumulative roll bonding. Mater. Sci. Eng. A 559, 345–351 (2013). https://doi.org/10.1016/j.msea.2012.08.109
M.S. Bayati, H. Sharifi, M. Tayebi, T. Isfahani, Effect of Al–B4C nanocomposite filler manufactured by accumulative roll bonding (ARB) method on the microstructure and mechanical properties of weldings prepared by tungsten inert gas welding. Mater. Res. Express 6, 106529 (2019). https://doi.org/10.1088/2053-1591/ab33a0
S. Pasebani, M.R. Toroghinejad, Nano-grained 70/30 brass strip produced by accumulative roll-bonding (ARB) process. Mater. Sci. Eng. A 527, 491–497 (2010). https://doi.org/10.1016/j.msea.2009.09.029
F.J. Humphreys and M. Hatherly, Recrystallization and Related Annealing Phenomena, 2nd edn. (Pergamon, Oxford, 2004)
H. Park, J. Lee, R.E. Kim, S. Son, S.Y. Ahn, H.S. Kim, Effect of warm rolling on the structure and tensile properties of a metastable Fe-based medium entropy alloy. Met. Mater. Int. (2023). https://doi.org/10.1007/s12540-023-01532-5
M.M. Mahdavian, A.R. Khodabandeh, H.R. Jafarian, S. Mirdamadi, Evaluation of the macro/microstructure of Al/Cu/Sn/Ni multi-layered composite produced by accumulative-roll-bonding (ARB) and post-heat treatment. J. Alloys Compd. 925, 166711 (2022). https://doi.org/10.1016/j.jallcom.2022.166711
M.D. Gholami, M. Salamat, R. Hashemi, Study of mechanical properties and wear resistance of Al 1050/Brass (70/30)/Al 1050 composite sheets fabricated by the accumulative roll bonding process. J. Manuf. Process. 71, 407–416 (2021). https://doi.org/10.1016/j.jmapro.2021.09.032
T. Huang, Z. Song, F. Chen, J. Guo, Y. Pei, B. Xing, N. Xiang, K. Song, Influence of the anisotropy on the microstructure and mechanical properties of Ti/Al laminated composites. Materials (Basel) 13, 3556 (2020). https://doi.org/10.3390/ma13163556
M. Tayebi, S. Nategh, H. Najafi, A. Khodabandeh, Tensile properties and microstructure of ZK60/SiCw composite after extrusion and aging. J. Alloys Compd. 830, 154709 (2020). https://doi.org/10.1016/j.jallcom.2020.154709
M. Tayebi, H. Najafi, S. Nategh, A. Khodabandeh, Creep behavior of ZK60 alloy and ZK60/SiCw composite after extrusion and precipitation hardening. Met. Mater. Int. 27, 3905–3917 (2021). https://doi.org/10.1007/s12540-020-00877-5
S.F. Mousavi, H. Sharifi, M. Tayebi, B. Hamawandi, Y. Behnamian, Thermal cycles behavior and microstructure of AZ31/SiC composite prepared by stir casting. Sci. Rep. 12, 15191 (2022). https://doi.org/10.1038/s41598-022-19410-2
S.V.A. Ana, M. Reihanian, B. Lotfi, Accumulative roll bonding (ARB) of the composite coated strips to fabricate multi-component Al-based metal matrix composites. Mater. Sci. Eng. A 647, 303–312 (2015). https://doi.org/10.1016/j.msea.2015.09.006
Y.-Y. Wang, C. Jia, M. Xu, M. Kaseem, M. Tayebi, Microstructural changes caused by the creep test in ZK60 alloy reinforced by SiCp at intermediate temperature after KOBO extrusion and aging. Materials (Basel) 16, 3885 (2023). https://doi.org/10.3390/ma16103885
M. Naseri, M. Reihanian, E. Borhani, Effect of strain path on microstructure, deformation texture and mechanical properties of nano/ultrafine grained AA1050 processed by accumulative roll bonding (ARB). Mater. Sci. Eng. A 673, 288–298 (2016). https://doi.org/10.1016/j.msea.2016.07.031
I. Barsoum, J. Faleskog, Rupture mechanisms in combined tension and shear—experiments. Int. J. Solids Struct. 44, 1768–1786 (2007). https://doi.org/10.1016/j.ijsolstr.2006.09.031
S.K. Moheimani, K. Azadeh, S. Khademzadeh, M. Tayebi, A. Rajaee, A. Saboori, Tribological behaviour of AZ31 magnesium alloy reinforced by bimodal size B4C after precipitation hardening. J. Magnes. Alloys 10, 3267–3280 (2022). https://doi.org/10.1016/j.jma.2021.05.016
M. Li, Q. Guo, L. Chen, L. Li, H. Hou, Y. Zhao, Microstructure and properties of graphene nanoplatelets reinforced AZ91D matrix composites prepared by electromagnetic stirring casting. J. Mater. Res. Technol. 21, 4138–4150 (2022). https://doi.org/10.1016/j.jmrt.2022.11.033
S. Wen, P. Huang, Principles of Tribology (Wiley, Hoboken, 2012)
L. Chen, Y. Zhao, J. Jing, H. Hou, Microstructural evolution in graphene nanoplatelets reinforced magnesium matrix composites fabricated through thixomolding process. J. Alloys Compd. 940, 168824 (2023). https://doi.org/10.1016/j.jallcom.2023.168824
X. Wang, M. Huang, Y. Zheng, J. Yang, P. Chi, M. Tayebi, Hot temperature tribological behavior of Mg–Zn–Gd alloy under graphite surfactant functionalized SN500. J. Alloys Compd. 967, 171843 (2023). https://doi.org/10.1016/j.jallcom.2023.171843
M. Karimi, M. Bozorg, Wear behavior of laminated nanostructured CP–Ti sheets fabricated by severe plastic deformation. Mater. Chem. Phys. 290, 126634 (2022). https://doi.org/10.1016/j.matchemphys.2022.126634
E. Ahmadi, M. Goodarzi, Mechanical response and wear behavior of graphene reinforced inconel 718 composite produced via hybrid accumulative roll bonding and gas tungsten arc welding process. J. Mater. Res. Technol. 19, 3059–3072 (2022). https://doi.org/10.1016/j.jmrt.2022.06.013
N. Bay, Cold welding: Part 1. characteristics, bonding mechanisms, bond strength, in Metal Construction, vol. 18 (Welding Institute Journal, Cambridge, 1986)
M. Eizadjou, H.D. Manesh, K. Janghorban, Microstructure and mechanical properties of ultra-fine grains (UFGs) aluminum strips produced by ARB process. J. Alloys Compd. 474, 406–415 (2009). https://doi.org/10.1016/j.jallcom.2008.06.161
A.A. Javidparvar, R. Naderi, B. Ramezanzadeh, L-cysteine reduced/functionalized graphene oxide application as a smart/control release nanocarrier of sustainable cerium ions for epoxy coating anti-corrosion properties improvement. J. Hazard. Mater. 389, 122135 (2020). https://doi.org/10.1016/j.jhazmat.2020.122135
Z. Gao, D. Zhang, S. Jiang, Q. Zhang, X. Li, XPS investigations on the corrosion mechanism of V(IV) conversion coatings on hot-dip galvanized steel. Corros Sci 139, 163–171 (2018). https://doi.org/10.1016/j.corsci.2018.04.030
X.-J. Zhang, F. Gao, Z.-Y. Liu, Effect of Sn on corrosion behavior of ultra-pure 17 mass% cr ferritic stainless steels in sulphuric acid. J. Iron Steel Res. Int. 23, 1044–1053 (2016). https://doi.org/10.1016/S1006-706X(16)30156-X
Y. Hao, Y. Zhao, B. Li, L. Song, Z. Guo, Self-healing effect of graphene@PANI loaded with benzotriazole for carbon steel. Corros. Sci. 163, 108246 (2020). https://doi.org/10.1016/j.corsci.2019.108246
S. Feliu, Electrochemical impedance spectroscopy for the measurement of the corrosion rate of magnesium alloys: brief review and challenges. Metals (Basel) 10, 775 (2020). https://doi.org/10.3390/met10060775
M. Furko, Y. Jiang, T.A. Wilkins, C. Balázsi, Electrochemical and morphological investigation of silver and zinc modified calcium phosphate bioceramic coatings on metallic implant materials. Mater. Sci. Eng. C 62, 249–259 (2016). https://doi.org/10.1016/j.msec.2016.01.060
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Esmaeil Zadeh, M., Ghalandari, L., Sani, R. et al. Microstructural Evaluation, Mechanical Properties, and Corrosion Behavior of the Al/Cu/Brass Multilayered Composite Produced by the ARB Process. Met. Mater. Int. 30, 1123–1144 (2024). https://doi.org/10.1007/s12540-023-01557-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12540-023-01557-w