Measurements of the Viscosity of Hydrogen and a (Hydrogen + Methane) Mixture with a Two-Capillary Viscometer

Abstract

Measurements of the viscosity of pure hydrogen and a binary (hydrogen + methane) mixture with a nominal composition 90 mol % hydrogen are presented. The measurements were conducted with a two-capillary viscometer relative to helium along three isotherms of (298.15, 323.15, and 348.15) K and at pressures of up to 18 MPa. Expanded relative combined uncertainties in viscosity range from (0.65 to 2.7) % (k = 2) for the hydrogen data, and from (0.91 to 3.2) % (k = 2) for the (hydrogen + methane) data. The viscosity data are compared to experimental literature data and viscosity correlations implemented in the NIST REFPROP v10.0 database. Good agreement between this work’s data, literature data, and the viscosity correlation was achieved for pure hydrogen. The (hydrogen + methane) mixture was compared to the Extended Corresponding States (ECS) model implemented in REFPROP v10.0. Relative deviations between the experimental data and the ECS model exceed the experimental uncertainty and were found to exhibit a positive trend with increasing density and a weakly pronounced negative trend with increasing temperature. No experimental literature data are available at overlapping state regions. Nonetheless, deviations to the ECS model imply reasonable consistency of this work’s data and literature data. In addition to experimental viscosities, experimental zero-density viscosity ratios of the fluids under investigation and helium are reported. Fairly good agreement within the experimental uncertainty of this work with a highly accurate literature value and a value obtained from accurate ab initio calculated data was achieved for hydrogen.

1 Introduction

The implementation of the 2015 Paris agreement to hold the increase of the global average temperature below 2 °C and if possible below 1.5 °C compared to pre-industrialized levels, requires large-scale deployment of renewable energy sources. However, a substantial increase of renewable energy sources in the energy mix comes with challenges for power grid stability. In contrast to fossil-fueled power plants, base-load capacities cannot be readily provided by fluctuating renewables, such as wind and solar. Therefore, large-scale energy storage systems need to be employed, to balance the mismatch of renewable energy supply and demand. Hydrogen production from excess renewable energy, and underground storage in geological formations, such as salt caverns, aquifers, and depleted oil and gas reservoirs, offers large storage capacities over seasonal timescales. Depleted oil and gas reservoirs qualify for several reasons as suited storage sites, such as extensive storage capacities, gas tightness of the reservoirs over large timescales, well characterized storage properties, and the opportunity to re-purpose already existing infrastructure for injection and depletion [1, 2]. Little experience with hydrogen storage in depleted oil and gas reservoirs has been made so far [2] and, thus, accurate simulation tools need to be employed, to allow for safe, cost-effective, and efficient operation. Nonetheless, for accurate and reliable simulations of e.g., reservoir flows, basic knowledge gaps in the description of thermophysical properties of hydrogen and mixtures of hydrogen with remaining reservoir or cushion gases have to be addressed. As shown by Cai et al. [3], predictive viscosity models, as they are used in simulation tools such as GPSFLOW, are not capable to provide data with sufficient accuracy without adjustment to reference data. However, at high hydrogen concentrations the existing database for viscosities of mixtures of hydrogen with typical reservoir gases like methane does not cover the temperature and pressure ranges, which are most relevant in the context of underground hydrogen storage (cf. Sect. 3.4). Therefore, to enhance the database, measurements of the viscosity of a binary mixture with a nominal composition of 90 mol % hydrogen and 10 mol % methane were carried out within this work, covering typical reservoir conditions. Additionally, validation measurements on pure hydrogen were conducted at the same temperatures and pressure range.

2 Experimental Section

2.1 Hydrodynamic Model

The viscosity measurements presented here, were carried out with a two-capillary viscometer. The measurement method is based on the Hagen-Poiseuille equation, which relates the volume flow rate Q of a fluid with viscosity η through a circular capillary with radius R to the pressure gradient along the capillary’s longitudinal axis dP/dz

$$- \frac{8\eta Q}{{\pi R^{4} }} = \frac{{{\text{d}}P}}{{{\text{d}}z}}.$$

(1)

Substitution of Q = $\dot{n}$/ρ and assuming the radius to be constant along the length of the capillary, integration of Eq. 1 from inlet to outlet of the capillary yields

$$-\frac{8\dot{n}}{\pi {R}^{4}}\int_{0}^{L}{\text{d}}z=\int_{{P}_{{\text{in}}}}^{{P}_{{\text{out}}}}\frac{\rho }{\eta }{\text{d}}P,$$

(2)

where P_in and P_out are the pressures at the inlet and outlet of the capillary, respectively, ρ is the molar density, $\dot{n}$ is the molar flow rate, and L is the length of the capillary. Approximation of the viscosity with the pressure independent zero-density viscosity and assuming isothermal flow and a linear pressure dependency of the density, the integral on the right-hand side of Eq. 2 can be approximated by

$$\int_{{P}_{{\text{in}}}}^{{P}_{{\text{out}}}}\frac{\rho }{\eta }{\text{d}}P=\frac{\frac{1}{2}({\rho }_{{\text{in}}}+{\rho }_{{\text{out}}})({P}_{{\text{out}}}-{P}_{{\text{in}}})}{{\eta }_{0}}.$$

(3)

Here, η₀ is the zero-density viscosity, and ρ_in and ρ_out are the temperature, pressure, and fluid dependent molar densities at the inlet and outlet of the capillary, respectively,

$${\rho }_{{\text{in}}}=\rho \left(T,{P}_{{\text{in}}},\overline{x }\right)\mathrm{ and} {\rho }_{{\text{out}}}=\rho \left(T,{P}_{{\text{out}}},\overline{x }\right),$$

(4)

where T is the temperature and $\overline {x}$ is the vector of the molar composition. Combining Eqs. 2 and 3, yields an expression for the ideal flow rate $\dot{n}_0$ of a compressible, non-ideal fluid

$${\dot{n}}_{0}=\frac{\pi {R}^{4}\cdot \Delta {P}_{{\text{in}},{\text{out}}}\cdot ({\rho }_{{\text{in}}}+{\rho }_{{\text{out}}})}{16L{\eta }_{0}},$$

(5)

as derived by van den Berg et al. [4], where ΔP_in,out = P_in – P_out. Equation 5 is applicable for a laminar flow of a Newtonian fluid through a straight capillary with constant cross section. In addition to the above made simplifications of isothermal flow and neglected pressure dependency of the viscosity, it is assumed: no slip flow occurs at the walls of the capillary, the flow profile is fully established at the inlet of the capillary, and the kinetic energy of the fluid before entering and after exiting the capillary does not contribute to the pressure gradient. Berg [5] introduced a flow model for the molar flow rate, comprising six correction terms to account for most of these simplifications:

$$\begin{aligned}\dot{n}={\dot{n}}_{0}\bigg[1+{g}_{{\text{virial}}}\left({P}_{{\text{in}}},{P}_{{\text{out}}}\right)+4{K}_{{\text{slip}}}Kn+\frac{{K}_{{\text{ent}}}}{16}\frac{R}{L}Re\\+\left(\frac{{K}_{{\text{exp}}}}{8}+\frac{{K}_{{\text{therm}}}}{16}\right)\frac{R}{L}Re {\text{ln}}\left(\frac{{P}_{{\text{out}}}}{{P}_{{\text{in}}}}\right)\bigg]{f}_{{\text{cent}}}\left(De\right),\end{aligned}$$

(6)

The term g_virial was initially introduced to account for non-ideal gas behavior and the pressure dependency of the viscosity. Berg [5] used an expression for the ideal flow rate $\dot{n}_0$, as derived by Kawata et al. [6] with the ideal gas equation of state. However, in this work, multiparameter Helmholtz equations of state are used to calculate the fluid density and, thus, non-ideal gas behavior is accounted for in Eq. 5. Hence, we adjusted the virial correction according to Berg [7], to correct for the departure from the zero-density viscosity according to Eq. 3

$${g}_{{\text{virial}}}=\frac{{b}_{\eta }}{{R}_{{\text{gas}}}T}\frac{\left({P}_{{\text{in}}}+{P}_{{\text{out}}}\right)}{\left({\rho }_{{\text{in}}}+{\rho }_{{\text{out}}}\right)}\left[-\overline{P }+\left({b}_{\eta }+2{B}_{P}-\frac{{c}_{\eta }}{{b}_{\eta }}\right)\frac{\left({P}_{{\text{in}}}^{2}+{P}_{{\text{out}}}^{2}\right)}{2}\right],$$

(7)

where R_gas is the universal gas constant, b_η and c_η are the second and third viscosity virial coefficients, B_P is the second virial coefficient of a pressure dependent expansion series of the compressibility factor, respectively, and $\overline {P}$ is obtained from

$$\overline{P }=\frac{2}{3}\frac{\left({P}_{{\text{in}}}^{3}-{P}_{{\text{out}}}^{3}\right)}{\left({P}_{{\text{in}}}^{2}-{P}_{{\text{out}}}^{2}\right)}.$$

(8)

A detailed derivation of the virial correction is given in section S1 in the supplementary material. The viscosity virial coefficients for hydrogen and helium were obtained from second-order polynomial fits to experimental viscosities as functions of pressure to data from Gracki et al. [8]. Viscosity virial coefficients for the (hydrogen + methane) mixture were obtained from this works data, and B_P was calculated with the respective equations of state [9,10,11]. The virial correction according to Eq. 7 applies at pressure ranges, where departures from the zero-density viscosity can be sufficiently accounted for by second-order virial expansions. At elevated pressures, the average viscosity between the inlet and outlet of the capillary should be used in Eq. 5 instead of η₀, given that the pressure difference ΔP_in,out is small. In that case the virial correction is not considered.

The remaining terms in the large bracket of Eq. 6 account for slip at the capillary wall, change of kinetic energy of the fluid when entering the capillary, change of kinetic energy, due to gas expansion along the capillary, and radial temperature gradients, resulting from viscous heating and cooling, caused by the Joule–Thomson effect, respectively. The factor f_cent corrects for centrifugal effects, due to the coiling of the capillary. In this work, f_cent was applied as given in the publication of Berg [7]

$${f}_{{\text{cent}}}={\left[1+16{\left(\frac{De}{{De}_{0}}\right)}^{4}\right]}^{-1/16},$$

(9)

which is based on investigations of van Dyke [12], but allows for a simpler calculation of the centrifugal correction. De₀ = 40.58385 is the reducing value and the Dean De number can be calculated according to

$$De = \sqrt {\frac{R}{{R_{{{\text{coil}}}} }}} Re,$$

(10)

where R_coil is the coil radius and Re is the Reynolds number. The Knudsen number Kn and Reynolds number Re were calculated according to Eqs. 11 and 12, respectively,

$$Kn = \frac{1}{R}\sqrt {\frac{{2R_{{{\text{gas}}}} T}}{M}} \frac{{\eta_{{{\text{in}}/{\text{out}}}} }}{{P_{{{\text{in}}/{\text{out}}}} }},$$

(11)

$$Re = \frac{{2M\dot{n}}}{\pi R\eta },$$

(12)

where M is the molar mass, and η_in/out is the viscosity at the average pressure P_in/out between the capillary’s inlet and outlet. For the calculation of Kn, viscosity correlations [13,14,15] as implemented in the thermophysical property database REFPROP v10.0 [16] were used. Berg [5] investigated the pressure dependence of flows of various fluids through a quartz capillary flow meter and found, that K_slip = 1 holds for most fluids, except for helium. This was confirmed by measurements of May et al. [17] on (among others) hydrogen, methane, and helium. Hence, K_slip = 1 for hydrogen and the (hydrogen + methane) mixture, and K_slip = 1.18 for helium were chosen according to May et al. [17]. The factors K_ent =  − 1.14, K_exp = 1, and K_therm (cf. Eq. 13), were adopted from Berg [5], based on the publications of Kawata et al. [6], and van den Berg et al. [4, 18], respectively.

$$K_{{{\text{therm}}}} = - \left[ {1 + \frac{1}{3}\left( {\frac{T}{\eta }\frac{\partial \eta }{{\partial T}}} \right)} \right]\frac{{R_{{{\text{gas}}}} \eta }}{M\kappa },$$

(13)

where κ is the thermal conductivity.

For the sake of simplicity and consistency with earlier publications [17, 19,20,21], the temperature and pressure dependent impedance Z_T(P) of the capillary is denoted by

$$Z_{T} \left( P \right) = \frac{16L}{{\pi R^{4} }},$$

(14)

and the correction terms of Eq. 6 are summarized in a temperature, pressure and fluid dependent correction factor C^fluid

$$ \begin{aligned} C^{\text{fluid}} \left( {T, P_{\text{in}} ,P_{\text{out}} } \right) = \;&\bigg[1+{g}_{\text{virial}}\left({P}_{\text{in}},{P}_{\text{out}}\right)+4{K}_{\text{slip}}Kn+\frac{{K}_{\text{ent}}}{16}\frac{R}{L}Re\\&+\left(\frac{{K}_{\text{exp}}}{8}+\frac{{K}_{\text{therm}}}{16}\right)\frac{R}{L}Re {\text{ln}}\left(\frac{{P}_{\text{out}}}{{P}_{\text{in}}}\right)\bigg]f_{{\text{cent}}} \left( {De} \right). \end{aligned}$$

(15)

For fluid flow at low pressures, combination of Eqs. 5, 6, 14, and 15 yields

$$\dot{n} = \frac{{\Delta P_{{{\text{in}},{\text{out}}}} \left( {\rho_{{{\text{in}}}} + \rho_{{{\text{out}}}} } \right)}}{{Z_{T} \left( P \right)\eta_{0} }}C^{{{\text{fluid}}}} \left( {T, P_{{{\text{in}}}} ,P_{{{\text{out}}}} } \right).$$

(16)

At elevated pressures, the average viscosity between the inlet and outlet of the capillary is used instead of the zero-density viscosity, and a correction factor C*^fluid is applied, in which the virial correction is not considered.

2.2 Apparatus Description

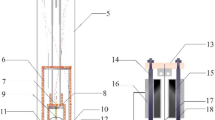
The two-capillary viscometer used in this work was comprehensively described in the work of Khosravi et al. [21]. Hence, only the main components are briefly described here. A simplified schematic of the two-capillary viscometer is shown in Fig. 1, which divides the setup into 11 subsections.

Fig. 1

Simplified schematic of the two-capillary viscometer [21]

All subsections can be separated from the rest of the system by pneumatic shut-off valves. E-01 is the gas supply cylinder. In case of the pure fluids hydrogen and helium, the cylinders were used as delivered by the gas supplier. In case of the (hydrogen + methane) mixture, a 10 L aluminum cylinder with inner surface treatment for long-term stability of mixture composition, as supplied by Scott Specialty Gases (Netherlands), was used. The high pressure delivery system, marked as E-02, consists of a syringe pump (model: PHMP 50-1000, Top Industrie, France) and a tubular buffer tank, with internal volumes of approximately 52 ml and 120 ml, respectively. The syringe pump pressurizes the system and was used to control the pressure at the inlet of the upstream capillary (P₁). The pressure inside the syringe pump (P₅) was monitored by a Keller pressure transmitter (series 33X, 0.1% precision, 100 MPa full scale). The buffer tank was introduced to enhance pressure stabilization, but also increases the fluid volume in the apparatus and, thus, extends the time for measurements. For simultaneous viscosity and density measurements, the setup incorporates a commercial vibrating tube densimeter (E-03) (DMA HPM, Anton Paar, Austria). However, since accurate equations of state for the investigated fluids are available in the literature, no density measurements were carried out in this work. Subsections E-04 and E-05 comprise the capillaries, thermostatted inner tanks and vacuum insulated (outer) tanks of the upstream and downstream part, respectively. The capillaries in the upstream part, also referred to as measurement capillaries, are operated at pressure and temperature of interest, whereas the capillaries in the downstream part, also referred to as reference capillaries, are maintained at reference conditions, except for the determination of ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ (cf. Eq. 19). In total four capillaries with different lengths and diameters are installed, two each in the upstream and downstream part, of which one upstream and one downstream capillary can be used simultaneously. With this, four different capillary configurations are possible, to enable measurements at optimal flow rates at different pressures and temperatures. For the measurements carried out in this work, only one configuration was used: the length and inner diameter of the upstream capillary are 11.671 m and 200 µm, respectively, and 8.563 m and 500 µm for the downstream capillary, respectively. The capillaries are made of fused silica with a polyimide coating and were supplied by Polymicro Technologies (USA). The capillaries were mounted on tubular stainless steel grids with a diameter of 0.49 m inside the inner tanks, which are continuously flushed with heat exchanging fluid. To achieve high temperature stability, the inner tanks are placed inside the vacuum tanks and are additionally insulated by several layers of aluminum coated plastic foil. Two flow thermostats (type: MA-12 and FP89-HL, Julabo, Germany) were used for thermostatting the heat exchanging fluid. In addition, heating elements were added to the supply pipes to achieve better temperature stability. To reduce the pressure from the upstream part to the reference pressure in the downstream part, a pressure reduction system (E-06) is installed between E-04 and E-05, which is shown in Fig. 2.

Fig. 2

Simplified schematic of the pressure reduction system (E-06) [21]

It consists of an actuated flow control valve (V-26) (type: SmallFlow-080000, Flowserve, Germany) and a cascade of five auxiliary capillaries, of which four are connected in series before V-26 and one in parallel. The flow control valve allows for precise control of the inlet pressure of the downstream capillaries (P₃). However, the performance particularly depends on the difference of the pressures before and after V-26. If the pressure difference is insufficiently low for precise flow control, the valve can be bypassed, utilizing the auxiliary capillary connected in parallel by opening a pneumatic shut-off valve (indicated as V-21 in Fig. 2). If the pressure difference is too high for precise flow control, the auxiliary capillaries connected in series before V-26 can be employed to reduce the pressure before V-26, by closing the pneumatic shut-off valves (indicated as V-22 to V-25 in Fig. 2), which are connected in parallel to the capillaries. However, at the time the measurements of this work were carried out, capillaries 22, 24, and 25, proved to be not pressure tight. Therefore, they were disconnected and the corresponding connections were blind plugged. Thus, mainly the flow control valve was used, to reduce the upstream pressure to the downstream pressure. Typically, at pressures beyond 10 MPa, this restriction led to high standard deviations in pressure difference, since the flow control valve was working close to its performance limitation. The pressure directly before V-26 was monitored with a pressure transmitter (indicated as P₇ in Fig. 2, series 3 PAA-35X HTC, Keller, Switzerland).

Subsection E-07 comprises the pressure sensor arrays, used for the pressure measurements at the inlet and outlet of the measurement capillaries. For each pressure tap, a sensor array of four pressure sensors was used, to cover the full pressure design range of the apparatus. In total six Paroscientific pressure transmitters with maximum pressure ranges of 2.1 MPa, 6.9 MPA, and 13.8 MPa, and two Keller pressure transmitters (series PAA-33X, Keller, Switzerland) with a maximum pressure range of 100 MPa were used for the upstream part, with identical sensors for the measurement of P₁ and P₂, respectively. Both sensor arrays can be connected directly by opening a pneumatic shut-off valve, bypassing the capillaries, to allow for the determination of the bias of the sensors in use. The sensors were housed in an aluminum box, which was constantly heated to approximately 313.15 K. A similar setup was used for the pressure measurement of the downstream part (E-08), which is placed in a separate aluminum box. Here, two pressure sensor arrays consisting each of two Paroscientific pressure transmitters with maximum pressure ranges of 0.21 MPa and 6.9 MPa, respectively, were used for the measurement of P₃ and P₄. Pressure calibration was carried out with a dynamometer (type: DH 26000, Desgranges et Huot, France), which could be fitted with three different piston cylinder units (type: 410, Desgranges et Huot, France) depending on the calibrated pressure range of up to 1 MPa, 5 MPa, and 20 MPa, respectively.

Subsection E-09 is only employed for flow calibration measurements and consists of a hollow sphere, made of aluminum with an internal volume of approximately 963 ml. The top end was threaded and fitted with a T-piece (1/16’’, Swagelok, USA), which enabled a pressure tight installation of a Pt-100 Ω resistance thermometer in the sphere and simultaneously allowed filling and emptying of the sphere with the fluid under investigation. The other connection of the T-piece was connected via a manually operated and a pneumatic shut-off valve to the pressure reduction system (E-06), directly before the flow control valve. For precise control of the pressure at the outlet of the downstream capillaries (P₄), a leak valve (series: 590, VAT Group AG, Switzerland) (V-35) was installed. The leak valve is combined with a vacuum pump (E-11), which is connected downstream of the valve, to maintain a pressure gradient between the capillaries’ outlet and exhaust and, thus, assures continuous flow.

2.3 Working Equation

For the measurements carried out in this work, we followed an approach as proposed by Berg et al. [20]

$$\eta_{P,T}^{{{\text{fluid}}}} = \left( {\eta_{0,298}^{{{\text{He}}}} } \right)_{ab\, initio} \left( {\frac{{\eta_{0,T}^{{{\text{He}}}} }}{{\eta_{0,298}^{{{\text{He}}}} }}} \right)_{ab\, initio} \left( {\frac{{\eta_{0,298}^{{{\text{fluid}}}} }}{{\eta_{0,298}^{{{\text{He}}}} }}} \right)\left( {\frac{{\eta_{P,T}^{{{\text{He}}}} }}{{\eta_{0,T}^{{{\text{He}}}} }}} \right)\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0} ,$$

(17)

where the superscripts “fluid” and “He” denote the property of the fluid under test and helium, and the subscripts indicate the property at the corresponding pressure and temperature, respectively. The factor $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$ is the ratio of viscosity ratios, which is explained below. This approach is based on the measurement of viscosity ratios, instead of absolute viscosity measurements and, thus, only approximate values for the capillaries’ geometries are needed for the correction terms. The first two factors in Eq. 17, $\left( {\eta_{{0,298}}^{{{\text{He}}}} } \right)_{{{ab\, initio}}}$ and $\left( {\eta_{{{0,T}}}^{{{\text{He}}}} /\eta_{{0,298}}^{{{\text{He}}}} } \right)_{{{ab\, initio}}}$, are reference values for the viscosity of helium in the limit of zero-density and at reference temperature T_ref = 298.15 K and the temperature dependent viscosity ratio of helium in the limit of zero-density, respectively. These values were obtained from highly accurate ab initio calculations of Cencek et al. [22], with relative uncertainties of less than 0.001% (k = 1) for both values. The zero-density viscosity ratio of the fluid under test and helium at T_ref = 298.15 K, $\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}$, can be determined from the flow calibration measurements (cf. Section 2.3), applying a known flow rate to the downstream capillary of the two-capillary viscometer. Applying Eq. 16 for the test fluid and helium, the viscosity ratio yields

$$\frac{{\eta_{0,298}^{{{\text{fluid}}}} }}{{\eta_{0,298}^{{{\text{He}}}} }} = \frac{{\Delta P_{34}^{{{\text{fluid}}}} \left( {\rho_{3} + \rho_{4} } \right)^{{{\text{fluid}}}} C^{{{\text{fluid}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)\dot{n}^{{{\text{He}}}} }}{{\Delta P_{34}^{{{\text{He}}}} \left( {\rho_{3} + \rho_{4} } \right)^{{{\text{He}}}} C^{{{\text{He}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)\dot{n}^{{{\text{fluid}}}} }}.$$

(18)

The subscripts “3” and “4” indicate the property at the inlet and outlet of the downstream capillary, respectively. Analogous to Eq. 4, the molar densities were evaluated at the capillary’s inlet and outlet pressure, P₃ and P₄, at reference temperature T_ref = 298.15 K and at constant composition. For the calculation of the molar densities of helium and hydrogen, the equations of state of Ortiz-Vega et al. [10] and Leachman et al. [9], respectively, were used, which are implemented in REFPROP v10.0 [16]. For the (hydrogen + methane) mixture, the equation of state for binary (hydrogen + methane) mixtures of Beckmüller et al. [11] was used, as implemented in the thermodynamic software tool TREND [23].

The pressure and temperature dependent viscosity ratio of helium $\eta_{{{P,T}}}^{{{\text{He}}}} /\eta_{{{0,T}}}^{{{\text{He}}}}$, was determined from the ratio of measurements at both, the upstream and the downstream capillary, while maintaining both capillaries at the same temperature T,

$$\frac{{\eta_{P,T}^{{{\text{He}}}} }}{{\eta_{0,T}^{{{\text{He}}}} }} = \frac{{Z_{{{\text{down}},T}} \left( 0 \right)}}{{Z_{{{\text{up}},T}} \left( P \right)}}\frac{{\Delta P_{12}^{{{\text{He}}}} \left( {\rho_{1} + \rho_{2} } \right)^{{{\text{He}}}} C^{{\text{*He}}} \left( {T, P_{1} ,P_{2} } \right)}}{{\Delta P_{34}^{{{\text{He}}}} \left( {\rho_{3} + \rho_{4} } \right)^{{{\text{He}}}} C^{{{\text{He}}}} \left( {T, P_{3} ,P_{4} } \right)}},$$

(19)

where the subscripts “1” and “2” indicate the property at the inlet and outlet of the upstream capillary, respectively. Z_down,T(0)/Z_up,T(P) is the ratio of the impedances of the downstream capillary at low pressure and the upstream capillary at target pressure. This impedance ratio can be expressed as

$$\frac{{Z_{{{\text{down}},T}} \left( 0 \right)}}{{Z_{{{\text{up}},T}} \left( P \right)}} = \frac{{Z_{{{\text{up}},T}} \left( 0 \right)}}{{Z_{{{\text{up}},T}} \left( P \right)}}\frac{{Z_{{{\text{down}},T}} \left( 0 \right)}}{{Z_{{{\text{up}},T}} \left( 0 \right)}},$$

(20)

where Z_up,T(0)/Z_up,T(P) accounts for the pressure induced dilation of the capillary’s inner radius, which was calculated from the pressure, the capillary’s dimensions, and material properties. Z_down,T(0)/Z_up,T(0) was determined from a second set of helium measurements, operating both capillaries at low pressure and identical temperature

$$\frac{{Z_{{{\text{down}},T}} \left( 0 \right)}}{{Z_{{{\text{up}},T}} \left( 0 \right)}} = \frac{{\Delta P_{{34,{\text{LP}}}}^{{{\text{He}}}} (\rho_{3} + \rho_{4} )_{{{\text{LP}}}}^{{{\text{He}}}} C^{{{\text{He}}}} \left( {T, P_{{3,{\text{LP}}}} ,P_{{4,{\text{LP}}}} } \right)}}{{\Delta P_{{12,{\text{LP}}}}^{{{\text{He}}}} (\rho_{1} + \rho_{2} )_{{{\text{LP}}}}^{{{\text{He}}}} C^{{{\text{He}}}} \left( {T, P_{{1,{\text{LP}}}} ,P_{{2,{\text{LP}}}} } \right)}},$$

(21)

where the subscript “LP” denotes the low-pressure measurements. The fifth factor in Eq. 17 is the ratio of viscosity ratios

$$\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0} = \frac{{\eta_{P,T}^{{{\text{fluid}}}} /\eta_{0,298}^{{{\text{fluid}}}} }}{{\eta_{P,T}^{{{\text{He}}}} /\eta_{0,298}^{{{\text{He}}}} }},$$

(22)

where the viscosity ratios in the numerator and denominator were obtained by operating the upstream capillary at target pressure P and temperature T, and the downstream capillary at reference conditions. $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$ was obtained from

$$\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0} = \frac{{\Delta P_{12}^{{{\text{fluid}}}} \left( {\rho_{1} + \rho_{2} } \right)^{{{\text{fluid}}}} C^{{\text{*fluid}}} \left( {T, P_{1} ,P_{2} } \right)}}{{\Delta P_{34}^{{{\text{fluid}}}} \left( {\rho_{3} + \rho_{4} } \right)^{{{\text{fluid}}}} C^{{{\text{fluid}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)}}\frac{{\Delta P_{34}^{{{\text{He}}}} \left( {\rho_{3} + \rho_{4} } \right)^{{{\text{He}}}} C^{{{\text{He}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)}}{{\Delta P_{12}^{{{\text{He}}}} \left( {\rho_{1} + \rho_{2} } \right)^{{{\text{He}}}} C^{{\text{*He}}} \left( {T, P_{1} ,P_{2} } \right)}}.$$

(23)

2.4 Experimental Procedure

Before measurements with a new fluid were started, the remaining fluid in the whole system was released down to ambient pressure and the apparatus was evacuated for 5 min to 10 min, including the pump and supply tubes, the capillaries in the upstream and downstream part, the pressure sensor arrays, and the pressure reduction system. Afterwards, the syringe pump, the upstream part, and the pressure reduction system were pressurized with the fluid under investigation to approximately 1 MPa. The flow control valve (V-26) and leak valve (V-35) were set to control the fluid flow to continuously flush the downstream part, while not exceeding a pressure of 0.15 MPa at the pressure taps of P₃ and P₄. This procedure was repeated at least two times. In case of the volume calibration and flow calibration measurements, additionally the sphere was evacuated for at least 15 min and subsequently pressurized to at least 1 MPa. This procedure was repeated three times, before the volume or flow calibration measurements were started.

Flow calibration measurements were carried out for each fluid investigated in this work, to determine the zero-density viscosity ratio of the test fluid and helium at reference temperature, $\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}$, and to provide a value for the flow rate, which is needed for the Reynolds number-dependent corrections (cf. Eq. 6). For this purpose, subsection E-09 was employed, to apply a continuous fluid flow from the sphere through the reference capillary, while simultaneously controlling the pressures at the inlet (P₃) and outlet (P₄) of the reference capillary within narrow limits. The sphere served as a fluid reservoir, to provide an appropriate amount of fluid for the measurements, and as a reference volume, for the determination of the flow rate. The flow calibration measurements were carried out at reference temperature T_ref = 298.15 K and at previously selected pressure differences along the reference capillary, whereby P₃ and P₄ were chosen so, that they averaged to approximately 0.1 MPa. Once temperature equilibrium in the downstream part was achieved, the measurement procedure was carried out as follows: (1) Filling of the sphere. (2) Determination of the bias between the pressure sensors at the inlet and outlet of reference capillary. (3) Flow calibration measurements under the condition of stationary flow. (4) Repetition of the bias measurements. The sphere was filled through the upstream part to approximately 3 MPa and the pressure was maintained constant, utilizing the syringe pump, while the sphere’s temperature equilibrated with the ambient temperature. In the meantime, bias measurements of the pressure sensors used for the downstream part were conducted. The bias was determined from the apparent pressure difference at identical pressure between the pressure sensors used for the pressure taps at the inlet and outlet. Therefore, the reference capillary was bypassed by opening the pneumatic shut-off valves, which separates the pressure sensor arrays from each other. To avoid additional contributions to the pressure difference, due to residual fluid flow, the reference capillary, including the pressure sensor arrays of the downstream part, were separated from the rest of the system. The bias measurements were conducted for 5 min to 10 min and the bias was assumed as the arithmetic mean of the two time-averaged bias measurements. With this, the impact of systematic errors in the pressure measurement on the uncertainty of the pressure difference was significantly reduced. Before the actual flow calibration measurements were started, stationarity of the flow in the reference capillary had to be achieved with the controlled operation of the flow control valve (V-26) and leak valve (V-35), which maintained P₃ and P₄ within narrow limits. Until stationarity in the downstream part was achieved, auxiliary fluid flow from the upstream part was sustained, to avoid unnecessary fluid losses in the sphere and, thus, extending the time of measurement. Once stationarity of the flow was established, the upstream part was separated from the downstream part, including the sphere and flow control valve. Thereby, fluid flow was achieved exclusively from the sphere. Temperature and pressure in the sphere, as well as temperature, pressures at the inlet and outlet of the reference capillary, and the pressure difference along the reference capillary were constantly recorded every second. Although P₃ and P₄ were continuously monitored and controlled within narrow limits, instationarities of the flow could not always be prevented. Hence, in the post-processing of the raw data, a suited time-frame was selected, where stationarity of the flow was achieved. For the selected time-frame, the measured properties at the reference capillary were time-averaged and the measured pressure difference was corrected for the bias

$$\Delta P_{{{\text{in}},{\text{ out}}}} = \left( {P_{{{\text{in}},{\text{M}}}} - P_{{{\text{out}},{\text{M}}}} } \right) - \left( {P_{{{\text{in}},{\text{B}}}} - P_{{{\text{out}},{\text{B}}}} } \right).$$

(24)

Here, the subscripts “M” and “B” indicate the measured pressure during the main measurements and bias measurements, respectively. In contrast to the work of Khosravi et al. [21], a modified setup of the sphere was used, to simplify the determination of the flow rate. As described in Sect. 2.2, the sphere was fitted with a Pt-100 Ω resistance thermometer to measure the temperature of the fluid inside the sphere. In addition, the pressure in the sphere could be measured with the pressure sensor (indicated as P₇ in Fig. 2), located between the sphere and the flow control valve. This setup allowed for a simple and fast determination of the amount of substance in the sphere, by calculating the fluid density with an equation of state at the measured temperature and pressure and at known composition

$$n = V\left( {T,P} \right)\, \cdot \,\rho \left( {T,P,\overline{x}} \right).$$

(25)

Here, n accounts for the amount of substance and V(T, P) for the internal volume of the sphere, at the corresponding temperature and pressure. The change of the internal volume with temperature and pressure was calculated from the sphere’s dimensions and material properties. The change of the volumes of the T-Piece, valve, tubing, and thermometer was considered to be negligible, due to the comparably large volume of the sphere. For the selected time-frame, the amount of substance in the sphere was calculated time resolved according to Eq. 25, and the molar flow rate was then obtained from the slope of a linear fit of the amount of substance as a function of time t

$$n\left( t \right) =- \dot{n}\, \cdot \,t + n\left( {t_{0} } \right).$$

(26)

Application of Eq. 25 required calibration of the internal volume of the sphere. Therefore, the mass difference of the sphere, once filled with nitrogen to approximately 3 MPa (purity class 5.0, Linde GmbH) and once at evacuated condition, was determined, utilizing a mass comparator (WAY 1.4Y.KO, RADWAG, Poland). The mass difference was obtained from comparative measurements to a reference sphere of similar mass and volume and, thus, the influence of buoyancy on the determination of the mass difference was diminished. The internal volume was then obtained via

$$V\left( {T,P} \right) = \frac{{\Delta m_{{{\text{Sphere}}}} }}{{\rho \left( {T,P} \right)M}},$$

(27)

where Δm_Sphere accounts for the mass difference of the nitrogen-filled and evacuated sphere, which equals the total mass of nitrogen in the sphere at filled condition. The density was calculated with the reference equation of state for nitrogen of Span et al. [24] at filling pressure and temperature.

The uncertainty of the pressure inside the sphere (P₇) contributes significantly to the uncertainty of the flow rate and internal volume of the sphere, and, thus, to the overall uncertainty of the viscosity measurements. The pressure was measured with a Keller pressure transmitter (series 35XHTC, Keller, Switzerland), with an uncertainty of 0.5% (full scale), as stated by the manufacturer. However, this uncertainty in pressure would result in unacceptable high uncertainties of the viscosity measurements. Therefore, the calibration of the pressure transmitter was regularly checked before, after, and in between the volume calibration and flow rate measurements, in the pressure range of P = (0.5 − 3.4) MPa, utilizing the dynamometer (type: DH 26000, Desgranges et Huot, France) fitted with a piston cylinder unit, capable of pressure calibration of up to 5 MPa. The calibration device (dynamometer and piston cylinder unit) was calibrated at IKM Laboratorium AS (Norway) and the uncertainty is stated as 0.001 bar + 0.01% RDG. Including the uncertainty due to calibration and drift of the sensor, the uncertainty in the measurement of P₇ was estimated to be 13.3 mbar (k = 1.73).

The measurements for the determination of the temperature and pressure dependent helium viscosity ratio ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ (cf. Eq. 19) and the ratio of viscosity ratios $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$ (cf. Eq. 23) were carried out at several pressures along isotherms, usually starting with the highest pressure of interest and then venting to the next lower pressure point. The isotherms were measured in the order of T = (298.15, 323.15, and 348.15) K, and T = 298.15 K again at selected pressures for repeatability check. Before the fluid was changed, measurements were conducted at all isotherms of interest. In contrast to the determination of $\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}$, measurements of ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ and $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$ are conducted employing the measurement and reference capillary simultaneously. Analogous to the flow calibration measurements, the bias between the pressure sensors used for the measurement and reference capillary was determined before and after the main measurements. Bias measurements for the measurement capillary were conducted at the same pressure as the main measurement, to account for a possible pressure dependency of the bias. $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$ was determined, operating the measurement capillary at the pressure and temperature of interest and the reference capillary at the previously calibrated inlet and outlet pressures, and at reference temperature T_ref = 298.15 K. Stationary flow had to be established in both capillaries. Therefore, the syringe pump was set to regulate the pressure at the inlet of the measurement capillary (P₁) at the pressure of interest, and V-26 and V-35 were set to regulate the pressures at the inlet (P₃) and outlet (P₄) of the reference capillary at the previously calibrated values. During the measurements, the pressures at the inlet and outlet of both capillaries (P₁, P₂, P₃, and P₄), as well as the pressure before V-26 (P₇) were continuously monitored to be stable within narrow limits and constant over time. If required and feasible, the auxiliary capillaries were employed to reduce the pressure before or bypass the flow control valve. Temperature and pressures were periodically recorded every second during the whole measurement procedure. In the post-processing of the raw data, a suited time-frame of at least 15 min was selected, where stationary flow was achieved, and the corresponding temperatures, pressures, and pressure differences along the capillaries were time-averaged. Subsequently, the measured pressure differences along the capillaries of the main measurements were corrected for the bias according to Eq. 24. The above described procedure was carried out for pure hydrogen and the (hydrogen + methane) mixture at T = (298.15, 323.15, and 348.15) K. The required experimental data for helium at T = (323.15 and 348.15) K for the determination of $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$, were adopted from measurements, carried out within the work of Khosravi et al. [25] and measurements at T = 298.15 K were repeated within this work.

Measurements of the temperature and pressure dependent helium viscosity ratio ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ were carried out, operating both capillaries at the same temperature. Additionally, measurements for the determination of the impedance ratio Z_down,T(0)/Z_up,T(0) (cf. Eq. 21) were conducted for each isotherm. Z_down,T(0)/Z_up,T(0) was obtained by operating both capillaries at low pressure. For the upstream capillary, operation at a minimum pressure of 1.4 MPa proved to be most feasible, to overcome the inherent impedance of the flow control valve and bypass capillary, and to achieve stationary flow for the targeted measurement duration of 15 min. Measurements of ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ were repeated in this work for T = (298.15 and 323.15) K. For the 348.15 K isotherm experimental data were used, which were measured within the work of Khosravi et al. [25]. The experimental data for ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ are given in Table S2 in section S2 in the supplementary material.

2.5 Experimental Material

The pure substances used for the measurements, mixture preparation, and volume calibration, are summarized in Table 1, including the mole fraction purity and impurities, as stated by the supplier. They were used as supplied, without further purification or gas analysis.

Table 1 Specification of materials and their suppliers

The (hydrogen + methane) mixture was prepared in a 10 L aluminum cylinder with special interior surface treatment (Scott Specialty Gases, Netherlands), supposed to ensure long-term stability of the mixture composition. Composition, molar mass, and uncertainty in composition of the (hydrogen + methane) mixture are given in Table 2.

Table 2 Composition (mole fraction of hydrogen ${x_{\text{H}_2}}$), molar mass M, and expanded combined uncertainty in composition U_c(${x_{\text{H}_2}}$) (k = 1.73), of the gravimetrically prepared (hydrogen + methane) mixture

The mixture preparation was carried out gravimetrically with comparative measurements of the mass difference between the sample cylinder and an identical reference cylinder, utilizing a mass comparator (type: XPR26003LC, Mettler-Toledo Inc., USA). To account for the drift of the comparator, an ABBA-type weighing scheme was applied, where A indicates the weighing of the reference, and B the weighing of the sample. Furthermore, errors arising from nonlinearities of the comparator’s characteristic curve were reduced, by equalizing the masses of the reference and sample with additional weights (OIML class F1). The mass differences were determined for the evacuated ($\Delta m_{{{\text{AB}},0}}^{*}$), hydrogen-filled ($\Delta m_{{{\text{AB}},1}}^{*}$), and (hydrogen + methane)-filled ($\Delta m_{{{\text{AB}},2}}^{*}$) sample cylinder, respectively. Hence, the filled masses of hydrogen (${m_{\text{H}_2}}$) and methane (${m_{\text{CH}_4}}$) were determined according to

$$m_{{{\text{H}}_{2} }} = \Delta m_{{{\text{AB}},1}}^{*} - \Delta m_{{{\text{AB}},0}}^{*} - V_{{{\text{Cylinder}},0}} \left[ {\rho_{{{\text{air}},0}} - \rho_{{{\text{air}},1}} \left( {1 + k_{p} \, \cdot \,P_{{{\text{Cylinder}},1}} } \right)} \right] + \left( {1 - \frac{{\rho_{{{\text{air}},1}} }}{{\rho_{{{\text{OIML}}}} }}} \right)\, \cdot \,\mathop \sum \limits_{j = 0}^{k} m_{{{\text{OIML}},j}} ,$$

(28)

and

$$m_{{{\text{CH}}_{4} }} = \Delta m_{{{\text{AB}},2}}^{*} - \Delta m_{{{\text{AB}},0}}^{*} - m_{{{\text{H}}_{2} }} - V_{{{\text{Cylinder}},0}} \left[ {\rho_{{{\text{air}},0}} - \rho_{{{\text{air}},2}} \left( {1 + k_{p} \, \cdot \,P_{{{\text{Cylinder}},2}} } \right)} \right] + \left( {1 - \frac{{\rho_{{{\text{air}},2}} }}{{\rho_{{{\text{OIML}}}} }}} \right)\mathop \sum \limits_{l = 0}^{m} m_{{{\text{OIML}},l}} ,$$

(29)

where the asterisks indicate the buoyancy affected mass differences, and the sums correspond to the total mass of OIML-weights used for mass equalization. The mass differences were determined from the average of 10 ABBA-weighing cycles, where the mass difference of one cycle was determined from the difference of the averaged weighings A and B, respectively. The terms proportional to the volume of the (empty) sample cylinder, V_Cylinder,0, correct for the buoyancy contribution arising from the pressure induced expansion of the cylinder. Before and after each weighing procedure, temperature, barometric pressure, and humidity were recorded and the density of the air ρ_air,i was calculated according to [26, 27]. The pressure inside the cylinder, P_Cylinder,i, was roughly estimated from the appropriate equations of state [9, 11], with temperature and fluid density as input parameters, whereby the density was determined from the filled masses and internal volume of the cylinder. The pressure expansion parameter k_p of the cylinder was obtained from a simple FEM-analysis. Before measurements for the determination of $\Delta m_{{{\text{AB}},0}}^{*}$ were conducted, the sample cylinder was evacuated to a pressure of approximately 2·10⁻² mbar. Filling and the subsequent weighing were conducted several hours apart, to assure thermal equilibrium between the sample cylinder and the environment. Before measurements on the mixture were carried out, the cylinder was rolled around its vertical axis for approximately two hours to homogenize the mixture.

3 Results

3.1 Uncertainty Analysis

The uncertainty of the experimental data presented in this work was estimated based on the Guide to the Expression of Uncertainty in Measurement (GUM) [28], according to which the expanded combined uncertainty U_c is estimated with

$$U_{{\text{c}}} \left( y \right) = k\, \cdot \,\sqrt {\mathop \sum \limits_{i = 1}^{N} \left( {\frac{\partial f}{{\partial x_{i} }}} \right)^{2} \, \cdot \,u^{2} \left( {x_{i} } \right) + 2\mathop \sum \limits_{i = 1}^{N - 1} \mathop \sum \limits_{j = i + 1}^{N} \frac{\partial f}{{\partial x_{i} }}\frac{\partial f}{{\partial x_{j} }}u\left( {x_{i} ,x_{j} } \right)} ,$$

(30)

where x_i and x_j are estimates of the input properties of the measurand y, which are related via a functional relationship f (for the sake of consistency with GUM [28], the former definition of x as the mole fraction is waved here). Furthermore, k is the coverage factor for a given confidence level and probability distribution, ∂f/∂x_i and ∂f/∂x_j are the partial derivatives of f with respect to x_i and x_j, respectively, u(x_i) is the standard uncertainty of x_i, and u(x_i, x_j) is the covariance associated with x_i and x_j, in case the input properties are correlated. If the input properties are uncorrelated the second term in the square root of Eq. 30 can be ignored. The uncertainties in viscosity reported in Tables 10 and 12 are given as expanded combined uncertainties U_c(η(T, P, $\overline {x}$)) (k = 2), including the standard uncertainties (k = 1) in viscosity measurement u(η), temperature u(T), pressure u(P). In case of the (hydrogen + methane) mixture the standard uncertainty in composition u($\overline {x}$) is also included. Provided that these input properties are not correlated, and applying Eq. 30, the expanded combined uncertainty in viscosity U_c(η(T, P, $\overline {x}$)) (k = 2) yields

$$U_{{\text{c}}} \left( {\eta \left( {T,P,\overline{x}} \right)} \right) = k\, \cdot \,\sqrt {u\left( \eta \right)^{2} + \left[ {\left( {\frac{\partial \eta }{{\partial T}}} \right)_{P,x} \, \cdot \,u\left( T \right)} \right]^{2} + \left[ {\left( {\frac{\partial \eta }{{\partial P}}} \right)_{T,x} \, \cdot \,u\left( P \right)} \right]^{2} + \left[ {\left( {\frac{\partial \eta }{{\partial x}}} \right)_{T,P} \, \cdot \,u\left( {\overline{x}} \right)} \right]^{2} } .$$

(31)

In Table 3, the uncertainty budget for the expanded combined uncertainty in viscosity for an exemplary measurement of the (hydrogen + methane) mixture at T = 298.15 K and P = 9.964 MPa is given. The weighted standard uncertainties in Tables 3, 4, 5, 6 and 7 were obtained from the expanded uncertainty of the respective uncertainty contribution divided by the coverage factor and multiplied with the sensitivity coefficient.

Table 3 Budget for the expanded combined uncertainty in viscosity U_c(η(T, P, $\overline {x}$)) (k = 2) at T = 298.15 K and P = 9.964 MPa for the (hydrogen + methane) mixture

Table 4 Budget for the expanded uncertainty in viscosity U(η) (k = 2) at T = 298.15 K and P = 9.964 MPa for the (hydrogen + methane) mixture

Table 5 Budget for the expanded uncertainty of the zero-density viscosity ratio U($\eta_{{0,298}}^{{{\text{mix}}}} /\eta_{{0,298}}^{{{\text{He}}}}$) (k = 2) for the (hydrogen + methane) mixture

Table 6 Budget for the expanded uncertainty of the helium viscosity ratio U($\eta_{{{P,T}}}^{{{\text{He}}}} /\eta_{{{0,T}}}^{{{\text{He}}}}$) (k = 2) at T = 298.15 K and P = 9.964 MPa

Table 7 Budget for the expanded uncertainty of the ratio of viscosity ratio $U\left(\left( {R_{T,298}^{{{\text{mix}},{\text{He}}}} } \right)_{P,0}\right)$ (k = 2) for the (hydrogen + methane) mixture at T = 298.15 K and P = 9.964 MPa

The main contribution to U_c(η) arises from u(η), which depends the uncertainties of the ab initio calculated reference data of helium, the measured viscosity ratios $\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}$ and ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$. , and ratio of viscosity ratios $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$, respectively (cf. Eq. 17). The impact of this contributions on the expanded uncertainty in viscosity U(η) = k⋅u(η) are broken down in Table 4.

As becomes apparent from Table 4, the uncertainties of the ab initio calculated parameters do not contribute significantly to U(η) and the main contributions arise from the measurements of $\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}$, ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$, and $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$. The individual uncertainty budgets for these inputs are listed in Tables 5, 6 and 7. The uncertainties $u\left(\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}\right)$, $u\left({\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}\right)$, and $\left(\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}\right)$ depend partly on the same input parameters (e.g., capillary dimensions, correction coefficients) and, thus, cannot be considered independent, which was accounted for in the determination of U(η). This was particularly the case for measurements at T = 298.15 K, where ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$, and $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$ were partly determined from the same set of helium measurements. The terms “Rest” in Tables 5, 6 and 7, summarize sources of uncertainty, contributing in sum less than 1 % to the overall variances ${u^{2}}\left(\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}\right)$, $u^{2}\left({\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}\right)$, and $u^{2}\left(\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}\right)$ and shall not be discussed in detail here. This includes uncertainty contributions such as from the capillaries’ dimensions, correction coefficients, and other parameters needed for the correction terms (cf. Eq. 15). Major contributions to $u\left(\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}\right)$, $u\left({\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}\right)$, and $u\left(\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}\right)$ result from the uncertainties in pressure differences. For the estimation of the uncertainty in pressure difference, we followed an approach according to [21]

$$u\left( {\Delta P_{{{\text{in}},{\text{out}}}} } \right) = \sqrt {u_{\text{r}}^{2} \left( {\Delta P_{{{\text{in}},{\text{out}}}} } \right) + \Delta P_{{{\text{in}},{\text{out}}}}^{2} \left( {\frac{{u_{P} }}{{P_{{{\text{max}}}} }}} \right)^{2} } ,$$

(32)

where u_r(ΔP_in,out) accounts for the uncertainty in pressure difference, arising from random errors during the measurements, for which the standard deviation was used as the best estimate. The second term in the square root accounts for the systematic uncertainty u_P, resulting from the calibration of the pressure sensors, which is assumed to scale with the full-scale pressure P_max of the sensor. For all measurements carried out in this work, u_r(ΔP_in,out) was the dominating uncertainty contribution to u(ΔP_in,out). This was particularly the case for measurements, which were conducted at pressures beyond 10 MPa in the upstream capillary. Due to performance limitations of the flow control valve at high pressure differences along the valve, these measurements were associated with high standard deviations of the downstream pressure difference ΔP₃₄. This affected the standard deviation of the upstream pressure difference ΔP₁₂ directly and, thus, these input quantities were considered to be correlated. Hence, the covariance u(ΔP₁₂, ΔP₃₄) was obtained from statistical analysis in accordance to GUM [28]

$$u\left( {\Delta P_{12} ,\Delta P_{34} } \right) = r\left( {\Delta P_{12} ,\Delta P_{34} } \right)\, \cdot \,u\left( {\Delta P_{12} } \right)\, \cdot \,u\left( {\Delta P_{34} } \right),$$

(33)

where r is the Pearson correlation coefficient. The values of r were always positive, and the derivatives of ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ and $\left( {R_{T,298}^{{{\text{fluid}},{\text{He}}}} } \right)_{P,0}$ with respect to ΔP₁₂ and ΔP₃₄, respectively, had opposite signs. Thus, consideration of u(ΔP₁₂, ΔP₃₄) resulted in slightly lower uncertainties. The weighted covariance in Tables 6, 7 was obtained from the covariance of the respective correlated input quantities multiplied with the product of their sensitivity coefficients.

3.2 Zero-Density Viscosity Ratio $\eta_{{0,298}}^{{{\text{fluid}}}} {/}\eta_{{0,298}}^{{{\text{He}}}}$

For the determination of the zero-density viscosity ratios of the fluids under test and helium, $\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}$, flow rate calibration measurements were conducted for helium, hydrogen, and the (hydrogen + methane) mixture at several different flow rates, as summarized in Table 8.

Table 8 Results of flow rate calibration measurements on helium, hydrogen, and the (hydrogen + methane) mixture

Applying Eq. 18 revealed a variation of the zero-density viscosity ratio for different flow rates. Therefore, the ratio Φ

$$\mathit{\Phi} = \frac{{\Delta P_{34} \left( {\rho_{3} + \rho_{4} } \right) C^{{{\text{fluid}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)/\dot{n}^{{{\text{fluid}}}} }}{{\mathop {\lim }\limits_{{{{Re}} \to 0}} \Delta P_{34} \left( {\rho_{3} + \rho_{4} } \right) C^{{{\text{fluid}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)/\dot{n}^{{{\text{fluid}}}} }}$$

(34)

of the individual flow rate measurements and their value extrapolated to Re = 0 were checked for their dependency on Re. Figure 3 shows Φ, obtained from the measurements on helium, hydrogen and the (hydrogen + methane) mixture, respectively, as a function of Re. As can be seen from Fig. 3, Φ appears to change systematically with Re. However, it is unclear, what effects caused this dependency.

Fig. 3

Values of Φ (cf. Eq. 34) as a function of the Reynolds number Re, obtained from flow calibration measurements on helium, hydrogen, and the (hydrogen + methane) mixture

The hydrodynamic model does not include corrections, accounting for the change of kinetic energy of the exit flow. However, according to Kestin et al. [29], the kinetic energy of the fluid at the outlet of the capillary is dissipated at constant pressure, and, thus, does not contribute to the pressure difference along the capillary. Another simplification, underlying the correction terms in Eq. 6, is the neglected dependency of the entrance correction coefficient K_ent on the Reynolds number. Kestin et al. [29] determined K_ent at different Reynolds numbers from numerical calculations and showed, that K_ent is proportional to Re⁻¹. For Reynolds numbers Re ≥ 100, their results were consistent with experimentally determined values for K_ent, according to Swindells et al. [30], Flynn et al. [31], and Kao et al. [32]; lower Re ranges were not covered by these publications.

The entrance correction coefficient can be experimentally determined from the slope of the property ΔP₃₄/$\dot{m}$ as a function of either $\dot{m}$ or Re, where $\dot{m}$ is the mass flow rate. However, an analogous determination of K_ent, based on the measurements carried out in this work, yielded results, which are one to two magnitudes larger, than the values reported in Kestin et al. [29] at corresponding Reynolds numbers. In addition, the slopes in Fig. 3 appear to be fluid dependent, which contradicts the definitions of the entrance correction, as well as of the expansion correction. Therefore, it is assumed, that the observed Re dependency cannot be attributed to an insufficient description of the entrance or expansion correction. Another correction term proportional to Re is the thermal correction, which is by definition of the thermal correction coefficient K_therm also fluid dependent (cf. Eq. 13). However, the thermal correction is almost one order of magnitude smaller than the entrance and expansion correction, respectively, and by a factor of approximately 1000 smaller than the slip correction, and, thus, considered to be almost negligible. Since the observed Reynolds number dependency could not be conclusively clarified, the zero-density viscosity ratios $\eta_{{0,298}}^{{{\text{H}}_{2} }} /\eta_{{0,298}}^{{{\text{He}}}}$ and $\eta_{{0,298}}^{{{\text{mix}}}} /\eta_{{0,298}}^{{{\text{He}}}}$ were determined according to Eq. 35 from the extrapolated values

$$\frac{{\eta_{0,298}^{{{\text{fluid}}}} }}{{\eta_{0,298}^{{{\text{He}}}} }} = \frac{{\mathop {\lim }\limits_{{{{Re}} \to 0}} \Delta P_{34}^{{{\text{fluid}}}} \left( {\rho_{3} + \rho_{4} } \right)^{{{\text{fluid}}}} C^{{{\text{fluid}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)/\dot{n}^{{{\text{fluid}}}} }}{{\mathop {\lim }\limits_{{{{Re}} \to 0}} \Delta P_{34}^{{{\text{He}}}} \left( {\rho_{3} + \rho_{4} } \right)^{{{\text{He}}}} C^{{{\text{He}}}} \left( {T_{{{\text{ref}}}} , P_{3} ,P_{4} } \right)/\dot{n}^{{{\text{He}}}} }}.$$

(35)

The resulting viscosity ratios are listed in Table 9, together with reference data for $\eta_{{0,298}}^{{{\text{H}}_{{2}} }} {/}\eta_{{0,298}}^{{{\text{He}}}}$ according to May et al. [17] and a value obtained from ab initio calculated viscosity data for hydrogen and helium, according to Mehl et al. [33] and Cencek et al. [22], respectively. The zero-density viscosity ratio of hydrogen and helium obtained from Eq. 35 agrees remarkably well with the reference values, with deviations of 0.00022 to both values, and, thus, within the experimental uncertainty of this work. Hence, the determination of $\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}$ according to Eq. 35 is assumed to be valid. Uncertainty contributions arising from the extrapolation were considered in the estimation of U$\left(\eta_{{0,298}}^{{{\text{fluid}}}} /\eta_{{0,298}}^{{{\text{He}}}}\right)$ (k = 2). In case of the zero-density viscosity ratio of hydrogen and helium, they contribute approximately 17% to the overall variance u²$\left(\eta_{{0,298}}^{{{\text{H}}_{2} }} /\eta_{{0,298}}^{{{\text{He}}}}\right)$, which is due to the comparably high scattering of the hydrogen data. In case of the (hydrogen + methane) mixture data, uncertainties resulting from the extrapolation, contribute approximately 0.66% to the overall variance u²$\left(\eta_{{0,298}}^{{{\text{mix}}}} /\eta_{{0,298}}^{{{\text{He}}}}\right)$. No data for the viscosity of (hydrogen + methane) mixtures were found in the literature at corresponding states. Hence, no comparison with reference mixture data can be made.

Table 9 Zero-density viscosity ratios for hydrogen $\left(\eta_{{0,298}}^{{{\text{H}}_{{2}} }} {/}\eta_{{0,298}}^{{{\text{He}}}}\right)$ and for the (hydrogen + methane) mixture $\left(\eta_{{0,298}}^{{{\text{mix}}}} {/}\eta_{{0,298}}^{{{\text{He}}}}\right)$ at T = 298.15 K and expanded uncertainties U$\left(\eta_{{0,298}}^{{{\text{fluid}}}} {/}\eta_{{0,298}}^{{{\text{He}}}}\right)$ (k = 2)

3.3 Measurements on Hydrogen

The viscosity of pure hydrogen was measured at 18 different state points along three isotherms of (298, 323, and 348) K and at pressures between (3 and 18) MPa. The experimental data for the ratio of ratios $\left( {R_{T,298}^{{{\text{H}}_{{2}} ,{\text{He}}}} } \right)_{P,0}$ and for the viscosity of hydrogen are listed in Table 10 together with their experimental uncertainties. Table 10 also includes viscosity data (${{\eta_{\text{exp}}^*}}$), which were evaluated applying the zero-density viscosity ratio $\eta_{{0,298}}^{{{\text{H}}_{{2}} }} {/}\eta_{{0,298}}^{{{\text{He}}}}$, measured by May et al. [17] (cf. Sect. 3.2), to Eq. 17. The corresponding viscosity data are (0.0043 to 0.0048) µPa·s lower, than the data, which were evaluated with the zero-density viscosity ratio measured within this work. These deviations correspond to a constant relative off-set of 0.048%. However, due to the considerably lower uncertainty of the zero-density viscosity ratio of May et al. [17], the expanded combined uncertainty of ${{\eta_{\text{exp}}^*}}$ (U_c(${{\eta_{\text{exp}}^*}}$) (k = 2)) of these data is partly lower than U_c(η_exp) (k = 2). The expanded combined uncertainty of η_exp yields between (0.058 and 0.27) µPa⋅s (k = 2), which corresponds to relative uncertainties between (0.65 and 2.7) % (k = 2). The expanded combined uncertainty of ${{\eta_{\text{exp}}^*}}$ is between (0.038 and 0.27) µPa·s (k = 2), which corresponds to relative uncertainties between (0.42 and 2.7) % (k = 2). U_c(${{\eta_{\text{exp}}^*}}$) is particularly lower for data measured at lower pressures, since the standard deviations of the pressure differences for the determination of ${\eta_{P,T}^{\rm{He}}} /{\eta_{0,T}^{\rm{He}}}$ and $\left( {R_{T,298}^{{{\text{H}}_{{2}} ,{\text{He}}}} } \right)_{P,0}$ were the dominating uncertainty contributions at pressures above 10 MPa. At lower pressures, the standard deviations in pressure differences were considerably lower and, thus, the contribution from the zero-density viscosity ratio was more significant. Reproducibility checks were conducted at 298.15 K and three different pressures; the corresponding data could be reproduced with relative deviations between (0.034 and 1.10)% and always within their respective experimental uncertainty. Higher deviations occurred at higher pressures, where the experimental uncertainty was higher anyways.

Table 10 Experimental (η, P, T) data for pure hydrogen, where T is the temperature, P is the pressure, ρ_calc is the molar density calculated with the equation of state for hydrogen of Leachman et al. [9], $\left( {R_{T,298}^{{{\text{H}}_{{2}} ,{\text{He}}}} } \right)_{P,0}$ is the experimental ratio of viscosity ratios for hydrogen and helium, η_exp and ${{\eta_{\text{exp}}^*}}$ are the experimental viscosities, evaluated with the zero-density measured in this work and by May et al. [17], respectively, U$\left(\left( {R_{T,298}^{{{\text{H}}_{{2}} ,{\text{He}}}} } \right)_{P,0}\right)$ is the expanded uncertainty (k = 2) of $\left( {R_{T,298}^{{{\text{H}}_{{2}} ,{\text{He}}}} } \right)_{P,0}$, and U_c(η_exp) and U_c(${{\eta_{\text{exp}}^*}}$) are the expanded combined uncertainties (k = 2) (including uncertainties in temperature^a and pressure^b) of η_exp and ${{\eta_{\text{exp}}^*}}$, respectively

In Fig. 4, relative deviations between our results and the viscosity correlation for hydrogen of Muzny et al. [14], as implemented in REFPROP v10.0 [16], are plotted versus molar density for each measured isotherm, together with selected experimental literature data, listed in Table 11. The molar density was calculated with the equation of state of Leachman et al. [9], as implemented in REFPROP v10.0 [16]. The deviations of the viscosity data of this work, which were evaluated with the zero-density viscosity ratio $\eta_{{0,298}}^{{{\text{H}}_{{2}} }} {/}\eta_{{0,298}}^{{{\text{He}}}}$ measured in this work, are shown in the left panels of Fig. 4, and data evaluated with the zero-density viscosity ratio of May et al. [17] are shown in the right panels. As becomes apparent from Fig. 4, reasonable agreement of our data with the viscosity correlation, as well as with experimental literature data, was achieved. Relative deviations to the viscosity correlation of the data set, evaluated with zero-density viscosity ratio measured in this work, are between (− 0.45 and 1.15)% and the averaged, absolute deviation yields 0.22%.

Fig. 4

Percentage deviations of experimental viscosity data η_exp for hydrogen from calculated values η_calc according to the viscosity correlation of Muzny et al. [14], as implemented in REFPROP v10.0 [16], at selected isotherms. Deviations are plotted vs. molar density, calculated with the equation of state of Leachman et al. [9]. The deviations in the right panel show data of this work marked with an asterix (This work*), which were evaluated with the zero-density viscosity ratio $\eta_{{0,298}}^{{{\text{H}}_{{2}} }} {/}\eta_{{0,298}}^{{{\text{He}}}}$ as given in May et al. [17]

Table 11 Selected experimental viscosity data of hydrogen

For the data set evaluated with the zero-density viscosity ratio of May et al. [17], relative deviations are between (− 0.50 and 1.10)%, and the averaged, absolute deviation yields 0.22%. Fairly good agreement with the viscosity correlation [14] and the most accurate literature data [8, 35, 37] was achieved particularly at lower pressures. In the limited pressure range of up to 10 MPa, average absolute deviations of η_exp and ${{\eta_{\text{exp}}^*}}$ to the viscosity correlation are 0.080% and 0.010%, respectively. The uncertainty of the viscosity correlation for temperatures between (200 and 400) K is stated as 0.1% at a pressure of 0.1 MPa, and 4% at pressures of up to 200 MPa [14], respectively. Hence, both data sets agree with the viscosity correlation within its claimed uncertainty as well as within their respective experimental uncertainties.

3.4 Measurements on the (Hydrogen + Methane) Mixture

The viscosity of the (hydrogen + methane) mixture was measured at 18 different state points along three isotherms of (298, 323, and 348) K and pressures between (3 and 15) MPa, listed in Table 12. The expanded combined uncertainty in viscosity was estimated to be (0.09 to 0.35) µPa·s (k = 2), which corresponds to relative expanded combined uncertainties between (0.91 and 3.2) %. The experimental results could be reproduced with relative deviations between (− 0.28 and 0.80) % and always within the respective experimental uncertainty.

Table 12 Experimental (η, P, T) data for the (hydrogen + methane) mixture (${{x_{\text{H}_2}}}$ = 0.896111), where T is the temperature, P is the pressure, ρ_calc is the molar density calculated with the equation of state for (hydrogen + methane) mixtures of Beckmüller et al. [11], $\left( {R_{T,298}^{{{\text{mix}},{\text{He}}}} } \right)_{P,0}$ is the experimental ratio of viscosity ratios for the mixture and helium, η_exp is the experimental viscosity, U$\left(\left( {R_{T,298}^{{{\text{mix}},{\text{He}}}} } \right)_{P,0}\right)$ is the expanded uncertainty (k = 2) of $\left( {R_{T,298}^{{{\text{mix}},{\text{He}}}} } \right)_{P,0}$, and U_c(η_exp) is the expanded combined uncertainty (k = 2) (including uncertainties in temperature^a, pressure^b, and composition^c) of η_exp

The available database for viscosity data for binary (hydrogen + methane) mixtures covers a broad state region at temperatures from 173 K to 523 K and pressures of up to 51 MPa and various compositions. It comprises 755 data points from nine publications, as summarized in Table 13. Additionally, one data set of Nabizadeh and Mayinger [39] was found in the literature, reporting viscosities for mixtures of hydrogen and synthetic natural gas, with methane as major component. Although the measurements of Adzumi [34], Chuang et al. [44], Trautz and Sorg [45], Kobayashi et al. [46], Iwasaki and Takahashi [47], and Golubev and Gnezdilov [48] indicate, that the viscosity of (hydrogen + methane) mixtures changes significantly with changing composition at high hydrogen concentrations, the database for mixtures with hydrogen contents above 80 mol % is limited to two data sets at ambient pressure [45, 46]. Hence, no comparative data for the measurements carried out in this work are available at overlapping state ranges.

Table 13 Available experimental viscosity data of (hydrogen + methane) mixtures

In Fig. 5, relative deviations between experimental data and calculated viscosities according to the Extended Corresponding States (ECS) model of Chichester and Huber [15], implemented in REFPROP v10.0 [16], are shown. The ECS model includes four adjustable, binary interaction parameters, which can be fitted to experimental data. According to the corresponding parameter file in REFPROP v10.0 [16], all four binary interaction parameters were fitted. However, it is not apparent, which data sets were used for the parametrization. Relative deviations between the experimental data of this work and the ECS model vary between (− 0.85 and − 3.51) % and the average, absolute deviation yields 2.6%. Thus, the experimental data of this work are mostly not reproduced within their experimental uncertainty. The relative deviations exhibit a positive trend with increasing density, which is less pronounced at lower densities. With increasing temperature, the deviations show a slightly negative trend. Figure 5 also includes experimental data of Trautz and Sorg [45] and Kobayashi et al. [46] for mixtures with hydrogen mole fractions of 0.9223 and 0.9, respectively. It should be noted here, that the data in the publication of Kobayashi et al. [46] are not tabulated explicitly, but reported graphically in ${{\eta,x_{\text{H}_2}}}$-diagrams. Therefore, the reliability of this data set might be affected by errors, introduced during the data conversion. Relative deviations to the ECS model yield − 3.23 % for the data point of Trautz and Sorg [45] and (− 2.75 to − 3.38) % for the data set of Kobayashi et al. [46]. Although none of the measurements of this work was carried out in regions overlapping with the literature data, the deviation plots in Fig. 5 indicate reasonable consistency with the data sets of Trautz and Sorg [45] and Kobayashi et al. [46].

Fig. 5

Percentage deviations of experimental viscosity data η_exp for binary (hydrogen + methane) mixtures from calculated values η_calc according to the ECS model of Chichester and Huber [15], as implemented in REFPROP v10.0 [16], at selected isotherms. Deviations are plotted vs. molar density, calculated with the equation of state of Beckmüller et al. [11], as implemented in TREND 5.0 [23]

4 Conclusion

In this work, measurements on pure hydrogen and a binary (hydrogen + methane) mixture with a nominal composition of 90 mol % hydrogen and 10 mol % methane were carried at temperatures of (298.15, 323.15 and 348.15) K and pressures of up to 18 MPa with a two-capillary viscometer. Relative expanded combined uncertainties in viscosity yield between (0.65 and 2.7) % (k = 2) for the hydrogen data and between (0.91 and 3.2) % for the (hydrogen + methane) mixture data. Re-evaluation of the experimental data of hydrogen with a highly accurate reference value for the zero-density viscosity ratio of hydrogen and helium [17] indicate, that the experimental uncertainty can be significantly reduced, provided that accurate zero-density viscosity data are available. The measurements on hydrogen were compared to the viscosity correlation of Muzny et al. [14] and to selected literature data. The average absolute deviation to the viscosity correlation is 0.22% and maximum deviations do not exceed 1.15%. Hence, good agreement with the viscosity correlation within the experimental uncertainty was achieved. The results for the (hydrogen + methane) mixture were compared to viscosities calculated with an ECS model [15], as implemented in REFPROP v10.0 [16]. Deviations between this model and of this work’s data are between (− 0.85 to − 3.51) % and, thus, are larger than the experimental uncertainty of the data. No experimental data at overlapping state regions are available for (hydrogen + methane) mixtures in the literature. Nonetheless, deviations to the ECS model of the measurements carried out in this work and of low-pressure literature data with similar composition appear to be consistent.