Anisotropic Elastic Strain-Gradient Continuum from the Macro-Scale to the Granular Micro-Scale

Abstract

A multi-scale framework is constructed for the computation of the stiffness tensors of an elastic strain-gradient continuum endowed with an anisotropic microstructure of arbitrarily-shaped particles. The influence of microstructural features on the macroscopic stiffness tensors is demonstrated by comparing the fourth-order, fifth-order and sixth-order stiffness tensors obtained from macro-scale symmetry considerations to the stiffness tensors deduced from homogenizing the elastic response of the granular microstructure. Special attention is paid to systematically relating the particle properties to the probability density function describing their directional distribution, which allows to explicitly connect the level of anisotropy of the particle assembly to local variations in particle stiffness and morphology. The applicability of the multi-scale framework is exemplified by computing the stiffness tensors for various anisotropic granular media composed of equal-sized spheres. The number of independent coefficients of the homogenized stiffness tensors appears to be determined by the number of independent microstructural parameters, which is equal to, or less than, the number of independent stiffness coefficients following from macro-scale symmetry considerations. Since the modelling framework has a general character, it can be applied to different higher-order granular continua and arbitrary types of material anisotropy.

1 Introduction

In a classical Boltzmann continuum the deformation is considered to be homogeneous, as described by the symmetric part of the first-order gradient of the displacement field, i.e., the macroscopic strain. In order to account for heterogeneous deformations characterized by strong time and/or spatial variations, such as those induced during high-frequency wave propagation or localized failure (i.e., shear bands, localized damage), or deformations characterizing size effects and surface tension phenomena, the kinematic description of the continuum needs to be enhanced by (gradients of) micro-deformation, and/or higher gradients of macroscopic deformation. Along this way, various types of elastic and inelastic enhanced continuum models – commonly referred to as higher-order continuum models – have been developed and applied, such as i) micro-polar models (or Cosserat models), whereby at constitutive level the kinematic description is enhanced by incorporating a micro-rotational degree of freedom and its first gradient [12, 15, 19, 21, 23, 25, 48, 55, 59–61], ii) strain-gradient models, in which at constitutive level the kinematic description is extended by including first/second-order gradients of macroscopic strain [1, 2, 4, 11, 13, 22, 26, 27, 37, 41, 44, 46, 49, 56, 58–60, 62, 63, 65] and also fourth-order gradients of macroscopic strain [3, 4, 37, 46, 58], and iii) general higher-gradient models, in which the constitutive expressions include both (gradients of) micro-deformation and higher gradients of macroscopic deformation [5, 9, 14, 40, 42, 47, 53, 58, 62, 63].

Although most of the higher-order continuum models presented in the literature refer to isotropic materials, see the references above, several studies on anisotropic higher-order models have been presented. In [45, 64], a third-order shear deformable plate theory is derived from the three-dimensional anisotropic elastic strain-gradient continuum theory. The model is applied for the analysis of centrosymmetric anisotropic plate structures, whereby various levels of anisotropy are considered and the influence of internal length scales on the deformation characteristics and buckling behaviour is assessed. It is further demonstrated that the model is able to adequately capture size effects. In [32], the three-dimensional Green tensor is derived for an anisotropic gradient elastic continuum model of the Helmholtz type, which is used to study the Kelvin problem. It is shown that the Green tensor provides a physically-based regularization of the classical anisotropic Green tensor. An anisotropic Cosserat continuum model for cancellous bone is elaborated in [28] from asymptotic homogenization of the microstructure. The effective elastic moduli of periodic bone cell structures are computed for different bone densities, and a study of cracked bone samples reveals the regularizing effect of the Cosserat continuum model in comparison to a classical continuum model. In [50], an orthotropic elastic second-gradient continuum model is developed that is representative of a pantographic structure composed of identical orthogonal fibers. The macro-scale constitutive parameters are derived in terms of geometrical and mechanical properties of the pantographic microstructure, and the model is validated by solving basic analytical boundary value problems that consider various loading modes, as well as a more sophisticated numerical boundary value problem that includes a boundary layer effect. In [6, 7], the anisotropy of a strain-gradient elastic continuum is explored at the macro-scale by performing a classification of all possible symmetry classes of the macroscopic stiffness tensors. The matrix representations of the fourth-order, fifth-order and sixth-order stiffness tensors are established in a compact and structured fashion, illustrating the versatility and complexity of the constitutive formulation.

In the present contribution, a multi-scale framework is constructed that connects the macro-scale stiffness tensors of an anisotropic elastic strain-gradient continuum to the characteristics of a granular microstructure of arbitrarily-shaped particles. At the macro-scale, the strain and micro-deformation gradient of the strain-gradient model are energetically-conjugated to, respectively, the Cauchy stress and double stress, in correspondence with a reduced form of the well-established higher-order continuum model developed by Mindlin [40]. Considering different levels of material anisotropy, the macro-scale stiffness tensors of the strain-gradient model are developed in single-matrix format from elastic symmetry considerations. In order to reveal the influence of microstructural features on the level of elastic anisotropy, the fourth-order, fifth-order and sixth-order macro-scale stiffness tensors are compared to the stiffness tensors deduced from homogenizing the elastic response of the granular microstructure. The applied homogenization method is the Granular Micromechanics Approach (GMA), which has been used by various investigators to derive the isotropic stiffness tensors for classical granular continua [10, 24, 33, 54, 66] and higher-order granular continua [11–15, 42, 53, 58, 62, 63]. The application of GMA homogenization for the derivation of the constitutive response of anisotropic granular media has been limited to classical continuum formulations [16, 17, 43, 51, 57]. In elaborating the GMA formulation for the anisotropic elastic strain-gradient continuum considered in this work, special attention is paid to systematically relating the particle properties to the probability density function describing their directional distribution, which allows to explicitly connect the level of anisotropy of the particle assembly to local variations in particle stiffness and morphology. With the constructed GMA framework, the coefficients are computed for the stiffness tensors of various anisotropic granular media composed of equal-sized spheres, whereby it is exemplified how, and up to which extent, the microstructural features reduce the number of independent elastic coefficients identified from symmetry considerations at the macro-scale. Since the modelling framework has a general character, it can be applied to different higher-order granular continua and arbitrary types of anisotropy.

The paper is organized as follows. In Sect. 2 the macro-scale formulation of the elastic strain-gradient model is reviewed. The constitutive relations are formulated, and the major and minor symmetries of the fourth-order, fifth-order and sixth-order elastic tensors are specified. In Sect. 3 the stiffness tensors of the strain-gradient model are elaborated for different types of anisotropy, by imposing the corresponding degree of elastic symmetry and identifying the nonzero stiffness components. In Sect. 4 the anisotropic strain-gradient continuum is endowed with a granular microstructure. The GMA-based homogenization framework is constructed, resulting in expressions for the elastic stiffness tensors in terms of the granular, microstructural properties. The particle properties are systematically related to the probability density function describing their directional distribution, after which the resulting modelling framework is used to compute the coefficients for the elastic stiffness tensors of various anisotropic granular media composed of equal-sized spheres. The structures of the stiffness tensors are compared to those derived from macro-scale symmetry considerations, in order to identify and assess differences in the numbers of independent elastic coefficients. Section 5 presents some concluding remarks.

2 Review of Elastic Strain-Gradient Model

The formulation of the elastic strain-gradient model considered in this study is a reduced form of the well-established higher-order continuum model developed by Mindlin [40]. In this section, the macroscopic constitutive relations of the strain-gradient model are reviewed, for which the major and minor symmetries of the elastic stiffness tensors are specified from the symmetries of the deformation measures and the energetically-conjugated stresses. The constitutive relations are subsequently converted into a basic matrix-vector format, which helps to clarify the analysis of various levels of anisotropy of granular materials, as presented further in this paper.

2.1 Governing Equations

Within a framework of small deformations, a material point in a classical Boltzmann continuum is characterized by a potential energy density $W$ (per unit volume) of the form

$$ W=\frac{1}{2}C_{ijkl}\epsilon ^{e}_{ij}\epsilon ^{e}_{kl} \, , $$

(1)

where $C_{ijkl}$ reflects the components of the fourth-order elasticity tensor $\mathbf{C}$, and $\epsilon _{ij}^{e}$ are the components of the infinitesimal, macroscopic elastic strain tensor $\boldsymbol{\epsilon}^{e}$. Here and in the following, Einstein’s summation convention is applied on repeated tensor indices, unless stated otherwise. In the landmark paper of Mindlin [40], the potential energy density, Eq. (1), is extended by including, in addition to the macroscopic strain $\boldsymbol{\epsilon}$ (whereby the superscript “$e$” denoting that the strain is “elastic” henceforth will be omitted for notational convenience), two deformation measures, namely the relative deformation $\boldsymbol{\gamma}$ and the micro-deformation gradient $\boldsymbol{\kappa}$. In component form, these three deformation measures are defined by [40]¹

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \epsilon _{ij} & = & \frac{1}{2} \left ( u_{i,j} + u_{j,i} \right ) \, , \\ \gamma _{ij} & = & u_{j,i} - \psi _{ij} \, , \\ \kappa _{kji} & = & \psi _{jk,i} \, , \end{array} $$

(2)

with $\psi _{ij}$ reflecting the components of the micro-deformation $\boldsymbol{\psi}$. In the present work, the microscopic and macroscopic deformations are assumed to be equal, $\psi _{ij}=u_{j,i}$, as a result of which the relative deformation $\boldsymbol{\gamma}$ given by Eq. (2)₂ vanishes, and the micro-deformation gradient $\boldsymbol{\kappa}$ in Eq. (2)₃ becomes

$$ \kappa _{kji} = u_{k,ji} \, . $$

(3)

With the deformation measures given by Eqs. (2)₁ and (3), the kinematic formulation of the higher-order continuum model only depends on first-order and second-order gradients of the macroscopic displacement $\boldsymbol{u}$. The potential energy density of this so-called strain-gradient model can be formulated as

$$ W=\frac{1}{2}C_{ijkl}\epsilon _{ij}\epsilon _{kl} +F_{ijklm}\kappa _{ijk} \epsilon _{lm} +\frac{1}{2}A_{ijklmn}\kappa _{ijk}\kappa _{lmn} \, , $$

(4)

where $F_{ijklm}$ and $A_{ijklmn}$ represent the components of the fifth-order and sixth-order elasticity tensors $\mathbf{F}$ and $\mathbf{A}$, respectively. The energetically-conjugated stress measures of the deformations $\boldsymbol{\epsilon}$ and $\boldsymbol{\kappa}$ respectively are the Cauchy stress $\boldsymbol{\tau}$ and double stress $\boldsymbol{\mu}$, as defined by [40]

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{1mm} \tau _{ij} & = & \displaystyle{ \frac{\partial W}{\partial \epsilon _{ij}} } \, , \\ \mu _{ijk} & = & \displaystyle{ \frac{\partial W}{\partial \kappa _{ijk}} } \, . \end{array} $$

(5)

Inserting Eq. (4) into Eq. (5) results into the following constitutive relationships:

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \tau _{ij} & = & C_{\underline{(ij)}\;\underline{(kl)}}\epsilon _{kl} + F_{k(lm)(ij)}\kappa _{klm} \, , \\ \mu _{ijk} & = & F_{i(jk)(lm)}\epsilon _{lm} + A_{\underline{i(jk)}\; \underline{l(mn)}}\kappa _{lmn} \, . \end{array} $$

(6)

Here, the notations ... and (..) used for the tensor indices respectively designate the major and minor symmetries of the tensors. The major symmetries result from the existence of a potential energy density function, while the minor symmetries originate from symmetries of the deformation measures Eqs. (2)₁ and (3), and the energetically-conjugated stress measures, Eq. (5)_1,2. Specifically, the minor symmetries are in accordance with the symmetry of the macroscopic strain, $\epsilon _{ij}=\epsilon _{ji}$, and, through Eq. (5)₁, with the symmetry of the associated Cauchy stress, $\tau _{ij}=\tau _{ji}$, and further with the symmetry of the higher-order deformation, $\kappa _{ijk}=\kappa _{ikj}$, and the associated double stress, $\mu _{ijk}=\mu _{ikj}$. Note that the latter symmetry follows from Eqs. (3) and (5)₂, considering the reversibility in the order of differentiation, $u_{i,jk}=u_{i,kj}$. Without these major and minor symmetries, the numbers of independent components of the elasticity tensors, $\mathbf{C}$, $\mathbf{F}$, and $\mathbf{A}$, are equal to 81, 243, and 729, respectively. The major and minor symmetries indicated in Eq. (6) reduce these numbers to 21, 108, and 171, respectively. Note that this reduction is independent of the reduction in components following from specific planes or axes of elastic symmetry. Correspondingly, a solid that possesses onefold symmetry that is equal to no symmetry at all – as representative of the most disordered material structure – is referred to as triclinic, and contains fully occupied $\mathbf{C}$, $\mathbf{F}$, and $\mathbf{A}$ elastic stiffness tensors with 21, 108, and 171 independent, nonzero components, respectively.

With Eqs. (4) and (6), the variation of the potential energy for a volume $V$ can be developed as

$$ \begin{aligned}[b] \int _{V} \delta W \text{d} V &= - \int _{V} \left ( \tau _{ij,j} - \mu _{ijk,jk} \right ) \delta u_{i} \, \text{d} V + \int _{S} \left ( \tau _{ij} - \mu _{ijk,k} \right ) n_{j} \, \delta u_{i}\, \text{d} S \\ &\quad {}+ \int _{S} \mu _{ijk} n_{j} \, \delta u_{i,k}\, \text{d} S \, , \end{aligned} $$

(7)

whereby the divergence theorem has been applied to obtain the resulting expression. Here, $\mathbf{n}$ designates the normal direction and $S$ represents the boundary of volume $V$. From the variational principle for Eq. (7), the volume integral in the right-hand side results in the following equilibrium equation:

$$ \tau _{ij,j} - \mu _{ijk,jk} = 0 \, , $$

(8)

where body forces are assumed to be absent. Equation (7) can also be found in [40], in which it follows from a reduction of the general model formulation through the application of the kinematic constraint, Eq. (3). As pointed out in [40], the term $\delta u_{i,k}$ appearing in the last integral in the right-hand side of Eq. (7) is not independent of $\delta u_{i}$ on the boundary $S$, since if $\delta u_{i}$ is known, so is the surface-gradient of $\delta u_{i}$. In other words, only the normal component $\delta u_{i,k} n_{k}$ can be varied independently. The strategy to correctly extract the independent boundary conditions in a variational principle based on Eq. (7) is given in [40].

2.2 Matrix Representation of the Constitutive Relation

As shown in [6, 7], Eq. (6) can be conveniently reformulated using matrix notation, whereby the stress and deformation measures are written in vector form and the stiffness tensors are expressed in matrix form, with their components related as:

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l@{\quad}l@{\quad}l@{\quad}l} \vspace{2mm} \tau _{\alpha }& = & C_{\alpha \beta}\epsilon _{\beta}+F_{\alpha \gamma}\kappa _{\gamma },& \qquad \alpha : \text{1 to 6}, & \quad \beta : \text{1 to 6}, & \quad \gamma : \text{1 to 18} \, , \\ \mu _{\alpha }& = & F_{\beta \alpha}\epsilon _{\beta}+A_{\alpha \gamma}\kappa _{\gamma}, & \qquad \alpha : \text{1 to 18}, & \quad \beta : \text{1 to 6}, & \quad \gamma : \text{1 to 18} \, . \end{array} $$

(9)

Here, $\boldsymbol{\tau}$ and $\boldsymbol{\epsilon}$ are $6\times 1$ vectors containing the components of the Cauchy stress and macroscopic strain, respectively, and $\boldsymbol{\mu}$ and $\boldsymbol{\kappa}$ are $18 \times 1$ vectors representing the components of the double stress and higher-order deformation components, respectively. Additionally, $\mathbf{C}$, $\mathbf{F}$, and $\mathbf{A}$ respectively are $6\times 6$, $6 \times 18$, and $18\times 18$ matrices containing the corresponding elasticity parameters. Note that the tensor indices $ij$, $kl$, and $klm$ in Eq. (6)₁ are respectively replaced by the matrix indices $\alpha$, $\beta$, and $\gamma$ in Eq. (9)₁. Further, the tensor indices $ijk$, $lm$, and $lmn$ in Eq. (6)₂ are converted to the matrix/vector indices $\alpha$, $\beta$, and $\gamma$ in Eq. (9)₂, respectively. Similar as in [6, 7], the two-to-one and three-to-one index relations that define this conversion can be orderly summarized in a table, see Tables 1 and 2. In accordance with these conversions and the symmetries indicated in Eq. (6), the equivalences between the specific tensor symbols and matrix/vector symbols are

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \tau _{\alpha }& \equiv & \tau _{ij} \, , \\ \vspace*{1mm} \mu _{\alpha }& \equiv & \mu _{ijk} \, , \\ \vspace*{1mm} \epsilon _{\beta }& \equiv & \: \textstyle\begin{cases} \epsilon _{lm} \:\:\:\:\quad \text{if}\ l=m \, , \\ 2\epsilon _{lm} \:\:\quad \text{if}\ l\ne m \, , \end{cases}\displaystyle \\ \vspace*{2mm} \kappa _{\gamma }& \equiv & \textstyle\begin{cases} \kappa _{lmn} \:\:\quad \text{if}\ m=n \, , \\ 2\kappa _{lmn} \quad \text{if}\ m\ne n \, , \end{cases}\displaystyle \\ \vspace*{2mm} C_{\alpha \beta} & \equiv & \displaystyle{ \frac{C_{ijkl}+C_{jikl}+C_{ijlk}+C_{jilk}}{4} } \, , \\ \vspace*{2mm} F_{\alpha \beta} & \equiv & \displaystyle{ \frac{F_{ijklm}+F_{ikjlm}+F_{ijkml}+F_{ikjml}}{4} } \, , \\ A_{\alpha \gamma} & \equiv & \displaystyle{ \frac{A_{ijklmn}+A_{ikjlmn}+A_{ijklnm}+A_{ikjlnm}}{4} } \, . \end{array} $$

(10)

Table 1 Two-to-one index relations for conversion from tensor to matrix notation

Table 2 Three-to-one index relations for conversion from tensor to matrix notation

3 Various Degrees of Elastic Symmetry

Most materials possess some form of elastic symmetry, which may originate from crystallographic symmetry, i.e., symmetries of single crystals as determined by the chemical constituents of the material, or textural symmetry, i.e., symmetries determined by the microstructural organization (or texture) of the material. Examples of materials with textural symmetry are geomaterials, plant and animal tissues, and almost all manufactured materials [20]. The increase in elastic symmetry results in a reduction of the number of independent elastic parameters required to uniquely characterize the elastic material behaviour. Different degrees of symmetry can be explored by subjecting the stiffness tensors of the strain-gradient model in the three-dimensional Euclidian space to an orthogonal transformation $\mathbf{Q}$, with $\mathbf{Q}^{-1}=\mathbf{Q}^{T}$, under which the components of the stiffness tensor should remain unchanged. For a given tensor $\mathbf{T}$ of arbitrary order, this mathematical operation can be formally expressed as

$$ {T}'_{op...qr}=Q_{io}Q_{jp}...Q_{kq}Q_{lr}T_{ij...kl} \, , $$

(11)

whereby ${T}'_{op...qr}$ and $T_{ij...kl}$ respectively represent the components of tensor $\mathbf{T}$ in the new (${\mathbf{x}'}$) and reference ($\mathbf{x}$) Cartesian coordinate systems. Note that these two coordinate systems are related as ${\mathbf{x}'}=\mathbf{Q} \mathbf{x}$. Accordingly, the orthogonal transformations of the fourth-order, fifth-order and sixth-order elasticity tensors $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ defining the constitutive expressions, Eq. (6), read

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{1mm} {C}'_{opqr} & = & Q_{io}Q_{jp}Q_{kq}Q_{lr} C_{ijkl} \, , \\ \vspace*{1mm} {F}'_{opqrs} & = & Q_{io}Q_{jp}Q_{kq}Q_{lr}Q_{ms}F_{ijklm} \, , \\ {A}'_{opqrst} & = & Q_{io}Q_{jp}Q_{kq}Q_{lr}Q_{ms}Q_{nt}A_{ijklmn} \, , \end{array} $$

(12)

where ${C}'_{opqr}$, ${F}'_{opqrs}$ and ${A}'_{opqrst}$ respectively are the components of fourth-order, fifth-order and sixth-order elasticity tensors in the new Cartesian coordinate system. In case of elastic symmetry, it is required that the components of the elastic tensors meet the following conditions

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{1mm} {C}'_{opqr} & = & {C}_{opqr} \, , \\ \vspace*{1mm} {F}'_{opqrs} & = & {F}_{opqrs} \, , \\ {A}'_{opqrst} & = & A_{opqrst} \, , \end{array} $$

(13)

whereby $\mathbf{Q}$ in Eq. (12) represents an orthogonal transformation in the materials’ symmetry group. In the subsections below, for the strain-gradient continuum model, Eq. (6), various degrees of elastic symmetry are elaborated, whereby the identified nonzero components and their mutual relations define the structures of the elastic stiffness tensors.

3.1 One Plane of Elastic Symmetry: Monoclinic

A solid characterized by one plane of elastic symmetry is referred to as a monoclinic material. In a Cartesian coordinate system $\mathbf{x} = (x_{1},x_{2},x_{3})$, elastic symmetry with respect to the $x_{3}$-plane is specified by a reflection in this plane, as defined by the orthogonal transformation:

$$ \mathbf{Q}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{bmatrix} \, . $$

(14)

Note that the reflection has the common characteristic that $\text{det} \, \mathbf{Q}=-1$. Combining Eq. (14) with Eqs. (12) and (13) results in the following conditions for the stiffness components:

$$ \begin{aligned} C_{ijkl}, \, F_{ijklm}, \, A_{ijklmn}=\; \textstyle\begin{cases} \text{nonzero} & \text{if tensor index 3 appears an even number of times,} \\ \text{zero} & \text{if tensor index 3 appears an odd number of times. } \end{cases}\displaystyle \end{aligned} $$

(15)

With the conversions presented in Tables 1 and 2, from Eq. (15) the stiffness matrices for $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ follow as

$$ \mathbf{C}= \begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & C_{16} \\ & C_{22} & C_{23} & 0 & 0 & C_{26} \\ & & C_{33} & 0 & 0 & C_{36} \\ & \text{symm.}& & C_{44} & C_{45} & 0 \\ & & & & C_{55} & 0 \\ & & & & & C_{66} \end{bmatrix} \, , $$

(16)

and

and

in which the denotation “symm.” refers to the symmetry of the matrix. Observe from Eqs. (16), (17) and (18) that the formulation of the monoclinic stiffness tensors $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ requires the definition of 13, 56 and 91 independent coefficients, respectively. The expression for the fourth-order elastic stiffness tensor $\mathbf{C}$ in Eq. (16) is in agreement with the formulation presented in reference works on continuum mechanics theory, e.g., [36]. Obviously, the above expressions for elastic symmetry in the $x_{3}$-direction are similar if the symmetry plane is taken in the $x_{1}$- or $x_{2}$-direction: this only leads to a shift of nonzero stiffness coefficients in the three stiffness matrices, as follows from replacing the tensor index ‘3’ in Eq. (15) by respectively ‘1’ or ‘2’.

3.2 Two Perpendicular Planes of Elastic Symmetry

In order to determine the specific forms of the stiffness tensors $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ for the case of two mutually perpendicular planes of elastic symmetry, the $x_{2}$- and $x_{3}$-planes are considered as symmetry planes. The determination of the stiffness tensors then follows from assuming an orthogonal transformation that represents symmetry in the $x_{3}$- direction, Eq. (14), followed by an orthogonal transformation defining symmetry in the $x_{2}$-direction:

$$ \mathbf{Q}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \, . $$

(19)

It is emphasized that the resulting stiffness tensors are independent of the order of application of these two transformations. Combining Eqs. (14) and (19) with Eqs. (12) and (13) leads to the following conditions for the stiffness components:

$$ \begin{aligned}[b] &C_{ijkl}, \, F_{ijklm}, \, A_{ijklmn} \\ &\quad =\; \textstyle\begin{cases} \text{nonzero} & \text{if tensor indices 2 } \textit{and}\text{ 3 appear an even number of times,} \\ \text{zero} & \text{if tensor index 2 }\textit{or}\text{ 3 appears an odd number of times.} \end{cases}\displaystyle \end{aligned} $$

(20)

Using the conversions listed in Tables 1 and 2, from Eq. (20) the stiffness matrices $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ can be derived as

$$ \mathbf{C}= \begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ & C_{22} & C_{23} & 0 & 0 & 0 \\ & & C_{33} & 0 & 0 & 0 \\ & \text{symm.}& & C_{44} & 0 & 0 \\ & & & & C_{55} & 0 \\ & & & & & C_{66} \end{bmatrix} \, , $$

(21)

and

and

The three expressions above show that the number of independent coefficients of the $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ stiffness tensors equals 9, 28 and 51, respectively, with Eq. (21) corresponding to the definition provided in standard reference works on continuum mechanics theory, e.g., [36]. Trivially, when considering elastic symmetry in the $x_{1}$- and $x_{2}$-directions, or in the $x_{1}$- and $x_{3}$-directions, the tensor indices ‘2’ and ‘3’ defining Eq. (20) are replaced by ‘1’ and ‘2’, and ‘1’ and ‘3’, respectively. For the stiffness tensors $\mathbf{C}$ and $\mathbf{A}$ of even rank, two perpendicular planes of elastic symmetry automatically impose an additional plane of elastic symmetry in the third perpendicular direction, as a result of which these stiffness tensors are orthotropic. Conversely, as will be demonstrated in the subsection below, for the stiffness tensor $\mathbf{F}$ of odd rank the expression obtained under two perpendicular planes of symmetry, Eq. (22), is different than under three perpendicular planes of symmetry.

3.3 Three Perpendicular Planes of Elastic Symmetry: Orthotropic

The stiffness tensors for an orthotropic solid with three perpendicular planes of elastic symmetry are obtained by subsequently applying the orthogonal transformations, Eqs. (14) and (19), that reflect symmetries with respect to the $x_{3}$- and $x_{2}$-planes, followed by applying the transformation representing symmetry with respect to the $x_{1}$-plane:

$$ \mathbf{Q}= \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \, . $$

(24)

The successive application of Eqs. (14), (19) and (24) to Eqs. (12) and (13) results in the following conditions for the stiffness components:

$$ \begin{aligned}[b] &C_{ijkl}, \, F_{ijklm}, \, A_{ijklmn} \\ &\quad =\; \textstyle\begin{cases} \text{nonzero} & \text{if tensor indices 1 }\textit{and}\text{ 2 }\textit{and}\text{ 3 appear an even number of times,} \\ \text{zero} & \text{if tensor index 1 }\textit{or}\text{ 2 }\textit{or}\text{ 3 appears an odd number of times.} \end{cases}\displaystyle \end{aligned} $$

(25)

With the conversions listed in Tables 1 and 2, from Eq. (25) it follows that the fourth-order tensor $\mathbf{C}$ and the sixth-order tensor $\mathbf{A}$ indeed have the same form as for the case of two orthogonal planes of elastic symmetry, see Eqs. (21) and (23). In fact, when for an even-rank tensor the indices referring to two different perpendicular directions appear an even number of times, the tensor index referring to the third perpendicular direction automatically also appears an even number of times, by which the condition in Eq. (25)₁ is satisfied. In contrast, the fifth-order tensor $\mathbf{F}$ reduces to the null tensor $\mathbf{F=0}$, and thus differs from Eq. (22) deduced for two orthogonal planes of symmetry. In fact, for any odd-rank stiffness tensor all coefficients are equal to zero for an orthotropic material characterized by three orthogonal planes of symmetry, since in that case all stiffness components contain an uneven number of tensor indices related to one (or all three) symmetry direction(s), $x_{1}$, $x_{2}$ or $x_{3}$, as also discussed in [31].

The consecutive application of the three plane reflections, Eqs. (14), (19) and (24) to Eqs. (12) and (13) thus leads to the orthotropic stiffness tensors; it is emphasized that this result is different from that obtained after applying a single point reflection through the origin of the $x_{1}$-$x_{2}$-$x_{3}$ frame of reference, as defined by

$$ \mathbf{Q}= \begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix} \, . $$

(26)

Specifically, stiffness tensors that remain unchanged after a point reflection are referred to as centrosymmetric tensors, whereas those that do not are referred to as non-centrosymmetric tensors. Since Eq. (26) essentially represents the negative of the second-order identity tensor $\mathbf{I}$, after substituting Eq. (26) into Eq. (12) it may be concluded that the even-rank tensors $\mathbf{C}$ and $\mathbf{A}$ are centrosymmetric, and the odd-rank tensor $\mathbf{F}$ is non-centrosymmetric, see also [6, 30]. Hence, for the class of (strain-gradient) models considered in the present work, non-centrosymmetry only plays a role when $\mathbf{F} \neq \mathbf{0}$, which, as shown in the sections above, is the case for no plane of elastic symmetry (triclinic materials), one plane of elastic symmetry (monoclinic materials), and two planes of elastic symmetry. Other examples of odd-rank, non-centrosymmetric stiffness tensors may be found in the constitutive formulations of micro-polar media [31] and chiral materials [30], where the relative deformation $\boldsymbol{\gamma}$ given by Eq. (2)₂ is accounted for in the model formulation [40]. In the case of granular materials, the relative deformation $\boldsymbol{\gamma}$ becomes non-zero when the effect of particle rotations is incorporated in the description of the particle interactions, see [14, 58]. However, as stated in Sect. 2.1, this class of materials falls beyond the scope of the present work.

It is further interesting to mention that the consecutive application of the three plane reflections Eqs. (14), (19) and (24) to Eqs. (12) and (13) leads to the same result as the consecutive application of two plane reflections, Eqs. (14) and (19) (or one of the other two possible combinations), followed by a point reflection, Eq. (26). As a consequence of this resemblance, it can be concluded that even-rank (centrosymmetric) stiffness tensors for a material with two perpendicular planes of elastic symmetry automatically impose a third mutually perpendicular plane of elastic symmetry, and thus are orthotropic, in accordance with the discussion in Sect. 3.2 above. Furthermore, the point reflection, Eq. (26), thus represents an orthogonal transformation that is in the symmetry group of the orthotropic material, which means that for this material the conditions given by Eq. (13) must hold under the application of Eq. (26). Accordingly, the odd-rank tensor $\mathbf{F}$ vanishes under the point reflection Eq. (26), $\mathbf{F}=\mathbf{0}$, which indeed is in agreement with the computational result $\mathbf{F}=\mathbf{0}$ presented below Eq. (25). Clearly, for materials with a higher elastic symmetry than the orthotropic material (i.e., transversely isotropic and isotropic materials), the point reflection is also included in the materials’ symmetry group, thus leading to $\mathbf{F}=\mathbf{0}$.

3.4 Three Perpendicular Planes of Elastic Symmetry and an Axis of Rotational Symmetry: Transversely Isotropic

A material that has three mutually orthogonal planes of elastic symmetry and additionally has an axis of rotational symmetry perpendicular to one of these planes is called transversely isotropic. For the computation of the stiffness tensors, without loss of generality the $x_{3}$-axis is considered as the axis of rotational symmetry. Figure 1 shows the new Cartesian coordinate system $\mathbf{x}'$ after applying an arbitrary rotation $\alpha$ about the $x_{3}$-axis of the reference Cartesian coordinate system $\mathbf{x}$. The transformation matrix defining an arbitrary rotation $\alpha$ about the $x_{3}$-axis is:

$$ \mathbf{Q}= \begin{bmatrix} \cos \alpha & \sin \alpha & 0 \\ -\sin \alpha & \cos \alpha & 0 \\ 0& 0& 1 \end{bmatrix} \, . $$

(27)

It can be confirmed that the rotation has the common characteristic that $\text{det} \, \mathbf{Q}=1$. Considering that the stiffness tensors $\mathbf{C}$ and $\mathbf{A}$ for a transversely isotropic material have the same format as for an orthotropic material (i.e., there are no additional zero components, see Eqs. (21) and (23)), and that the uneven, fifth-order tensor vanishes, $\mathbf{F}=\mathbf{0}$, combining Eq. (27) with Eqs. (12) and (13) results in the following symmetry relations for $\mathbf{C}$:

$$ \textstyle\begin{array}{l} \vspace*{1mm} C_{11} = C_{22} \, , \\ \vspace*{1mm} C_{13} = C_{23} \, , \\ C_{44} = C_{55} \, , \\ C_{66} = \displaystyle{ \frac{1}{2} \left ( C_{11} - C_{12} \right )} \, , \end{array} $$

(28)

and for $\mathbf{A}$:

$$ \begin{aligned} &A_{0101}=A_{0808}, \quad A_{0102}=A_{0708}, \quad A_{0103}=A_{0809}, \quad A_{0112}=A_{0608}, \\ &A_{0117}=A_{0816}, \quad A_{0202}=A_{0707}, \quad A_{0203}=A_{0709}, \quad A_{0212}=A_{0607}, \\ &A_{0217}=A_{0716}, \quad A_{0303}=A_{0909}, \quad A_{0312}=A_{0609}, \quad A_{0317}=A_{0916}, \\ &A_{0404}=A_{1111}, \quad A_{0418}=A_{1118}, \quad A_{0505}=A_{1010}, \quad A_{0513}=A_{1014}, \\ &A_{0514}=A_{1013}, \quad A_{0515}=A_{1015}, \quad A_{0606}=A_{1212}, \quad A_{0616}=A_{1217}, \\ &A_{1313}=A_{1414}, \quad A_{1315}=A_{1415}, \quad A_{1616}=A_{1717} , \\ &A_{0212}=\frac{1}{2}(A_{0101}-A_{0202}-2A_{0112}), \\ &A_{0312}=\frac{1}{2}(A_{0103}-A_{0203}), \\ &A_{0418}=\frac{1}{2}(A_{0513}-A_{0514}), \\ &A_{0510}=A_{0505}- A_{0404}-A_{0411}, \\ &A_{0606}=\frac{1}{4}(A_{0101}+A_{0202})-\frac{1}{2} A_{0102} , \\ &A_{0616}=\frac{1}{2}(A_{0117}-A_{0217}), \\ &A_{1818}=\frac{1}{2}(A_{1313}-A_{1314}) \, . \end{aligned} $$

(29)

Using these relationships, the stiffness matrices $\mathbf{C}$ and $\mathbf{A}$ can be respectively represented as

$$ \mathbf{C}= \begin{bmatrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ & C_{11} & C_{13} & 0 & 0 & 0 \\ & & C_{33} & 0 & 0 & 0 \\ & \text{symm.}& & C_{44} & 0 & 0 \\ & & & & C_{44} & 0 \\ & & & & & \frac{1}{2} \left ( C_{11} - C_{12} \right ) \end{bmatrix} \, , $$

(30)

and

$$ \mathbf{A}= \begin{bmatrix} \mathbf{A}_{1} & \mathbf{A}_{2} \end{bmatrix} \, , $$

(31)

with the $18\times 9$ submatrices $\mathbf{A}_{1}$ and $\mathbf{A}_{2}$ as

$$ \mathbf{A}_{1} = \begin{bmatrix} A_{0101} &A_{0102} &A_{0103} &0 &0 &0 &0 &0 &0 \\ &A_{0202} &A_{0203} &0 &0 &0 &0 &0 &0 \\ & &A_{0303} &0 &0 &0 &0 &0 &0 \\ & & &A_{0404} &0 &0 &0 &0 &0 \\ & & & &A_{0505} &0 &0 &0 &0 \\ & & & & &\frac{1}{4}(A_{0101}+A_{0202})-\frac{1}{2} A_{0102} & \frac{1}{2}(A_{0101}-A_{0202}-2A_{0112}) &A_{0608} &\frac{1}{2}(A_{0103}-A_{0203}) \\ & & & & & &A_{0202} &A_{0102} &A_{0203} \\ & & & & & & &A_{0101} &A_{0103} \\ & & & & & & & &A_{0303} \\ & & & & & & & & \\ & & & & & & & & \\ & & & \text{symm.} & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \end{bmatrix} \,, $$

(32)

and

$$ \mathbf{A}_{2} = \begin{bmatrix} &0 &0 &A_{0112} &0 &0 &0 &0 &A_{0117} &0 \\ &0 &0 &\frac{1}{2}(A_{0101}-A_{0202}-2A_{0112}) &0 &0 &0 &0 &A_{0217} &0 \\ &0 &0 &\frac{1}{2}(A_{0103}-A_{0203}) &0 &0 &0 &0 &A_{0317} &0 \\ &0 &A_{0411} &0 &0 &0 &0 &0 &0 &\frac{1}{2}(A_{0513}-A_{0514}) \\ &A_{0505}- A_{0404}-A_{0411} &0 &0 &A_{0513} &A_{0514} &A_{0515} &0 &0 &0 \\ &0 &0 &0 &0 &0 &0 &\frac{1}{2}(A_{0117}-A_{0217}) &0 &0 \\ &0 &0 &0 &0 &0 &0 &A_{0217} &0 &0 \\ &0 &0 &0 &0 &0 &0 &A_{0117} &0 &0 \\ &0 &0 &0 &0 &0 &0 &A_{0317} &0 &0 \\ &A_{0505} &0 &0 &A_{0514} &A_{0513} &A_{0515} &0 &0 &0 \\ & &A_{0404} &0 &0 &0 &0 &0 &0 &\frac{1}{2}(A_{0513}-A_{0514}) \\ & & &\frac{1}{4}(A_{0101}+A_{0202})-\frac{1}{2} A_{0102} &0 &0 &0 &0 & \frac{1}{2}(A_{0117}-A_{0217}) &0 \\ & & & &A_{1313} &A_{1314} &A_{1315} &0 &0 &0 \\ & & & & &A_{1313} &A_{1315} &0 &0 &0 \\ & & & & & &A_{1515} &0 &0 &0 \\ & & \text{symm.} & & & & &A_{1616} &0 &0 \\ & & & & & & & &A_{1616} &0 \\ & & & & & & & & &\frac{1}{2}(A_{1313}-A_{1314}) \end{bmatrix} \,, $$

(33)

whereby it is emphasized that the denotation “symm.” refers to the symmetry of the complete $18\times 18$ square matrix $\mathbf{A}$, Eq. (31).

Fig. 1

New Cartesian coordinate system $\mathbf{x}'$ after a rotation $\alpha$ about the $x_{3}$-axis of the reference Cartesian coordinate system $\mathbf{x}$

As a result of the 4 symmetry relations for $\mathbf{C}$ and the 30 symmetry relations for $\mathbf{A}$ as given by Eqs. (28) and (29), the corresponding numbers of 9 and 51 independent coefficients for an orthotropic elastic material in Eqs. (21) and (23) reduce to 5 and 21 independent coefficients for a transversely isotropic material, see Eqs. (30), (32) and (33). Note that the classical stiffness matrix given by Eq. (30) is in correspondence with the common form presented in continuum mechanics textbooks, see, e.g., [36].

3.5 Arbitrary Planes of Elastic Symmetry and Axes of Rotational Symmetry: Isotropic

The elastic stiffness tensors of an isotropic material are symmetric with respect to any plane of symmetry and any rotational axis. In other words, this symmetry group contains the full set of orthogonal transformations (i.e., rotations and reflections), as a result of which the elastic tensors are invariant in both right-handed and left-handed orthogonal coordinate systems.² As demonstrated in [56], the components of isotropic tensors of arbitrary order can be systematically derived from Weyl’s theory on formal orthogonal invariant polynomial functions [67], leading for $\mathbf{C}$ and $\mathbf{A}$ to:

$$ C_{ijkl} = c_{1} \delta _{ij} \delta _{kl} + c_{2} \delta _{ik} \delta _{jl} + c_{3} \delta _{il}\delta _{jk} \, , $$

(34)

and

$$ \begin{aligned}[b] A_{ijklmn}& = a_{1}\delta _{ij}\delta _{kl}\delta _{mn} \, + \, a_{2} \delta _{ij}\delta _{km}\delta _{ln} \, + \, a_{3}\delta _{ij}\delta _{kn} \delta _{lm} \\ &{} + a_{4}\delta _{ik}\delta _{jl}\delta _{mn} \, + \, a_{5}\delta _{ik} \delta _{jm}\delta _{ln} \, + \, a_{6}\delta _{ik}\delta _{jn}\delta _{lm} \\ &{} + a_{7}\delta _{il}\delta _{jk}\delta _{mn} \, + \, a_{8}\delta _{il} \delta _{jm}\delta _{kn} \, + \, a_{9}\delta _{il}\delta _{jn}\delta _{km} \\ &{} + a_{10}\delta _{im}\delta _{jk}\delta _{ln} \, + \, a_{11} \delta _{im}\delta _{jl}\delta _{kn} \, + \, a_{12}\delta _{im} \delta _{jn}\delta _{kl} \\ &{} + a_{13}\delta _{in}\delta _{jk}\delta _{lm} \, + \, a_{14} \delta _{in}\delta _{jl}\delta _{km} \, + \, a_{15}\delta _{in} \delta _{jm}\delta _{kl} \, . \end{aligned} $$

(35)

Imposing the minor symmetries discussed in Sect. 2.1 on Eq. (34) leads to an equality for the coefficients $c_{2}$ and $c_{3}$ of the fourth-order elastic tensor $\mathbf{C}$:

$$ c_{2} = c_{3} . $$

(36)

Further, imposing both major and minor symmetries on Eq. (35) results in the following equalities between coefficients of the sixth-order elastic tensor $\mathbf{A}$:

$$ \textstyle\begin{array}{l} a_{1}=a_{4}=a_{10}=a_{13} \, , \\ a_{2}=a_{3}=a_{5}=a_{6} \, , \\ a_{8}=a_{9} \, , \\ a_{11}=a_{12}=a_{14}=a_{15} \, . \end{array} $$

(37)

With Eqs. (36) and (37) the fourth-order elastic tensor $\mathbf{C}$, Eq. (34), and the sixth-order elastic tensor $\mathbf{A}$, Eq. (35), are defined by 2 and 5 independent components, respectively, in accordance with:

$$ C_{ijkl} = c_{1} \delta _{ij} \delta _{kl} + c_{2} \left ( \delta _{ik} \delta _{jl} + \delta _{il} \delta _{jk} \right ) \, , $$

(38)

and

$$ \begin{aligned}[b] A_{ijklmn}& = a_{1}(\delta _{ij}\delta _{kl}\delta _{mn}+\delta _{ik} \delta _{jl}\delta _{mn}+\delta _{im}\delta _{jk}\delta _{ln}+\delta _{in} \delta _{jk}\delta _{lm}) \\ &{} + a_{2}(\delta _{ij}\delta _{km}\delta _{ln}+\delta _{ij}\delta _{kn} \delta _{lm}+\delta _{ik}\delta _{jm}\delta _{ln}+\delta _{ik}\delta _{jn} \delta _{lm}) \\ &{} + a_{7}(\delta _{il}\delta _{jk}\delta _{mn}) \\ &{} + a_{8}(\delta _{il}\delta _{jm}\delta _{kn}+\delta _{il}\delta _{jn} \delta _{km}) \\ &{} + a_{11}(\delta _{im}\delta _{jl}\delta _{kn}+\delta _{im}\delta _{jn} \delta _{kl}+\delta _{in}\delta _{jl}\delta _{km}+\delta _{in}\delta _{jm} \delta _{kl}) \, . \end{aligned} $$

(39)

Correspondingly, using Tables 1 and 2, the above tensorial forms of the stiffness tensors for an isotropic material can be represented in matrix form as

$$ \mathbf{C}= \begin{bmatrix} c_{1}+2c_{2} & c_{1} & c_{1} & 0 & 0 & 0 \\ & c_{1}+2c_{2} & c_{1} & 0 & 0 & 0 \\ & & c_{1}+2c_{2} & 0 & 0 & 0 \\ & \text{symm.}& & c_{2} & 0 & 0 \\ & & & & c_{2} & 0 \\ & & & & & c_{2} \end{bmatrix} \, , $$

(40)

and

$$ \mathbf{A}= \begin{bmatrix} \mathbf{A}_{1} & \mathbf{A}_{2} \end{bmatrix} \, , $$

(41)

with the $18\times 9$ submatrices $\mathbf{A}_{1}$ and $\mathbf{A}_{2}$ given by

$$ \mathbf{A}_{1} = \begin{bmatrix} 4a_{1} + 4a_{2} + a_{7} + 2a_{8} + 4a_{11} &2a_{1}+a_{7} &2a_{1}+a_{7} &0 &0 &0 &0 &0 &0 \\ &a_{7}+2a_{8} &a_{7} &0 &0 &0 &0 &0 &0 \\ & &a_{7}+2a_{8} &0 &0 &0 &0 &0 &0 \\ & & &a_{8} &0 &0 &0 &0 &0 \\ & & & &a_{2}+a_{8}+a_{11} &0 &0 &0 &0 \\ & & & & &a_{2}+a_{8}+a_{11} &a_{1}+2a_{11} &a_{1}+2a_{2} &a_{1} \\ & & & & & &a_{7}+2a_{8} &2a_{1}+a_{7} &a_{7} \\ & & & & & & &4a_{1} + 4a_{2} + a_{7} + 2a_{8} + 4a_{11} &2a_{1}+a_{7} \\ & & & & & & & &a_{7}+2a_{8} \\ & & & & & & & & \\ & & & & & & & & \\ & & & \text{symm.} & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \\ & & & & & & & & \end{bmatrix} \,, $$

(42)

and

$$ \mathbf{A}_{2} = \begin{bmatrix} 0 &0 &a_{1}+2a_{2} &0 &0 &0 &0 &a_{1}+2a_{2} &0 \\ 0 &0 &a_{1}+2a_{11} &0 &0 &0 &0 &a_{1} &0 \\ 0 &0 &a_{1} &0 &0 &0 &0 &a_{1}+2a_{11} &0 \\ 0 &a_{11} &0 &0 &0 &0 &0 &0 &a_{11} \\ a_{2} &0 &0 &a_{1}+2a_{11} &a_{1} &a_{1}+2a_{2} &0 &0 &0 \\ 0 &0 &0 &0 &0 &0 &a_{2} &0 &0 \\ 0 &0 &0 &0 &0 &0 &a_{1} &0 &0 \\ 0 &0 &0 &0 &0 &0 &a_{1}+2a_{2}&0 &0 \\ 0 &0 &0 &0 &0 &0 &a_{1}+2a_{11} &0 &0 \\ a_{2}+a_{8}+a_{11} &0 &0 &a_{1} &a_{1}+2a_{11} &a_{1}+2a_{2} &0 &0 &0 \\ &a_{8} &0 &0 &0 &0 &0 &0 &a_{11} \\ & &a_{2}+a_{8}+a_{11} &0 &0 &0 &0 &a_{2} &0 \\ & & &a_{7}+2a_{8} &a_{7} &2a_{1}+a_{7} &0 &0 &0 \\ & & & &a_{7}+2a_{8} &2a_{1}+a_{7} &0 &0 &0 \\ & & & & &4a_{1} + 4a_{2} + a_{7} + 2a_{8} + 4a_{11} &0 &0 &0 \\ & & \text{symm.} & & & &a_{2}+a_{8}+a_{11} &0 &0 \\ & & & & & & &a_{2}+a_{8}+a_{11} &0 \\ & & & & & & & & a_{8} \end{bmatrix} \,. $$

(43)

Note that the coefficients $c_{1}$ and $c_{2}$ defining the classic elastic stiffness matrix in Eq. (40) respectively are equal to the Lamé constants $\lambda$ and $\mu$. For the different degrees of elastic symmetry considered in this section, Table 3 summarizes the number of independent coefficients $N_{i}$ required for fully characterizing the elastic behaviour of the strain-gradient continuum model. The values of $N_{i}$ listed for the fourth-order elastic tensor $\mathbf{C}$ and sixth-order elastic tensor $\mathbf{A}$ are in agreement with those presented in [20] and [6], respectively. The values listed for the fifth-order elastic tensor $\mathbf{F}$ are also reported in [7], however, within the definitions of an alternative, more detailed classification scheme for crystal systems.

Table 3 Overview of the number of independent elastic coefficients $N_{i}$ for the fourth- fifth- and sixth-order elasticity tensors $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ of the strain-gradient continuum model for various degrees of elastic symmetry

4 Anisotropic Strain-Gradient Continuum with a Granular Microstructure

In this section the anisotropic strain-gradient continuum is endowed with a granular microstructure. The GMA-based homogenization framework is presented, which connects the micro-scale particle properties to the mechanical characteristics at the macro-scale. The particle properties are systematically related to the probability density function describing their directional distribution, after which the resulting modelling framework is used to deduce the stiffness tensors for various anisotropic granular media composed of equal-sized spheres. The structures of the corresponding elastic tensors are compared to those derived in Sect. 3 from macro-scale symmetry considerations, in order to identify and assess differences in the numbers of independent elastic coefficients.

4.1 GMA-Based Homogenization Framework

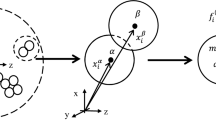
Consider two neighbouring grains $p$ and $q$ in a representative granular microstructure that characterizes the macroscopic response of the strain-gradient continuum, Eq. (6). Denoting the displacement field in a Cartesian coordinate system as $\boldsymbol{u} = (u_{1}, u_{2}, u_{3})$, a displacement component $u_{i}^{q}$ at grain q, with $i \in \{1,2,3 \}$, may be expressed as a Taylor expansion of the displacement field evaluated at the neigbouring grain $p$:

$$ u_{i}^{q}=u_{i}^{p}+u_{i,j}^{p}\big(x_{j}^{q}-x_{j}^{p}\big) + \frac{1}{2}u_{i,jk}^{p}\big(x_{j}^{q}-x_{j}^{p}\big)\big(x_{k}^{q}-x_{k}^{p} \big) + \mathcal{O} \! \left ( \left ( \sqrt{\sum _{i=1}^{3} \left (x_{i}^{q}-x_{i}^{p} \right )^{2} } \right )^{\! \! \! 3} \right ) \, , $$

(44)

in which the vectors $\boldsymbol{x}^{p}$ and $\boldsymbol{x}^{q}$ designate the centroidal positions of the neigbouring grains $p$ and $q$, respectively, and the Landau symbol $\mathcal{O}(.)$ denotes the order of magnitude of the corresponding term. In accordance with the definition of the kinematic variables in Eqs. (2) and (3), in Eq. (44) the terms of the order three and higher are neglected. The next step is to use Eq. (44) for defining the potential energy at the particle contact level. The antisymmetric part of the displacement gradient reflects the rigid body rotation of the material point, which does not contribute to the potential energy density. Hence, the term $u_{i,j}^{p}$ in the right-hand side of Eq. (44) may be replaced by the symmetric part of the displacement gradient, which equals the strain $\epsilon _{ij}^{p}$, see Eq. (2)₁. Further, in accordance with Eq. (3), the term $u_{i,jk}^{p}$ is replaced by the micro-deformation gradient $\kappa _{ijk}^{p}$, by which the relative displacement $\delta _{i}^{\alpha}$ at the contact $\alpha$ between the two neighbouring particles $p$ and $q$ follows from Eq. (44) as

$$ \delta _{i}^{\alpha}=\delta _{i}^{pq} = u_{i}^{q}-u_{i}^{p} \approx \epsilon _{ij}^{p} \big(x_{j}^{q}-x_{j}^{p}\big)+\frac{1}{2}\kappa _{ijk}^{p} \big(x_{j}^{q}-x_{j}^{p}\big)\big(x_{k}^{q}-x_{k}^{p}\big)=\epsilon _{ij}^{p}l_{j}^{ \alpha}+ \frac{1}{2} \kappa _{ijk}^{p} l_{j}^{\alpha }l_{k}^{\alpha } \, , $$

(45)

where in the final expression $l_{j}^{\alpha}=x_{j}^{q}-x_{j}^{p}$ is the branch vector that connects the centres of the two neighbouring particles. In accordance with the so-called kinematic hypothesis, the strain $\epsilon _{ij}^{p}$ and micro-deformation gradient $\kappa _{ijk}^{p}$ defined at the particle level are replaced by their mean values $\epsilon _{ij}$ and $\kappa _{ijk}$ over the volume $V$ of the particle assembly. This approximation of the micro-scale kinematic field induces a constraint that will cause the homogenized material response to be somewhat stiffer than the true macroscopic response [8, 12, 33], i.e., it leads to an overestimation of the true macroscopic response. The kinematic hypothesis has been regularly applied in homogenization procedures for granular media, both for the derivation of classical continua [10, 24, 66] and higher-order continua [11, 14, 15, 47, 58, 62]. Applying the kinematic hypothesis to Eq. (45) leads to

$$ \delta _{i}^{\alpha}= \delta _{i}^{\alpha s}+\delta _{i}^{\alpha m} = \epsilon _{ij}l_{j}^{\alpha}+ \frac{1}{2} \kappa _{ijk}l_{j}^{\alpha }l_{k}^{ \alpha }\, , $$

(46)

whereby the displacement $\delta _{i}^{\alpha s}$ is related to the strain $\epsilon _{ij}$ and the displacement $\delta _{i}^{\alpha m}$ is related to the micro-deformation gradient $\kappa _{ijk}$, as designated by the superscripts s and m, respectively. With Eq. (46), the potential energy stored at each grain contact can be formulated as

$$ W^{\alpha}= \frac{1}{2}K_{ik}^{\alpha} \delta _{i}^{\alpha s} \delta _{k}^{ \alpha s} +K_{ik}^{\alpha}\delta _{i}^{\alpha s} \delta _{k}^{\alpha m} +\frac{1}{2}K_{il}^{\alpha}\delta _{i}^{\alpha m} \delta _{l}^{ \alpha m} \, . $$

(47)

in which $K_{ij}^{\alpha}$ is the particle contact stiffness, which will be specified further in this section. With Eq. (47), the potential energy density in a macroscopic material point can be expressed as the volume average of the potential energies at all grain contacts, i.e.,

$$ W=\frac{1}{V}\sum _{\alpha =1}^{N_{c}}W^{\alpha}= \frac{1}{2V}\sum _{ \alpha =1}^{N_{c}}\left (K_{ik}^{\alpha}\delta _{i}^{\alpha s} \delta _{k}^{\alpha s} + 2 K_{ik}^{\alpha }\delta _{i}^{\alpha s} \delta _{k}^{\alpha m} + K_{il}^{\alpha}\delta _{i}^{\alpha m} \delta _{l}^{\alpha m}\right ) \, , $$

(48)

where $N_{c}$ and $V$ respectively are the total number of inter-particle contacts and the volume characterizing the granular microstructure represented in the macroscopic material point. In correspondence with the so-called Hill-Mandel micro-heterogeneity condition [29], the volume average of the variational (or virtual) work applied at the boundaries of the representative micro-scale particle volume needs to be equal to the local variational work per unit volume at the macro-scale, see also [34, 35, 38, 39, 52]. For a conservative, elastic material (which does not dissipate energy into heat), the variational work per unit volume directly follows from the variation of the potential energy density $\delta W$, which, by using Eq. (4), may be formally expressed as

$$ \delta W = \frac{\partial W}{\partial \epsilon _{ij}} \delta \epsilon _{ij} + \frac{\partial W}{\partial \kappa _{ijk}} \delta \kappa _{ijk} \, . $$

(49)

For a macroscopic material point, Eq. (49) can be further developed by inserting Eqs. (5) and (6). In addition, the volume average of the variation of the potential energy in the representative granular microstructure is obtained by inserting Eq. (46) into Eq. (48), followed by substituting the resulting expression into Eq. (49). With these two expressions for $\delta W$, the Hill-Mandel micro-heterogeneity condition becomes

$$ \begin{aligned}[b] \delta W &\quad = \quad C_{ijkl} \epsilon _{kl} \delta \epsilon _{ij} + F_{klmij} \kappa _{klm} \delta \epsilon _{ij} + F_{ijklm} \epsilon _{lm} \delta \kappa _{ijk} + A_{ijklmn} \kappa _{lmn} \delta \kappa _{ijk} \\ &\quad =\quad \displaystyle{ \frac{1}{V}\sum _{\alpha =1}^{N_{c}} \left ( K_{ik}^{\alpha} l_{j}^{\alpha }l_{l}^{\alpha} \epsilon _{kl} \delta \epsilon _{ij} + \frac{1}{2} K_{ik}^{\alpha} l_{j}^{ \alpha} l_{l}^{\alpha} l_{m}^{\alpha} \kappa _{klm} \delta \epsilon _{ij} + \frac{1}{2} K_{li}^{\alpha} l_{j}^{\alpha} l_{k}^{\alpha} l_{m}^{ \alpha} \epsilon _{lm} \delta \kappa _{ijk} \right . } \\ & \quad \qquad \qquad {}+ \quad \displaystyle{ \left . \frac{1}{4} K_{il}^{\alpha} l_{j}^{ \alpha }l_{k}^{\alpha }l_{m}^{\alpha }l_{n}^{\alpha }\kappa _{lmn} \delta \kappa _{ijk} \right ) } \, . \end{aligned} $$

(50)

Equation (50) holds for arbitrary deformations $\epsilon _{ij}$ and $\kappa _{ijk}$ and arbitrary deformation variations $\delta \epsilon _{ij}$ and $\delta \kappa _{ijk}$, and leads to the following expressions for the macroscopic stiffness tensors in terms of the particle contact stiffness $K^{\alpha}_{ij}$ and branch vector $l^{\alpha}_{j}$ at particle contact $\alpha$:

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} C_{ijkl} & = & \displaystyle{ \frac{1}{V}\sum _{\alpha =1}^{N_{c}} K_{ik}^{ \alpha}l_{j}^{\alpha }l_{l}^{\alpha }\, , } \\ F_{ijklm} & = & \displaystyle{ \frac{1}{2V}\sum _{\alpha =1}^{N_{c}}K_{il}^{ \alpha}l_{j}^{\alpha }l_{k}^{\alpha }l_{m}^{\alpha }\, , } \\ A_{ijklmn} & = & \displaystyle{ \frac{1}{4V}\sum _{\alpha =1}^{N_{c}}K_{il}^{ \alpha}l_{j}^{\alpha }l_{k}^{\alpha }l_{m}^{\alpha }l_{n}^{\alpha }\, . } \end{array} $$

(51)

Here, the elastic contact stiffness tensor $K_{ij}^{\alpha}$ has the usual expression

$$ K_{ij}^{\alpha} = k_{\text{n}}^{\alpha} n_{i}^{\alpha} n_{j}^{\alpha} + k_{\text{s}}^{\alpha} s_{i}^{\alpha }s_{j}^{\alpha }+ k_{\text{t}}^{ \alpha} t_{i}^{\alpha }t_{j}^{\alpha }\, , $$

(52)

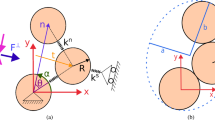
where $k_{\text{n}}^{\alpha}$ is the contact stiffness in the direction normal to the contact plane, and $k_{\text{s}}^{\alpha}$ and $k_{\text{t}}^{\alpha}$ are the contact stiffnesses in two perpendicular directions tangential to the contact plane. Note from Eq. (52) that the contact stiffness is symmetric, $K_{ij}^{\alpha}=K_{ji}^{\alpha}$. Further, $\mathbf{n}^{\alpha}$ represents the orthonormal base vector normal to the contact plane, and $\mathbf{s}^{\alpha}$ and $\mathbf{t}^{\alpha}$ are the orthonormal base vectors tangential to the contact plane. In accordance with the schematization in Fig. 2, the orthonormal base vectors ($\mathbf{n}^{ \alpha}$, $\mathbf{s}^{\alpha}$, $\mathbf{t}^{\alpha}$) defining the local particle contact plane are related to the orthonormal base vectors ($\mathbf{e}_{1}$, $\mathbf{e}_{2}$, $\mathbf{e}_{3}$) of the global Cartesian coordinate system $\mathbf{x} = (x_{1}, x_{2}, x_{3})$ via

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \mathbf{n}^{\alpha} & = & \text{sin} \, \theta ^{\alpha} \, \text{cos} \, \phi ^{\alpha} \, \mathbf{e}_{1} + \text{sin} \, \theta ^{\alpha} \, \text{sin} \, \phi ^{\alpha} \, \mathbf{e}_{2} + \text{cos} \, \theta ^{\alpha} \, \mathbf{e}_{3} \, , \\ \mathbf{s}^{\alpha} & = & \text{cos} \, \theta ^{\alpha} \, \text{cos} \, \phi ^{\alpha} \, \mathbf{e}_{1} + \text{cos} \, \theta ^{\alpha} \, \text{sin} \, \phi ^{\alpha} \, \mathbf{e}_{2} \, - \text{sin} \, \theta ^{\alpha} \, \mathbf{e}_{3} \, , \\ \mathbf{t}^{\alpha }& = & \mathbf{n}^{\alpha} \times \mathbf{s}^{ \alpha} = - \text{sin} \, \phi ^{\alpha} \, \mathbf{e}_{1} + \text{cos} \, \phi ^{\alpha} \, \mathbf{e}_{2} \, , \end{array} $$

(53)

in which the coordinates $\theta \in [0,\pi ]$ and $\phi \in [0, 2 \pi ]$ of the spherical coordinate system $(\rho , \theta , \phi )$ are the polar angle and the azimuthal angle, respectively, and $\rho$ is the radial coordinate. With the elastic contact stiffness, Eq. (52), the contact displacement, Eq. (46), can be related to the contact force $f_{i}^{\alpha}$ as

$$ f_{i}^{\alpha }= K_{ij}^{\alpha }\, \delta _{j}^{\alpha }\, , $$

(54)

which, after inserting Eq. (46), turns into

$$ f_{i}^{\alpha }= K_{ik}^{\alpha }l_{l}^{\alpha }\epsilon _{kl} + \frac{1}{2} K_{ik}^{\alpha }l_{l}^{\alpha }l_{m}^{\alpha }\kappa _{klm} \, . $$

(55)

Substituting the expressions for the stiffness tensors, Eq. (51), into the macroscopic constitutive relations, Eq. (6), and comparing the result with Eq. (55), it follows that the Cauchy stress $\tau _{ij}$ and double stress $\mu _{ijk}$ can be expressed in terms of the contact force $f_{i}^{\alpha}$ and branch vector $l_{j}^{\alpha}$ as

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \tau _{ij} & = & \displaystyle{ \frac{1}{V} \sum _{\alpha =1}^{N_{c}} f_{i}^{ \alpha }l_{j}^{\alpha }} \, , \\ \mu _{ijk} & = & \displaystyle{ \frac{1}{2V} \sum _{\alpha =1}^{N_{c}} f_{i}^{\alpha }l_{j}^{\alpha }l_{k}^{\alpha }} \, , \end{array} $$

(56)

which obey the symmetry conditions $\tau _{ij}=\tau _{ji}$ and $\mu _{ijk}=\mu _{ikj}$ discussed in Sect. 2.1. The expression for the Cauchy stress, Eq. (56)₁, is well-known, and has been presented previously in other works on homogenization of granular media, see, e.g., [8, 10, 14, 15, 18, 54, 58, 62]. The expression for the double stress, Eq. (56)₂, is far less familiar, but can be found in [14], together with the corresponding expressions for the homogenized stiffness tensors Eq. (51). It should be mentioned, however, that the expressions derived in [14] were obtained by applying an alternative, more elaborative derivation procedure based on equilibrium considerations of the local contact forces in the granular microstructure.

Fig. 2

Two grains in contact and the local and global coordinate systems

In order to relate macro-scale anisotropy to the particle properties at the microstructural scale, the stiffness tensors in Eq. (51) are further developed for the general case of a packing composed of arbitrarily-shaped particles. As pointed out in [43], in Eq. (51) the summation over the particle contacts $\alpha$ in the granular volume $V$ can be reformulated into particle contact summations over the three spherical coordinates $(\phi ,\theta ,\rho )$ illustrated in Fig. 2. Hence, writing the branch vector as $\mathbf{l}^{\alpha}= l^{\alpha} \mathbf{n}^{\alpha}$, whereby $l^{\alpha}$ is the magnitude of the branch vector, and invoking Eq. (52), Eq. (51) becomes

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{1mm} C_{ijkl} & = & \displaystyle{ \frac{1}{V}\sum _{\phi ^{*}_{p}} \sum _{ \theta ^{*}_{q}} \biggl[ \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{n}}^{\alpha} l^{\alpha} l^{\alpha} \biggr) n_{i} n_{k} n_{j} n_{l} + \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{s}}^{ \alpha} l^{\alpha} l^{\alpha} \biggr) s_{i} s_{k} n_{j} n_{l} } \\ \vspace*{1mm} & + & \displaystyle{ \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{t}}^{\alpha} l^{\alpha} l^{\alpha} \biggr) t_{i} t_{k} n_{j} n_{l} \biggr] , } \\ \vspace*{1mm} F_{ijklm} & = & \displaystyle{ \frac{1}{2V}\sum _{\phi ^{*}_{p}} \sum _{\theta ^{*}_{q}} \biggl[ \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{n}}^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} \biggr) n_{i} n_{l} n_{j} n_{k} n_{m} + \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{ \text{s}}^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} \biggr) s_{i} s_{l} n_{j} n_{k} n_{m} } \\ & + & \displaystyle{ \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{t}}^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} \biggr) t_{i} t_{l} n_{j} n_{k} n_{m} \biggr] , } \end{array} $$

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{1mm} A_{ijklmn} & = & \displaystyle{ \frac{1}{4V}\sum _{\phi ^{*}_{p}} \sum _{\theta ^{*}_{q}} \biggl[ \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{n}}^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} \biggr) n_{i} n_{l} n_{j} n_{k} n_{m} n_{n} } \\ & + & \displaystyle{ \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{s}}^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} \biggr) s_{i} s_{l} n_{j} n_{k} n_{m} n_{n} } + \displaystyle{ \biggl( \sum _{\alpha =\alpha _{\rho ^{*}_{pq}}} k_{\text{t}}^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha} \biggr) t_{i} t_{l} n_{j} n_{k} n_{m} n_{n} \biggr] , } \end{array} $$

(57)

where $\alpha _{\rho ^{*}_{pq}}$ denotes a particle contact along the radial $\rho ^{*}_{pq}$-direction that is set by the discrete spherical polar coordinates $\phi ^{*}_{p}$ and $\theta ^{*}_{q}$, see also Fig. 2. Note that in Eq. (57) the superscript $\alpha$ for the orthonormal base vectors $\mathbf{n}$, $\mathbf{s}$ and $\mathbf{t}$ given by Eq. (53) has vanished, as these vectors now are evaluated at discrete spherical polar coordinates instead of at the particle contacts, i.e., $\mathbf{n}=\mathbf{n}(\phi _{p}^{*},\theta _{q}^{*})$, $\mathbf{s}=\mathbf{s}(\phi _{p}^{*},\theta _{q}^{*})$ and $\mathbf{t}=\mathbf{t}(\phi _{p}^{*},\theta _{q}^{*})$. The discrete spherical polar coordinates $\phi ^{*}_{p}$ and $\theta ^{*}_{q}$ should have representative values within the small, finite interval considered, $\phi ^{*}_{p} \in [ \phi _{p-1}, \phi _{p} ] \, \wedge \, \theta ^{*}_{q} \in [ \theta _{q-1}, \theta _{q}]$, whereby all particle contacts $\alpha _{\rho ^{*}_{pq}}$ within this interval are identified and accounted for. The incremental solid angle related to this interval then follows as

$$ \Delta \Omega _{pq} = \text{sin} \, \theta ^{*}_{q} \, \Delta \theta _{q} \, \Delta \phi _{p} \qquad \text{with} \qquad p,q \in [1,2, \ldots \infty \! > \, , $$

(58)

where the incremental spherical polar coordinates are given by $\Delta \phi _{p} = \phi _{p} - \phi _{p-1}$ and $\Delta \theta _{q}=\theta _{q} - \theta _{q-1}$. Accordingly, the probability $P^{n}_{\Delta \Omega _{pq}}$ that the “combined contact parameter” $k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}$ appearing in Eq. (57) lies within the finite interval $\Delta \Omega _{pq}$ can be expressed as

$$ P^{n}_{\Delta \Omega _{pq}} = \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}} \, . $$

(59)

Similarly, the probabilities $P^{s}_{\Delta \Omega _{pq}}$ and $P^{t}_{\Delta \Omega _{pq}}$ related to the combined contact parameters $k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha}$ and $k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha}$ appearing in Eq. (57) read

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{2mm} P^{s}_{\Delta \Omega _{pq}} & = & \displaystyle{ \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha}} \, ,} \\ P^{t}_{\Delta \Omega _{pq}} & = & \displaystyle{ \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha}} \, .} \end{array} $$

(60)

For simplicity, it is assumed that the three probabilities in Eqs. (59) and (60) are equal, and thus are represented by one and the same probability $P_{\Delta \Omega _{pq}}$, i.e.,

$$ P_{\Delta \Omega _{pq}}=P^{n}_{\Delta \Omega _{pq}}=P^{s}_{\Delta \Omega _{pq}}=P^{t}_{\Delta \Omega _{pq}} \, , $$

(61)

which can be expressed in terms of a probability density $\xi =\xi (\theta _{q}^{*}, \phi _{p}^{*})$ as

$$ \begin{aligned}[b] P_{\Delta \Omega _{pq}} &\quad = \quad \xi (\theta ^{*}_{q}, \phi ^{*}_{p}) \Delta \Omega _{pq} \\ &\quad = \quad \xi (\theta ^{*}_{q}, \phi ^{*}_{p}) \, \text{sin} \, \theta ^{*}_{q} \, \Delta \theta _{q} \, \Delta \phi _{p} \, , \end{aligned} $$

(62)

whereby Eq. (58) has been substituted to obtain the final expression. Note that the sum of all discrete probabilities needs to be equal to unity, i.e.,

$$ \sum _{p=1}^{\infty} \sum _{q=1}^{\infty} P_{\Delta \Omega _{pq}} = 1 \, . $$

(63)

Analogous to Eq. (59), $P_{\Delta _{pq}}$ is further supposed to reflect the probabilities regarding the “higher-order combined contact parameters” in normal particle contact direction, $k_{\text{n}}^{\alpha}l^{\alpha} l^{\alpha} l^{\alpha}$ and $k_{\text{n}}^{\alpha}l^{\alpha} l^{\alpha} l^{\alpha} l^{\alpha}$, that appear in Eq. (57):

$$ P_{\Delta \Omega _{pq}} = \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}} = \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}} \, , $$

(64)

and, similar to Eq. (60), the probabilities with respect to higher-order combined contact parameters in the two tangential particle contact directions:

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{2mm} P_{\Delta \Omega _{pq}} & = & \displaystyle{ \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}} = \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}} } \, , \\ P_{\Delta \Omega _{pq}} & = & \displaystyle{ \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}} = \frac{\sum _{\alpha =\alpha _{\rho ^{*}_{pq}}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}}{\sum _{\alpha =1}^{N_{c}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}l^{\alpha}} } \, . \end{array} $$

(65)

Hence, in accordance with Eqs. (59), (60), (61), (64) and (65), all combined contact parameters for simplicity reasons are assumed to be related to one common probability $P_{\Delta \Omega _{pq}}$. In addition, for the combined contact parameters appearing in the denominators of Eqs. (59), (60), (64) and (65), the average values across the particle volume $V$ can be calculated as

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \overline{k_{\text{n}} l l } = \displaystyle{\frac{1}{N_{c}} \sum _{ \alpha =1}^{N_{c}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha}} \, , & \overline{k_{\text{n}} l l l} = \displaystyle{\frac{1}{N_{c}} \sum _{ \alpha =1}^{N_{c}}k_{\text{n}}^{\alpha}l^{\alpha}l^{\alpha} l^{\alpha}} \, , & \overline{k_{\text{n}} l l l l} = \displaystyle{ \frac{1}{N_{c}} \sum _{\alpha =1}^{N_{c}}k_{\text{n}}^{\alpha}l^{ \alpha}l^{\alpha} l^{\alpha} l^{\alpha}} \, , \\ \overline{k_{\text{s}} l l } = \displaystyle{ \frac{1}{N_{c}} \sum _{ \alpha =1}^{N_{c}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha} } \, , & \overline{k_{\text{s}} l l l} = \displaystyle{\frac{1}{N_{c}} \sum _{ \alpha =1}^{N_{c}}k_{\text{s}}^{\alpha}l^{\alpha}l^{\alpha} l^{\alpha}} \, , & \overline{k_{\text{s}} l l l l} = \displaystyle{ \frac{1}{N_{c}} \sum _{\alpha =1}^{N_{c}}k_{\text{s}}^{\alpha}l^{ \alpha}l^{\alpha} l^{\alpha} l^{\alpha}} \, , \\ \overline{k_{\text{t}} l l } = \displaystyle{ \frac{1}{N_{c}} \sum _{ \alpha =1}^{N_{c}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha} } \, , & \overline{k_{\text{t}} l l l} = \displaystyle{\frac{1}{N_{c}} \sum _{ \alpha =1}^{N_{c}}k_{\text{t}}^{\alpha}l^{\alpha}l^{\alpha} l^{\alpha}} \, , & \overline{k_{\text{t}} l l l l} = \displaystyle{ \frac{1}{N_{c}} \sum _{\alpha =1}^{N_{c}}k_{\text{t}}^{\alpha}l^{ \alpha}l^{\alpha} l^{\alpha} l^{\alpha}} \, , \end{array} $$

(66)

with the superimposed bar indicating the average of the corresponding parameter. Substituting Eqs. (59) to (66) into Eq. (57) leads to

$$ \begin{aligned} C_{ijkl} & = \displaystyle{ \frac{N_{c}}{V} \sum _{\phi ^{*}_{p}} \sum _{\theta ^{*}_{q}} \left ( \overline{k_{\text{n}} l l} \, n_{i} n_{k} + \overline{k_{\text{s}} l l} \, s_{i} s_{k} + \overline{k_{\text{t}} l l} \, t_{i} t_{k} \right ) n_{j} n_{l} } \, \xi (\theta ^{*}_{q}, \phi ^{*}_{p}) \, \text{sin} \, \theta ^{*}_{q} \, \Delta \theta _{q} \, \Delta \phi _{p} \, , \\ F_{ijklm} & = \displaystyle{ \frac{N_{c}}{2V} \sum _{\phi ^{*}_{p}} \sum _{\theta ^{*}_{q}} \left ( \overline{k_{\text{n}} l l l} \, n_{i} n_{l} + \overline{k_{\text{s}} l l l} \, s_{i} s_{l} + \overline{k_{\text{t}} l l l} \, t_{i} t_{l} \right ) n_{j} n_{k} n_{m} \, \xi (\theta ^{*}_{q}, \phi ^{*}_{p}) \, \text{sin} \, \theta ^{*}_{q} \, \Delta \theta _{q} \, \Delta \phi _{p}} \, , \\ A_{ijklmn} & = \displaystyle{ \frac{N_{c}}{4V} \sum _{\phi ^{*}_{p}} \sum _{\theta ^{*}_{q}} \left ( \overline{k_{\text{n}} l l l l} \, n_{i} n_{l} + \overline{k_{\text{s}} l l l l} \, s_{i} s_{l} + \overline{k_{\text{t}} l l l l} \, t_{i} t_{l} \right ) n_{j} n_{k} n_{m} n_{n} \, \xi (\theta ^{*}_{q}, \phi ^{*}_{p}) \, \text{sin} \, \theta ^{*}_{q} \, \Delta \theta _{q} \, \Delta \phi _{p} } \, . \end{aligned} $$

(67)

In the limit of the intervals $\Delta \phi _{p}$ and $\Delta \theta _{q}$ approaching to zero, the finite sums defining the elastic stiffness tensors in Eq. (67) turn into corresponding integral expressions:

$$ \begin{aligned} C_{ijkl} & = \displaystyle{ \frac{N_{c}}{V} \int _{\phi =0}^{2 \pi} \int _{\theta =0}^{\pi} \left ( \overline{k_{\text{n}} l l} \, n_{i} n_{k} + \overline{k_{\text{s}} l l} \, s_{i} s_{k} + \overline{k_{\text{t}} l l} \, t_{i} t_{k} \right ) n_{j} n_{l} } \, \xi (\theta , \phi ) \, \text{sin} \, \theta \, \text{d} \theta \, \text{d} \phi \, , \\ F_{ijklm} & = \displaystyle{ \frac{N_{c}}{2V} \int _{\phi =0}^{2 \pi} \int _{\theta =0}^{\pi} \left ( \overline{k_{\text{n}} l l l} \, n_{i} n_{l} + \overline{k_{\text{s}} l l l} \, s_{i} s_{l} + \overline{k_{\text{t}} l l l} \, t_{i} t_{l} \right ) n_{j} n_{k} n_{m} } \, \xi (\theta , \phi ) \, \text{sin} \, \theta \, \text{d} \theta \, \text{d} \phi \, , \\ A_{ijklmn} & = \displaystyle{ \frac{N_{c}}{4V} \int _{\phi =0}^{2 \pi} \int _{\theta =0}^{\pi} \left ( \overline{k_{\text{n}} l l l l} \, n_{i} n_{l} + \overline{k_{\text{s}} l l l l} \, s_{i} s_{l} + \overline{k_{\text{t}} l l l l} \, t_{i} t_{l} \right ) n_{j} n_{k} n_{m} n_{n} } \, \xi (\theta , \phi ) \, \text{sin} \, \theta \, \text{d} \theta \, \text{d} \phi \, . \end{aligned} $$

(68)

The above equations are valid for packings composed of arbitrarily-shaped particles, whereby, as can be concluded from the discretized expressions Eqs. (62) and (63), the probability density function $\xi$ needs to satisfy the condition

$$ \int _{\phi =0}^{2 \pi} \int _{\theta =0}^{\pi} \xi (\theta , \phi ) \sin \theta \, \mathrm{d} \theta \, \mathrm{d} \phi = 1 \, . $$

(69)

Observe from Eqs. (59) to (65) that the probability density function is determined by a combined directional distribution of i) the particle contact stiffnesses, ii) the branch vectors (i.e., the local particle geometries), and iii) the number of particle contacts and, in this way, effectively characterizes the anisotropic properties of the particle packing. Note that the current, microstructural definition for the probability density function $\xi$ allows for a more complete interpretation of anisotropy compared to the interpretation commonly used in other works, in which anisotropy is phenomenologically ascribed to spatial variations in the “density of particle contacts”, see e.g., [16, 17]. Although anisotropy aspects can be studied for packings of arbitrarily-shaped particles by applying Eq. (68), from hereon a monodisperse packing composed of spheres will be considered. This specific choice will not affect the nature and main features of the modelling results, and has the advantage that the closed-form expressions calculated for the elastic coefficients remain relatively simple.

For a monodisperse packing composed of spheres made of one and the same elastic material, the linear elastic contact stiffnesses may be assumed to be uniform across the granular volume $V$, i.e., $k_{\text{n}}^{\alpha} = k_{\text{n}}$, $k_{\text{s}}^{\alpha} = k_{\text{s}}$ and $k_{\text{t}}^{\alpha} = k_{\text{t}}$, $\forall \alpha$, and the branch vector between the particles is expressed by $\mathbf{l}=2r \mathbf{n}$, with $r$ the particle radius. In addition, the contact area between two particles has a circular shape, so that the two shear stiffnesses defining the contact stiffness tensor, Eq. (52), can be assumed identical, i.e., $k_{\text{s}}=k_{\text{t}}$. Furthermore, the averages of the combined contact parameters presented in Eq. (66) may be replaced by products of the associated, individual contact parameters, as in $\overline{k_{\text{n}}ll}=k_{\text{n}} l^{2}$, by which Eq. (68) specifies to

$$ \begin{aligned} C_{ijkl} & = \displaystyle{ \rho _{c} \, l^{2} \int _{\phi =0}^{2 \pi} \int _{\theta =0}^{\pi} \left ( k_{\text{n}} \, n_{i} n_{k} + k_{\text{s}} \left ( s_{i} s_{k} + t_{i} t_{k} \right ) \right ) n_{j} n_{l} } \, \xi \, \text{sin} \, \theta \, \text{d} \theta \, \text{d} \phi \, , \\ F_{ijklm} & = \displaystyle{ \frac{\rho _{c} \, l^{3}}{2} \int _{ \phi =0}^{2 \pi} \int _{\theta =0}^{\pi} \left ( k_{ \text{n}} \, n_{i} n_{l} + k_{\text{s}} \left ( s_{i} s_{l} + t_{i} t_{l} \right ) \right ) n_{j} n_{k} n_{m} } \, \xi \, \text{sin} \, \theta \, \text{d} \theta \, \text{d} \phi \, , \\ A_{ijklmn} & = \displaystyle{ \frac{\rho _{c} \, l^{4}}{4} \int _{ \phi =0}^{2 \pi} \int _{\theta =0}^{\pi} \left ( k_{ \text{n}} \, n_{i} n_{l} + k_{\text{s}} \left ( s_{i} s_{l} + t_{i} t_{l} \right ) \right ) n_{j} n_{k} n_{m} n_{n} } \, \xi \, \text{sin} \, \theta \, \text{d} \theta \, \text{d} \phi \, , \end{aligned} $$

(70)

with $\rho _{\text{c}}=N_{\text{c}}/V$ the volume number density of the particle contacts. For reasons of brevity, the dependencies of $\mathbf{n}$, $\mathbf{s}$, $\mathbf{t}$ and $\xi$ on the spherical polar coordinates $\theta$ and $\phi$ have been omitted in Eq. (70).

Through Eq. (70), the probability density function $\xi =\xi (\theta , \phi )$ effectively incorporates the anisotropic characteristics of the monodisperse particle structure in the macrocopic stiffness tensors characterizing the strain-gradient continuum. Since the particle contacts stiffness and particle geometry are uniform across a monodisperse packing of spheres, the probability density function is solely characterized by the directional distribution of the number of particle contacts. In the subsections below, micromechanics-based stiffness tensors for the strain-gradient continuum are derived by including in Eq. (70) functional forms for $\xi (\theta ,\phi )$ that reflect various degrees of elastic symmetry, as considered in Sect. 3.

4.2 Directional Distribution of Particle Contact Properties

Following the pioneering work of Chang and Misra [16], the directional distribution of particle contacts properties $\xi = \xi (\theta ,\phi )$ that appears in Eq. (70) is expressed by means of a spherical harmonics expansion:

$$ \xi (\theta ,\phi )=\frac{1}{4\pi} \! \left [1+\sum _{k=2}^{\infty}{}^{\prime } \left [a'_{k0}P_{k} \! \left (\cos \theta \right )+\sum _{m=1}^{k}P_{k}^{m} \! \left (\cos \theta \right )\left [a'_{km}\cos m\phi +b'_{km}\sin m \phi \right ]\right ]\right ] \, , $$

(71)

where $a'_{k0}$, $a'_{km}$, and $b'_{km}$ denote fabric parameters that represent the directional dependence of the contact properties between particles, $P_{k} \! \left (\cos \theta \right )$ is the Legendre polynomial of degree $k$ with respect to $\cos \theta$, and $P_{k}^{m}\left (\cos \theta \right )$ is its associated Legendre function of degree $m$. The special summation symbol $\Sigma '$ indicates that the summation is performed only with respect to even integers $k$. Note that the upper limit of the second summation in Eq. (71) has been set to $k$ instead of infinity, as for $m > k$ the associated Legendre function is equal to zero, $P_{k}^{m}(\text{cos} \, \theta )=0$. Defining the probability density function in terms of Legendre polynomials and associated Legendre functions guarantees that (i) the directional distribution of particle contacts is described by a series of orthonormal functions whose integral over the surface of a sphere is always equal to unity, in accordance with Eq. (69), and (ii) allows for a systematic inclusion of the effects of reflection and rotation symmetries that characterise the planes and axes of elastic symmetry. Accordingly, the elastic stiffness tensors of isotropic, transversely isotropic, orthotropic, monoclinic and triclinic granular materials are respectively studied in Sects. 4.3, 4.4, 4.5, 4.6 and 4.7, by defining a proper density distribution function for these materials based on the general expression, Eq. (71).

4.3 Elastic Stiffness Components for an Isotropic Granular Material

An isotropic granular material is represented by a uniform directional distribution of particle contact characteristics. Hence, the contributions of the fabric parameters $a'_{k0}$, $a'_{km}$, and $b'_{km}$ to the probability density function, Eq. (71), vanish, and only the first, constant term in the right-hand side of the expression is preserved:

$$ \xi = \frac{1}{4\pi} \, . $$

(72)

By substituting Eq. (72) into Eq. (70), closed-form expressions can be derived for the stiffness tensors of the isotropic elastic granular material. Accordingly, the fourth-order and sixth-order stiffness tensors $\mathbf{C}$ and $\mathbf{A}$ given by Eqs. (40) to (43) are respectively characterized by the nonzero components

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{1mm} c_{1} & = & \displaystyle{\frac{\rho _{\text{c}} \, l^{2}}{15} (k_{ \text{n}}-k_{\text{s}}) \, ,} \\ c_{2} & = & \displaystyle{ \frac{\rho _{\text{c}} \, l^{2}}{30} (2k_{ \text{n}}+3k_{\text{s}}) \, ,} \end{array} $$

(73)

and

$$ \textstyle\begin{array}{l} \vspace*{1mm} a_{1}=a_{2}=a_{11}= \displaystyle{ \frac{\rho _{\text{c}} \, l^{4} }{420} (k_{\text{n}}-k_{\text{s}}) \, ,} \\ a_{7}=a_{8}= \displaystyle{ \frac{\rho _{\text{c}} \, l^{4}}{420} (k_{ \text{n}}+6k_{\text{s}}) \, ,} \end{array} $$

(74)

while the components of the fifth-order stiffness tensor vanish, $\mathbf{F}=\mathbf{0}$. The above expressions for the elastic coefficients $c_{i}$ of the fourth-order stiffness tensor $\mathbf{C}$ are in agreement with those computed for other isotropic GMA-based models [11, 15, 16, 58, 62]. Furthermore, the components $c_{i}$ and $a_{i}$ in Eqs. (73) and (74) satisfy the equalities in Eqs. (36) and (37) regarding the other nonzero components, and the result $\mathbf{F}=\mathbf{0}$ is in agreement with the macro-scale outcome presented in Table 3. Nevertheless, from the GMA homogenization procedure the number of independent coefficients $a_{i}$ of the sixth-order tensor $\mathbf{A}$ is equal to two, see Eq. (74), while from symmetry considerations at the macro-scale it comes out as 5, see Eq. (39). It may thus be concluded that the specific granular microstructure of equal-sized spheres considered in the GMA approach imposes additional constraints on the coefficients of the sixth-order elastic tensor $\mathbf{A}$. Indeed, Eqs. (73) and (74) show that at the microstructural level the higher-order continuum model is characterized by only three independent parameters in total, which are the parameters $\rho _{c} l^{2} k_{\text{n}}$ and $\rho _{c} l^{2} k_{\text{s}}$ related to the normal and shear contact stiffnesses, and the magnitude of the branch vector $l(=2r)$. The latter parameter induces a length scale dependency $l^{2}$ in the coefficients $a_{i}$ of the sixth-order stiffness tensor $\mathbf{A}$, as can be concluded from the difference in dimension of the coefficients $a_{i}$ and $c_{i}$, see Eqs. (73) and (74).

The fact that the characteristics of the granular microstructure can reduce the number of independent coefficients of the macroscopic stiffness tensors has also been reported for other GMA-based higher-order continuum models [56, 58]. In specific, a reduction of the number of independent coefficients caused by the granular microstructure narrows the conditions that the elastic constants need to satisfy from macro-scale elastic stability considerations. As a basic example: if the monodisperse packing is assumed to consist of perfectly smooth spheres for which the shear stiffness is zero, $k_{\text{s}}=0$, it follows from Eq. (73) that the two elastic coefficients defining the fourth-order stiffness tensor $\mathbf{C}$ become equal, $c_{1}$ (= $\lambda$) = $c_{2}$ (= $\mu$) = $\rho _{c} l^{2} k_{\text{n}}/15$; the characterization of $\mathbf{C}$ by only one independent elastic coefficient corresponds to an isotropic elastic material with a specific Poisson’s ratio of $\nu =0.25$, which is a clear restriction of the common range of possible values $-1 < \nu < 0.5$ that follows from elastic stability requirements. Furthermore, in the general case of $0 \leq k_{\text{s}} < \infty$, the two coefficients given by Eq. (73) correspond to a range of Poisson’s ratios of $-1 < \nu \leq 0.25$; despite that the number of two independent coefficients for $\mathbf{C}$ equals the number following from symmetry considerations at the macro-scale, see Table 3, this range of Poisson’s ratios still is somewhat smaller than that determined from elastic stability requirements, which is due to the constraining effect caused by the kinematic hypothesis Eq. (46), see also [12].

4.4 Elastic Stiffness Components for a Transversely Isotropic Granular Material

A transversely isotropic elastic material is characterized by three orthogonal planes of elastic symmetry and one axis of rotational symmetry. Without loss of generality, in Sect. 3.4 the normal directions of the planes of elastic symmetry are taken in accordance with the $x_{1}$-, $x_{2}$- and $x_{3}$-directions illustrated in Fig. 2, and the axis of rotational symmetry is assumed to correspond with the $x_{3}$-direction. The $x_{3}$-plane thus represents the plane of isotropy, so that the directional distribution of the elastic properties is independent of the (in-plane) azimuthal angle $\phi$ in Fig. 2, and only depends on the polar angle $\theta$. Correspondingly, the fabric parameters $a'_{km}$ and $b'_{km}$ in the probability distribution function Eq. (71) vanish, by which the expression reduces to

$$ \xi (\theta )=\frac{1}{4\pi}\left [1+\sum _{k=2}^{\infty}{}^{\prime }{a'_{k0}P_{k} \left (\cos \theta \right )}\right ] . $$

(75)

After inserting Eq. (75) into Eq. (70) and carrying out the integration procedure, the macroscopically independent components of the stiffness tensors $\mathbf{C}$ and $\mathbf{A}$ in Eqs. (30) to (33) are obtained as

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} \vspace*{2mm} C_{11} & = & \displaystyle{ \frac{\rho _{\text{c}} \, l^{2}}{420} \left ( 4(21-6a'_{20}+a'_{40})k_{\text{n}}+(56-4a'_{20}-4a'_{40})k_{ \text{s}} \right ) ,} \\ \vspace*{2mm} C_{12} & = & \displaystyle{ \frac{\rho _{\text{c}} \, l^{2}}{315}(21-6a'_{20}+a'_{40})(k_{ \text{n}}-k_{\text{s}}) ,} \\ \vspace*{2mm} C_{13} & = & \displaystyle{ \frac{\rho _{\text{c}} \, l^{2}}{315}(21+3a'_{20}-4a'_{40})(k_{ \text{n}}-k_{\text{s}}) , } \\ \vspace*{2mm} C_{33} & = & \displaystyle{ \frac{\rho _{\text{c}} \, l^{2}}{315} \left ( 63+36a'_{20}+8a'_{40})k_{\text{n}}+2(21+3a'_{20}-4a'_{40})k_{ \text{s}} \right ) , } \\ C_{44} & = & \displaystyle{ \frac{\rho _{\text{c}} \, l^{2}}{1260} \left ( 4(21+3a'_{20}-4a'_{40})k_{\text{n}}+(126+9a'_{20}+16a'_{40})k_{ \text{s}} \right ) ,} \end{array} $$

(76)

and

$$ \begin{aligned} &A_{0101}=\frac{\rho _{\text{c}} \, l^{4}}{60060}\left ( 5(429-143a'_{20}+39a'_{40}-5a'_{60})k_{\text{n}}+(858-143a'_{20}-52a'_{40}+25a'_{60} )k_{\text{s}} \right ), \\ &A_{0102}=\frac{\rho _{\text{c}} \, l^{4}}{180180}\left ( 3(429-143a'_{20}+39a'_{40}-5a'_{60})k_{\text{n}}+(1716-429a'_{20}+26a'_{40}+15a'_{60})k_{ \text{s}} \right ), \\ &A_{0103}=\frac{\rho _{\text{c}} \, l^{4}}{180180} \left ( 3(429-91a'_{40}+30a'_{60})k_{\text{n}}+(1716+429a'_{20}-299a'_{40}-90a'_{60})k_{ \text{s}} \right ), \\ &A_{0112}=\frac{\rho _{\text{c}} \, l^{4}}{60060} (429-143a'_{20}+39a'_{40}-5a'_{60})(k_{ \text{n}}-k_{\text{s}}), \\ &A_{0117}=\frac{\rho _{\text{c}} \, l^{4}}{60060}(429-91a'_{40}+30a'_{60})(k_{ \text{n}}-k_{\text{s}}), \\ &A_{0202}=\frac{\rho _{\text{c}} \, l^{4}}{60060} \left ( (429-143a'_{20}+39a'_{40}-5a'_{60})k_{\text{n}}+(2574-715a'_{20}+104a'_{40}+5a'_{60})k_{ \text{s}} \right ), \\ &A_{0203}=\frac{\rho _{\text{c}} \, l^{4}}{180180} \left ( (429-91a'_{40}+30a'_{60})k_{\text{n}}+(2574+429a'_{20}-481a'_{40}-30a'_{60})k_{ \text{s}} \right ), \end{aligned} $$

$$ \begin{aligned} &A_{0217}=\frac{\rho _{\text{c}} \, l^{4}}{180180}(429-91a'_{40}+30a'_{60})(k_{ \text{n}}-k_{\text{s}}), \\ &A_{0303}=\frac{\rho _{\text{c}} \, l^{4}}{180180}\left ( (1287+429a'_{20}-208a'_{40}-120a'_{60})k_{\text{n}}+(7722+4719a'_{20}+1352a'_{40}+120a'_{60})k_{ \text{s}} \right ), \\ &A_{0317}=\frac{\rho _{\text{c}} \, l^{4}}{180180}(1287+429a'_{20}-208a'_{40}-120a'_{60})(k_{ \text{n}}-k_{\text{s}}), \\ &A_{0404}=\frac{\rho _{\text{c}} \, l^{4}}{180180} \left ( (429-91a'_{40}+30a'_{60})k_{\text{n}}+(2574+429a'_{20}-481a'_{40}-30a'_{60})k_{ \text{s}} \right ), \\ &A_{0411}=\frac{\rho _{\text{c}} \, l^{4}}{180180} (429-91a'_{40}+30a'_{60})(k_{ \text{n}}-k_{\text{s}}) , \\ &A_{0505}=\frac{\rho _{\text{c}} \, l^{4}}{180180} \left ( 3(429-91a'_{40}+30a'_{60})k_{\text{n}}+(1716+429a'_{20}-299a'_{40}-90a'_{60})k_{ \text{s}} \right ), \\ &A_{0513}=\frac{\rho _{\text{c}} \, l^{4}}{60060}(429-91a'_{40}+30a'_{60})(k_{ \text{n}}-k_{\text{s}}), \\ &A_{0514}=\frac{\rho _{\text{c}} \, l^{4}}{180180}(429-91a'_{40}+30a'_{60})(k_{ \text{n}}-k_{\text{s}}), \\ &A_{0515}=\frac{\rho _{\text{c}} \, l^{4}}{180180}(1287+429a'_{20}-208a'_{40}-120a'_{60})(k_{ \text{n}}-k_{\text{s}}), \\ &A_{1313}=\frac{\rho _{\text{c}} \, l^{4}}{60060} \left ( (429-91a'_{40}+30a'_{60})k_{\text{n}}+6(429-143a'_{20}+39a'_{40}-5a'_{60})k_{ \text{s}} \right ), \\ &A_{1314}=\frac{\rho _{\text{c}} \, l^{4}}{180180} \left ( (429-91a'_{40}+30a'_{60})k_{\text{n}}+6(429-143a'_{20}+39a'_{40}-5a'_{60})k_{ \text{s}} \right ), \\ &A_{1315}=\frac{\rho _{\text{c}} \, l^{4}}{180180}\left ( (1287+429a'_{20}-208a'_{40}-120a'_{60})k_{\text{n}}+4(429-91a'_{40}+30a'_{60})k_{ \text{s}} \right ), \\ &A_{1515}=\frac{\rho _{\text{c}} \, l^{4}}{180180}\left ( 15(429+286a'_{20}+104a'_{40}+16a'_{60})k_{\text{n}}+2(1287+429a'_{20}-208a'_{40}-120a'_{60})k_{ \text{s}} \right ), \\ &A_{1616}=\frac{\rho _{\text{c}} \, l^{4}}{180180}\left ( (1287+429a'_{20}-208a'_{40}-120a'_{60})k_{\text{n}}+4(429-91a'_{40}+30a'_{60})k_{ \text{s}} \right ) . \end{aligned} $$

(77)

As for the isotropic material, the components of the fifth-order stiffness tensor are zero, $\mathbf{F}=\mathbf{0}$, which is consistent with the macro-scale result reported in Table 3. It has been further confirmed that the nonzero coefficients in Eqs. (76) and (77) satisfy the equalities given by Eqs. (28) and (29) regarding the other nonzero coefficients. Observe from Eqs. (76) and (77) that the transversely isotropic material is characterized by 6 independent micro-scale parameters in total, which are the contact stiffness-related parameters $\rho _{c} l^{2} k_{\text{n}}$ and $\rho _{c} l^{2} k_{\text{s}}$ and the length scale parameter $l$ (which were also identified for the isotropic material in Sect. 4.3), and the fabric parameters $a'_{20}$, $a'_{40}$ and $a'_{60}$. Essentially, the higher-order fabric parameters $a'_{80}, a'_{100}, a'_{120}, \ldots \text{etc.}$ vanish after carrying out the integration in Eq. (70), and thus have no influence on the properties of the transversely isotropic elastic material. Out of the 6 independent micro-scale parameters, the fourth-order stiffness tensor $\mathbf{C}$ is defined by 4 independent parameters, i.e., the two contact stiffness-related parameters $\rho _{c} l^{2} k_{\text{n}}$ and $\rho _{c} l^{2} k_{\text{s}}$ and the two fabric parameters $a'_{20}$ and $a'_{40}$, see Eq. (76), while the sixth-order stiffness tensor $\mathbf{A}$ is characterized by 5 independent parameters, i.e., two contact stiffness-related parameters $\rho _{c} l^{4} k_{\text{n}}$ and $\rho _{c} l^{4} k_{\text{s}}$, and the three fabric parameters $a'_{20}$, $a'_{40}$ and $a'_{60}$, see Eq. (77). Conversely, from macro-scale symmetry considerations, the stiffnesses $\mathbf{C}$ and $\mathbf{A}$ of the transversely isotropic material are respectively defined by 5 and 21 independent coefficients, see Table 3 and Eqs. (76) and (77). Hence, in contrast to the isotropic elastic material, the number of independent coefficients of both $\mathbf{C}$ and $\mathbf{A}$ are reduced by the constraints imposed by the microstructure of equal-sized spheres.

4.5 Elastic Stiffness Components for an Orthotropic Granular Material

For the modelling of an orthotropic granular material, the probability density function, Eq. (71), needs to represent the materials’ elastic symmetry with respect to three mutually orthogonal ($x_{1}$-, $x_{2}$- and $x_{3}$) planes. In accordance with Fig. 2, these three reflections lead to the following conditions for the probability density function:

$$ \textstyle\begin{array}{l} \xi (\theta ,\phi )=\xi (\pi -\theta ,\phi ) \:\:\:\:\:\quad \text{reflection with respect to the $x_{3}$-plane,} \\ \xi (\theta ,\phi )=\xi (\theta ,-\phi ) \:\:\:\:\: \quad \quad \text{reflection with respect to the $x_{2}$-plane,} \\ \xi (\theta ,\phi )=\xi (\theta ,\pi -\phi ) \:\:\:\:\:\quad \text{reflection with respect to the $x_{1}$-plane}. \end{array} $$

(78)

In correspondence with Eq. (78), in Eq. (71) the fabric parameters $a'_{km}$ related to uneven values of m and the fabric parameters $b'_{km}$ must vanish, by which the probability density function becomes

$$ \xi (\theta ,\phi )=\frac{1}{4\pi}\left [1+\sum _{k=2}^{\infty}{}^{\prime } \left [a'_{k0}P_{k}\left (\cos \theta \right )+\sum _{m=2}^{k}{}^{\prime}P_{k}^{m} \left (\cos \theta \right )\left [a'_{km}\cos m\phi \right ]\right ] \right ] . $$

(79)

Here, the summations over $k$ and $m$ are both performed with respect to even indices, as designated by the special summation symbol $\Sigma '$. Inserting the above probability density function into Eq. (70), the components of fourth-, fifth-, and sixth-order elasticity tensors of the orthotropic material can be calculated. Similar to the transversely isotropic material, for the fabric parameter $a'_{k0}$ the first three components $a'_{20}$, $a'_{40}$ and $a'_{60}$ survive the integration in Eq. (70), and the rest of the components vanishes. Additionally, for the fabric parameter $a'_{km}$ only the first 6 components $a'_{22}$, $a'_{42}$, $a'_{44}$, $a'_{62}$, $a'_{64}$ and $a'_{66}$ survive the integration. Together with the 6 independent micro-scale parameters identified for the transversely isotropic material, these 6 fabric parameters lead to a total of 12 independent parameters for the orthotropic material. Out of these 12 parameters, the fourth-order orthotropic elastic tensor $\mathbf{C}$ is defined by 7 independent micro-scale parameters, i.e., the two contact stiffness-related parameters $\rho _{c} l^{2} k_{\text{n}}$ and $\rho _{c} l^{2} k_{\text{s}}$, and the 5 fabric parameters $a'_{20}$, $a'_{40}$, $a'_{22}$, $a'_{42}$, $a'_{44}$. Further, the sixth-order tensor $\mathbf{A}$ is defined by 11 independent micro-scale parameters, namely the two contact stiffness-related parameters $\rho _{c} l^{4} k_{\text{n}}$ and $\rho _{c} l^{4} k_{\text{s}}$, and the three fabric parameters $a'_{ko}$ and 6 fabric parameters $a'_{km}$ mentioned above. Note that the 12-th independent micro-scale parameter is the mico-structural length scale $l$ that is responsible for the difference in dimension between the stiffness tensors $\mathbf{C}$ and $\mathbf{A}$. It has been confirmed that the non-zero and zero components of $\mathbf{C}$ and $\mathbf{A}$ are in a agreement with the stiffness matrices given by Eqs. (21) and (23). The number of independent coefficients as obtained from macro-scale symmetry considerations is equal to 9 for $\mathbf{C}$ and 51 for $\mathbf{A}$, see Table 3, illustrating that the independent components of both $\mathbf{C}$ and $\mathbf{A}$ are reduced by the granular microstructure of equal-sized spheres. Finally, from Eq. (70)₂ the components of fifth-order stiffness tensor $\mathbf{F}$ appear to be equal to zero, $\mathbf{F}=\mathbf{0}$, which is in agreement with the result from macro-scale symmetry considerations.

The total number of 60 macroscopically independent stiffness components of the orthotropic elastic strain-gradient material is too large for presenting the closed-form expressions of the components, as obtained from solving Eq. (70). Instead, the stiffness response is plotted for a relatively simple orthotropic elastic material, for which the probability density function, Eq. (79), is defined by a single fabric parameter $a'_{22}$. The 9 components of the fourth-order orthotropic stiffness tensor $\mathbf{C}$ and a selection of 9 components of the sixth-order orthotropic stiffness tensor $\mathbf{A}$ are analyzed by varying this fabric parameter in the range $0 \leq a'_{22} \leq 0.2$. In addition, a simple transversely isotropic material characterized by a single fabric parameter $a'_{20}$ is considered for comparison, for which the above-mentioned stiffness components are analyzed in a similar range of the fabric parameter, $0 \leq a'_{20} \leq 0.2$.

The influence of the fabric parameters $a'_{22}$ and $a'_{20}$ on the components of the fourth-order elastic tensor $\mathbf{C}$ of, respectively, the orthotropic granular material and the transversely isotropic granular material are shown in Figs. 3(a) and (b), while for selected components of the sixth-order elastic tensor $\mathbf{A}$ the dependencies on $a'_{22}$ and $a'_{20}$ are displayed in Figs. 3(c) and (d), respectively. Further, the probability density functions for the orthotropic and transversely isotropic materials are respectively depicted at the minimum and maximum fabric parameter values of 0.0 and 0.2, with the former case representing the isotropic limit for which these probability density functions become spherical. For the generation of the computational results, the shear contact stiffness has been set equal to one half of the normal contact stiffness, $k_{\text{s}}=k_{\text{n}}/2$. The stiffness components in Fig. 3 are presented in dimensionless form, whereby their subindices should be interpreted in accordance with the notation summarized in Tables 1 and 2. At the isotropic limit, $a'_{22}=0$, $a'_{20}=0$, the stiffness components of $\mathbf{C}$ and $\mathbf{A}$ of the granular material indeed satisfy the symmetry conditions given by Eq. (40) and Eqs. (41) to (43), i.e.,

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l@{\quad}c@{\quad}l@{\quad}c@{\quad}l} C_{11}& =& C_{22}& =& C_{33} \, , \\ C_{12} & = & C_{13} & = & C_{23} \, , \\ C_{44}& = & C_{55} & = & C_{66} & = & \displaystyle{\frac{1}{2}} \left (C_{11}-C_{12}\right ) \, , \end{array} $$

(80)

and

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l@{\quad}c@{\quad}l} A_{0101} & = & A_{0808} & = & A_{1515} \, , \\ A_{0112} & = & A_{0117} & = & A_{0608} \, , \\ A_{0202} & = & A_{0303} & = & A_{0707} \, . \end{array} $$

(81)

Observe that for nonzero values of the fabric parameters $a'_{22}$ and $a'_{20}$ the elastic symmetry expressed by Eqs. (80) and (81) is released, whereby the granular material respectively becomes increasingly orthotropic and transversely isotropic for a larger value of the corresponding fabric parameter. It can be confirmed that for the transversely isotropic granular material the stiffness components of $\mathbf{C}$ and $\mathbf{A}$ depicted in Figs. 3(b) and (d) meet the symmetry conditions given by Eq. (30) and Eqs. (31) to (33), i.e.,

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} C_{11} & = & C_{22} \, , \\ C_{13} & = & C_{23} \, , \\ C_{44} & = & C_{55} \, , \\ C_{66} & = & \displaystyle{\frac{1}{2}}\left (C_{11}-C_{12}\right ) \, , \end{array} $$

(82)

and

$$ \textstyle\begin{array}{l@{\quad}c@{\quad}l} A_{0101} & = & A_{0808} \, , \\ A_{0112} & = & A_{0608} \, , \\ A_{0202} & = & A_{0707} \, . \end{array} $$

(83)

Further, for the orthotropic granular material the stiffness components of $\mathbf{C}$ and $\mathbf{A}$ displayed in Figs. 3(a) and (c) all have different values, in accordance with Eqs. (21) and (23).

Fig. 3

Influence of the fabric parameters $a'_{22}$ and $a'_{20}$ on, respectively, the components of the fourth-order elastic tensor $\mathbf{C}$ and selected components of the sixth-order elastic tensor $\mathbf{A}$ of orthotropic and transversely isotropic materials. The probability density functions of these materials are depicted at the minimum and maximum fabric parameter values of 0.0 and 0.2, respectively. (a) Components of the fourth-order stiffness tensor $\mathbf{C}$ of an orthotropic material. (b) Components of the fourth-order stiffness tensor $\mathbf{C}$ of a transversely isotropic material. (c) Selected components of the sixth-order stiffness tensor $\mathbf{A}$ of an orthotropic material. (d) Selected components of the sixth-order stiffness tensor $\mathbf{A}$ of a transversely isotropic material

4.6 Elastic Stiffness Components for a Monoclinic Granular Material

For a monoclinic granular material, the probability density function, Eq. (71), should represent one plane of elastic symmetry. Assuming the $x_{3}$-plane as the plane of elastic symmetry, in accordance with Fig. 2 the probability density function needs to satisfy the condition

$$ \xi (\theta ,\phi )=\xi (\pi -\theta ,\phi ). $$

(84)

Consequently, in Eq. (71) the fabric parameters $a'_{km}$ and $b'_{km}$ related to uneven values of m vanish, by which the expression reduces to

$$ \xi (\theta ,\phi )=\frac{1}{4\pi}\left [1+\sum _{k=2}^{\infty}{}^{\prime } \left [a'_{k0}P_{k}\left (\cos \theta \right )+\sum _{m=2}^{k}{}^{\prime}P_{k}^{m} \left (\cos \theta \right )\left [a'_{km}\cos m\phi +b'_{km}\sin m \phi \right ]\right ]\right ] \, . $$

(85)

Inserting Eq. (85) into Eq. (70) shows that for the fabric parameter $b'_{km}$ the first 6 components $b'_{22}$, $b'_{42}$, $b'_{44}$, $b'_{62}$, $b'_{64}$ and $b'_{66}$ survive the integration, and the rest of the components vanishes. In addition to the 12 independent micro-scale parameters identified for the orthotropic material, these 6 fabric parameters result in a total of 18 independent micro-scale parameters for the monoclinic material. Out of these 18 parameters, the fourth-order elasticity tensor $\mathbf{C}$ is characterized by 10 independent micro-scale parameters, namely the 7 independent parameters identified for the orthotropic material and the three fabric parameters $b'_{22}$, $b'_{42}$, $b'_{44}$. The sixth-order elasticity tensor $\mathbf{A}$ is characterized by 17 independent micro-scale parameters, which are the 11 independent parameters identified for the orthotropic material and the 6 fabric parameters $b'_{km}$ mentioned above. The zero and non-zero components of $\mathbf{C}$ and $\mathbf{A}$ agree with those of the macro-scale stiffness tensors given by Eqs. (16) and (18). Further, from Eq. (70)₂ the components of the fifth-order elasticity tensor appear to be zero, $\mathbf{F}=\mathbf{0}$. It may thus be concluded that the generation of non-zero stiffness components for $\mathbf{F}$, as dictated from macro-scale symmetry requirements for the monoclinic material, see Table 3, requires a more extensive description of the directional distribution of the particle contact characteristics than provided by the spherical harmonics expansion, Eq. (85).

4.7 Elastic Stiffness Components for a Triclinic Granular Material

For the modelling of a triclinic granular material, the complete form of the probability density function, Eq. (71), must be applied, which, after substitution into Eq. (70), shows that for the fabric parameter $a'_{k0}$ the first three components, $a'_{20}$, $a'_{40}$ and $a'_{60}$, are preserved after the integration, while for the fabric parameter $a'_{km}$, the first 12 components $a'_{21}$, $a'_{22}$, $a'_{41}$, $a'_{42}$, $a'_{43}$, $a'_{44}$, $a'_{61}$, $a'_{62}$, $a'_{63}$, $a'_{64}$, $a'_{65}$ and $a'_{66}$ are preserved, and for the fabric parameter $b'_{km}$ also the first 12 components $b'_{21}$, $b'_{22}$, $b'_{41}$, $b'_{42}$, $b'_{43}$, $b'_{44}$, $b'_{61}$, $b'_{62}$, $b'_{63}$, $b'_{64}$, $b'_{65}$ and $b'_{66}$ are preserved. Accordingly, the triclinic granular material is characterized by 30 independent micro-scale parameters, which are the 27 fabric parameters mentioned above, the stiffness-related parameters $\rho _{c} l^{2} k_{\text{n}}$ and $\rho _{c} l^{2} k_{\text{s}}$, and the magnitude of the branch vector $l$. From these 30 parameters, the fourth-order elasticity tensor $\mathbf{C}$ is defined by 16 independent micro-scale parameters, which are the two contact stiffness-related parameters $\rho _{c} l^{2} k_{\text{n}}$ and $\rho _{c} l^{2} k_{\text{s}}$, and the 14 fabric parameters $a'_{20}$, $a'_{40}$, $a'_{21}$, $a'_{22}$, $a'_{41}$, $a'_{42}$, $a'_{43}$, $a'_{44}$, $b'_{21}$, $b'_{22}$, $b'_{41}$, $b'_{42}$, $b'_{43}$, $b'_{44}$. In addition, the sixth-order elasticity tensor $\mathbf{A}$ is defined by 29 independent micro-scale parameters, namely the two contact stiffness-related parameters $\rho _{c} l^{4} k_{\text{n}}$ and $\rho _{c} l^{4} k_{\text{s}}$ and the 27 fabric parameters mentioned above. As for the monoclinic material, the components of the fifth-order elasticity tensor of the triclinic material vanish, $\mathbf{F}=\mathbf{0}$. Accordingly, irrespective of the level of anisotropy as defined via Eq. (71), for the granular system of equal-sized spheres the interaction between the Cauchy stress $\boldsymbol{\sigma}$ and double stress $\boldsymbol{\mu}$ disappears from the general constitutive expressions, Eq. (6), and only takes place via the equilibrium condition, Eq. (8).

Table 4 summarizes the number of independent parameters $N_{i}$ that define the fourth-order and sixth-order elasticity tensors of granular materials with different degrees of elastic symmetry, as following from the GMA-based homogenization procedure. For comparison, the corresponding number of independent components following from macro-scale symmetry considerations are given between parentheses, as taken from Table 3. The overview clearly shows that the discrepancy between the number of independent micro-scale and macro-scale parameters for the sixth-order tensor $\mathbf{A}$ is larger than for the fourth-order tensor $\mathbf{C}$, and grows when the degree of elastic symmetry decreases.

Table 4 Overview of the number of independent elastic coefficients $N_{i}$ for the fourth-order and sixth-order elasticity tensors $\mathbf{C}$ and $\mathbf{A}$, as obtained from GMA-based homogenization solution for a system of equal-sized spheres with various degrees of elastic symmetry. For comparison, the corresponding number of independent components following from macro-scale symmetry considerations are given between parentheses, as taken from Table 3. The components of the GMA-based fifth-order elasticity tensor are zero for all degrees of symmetry, $\mathbf{F}=\mathbf{0}$

The assessment of the effect of the granular microstructure on the stiffness tensors $\mathbf{C}$, $\mathbf{F}$ and $\mathbf{A}$ of relatively complicated anisotropic granular materials, as characterized by a more advanced directional distribution of the particle contact characteristics than Eq. (71), can be studied in a comparable fashion as shown above. Similarly, the framework can be extended to alternative higher-order continua.

5 Concluding Remarks

A multi-scale framework is constructed for the computation of the stiffness tensors of an elastic strain-gradient continuum endowed with an anisotropic microstructure of arbitrarily-shaped particles. The influence of microstructural features on the macroscopic stiffness tensors is demonstrated by comparing the fourth-order, fifth-order and sixth-order elastic stiffness tensors obtained from macro-scale symmetry considerations to the stiffness tensors deduced from homogenizing the elastic response of the granular microstructure. The applied homogenization procedure is the Granular Micromechanics Approach (GMA), in which the effective behaviour of an assembly of arbitrarily-shaped particles is deduced from the local interactions and properties at the particle level. In elaborating the GMA formulation, special attention is paid to systematically relating the particle properties to the probability density function describing their directional distribution, which allows to explicitly connect the level of anisotropy of the particle assembly to local variations in particle stiffness and morphology.

The applicability of the multi-scale framework is exemplified by computing the stiffness tensors for various anisotropic granular media composed of equal-sized spheres. Independent of the degree of anisotropy, the locations of the nonzero and zero coefficients defining the structure of the homogenized elastic stiffness tensors agree with those obtained from macro-scale symmetry considerations. Further, the number of independent coefficients of the homogenized stiffness tensors appears to be determined by the number of independent microstructural parameters, which is equal to, or less than, the number of independent stiffness coefficients following from macro-scale symmetry considerations. Since the modelling framework has a general character, it can be applied to different higher-order granular continua and arbitrary types of material anisotropy.