Cosserat Elasticity of Lattice Solids

Abstract

We discuss a model of fibrous solids composed of three families of continuously distributed Kirchhoff rods embedded in a matrix material. This is a special case of Cosserat elasticity in which the basic kinematic descriptors are a single deformation field and three rotation fields, one for each fiber family. The fibers are assumed to convect with the underlying continuum deformation as material curves. Various kinds of internal connectivity, imposing restrictions of the fiber rotations fields, are considered.

1 Introduction

In this work we aim for a fairly general framework suitable for analyzing equilibria of so-called mechanical metamaterials [1–4] characterized by a lattice-like substructure. We base our model on a variant of Cosserat elasticity theory in which the fibers of the lattice are regarded as continuously distributed stretchable, unshearable rods of the Kirchhoff type. This furnishes the simplest way to account for the fiber flexural and torsional stiffnesses dominating the mechanical behavior of metamaterials. The kinematics of a fiber family are controlled by a fiber-specific rotation field and its gradient in addition to a conventional underlying continuum deformation. Accordingly, three-dimensional Cosserat elasticity, suitably extended, furnishes the appropriate conceptual framework [2, 5–7]. In contrast to conventional Cosserat elasticity [8–14], the fibers induce a directional Cosserat effect and convect with the continuum deformation as material curves. These effects are represented by constraints involving the deformation and rotation fields.

The kinematics of a single fiber family are outlined in Sect. 2. The results therein are used in Sect. 3 to establish the kinematical and constitutive framework of a continuum theory of lattice materials consisting of three families of fibers. Much of the theory extends in an obvious way to lattices consisting of four or more families, but for the sake of brevity and simplicity such extensions are not pursued here. In Sects. 4 and 5 we use a partwise virtual power postulate to extract the local equilibrium equations associated with various kinds of internal lattice connectivity, and conclude, in Sect. 6, with an example designed to furnish a simple illustration of the theory.

We use the standard symbols $\boldsymbol{A}^{t}$, $\boldsymbol{A}^{-1}$, $\boldsymbol{A}^{\ast }$, $\mathit{Skw}\boldsymbol{A}$ and $\det \boldsymbol{A}$. These are respectively the transpose, inverse, cofactor, skew part and determinant of a 2nd-order tensor $\boldsymbol{A}$. The axial vector $\mathit{ax}(\mathit{Skw}\boldsymbol{A)}$ of $\mathit{Skw}\boldsymbol{A}$ is defined by $\mathit{ax}(\mathit{Skw}\boldsymbol{A})\times \boldsymbol{v}=(\mathit{Skw}\boldsymbol{A})\boldsymbol{v}$ for any vector $\boldsymbol{v}$. The tensor product of three-vectors is indicated by interposing the symbol ⊗, and the Euclidean inner product of tensors $\boldsymbol{A}, \boldsymbol{B}$ is denoted and defined by $\boldsymbol{A}\cdot \boldsymbol{B}=\mathit{tr}(\boldsymbol{AB}^{t})$, where $\mathit{tr}(\cdot )$ is the trace; the induced norm is $\left \vert \boldsymbol{A}\right \vert =\sqrt{\boldsymbol{A}\cdot \boldsymbol{A}}$. The symbol $\left \vert \cdot \right \vert$ is also used to denote the usual Euclidean norm of three-vectors. Latin and Greek indices take values in $\{1,2,3\}$ and $\{2,3\}$, respectively, and, when repeated, are summed over their ranges. However, Latin indices enclosed in parentheses are not summed. Finally, bold subscripts are used to denote derivatives of scalar functions with respect to their vector or tensor arguments.

2 Kinematics of a Single Fiber Family

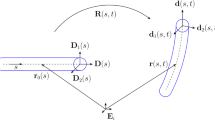
Cosserat elasticity theory furnishes the natural setting for elastic solids with embedded fibers - modeled as continuously distributed Kirchhoff rods - that support bending and twisting moments. The fibers of a given family are assumed to be perfectly bonded to an underlying matrix material and aligned locally with a unit-vector field $\boldsymbol{D(X)}$, where $\boldsymbol{X}$ is the position of a material point in a fixed reference configuration $\kappa$. Here the term ‘matrix’ encompasses the elasticity of the junctions of the different fiber families at the points where they intersect, i.e., at the material points of the continuum. If a fiber is sufficiently stiff relative to the matrix then its deformation gradient is approximated by a rotation field $\boldsymbol{R(X)}$. In Dill’s interpretation of the Kirchhoff theory [15] this is accompanied by a small axial strain. Kirchhoff’s theory is subsumed under the Special Cosserat Theory of rods, extensively treated in Chap. 8 of Antman’s book [16].

We assume that fibers convect as material curves with respect to the underlying matrix deformation. Thus,

$$ \boldsymbol{FD}=\lambda \boldsymbol{d,}\quad \textrm{where}\quad \boldsymbol{d}=\boldsymbol{RD}\quad \textrm{and}\quad \lambda =\left \vert \boldsymbol{FD}\right \vert , $$

(1)

where $\lambda$ is the fiber stretch, $\boldsymbol{d}$ is the unit tangent to the fiber after deformation and $\boldsymbol{F}=\nabla \boldsymbol{\chi }$ is the gradient of a deformation field $\boldsymbol{\chi (X)}$. The fields $\boldsymbol{F}$ and $\boldsymbol{R}$ are otherwise independent. Hence the two constraints

$$ \boldsymbol{D}_{\alpha }\cdot \boldsymbol{ED}=0;\quad \alpha =2,3, $$

(2)

involving the fiber rotation and matrix deformation, where

$$ \boldsymbol{E=R}^{t}\boldsymbol{F} $$

(3)

and $\boldsymbol{D}_{\alpha }$ are cross-sectional vectors embedded in the fiber, but not in the matrix. We arrange $\{\boldsymbol{D}_{i}\}=\{\boldsymbol{D},\boldsymbol{D}_{\alpha }\}$ to be a right-handed set. The images, $\boldsymbol{d}_{\alpha }=\boldsymbol{RD}_{\alpha }$, of $\boldsymbol{D}_{\alpha }$ after deformation are free to shear relative to the matrix while remaining mutually orthogonal and perpendicular to $\boldsymbol{d}$. The fiber rotation field $\boldsymbol{R}$ is thus given simply by

$$ \boldsymbol{R=d}_{i}\otimes \boldsymbol{D}_{i}, $$

(4)

where $\{\boldsymbol{d}_{i}\}=\{\boldsymbol{d,d}_{\alpha }\}$.

In Kirchhoff’s theory a fiber is assumed to respond constitutively to a flexure/twist-strain vector [15–17]. This involves the derivatives $\boldsymbol{d}_{i}^{\prime }$, where $(\cdot )^{\prime }$ is a directional derivative along $\boldsymbol{D}$. Thus,

$$ \boldsymbol{d}_{i}^{\prime }=\boldsymbol{R}^{\prime }\boldsymbol{D}_{i}+\boldsymbol{RD}_{i}^{\prime }. $$

(5)

Let $\{\boldsymbol{E}_{i}\}$ be a fixed right-handed orthonormal background frame. Then $\boldsymbol{D}_{i}(\boldsymbol{X)}=\boldsymbol{A}(\boldsymbol{X})\boldsymbol{E}_{i}$, where $\boldsymbol{A}$ is a rotation field, and

$$ \boldsymbol{d}_{i}^{\prime }=\boldsymbol{Wd}_{i}=\boldsymbol{w\times d}_{i}, $$

(6)

where

$$ \boldsymbol{W}=\boldsymbol{R}^{\prime }\boldsymbol{R}^{t}+\boldsymbol{RA}^{\prime }\boldsymbol{A}^{t}\boldsymbol{R}^{t}, $$

(7)

with axial vector

$$ \boldsymbol{w}=\mathit{ax}\boldsymbol{W}=\kappa _{i}\boldsymbol{d}_{i}, $$

(8)

with components

$$ \kappa _{i}=\frac{1}{2}e_{\mathit{ijk}}\boldsymbol{d}_{k}\cdot \boldsymbol{d}_{j}^{\prime }. $$

(9)

Here $e$ is the permutation symbol ($e_{123}=+1$, etc.), $\kappa _{1}$ is the twist of the rod and $\kappa _{\alpha }$ are the curvatures. These in turn generate a Galilean-invariant curvature/twist vector

$$ \boldsymbol{\kappa }=\kappa _{i}\boldsymbol{\boldsymbol{D}}_{i}=\boldsymbol{R}^{t}\boldsymbol{w}=\mathit{ax}(\boldsymbol{R}^{t}\boldsymbol{WR).} $$

(10)

From (7) we have

$$ \boldsymbol{\kappa =\gamma +\bar{\kappa }}, $$

(11)

where

$$ \boldsymbol{\bar{\kappa }}=\mathit{ax}(\boldsymbol{A}^{\prime }\boldsymbol{A}^{t})=\bar{\kappa }_{i}\boldsymbol{D}_{i}, $$

(12)

with

$$ \bar{\kappa }_{i}=\frac{1}{2}e_{\mathit{ijk}}\boldsymbol{D}_{k}\cdot \boldsymbol{D}_{j}^{\prime }, $$

(13)

and where

$$ \boldsymbol{\gamma }=\mathit{ax}(\boldsymbol{R}^{t}\boldsymbol{R}^{\prime })=\gamma _{i}\boldsymbol{D}_{i} $$

(14)

is the flexure/twist strain, with

$$ \gamma _{i}=\kappa _{i}-\bar{\kappa }_{i}=\frac{1}{2}e_{\mathit{ijk}}\boldsymbol{D}_{k}\cdot \boldsymbol{R}^{t}\boldsymbol{R}^{\prime }\boldsymbol{D}_{j}. $$

(15)

To facilitate analysis we adopt the Cartesian index notation

$$ \boldsymbol{F}=F_{\mathit{iA}}\boldsymbol{e}_{i}\otimes \boldsymbol{E}_{A},\quad \boldsymbol{R}=R_{\mathit{iA}}\boldsymbol{e}_{i}\otimes \boldsymbol{E}_{A}\quad \text{and}\quad \nabla \boldsymbol{R}=R_{\mathit{iA},B}\boldsymbol{e}_{i}\otimes \boldsymbol{E}_{A}\otimes \boldsymbol{E}_{B} $$

(16)

with

$$ F_{\mathit{iA}}=\chi _{i,A}, $$

(17)

where $(\cdot ),_{A}=\partial (\cdot )/\partial X_{A}$ and where $\{\boldsymbol{e}_{i}\}$ and $\{\boldsymbol{E}_{A}\}$ are fixed orthonormal bases associated with the Cartesian coordinates $x_{i}$ and $X_{A}$, with $x_{i}=\chi _{i}(X_{A})$. Using $R_{\mathit{iA}}^{\prime }=R_{\mathit{iA},B}D_{B}$ we derive

$$ \boldsymbol{R}^{t}\boldsymbol{R}^{\prime }=R_{\mathit{iC}}R_{\mathit{iA},B}D_{B}\boldsymbol{E}_{C}\otimes \boldsymbol{E}_{A}=e_{\mathit{ACD}}\Gamma _{\mathit{DB}}D_{B}\boldsymbol{E}_{C}\otimes \boldsymbol{E}_{A}, $$

(18)

in which $e$ is again the permutation symbol, and where

$$ \Gamma _{\mathit{DC}}=\frac{1}{2}e_{\mathit{BAD}}R_{\mathit{iA}}R_{\mathit{iB},C} $$

(19)

are the components of the wryness tensor [13]

$$ \boldsymbol{\Gamma }=\Gamma _{\mathit{DC}}\boldsymbol{E}_{D}\otimes \boldsymbol{E}_{C}. $$

(20)

The wryness tensor and the flexure/twist strain vector are related by

$$ \boldsymbol{\gamma} =\boldsymbol{\Gamma D.} $$

(21)

To demonstrate this we combine (15) and (18), reaching

$$ \gamma _{i}=G_{\mathit{iD}}^{\ast }\Gamma _{\mathit{DB}}D_{B}, $$

(22)

where

$$ G_{\mathit{iD}}^{\ast }=\frac{1}{2}e_{\mathit{ijk}}e_{\mathit{DAC}}G_{\mathit{jA}}G_{\mathit{kC}} $$

(23)

are the elements of the cofactor matrix of the matrix with components $G_{\mathit{jA}}=\boldsymbol{D}_{j}\cdot \boldsymbol{E}_{A}$. The latter induce the tensor $\boldsymbol{G}=G_{\mathit{iA}}\boldsymbol{D}_{i}\otimes \boldsymbol{E}_{A}$, and from $\boldsymbol{D}_{i}=(\boldsymbol{D}_{i}\cdot \boldsymbol{E}_{B})\boldsymbol{E}_{B}=G_{\mathit{iB}}\boldsymbol{E}_{B}$ it follows that

$$ \boldsymbol{G}=G_{\mathit{iA}}G_{\mathit{iB}}\boldsymbol{E}_{B}\otimes \boldsymbol{E}_{A}, $$

(24)

with

$$ G_{\mathit{iA}}G_{\mathit{iB}}=(\boldsymbol{D}_{i}\cdot \boldsymbol{E}_{A})(\boldsymbol{D}_{i}\cdot \boldsymbol{E}_{B})= \boldsymbol{I}\cdot \boldsymbol{E}_{A}\otimes \boldsymbol{E}_{B}=\delta _{\mathit{AB}}, $$

(25)

where $\boldsymbol{I}=\boldsymbol{D}_{i}\otimes \boldsymbol{D}_{i}$ is the identity for 3-space and $\delta _{\mathit{AB}}$ is the Kronecker delta. Thus $\boldsymbol{G}=\boldsymbol{I}$ and the formula $\boldsymbol{G}^{t}\boldsymbol{G}^{\ast }=(\det \boldsymbol{G)I}$ leads, with (22), to

$$ G_{\mathit{iC}}\gamma _{i}=G_{\mathit{iC}}G_{\mathit{iD}}^{\ast }\Gamma _{\mathit{DB}}D_{B}=\delta _{\mathit{CD}} \Gamma _{\mathit{DB}}D_{B}=\Gamma _{\mathit{CB}}D_{B}. $$

(26)

Equation (14), expressed in the form $\boldsymbol{\gamma }=G_{\mathit{iC}}\gamma _{i}\boldsymbol{E}_{C}$, is thus equivalent to (21).

3 Three Families of Fibers: Kinematics and Constitutive Response

We consider an elastic solid with three families of embedded fibers having unit tangents $\boldsymbol{D}_{(k)}(\boldsymbol{X})$; $k=1,2,3$, in $\kappa$. These are modeled as continuously distributed curves endowed with the mechanical properties of extensible, but unshearable, rods. Here and henceforth subscripts enclosed in parentheses are exempted from the summation convention for repeated indices. Thus each point of the continuum is a point of intersection of three fibers, one from each family. We assume the set $\{\boldsymbol{D}_{(k)}\}$ to be linearly independent and positively oriented at each $\boldsymbol{X}\in \kappa$. This set is used to define a local lattice basis $\{\boldsymbol{L}_{i}\}$, with $\boldsymbol{L}_{i}=\boldsymbol{D}_{(i)}$, and an associated reciprocal basis $\boldsymbol{L}^{i}$.

The rotation field associated with the $k^{\mathit{th}}$ fiber family is (cf. (4))

$$ \boldsymbol{R}_{(k)}=\boldsymbol{d}_{(k)i}\otimes \boldsymbol{D}_{(k)i}, $$

(27)

in which $\{\boldsymbol{D}_{(k)i}\}=\{\boldsymbol{D}_{(k)},\boldsymbol{D}_{(k)\alpha }\}$ and $\{\boldsymbol{d}_{(k)i}\}=\{\boldsymbol{d}_{(k)},\boldsymbol{d}_{(k)\alpha }\}$ are right-handed orthonormal triads with $\boldsymbol{d}_{(k)}$ the unit tangent to the $k^{\mathit{th}}$ fiber after deformation. The latter are used to define the deformed lattice basis $\{\boldsymbol{l}_{i}\}$, with $\boldsymbol{l}_{i}=\boldsymbol{d}_{(i)}$. The fibers are assumed to convect with the continuum deformation. Accordingly, as in (2),

$$ \boldsymbol{D}_{(k)\alpha }\cdot \boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}=0;\quad \alpha =2,3; \quad k=1,2,3, $$

(28)

with

$$ \boldsymbol{E}_{(k)}=\boldsymbol{\boldsymbol{R}}_{(k)}^{t}\boldsymbol{F}. $$

(29)

With (1)₃ and (29) the fiber stretches are given simply by

$$ \lambda _{(k)}=\left \vert \boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}\right \vert . $$

(30)

Pursuant to the discussion in Sect. 2, we assume the constitutive response of the fibrous material to be embodied in a strain-energy density

$$ U(\boldsymbol{F},\boldsymbol{R}_{(1)},\boldsymbol{R}_{(2)},\boldsymbol{R}_{(3)},\nabla \boldsymbol{R}_{(1)},\nabla \boldsymbol{R}_{(2)},\nabla \boldsymbol{R}_{(3)};\boldsymbol{X}), $$

(31)

per unit volume of $\kappa$, where $\nabla \boldsymbol{R}_{(k)}$ are the rotation gradients. We show in Appendix A that this energy is Galilean invariant if and only if

$$ U=W(\boldsymbol{E}_{(1)},\boldsymbol{E}_{(2)},\boldsymbol{E}_{(3)}, \boldsymbol{\Gamma }_{(1)},\boldsymbol{\Gamma }_{(2)},\boldsymbol{\Gamma }_{(3)};\boldsymbol{X}), $$

(32)

where $W$ is the reduced strain-energy function, and (cf. Equation (19), (20))

$$ \boldsymbol{\Gamma }_{(k)}=\Gamma _{(k)\mathit{DC}}\boldsymbol{E}_{D}\otimes \boldsymbol{E}_{C};\quad \Gamma _{(k)\mathit{DC}}=\frac{1}{2}e_{\mathit{BAD}}R_{(k)\mathit{iA}}R_{(k)\mathit{iB},C} $$

(33)

are the fiber wryness tensors.

Because the Cosserat effect is conferred by the fibers, it is appropriate to require that the strain energy depend on the $\boldsymbol{\Gamma }_{(k)}$ via the fiber flexure/twist strain vectors (cf. Equation (21))

$$ \boldsymbol{\gamma }_{(k)}=\boldsymbol{\Gamma }_{(k)}\boldsymbol{D}_{(k)}, $$

(34)

and hence that

$$ W=w(\boldsymbol{E}_{(1)}\boldsymbol{,\boldsymbol{E}}_{(2)},\boldsymbol{\boldsymbol{E}}_{(3)},\boldsymbol{\gamma }_{(1)},\boldsymbol{\gamma }_{(2)},\boldsymbol{\gamma }_{(3)};\boldsymbol{X}), $$

(35)

for some function $w$. Evidently $W$ depends explicitly on $\boldsymbol{X}$ (via the $\boldsymbol{D}_{(k)}(\boldsymbol{X})$) even if there is no such explicit dependence in $w$.

We introduce Cosserat stresses $\boldsymbol{\sigma }_{(k)}$ and couple stresses $\boldsymbol{\mu }_{(k)}$. These are power-conjugate to $\boldsymbol{E}_{(k)}$ and $\boldsymbol{\Gamma }_{(k)}$, respectively, i.e.,

$$ \dot{W}=\sum (\boldsymbol{\sigma }_{(k)}\cdot \dot{\boldsymbol{E}}_{(k)}+\boldsymbol{\mu }_{(k)} \cdot \dot{\boldsymbol{\Gamma }}_{(k)}), $$

(36)

where superposed dots refer to derivatives, with respect to a parameter, of one-parameter families of deformation and fiber-rotation fields, and the sum is on $k$ from 1 to 3. Thus,

$$ \boldsymbol{\sigma }_{(k)}=W_{\boldsymbol{E}_{(k)}}\quad \mbox{and}\quad \boldsymbol{\mu }_{(k)}=W_{ \boldsymbol{\Gamma }_{(k)}}. $$

(37)

These presume that the $\boldsymbol{E}_{(k)}$ and $\boldsymbol{\Gamma }_{(k)}$ may be varied independently. Accordingly $W$ is regarded here and henceforth as an extension of the actual energy from the manifold defined by the constraints (28).

In terms of the (extended) energy $w$ we have

$$ \boldsymbol{\sigma }_{(k)}=w_{\boldsymbol{E}_{(k)}}, $$

(38)

whereas the couple stresses follow by varying the energy at fixed $\boldsymbol{E}_{(k)}$ and fixing all but one of the $\boldsymbol{\Gamma }_{(k)}$ in succession. With $\dot{\boldsymbol{\gamma }}_{(k)}=\dot{\boldsymbol{\Gamma }}_{(k)}\boldsymbol{D}_{(k)}$ it then follows that

$$ \boldsymbol{\mu }_{(k)}\cdot \dot{\boldsymbol{\Gamma }}_{(k)}=\dot{W}=\dot{w}=w_{\boldsymbol{\gamma }_{(k)}}\cdot \dot{\boldsymbol{\gamma }}_{(k)}=\boldsymbol{M}_{(k)}\otimes \boldsymbol{D}_{(k)}\cdot \dot{\boldsymbol{\Gamma }}_{(k)}, $$

(39)

where

$$ \boldsymbol{M}_{(k)}=w_{\boldsymbol{\gamma }_{(k)}}. $$

(40)

Finally,

$$ \boldsymbol{\mu }_{(k)}=\boldsymbol{M}_{(k)}\otimes \boldsymbol{D}_{(k)}\quad \textrm{and}\quad \boldsymbol{R}_{(k)}\boldsymbol{\mu }_{(k)}=\boldsymbol{m}_{(k)}\otimes \boldsymbol{D}_{(k)}, \quad \mbox{where}\quad \boldsymbol{m}_{(k)}=\boldsymbol{R}_{(k)}\boldsymbol{M}_{(k)}. $$

(41)

We shall see later that the vector $\boldsymbol{m}_{(k)}$ may be interpreted as the moment per unit area acting on the ‘cross sections’ of the fibers of the $k^{\mathit{th}}$ family.

4 Partwise Virtual Power and Equilibrium

We define equilibria to be states that satisfy the virtual-power statement

$$ \dot{E}=P, $$

(42)

where $P$ is the virtual power of agencies acting on an arbitrary subvolume $\pi \subset \kappa$ of the body,

$$ E=\int _{\pi }[W+\sum \Lambda _{(k)\alpha }\boldsymbol{D}_{(k)\alpha }\cdot \boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}]dv $$

(43)

is the extended energy of $\pi$, $\Lambda _{(k)\alpha }$ are Lagrange multipliers associated with the constraints (28) [18], and superposed dots are used to denote variational derivatives, evaluated at the considered equilibrium state.

The variation of the extended energy is

$$ \dot{E}=\int _{\pi }\{\sum [(\boldsymbol{\sigma }_{(k)}+\boldsymbol{\Lambda }_{(k)}\otimes \boldsymbol{D}_{(k)})\cdot \dot{\boldsymbol{E}}_{(k)}+\boldsymbol{\mu }_{(k)}\cdot \dot{\boldsymbol{\Gamma }}_{(k)}]\}dv, $$

(44)

where

$$ \boldsymbol{\Lambda }_{(k)}=\Lambda _{(k)\alpha }\boldsymbol{D}_{(k)\alpha } $$

(45)

and the variations $\dot{\Lambda }_{(k)\alpha }$ have been suppressed as these merely return the constraints as Euler equations.

To reduce this we use (29) in the form

$$ \dot{\boldsymbol{E}}_{(k)}=\boldsymbol{R}_{(k)}^{t}(\nabla \boldsymbol{u}-\boldsymbol{\Omega }_{(k)} \boldsymbol{F}),\quad \mbox{where}\quad \boldsymbol{u}=\dot{\boldsymbol{\chi }} \quad \mbox{and}\quad \boldsymbol{\Omega }_{(k)}=\dot{\boldsymbol{R}}_{(k)}\boldsymbol{R}_{(k)}^{t}. $$

(46)

We also have (see Appendix B)

$$ \dot{\boldsymbol{\Gamma }}_{(k)}=\boldsymbol{R}_{(k)}^{t}\nabla \boldsymbol{\omega }_{(k)}\boldsymbol{,} $$

(47)

where $\boldsymbol{\omega }_{(k)}=\mathit{ax}\boldsymbol{\Omega }_{(k)}\boldsymbol{.}$ We combine these results with (44) and integrate by parts, reaching

$$\begin{aligned} \dot{E} =&\int _{\partial \pi }(\boldsymbol{P\nu \cdot u}+\sum \boldsymbol{R}_{(k)}\boldsymbol{\mu }_{(k)}\boldsymbol{\nu }\cdot \boldsymbol{\omega }_{(k)})\mathit{da}-\int _{\pi }\boldsymbol{u}\cdot \mathit{Div}\boldsymbol{P}dv \\ &-\int _{\pi }\sum \boldsymbol{\omega }_{(k)}\cdot \{\mathit{Div}(\boldsymbol{R}_{(k)} \boldsymbol{\mu }_{(k)}\boldsymbol{)}+2ax(\boldsymbol{R}_{(k)}\mathit{Skw}[(\boldsymbol{\sigma }_{(k)}+\boldsymbol{\Lambda }_{(k)}\otimes \boldsymbol{D}_{(k)}\boldsymbol{)E}_{(k)}^{t}]\boldsymbol{R}_{(k)}^{t})\}dv, \end{aligned}$$

(48)

where $\boldsymbol{\nu }$ is the exterior unit normal to $\partial \pi$; where

$$ \boldsymbol{P}=\sum (\boldsymbol{R}_{(k)}\boldsymbol{\sigma }_{(k)}+\boldsymbol{\lambda }_{(k)}\otimes \boldsymbol{D}_{(k)}),\quad \text{with}\quad \boldsymbol{\lambda }_{(k)}=\boldsymbol{R}_{(k)}\boldsymbol{\Lambda }_{(k)}=\Lambda _{(k)\alpha }\boldsymbol{d}_{(k)\alpha }, $$

(49)

and where $\mathit{Div}$ is the divergence with respect to $\boldsymbol{X}$.

Remarks 1

1. Fiber inextensibility is accommodated by appending the constraints $\left \vert \boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}\right \vert =1$. With

$$ \left \vert \boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}\right \vert ^{\cdot }=\left \vert \boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}\right \vert ^{-1}\boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}\otimes \boldsymbol{D}_{(k)}\cdot \dot{\boldsymbol{E}}_{(k)} $$

(50)

and (cf. Equation (1)) $\lambda _{(k)}\boldsymbol{D}_{(k)}=\boldsymbol{E}_{(k)}\boldsymbol{D}_{(k)}$, we find that $\boldsymbol{\Lambda }_{(k)}$ and $\boldsymbol{\lambda }_{(k)}$ in the foregoing are now 3-vectors given respectively by $\Lambda _{(k)i}\boldsymbol{D}_{i}$ and $\Lambda _{(k)i}\boldsymbol{d}_{i}$ in which $\Lambda _{(k)1}$ are constitutively indeterminate axial stresses transmitted by the fibers [19].

2. Incompressibility entails the constraint $\det \boldsymbol{F}=1$, the effect of which is to replace $\boldsymbol{P}$ in (49) by

$$ \boldsymbol{P}=\sum (\boldsymbol{R}_{(k)}\boldsymbol{\sigma }_{(k)}+\boldsymbol{\lambda }_{(k)}\otimes \boldsymbol{D}_{(k)}\boldsymbol{)}-p\boldsymbol{F}^{\ast }, $$

(51)

where $p$ is a constitutively indeterminate pressure field [20].

5 Lattice Connectivity

Inspired by the mechanics of a lattice of discrete rods [21], we contemplate three distinct types of interaction of the fibers at their points of intersection, i.e., at the material points of the continuum.

5.1 Independent Fiber Rotations

This models ball-and-socket joints in a discrete lattice [21]. In the present context, however, we have in mind solid junctions of intersecting fibers that offer elastic resistance to relative fiber shear and rotation. This seems to us to furnish a faithful representation of the actual situation in a manufactured fibrous metamaterial [1, 4].

In this case the virtual spin velocities $\boldsymbol{\omega }_{(k)}$ are independent and (42), (48) furnish the virtual power

$$ P=\int _{\partial \pi }(\boldsymbol{t}\cdot \boldsymbol{u}+\sum \boldsymbol{c}_{(k)}\cdot \boldsymbol{\omega }_{(k)})da+\int _{\pi }(\boldsymbol{g}\cdot \boldsymbol{u}+\sum \boldsymbol{\pi }_{(k)}\cdot \boldsymbol{\omega }_{(k)})dv, $$

(52)

where $\boldsymbol{t}$ is the traction, $\boldsymbol{g}$ is the body force, and $\boldsymbol{c}_{(k)}$ and $\boldsymbol{\pi }_{(k)}$ respectively are the couple traction and body couple acting on the $k^{\mathit{th}}$ fiber family, with

$$ \boldsymbol{g}=-\mathit{Div}\boldsymbol{P}\quad \text{and}\quad \boldsymbol{\pi }_{(k)}=-\mathit{Div}(\boldsymbol{R}_{(k)}\boldsymbol{\mu }_{(k)})-2ax\{\boldsymbol{R}_{(k)}\mathit{Skw}[(\boldsymbol{\sigma }_{(k)}+\boldsymbol{\Lambda }_{(k)}\otimes \boldsymbol{D}_{(k)})\boldsymbol{E}_{(k)}^{t}]\boldsymbol{R}_{(k)}^{t}\}, $$

(53)

and with

$$ \boldsymbol{t}=\boldsymbol{P\nu }\quad \text{and}\quad \boldsymbol{c}_{(k)}=\boldsymbol{R}_{(k)}\boldsymbol{\mu }_{(k)}\boldsymbol{\nu }. $$

(54)

We use (41)₂ to recast the force and couple tractions as

$$ \boldsymbol{t}=\sum (\boldsymbol{R}_{(k)}\boldsymbol{\sigma }_{(k)}\boldsymbol{\nu} +(\boldsymbol{D}_{(k)}\cdot \boldsymbol{\nu} )\boldsymbol{\lambda }_{(k)})\quad\text{and}\quad \boldsymbol{c}_{(k)}=(\boldsymbol{D}_{(k)}\cdot \boldsymbol{\nu} )\boldsymbol{m}_{(k)}, $$

(55)

and thus interpret $\boldsymbol{\lambda }_{(k)}$ and $\boldsymbol{m}_{(k)}$, respectively, as shear force and moment densities acting on the ‘cross sections’ of the fibers of the $k^{\mathit{th}}$ family; that is, on surfaces that intersect the fibers orthogonally $(\boldsymbol{D}_{(k)}\cdot \boldsymbol{\nu }=\pm 1)$.

5.2 Rotations with a Common Orientation

Here we contemplate nodal pivots in a discrete lattice [21] at which the intersecting rods are pinned in such a way as to allow them to undergo rotations having a common orientation. In the present context this is modeled as

$$ \boldsymbol{R}_{(k)}\boldsymbol{N}=\boldsymbol{ n}, $$

(56)

in which $\boldsymbol{N}(\boldsymbol{X})$ is an assigned unit-vector field aligned locally with the axes of the pivots. These are acted upon by the $\boldsymbol{R}_{(k)}$ to generate a field of pivotal axes that evolve in the course of deformation. It may be helpful to think of $\boldsymbol{N}$ as a field of unit normals to a surface consisting of continuously distributed pivots. Then $\boldsymbol{n}$ is the field of unit vectors aligned with the pivot axes after deformation. A 3D-printed pantographic lattice of this kind is depicted in the cover image of [3].

The variational form of (56) is $\dot{\boldsymbol{R}}_{(k)}\boldsymbol{N=\dot{n}}$, i.e.,

$$ \boldsymbol{\omega }_{(k)}\times \boldsymbol{n}=\boldsymbol{\beta} \times \boldsymbol{n}, $$

(57)

where $\boldsymbol{\beta }$ is an arbitrary vector field. Then,

$$ \boldsymbol{\omega }_{(k)}=\alpha _{(k)}\boldsymbol{n}+\boldsymbol{n}\times (\boldsymbol{\beta} \times \boldsymbol{n}), $$

(58)

where the $\alpha _{(k)}$ are arbitrary scalar fields. The virtual power takes the form

$$ P=\int _{\partial \pi }(\boldsymbol{t}\cdot \boldsymbol{u}+\boldsymbol{\delta} \cdot \boldsymbol{\beta }+\sum c_{(k)} \alpha _{(k)})da+\int _{\pi }(\boldsymbol{g}\cdot \boldsymbol{u}+\boldsymbol{\phi} \cdot \boldsymbol{\beta }+ \sum \pi _{(k)}\alpha _{(k)})dv, $$

(59)

where $\boldsymbol{g}$ and $\boldsymbol{t}$ are given by (53)₁ and (54)₁; and

$$ c_{(k)}=\boldsymbol{c}_{(k)}\cdot \boldsymbol{n}\quad \text{and}\quad \pi _{(k)}=\boldsymbol{\pi }_{(k)}\cdot \boldsymbol{n} $$

(60)

are axial couple tractions and body couples acting on the pivots, with $\boldsymbol{\pi }_{(k)}$ and $\boldsymbol{c}_{(k)}$ given by (53)₂ and (54)₂, respectively; and

$$ \boldsymbol{\delta }=\boldsymbol{n}\times (\boldsymbol{c}\times \boldsymbol{n})\quad \mbox{and}\quad \boldsymbol{\phi} =\boldsymbol{n}\times (\boldsymbol{\pi} \times \boldsymbol{n}) $$

(61)

are bending couples, where

$$ \boldsymbol{c}=\sum \boldsymbol{c}_{(k)} $$

(62)

is the net couple traction and

$$ \boldsymbol{\pi }=\sum \boldsymbol{\pi }_{(k)} $$

(63)

is the net body couple.

5.3 Rigid Joints

It is appropriate to idealize the solid joints of a lattice as rigid if they are sufficiently stiff. This is modeled by assigning a common rotation to each fiber family. Thus,

$$ \boldsymbol{R}_{(k)}=\boldsymbol{R}, $$

(64)

implying that all fibers suffer the same Cosserat strain:

$$ \boldsymbol{E}_{(k)}=\boldsymbol{E=R}^{t}\boldsymbol{F}. $$

(65)

The virtual fiber spins are also equal, i.e., $\boldsymbol{\omega }_{(k)}=\boldsymbol{\omega }$, where $\boldsymbol{\omega }=\mathit{ax}(\dot{\boldsymbol{R}R}^{t})$, and (42), (48) deliver the virtual power

$$ P=\int _{\partial \pi }(\boldsymbol{t}\cdot \boldsymbol{u}+ \boldsymbol{c}\cdot \boldsymbol{\omega} )da+\int _{\pi }(\boldsymbol{g}\cdot \boldsymbol{u}+\boldsymbol{\pi} \cdot \boldsymbol{\omega} )dv. $$

(66)

Remarks 2

1. From (1) it follows that the deformation gradient may be represented in terms of the lattice bases, defined in Sect. 3, as

$$ \boldsymbol{F}=\boldsymbol{FL}_{i}\otimes \boldsymbol{L}^{i}=\sum \lambda _{(i)}\boldsymbol{l}_{i}\otimes \boldsymbol{L}^{i}=\sum \lambda _{(i)}\boldsymbol{R}_{(i)}\boldsymbol{L}_{i}\otimes \boldsymbol{L}^{i}, $$

(67)

so that, for a rigidly connected lattice,

$$ \boldsymbol{E}=\sum \lambda _{(i)}\boldsymbol{L}_{i}\otimes \boldsymbol{L}^{i}\quad \text{and}\quad \boldsymbol{R}=\boldsymbol{l}_{i}\otimes \boldsymbol{L}^{i}. $$

(68)

We conclude that if the fibers are inextensible, i.e., if $\lambda _{(i)}=1$, then $\boldsymbol{E}=\boldsymbol{L}_{i}\otimes \boldsymbol{L}^{i}=\boldsymbol{I}$, $\boldsymbol{R}=\nabla \boldsymbol{\chi }$ and $\boldsymbol{\chi }$ is thus a rigid-body deformation. Accordingly, we expect a rigidly connected lattice to be extremely stiff if the extensional stiffnesses of the fibers are large. Indeed this is a principal feature of lattice-type metamaterials [1, 4].

Further, as $\lambda _{(i)}=\left \vert \boldsymbol{FL}_{i}\right \vert$ it follows that $\boldsymbol{E}$ and $\boldsymbol{R}$ are determined by $\boldsymbol{F}$. Because the strain-energy function depends on $\nabla \boldsymbol{R}$, we conclude that rigidly connected lattices furnish examples of second-grade elastic materials. In this case the virtual spin $\boldsymbol{\omega }$ in (66) may be expressed as a linear form in $\nabla \boldsymbol{u}$ [2].

2. Equation (68) implies that

$$ \boldsymbol{EL}_{i}=\lambda _{(i)}\boldsymbol{L}_{i}, $$

(69)

and hence that $\boldsymbol{L}^{i}\cdot \boldsymbol{EL}_{j}=\lambda _{(j)}\delta _{j}^{i}$, where $\delta _{j}^{i}$ is the Kronecker delta. Thus,

$$ \boldsymbol{L}^{i}\cdot \boldsymbol{EL}_{j}=0;\quad i\neq j. $$

(70)

These furnish constraints on $\boldsymbol{F}$. To proceed with the derivation of the equilibrium equations via (42), (48) and (66), we impose them in lieu of (28). Accordingly the $\Lambda _{(k)\alpha }$ are suppressed in the foregoing formulae. Because $\boldsymbol{F}$ is a gradient these constraints give rise to distinct sets of alternative Lagrange multipliers in the interior and at the boundary [2].

In the case of a rigidly connected orthogonal lattice we have $\boldsymbol{L}^{i}=\boldsymbol{L}_{i}$, and (65), (68) then imply that $\boldsymbol{E}$ is the right-stretch factor in the polar decomposition of the deformation gradient, whereas $\boldsymbol{R}$ is simply the rotation factor. This case is studied in detail in [2], where the constraints (70) are imposed in the form

$$ \boldsymbol{FL}_{i}\cdot \boldsymbol{FL}_{j}=0;\quad i\neq j. $$

(71)

3. Because the energy is Galilean invariant, with the constraints in effect arbitrary rigid-body variations yield $P=0$, where $P$ is given by (60) in which $\boldsymbol{\omega }$ is uniform and $\boldsymbol{u}=\boldsymbol{\omega} \times \boldsymbol{x}+\boldsymbol{a}$, where $\boldsymbol{a}$ is also uniform and $\boldsymbol{x}=\boldsymbol{\chi} (\boldsymbol{X})$ is an equilibrium deformation. For this it is necessary and sufficient that the global force and moment balances

$$ \int _{\partial \pi }\boldsymbol{t}\mathit{da}+\int _{\pi }\boldsymbol{g}dv=\boldsymbol{0}\quad \text{and}\quad \int _{\partial \pi }(\boldsymbol{x\times t+c)}da+\int _{ \pi }(\boldsymbol{x}\times \boldsymbol{g}+\boldsymbol{\pi} )dv=\boldsymbol{0}, $$

(72)

respectively, be satisfied. These are necessary, but not sufficient, for the equilibrium Eqs. (53)₂, (54)₂ and (60), (61), the arbitrariness of $\pi$ notwithstanding. A similar conclusion follows in the case of rigid connectivity, with (72) modified to take account of edge forces - operative if $\partial \pi$ is piecewise smooth - and a double force, both types being associated with second-grade elasticity [2]. This situation stands in contrast to conventional elasticity theory in which partwise global balances of force and moment are both necessary and sufficient for equilibrium.

6 Example: Finite Torsion

To illustrate the theory we consider finite torsion of a right circular cylinder of annular cross section composed of a uniform incompressible material, with response functions contrived so as to facilitate the appropriation of standard results from conventional elasticity theory. We adopt the decoupled energy

$$ w(\boldsymbol{E}_{(1)},\boldsymbol{E}_{(2)},\boldsymbol{E}_{(3)}, \boldsymbol{\gamma }_{(1)},\boldsymbol{\gamma }_{(2)},\boldsymbol{\gamma }_{(3)})=\varpi ( \boldsymbol{E}_{(1)},\boldsymbol{E}_{(2)},\boldsymbol{E} _{(3)})+\varphi (\boldsymbol{\gamma }_{(1)},\boldsymbol{\gamma }_{(2)},\boldsymbol{\gamma }_{(3)}), $$

(73)

in which $\varphi$ is a homogeneous quadratic function. As justification we note that the dependence of $w$ on the $\boldsymbol{\gamma }_{(k)}$ introduces natural length scales into the constitutive theory which are on the order of the diameters of the actual fiber cross sections or the fiber spacings. We use $l$, the largest of these, to define the dimensionless flexure/twist strains $l\boldsymbol{\gamma }_{(k)}$. Assuming $\left \vert l\boldsymbol{\gamma }_{(k)}\right \vert \ll 1$ in typical applications and that the moments $\boldsymbol{m}_{(k)}$ vanish when the $\boldsymbol{\gamma }_{(k)}$ vanish, we arrive at (73) provided that $w$ is a differentiable function and $\left \vert \boldsymbol{E}_{(k)}-\boldsymbol{I}\right \vert$ are small. Drawing on the mechanics of discrete lattices [21] for motivation, we further assume that $\varphi$ is decoupled, i.e.,

$$ \varphi =\sum \varphi _{k}(\boldsymbol{\gamma }_{(k)}), $$

(74)

in which each $\varphi _{k}$ is a homogeneous quadratic function, yielding

$$ \boldsymbol{m}_{(k)}=(\varphi _{k})_{\boldsymbol{\gamma }_{(k)}}. $$

(75)

For $\varpi$ we take

$$ \varpi =\frac{\mu }{6}[\sum \mathit{tr}(\boldsymbol{E}_{(k)}^{t}\boldsymbol{E}_{(k)})-3], $$

(76)

in which $\mu$ is a positive constant. The sum is $3\mathit{tr}(\boldsymbol{F}^{t}\boldsymbol{F)}$ and $\varpi$ is simply the conventional neo-Hookean energy. This furnishes

$$ \boldsymbol{\sigma }_{(k)}=\frac{\mu }{3}\boldsymbol{E}_{(k)} \quad \mbox{and}\quad \boldsymbol{R}_{(k)}\boldsymbol{\sigma }_{(k)}=\frac{\mu }{3}\boldsymbol{F}, $$

(77)

yielding (cf. (49))

$$ \boldsymbol{P}=\mu \boldsymbol{F}-p\boldsymbol{F}^{\ast }+\sum \boldsymbol{\lambda }_{(k)}\otimes \boldsymbol{D}_{(k)}, $$

(78)

in which the $\boldsymbol{D}_{(k)}$ remain to be specified. In the absence of body force and with the incompressibility constraint in effect, (53)₁ then reduces to

$$ \mu \mathit{div}\boldsymbol{B}+\sum [(\nabla \boldsymbol{\lambda }_{(k)})\boldsymbol{D}_{(k)}+(\mathit{Div}\boldsymbol{D}_{(k)}) \boldsymbol{\lambda }_{(k)}]=\mathit{gradp}, $$

(79)

where $\boldsymbol{B}=\boldsymbol{FF}^{t}$ is the left Cauchy-Green deformation tensor and $\mathit{div}$ and $\mathit{grad}$ are the divergence and gradient with respect to $\boldsymbol{x}=\boldsymbol{\chi} (\boldsymbol{X})$.

We assume the fiber rotations to be independent as described in Sect. 5.1. In this case (53)₂ is operative and reduces, in the absence of body couples and with the aid of (41)₂, to

$$ (\nabla \boldsymbol{m}_{(k)})\boldsymbol{D}_{(k)}+(\mathit{Div}\boldsymbol{D}_{(k)})\boldsymbol{m}_{(k)}+2ax\{\boldsymbol{R}_{(k)}\mathit{Skw}[(\boldsymbol{\sigma }_{(k)}+\boldsymbol{\Lambda }_{(k)}\otimes \boldsymbol{D}_{(k)})\boldsymbol{E}_{(k)}^{t}]\boldsymbol{R}_{(k)}^{t}\}=\boldsymbol{0}, $$

(80)

where

$$\begin{aligned} 2ax\{\boldsymbol{R}_{(k)}\mathit{Skw}[(\boldsymbol{\Lambda }_{(k)}\otimes \boldsymbol{D}_{(k)})\boldsymbol{E}_{(k)}^{t}]\boldsymbol{R}_{(k)}^{t}\} =&2ax\{\mathit{Skw}[\boldsymbol{R}_{(k)}(\boldsymbol{\Lambda }_{(k)}\otimes \boldsymbol{D}_{(k)})\boldsymbol{E}_{(k)}^{t}\boldsymbol{R}_{(k)}^{t}]\} \\ =&2ax[\mathit{Skw}(\boldsymbol{\lambda }_{(k)}\otimes \boldsymbol{FD}_{(k)})] \\ =&\mathit{ax}(\boldsymbol{\lambda }_{(k)}\otimes \boldsymbol{FD}_{(k)}-\boldsymbol{FD}_{(k)}\otimes \boldsymbol{\lambda }_{(k)}) \\ =&\boldsymbol{FD}_{(k)}\times \boldsymbol{\lambda }_{(k)}. \end{aligned}$$

(81)

From (77)₁ we have $\mathit{Skw}(\boldsymbol{\sigma }_{(k)}\boldsymbol{E}_{(k)}^{t})=\boldsymbol{0}$, implying that there are no distributed couples transmitted to the fibers. Nevertheless the energy (76) assigns elastic resistance to the fiber junctions. Thus the moment balance for the $k^{\mathit{th}}$ fiber family reduces to

$$ (\nabla \boldsymbol{m}_{(k)})\boldsymbol{D}_{(k)}+(\mathit{Div}\boldsymbol{D}_{(k)})\boldsymbol{m}_{(k)}+\boldsymbol{FD}_{(k)}\times \boldsymbol{\lambda }_{(k)}=\boldsymbol{0}. $$

(82)

We are finally in a position to analyze the torsion problem. We assume the reference configuration to be the region defined by $(0<)A\leq R\leq B$, $0\leq \theta <2\pi$, $0\leq Z\leq L$ in a cylindrical polar coordinate system $(R,\theta ,Z)$. Position of a material point in this region is given by

$$ \boldsymbol{X}=R\boldsymbol{e}_{r}(\theta )+Z\boldsymbol{k}, $$

(83)

where $\boldsymbol{e}_{r}(\theta )$ is the radial unit vector at azimuth $\theta$, directed away from the cylinder axis, $\boldsymbol{k}$ is the fixed unit vector directed along the axis, and $\boldsymbol{e}_{\theta }(\theta )=\boldsymbol{k\times e}_{r}$. We assume a deformation of the form

$$ \boldsymbol{\chi} (\boldsymbol{X})=r(R)\boldsymbol{e}_{r}(\phi )+Z\boldsymbol{k}, \quad \mbox{where}\quad \phi =\theta +\tau Z $$

(84)

in which $\tau$ - the twist per unit length - is a specified constant. The deformation gradient is

$$ \boldsymbol{F}=\boldsymbol{Q}\bar{\boldsymbol{F}},\quad \text{with}\quad \bar{\boldsymbol{F}}=r^{\prime }(R)\boldsymbol{e}_{r}(\theta )\otimes \boldsymbol{e}_{r}(\theta )+(r/R)\boldsymbol{e}_{\theta }(\theta )\otimes \boldsymbol{e}_{\theta }(\theta )+r\tau \boldsymbol{e}_{\theta }(\theta )\otimes \boldsymbol{k}+\boldsymbol{k}\otimes \boldsymbol{k}, $$

(85)

where

$$ \boldsymbol{Q} =\boldsymbol{e}_{r}(\phi )\otimes \boldsymbol{e}_{r}(\theta )+\boldsymbol{e}_{\theta }(\phi )\otimes \boldsymbol{e}_{\theta }(\theta )+\boldsymbol{k}\otimes \boldsymbol{k} $$

(86)

is a rotation, and the deformation is isochoric provided that $\mathit{rr}^{\prime }(R)=R$, i.e.,

$$ r^{2}-a^{2}=R^{2}-A^{2},\quad \text{with}\quad a=r(A). $$

(87)

We assume the fibers to be initially orthogonal and aligned with the coordinate axes: $\boldsymbol{D}_{(1)}=\boldsymbol{e}_{r}(\theta )$, $\boldsymbol{D}_{(2)}=\boldsymbol{e}_{\theta }(\theta )$ and $\boldsymbol{D}_{(3)}=\boldsymbol{k}$. Then (1) and (85) yield the fiber stretches $\lambda _{(1)}=R/r$, $\lambda _{(2)}=r/R$ and $\lambda _{(3)}=\sqrt{r^{2}\tau ^{2}+1}$, together with the fiber direction fields

$$ \boldsymbol{d}_{(1)}=\boldsymbol{e}_{r}(\phi ),\quad \boldsymbol{d}_{(2)}=\boldsymbol{e}_{\theta }(\phi )\quad \text{and}\quad \boldsymbol{d}_{(3)}=\lambda _{(3)}^{-1}(r \tau \boldsymbol{e}_{\theta }(\phi )+\boldsymbol{k}), $$

(88)

after deformation. Accordingly (27) implies that $\boldsymbol{R}_{(1)}\boldsymbol{e}_{r}(\theta )=\boldsymbol{e}_{r}(\phi )$ and $\boldsymbol{R}_{(2)}\boldsymbol{e}_{\theta }(\theta )=\boldsymbol{e}_{\theta }(\phi )$. Thus we satisfy the constraints (28), with $\{\boldsymbol{D}_{(1)\alpha }\}=\{\boldsymbol{e}_{\theta }(\theta ),\boldsymbol{k\}}$ and $\{\boldsymbol{D}_{(2)\alpha }\}=\{\boldsymbol{k,\boldsymbol{e}}_{r}(\theta )\}$, by taking

$$ \boldsymbol{R}_{(1)}=\boldsymbol{R}_{(2)}=\boldsymbol{Q}. $$

(89)

To compute the induced flexure/twist strains $\boldsymbol{\gamma }_{(1)}$, $\boldsymbol{\gamma }_{(2)}$ we use (14), i.e., $\boldsymbol{\gamma }_{(1)}=\mathit{ax}(\boldsymbol{R}_{(1)}^{t}\boldsymbol{R}_{(1)}^{\prime })$, with $(\cdot )^{\prime }=\partial (\cdot )/\partial R$; and $\boldsymbol{\gamma }_{(2)}=\mathit{ax}(\boldsymbol{R}_{(2)}^{t}\boldsymbol{R}_{(2)}^{\prime })$, with $(\cdot )^{\prime }=R^{-1}\partial (\cdot )/\partial \theta$. In the first instance $\boldsymbol{R}_{(1)}^{\prime }$, and hence $\boldsymbol{\gamma }_{(1)}$, vanish trivially. In the second, we have

$$ \boldsymbol{R}_{(2)}^{\prime }=(\theta ^{\prime }-\phi ^{\prime })[\boldsymbol{e}_{r}(\phi )\otimes \boldsymbol{e}_{\theta }(\theta )-\boldsymbol{e}_{\theta }(\phi ) \otimes \boldsymbol{e}_{r}(\theta )], $$

(90)

and this vanishes because $\theta ^{\prime }=\phi ^{\prime }(=R^{-1})$. Thus $\boldsymbol{\gamma }_{(2)}$ also vanishes. This is due to the fact that the $\boldsymbol{\gamma }_{(k)}$ are computed using referential arclength derivatives along the fibers. Thus, whereas the actual curvatures of the circular fibers of the azimuthal fiber family change in the course of deformation, the Galilean-invariant measure (10) retains its original value and $\boldsymbol{\gamma }_{(2)}$ vanishes (cf. (11)). Our assumptions then imply that $\boldsymbol{m}_{(1)}$ and $\boldsymbol{m}_{(2)}$ vanish identically, and (82) reduces to

$$ \boldsymbol{d}_{(k)}\times \boldsymbol{\lambda }_{(k)}=\boldsymbol{0};\quad k=1,2. $$

(91)

Because $\boldsymbol{d}_{(k)}\cdot \boldsymbol{\lambda }_{(k)}=0$ (cf. (49)) these imply that $\boldsymbol{\lambda }_{(1)}$ and $\boldsymbol{\lambda }_{(2)}$ vanish and hence that (79) and (82) become

$$ \mu \mathit{div}\boldsymbol{B}+\boldsymbol{\lambda }^{\prime }=\mathit{gradp}\quad \textrm{and}\quad \boldsymbol{m}^{\prime }+\boldsymbol{\chi }^{\prime }\times \boldsymbol{\lambda} =\boldsymbol{0}, $$

(92)

respectively, where $\boldsymbol{\lambda} =\boldsymbol{\lambda }_{(3)}$, $\boldsymbol{m}=\boldsymbol{m}_{(3)}$ and $(\cdot )^{\prime }=\partial (\cdot )/\partial Z$. The second of these is the standard moment balance for an isolated rod, and the first yields the interpretation of $\mu \mathit{div}\boldsymbol{B}-\mathit{gradp}$ as a density of distributed force transmitted to the rod by the matrix material in which it is embedded.

With (88)₃ in hand we could undertake the arduous task of determining $\boldsymbol{R}_{(3)}$, but we avoid this by adopting the simple strain-energy function

$$ \varphi _{3}=\frac{1}{2}(T\kappa _{(3)1}^{2}+F\kappa _{(3)\alpha } \kappa _{(3)\alpha }) $$

(93)

- appropriate for an initially straight fiber of circular cross section composed of an isotropic material [7, 17] - in which $T$ and $F$ respectively are the constant torsional and flexural stiffnesses. As explained in [7, 17] this furnishes

$$ \boldsymbol{m}=T\kappa \boldsymbol{d}+F\boldsymbol{d}\times \boldsymbol{d}^{\prime }, $$

(94)

where $\kappa =\kappa _{(3)1}$ is the twist and $\boldsymbol{d}=\boldsymbol{d}_{(3)}$.

With these results the solution proceeds as in [5, 6] for the case of a single fiber family initially aligned with the axis of the cylinder. We present it in outline here.

It is well known that (84) furnishes a solution to the equilibrium equations for any uniform isotropic incompressible material in the absence of body force. For the neo-Hookean material this problem amounts to finding a pressure field $p$ such that

$$ \mu \mathit{div}\boldsymbol{B}=\mathit{gradp}, $$

(95)

yielding $p$ as a function of $r$ in the present example, with derivative depending parametrically on the (unknown) inner cylinder radius $a$. Integration then furnishes $p$ in terms of $a$ and another constant.

If (92)₂ is scalar-multiplied by $\boldsymbol{d}$ we find, with (94), that the fiber twist $\kappa$ is such that $\kappa ^{\prime }=0$, i.e. $\kappa$ is independent of $Z$. Using the expression (88)₃ for $\boldsymbol{d,}$ together with

$$ \boldsymbol{d}\times \boldsymbol{d}^{\prime }=\lambda ^{-2}r\tau ^{2}[r\tau \boldsymbol{k}-\boldsymbol{e}_{\theta }(\phi )], $$

(96)

where $\lambda =\lambda _{(3)}$, we then derive

$$ \boldsymbol{m}^{\prime }=\lambda ^{-1}r\tau ^{2}(\lambda ^{-1}F\tau -T\kappa )\boldsymbol{e}_{r}(\phi ). $$

(97)

This is used in (92)₂ and (94), with $\boldsymbol{\chi }^{\prime }=\lambda \boldsymbol{d}$, to find $\boldsymbol{\lambda} \times \boldsymbol{d}$, yielding

$$ \boldsymbol{\lambda} =\boldsymbol{d}\times (\boldsymbol{\lambda} \times \boldsymbol{d})=-\lambda ^{-3}r\tau ^{2}( \lambda ^{-1}F\tau -T\kappa )[r\tau \boldsymbol{k}-\boldsymbol{e}_{\theta }(\phi )]. $$

(98)

From (92)₁ and (95) we have that $\boldsymbol{\lambda }^{\prime }=\boldsymbol{0}$. Because $\partial \boldsymbol{e}_{\theta }(\phi )/\partial Z=-\tau \boldsymbol{e}_{r}(\phi )$ is non-zero, this in turn requires that

$$ \kappa =\lambda ^{-1}(F/T)\tau , $$

(99)

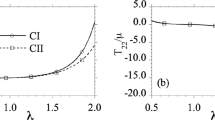
furnishing the fiber twist $\kappa$ as a function of $r$. With this result $\boldsymbol{\lambda }$ and $\boldsymbol{m}^{\prime }$ vanish separately, so that (92)₂ is identically satisfied, and after some algebra we find that (94) furnishes the simple result

$$ \boldsymbol{m}=F\tau \boldsymbol{k}. $$

(100)

To determine $a$ and the remaining constant in the function $p$, we impose zero tractions at $r=a$ and $r=b$, where $b^{2}=a^{2}+B^{2}-A^{2}$. With all $\boldsymbol{\lambda }_{(k)}$ vanishing, this results in

$$ \mu (A/a)^{2}=p\quad \mbox{at}\quad r=a\quad \text{and}\quad \mu (B/b)^{2}=p \quad \mbox{at}\quad r=b. $$

(101)

Appendices

Appendix A: Galilean invariance

We require the energy to be Galilean invariant; that is,

$$\begin{aligned} &U(\boldsymbol{F},\boldsymbol{R}_{(1)},\boldsymbol{R}_{(2)},\boldsymbol{R}_{(3)},\nabla \boldsymbol{R}_{(1)},\nabla \boldsymbol{R}_{(2)},\nabla \boldsymbol{R}_{(3)};\boldsymbol{X}) \\ =&U(\boldsymbol{QF},\boldsymbol{QR}_{(1)},\boldsymbol{QR}_{(2)},\boldsymbol{QR}_{(3)},\boldsymbol{Q}\nabla \boldsymbol{R}_{(1)},\boldsymbol{Q}\nabla \boldsymbol{R}_{(2)},\boldsymbol{Q}\nabla \boldsymbol{R}_{(3)};\boldsymbol{X}), \end{aligned}$$

(102)

for arbitrary spatially uniform rotations $\boldsymbol{Q}$, with $(\boldsymbol{Q}\nabla \boldsymbol{R}_{(k)})_{\mathit{iAB}}=(Q_{\mathit{ij}}R_{{(k)}\mathit{jA}}),{}_{B}=Q_{\mathit{ij}}R_{(k)\mathit{jA},B}$.

For example, by taking $\boldsymbol{Q}=\boldsymbol{R}_{(1)\mid X}^{t}$, where $X$ is the material point in question, we conclude that $U$ depends on its arguments via the list

$$ \{\boldsymbol{E}_{(1)},\boldsymbol{R}_{(1)}^{t}\boldsymbol{\boldsymbol{R}}_{(2)},\boldsymbol{R}_{(1)}^{t}\boldsymbol{\boldsymbol{R}}_{(3)},\boldsymbol{R}_{(1)}^{t}\nabla \boldsymbol{R}_{(1)},\boldsymbol{R}_{(1)}^{t}\nabla \boldsymbol{R}_{(2)},\boldsymbol{R}_{(1)}^{t}\nabla \boldsymbol{R}_{(3)}\}. $$

(103)

Here we note that

$$ \boldsymbol{R}_{(1)}^{t}{\boldsymbol{R}}_{(2)}=\boldsymbol{R}_{(1)}^{t}\boldsymbol{F}(\boldsymbol{R}_{(2)}^{t}\boldsymbol{F})^{-1}=\boldsymbol{E}_{(1)}\boldsymbol{E}_{(2)}^{-1} $$

(104)

and

$$ \boldsymbol{R}_{(1)}^{t}\nabla \boldsymbol{R}_{(2)}=\boldsymbol{E}_{(1)}\boldsymbol{E}_{(2)}^{-1}\boldsymbol{R}_{(2)}^{t}\nabla \boldsymbol{R}_{(2)}, $$

(105)

etc. Thus $U$ is determined by the equivalent list

$$ \{\boldsymbol{E}_{(1)},\boldsymbol{E}_{(2)},\boldsymbol{E}_{(3)},\boldsymbol{R}_{(1)}^{t}\nabla \boldsymbol{R}_{(1)},\boldsymbol{R}_{(2)}^{t}\nabla \boldsymbol{R}_{(2)},\boldsymbol{R}_{(3)}^{t}\nabla \boldsymbol{R}_{(3)}\}. $$

(106)

For $\boldsymbol{R}\in \{\boldsymbol{R}_{(k)}\}$ we have $(\boldsymbol{R}^{t}\nabla \boldsymbol{R})_{\mathit{ABC}}=R_{\mathit{iA}}R_{\mathit{iB},C}$. For each fixed $C\in \{1,2,3\}$, the matrix $R_{\mathit{iA}}R_{\mathit{iB},C}$ is skew. The elements of this matrix stand in one-to-one relation to

$$ \gamma _{D(C)}=\frac{1}{2}e_{\mathit{BAD}}R_{\mathit{iA}}R_{\mathit{iB},C}, $$

(107)

which furnish the axial vectors $\boldsymbol{\gamma }_{C}=\gamma _{D(C)}\boldsymbol{E}_{D}$, yielding (cf. (19), (20))

$$ \boldsymbol{\Gamma }=\boldsymbol{\gamma }_{C}\otimes \boldsymbol{E}_{C}. $$

(108)

Accordingly $\boldsymbol{\Gamma }$ is isomorphic to $\boldsymbol{R}^{t}\nabla \boldsymbol{R}$. The strain measures $\boldsymbol{E}$ and $\boldsymbol{\Gamma }$ are generally non-symmetric.

We have established that $U$ is determined by the list

$$ \{\boldsymbol{E}_{(1)},\boldsymbol{E}_{(2)},\boldsymbol{E}_{(3)},\boldsymbol{\Gamma }_{(1)},\boldsymbol{\Gamma }_{(2)},\boldsymbol{\Gamma }_{(3)}\} $$

(109)

and hence that (32) is necessary for Galilean invariance. Sufficiency is immediate.

Appendix B: Variation of the wryness tensor

We suppress the fiber label $(k)$ for the sake of clarity. To establish (47) we combine (19) and (46)₃, obtaining

$$\begin{aligned} \dot{\Gamma }_{\mathit{DC}} =&\frac{1}{2}e_{\mathit{BAD}}(\dot{R}_{\mathit{iA}}R_{\mathit{iB},C}+R_{\mathit{iA}} \dot{R}_{\mathit{iB},C}) \\ =&\frac{1}{2}e_{\mathit{BAD}}[\Omega _{\mathit{im}}R_{\mathit{mA}}R_{\mathit{iB},C}+R_{\mathit{mA}}(\Omega _{\mathit{mj},C}R_{\mathit{jB}}+ \Omega _{\mathit{mj}}R_{\mathit{jB},C})] \\ =&\frac{1}{2}e_{\mathit{BAD}}R_{\mathit{mA}}[\Omega _{\mathit{mi},C}R_{\mathit{iB}}+(\Omega _{\mathit{mi}}+ \Omega _{\mathit{im}})R_{\mathit{iB},C}] \\ =&\frac{1}{2}e_{\mathit{BAD}}R_{\mathit{iB}}R_{\mathit{mA}}\Omega _{\mathit{mi},C}. \end{aligned}$$

(110)

Because $\det \boldsymbol{R}=1$ we have $e_{\mathit{BAD}}R_{\mathit{iB}}R_{\mathit{mA}}R_{\mathit{jD}}=e_{\mathit{imj}}$, and thus $e_{\mathit{BAC}}R_{\mathit{iB}}R_{\mathit{mA}}=e_{\mathit{imj}}R_{\mathit{jC}}$, where use has been made of $R_{\mathit{jD}}R_{\mathit{jC}}=\delta _{\mathit{DC}}$. Altogether, we find

$$ \dot{\Gamma }_{\mathit{DC}}=R_{\mathit{jD}}\omega _{j,C}, $$

(111)

where $\omega _{j}=\frac{1}{2}e_{\mathit{imj}}\Omega _{\mathit{mi}}$, and thus verify (47).