Skip to main content
SpringerLink
Log in

A micromechanics-based elasto-plastic model for granular media combined with Cosserat continuum theory

  • Research Paper
  • Published:
Acta Geotechnica Aims and scope Submit manuscript

Abstract

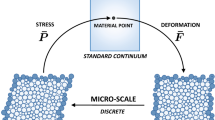
This paper is devoted to the micromechanical model of granular materials based on the Cosserat continuum theory. The generalised stress–strain relationships of a representative element volume are closely related to the micro elasto-plastic force–displacement and moment–rotation laws. With the help of generalised micro–macro relations, a micromechanical model is presented by aggregating the generalised micro elasto-plastic inter-particle contact laws in each contact orientation. A corresponding implicit multiscale integration algorithm for integrating the micromechanical model is proposed. Furthermore, the micromechanical model and implicit multiscale integration algorithm are simplified to consider a two-dimensional condition, and the Romberg integration of the numerical quadrature formula is also introduced in this condition. Compared with the data of Hostun sand and the results of DEM simulations for different particle shapes, it is demonstrated that the proposed micromechanical model can describe both the macro and micro responses of granular materials relatively well, such as strain softening/hardening, volumetric compaction/dilatancy, particle rotation, and evolution of the coordination number.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Abbreviations

\(\sigma_{ij}\) :

The stress tensor of the REV

\(\mu_{ij}\) :

The couple stress tensor of the REV

\(\gamma_{ij}\) :

The strain tensor of the REV

\(\kappa_{ij}\) :

The curvature tensor of the REV

\(f_{i}^{c}\) :

The inter-particle contact force

\(m_{i}^{c}\) :

The inter-particle contact moment

\(l_{i}^{c}\) :

The branch vector joining the centres of two contact particles

\(x_{i}^{c}\) :

The Cartesian coordinate of inter-particle contact

\(A_{ij}\) :

The fabric tensor

\(P_{ij}\) (\(PP_{ij}\)):

The transform matrix

\(u_{i}^{ce}\) :

The elastic displacement of inter-particle contact

\(\omega_{i}^{ce}\) :

The elastic rotation of inter-particle contact

\(k_{n}\) :

The normal stiffness of inter-particle contact

\(k_{r}\) :

The shear stiffness of inter-particle contact

\(g_{n}\) :

The torsion stiffness of inter-particle contact

\(g_{r}\) :

The bending stiffness of inter-particle contact

\(du_{i}^{cp}\) :

The plastic displacement increment of inter-particle contact

\(d\omega_{i}^{cp}\) :

The plastic rotation increment of inter-particle contact

\({\Delta }_{r}^{cp}\) :

The generalised tangential plastic displacement of inter-particle contact

\(T\) :

The generalised shear force of inter-particle contact

\(x^{c}\) :

The material constant with dimension of length

\(\alpha\) :

The hardening/softening parameter for inter-particle contact

\(\alpha_{m}\) :

The peak inter-particle friction coefficient

\(e_{c}\) :

The void ratio at the critical state

\(e\) :

The void ratio of granular materials

\(\phi_{\mu }^{c}\) :

The inter-particle sliding friction angle

\(\psi^{c}\) :

The material constant in the dilatancy equation

\(\eta\) :

The non-dimensional parameter relating to coefficient of rolling friction

\(k_{p}^{c}\) :

The material constant that controls the hardening/softening speed

\(d\lambda\) :

The plastic multiplier

\(H\) :

The plastic hardening modulus

\(Z\) :

The coordination number

\(d_{50}\) :

The mean particle diameter

\(d{\varvec{\sigma}}\) :

The generalised stress increment

\({\varvec{\sigma}}\) :

The generalised stress

\(d{\varvec{\gamma}}\) :

The generalised strain increment

\({\varvec{\gamma}}\) :

The generalised strain

\({\varvec{S}}\) :

The matrix of loading constraint of the generalised stress increment

\({\varvec{E}}\) :

The matrix of loading constraint of the generalised strain increment

\(d{\varvec{X}}\) :

The imposed driven vector

\(d{\varvec{X}}^{{ \star }}\) :

The new imposed driven vector

\({\varvec{R}}\) :

The residual vector

References

  1. Anandarajah A (2008) Critical state of granular materials based on the sliding-rolling theory. J Geotech Geoenvironmental Eng 134(1):125–135

    Article  Google Scholar 

  2. Bardet JP, Choucair W (1991) A linearized integration technique for incremental constitutive equations. Int J Numer Anal Methods Geomech 15(1):1–19

    Article  MATH  Google Scholar 

  3. Bardet JP, Vardoulakis I (2001) The asymmetry of stress in granular media. Int J Solids Struct 38(2):353–367

    Article  MATH  Google Scholar 

  4. Bažant ZP, Oh BH (1986) Efficient numerical integration on the surface of a sphere. J Appl Math Mech 66(1):37–49

    MathSciNet  MATH  Google Scholar 

  5. Bažant ZP, Oh BH (1985) Microplane model for progressive fracture of concrete and rock. J Eng Mech 111(4):559–582

    Google Scholar 

  6. Biarez J, Hicher P-Y (1994) Elementary mechancis of soil behaviour. AA Balkema, Avereest

    Google Scholar 

  7. Bouvard D (1982) Rhéologie des milieux pulvérulents: étude expérimentale et identification d’une loi de comportement. Université de Grenoble

  8. Chang CS, Chao SJ, Chang Y (1995) Estimates of elastic moduli for granular material with anisotropic random packing structure. Int J Solids Struct 32(14):1989–2008

    Article  MATH  Google Scholar 

  9. Chang CS, Gao J (1996) Kinematic and static hypotheses for constitutive modelling of granulates considering particle rotation. Acta Mech 115(1):213–229

    Article  MATH  Google Scholar 

  10. Chang CS, Hicher P-Y (2005) An elasto-plastic model for granular materials with microstructural consideration. Int J Solids Struct 42(14):4258–4277

    Article  MATH  Google Scholar 

  11. Chang CS, Kuhn MR (2005) On virtual work and stress in granular media. Int J Solids Struct 42(13):3773–3793

    Article  MATH  Google Scholar 

  12. Chang CS, Ma L (1992) Elastic material constants for isotropic granular solids with particle rotation. Int J Solids Struct 29(8):1001–1018

    Article  MATH  Google Scholar 

  13. Chang CS, Sundaram SS, Misra A (1989) Initial moduli of particulated mass with frictional contacts. Int J Numer Anal Methods Geomech 13(6):629–644

    Article  MATH  Google Scholar 

  14. Cudny M, Vermeer PA (2004) On the modelling of anisotropy and destructuration of soft clays within the multi-laminate framework. Comput Geotech 31(1):1–22

    Article  Google Scholar 

  15. Dashti H, Sadrnejad SA, Ganjian N (2019) A novel semi-micro multilaminate elasto-plastic model for the liquefaction of sand. Soil Dyn Earthq Eng 124:121–135

    Article  Google Scholar 

  16. Davis PJ, Rabinowitz P (1984) Methods of numerical integration. Elsevier, London

    MATH  Google Scholar 

  17. de Borst R (1993) A generalization of J2-flow theory for polar continua. Comput Methods Appl Mech Eng 103(3):347–362

    Article  MATH  Google Scholar 

  18. Di Luzio G (2007) A symmetric over-nonlocal microplane model M4 for fracture in concrete. Int J Solids Struct 44(13):4418–4441

    Article  MATH  Google Scholar 

  19. Ehlers W, Ramm E, Diebel S, D’Addetta GA (2003) From particle ensembles to Cosserat continua: homogenization of contact forces towards stresses and couple stresses. Int J Solids Struct 40(24):6681–6702

    Article  MathSciNet  MATH  Google Scholar 

  20. Emeriault F, Cambou B (1996) Micromechanical modelling of anisotropic non-linear elasticity of granular medium. Int J Solids Struct 33(18):2591–2607

    Article  MATH  Google Scholar 

  21. Gao Z, Zhao J (2017) A non-coaxial critical-state model for sand accounting for fabric anisotropy and fabric evolution. Int J Solids Struct 106–107:200–212

    Article  Google Scholar 

  22. Gardiner BS, Tordesillas A (2004) Micromechanics of shear bands. Int J Solids Struct 41(21):5885–5901

    Article  MATH  Google Scholar 

  23. Hicher P-Y, Chang CS (2005) Evaluation of two homogenization techniques for modeling the elastic behavior of granular materials. J Eng Mech 131(11):1184–1194

    Google Scholar 

  24. Hill R (1966) Generalized constitutive relations for incremental deformation of metal crystals by multislip. J Mech Phys Solids 14(2):95–102

    Article  Google Scholar 

  25. Hu N, Yu H-S, Yang D-S, Zhuang P-Z (2020) Constitutive modelling of granular materials using a contact normal-based fabric tensor. Acta Geotech 15(5):1125–1151

    Article  Google Scholar 

  26. Huang W, Nübel K, Bauer E (2002) Polar extension of a hypoplastic model for granular materials with shear localization. Mech Mater 34(9):563–576

    Article  Google Scholar 

  27. Iwashita K, Oda M (1998) Rolling resistance at contacts in simulation of shear band development by DEM. J Eng Mech 124(3):285–292

    Google Scholar 

  28. Kabilamany K, Ishihara K (1991) Cyclic behaviour of sand by the multiple shear mechanism model. Soil Dyn Earthq Eng 10(2):74–83

    Article  Google Scholar 

  29. Ken-Ichi K (1984) Distribution of directional data and fabric tensors. Int J Eng Sci 22(2):149–164

    Article  MathSciNet  MATH  Google Scholar 

  30. Kruyt NP, Rothenburg L (2016) A micromechanical study of dilatancy of granular materials. J Mech Phys Solids 95:411–427

    Article  MathSciNet  Google Scholar 

  31. La Ragione L, Prantil VC, Sharma I (2008) A simplified model for inelastic behavior of an idealized granular material. Int J Plast 24(1):168–189

    Article  MATH  Google Scholar 

  32. Li X-S, Dafalias YF, Wang Z-L (1999) State-dependent dilatancy in critical-state constitutive modelling of sand. Can Geotech J 36(4):599–611

    Article  Google Scholar 

  33. Li X, Yu HS, Li XS (2009) Macro-micro relations in granular mechanics. Int J Solids Struct 46(25):4331–4341

    Article  MATH  Google Scholar 

  34. Li XS, Dafalias YF (2012) Anisotropic critical state theory: role of fabric. J Eng Mech 138(3):263–275

    Google Scholar 

  35. Liao CL, Chan TC, Suiker ASJ, Chang CS (2000) Pressure-dependent elastic moduli of granular assemblies. Int J Numer Anal Methods Geomech 24(3):265–279

    Article  MATH  Google Scholar 

  36. Liao C-L, Chang T-P, Young D-H, Chang CS (1997) Stress–strain relationship for granular materials based on the hypothesis of best fit. Int J Solids Struct 34(31–32):4087–4100

    Article  MATH  Google Scholar 

  37. Lin J, Wu W, Borja RI (2015) Micropolar hypoplasticity for persistent shear band in heterogeneous granular materials. Comput Methods Appl Mech Eng 289:24–43

    Article  MathSciNet  MATH  Google Scholar 

  38. Liu EL, Lai YM (2020) Thermo-poromechanics-based viscoplastic damage constitutive model for saturated frozen soil. Int J Plast 128:102683

    Article  Google Scholar 

  39. Liu EL, Wong H, Feng J, Lai YM (2018) An elastoplastic model for saturated freezing soils based on thermo-poromechanics. Int J Plast 107:246–285

    Article  Google Scholar 

  40. Matsuoka H (1974) Stress-strain relationships of sands based on the mobilized plane. Soils Found 14(2):47–61

    Article  Google Scholar 

  41. Misra A, Poorsolhjouy P (2016) Granular micromechanics model of anisotropic elasticity derived from Gibbs potential. Acta Mech 227(5):1393–1413

    Article  MATH  Google Scholar 

  42. Mühlhaus H-B, Vardoulakis I (1987) The thickness of shear bands in granular materials. Géotechnique 37(3):271–283

    Article  Google Scholar 

  43. Nemat-Nasser S, Zhang J (2002) Constitutive relations for cohesionless frictional granular materials. Int J Plast 18(4):531–547

    Article  MATH  Google Scholar 

  44. Nicot F, Darve F (2011) The H-microdirectional model: accounting for a mesoscopic scale. Mech Mater 43(12):918–929

    Article  Google Scholar 

  45. Nicot F, Darve F (2007) Micro-mechanical bases of some salient constitutive features of granular materials. Int J Solids Struct 44(22):7420–7443

    Article  MATH  Google Scholar 

  46. Nicot F, Darve F, RNVO Group: Natural Hazards and Vulnerability of Structures (2005) A multi-scale approach to granular materials. Mech Mater 37(9):980–1006

    Google Scholar 

  47. Oda M, Iwashita K (2000) Study on couple stress and shear band development in granular media based on numerical simulation analyses. Int J Eng Sci 38(15):1713–1740

    Article  Google Scholar 

  48. Ortiz M, Simo JC (1986) An analysis of a new class of integration algorithms for elastoplastic constitutive relations. Int J Numer Methods Eng 23(3):353–366

    Article  MathSciNet  MATH  Google Scholar 

  49. Pagano AG, Tarantino A, Magnanimo V (2019) A microscale-based model for small-strain stiffness in unsaturated granular geomaterials. Géotechnique 69(8):687–700

    Article  Google Scholar 

  50. Pande GN, Sharma KG (1983) Multi-laminate model of clays—a numerical evaluation of the influence of rotation of the principal stress axes. Int J Numer Anal Methods Geomech 7(4):397–418

    Article  MATH  Google Scholar 

  51. Roscoe KH, Schofield AN, Wroth CP (1958) On the yielding of soils. Géotechnique 8(1):22–53

    Article  Google Scholar 

  52. Schuller H, Schweiger HF (2002) Application of a multilaminate model to simulation of shear band formation in NATM-tunnelling. Comput Geotech 29(7):501–524

    Article  Google Scholar 

  53. Tang H, Dong Y, Wang T, Dong Y (2019) Simulation of strain localization with discrete element-Cosserat continuum finite element two scale method for granular materials. J Mech Phys Solids 122:450–471

    Article  MathSciNet  Google Scholar 

  54. Tian J, Liu E (2019) Influences of particle shape on evolutions of force-chain and micro-macro parameters at critical state for granular materials. Powder Technol 354:906–921

    Article  Google Scholar 

  55. Tian J, Liu E (2018) Effect of particle shape on micro- and mesostructure evolution of granular assemblies under biaxial loading conditions. C R Mécanique 346(12):1233–1252

    Article  Google Scholar 

  56. Tian J, Liu E, He C (2020) Shear band analysis of granular materials considering effects of particle shape. Acta Mech. https://doi.org/10.1007/s00707-020-02771-y

    Article  Google Scholar 

  57. Tordesillas A, Liu E (2015) Evolution of mesoscopic granular clusters in comminution systems: a structural mechanics model of grain breakage and force chain buckling. Contin Mech Thermodyn 27(1–2):105–132

    Article  MathSciNet  MATH  Google Scholar 

  58. Tordesillas A, Walsh DCS (2002) Incorporating rolling resistance and contact anisotropy in micromechanical models of granular media. Powder Technol 124:106–111

    Article  Google Scholar 

  59. Vardoulakis I (2019) Cosserat continuum mechancis. Springer, Berlin

    Book  MATH  Google Scholar 

  60. Voyiadjis GZ, Alsaleh MI, Alshibli KA (2005) Evolving internal length scales in plastic strain localization for granular materials. Int J Plast 21(10):2000–2024

    Article  MATH  Google Scholar 

  61. Walton K (1987) The effective elastic moduli of a random packing of spheres. J Mech Phys Solids 35(2):213–226

    Article  MATH  Google Scholar 

  62. Yin Z-Y, Chang CS, Hicher P-Y, Karstunen M (2009) Micromechanical analysis of kinematic hardening in natural clay. Int J Plast 25(8):1413–1435

    Article  MATH  Google Scholar 

  63. Yin Z-Y, Zhao J, Hicher P-Y (2014) A micromechanics-based model for sand-silt mixtures. Int J Solids Struct 51(6):1350–1363

    Article  Google Scholar 

  64. Zhao C (2017) Multiscale modelling of granular soils: from the grain to the structure scale. École centrale de Nantes

  65. Zhao C-F, Yin Z-Y, Hicher P-Y (2018) Integrating a micromechanical model for multiscale analyses. Int J Numer Methods Eng 114(2):105–127

    Article  MathSciNet  Google Scholar 

  66. Zhu H, Mehrabadi MM, Massoudi M (2006) Three-dimensional constitutive relations for granular materials based on the dilatant double shearing mechanism and the concept of fabric. Int J Plast 22(5):826–857

    Article  MATH  Google Scholar 

  67. Zhu QZ, Shao JF, Mainguy M (2010) A micromechanics-based elastoplastic damage model for granular materials at low confining pressure. Int J Plast 26(4):586–602

    Article  MATH  Google Scholar 

  68. Zreid I, Kaliske M (2016) An implicit gradient formulation for microplane Drucker–Prager plasticity. Int J Plast 83:252–272

    Article  Google Scholar 

Download references

Acknowledgements

The authors appreciate the financial support from the National Key Research and Development Program of China (Project Nos. 2017YFC1501003; 2018YFC0809605).

Author information

Authors and Affiliations

  1. State Key Laboratory of Hydraulics and Mountain River Engineering, College of Water Resource and Hydropower, Sichuan University, Chengdu, 610065, People’s Republic of China

    Jianqiu Tian & Enlong Liu

  2. State Key Laboratory of Frozen Soil Engineering, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou, 730000, People’s Republic of China

    Yuanming Lai & Enlong Liu

  3. Ningbo Nottingham New Materials Institute, University of Nottingham Ningbo China, Ningbo, 315100, People’s Republic of China

    Yunming Yang

Authors
  1. Jianqiu Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuanming Lai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Enlong Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yunming Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Enlong Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

Constraints matrices and evolution vector (3D)

$${\varvec{S}} = \left[ {\begin{array}{*{20}c} {{\varvec{S}}_{11} } & {{\varvec{S}}_{12} } \\ {{\varvec{S}}_{21} } & {{\varvec{S}}_{22} } \\ \end{array} } \right].$$
(65)
$${\varvec{E}} = \left[ {\begin{array}{*{20}c} {{\varvec{E}}_{11} } & {{\varvec{E}}_{12} } \\ {{\varvec{E}}_{21} } & {{\varvec{E}}_{22} } \\ \end{array} } \right].$$
(66)

Stress-controlled compression:

$${\varvec{S}}_{11} = {\varvec{S}}_{22} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \\ \end{array} } \right].$$
(67)
$${\varvec{S}}_{12} = {\varvec{S}}_{21} = {\varvec{E}}_{11} = {\varvec{E}}_{12} = {\varvec{E}}_{21} = {\varvec{E}}_{22} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right].$$
(68)
$${\text{d}}{\varvec{X}} = \left[ {{\text{d}}x_{1} , {\text{d}}x_{2} , {\text{d}}x_{3} , 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} \right]^{{\text{T}}} .$$
(69)

Strain-controlled drained triaxial:

$${\varvec{S}}_{11} = {\varvec{S}}_{22} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \\ \end{array} } \right].$$
(70)
$${\varvec{S}}_{12} = {\varvec{S}}_{21} = {\varvec{E}}_{12} = {\varvec{E}}_{21} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right].$$
(71)
$${\varvec{E}}_{11} = {\varvec{E}}_{22} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right].$$
(72)
$${\text{d}}{\varvec{X}} = \left[ {{\text{d}}x_{1} , 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0} \right]^{{\text{T}}} .$$
(73)

Constraints matrices and evolution vector (2D)

Stress-controlled compression:

$${\varvec{S}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \\ \end{array} } \right].$$
(74)
$${\varvec{E}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right].$$
(75)
$${\text{d}}{\varvec{X}} = \left[ {{\text{d}}x_{1} ,{\text{d}}x_{2} , 0, 0, 0, 0} \right]^{{\text{T}}} .$$
(76)

Strain-controlled drained biaxial:

$${\varvec{S}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \\ \end{array} } \right].$$
(77)
$${\varvec{E}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right].$$
(78)
$${\text{d}}{\varvec{X}} = \left[ {{\text{d}}x_{1} ,0, 0, 0, 0, 0} \right]^{{\text{T}}} .$$
(79)

Appendix B

The stress–strain relationships are closely related to the plastic part of the inter-particle contact and macro parameters (i.e. the reference pressure \(p_{{{\text{ref}}}}\), the reference void ratio \(e_{{{\text{ref}}}}\), and the slope of the critical state line \(\lambda\)) of the plastic part for inter-particle contact are determined directly from the critical state of the Hostun sand. So the micro parameters (i.e. material constant \(k_{p}^{c}\), the inter-particle sliding friction angle \(\phi_{\mu }^{c}\), and material constant \(\psi^{c}\)) of the plastic part for inter-particle contact are discussed here. Based on parameters for Hostun sand, the confining pressure 800 kPa and initial void ratio 0.72, \(k_{p}^{c}\), \(\phi_{\mu }^{c}\), and \(\psi^{c}\) are discussed.

The effects of micro parameters on the stress–strain relationships are illustrated in Fig. 

Fig. 15
figure 15

The parametric study for \(k_{p}^{c}\), \(\phi_{\mu }^{c}\), and \(\psi^{c}\)

Full size image

15. Figure 15a depicts effects of \(k_{p}^{c}\) on the stress–strain relationships. The speed of hardening is faster and volumetric compaction is smaller for larger values of \(k_{p}^{c}\). According to Coulomb type yield function (Eq. 16) and definition of the hardening/softening parameter (Eq. 18), the contact force and moment increase faster with larger \(k_{p}^{c}\). After relationship between macro and micro variables (Sect. 2.1) and homogenisation method (Sect. 2.5) are applied, we can see that the deviatoric stress increases faster for larger values of \(k_{p}^{c}\). According to the dilatancy equation (Eq. 20), the direction of plastic contact displacement increment is closer to the direction of \(d\Delta_{r}^{cp}\) for larger values of \(k_{p}^{c}\). After relationship between macro and micro variables (Sect. 2.1) and homogenisation method (Sect. 2.5) are applied, we can see that the volumetric compaction is smaller for larger values of \(k_{p}^{c}\). Figure 15b depicts effects of \(\phi_{\mu }^{c}\) on the stress–strain relationships. The deviatoric stress is larger and volumetric compaction is smaller for larger values of \(\phi_{\mu }^{c}\). Figure 15c depicts effects of \(\psi^{c}\) on the stress–strain relationships. The deviatoric stress is larger and volumetric compaction is larger for larger \(\psi^{c}\). These phenomena in Fig. 15b, c can be also analysed like discussions for Fig. 15a.

Appendix C

Based on the parameters of square particles, the micromechanical model proposed here is used to predict the stress–strain relations of square particles with relative density 40% (i.e. initial void ratio 0.206) [55]. In Fig. 

Fig. 16
figure 16

The stress–strain curves of medium dense sand predicted by micromechanical model

Full size image

16, under a low confining pressure the strain softening and volumetric dilatancy after volumetric compaction are observed, and under a high confining pressure the strain hardening and a light volumetric dilatancy after volumetric compaction are observed. These characteristics belong to medium dense sand.

The representative volume element for simple shear is shown in Fig. 

Fig. 17
figure 17

The schematic of specimen and stress–strain curves of simple shear

Full size image

17a. Initially, an isotropic compressive stress (200 kPa, 400 kPa, and 600 kPa) is applied on the representative volume element, and with shear strain increasing, the vertical and horizontal stresses (i.e. \(\sigma_{xx}\) and \(\sigma_{yy}\)) remain constant. Based on the parameters of the elongated grains (Table 4), the stress–strain relations are predicted by the micromechanical model (Fig. 17b). Figure 17b depicts the evolution of shear stress versus shear strain. The strain softening is observed and the shear stress is higher for higher isotropic compressive stresses. Figure 17b also depicts the evolution of volumetric strain versus shear strain. After an initial stage of volumetric compaction, volumetric dilatancy occurs during a large range of shear strain until the critical state is reached. The volumetric compaction is larger and dilatancy is lower for higher isotropic compressive stresses. These stress–strain relations of simple shear predicted by the micromechanical model conform to the rule of dense granular materials sheared under simple shear condition.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tian, J., Lai, Y., Liu, E. et al. A micromechanics-based elasto-plastic model for granular media combined with Cosserat continuum theory. Acta Geotech. 17, 2259–2285 (2022). https://doi.org/10.1007/s11440-021-01336-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11440-021-01336-0

Keywords

Search

Navigation