1 Introduction

Mechanical forces and signals have recently been identified as an important influencing factor for brain development, injury, and disease [22, 29]. Consequently, continuum-mechanics-based computational models have gained considerable interest in the context of targeting open challenges associated with physiological and pathological processes in the brain. Numerical simulations have advanced our understanding of cortical folding during brain development [5, 11] and the interplay of biochemical and biomechanical degeneration in Alzheimer’s disease [45]. In addition, mechanical models have been applied to assess the risk during traumatic brain injury (TBI) [31] and establish corresponding injury thresholds [37], or to inform neurosurgeons on the optimization of neurosurgical procedures [52].

From a mechanics point of view, brain tissue is an exceptional material due its extreme compliance and mechanical complexity [15]. The mechanical response highly depends on length and time scales as well as loading conditions and has been subject of numerous studies throughout the last half century [15, 17]. The main mechanical characteristics are nonlinearity, compression-tension asymmetry, and – especially for short and intermediate time scales – pronounced conditioning and hysteresis [12, 41]. The latter can only partially be attributed to the biphasic nature of brain tissue and poroelastic effects [18, 21].

Not only the mechanical response of brain tissue is complex but also its structure, both on macroscopic and microscopic scales [11, 16, 30, 47]. The brain consists of the cerebrum (with telencephalon and diencephalon), the cerebellum, and the brain stem (with mesencephalon, pons, and medulla oblongata), as illustrated in Fig. 1. Macroscopically, we may distinguish between two tissue types, gray and white matter, or more refined between the cortex (outer gray matter), the corona radiata (central white matter), the basal ganglia (part of the inner gray matter including the putamen), and inner white matter, with highly aligned nerve fibers in the corpus callosum (which connects the two hemispheres) and the brain stem. But even within gray and white matter regions, the brain’s microstructure consisting of cells, extracellular matrix, and interstitial fluid may vary significantly due to differences in local functional demands. This is clearly visible when comparing the microstructure of the corona radiata and the brain stem (both white matter regions) in Figs. 1b and e, respectively. The microstructure of brain tissue is interesting from a mechanics point of view as it lacks fibrillar extracellular matrix components, such as elastin and fibrillar collagen [3], which control the overall mechanical behavior of other soft tissues like arteries [23, 24]. Consequently, the much softer cellular and non-fibrillar extracellular components may become decisive [3, 50]. In addition, brain cells ‘actively’ respond to their mechanical environment through ‘mechanosensing’ [8, 29, 38, 49]: They may adapt their migration, differentiation and proliferation behavior, or even their mechanical environment through secretion of extracellular matrix components resulting in additional coupling effects [9].

Fig. 1
figure 1

Structure of the porcine brain with (a) different macroscopic components (cerebrum, cerebellum, and brain stem) and anatomical regions (corona radiata and putamen) and the corresponding microstructure in (b) the corona radiata, (c) the putamen, (d) the cerebellar white matter, and (e) the brain stem. Scale bars indicate 100 μm

Full size image

While computational modeling based on nonlinear continuum mechanics has been appreciated as a promising tool to advance our understanding of brain mechanics and better understand mechanics-driven processes associated with injury and disease, it remains challenging to provide appropriate constitutive models that capture brain tissue complexity in space and time. Those are key to perform predictive simulations that are eventually useful to the biomedical and clinical communities. Currently used constitutive models are mostly phenomenological [12, 19, 34, 35, 43]. It has been shown that the Ogden model well represents the time-independent, hyperelastic response of brain tissue under different loading modes [12, 34, 36], and that its viscoelastic extension is capable of additionally capturing conditioning effects and hysteresis [13]. However, the corresponding material parameters have varied greatly depending on the experimental data used for calibration. In addition, those models can only implicitly account for regional differences through individual parameter sets for different anatomical regions [12, 13], while it is not possible to capture the heterogeneities that are present even within a certain anatomical region.

A possible solution to this problem is to incorporate microstructural information into constitutive models for brain tissue [7], which has been successfully realized for other tissues, such as arterial tissue, especially by Gerhard A. Holzapfel and his co-workers [24]. An additional advantage of microstructure-informed constitutive models is that they enable us to predict how (local) changes in the tissue’s microstructure that may occur during development and aging or due to injury and disease translate into changes in macroscopic mechanical properties. This is highly relevant in the context of certain diseases, where microstructural changes are known but the link to the corresponding tissue mechanics remains unclear [6, 16]. Importantly, such changes in mechanical properties can in turn affect cell behavior [29].

Recent efforts towards micromechanical modeling of brain tissue have proposed to include the individual contributions of axons and extracellular matrix in white matter tissue [25, 42] or the brain stem [2, 26] through representative volume elements accounting for the distribution and orientation of nerve fiber bundles from magnetic resonance and diffusion tensor imaging data. However, it remains controversial whether axons indeed majorly contribute to the mechanical response of brain tissue [12, 15, 20, 51] and such models would only be valid for certain white matter areas. Other studies have expanded phenomenological models to account for a cell-density dependent tissue stiffness [1, 16, 28]. So far, such models have been limited to linear elastic [1, 28] or hyperelastic models [16], but have not accounted for viscoelastic effects. In addition, tissue samples were first subjected to mechanical loading and afterwards examined histologically or immunohistologically [16, 28], or even separate sets of samples were used for mechanical and microstructural analyses [1]. Therefore, it still remains unclear how deformations on the tissue scale are transferred to the different elements on the microscopic scale (cells, extracellular matrix components, blood vessels) and which microstructural components contribute to the hyper- and viscoelastic tissue behavior.

The aim of this study is to further advance microstructure-informed constitutive models for brain tissue. We will first introduce the modeling framework in Sect. 2.1, and then simultaneously record the mechanical response and microstructural rearrangement during compressive loading of porcine brain tissue in Sect. 2.2. Like this, we identify the key microstructural elements that are relevant for the macroscopic mechanical response and propose a microstructure-informed finite viscoelastic constitutive model for brain tissue in Sect. 2.3. We include microstructural parameters from imaging data and calibrate the remaining model parameters by simultaneously considering cyclic loadings and stress relaxation experiments in Sect. 2.4. Finally, we conclude in Sect. 3 with a summary on the main findings and prospects for microstructure-informed constitutive modeling of brain tissue in the future.

2 Microstructure-Informed Modeling of Brain Viscoelasticity

2.1 Kinematics of Finite Viscoelasticity

To model the finite viscoelasticity of brain tissue, we use the nonlinear equations of continuum mechanics and introduce the deformation map \(\boldsymbol{\varphi }\, (\mathbf{X},t)\) to map tissue from its undeformed, unloaded state with the position vector \(\mathbf{X}\) at time \(t_{0}\) to its deformed, loaded state with the position vector \(\mathbf{x}= \boldsymbol{\varphi }\, (\mathbf{X},t)\) at time \(t\). We determine the associated deformation gradient \(\mathbf{F}\) in its spectral representation in terms of the eigenvalues \(\lambda _{\mathrm{a}}\) and the undeformed and deformed eigenvectors \(\mathbf{N}_{\mathrm{a}}\) and \(\mathbf{n}_{\mathrm{a}}=\mathbf{F}\cdot \mathbf{N}_{\mathrm{a}}\),

$$ \mathbf{F}= \nabla _{\mathbf{X}} \boldsymbol{\varphi }= \sum _{ \mathrm{a =1}}^{3} \lambda _{\mathrm{a}} \, \mathbf{n}_{\mathrm{a}} \otimes \mathbf{N}_{\mathrm{a}} \,. $$
(1)

From the deformation gradient, we may further determine the left Cauchy Green deformation tensor \(\mathbf{b}\) and its spectral representation

$$ \mathbf{b}= \mathbf{F}\cdot \mathbf{F}^{\mathrm{t}} = \sum _{\mathrm{a =1}}^{3} \lambda _{\mathrm{a}}^{2} \mathbf{n}_{\mathrm{a}} \otimes \mathbf{n}_{\mathrm{a}} \,. $$
(2)

To capture viscoelastic effects, we decompose the deformation gradient into elastic and viscous parts,

$$ \mathbf{F}=\mathbf{F}^{\mathrm{e}}_{i} \cdot \mathbf{F}^{\mathrm{v}}_{i} \qquad \forall \quad i=1,..,m \,, $$
(3)

where \(i\) denotes the parallel arrangement of \(m\) viscoelastic elements [46], as illustrated in Fig. 2. We can then introduce the spatial velocity gradient,

$$ \mathbf{l}= \nabla _{\mathbf{x}} \mathbf{v}= \dot{\mathbf{F}} \cdot \mathbf{F}^{-1} = \mathbf{l}_{i}^{\mathrm{e}} +\mathbf{l}_{i}^{ \mathrm{v}} \, , $$
(4)

and decompose it additively into elastic parts, \(\mathbf{l}_{i}^{\mathrm{e}} = \dot{\mathbf{F}}{}^{\mathrm{e}} \cdot ( \mathbf{F}_{i}^{\mathrm{e}}){}^{-1}\), and viscous parts, \(\mathbf{l}_{i}^{\mathrm{v}} = \mathbf{F}_{i}^{\mathrm{e}} \cdot \dot{\mathbf{F}}{}_{i}^{\mathrm{v}} \cdot (\mathbf{F}_{i}^{\mathrm{v}}){}^{-1} \cdot (\mathbf{F}_{i}^{\mathrm{e}}){}^{-1}\).

Fig. 2
figure 2

Multiplicative decomposition model, where \(\mathbf{F}\) is associated with the main elastic network, \(\mathbf{F}^{{\mathrm{v}}}_{1}\) is the viscous damper associated with fluid flow inside the tissue with the corresponding hyperelastic spring \(\mathbf{F}^{{\mathrm{e}}}_{1}\), and \(\mathbf{F}^{{\mathrm{v}}}_{2}\) and \(\mathbf{F}^{{\mathrm{e}}}_{2}\) are the viscous damper and the corresponding hyperelastic spring associated with the viscoelasticity of the network of cells and extracellular matrix. Adapted from [14]

Full size image

It proves convenient to also introduce the elastic left Cauchy Green deformation tensor for each mode,

$$ \mathbf{b}^{\mathrm{e}}_{i} = \mathbf{F}^{\mathrm{e}}_{i} \cdot (\mathbf{F}^{ \mathrm{e}}_{i}){}^{\mathrm{t}} = \sum _{\mathrm{a =1}}^{3} [\lambda _{i\,\mathrm{a}}^{{ \mathrm{e}}}]^{2} \; \mathbf{n}_{i\,\mathrm{a}}^{\mathrm{e}} \otimes \mathbf{n}_{i \,\mathrm{a}}^{\mathrm{e}} \,, $$
(5)

with eigenvalues \(\lambda _{i\,\mathrm{a}}^{{\mathrm{e}}}\) and eigenvectors \(\mathbf{n}_{i\,\mathrm{a}}^{\mathrm{e}}\), which are, in general, not identical to the eigenvectors of the total left Cauchy Green deformation tensor in Equation (2), \(\mathbf{n}_{i\,\mathrm{a}}^{\mathrm{e}} \neq \mathbf{n}_{\mathrm{a}}\). The material time derivative of the elastic left Cauchy Green deformation tensor,

$$ \dot{\mathbf{b}}{}^{\mathrm{e}}_{i} = 2\,[\,\mathbf{l}_{i}^{\mathrm{e}} \cdot \mathbf{b}^{\mathrm{e}}_{i}\,]^{\mathrm{sym}} = 2\,[\,\mathbf{l}\cdot \mathbf{b}^{\mathrm{e}}_{i}\,]^{\mathrm{sym}} - 2\,[\,\mathbf{l}^{\mathrm{v}}_{i} \cdot \mathbf{b}^{\mathrm{e}}_{i}\,]^{\mathrm{sym}} , $$
(6)

introduces the Lie-derivative,

$$ {\mathscr{L}}_{v} \, \mathbf{b}^{\mathrm{e}}_{i} = - 2\,[\, \mathbf{l}^{ \mathrm{v}}_{i} \cdot \mathbf{b}^{\mathrm{e}}_{i}\, ]^{\mathrm{sym}} \,, $$
(7)

along the velocity field of the material motion.

2.2 Experimental Analyses

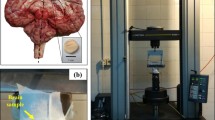
To experimentally assess the microstructural origin of brain tissue viscoelasticity, we used a Discovery HR-3 Rheometer from TA instruments (New Castle, Delaware, USA) with the corresponding microscope module. We visualized the cells inside the cylindrical tissue sample of approximately \(R=4\) mm diameter and \(H=4\) mm height by using methylene blue, which is a water-based dye that stains the fresh tissue without significantly altering its mechanical properties. Figure 3 shows the experimental setup for unconfined compression experiments with simultaneous cell tracking. The stained specimens were fixed to the bottom glass plate and upper specimen holder and immersed in phosphate buffered saline solution (PBS). The microscope objective and light source were located underneath the glass plate. We used a 20× magnification since, on the one hand, it allowed us to distinguish individual larger cell bodies and track their deformations, and, on the other hand, it was still small enough so that the observed cells did not leave the field of view during the experiments with low to medium compressive strains.

Fig. 3
figure 3

Experimental setup. Rheometer with microscope module (left). Specimen mounted to the testing device (right)

Full size image

We assumed that our brain samples deformed isochorically, \(J=\det (\mathbf{F}) =\lambda _{1}\lambda _{2}\lambda _{3} = 1\), and homogeneously during all experiments [12]. This implies that we neglect boundary effects and assume a constant deformation gradient \(\mathbf{F}\) across the sample [43]. For the case of uniaxial compression, we then obtain

$$ [\mathbf{F}] = \begin{bmatrix} 1/\sqrt{\lambda } & 0 & 0 \\ 0 & 1/\sqrt{\lambda } & 0 \\ 0 & 0 & \lambda \end{bmatrix} , $$
(8)

where the stretch \(\lambda \) is computed as \(\lambda =1+\Delta z / H\) with z-displacement \(\Delta z\). We further computed the Piola stress \(P_{zz}\) as the force \(f_{z}\) recorded during the experiments divided by the cross-sectional area \(A\) of the specimen in its unloaded state, i.e., \(P_{zz}=f_{z}/A\) with \(A=\pi R^{2}\).

2.2.1 The Limit of Brain Viscoelasticity

In an initial test series, we aimed to define the limit of brain viscoelasticity, i.e. the macroscopic loading that still allows for the full recovery of the mechanical response of brain tissue. To this end, we performed cyclic compression experiments with three loading/unloading cycles and a recovery period of 20 minutes for compressive strains of up to 50%.

Figure 4 demonstrates that porcine brain tissue can recover from compressive loadings of up to 30% strain within a 20 minute recovery period. We note that preliminary studies had shown that shorter recovery periods were not sufficient for the tissue to reach full recovery. For longer periods, in turn, the specimens may start to swell, which leads to artefacts in the measured stress response. For higher compressive strains, i.e., 40% and 50%, we observe permanent softening of the tissue response, which is presumably associated with tissue damage. The latter is also supported by the observation that specimens subjected to 50% strain were visibly torn after testing.

Fig. 4
figure 4

Limit of brain viscoelasticity. Representative nominal stress versus stretch behavior of specimens from the corona radiata loaded with two sets of three loading cycles under compression, separated by a 20 min recovery period, with different maximum strains of 30%, 40%, and 50%. The tissue recovers from strains up to 30%, while higher strains lead to permanent softening of the tissue response

Full size image

2.2.2 Deformations on the Cellular Level

By tracking the motion and deformation of individual cells during compression loading, we observed that most cell bodies undergo large displacements without being deformed, as exemplarily illustrated in Fig. 5. Only few cells deformed visibly, but still returned to their original shape upon unloading (see Fig. 6). This suggests that cell bodies move with the inter-cellular network consisting of dendrites, synapses, and extracellular matrix, but hardly experience any deformation. Interestingly, also relative movements between neighboring cells are minor compared to the overall cell displacement. We may conclude that the mechanical loading is rather transferred to the inter-cellular network than the cell bodies themselves. Accordingly, the stiffness of individual brain cells, which have been previously probed [33], seems rather irrelevant for tissue mechanics.

Fig. 5
figure 5

Rigid body displacement of a cell body in the brain stem during compressive loading (a) and unloading (b). The colored lines depict the shape of the cell body in the undeformed (orange) and deformed (blue) specimen. The black arrow indicates the displacement of the nucleus

Full size image
Fig. 6
figure 6

Deformation of a cell body in the brain stem during compressive loading (a) and unloading (b). The colored lines depict the shape of the cell body in the undeformed (orange) and deformed (blue) configuration. The black arrows indicate the displacements of the surrounding cell nuclei

Full size image

2.2.3 Stress Relaxation Behavior Across Scales

In a next step, we aimed to unravel how rearrangements on the cellular scale are linked to time-dependent effects and the stress relaxation behavior of brain tissue. We performed stress relaxation experiments in compression with maximum strains of 7.5% (for higher strains the cells would have moved out of focus) and a holding period of 600 s. When a sample was loaded, the cells inside the tissue started moving, as exemplarily shown in Fig. 7a (black dotted line). Interestingly, during the holding period, the cells kept moving in the same direction as during the loading phase, but their velocity decreased over time. We note that in previous studies, we had used a holding period of 300 s for stress relaxation tests. However, as cell displacement curves take at least 600 s to reach equilibrium, we chose a holding period of 600 s here. For even longer testing times, we could not have analyzed the cell displacements as the staining washes out after around ten minutes. The cell displacement curves were similar for all tested specimens. Consequently, they were much less affected by measurement inaccuracies and boundary effects than the corresponding stress data (blue solid line). In addition, the cell displacement data are extracted from microscope videos and, thus, inherently less noisy. Therefore, we render them suitable for the determination of microstructurally motivated relaxation time constants, as further discussed in Sect. 2.3.2.

Fig. 7
figure 7

Stress relaxation behavior on the cell and tissue scale. During stress relaxation, cells keep moving in the same direction as during loading (a). The maximum cell displacement correlates with the peak stress inside the respective specimen with a correlation coefficient \(r = 0.71\) (b). The cell displacements during the relaxation period can be fitted with a one-term Prony series (c)

Full size image

Figure 7b shows the correlation between the maximum cell displacement inside a specimen and the peak stress of the corresponding stress relaxation curve. Higher peak stresses are associated with larger cell displacements. This seems to hold true for all the different regions introduced in Fig. 1, the corona radiata, putamen, brain stem, and cerebellum.

2.3 Microstructure-Informed Constitutive Modeling

Based on our previous experimental findings [12], we assume that both the elastic and viscoelastic behavior of brain tissue are isotropic. Following the considerations in [44] and [13], we introduce the viscoelastic free energy function \(\psi \) as the sum of three terms, an equilibrium part \(\psi ^{\mathrm{eq}}\) in terms of the total principal stretches \(\lambda _{\mathrm{a}}\), a non-equilibrium part \(\psi ^{\mathrm{neq}} = \sum _{i=1}^{m} \psi _{i}\) in terms of the \(i,..,m\) elastic principal stretches \(\lambda _{i{\mathrm{a}}}^{\mathrm{e}}\), and a term \(p \, [\,J-1\,]\) that enforces the incompressibility constraint, \(J-1=0\), via the Lagrange multiplier \(p\) [13, 14],

$$ \psi = \psi ^{\mathrm{eq}} + \psi ^{\mathrm{neq}} - p \, [\,J-1\,] \,. $$
(9)

As we have previously shown that two viscoelastic elements are sufficient to accurately capture the viscoelastic response of brain tissue [10, 13], we set \(m=2\) (see Fig. 2).

Corresponding to Equation (9), we introduce the stress power \(\mathcal{P}\) as the sum of an equilibrium part \(\mathcal{P}^{\mathrm{eq}}=\boldsymbol{\tau }^{\mathrm{eq}}:\mathbf{l}\) in terms of the equilibrium Kirchoff stress \(\boldsymbol{\tau }^{\mathrm{eq}}\) and a non-equilibrium part \(\mathcal{P}^{\mathrm{neq}}=\boldsymbol{\tau }^{\mathrm{neq}}:\mathbf{l}\) in terms of the non-equilibrium Kirchoff stress \(\boldsymbol{\tau }^{\mathrm{neq}} = \sum _{i=1}^{2} \boldsymbol{\tau }_{i}\),

$$ \mathcal{P} = \mathcal{P}^{\mathrm{eq}} + \mathcal{P}^{\mathrm{neq}} =[\, \boldsymbol{\tau }^{\mathrm{eq}} + \boldsymbol{\tau }^{\mathrm{neq}} \,] : \mathbf{l}\,. $$
(10)

We can then evaluate the dissipation inequality, \(\mathcal{D} =\mathcal{P} - \dot{\psi } \ge 0\), in terms of the individual equilibrium and non-equilibrium contributions,

$$ \mathcal{D} =[\, \mathcal{P}^{\mathrm{eq}} + \mathcal{P}^{\mathrm{neq}}\,] -[\, \dot{\psi }^{\mathrm{eq}} + \dot{\psi }^{\mathrm{neq}} \,] \ge 0 . $$
(11)

Based on the assumption of isotropy, we may express the non-equilibrium stress power in terms of the Lie derivative of the elastic left Cauchy Green deformation tensor \(\mathbf{b}^{\mathrm{e}}_{i}\) in Equation (7), \(\mathcal{P}^{\mathrm{neq}} = \sum _{i=1}^{2} [{\boldsymbol{\tau }}_{i} \cdot (\mathbf{b}^{\mathrm{e}}_{i})^{-1} ]{:}\; \mbox{$\frac{1}{2}$} [\, \dot{\mathbf{b}}^{\mathrm{e}} - {\mathscr{L}}_{v} \mathbf{b}^{\mathrm{e}}_{i} \,]\), and obtain the following explicit representation of the dissipation inequality,

$$ \textstyle\begin{array}{l@{\,}l@{\, }l@{\ }l} \mathcal{D} &=&\displaystyle { \left [ \boldsymbol{\tau }^{\mathrm{eq}} - 2 \frac{\partial {\psi }^{\mathrm{eq}}}{\partial \mathbf{b}} \cdot \mathbf{b}\right ]} &: \mathbf{l} \\ &{}+ \displaystyle {\sum _{i=1}^{2}} & \displaystyle { \left [ \frac{1}{2} \boldsymbol{\tau }_{i} \cdot (\mathbf{b}_{i}^{\mathrm{e}})^{-1} - \frac{\partial {\psi }_{i}}{\partial \mathbf{b}_{i}^{\mathrm{e}}} \right ]} &: \dot{\mathbf{b}}_{i}^{\mathrm{e}} \\ &{}- \displaystyle {\sum _{i=1}^{2}} & \displaystyle { \left [ \frac{1}{2} \boldsymbol{\tau }_{i} \cdot (\mathbf{b}_{i}^{\mathrm{e}})^{-1} \right ]} &:{\mathscr{L}}_{v} \mathbf{b}_{i}^{\mathrm{e}} \ge 0 \,. \end{array} $$
(12)

Following standard arguments of thermodynamics, we obtain the definition of the equilibrium Kirchhoff stress,

$$ \boldsymbol{\tau }^{\mathrm{eq}} = 2 \frac{\partial \psi ^{\mathrm{eq}}}{\partial \mathbf{b}} \cdot \mathbf{b}= \sum _{\mathrm{a=1}}^{3} \frac{\partial \psi ^{\mathrm{eq}}}{\partial \lambda _{\mathrm{a}}}\lambda _{ \mathrm{a}} \mathbf{n}_{\mathrm{a}} \otimes \mathbf{n}_{\mathrm{a}} \,, $$
(13)

the definition of the non-equilibrium Kirchhoff stresses,

$$ \boldsymbol{\tau }_{i} = 2 \frac{\partial \psi _{i}}{\partial \mathbf{b}^{\mathrm{e}}_{i}} \cdot \mathbf{b}^{\mathrm{e}}_{i} = \sum _{\mathrm{a=1}}^{3} \frac{\partial \psi _{i}}{\partial \lambda _{i\, \mathrm{a}}^{\mathrm{e}}} \lambda _{i\, \mathrm{a}}^{\mathrm{e}} \mathbf{n}_{i\, \mathrm{a}}^{\mathrm{e}} \otimes \mathbf{n}_{i\, \mathrm{a}}^{\mathrm{e}} \,, $$
(14)

and the reduced dissipation inequalities for each individual mode \(i\),

$$ \mathcal{D}^{\mathrm{red}}_{i} =- \boldsymbol{\tau }_{i} : \mbox{$\frac{1}{2}$} \, [{\mathscr{L}}_{v} \mathbf{b}^{\mathrm{e}}_{i} \cdot (\mathbf{b}^{\mathrm{e}}_{i})^{-1}] \ge 0 \,. $$
(15)

It remains to specify the equilibrium and non-equilibrium parts of the free energy, \(\psi ^{\mathrm{eq}}\) and \(\psi ^{\mathrm{neq}}\) (Sect. 2.3.1), and the evolution of the internal variables \(\mathbf{b}_{i}^{\mathrm{e}}\) (Sect. 2.3.2), based on the insights into the microstructural origin of brain viscoelasticity gained in Sect. 2.2.

2.3.1 Microstructure-Informed Hyperelastic Constitutive Models

We have previously shown that the hyperelastic behavior of brain tissue under multiple loading modes is best represented by the one-term Ogden model [40] with the strain energy function \(\psi =2\mu /\alpha ^{2}[\lambda _{1}^{\alpha }+\lambda _{2}^{\alpha }+ \lambda _{3}^{\alpha }-3]\), which we have reformulated in terms of the classical shear modulus \(\mu \) and the nonlinearity parameter \(\alpha \) here [12, 13]. In addition, we have found that both the initial shear modulus and the nonlinearity parameter correlate linearly with the density of cell nuclei in the fully developed human brain. This has motivated us to introduce these two parameters as a linear function of the cell density \(\rho _{{\mathrm{c}}}\) [16]. We have demonstrated that this microstructure-informed hyperelastic model is capable of simultaneously predicting the response of brain tissue from different regions, the corona radiata, cortex, corpus callosum, and basal ganglia, with a single set of model parameters.

Following these considerations, we propose a similar approach for the equilibrium strain energy

$$ \psi ^{\mathrm{eq}}(\lambda _{{\mathrm{a}}}, \rho _{{\mathrm{c}}}) = \frac{2 \mu _{\infty }(\rho _{{\mathrm{c}}})}{\alpha _{\infty }(\rho _{{\mathrm{c}}})^{2}} \, [\, \lambda _{1}^{\alpha _{\infty }(\rho _{{\mathrm{c}}})} + \lambda _{2}^{\alpha _{\infty }(\rho _{{\mathrm{c}}})} +\lambda _{3}^{ \alpha _{\infty }(\rho _{{\mathrm{c}}})}-3 \,] \,, $$
(16)

parameterized in terms of the total stretches \(\lambda _{{\mathrm{a}}}\), with

$$ \mu _{\infty }(\rho _{{\mathrm{c}}}) = m_{\infty }^{\mu } \, \rho _{{ \mathrm{c}}} + c_{\infty }^{\mu } \quad \mbox{and} \quad \alpha _{ \infty }(\rho _{{\mathrm{c}}}) = m_{\infty }^{\alpha } \, \rho _{{ \mathrm{c}}} + c_{\infty }^{\alpha }, $$
(17)

and the non-equilibrium strain energies

$$ \psi _{i} (\tilde{\lambda }^{\mathrm{e}}_{i\,{\mathrm{a}}}, \rho _{{\mathrm{c}}}) = \frac{2 \mu _{i}(\rho _{{\mathrm{c}}})}{\alpha _{i}(\rho _{{\mathrm{c}}})^{2}} \; [\, (\tilde{\lambda }^{\mathrm{e}}_{i1}){}^{\alpha _{i}(\rho _{{ \mathrm{c}}})} +(\tilde{\lambda }^{\mathrm{e}}_{i2}){}^{\alpha _{i}(\rho _{{ \mathrm{c}}})} +(\tilde{\lambda }^{\mathrm{e}}_{i3}){}^{\alpha _{i}(\rho _{{ \mathrm{c}}})}-3 \,] \, , $$
(18)

parameterized in terms of the deviatoric elastic principal stretches \(\tilde{\lambda }^{\mathrm{e}}_{i} =(J^{\mathrm{e}}_{i})^{-1/3} \lambda ^{\mathrm{e}}_{i}\), the square roots of the eigenvalues of the isochoric part of the elastic left Cauchy Green tensor, \(\tilde{\mathbf{b}}^{\mathrm{e}}_{i}=(J^{\mathrm{e}}_{i}){}^{-2/3} \mathbf{b}^{\mathrm{e}}_{i}\), with

$$ \mu _{i}(\rho _{{\mathrm{c}}}) = m_{i}^{\mu } \, \rho _{{\mathrm{c}}} + c_{i}^{\mu } \quad \mbox{and} \quad \alpha _{i}(\rho _{{ \mathrm{c}}}) = m_{i}^{\alpha } \, \rho _{{\mathrm{c}}} + c_{i}^{ \alpha }. $$
(19)

The derivatives in Equations (13) and (14) then yield

$$ \frac{\partial \psi ^{\mathrm{eq}}}{\partial \lambda _{\mathrm{a}}} = 2 \mu _{ \infty } \; \frac{\lambda _{\mathrm{a}}^{\alpha _{\infty }-1}}{\alpha _{\infty }} $$
(20)

and

$$ \frac{\partial \psi _{i}}{\partial \lambda _{i\, \mathrm{a}}^{\mathrm{e}}} \lambda _{i\, \mathrm{a}}^{\mathrm{e}} =\frac{2\mu _{i}}{\alpha _{i}} \left [ \frac{2}{3} (\tilde{\lambda }_{{i \, \mathrm{a}}}^{\mathrm{e}})^{\alpha _{i}} - \frac{1}{3} (\tilde{\lambda }_{{i \, \mathrm{b}}}^{\mathrm{e}})^{\alpha _{i}} - \frac{1}{3} (\tilde{\lambda }_{{i \, \mathrm{c}}}^{\mathrm{e}})^{\alpha _{i}} \right ] , $$
(21)

where \({\mathrm{a}}, {\mathrm{b}}, {\mathrm{c}} = \{ 1, 2, 3 \}\) and \({\mathrm{a}} \neq {\mathrm{b}}\), \({\mathrm{a}} \neq {\mathrm{c}}\), and \({\mathrm{b}} \neq {\mathrm{c}}\).

Considering the finding that a single nonlinearity parameter \(\alpha = \alpha _{\infty } = \alpha _{1}= \alpha _{2}\) can capture the nonlinearity of brain tissue with sufficient accuracy [14], this introduces a total of eight model parameters, \(m^{\alpha }\), \(c^{\alpha }\), \(m_{\infty }^{\mu }\), \(c_{\infty }^{\mu }\), \(m_{1}^{ \mu }\), \(c_{1}^{\mu }\), \(m_{2}^{\mu }\), and \(c_{2}^{\mu }\), while the cell density \(\rho _{{\mathrm{c}}}\) is a microstructural parameter that needs to be determined through histological staining of the tested specimens [16], as discussed in detail in Sect. 2.4.

2.3.2 Microstructure-Based Relaxation Times

For the evolution of the internal variables \(\mathbf{b}_{i}^{\mathrm{e}}\), we choose evolution equations that a priori satisfy the reduced dissipation inequality (15) [13, 44],

$$ - \, {\mathscr{L}}_{v} \mathbf{b}^{\mathrm{e}}_{i} \cdot (\mathbf{b}^{ \mathrm{e}}_{i})^{-1} = \frac{1}{\eta _{i}} \, {\boldsymbol{\tau }}_{i} \, , $$
(22)

which introduces a total of two additional parameters, the viscosities \(\eta _{1}>0\) and \(\eta _{2}>0\), or, when scaled with the corresponding shear modulus \(\mu _{i}\), the associated relaxation times, \(\tau _{i} = {\eta _{i}}/{\mu _{i}}\) [13, 44].

Based on the observations in Sect. 2.2.3, we propose to determine one relaxation time constant from the cell displacement curves during stress relaxation experiments (see Fig. 7a). In addition to their physical interpretation, those curves were more robust and less noisy than the stress data. The corresponding time constant is supposed to represent the viscoelasticity of the network of cells and extracellular matrix. Since the displacement curves were surprisingly consistent between the individual samples originating from different brain regions (see also Fig. 7b), we decided to determine a single time constant valid for brain tissue as a whole, independent of the local microstructure. To this end, we adopted a one-term Prony series for each of the displacement curves, as exemplarily shown in Fig. 7c, and determined the average relaxation time from \(n=17\) samples to \(\tau _{\mathrm{network}} = 80 s \pm 27.48s\). We note that, while we universally set \(\tau _{\mathrm{network}} = 80\,s\), the viscosity \(\eta _{\mathrm{network}}(\rho _{{\mathrm{c}}}) = \tau _{\mathrm{network}}\, \mu _{\mathrm{network}}(\rho _{{\mathrm{c}}})\) is still a function of the cell density \(\rho _{{\mathrm{c}}}\) and may vary from one sample or region to the other – depending on the underlying microstructure.

2.3.3 Overall Tissue Response

Finally, for comparison with experimental measurements, we calculate the Piola stress \(\mathbf{P}^{\psi }\) as the partial pullback of the Kirchhoff stress \(\boldsymbol{\tau }\),

$$ \mathbf{P}^{\psi } = \boldsymbol{\tau } \cdot \mathbf{F}^{-{\mathrm{t}}} = [\, \boldsymbol{\tau }^{\mathrm{eq}} + \boldsymbol{\tau }^{\mathrm{neq}} - p \, \boldsymbol{I} \,] \cdot \mathbf{F}^{-{\mathrm{t}}} \,. $$
(23)

In unconfined compression, the Lagrange multiplier \(p\) follows from the lateral boundary conditions, \(P_{xx}=P_{yy} \doteq 0\). To advance the non-equilibrium part of the constitutive equations in time, we perform an implicit time integration with exponential update [13, 44]. For details, we refer to [13].

2.4 Parameter Identification

Our viscoelastic model has two microstructural parameters \(\rho _{{\mathrm{c}}}\) and \(\tau _{\mathrm{network}}\), which we obtain from microstructural imaging data, and nine model parameters, which we calibrate by using experimental data, as described in detail in Sect. 2.4.1. The parameters \(m^{\alpha }\) and \(c^{\alpha }\) characterize the nonlinearity of the hyperelastic spring elements, \(m_{\infty }^{\mu }\), \(c_{\infty }^{\mu }\), \(m_{1}^{\mu }\), \(c_{1}^{\mu }\), \(m_{2}^{\mu }\) and \(c_{2}^{\mu }\) characterize the corresponding shear moduli, and \(\eta \) characterizes the unknown viscosity. While the microstructurally motivated time constant \(\tau _{\mathrm{network}}\) is constant for all specimens, the cell density \(\rho _{{\mathrm{c}}}\) has to be determined individually through microstructural analyses subsequent to the mechanical measurements. While the free model parameters are solely identified based on mechanical measurements (see Sect. 2.4.2), they may be physically interpreted based on the insights in Sect. 2.2 (see Sect. 2.4.3).

2.4.1 Mechanical and Microstructural Protocols for Parameter Identification

To determine the free model parameters, we performed a separate set of experiments combining cyclic loadings and stress relaxation experiments on the same sample. We restricted ourselves to specimens from the corona radiata, as only few of the brains, which we obtained from a local slaughterhouse, included the brain stem and/or the cerebellum. Specimens extracted from the porcine putamen proved to be susceptible to swelling when immersed in PBS for longer time spans, especially during stress relaxation tests. We first performed three cycles of compression with a maximum strain of 7.5% and a loading velocity of 100 μm/s. Subsequently, we performed a stress relaxation test with a maximum strain of 7.5% and a holding period of 600 s, similar to the experiments in Sect. 2.2.3. In total, we tested \(n=5\) specimens.

Immediately after testing, we fixed each sample using 4% Formaldehyde to determine the corresponding cell density \(\rho _{{\mathrm{c}}}\). We washed the specimens with PBS, soaked them in 30% sucrose overnight at 4 ∘C in the refrigerator, embedded them in optimal cutting temperature compound, and cryosectioned 6 μm thick slices. We then used Nissl staining, which stains nuclei in dark blue and neuropil in a granular purple-blue, to visualize the cell nuclei and cell bodies. In order to account for potential cell density variations within each specimen, we took images at four different specimen planes. We analyzed the images using a custom-written MATLAB code that first converts them into gray scale images and then applies a TV-L1 denoising algorithm [32] as well as an optimized Kuwahara algorithm for edge preservation [4]. Subsequently, the images were binarized using a Niblack algorithm [39]. In the binarized image, cell nuclei appear as black spots on a white background and can be counted. For each specimen, the cell density averaged over the four planes was considered as microstructural parameter, as reported in Fig. 8.

Fig. 8
figure 8

Model calibration. Mechanical response and microstructure of five specimens from the corona radiata of porcine brain tissue. Representative histologically stained images of each specimen used to determine the cell density \(\rho _{{\mathrm{c}}}\) as microstructural parameter (left). Experimentally recorded mechanical response during cyclic loadings and stress relaxation experiments (blue dotted line) used for model parameter identification and corresponding model fit (black solid line) with coefficients of determination \(R^{2}\) (right). Scale bars in microscope images indicate 100 μm

Full size image

2.4.2 Calibration of Free Model Parameters

After defining the microstructural parameters for each specimen, we identified the free model parameters by using the nonlinear least-squares algorithm lsqnonlin in MATLAB Release 2019b. We minimized the objective function,

$$ \chi ^{2} =\sum _{i=1}^{n} [ P_{zz} - P^{\psi }_{zz} ]^{2}_{i} , $$
(24)

where \(n\) is the number of considered experimental data points. \(P_{zz}\) and \(P^{\psi }_{zz}\) are the experimentally measured and model predicted Piola stresses, respectively. To evaluate the ‘goodness of fit’, we determined the coefficient of determination, \(R^{2} = 1-P^{\mathrm{{res}}}/P^{\mathrm{{tot}}}\), where \(P^{\mathrm{{res}}} = \sum _{i=1}^{n} [P_{i}-P^{\psi }_{i}]^{2}\) is the sum of the squares of the residuals with the experimental data \(P_{i}\), the corresponding model data \(P^{\psi }_{i}\), and the number of data points \(n\), and \(P^{\mathrm{{tot}}} = \sum _{i=1}^{n} [P_{i}-\bar{P}]^{2}\) is the total sum of squares with the mean of the experimental data \(\bar{P} = 1/n \sum _{i=1}^{n} P_{i}\).

Although the presented experimental setup only allowed us to perform a single loading mode, i.e., compression, and we had to limit ourselves to samples from a single region, i.e., the corona radiata, we were able to include our previous findings towards mode-specific and regional trends through the considerations in Sect. 2.3.1. On the one hand, we had previously shown that the one-term Ogden model is capable of simultaneously capturing the behavior of brain tissue under compression, tension, and shear – and especially the characteristic compression-tension asymmetry – when the nonlinearity parameter \(\alpha \) adopts negative values. Therefore, we restricted the parameters \(m^{\alpha }\) and \(c^{\alpha }\) accordingly. On the other hand, we anticipated that by accounting for the linear dependence of the shear modulus and the nonlinearity parameter on the cell density, the calibrated model would also be valid for regions different from the corona radiata, according to the results in [16].

Figure 8 shows the performance of the calibrated microstructure-informed viscoelastic constitutive model for brain tissue. Table 1 summarizes the corresponding model parameters. The model well captures the slope of the stress-stretch response during cyclic experiments for all specimens and only slightly underestimates the hysteresis area, achieving coefficients of determination between \(R^{2}=0.82\) and 0.97. We note that, while we had previously only calibrated our constitutive models with either the first or the third loading cycle [13,14,15], here we consider the entire loading history including three loading cycles in addition to the stress relaxation response. For the stress relaxation experiments, the agreement between model predictions and experimental data is slightly worse with coefficients of determination between \(R^{2}=0.82\) and 0.95. For these data, we struggled with extremely low forces that approach the resolution limit of our testing device, especially during the holding period of stress relaxation experiments. Smoothing the noisy data could have introduced artefacts and especially the relaxation curves of the samples three and four show an uncommon shape and should be treated with caution. Overall, the model is capable of predicting the mechanical response of all specimens with reasonable accuracy.

Table 1 Calibrated model parameters∗
Full size table

2.4.3 Physical Interpretation of Free Model Parameters

Interestingly, the viscoelasticity of the network determined from microstructural data in Sect. 2.2.3 seems to be associated with the longer time scale, \(\tau _{\mathrm{network}} = \tau _{2} = 80\) s, contrary to our previous assumptions in [13], while the first viscoelastic element with \(\eta _{1}=1.7025\) kPa s yields time constants between \(\tau _{1}= 5.33\) s and 7.06 s. The latter may represent the fluid movement through the network of cells and extracellular matrix, as indicated in Fig. 2. We further observed that all nonlinear spring elements needed to be cell-density-dependent in order to accurately predict the viscoelastic behavior of each specimen and specifically the hysteresis. This dependence is plausible for the equilibrium response and the non-equilibrium element associated with the viscoelasticity of the network of cells and matrix (\(i = 2\)) according to the findings in [16]: With fewer cells, there is more space for interconnections and matrix leading to a stiffer response. For the first viscoelastic element potentially associated with fluid movement, however, the observation is interesting and may be associated with a cell-density-dependent permeability. Importantly, the corresponding \(m_{1}^{\mu }\) is positive, contrary to the negative \(m_{\infty }^{\mu }\) and \(m_{2}^{\mu }\). This means that an increase in the cell density leads to an increase in the stiffness of the first viscoelastic element.

The values obtained for \(c_{\infty }^{\mu }\) and \(c_{2}^{\mu }\) are close, which makes sense considering the fact that we associate both with the contribution of the network of cells, cellular processes, and extracellular matrix. The value for \(c_{1}^{\mu }\), in contrast, is an order of magnitude smaller. This suggests that the first viscoelastic element indeed rather contributes to the viscous than the elastic behavior of the tissue.

3 Conclusions

We have provided important insights into the microstructural origin of brain viscoelasticity through the simultaneous analysis of the macroscopic mechanical response and microstructural rearrangements of porcine brain tissue samples. We have shown that cell bodies are displaced but hardly deformed upon compressive mechanical loading, which suggests that the network of dendrites, glial cell processes, and extracellular matrix controls the mechanical response of brain tissue. In addition, we have identified the limit of finite viscoelasticity of brain tissue in compression to be 30% strain. For higher strains, permanent softening occurred.

As cells are embedded in the extracellular matrix and firmly connected through the network of cell processes, the deformation of the network can be tracked through the displacements of cell bodies or cell nuclei. In a recent study, fluorescent beads have been embedded in collagen gels to track the deformation that cells impose on their surrounding matrix and to uncover the role of three-dimensional traction forces in cancer cell invasion [27]. In brain tissue, the displacements of cell nuclei could similarly be used to determine local tissue deformation. Here, we have exploited this effect to determine microstructurally motivated relaxation time constants from cell displacement data during stress relaxation experiments. Besides the physical relevance, an advantage of this approach is that we can circumvent the previously identified issue that relaxation times for brain tissue largely depend on the holding time during stress relaxation experiments [19]. In addition, due to the extreme compliance of brain tissue, stress relaxation data are often noisy and, therefore, less suitable for the identification of highly sensitive parameters.

Based on these considerations, we have proposed a microstructure-informed finite viscoelastic constitutive model for brain tissue, where one of two time constants is determined from cell displacement curves and universally fixed for brain tissue in general, and the hyperelastic model parameters are introduced as linear functions of the cell density. The model is intended to inherently capture regional differences in the mechanical response through the spatial distribution of the cell density. Even within a certain anatomical region, e.g. the corona radiata (see Fig. 1), the microstructure may vary notably. Here we have demonstrated that our proposed model captures the variation in the mechanical response of brain tissue through the consideration of the average cell density in each tested sample with reasonable accuracy (see Fig. 8).

Taken together, the results in Sect. 2.2.2 and 2.2.3 along with the time constants from cell displacement curves in Sect. 2.3.2 suggest that the short time scale of approximately \(\tau _{1} \approx 6\) s is associated with fluid movement within the solid skeleton consisting of the cellular network and the extracellular matrix, while the longer time scale of approximately \(\tau _{2} \approx 80\) s represents the viscoelasticity of the network itself, as illustrated in Fig. 2. This is consistent with the results of a recent study on poro-viscoelastic modeling of brain tissue, suggesting that fluid squeezed out during loading immediately flows back upon unloading [18]. However, a clear physical interpretation of the first viscoelastic element will require additional studies, for instance with focus on the distinction between viscoelastic and poroelastic effects of brain tissue behavior [18, 21]. It is interesting to note, however, that our model calibration yielded a positive correlation between the cell density and the shear modulus in this particular element, while we find the opposite trend for the equilibrium response (see also [16]) and the second viscoelastic element.

The negative values of the parameters \(m_{\infty }^{\mu }\) and \(m_{2}^{\mu }\) further confirm that the mechanical response of brain tissue is largely controlled by the network of dendrites, synapses, and extracellular matrix, rather than the cell nuclei themselves. This, however, only holds for the fully developed brain, since experiments have shown that the trend between the density of nuclei and stiffness is reversed in the early stages of development [48]. In this case, the network of connections has not formed yet, such that cell nuclei take over a more important role in the mechanical response of brain tissue, which diminishes over time. Therefore, the microstructure-informed viscoelastic constitutive model presented in this study is only valid for the fully developed brain under physiological conditions, at least with the set of parameters provided in Table 1. Still, the reversed trend in early stages of development could easily be implemented through a positive model parameter \(m_{\infty }^{\mu }\).

As the cell density for the porcine brain samples tested in this study was slightly higher than for our previously tested human brain samples [16], the slope \(m_{\infty }^{\mu }\) is smaller. Hypothetically, this could be attributed to the fact that the porcine brain tissue tested here originates from relatively young animals, while for the relatively old human body donors in [16] certain neuron loss has already taken place. The main focus of the present work was to establish and validate the modeling framework. Still, we plan to repeat the experiments on human brain samples from different regions in the future to account for possible inter-species variations. We note, however, that we only expect effects on the quantitative parameters (if at all) and not on the qualitative considerations presented here.