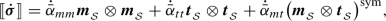On the mechanics of strain localization in plasticity: isotropic and orthotropic, elasto- and rigid-plastic, associated and non-associated models

Abstract

As strain localization is usually prognostics of localized failure in solids and structures, prediction of its occurrence and quantification of its adverse effects are of both theoretical and practical significance. Regarding plastic solids, onset of strain localization was presumed to be coincident with strain bifurcation, and the discontinuous bifurcation analysis was usually adopted to determine the discontinuity orientation though it does not apply to rigid-plastic solids. However, recent studies indicate that strain bifurcation and localization correspond to distinct stages of localized failure and should be dealt with separately. In this work, the mechanics of strain localization is addressed for perfect and softening plasticity in the most general context. Both isotropic and orthotropic, elasto- and rigid-plastic solids with associated and non-associated flow rules are analytically considered and numerically validated, extending our previous work on softening plasticity with associated evolution laws. In addition to Maxwell’s kinematics and continuity of the traction rate for strain bifurcation, a novel necessary condition, i.e., the stress rate objectivity (independent from the discontinuity bandwidth), and the resulting kinematic and static constraints, are derived for the occurrence of strain localization. In particular, the localization angles of the discontinuity band (surface) depend only on the specific stress state and the plastic flow tensor, irrespective from the material elastic constants and from the plastic yield function. Moreover, it is found that a transition stage generally exists in the case of plane strain during which the orientation of plastic flow rotates progressively such that strain localization may occur. Back-to-back numerical predictions of some benchmark problems, involving both perfect and softening plasticity, also justify the analytical results.

1 Introduction

As a typical phenomenon of localized failure in solids and structures, strain localization is manifested by highly non-uniform deformations concentrated within narrow bands of dimensions much smaller than the structural size. It leads to strain (weak) or even displacement (strong) discontinuities across the localization band, triggering substantial loss of integrity and safety or even collapse of structures. Consequently, quantification of strain localization is of both theoretical and practical significance in the prevention of localized failure for structural designs.

Historically, studies in strain localization originally stem from the interest in uncovering the mechanisms of shear banding in cohesive frictional (associated and non-associated) geotechnical materials like soils [25, 35, 42] and of extrusion and necking in bulk and sheet metal forming [23]. For the sake of brevity, in this work the material is assumed to be perfectly homogeneous; that is, only strain localization occurring spontaneously is considered. This is different from the Marciniak and Kucynski [33] criterion, widely adopted in the field of sheet metal forming, in which strain localization is initiated by a preexisting geometric and/or structural non-homogeneity [1, 31, 47].

In the context of shear-driven “slip lines” in pressure-independent rigid-plastic solids, strain localization was studied in the seminal works of Prandtl, Hencky and Mandel [21, 22, 32, 42]. This problem was later revisited by Hill [24] and the “slip lines” were interpreted as the characteristic lines of the underlying governing equations of hyperbolic type. In these early works, only rigid plasticity with no elastic deformations was considered, and incompressible behavior prior to shear-driven plastic yielding was assumed.

Strain localization in elastoplastic solids was later investigated by Hill, Thomas and Rice [25, 26, 44, 53] as a bifurcation problem. Upon the assumption of linear comparison (artificial) solids (i.e., plastic loading both inside and outside the discontinuity band), a strain bifurcation condition, i.e., singularity of the elastoplastic acoustic tensor, is derived from the combination of Maxwell’s kinematics and traction rate continuity condition across the discontinuity band. One noteworthy result is that strain bifurcation occurs at the hardening stages $H_{b} \ge 0$, for non-associated plastic materials [49]. Moreover, closed-form results for the discontinuity orientation and the associated hardening/softening moduli were obtained for the 2-D plane stress and plane strain conditions [50]. In the computational context, the above bifurcation condition with null hardening modulus was recommended to determine the discontinuity orientation in embedding weak or strong discontinuities into finite elements [36, 38, 52].

Though the above bifurcation analysis has been widely adopted, two issues cannot be overlooked. On the one hand, the strain bifurcation analysis does not apply to rigid-plastic solids since there is no elastic strain and the stiffness tensor is undetermined. Consequently, the stress cannot be directly given from the elastoplastic constitutive relation, and the elastoplastic acoustic tensor is no longer well defined. This makes unseemly the strain bifurcation analysis in rigid-plastic solids since it cannot be formulated as an equilibrium/stiffness problem.

On the other hand, the elastoplastic acoustic tensor depends on the hardening/softening modulus H, and so do the bifurcation condition and the resulting discontinuity orientation. As clarified in [6, 46], for the more frequently encountered incrementally nonlinear (real) material (i.e., inelastic loading inside the discontinuity band and elastic unloading outside it) the standard bifurcation analysis gives only the upper bound of strain localization. That is, though the initial bifurcation point corresponding to the largest hardening/softening modulus $H_{b}$ can be uniquely determined, strain localization is still indefinite and it can occur at any instant for $H \le H_{b}$. Moreover, even if the hardening/softening modulus H is specified a priori in an ad hoc manner, there may exist several solutions that fulfill the bifurcation condition. For instance, regarding the non-associated Mohr elastoplastic material, at least two valid solutions, one corresponding to Mohr’s solution [35] and the other to Roscoe’s solution [48], exist at the peak of the stress–strain relation ($H = 0$); see [40]. Consequently, if the discontinuity orientation is fixed at such detected bifurcation points, it is unavoidable to get pathological results in the computational context [38]. In particular, stress locking occurs due to the mis-prediction of the discontinuity orientation [39].

As the standard bifurcation analysis is not sufficient to determine the occurrence of strain localization, a more stringent condition needs to be introduced. To this end, the authors [13] proposed using the stress (rate) boundedness condition to determine the discontinuity orientation of associated von Mises ($J_{2}$) plastic materials. This condition was extended to isotropic elastoplastic models with general failure criteria (e.g., Rankine, von Mises, Mohr–Coulomb, Drucker–Prager and other more complex ones) [57,58,59], to orthotropic plastic ones [15, 29], and also to strain-based damage models [60]. Not only the discontinuity orientation but also the localized model upon strain localization, i.e., constitutive relations, evolution equations, traction-based failure criterion, softening functions, etc., can be determined consistently from a given material model [58, 59].

For the case of inelastic loading inside the discontinuity band and elastic unloading outside it, the stress (rate) boundedness condition is more constrictive than the traction (rate) continuity adopted in the strain bifurcation one. Remarkably, for isotropic and orthotropic elastoplastic materials with associated evolution laws, the discontinuity orientation predicted from the stress (rate) boundedness condition depends exclusively on the plastic flow tensor, independent of the elastic properties and the hardening/softening modulus. This is in contrast to the predictions given by the strain bifurcation condition. Extensive numerical simulations [10, 13, 15, 30] confirmed the analytical solutions with no a priori known information in the finite element simulations. These numerical results justify the stress (rate) boundedness condition for strain localization in plastic solids with associated flow rules and under the loading/unloading scenarios. Nevertheless, the not unusual loading/loading scenarios and the practically more encountered non-associated plastic flow rules remain to be investigated.

In this work, the mechanics of strain localization is addressed in the more general cases. Isotropic and orthotropic, rigid-plastic or elastoplastic solids with associated or non-associated evolution laws are analytically considered and numerically validated, extending our previous work on softening plasticity with associated evolution laws. An extra necessary condition, i.e., the stress rate objectivity (independent of the discontinuity bandwidth), in addition to Maxwell’s kinematics and continuity of the traction (rate) for strain bifurcation, is postulated for the occurrence of strain localization in perfectly or softening plastic solids. Both the loading/unloading and loading/loading scenarios are accounted for. This incorporates the “slip line” or “zero rate of extension” for rigid-plastic solids [24] and elastoplastic soils [48] as particular cases. Moreover, the previously proposed stress rate boundedness condition is also recovered as a particular case of strong discontinuities or regularized ones with a vanishing bandwidth, respectively, under the loading/unloading scenario.

The remainder of this paper is structured as follows. Section 2 presents briefly the kinematics, constitutive relations and statics for the analysis of strain localization. Section 3 is devoted the mechanics of strain localization in the continuum setting. Plastic yielding, strain bifurcation and strain localization are regarded as distinct stages of the whole failure process of elasto- and rigid-plastic solids. The difference and correlation between stain bifurcation and strain localization is discriminated. The analytical results for the localization angles in 2-D plane stress and plane strain conditions are also presented. Numerical validation of the proposed strain localization condition and the derived analytical results is addressed in Sect. 4 using the stabilized mixed ${\varvec{u}}/p$ finite elements, regarding the von Mises and Hill models with associated and non-associated plastic flow rules. A horizontal slit under vertical stretch and the Prandtl punch test are further considered in Sect. 5, further justifying the proposed condition for strain localization. The most relevant conclusions are drawn in Sect. 6 to close the paper.

2 General setting of discontinuities

Let us consider the reference configuration of an inelastic (elasto- and rigid-plastic in this work) solid $\varOmega \subset {\mathbb {R}}^{n_{\dim }} \; (n_{\dim } = 1, 2, 3)$. The external boundary is denoted by $\partial \varOmega \subset {\mathbb {R}}^{n_{\dim } - 1}$, with ${\varvec{n}}^{*}$ being the outward unit normal vector. Deformations of the solid are characterized by the displacement field ${\varvec{u}} ({\varvec{x}})$ and infinitesimal strain field $\varvec{\epsilon }({\varvec{x}}) := \nabla ^{\text {sym}} {\varvec{u}} ({\varvec{x}})$, for the symmetric gradient operator $\nabla ^{\text {sym}} (\cdot )$ with respect to the spatial coordinate ${\varvec{x}}$. Prescribed displacements ${\varvec{u}}^{*} ({\varvec{x}})$ and tractions ${\varvec{t}}^{*} ({\varvec{x}})$ are applied to two disjointed parts $\partial \varOmega _{u}$ and $\partial \varOmega _{t}$ of the boundary $\partial \varOmega$, respectively. The distributed body forces (per unit volume) are denoted by ${\varvec{b}}^{*}$. It is assumed in this work that only small deformations occur prior to strain localization; the extension to finite deformations in, e.g., soft materials, can be addressed with analogous hypotheses in the appropriate kinematic and constitutive frameworks.

2.1 Kinematics of discontinuities

Initially both the displacement and strain fields are continuous everywhere in the solid. In this case, the standard kinematics applies. Upon a specific condition and thereafter, either a discontinuity band or a discontinuity surface may form, depending on the localization band width. A discontinuity band can be regarded as a geometric regularization of a discontinuity surface (line) while the latter is recovered as bandwidth of the former vanishes in the limit.

Fig. 1

An inelastic solid with a discontinuity band

2.1.1 Discontinuity band

As shown in Fig. 1a, let us first consider the discontinuity band ${\mathcal {B}}$ of a finite width $b \ll L$, with L being the structural characteristic length. Note that in the continuum setting the bandwidth b is a numerical regularization parameter so that its value can be taken as small as possible. In the discrete (finite element) setting, b may be dependent on the mesh resolution. The discontinuity band ${\mathcal {B}}$ is delimited by two parallel surfaces ${\mathcal {S}}^{+}$ and ${\mathcal {S}}^{-}$, with the center one denoted by ${\mathcal {S}}$, i.e., $\varOmega ^{+} \cup \varOmega ^{-} \cup {\mathcal {B}} = \varOmega$. Let (n, m, t) be a set of orthogonal local axes, with ${\varvec{n}}_{_{\mathcal {S}}}$, ${\varvec{m}}_{_{\mathcal {S}}}$ and ${\varvec{t}}_{_{\mathcal {S}}}$ being the normal vector, the in-plane and out-of-plane tangential ones of the surface ${\mathcal {S}}$, respectively.

In this case, the displacement rate (velocity) field $\dot{{\varvec{u}}} ({\varvec{x}})$ is continuous, with an apparent velocity jump $\dot{{\varvec{w}}} := \dot{{\varvec{u}}} ({\varvec{x}} \in \varOmega ^{+} \cap {\mathcal {S}}^{+}) - \dot{{\varvec{u}}} ({\varvec{x}} \in \varOmega ^{-} \cap {\mathcal {S}}^{-})$ across the discontinuity band ${\mathcal {B}}$, where $\dot{(\;)}$ signifies the time derivative. The resulting strain rate field can be given by

(2.1)

for the collocation function $\varXi _{_{\mathcal {B}}} ({\varvec{x}})$ within the discontinuity band ${\mathcal {B}}$

$$\begin{aligned} \varXi _{_{\mathcal {B}}} ({\varvec{x}}) = {\left\{ \begin{array}{ll} 1 &{} \qquad {\varvec{x}} \in {\mathcal {B}}, \\ 0 &{} \qquad {\varvec{x}} \in \varOmega \backslash {\mathcal {B}}. \\ \end{array}\right. } \end{aligned}$$

(2.2)

Note that the strain rate field $\dot{\bar{\varvec{\epsilon }}} ({\varvec{x}})$ outside the discontinuity band ${\mathcal {B}}$ is independent of the bandwidth b, while the magnitude of the localized one $\dot{\tilde{\varvec{\epsilon }}}$ is inversely proportional to it: The smaller the bandwidth b is, the larger the localized strain becomes; see Fig. 1(b). Hereafter, the bar symbols $\bar{(\cdot )}$ are associated with the material points outside the discontinuity band (surface).

Remark 1

Note that in the kinematics (2.1) the collocation function $\varXi _{_{\mathcal {B}}} ({\varvec{x}})$ can be replaced by a bell-shaped continuous function localized within the discontinuity band ${\mathcal {B}}$. In this case, the localized strain rate $\dot{\tilde{\varvec{\epsilon }}} ({\varvec{x}})$ is continuous across the localization band, but it is still inversely proportional to the bandwidth b. $\square$

2.1.2 Discontinuity surface

As mentioned, the bandwidth b is a numerical parameter that can be made as small as desired. In the limit case $b \rightarrow 0$, the discontinuity band ${\mathcal {B}}$ becomes a discontinuity surface ${\mathcal {S}}$. It then follows that

$$\begin{aligned} \lim _{b \rightarrow 0} \dfrac{1}{b} \varXi _{_{\mathcal {B}}} ({\varvec{x}}) = \delta _{_{\mathcal {S}}} ({\varvec{x}}) = {\left\{ \begin{array}{ll} +\infty &{} \qquad {\varvec{x}} \in {\mathcal {S}} \\ 0 &{} \qquad {\varvec{x}} \in \varOmega \backslash {\mathcal {S}} \\ \end{array}\right. } \end{aligned}$$

(2.3)

for the Dirac-delta $\delta _{_{\mathcal {S}}} ({\varvec{x}})$ defined at the discontinuity surface ${\mathcal {S}}$.

Fig. 2

An inelastic solid with a discontinuity surface

Accordingly, the strain rate field becomes singular

(2.4)

Similarly, the strain rate field $\dot{\bar{\varvec{\epsilon }}} ({\varvec{x}})$ outside the discontinuity band ${\mathcal {B}}$ is independent of the bandwidth b, while the localized one $\dot{\tilde{\varvec{\epsilon }}} ({\varvec{x}})$ is singular. The above kinematics is shown in Fig. 2.

Remark 2

As the discontinuity surface can be recovered from the discontinuity band upon a vanishing bandwidth $b \rightarrow 0$, hereafter only the kinematics of the discontinuity band is considered. $\square$

2.2 Elastoplastic stress–strain relations

For elastoplastic models, the constitutive relation is expressed in rate form as

$$\begin{aligned} {\dot{\varvec{\epsilon }}} = {\dot{\varvec{\epsilon }}}^{e} + {\dot{\varvec{\epsilon }}}^{p}, \qquad {\dot{\varvec{\sigma }}} = {\mathbb {E}}_{0} : {\dot{\varvec{\epsilon }}}^{e} = {\mathbb {E}}_{0} : \big ({\dot{\varvec{\epsilon }}} - {\dot{\varvec{\epsilon }}}^{p} \big ) \end{aligned}$$

(2.5)

where the second-order tensors $\varvec{\sigma }$ and $\varvec{\epsilon }$ represent the stress and strain, respectively, with $\varvec{\epsilon }^{e}$ and $\varvec{\epsilon }^{p}$ being the elastic and plastic parts of the latter; the fourth-order material elasticity tensor ${\mathbb {E}}_{0}$ can be either isotropic or orthotropic.

Without loss of generality, the plastic strain rate is given by the following evolution laws

$$\begin{aligned} {\dot{\varvec{\epsilon }}}^{p} = {\dot{\lambda }} \varvec{\varLambda }^{p}, \qquad {\dot{\kappa }} = {\dot{\lambda }} h^{p} \end{aligned}$$

(2.6)

for the plastic multiplier ${\dot{\lambda }}$ satisfying the classical Karush–Kuhn–Tucker conditions

$$\begin{aligned} {\dot{\lambda }} \ge 0, \qquad f (\varvec{\sigma }, q) \le 0, \qquad {\dot{\lambda }} f (\varvec{\sigma }, q) \equiv 0, \end{aligned}$$

(2.7)

where a stress-based yield function $f (\varvec{\sigma }, q) \le 0$, with q being the stress-like internal variable (yield stress) conjugate to the strain-like one $\kappa$ which measure the plastic state, is introduced. The flow tensor $\varvec{\varLambda }^{p} := \partial f^{p} / \partial \varvec{\sigma }$ and the derivative $h^{p} := -\partial f^{p} / \partial q$ are normal to the potential function $f^{p} (\varvec{\sigma }, q)$ — if the latter is identical (or more generally, proportional) to the yield function $f (\varvec{\sigma }, q)$, the plastic flow is associated, and is non-associated otherwise. In the absence of plastic flow or in the case of elastic unloading, i.e., ${\dot{\lambda }} = 0$, the yield condition is not activated, i.e., $f (\varvec{\sigma }, q) < 0$; otherwise, plastic flow occurs. In this work, both perfect plasticity and softening one are addressed.

2.3 Statics of discontinuities

For elastoplastic solids, the stress rates inside the discontinuity band (surface) and outside it are given by

$$\begin{aligned}&{\dot{\varvec{\sigma }}} = {\mathbb {E}}_{0} : \big ( {\dot{\varvec{\epsilon }}} - {\dot{\varvec{\epsilon }}}^{p} \big ) = {\mathbb {E}}_{0} : \big ( {\dot{\varvec{\epsilon }}} - {\dot{\lambda }} \varvec{\varLambda }^{p} \big ), \end{aligned}$$

(2.8a)

$$\begin{aligned}&\dot{\bar{\varvec{\sigma }}} = {\mathbb {E}}_{0} : \big ( \dot{\bar{\varvec{\epsilon }}} - \dot{\bar{\varvec{\epsilon }}}^{p} \big ) = {\mathbb {E}}_{0} : \big ( \dot{\bar{\varvec{\epsilon }}} - \dot{\bar{\lambda }} \bar{\varvec{\varLambda }}^{p} \big ), \end{aligned}$$

(2.8b)

where the elastoplastic relations (2.5) and (2.6) have been recalled for both material points inside and outside the discontinuity band.

Accordingly, the resulting jump in the stress rate, $\llbracket {\dot{\varvec{\sigma }}} \rrbracket$, is expressed as

(2.9)

where the following Maxwell’s kinematic condition has been considered:

(2.10)

Equilibrium across the discontinuity band (surface) gives the following continuity condition of the traction rate:

(2.11)

where the scalars ${\dot{\alpha }}_\mathrm{mm}$, ${\dot{\alpha }}_\mathrm{tt}$ and ${\dot{\alpha }}_\mathrm{mt}$ can be either dependent on or independent of the bandwidth b, according to the deformation stage and stress state. Therefore, though stress rate discontinuities may occur, they can take place only on the plane of the discontinuity surface ${\mathcal {S}}$.

Remark 3

For rigid-plastic solids, the elastic strain $\varvec{\epsilon }^{e}$ vanishes such that

$$\begin{aligned} {\dot{\varvec{\epsilon }}} = {\dot{\varvec{\epsilon }}}^{p} = {\dot{\lambda }} \varvec{\varLambda }^{p}. \end{aligned}$$

(2.12)

In this case, the stress (rate) cannot be directly determined from the constitutive relation (2.5)$_{2}$. Consequently, only the compatibility condition, rather than the equilibrium one, applies to rigid-plastic solids. $\square$

3 The mechanics of strain localization: continuum setting

In this section, the mechanics of strain localization in plasticity is addressed in the continuum setting. The kinematics of discontinuities in an inelastic solid is first considered. After the classical concepts of plastic yielding (PY) and strain bifurcation (SB) are recalled, strain localization (SL) is further elaborated to general plastic models with associated and non-associated evolution laws.

3.1 Plastic yielding (PY)

Plastic yielding implies termination of linear elastic behavior. Plastic yielding occurs when the yield condition $f (\varvec{\sigma }, q) = 0$ is activated, i.e., ${\dot{\lambda }} > 0$. It then follows from the consistency condition ${\dot{f}} = 0$ that

$$\begin{aligned} {\dot{\lambda }} = \dfrac{\varvec{\varLambda }: {\mathbb {E}}_{0} : {\dot{\varvec{\epsilon }}}}{ \varvec{\varLambda }: {\mathbb {E}}_{0} : \varvec{\varLambda }^{p} + h \cdot H \cdot h^{p}} \end{aligned}$$

(3.1)

for the derivatives $\varvec{\varLambda }:= \partial f / \partial \varvec{\sigma }$ and $h := -\partial f / \partial q$ of the yield function $f (\varvec{\sigma }, q)$. Note that the hardening/softening modulus $H := \partial q / \partial \kappa$ is null for perfect plasticity and negative for softening one. Internal snap back is ruled out a priori with satisfaction of the condition $H > H_{c} := -\varvec{\varLambda }: {\mathbb {E}}_{0} : \varvec{\varLambda }^{p} / ( h \cdot h^{p} )$.

The corresponding constitutive relation in rate form then reads

$$\begin{aligned} {\dot{\varvec{\sigma }}} = {\mathbb {E}}_{0} : \big ({\dot{\varvec{\epsilon }}} - {\dot{\varvec{\epsilon }}}^{p} \big ) = {\mathbb {E}}^{ep} : {\dot{\varvec{\epsilon }}}, \end{aligned}$$

(3.2)

where the fourth-order elastoplasticity tangent ${\mathbb {E}}^{ep}$ is expressed as

(3.3)

For non-associated plasticity, i.e., $\varvec{\varLambda }^{p} \ne \varvec{\varLambda }$, the material tangent is not of major symmetry.

3.2 Strain bifurcation (SB)

Upon strain bifurcation, the strains inside and outside a small subdomain start deviating from each other, resulting in a discontinuity band with the strain rate jump given by Maxwell’s kinematics (2.10).

In this case, the material points inside the discontinuity band are in plastic loading, whereas those outside it can be in either plastic loading or elastic unloading, leading to the following continuous and discontinuous bifurcation scenarios, respectively:

• Loading–loading (i.e., the material is in loading both inside and outside the discontinuity band) or continuous bifurcation, i.e., ${\dot{\lambda }} > 0$ and $\dot{\bar{\lambda }} > 0$. Maxwell’s kinematics (2.10) and the traction (rate) continuity (2.11) give the following continuous bifurcation condition [43]

  $$\begin{aligned} \det {\varvec{Q}}^{ep} ({\varvec{n}}_{_{\mathcal {S}}}) = 0 \end{aligned}$$

  (3.4)

  for the elastoplastic acoustic tensor ${\varvec{Q}}^{ep} := {\varvec{n}}_{_{\mathcal {S}}} \cdot {\mathbb {E}}^{ep} \cdot {\varvec{n}}_{_{\mathcal {S}}}$ related to some normal vector ${\varvec{n}}_{_{\mathcal {S}}}$.

• Loading–unloading (i.e., the material is in loading inside the band and in elastic unloading outside it) or discontinuous bifurcation, i.e., ${\dot{\lambda }} > 0$ and $\dot{\bar{\lambda }} = 0$. Discontinuous strain bifurcation may occur provided the following condition holds [6, 46]

  $$\begin{aligned} \det {\varvec{Q}}^{ep} ({\varvec{n}}_{_{\mathcal {S}}}) \le 0 \end{aligned}$$

  (3.5)

  for some normal vectors ${\varvec{n}}_{_{\mathcal {S}}}$.

Note that the condition (3.4) of continuous bifurcation is the upper bound for that of discontinuous one (3.5). Accordingly, for incrementally nonlinear (real) materials, strain bifurcation is possible for any hardening/softening modulus $H_{c} < H \le H_{b}$ where the maximum value $H_{b}$ is determined from the criterion (3.4) for incrementally linear comparison (artificial) solids [2]; see [50] for the 2-D cases of plane stress and plane strain.

As the hardening/softening modulus H evolves with ongoing inelastic deformations, bifurcation first occurs as a continuous one at a point in the body where conditions are locally favorable. Once the continuous bifurcation is surpassed, deformations and strain concentrate further so that the discontinuous one becomes possible [46].

Remark 4

Regarding rigid-plastic solids, Young’s modulus goes to infinity, such that the elastoplastic acoustic tensor cannot be defined. The concept of strain bifurcation does not apply and the bifurcation analysis is unseemly. For isotropic elastoplastic models with associated or non-associated flow rules, [50] derived the analytical results for the bifurcation angle and the corresponding hardening/softening modulus $H_{b}$ in 2-D plane stress and plane strain conditions. It is found that the material under plane stress is more prone to strain localization compared to that under plane strain, and the bifurcation angle in the later case generally depends on Poisson’s ratio. Moreover, the occurrence of strain bifurcation depends on the hardening/softening modulus and is thus usually indefinite. Sometimes, multiple solutions exist at a given moment (with the hardening/softening modulus $H_{b}$ specified a priori) as discussed in [40]. The above facts imply that a more stringent condition is needed to determine the discontinuity band, motivating the strain localization criterion introduced in the next section. $\square$

3.3 Strain localization (SL)

After strain bifurcation occurs, deformations within the discontinuity band become more and more localized, affecting the stress rate (2.8a). Compared to the strain rate $\dot{\bar{\varvec{\epsilon }}}$ outside the band that is independent of the bandwidth b, the strain rate jump (2.10), inversely proportional to b, is much larger. Consequently, if it were not to cancel out by the third term, the stress rate ${\dot{\varvec{\sigma }}}$ would become unbounded for a vanishing bandwidth $b \rightarrow 0$, which is physically not allowable due to the plastic yielding condition $f (\varvec{\sigma }, q) \le 0$.

Therefore, in addition to Maxwell’s kinematics (2.10) and continuity of the traction rate (2.11), for the occurrence of strain localization, the stress rate within the discontinuity band has to be independent of the bandwidth whatever the localized strain rate is.

Remark 5

As the strain rate $\dot{\bar{\varvec{\epsilon }}}$ and stress rate $\dot{\bar{\varvec{\sigma }}}$ outside the discontinuity band are always independent of the bandwidth b, the above strain localization condition implies that the stress rate jump $\llbracket {\dot{\varvec{\sigma }}} \rrbracket$ across the band has also to be independent of it. $\square$

Remark 6

Regarding strain localization in strain-based elastic-damaging materials, not only the stress rate but also the stress itself have to be independent of the bandwidth; see [60]. It is interesting that the regularized XFEM [3,4,5] and the phase-field cohesive zone model [55, 56, 63, 64] both concur with the above statement. $\square$

3.3.1 Kinematic conditions

Now let us consider the kinematic conditions upon which the afore-defined strain localization occurs. As the strain rate $\dot{\bar{\varvec{\epsilon }}}$ outside the discontinuity band does not localize, for the stress rate (2.8a) inside the band to be independent of the bandwidth b, the plastic multiplier ${\dot{\lambda }} > 0$ has to admit the following additive expression

(3.6)

where the regular part ${\dot{\lambda }}_{0} \ge 0$ and the localized one $\dot{\tilde{\lambda }} > 0$ are both independent of the discontinuity bandwidth b.

Accordingly, for the stress rate (3.6) to be physically meaningful, the localized terms inversely proportional to the bandwidth b have to cancel out upon strain localization, i.e.,

(3.7)

That is, upon strain localization all of the strain rate jump, which is inversely proportional to the bandwidth b, has to be inelastic (plastic in this work). Note that the above kinematic condition depends only on the specific plastic flow tensor $\varvec{\varLambda }^{p}$ regardless it is associated or non-associated.

Remark 7

For rigid-plastic solids, the strain rate within the discontinuity band is purely plastic, such that

(3.8)

where the identity (3.6)$_{1}$ has been considered. As the strain rate $\dot{\bar{\varvec{\epsilon }}}$ does not localize, it follows that

(3.9a)

as well as

(3.9b)

where the localized plastic multiplier $\dot{\tilde{\lambda }} > 0$ does not vanish by definition. As can be seen, the strain rate (3.9b) outside the discontinuity is compatible with the assumed rigid behavior, if and only if the following condition is fulfilled:

$$\begin{aligned} {\dot{\lambda }}_{0} = 0 \qquad \Longleftrightarrow \qquad \dot{\bar{\varvec{\epsilon }}} = \varvec{ 0 }. \end{aligned}$$

(3.10)

That is, in this case strain localization occurs only for the loading/unloading scenarios, which is consistent with the classical result for rigid-plastic solids [24]. Note that there is no need to consider the equilibrium equation for strain localization in rigid-plastic solids. $\square$

3.3.2 Stress rate constraints

Upon satisfaction of the strain localization condition (3.7), the stress rate jump (2.9) is independent of the bandwidth b as expected:

$$\begin{aligned} \llbracket {\dot{\varvec{\sigma }}} \rrbracket = {\mathbb {E}}_{0} : \Big [ \dot{\bar{\lambda }} \bar{\varvec{\varLambda }}^{p} - {\dot{\lambda }}_{0} \dot{\tilde{\lambda }}^{-1} \big ( \dot{{\varvec{w}}} \otimes {\varvec{n}}_{_{\mathcal {S}}} \big )^{\text {sym}} \Big ]. \end{aligned}$$

(3.11)

Similarly to strain bifurcation, the material points outside the discontinuity band can be in plastic loading or elastic unloading/neutral loading, while those interior points are in plastic loading all along, i.e., $\dot{\tilde{\lambda }} > 0$ and $\dot{\bar{\lambda }} \ge 0$. Accordingly, the following two cases are distinguished:

• Loading–loading case (i.e., ${\dot{\lambda }} > 0$ and $\dot{\bar{\lambda }} > 0$). In this case, the stress rate jump is either null or orthogonal to the normal vector ${\varvec{n}}_{_{\mathcal {S}}}$, i.e.,

  

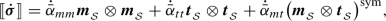  (3.12)

  where the scalars $\dot{\bar{\alpha }}_{mm}$, $\dot{\bar{\alpha }}_{tt}$ and $\dot{\bar{\alpha }}_{mp}$ are all independent of the discontinuity bandwidth b. This is a particular case of (2.11)$_{2}$ for strain bifurcation.

• Loading–unloading/neutral loading case (i.e., ${\dot{\lambda }} > 0$ and $\dot{\bar{\lambda }} = 0$): It then follows that

  $$\begin{aligned} \llbracket {\dot{\varvec{\sigma }}} \rrbracket =-{\dot{\lambda }}_{0} \dot{\tilde{\lambda }}^{-1} {\mathbb {E}}_{0} : \big ( \dot{{\varvec{w}}} \otimes {\varvec{n}}_{_{\mathcal {S}}} \big )^{\text {sym}} \qquad \Longrightarrow \qquad {\varvec{n}}_{_{\mathcal {S}}} \cdot \llbracket {\dot{\varvec{\sigma }}} \rrbracket =-{\dot{\lambda }}_{0} \dot{\tilde{\lambda }}^{-1} {\varvec{Q}}_{0} \cdot \dot{{\varvec{w}}} = \varvec{ 0 }. \end{aligned}$$

  (3.13)

  As the elastic acoustic tensor ${\varvec{Q}}_{0} := {\varvec{n}}_{_{\mathcal {S}}} \cdot {\mathbb {E}}_{0} \cdot {\varvec{n}}_{_{\mathcal {S}}}$ is symmetric and strictly positive-definite, this condition is fulfilled if and only if

  $$\begin{aligned} {\dot{\lambda }}_{0} = 0 \qquad \Longleftrightarrow \qquad \llbracket {\dot{\varvec{\sigma }}} \rrbracket = \varvec{ 0 }. \end{aligned}$$

  (3.14)

  Namely, in the loading–unloading/neutral loading case, the stress rate is continuous upon strain localization, even though the stress itself might be discontinuous due to the accumulation ever since strain bifurcation. This is the case we previously considered for strain softening solids with associated inelastic laws [13, 58, 59]; see [57].

Note that the above condition for strain localization, i.e., independence of the stress rate jump of the bandwidth b, applies to strain discontinuity bands and, in the limit of a vanishing bandwidth b, to strain localization surfaces.

3.3.3 Localization angles: analytical 2-D results

The strain localization condition (3.7) determines the structure of the flow tensor. More specifically, it implies the existence of a plastic flow vector $\varvec{\gamma }$ satisfying [37, 58, 59]

(3.15)

or in component form of the local axes system (n, m, t) defined at the discontinuity surface ${\mathcal {S}}$

$$\begin{aligned}&\varLambda _{nn}^{p} = \gamma _{n}, \qquad \varLambda _{nm}^{p} = \frac{1}{2} \gamma _{m}, \qquad \varLambda _{n t}^{p} = \frac{1}{2} \gamma _{t}, \end{aligned}$$

(3.16a)

$$\begin{aligned}&\varLambda _{mm}^{p} = 0, \qquad \varLambda _{tt}^{p} = 0, \qquad \qquad \varLambda _{mt}^{p} = 0. \end{aligned}$$

(3.16b)

From the kinematic constraint (3.15) or (3.16), the orientation of the discontinuity surface can be determined.

Regarding the 2-D case of plane stress and plane strain, the localization angle $\theta _{\ell }$ can be determined from the condition (3.16b). Interestingly, our previous analytical results for isotropic [57,58,59] and orthotropic [15] plasticity with associated evolution laws also applies to the non-associated case. Here these results are summarized for the sake of later validations.

• Orthotropic plasticity. As shown in Fig. 3a, let us consider the problem in the material axes (1, 2, 3). The orientation of the discontinuity band is characterized by the inclination angle (counterclockwise) $\theta _{\ell } \in [-\pi / 2, \pi / 2]$ between the normal vector ${\varvec{n}}_{_{\mathcal {S}}}$ and the material axis 1.

  In this case, the condition (3.16b)$_{2}$ gives [15]

  $$\begin{aligned} \tan \theta _{\ell } =-\dfrac{\varLambda _{12}^{p}}{\varLambda _{11}^{p}} \pm \sqrt{\bigg ( \dfrac{\varLambda _{12}^{p}}{\varLambda _{11}^{p}} \bigg )^{2} - \dfrac{\varLambda _{22}^{p}}{\varLambda _{11}^{p}}}. \end{aligned}$$

  (3.17)

  As can be seen, the discontinuity angle $\theta _{\ell }$ depends on the stress state upon strain localization.

• Isotropic plasticity. In this case, it is more convenient to define the discontinuity angles in the principal axes of the flow tensor $\varvec{\varLambda }^{p}$ (coincident with those of the stress tensor $\varvec{\sigma }$) as shown in Fig. 3b. The in-plane components along these principal axes are defined as $(\varLambda _{1}^{p}, \varLambda _{2}^{p})$, while $\varLambda _{3}^{p}$ are associated with the out-of-plane principal direction. The discontinuity angle (counterclockwise) $\theta _{\ell } \in [-\pi /2, \pi /2]$ between the normal vector ${\varvec{n}}_{_{\mathcal {S}}}$ and the principal vector ${\varvec{v}}_{1}$ of the stress tensor $\varvec{\sigma }$ is determined by [58, 59]

  $$\begin{aligned} \tan \theta _{\ell } = \pm \sqrt{-\dfrac{\varLambda _{2}^{p}}{\varLambda _{1}^{p}}}, \end{aligned}$$

  (3.18)

  which corresponds exactly to the case of $\varLambda _{12}^{p} = 0$ for the orthotropic result (3.17). Here axes are labeled so that $\varLambda _{1}^{p} \ge \varLambda _{2}^{p}$, and the magnitude of the out-of-plane components $\varLambda _{3}^{p}$ is not related directly to the magnitude of those in-plane.

For the plane stress case, (3.16b)$_{2}$ is automatically satisfied and thus (3.17) or (3.18) alone determines the localization angle $\theta _{\ell }$. Contrariwise, in the plane strain condition, the localization angle given by (3.17) or (3.18) is further constrained by the out-of-plane stress $\sigma _{3}$ that satisfies [59]

$$\begin{aligned} \varLambda _{33}^{p} (\theta _{\ell }) = 0 \end{aligned}$$

(3.19)

upon strain localization.

Fig. 3

Definitions of the discontinuity angle $\theta$ in isotropic and orthotropic plastic solids

Remark 8

The out-of-plane stress satisfying (3.19) is in general different from the elastic value

$$\begin{aligned} \sigma _{3} = \nu _{0} \big (\sigma _{1} + \sigma _{2} \big ). \end{aligned}$$

(3.20)

Therefore, in the case of plane strain, except for very particular cases, strain localization does not occur at the onset of plastic yielding. Rather, substantial plastic flows have to occur after plastic yielding (and possibly, strain bifurcation), until the out-of-plane stress fulfills (3.19).

Remark 9

As the localization angle $\theta _{\ell }$ is not affected by the elastic constants like Young’s modulus and Poisson’s ratio, the above results also apply to orthotropic elasticity. $\square$

3.4 Discussion

From the above analyses, the following comments can be made:

• (1) For both strain bifurcation and localization, the strain (rate) field exhibits discontinuities and the corresponding jump across the discontinuity band is given by Maxwell’s kinematics. Moreover, the material inside the band is in plastic loading, but the one outside it can be either in plastic/neutral loading or elastic unloading.

• (2) For both strain bifurcation and localization, continuity of the traction rate implies that stress rate discontinuities can take place only on the plane parallel to the discontinuity surface.

• (3) Strain bifurcation is only a necessary condition for strain localization, while the latter is more demanding with the extra condition that the stress rate within the discontinuity band has to be independent of the bandwidth.

• (4) In the plane strain condition, there is a transition stage between plastic yielding (and possibly, strain bifurcation) and strain localization. During this stage, the stress rate within the discontinuity band may depend on the bandwidth.

• (5) The occurrence of strain localization depends only on the plastic potential function, regardless of the flow rule is associated or non-associated. It depends neither on the plastic yield function (provided it is activated) nor on the elastic constants like Poisson’s ratio as that for strain bifurcation.

4 The mechanics of strain localization: discrete setting

In this section, the above strain localization condition and the analytical results for the discontinuity angles presented in 3.3.3 are numerically verified by finite element simulations. In particular, full boundary value problems (BVPs) are set up, discretized and solved, completed with the corresponding boundary conditions and increasing applied loading. Consequently, the obtained solutions have spatial variation and time evolution. Also, they are subjected to approximation errors (discretization in space and time, nonlinear tolerances, etc). Therefore, the comparison of the analytical results to the discrete solutions has to be interpreted on this regard.

In the numerical simulations, the plastic potential functions of the von Mises and the Hill criteria are considered, both being pressure independent and producing perfectly isochorich plastic flow by definition. Accordingly, for the occurrence of strain localization the plastic flow needs to be well developed and, at that stage, the incompressible plastic deformation is dominant over the elastic one. Standard displacement-based finite elements are not well suited to cope with this quasi-incompressibility situation in particular, if low-order finite elements are used. Mixed displacement/pressure (${\mathbf {u}}/p$) finite elements are far more suitable [51]; see our previous works on this topic [9, 11,12,13,14, 16, 17].

4.1 The stabilized mixed ${\varvec{u}} / p$ formulation

The strong form of the mixed ${\varvec{u}} / p$ formulation for mechanical problems is stated as: Given the elastic properties $(G_{0}, K_{0})$ and prescribed body forces ${\varvec{b}}^{*}$, find the displacement ${\varvec{u}}$ and pressure p, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \nabla \cdot {\varvec{s}} + \nabla p + {\varvec{b}}^{*} = \varvec{ 0 }, \\ \nabla \cdot {\varvec{u}} - \dfrac{1}{K_{0}} p = 0, \\ \end{array}\right. } \end{aligned}$$

(4.1)

where ${\varvec{s}} = 2 G_{0} \big ( {\varvec{e}} - {\varvec{e}}^{p} \big )$ is the deviatoric stress tensor, with ${\varvec{e}}$ and ${\varvec{e}}^{p}$ being the deviatoric strain tensor and its plastic component; $G_{0}$ and $K_{0}$ denote the shear and bulk moduli, respectively.

Standard arguments yield the following discrete form

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \int _{\varOmega } \nabla ^{\text {sym}} \delta {\varvec{u}}_{h} : {\varvec{s}}_{h} \; \text {d}V + \int _{\varOmega } \big ( \nabla \cdot \delta {\varvec{u}}_{h} \big ) p_{h} \; \text {d}V = \int _{\varOmega } \delta {\varvec{u}}_{h} \cdot {\varvec{b}}^{*} \; \text {d}V + \int _{\partial \varOmega _{t}} \delta {\varvec{u}}_{h} \cdot {\varvec{t}}^{*} \; \text {d}A &{} \qquad \forall \delta {\varvec{u}}_{h}, \\ \displaystyle \int _{\varOmega } \delta p_{h} \; \big ( \nabla \cdot {\varvec{u}}_{h} \big ) - \int _{\varOmega } \delta p_{h} \dfrac{1}{K_{0}} p_{h} \; \text {d}V = 0 &{} \qquad \forall \delta p_{h}, \\ \end{array}\right. } \end{aligned}$$

(4.2)

where $({\varvec{u}}_{h}, p_{h})$ and $(\delta {\varvec{u}}_{h}, \delta p_{h}) \in {\mathscr {V}}_{h} \times {\mathscr {Q}}_{h}$ denote the discrete displacement and pressure fields and their variations.

In mixed formulations, it is challenging to construct appropriate interpolating finite element spaces that satisfy the stability requirements on the spaces ${\mathscr {V}}_{h}$ and ${\mathscr {Q}}_{h}$ [7]. For instance, standard mixed elements with continuous equal-order linear/linear interpolation for both fields are not stable. Fortunately, stabilization methods [27, 28] can be developed to attain global stability with the desired choice of interpolation spaces. An appealing stabilization method is the orthogonal sub-grid scale method [19, 20], previously applied to the problem of incompressible elastoplasticity [9, 11,12,13,14, 16, 17].

The basic idea of the orthogonal sub-grid scale approach is to split the continuous displacement field into a coarse scale component and a fine one, corresponding to different scales or levels of resolution, i.e.,

$$\begin{aligned} {\varvec{u}} = {\varvec{u}}_{h} + {\varvec{u}}_{\perp }, \end{aligned}$$

(4.3)

where ${\varvec{u}}_{h} \in {\mathscr {V}}_{h}$ is the displacement field of the (coarse) finite element scale; ${\varvec{u}}_{\perp }$ is the enriched displacement field corresponding to the fine sub-grid scale, located in the space orthogonal to the finite element space and given by

$$\begin{aligned} {\varvec{u}}_{\perp } = \tau _{e} \big ( {\varvec{r}}_{h} - P_{h} ({\varvec{r}}_{h}) \big ) \qquad \text {with} \qquad {\varvec{r}}_{h} = \nabla \cdot {\varvec{s}}_{h} + \nabla p_{h} + {\varvec{b}}^{*} \end{aligned}$$

(4.4)

for the $L_{2}$-projection $P_{h}$ onto ${\mathscr {V}}_{h}$. Here, the stabilization parameter is determined by $\tau _{e} = c h_{e}^{2} / (2 G_{0})$ with $h_{e}$ being the characteristic length of the element and $c = {\mathcal {O}} (1)$ being a constant. As the stabilization (4.4) is residual-based, it is consistent; that is, it converges upon mesh refinement and vanishes for the continuous solution. The mesh size dependent stabilization parameter adopted achieves optimal convergence rate [19, 20].

Accordingly, the resulting stabilized mixed system of equations is expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \int _{\varOmega } \nabla ^{\text {sym}} \delta {\varvec{u}}_{h} : {\varvec{s}}_{h} \; \text {d}V + \int _{\varOmega } \big ( \nabla \cdot \delta {\varvec{u}}_{h} \big ) p_{h} \; \text {d}V = \int _{\varOmega } \delta {\varvec{u}}_{h} \cdot {\varvec{b}}^{*} \; \text {d}V + \int _{\partial \varOmega _{t}} \delta {\varvec{u}}_{h} \cdot {\varvec{t}}^{*} \; \text {d}A &{} \qquad \forall \delta {\varvec{u}}_{h}, \\ \displaystyle \int _{\varOmega } \delta p_{h} \; \big ( \nabla \cdot {\varvec{u}}_{h} \big ) - \int _{\varOmega } \delta p_{h} \dfrac{1}{K_{0}} p_{h} \; \text {d}V - \int _{\varOmega } \delta p_{h} \tau _{e} \big ( \nabla p_{h} - \pi _{h} \big ) \; \text {d}V = 0 &{} \qquad \forall \delta p_{h}, \\ \end{array}\right. } \end{aligned}$$

(4.5)

where the nodal variable $\pi _{h} = P_{h} (\nabla p_{h})$ is the $L_{2}$-projection of the pressure gradient.

4.2 Benchmark verification

The above mixed stabilized ${\varvec{u}}/p$ element is then applied to the strain localization analysis. The benchmark example is a 2-D strip loaded in uniaxial tension by stretching via imposed vertical displacements at the top and bottom ends; horizontal movement is not restrained. Figure 4a depicts the geometry of the problem with dimensions 10 $\times$ 20 $\times 1$ m (width $\times$ height $\times$ thickness). A sharp horizontal slit of length 2 m is inserted in the strip to introduce the perturbation necessary to trigger strain localization. As the plane stress condition has been previously numerically studied in [13] for isotropic plasticity and in [15] for orthotropic one, only the plane strain condition is considered in this work. The remote stress state corresponds to

$$\begin{aligned} \sigma _{xx} = 0, \qquad \sigma _{yy} = \sigma , \qquad \sigma _{xy} = 0. \end{aligned}$$

(4.6)

The numerical results are then used to validate the proposed strain localization criterion and verify the analytical results for the discontinuity orientation.

Fig. 4

A plane strain strip under vertical stretching: dimensions and finite element mesh. The bottom and top edges are vertically stretched along opposite directions but with equal magnitude. The flags in (b) indicate the actual elements inside and outside the localization band where the variables in Figs. 7, 9, 11 and 13 are sampled

Several elastoplastic models, i.e., the isotropic von Mises model and the orthotropic Hill model with associated flow rules, and the von Mises model with the non-associated Hill evolution law, all being isochoric, are considered for the material. Without loss of generality, the yield function is of the following form:

$$\begin{aligned} f (\varvec{\sigma }, q) : = \phi (\varvec{\sigma }) - q \le 0 \end{aligned}$$

(4.7)

for the loading function $\phi (\varvec{\sigma })$ and the yield strength q:

$$\begin{aligned} \phi (\varvec{\sigma }) = \sqrt{\dfrac{3}{2} \varvec{\sigma }^{\text {T}} \; {\mathbf {P}} \; \varvec{\sigma }}, \qquad q = \dfrac{3}{2} \big ( F + G + H \big )^{-1}, \end{aligned}$$

(4.8)

where $\varvec{\sigma }:= \big \{ \sigma _{11}, \sigma _{22}, \sigma _{33}, \sigma _{12}, \sigma _{13}, \sigma _{23} \big \}^{\text {T}}$ represents the stress vector in the Voigt notation, with $\sigma _{11}, \sigma _{22}, \sigma _{33}, \sigma _{12}, \sigma _{13}$ and $\sigma _{23}$ denoting the stress components in the material axes (1, 2, 3). Regarding the orthotropic Hill model, the projection matrix ${\mathbf {P}}$ is given by

$$\begin{aligned} {\mathbf {P}} = \dfrac{1}{F + G + H} \begin{bmatrix} F + G &{}\quad -F &{}\quad -G &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -F &{}\quad F + H &{}\quad -H &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -G &{}\quad -H &{}\quad G + H &{}\quad 0 &{}\quad 0 &{} 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 L &{}\quad 0 &{} 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 M &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 N \\ \end{bmatrix} \end{aligned}$$

(4.9)

for the following material parameters F, G, H, L, M and N:

$$\begin{aligned} F&= \frac{1}{2} \left[ \bigg (\dfrac{1}{\sigma _{Y, 11}} \bigg )^{2} + \bigg (\dfrac{1}{\sigma _{Y, 22}} \bigg )^{2} - \bigg (\dfrac{1}{\sigma _{Y, 33}} \bigg )^{2} \right] , \qquad L = \frac{1}{2} \bigg ( \dfrac{1}{\sigma _{Y, 12}} \bigg )^{2}, \end{aligned}$$

(4.10a)

$$\begin{aligned} G&= \frac{1}{2} \left[ \bigg (\dfrac{1}{\sigma _{Y,11}} \bigg )^{2} + \bigg (\dfrac{1}{\sigma _{Y, 33}} \bigg )^{2} - \bigg (\dfrac{1}{\sigma _{Y, 22}} \bigg )^{2} \right] , \qquad M = \frac{1}{2} \bigg ( \dfrac{1}{\sigma _{Y, 13}} \bigg )^{2}, \end{aligned}$$

(4.10b)

$$\begin{aligned} H&= \frac{1}{2} \left[ \bigg (\dfrac{1}{\sigma _{Y, 22}} \bigg )^{2} + \bigg (\dfrac{1}{\sigma _{Y, 33}} \bigg )^{2} - \bigg (\dfrac{1}{\sigma _{Y, 11}} \bigg )^{2} \right] , \qquad N = \frac{1}{2} \bigg ( \dfrac{1}{\sigma _{Y, 23}} \bigg )^{2}, \end{aligned}$$

(4.10c)

where those entities embellished by subscripts “Y” representing the corresponding yield strengths. The isotropic von Mises model is recovered with $\sigma _{Y, 11} = \sigma _{Y, 22} = \sigma _{Y, 33} = \sqrt{3} \sigma _{Y, 12} = \sqrt{3} \sigma _{Y, 13} = \sqrt{3} \sigma _{Y, 23} = \sigma _{Y}$ and $q = \sigma _{Y}$.

The following material properties are assumed in the numerical simulations: Young’s modulus $E_{0} = 10$ MPa, the yield strength $\sigma _{Y} = 10$ KPa for isotropic plastic models and $\sigma _{Y,11} = 15$ KPa with all the others equal to 10 kPa for orthotropic ones (no tilt is considered such that the material axes coincide with the global ones). It then follows that

$$\begin{aligned} {\left\{ \begin{array}{ll} F = G = H = \frac{1}{2} \Big (\frac{1}{\sigma _{Y}} \Big )^{2}, \quad M = N = L = \frac{3}{2 } \Big (\frac{1}{\sigma _{Y}} \Big )^{2} &{} \quad \text {the von Mises yield function}, \\ F = G = \frac{2}{9} \Big (\frac{1}{\sigma _{Y}} \Big )^{2}, \quad H = \frac{7}{9} \Big (\frac{1}{\sigma _{Y}} \Big )^{2}, \quad L = M = N = \frac{3}{2 } \Big (\frac{1}{\sigma _{Y}} \Big )^{2} &{} \quad \text {the Hill yield function}. \\ \end{array}\right. } \end{aligned}$$

(4.11)

The double symmetry of the problem and the solution allows to discretize a quarter of the domain. Various Poisson’s ratio $\nu _{0}$ are discussed for comparison purposes.

Fig. 5

Localization angles for the finite element meshes with various sizes

As the identity$\varLambda _{12}^{p} = 0$ holds for the von Mises potential function and the Hill one with no tilt, it follows from (4.16) that the localization angles are both $\theta _{\ell } = 45^{\circ }$; see Remark 10. Accordingly, structured triangular meshes are used in all the simulations to optimize the capacity of the linear triangles to represent a pure sliding mode, in parallel to one of the element sides; see Fig. 4b. In each example, three meshes of various sizes, i.e., $h_{e} = 0.02$ m, 0.01 m and 0.005 m, are considered. As shown in Fig. 5, for all cases the deformations are localized into narrow discontinuity bands of one single row of elements along $\pm 45^{\circ }$ directions, with the bandwidth proportional to the mesh size, i.e., $b = \sqrt{2} \; h_{e}$.

Calculations are performed with an enhanced version of the finite element program COMET [8], developed by the authors at the International Center for Numerical Methods in Engineering (CIMNE). Pre- and post-processing is done with GiD, also developed at CIMNE [18]. Loading is applied by imposed vertical displacements at both ends of the strip. The Newton–Raphson method is used to solve the nonlinear system of equations arising from the spatial and temporal discretization of the problem. An automatic procedure is used to adjust the step size, and about 200 steps are necessary to complete the analyses. Convergence of a time step is attained when the ratio between the norms of the residual and the total forces is smaller than $10^{-3}$.

The purpose of these benchmark examples is twofold: (1) to validate the proposed strain localization condition by comparing the mesh size (or, equivalently, bandwidth) independence of the stress (rate) inside the discontinuity band, and (2) to identify plastic yielding (PY), strain bifurcation (SB) and strain localization (SL) by monitoring stress and strain evolution of two neighboring points inside and right outside of the discontinuity band (see the flags in Fig. 4b):

• Plastic yielding (PY): PY is identified as the linear elastic limit of the stress–strain curves of the material point inside the discontinuity band. It can be determined by the change of slope observed in the evolution of the stresses and the Lode angle as plastic strains start to develop. For the current stress state and material parameters, it occurs when the vertical stress reaches

  $$\begin{aligned} \sigma _{yy} = {\left\{ \begin{array}{ll} \dfrac{\sigma _{Y}}{\sqrt{1 - \nu _{0} + \nu _{0}^{2}}} &{} \qquad \text {the von Mises yield function}, \\ \dfrac{\sigma _{Y}}{\sqrt{1 - \frac{14}{9} \nu _{0} + \nu _{0}^{2}}} &{} \qquad \text {the Hill yield function}. \end{array}\right. } \end{aligned}$$

  (4.12)

• Strain bifurcation (SB): SB is identified by definition as the moment right after the curves of the strain components of the material points inside and outside the discontinuity band start deviating. However, as the corresponding strains are small, the onset of strain bifurcation is not always easy to determine by inspection: It comes soon after plastic yielding and it triggers the transition phase into strain localization.

  Regarding the current example involving perfectly plasticity, SB is identified as the moment when the discontinuity band is passing through the material point, manifested by a local peak of the stress curves. After that, rotation of the discontinuity orientation occurs until the SL condition is activated.

• Strain localization (SL): SL is identified as the moment upon which the Lode angle corresponding to the strain localization condition $\varLambda _{33}^{p} (\theta _{\ell }) = 0$ is fulfilled at the material point inside the discontinuity band. This is feasible because plastic flow depends only on the deviatoric stresses and the strain localization condition is determined also by the corresponding Lode angle $\tilde{\theta }$. More specifically, for the von Mises and Hill potential functions, the out-of-plane stress $\sigma _{3}$ fulfilling the condition (3.19) is given by

  $$\begin{aligned} \sigma _{3} = {\left\{ \begin{array}{ll} \dfrac{1}{2} \sigma &{} \qquad \text {the von Mises potential function}, \\ \dfrac{7}{9} \sigma &{} \qquad \text {the Hill potential function}. \\ \end{array}\right. } \end{aligned}$$

  (4.13)

  Regarding the stress state (4.6) and (4.13), the Lode angle (positive cosine) $\tilde{\theta } \in [0, \pi /3]$ is determined as

  $$\begin{aligned} \tilde{\theta } = \dfrac{1}{3} \arccos \bigg [ \dfrac{J_{3}}{2} \Big ( \dfrac{3}{J_{2}} \Big )^{3/2} \bigg ] = {\left\{ \begin{array}{ll} 30^{\circ } &{} \qquad \text {the von Mises potential function}, \\ 47.78^{\circ } &{} \qquad \text {the Hill potential function}, \\ \end{array}\right. } \end{aligned}$$

  (4.14)

  where $J_{2}$ and $J_{3}$ denote the second and third invariants of the deviatoric stress tensor ${\varvec{s}}$.

Perfect plasticity is considered in Sects. 4.2.1–4.2.4, while the results presented in Sect. 4.2.5 indicate that the proposed strain localization condition also applies to softening plasticity [59].

Remark 10

For the plastic models with Eqs. (4.8)–(4.10) being the potential functions, in the plane strain cases ($\epsilon _{3} = 0$) the condition (3.19) gives the following out-of-plane stress:

$$\begin{aligned} \sigma _{33} = \dfrac{G \sigma _{11} + H \sigma _{22}}{G + H}, \qquad \varLambda _{11}^{p} + \varLambda _{22}^{p} =-\varLambda _{33}^{p} = 0. \end{aligned}$$

(4.15)

Accordingly, Eq. (3.17) becomes

$$\begin{aligned} \tan \theta _{\ell } =-\dfrac{\varLambda _{12}^{p}}{\varLambda _{11}^{p}} \pm \sqrt{\bigg ( \dfrac{\varLambda _{12}^{p}}{\varLambda _{11}^{p}} \bigg )^{2} + 1} \end{aligned}$$

(4.16)

for the ratio

$$\begin{aligned} \dfrac{\varLambda _{12}^{p}}{\varLambda _{11}^{p}} = \dfrac{\big (G + H \big ) L}{F G + F H + G H} \cdot \dfrac{\sigma _{12}}{\sigma _{11} - \sigma _{22}}. \end{aligned}$$

(4.17)

It follows from Eq. (4.16) that

$$\begin{aligned} \tan \theta _{\ell 1} \cdot \tan \theta _{\ell 2} = -1 \qquad \Longrightarrow \qquad \big | \theta _{\ell 1} - \theta _{\ell 2} \big | = 90^{\circ }. \end{aligned}$$

(4.18)

Accordingly, in the plane strain condition the discontinuity bands are perpendicular to each other. For the particular case of isotropic von Mises model, it follows from $\varLambda _{12}^{p} = 0$ that $\theta _{\ell } = \pm 45^{\circ }$. $\square$

4.2.1 The associated von Mises model with Poisson’s ratio $\nu _{0} = 0.0$

Let us first consider the associated von Mises model with Poisson’s ratio $\nu _{0} = 0.0$. For the material point within the discontinuity band, the evolution curves of the vertical strain, the vertical and out-of-plane stresses, and the Lode angle given by various mesh sizes are shown in Fig. 6.

Fig. 6

Strain, stresses and Lode angle of the von Mises model with Poisson’s ratio $\nu _{0} = 0.0$: Effect of the bandwidth (mesh size)

Fig. 7

Evolution curves of the von Mises model with Poisson’s ratio $\nu _{0} = 0.0$

As expected, the vertical strain $\epsilon _{yy}$ depends on the discontinuity bandwidth (or, equivalently, the mesh size): the less the bandwidth b is, the larger strain it reaches. Moreover, except during the intermediate transition stage, the stress components $\sigma _{yy}$ and $\sigma _{zz}$, and the Lode angle $\tilde{\theta }$, are all independent of the bandwidth b, validating the assumption postulated before: For the occurrence of strain localization, the stress rate inside the discontinuity band is independent from the mesh size and the resulting discontinuity bandwidth. Accordingly, termination of the transition stage can be identified as the strain localization point.

In order to identify plastic yielding (PY), strain bifurcation (SB) and strain localization (SL), the evolution curves of stress and strain at two neighboring points inside and right outside of the discontinuity band are considered in Fig. 7. Here only the results given by the mesh size $h_{e} = 0.005$ m are presented. In Fig. 7a, the evolution curves of the stress $\sigma _{yy}$ is shown. Plastic yielding is identified as the loss of linearity. For this case of vanishing Poisson’s ratio $\nu _{0} = 0.0$, another signal of plastic yielding is the occurrence of nonvanishing out-of-plane stress $\sigma _{zz}$ as depicted in Fig. 7b.

The evolution curves of the strain $\epsilon _{yy}$ are depicted in Fig. 7c. Though strain bifurcation is defined as the deviation of the strains inside and outside of the band, it corresponds to the peak points of the stress curves. The evolution curves of Lode angle $\tilde{\theta }$ are shown in Fig. 7d. Strain localization is identified as the moment upon which the Lode angle $\tilde{\theta } = 30^{\circ }$ for the material point inside the discontinuity band. Compared to strain bifurcation, strain localization occurs much later and there is a transition stage between them allowing the out-of-plane stress (3.19) to be attained.

As can be seen from the evolution curves of $\sigma _{yy}$ and $\sigma _{zz}$, upon strain bifurcation the stresses inside and outside the discontinuity band start deviating from each other. This stress jump that evolves during the transition phase from strain bifurcation to strain localization, remains constant, i.e., $\llbracket {\dot{\varvec{\sigma }}} \rrbracket = \varvec{ 0 }$, after strain localization, validating the stress rate continuity condition (3.14). This is because the material point outside the discontinuity band is in neutral loading.

4.2.2 The associated von Mises model with Poisson’s ratio $\nu _{0} = 0.5$

Let us next consider the associated von Mises model with Poisson’s ratio $\nu _{0} = 0.5$. As shown in Fig. 8, except for the vertical strain $\epsilon _{yy}$, the vertical and lateral stresses $(\sigma _{yy}, \sigma _{zz})$ as well as the Lode angle $\tilde{\theta }$ are all independent of the discontinuity bandwidth b almost during the whole deformation process. The observed very minor deviations are caused by stress perturbations during the formation of the discontinuity band and its passing through the sampling point.

As shown in Fig. 9 , in this case plastic yielding (PY), strain bifurcation (SB) and strain localization (SL) are very close to each other. This is because the out-of-plane stress (3.19) for $\nu _{0} = 0.5$ is coincident with the elastic value (3.20) and no transition stage exists. The minor differences between them is caused by the crossing of the discontinuity band through the material point. As there is no transition stage allowing stress discontinuities to develop, the stresses are continuous across the discontinuity band and the stress continuity holds together with the stress rate continuity, i.e., $\llbracket \varvec{\sigma }\rrbracket = \llbracket {\dot{\varvec{\sigma }}} \rrbracket = \varvec{ 0 }$.

Fig. 8

Strain, stresses and Lode angle of the von Mises model with Poisson’s ratio $\nu _{0} = 0.5$: Effect of the bandwidth (mesh size)

Fig. 9

Evolution curves of the von Mises model with Poisson’s ratio $\nu _{0} = 0.5$

4.2.3 The associated Hill model with Poisson’s ratio $\nu _{0} = 0.2$

Next the associated Hill model with Poisson’s ratio $\nu _{0} = 0.2$ is considered. Again, Fig. 10 confirms that the strain field inside the discontinuity band is dependent of the bandwidth b as expected, but the nonvanishing stress components $\sigma _{yy}$ and $\sigma _{zz}$ as well as the Lode angle $\tilde{\theta }$ are all independent of it except during the intermediate transition stage between strain bifurcation and localization.

Fig. 10

Strain, stresses and Lode angle of the associated Hill model with Poisson’s ratio $\nu _{0} = 0.2$: Effect of the bandwidth (mesh size)

In this case, plastic yielding (PY) and strain bifurcation (SB), which are identified from the evolution curves of $\sigma _{yy}$ and $\sigma _{zz}$ shown in the Fig. 11a, b as the loss of linearity of these curves and from Fig. 11c, d as the deviation of the strains inside and outside the discontinuity band, respectively. The latter is more easily identified as the peak points of the stress curves. As the out-of-plane stress (4.13)$_{2}$ cannot be attained at the onset of plastic yielding, there is a transition stage until the plane strain localization occurs with a Lode angle $\tilde{\theta } = 47.78^{\circ }$; see Fig. 11d.

Fig. 11

Evolution curves of the Hill model with Poisson’s ratio $\nu _{0} = 0.2$

Moreover, though the gaps between the stresses inside and outside the discontinuity band vary during the transition stage, the stress rate continuity condition $\llbracket {\dot{\varvec{\sigma }}} \rrbracket = \varvec{ 0 }$ holds upon strain localization (SL) and thereafter. That is, the postulated assumption of stress (rate) objectivity upon strain localization also applies to orthotropic plastic solids.

4.2.4 The non-associated von Mises/Hill model with Poisson’s ratio 0.2

Finally, let us consider the non-associated plastic model with the von Mises yield function and the Hill potential function. Poisson’s ratio $\nu _{0} = 0.2$ is assumed. Figure 12 depicts the evolution curves of the vertical strain, the nonvanishing stresses and the Lode angle inside the discontinuity band. As can be seen, for this non-associated plastic solid the stresses are also independent of the bandwidth upon strain localization and thereafter, though the strain becomes larger as the mesh size decreases.

Fig. 12

Strain, stresses and Lode angle of the non-associated von Mises/Hill model with Poisson’s ratio $\nu _{0} = 0.2$: Effects of the bandwidth

Fig. 13

Evolution curves of the non-associated von Mises/Hill model with Poisson’s ratio $\nu _{0} = 0.2$

Plastic yielding and strain bifurcation are easily identified from the loss of linearity and the peak load of the stress curves shown in Fig. 13a. Similarly, as the out-of-plane stress (4.13)$_{2}$ upon strain localization is not equal to the elastic one upon plastic yielding and strain bifurcation, a transition stage presents in Fig. 13d during which substantial deviatoric plastic flow occurs until the stress state inside the band corresponds to a Lode angle $\tilde{\theta } = 47.78^{\circ }$. Again, as can be seen from the evolution curves of $\sigma _{yy}$ and $\sigma _{zz}$, upon strain localization the stress discontinuities inside and outside the band stop increasing and the stress gaps maintain constant, i.e., $\llbracket {\dot{\varvec{\sigma }}} \rrbracket = \varvec{ 0 }$.

4.2.5 Localization in softening plasticity

In this subsection, the four cases studied in the preceding subsections for perfect plasticity are computationally re-analyzed for softening plasticity. For each case, three meshes of various sizes, i.e., $h_{e} = 0.02$ m, 0.01 m and 0.005 m, respectively, are considered as in the case of perfect plasticity. Exponential softening is considered for the yield stress q in (4.7). Dissipation is controlled by relating the softening parameters to the fracture energy [59] and the mesh size, though other strategies can be used as well [34, 41]. A fracture energy $G_{\text {f}} = 1,250$ J/m$^2$ is used in all cases.

Fig. 14

Evolution curves of Lode angle and vertical reaction for softening plasticity

For all the considered cases, the discontinuity bands form along as shown in Fig. 5, along the $45^{\circ }$ direction. Figure 14 shows the corresponding results. In the left column, the computed Lode angles for the elements inside the localization band are shown, corresponding exactly to the stress states that stem from satisfaction of the localization condition, i.e., $30^{\circ }$ for the isotropic von Mises potential function and $47.78^{\circ }$ for the Hill potential function. Note the resemblance to the corresponding results for the case of perfect plasticity shown in Figs. 6, 8, 10 and 12, respectively. In the right column, the global vertical reaction–displacement curves are shown; in all cases, the softening responses and the convergence upon mesh refinement are observed.

5 Numerical examples

In this section, two extra numerical examples are presented to further validate the obtained strain localization condition under more general conditions.

5.1 The plane strain strip under uniaxial stretching

Firstly, the plane strain strip under uniaxial stretching presented in Sect. 4.2 is re-analyzed. Different from the previous simulations, here quadrilateral ${\varvec{u}}/p$ elements are used to discretize the full computational domain. The mesh size is adopted as $h = 0.005$ m. In this way, two discontinuity bands that both satisfy the strain localization condition may form. Additionally, mesh alignment independence is also demonstrated for the discrete solution.

Four different models, i.e., the associated von Mises and Hill models, and the non-associated Hill/von Mises model (with the Hill criterion as the yielding function and the von Mises criterion as the potential one) and von Mises/Hill model (vice versa), are adopted in the simulation.

Fig. 15

A plane strain strip under uniaxial stretching: Localization angles for various models with no tilting

Fig. 16

Snapshots of the equivalent plastic strain at various applied displacements, showing rotation of the discontinuity orientation for the non-associated von Mises/Hill model

Let us first consider perfect plasticity. As mentioned before, for the case of no tilting, i.e., $\alpha = 0^{\circ }$, the analytical results predict discontinuity bands of $\pm \, 45^{\circ }$ directions for plastic models with either the von Mises or Hill potential function, and the yielding function does not alter the localization angle. The above results are exactly reproduced by the numerical simulations shown in Fig. 15. It is worth noting that even if the four final snapshots may look identical, they are not. The localization condition is identical for the four models, but the transition phases are different; distinct plastic strains accumulate during these phases. Minor differences can be observed around the horizontal slit, where plastic flows start.

Figure 16 presents three snapshots of the equivalent plastic strain at various applied displacements for the last model with the von Mises yielding function and the Hill potential one. The transition from plastic yielding/strain bifurcation to strain localization is evident, with the plastic strain evolving with increasing loading and the discontinuity angle eventually fixed at $\theta _{\ell } = 45^{\circ }$. Let us recall that for the von Mises model, the strain bifurcation angle $\theta _{b}$ depends on Poisson’s ratio, and $\theta _{b} > 45^{\circ }$ for $\nu _{0} < 0.5$ [50].

Let us now consider the tilt angle $\alpha = 60^{\circ }$. For the von Mises potential function, the flow tensor is isotropic and the same localization angles $\theta _{\ell } = \pm \, 45^{\circ }$ apply. As shown in Figs. 17a, b), the non-associated Hill/von Mises model shows the same localization as the associated von Mises model. The yield function does not alter the localization angle. Comparatively, for the Hill potential function, it follows from (4.16) that

$$\begin{aligned} \theta _{\ell } =-8.5^{\circ }; \; 81.5^{\circ }, \qquad \theta _{\ell } + \alpha = 51.5^{\circ }; \; 141.5^{\circ }, \end{aligned}$$

(5.1)

where $\theta _{\ell } + \alpha$ denotes the slopes of the upper discontinuity bands. As shown in Figs. 17c, d, the above analytical results are confirmed by the numerical simulations. Moreover, the non-associated von Mises/Hill model exhibits a localization pattern similar to that of the associated Hill model. Dependence of the localization angles only on the plastic potential function regardless the yield one is again confirmed.

Fig. 17

A plane strain strip under uniaxial stretching: Localization angles for various models with tilting angle $\alpha = 60^{\circ }$

Fig. 18

Snapshots of the equivalent plastic strain at various applied displacements, showing rotation of the discontinuity orientation for the non-associated von Mises/Hill model (with tilt angle $\alpha = 60^{\circ }$)

Figure 18 presents three snapshots of the equivalent plastic strain at various applied displacements for the non-associated von Mises/Hill model. In this peculiar instance, the four initial symmetric plastic bands rotate during the transition phase until two of them eventually localize at an angle compatible with the localization condition while the other two, orthogonal to the former, progressively fade into desactivation. As mentioned previously, even if the localization conditions of cases (a) and (b), and cases (c) and (d), are identical, respectively, the corresponding transition phases are not. This accounts for the slight curvature of the sliding lines in cases (b) and (d) around the slits.

Fig. 19

Snapshots of the equivalent plastic strain at various applied displacements, showing rotation of the discontinuity orientation for the softening non-associated von Mises/Hill model (with tilt angle $\alpha = 0^{\circ }$)

Fig. 20

Snapshots of the equivalent plastic strain at various applied displacements, showing rotation of the discontinuity orientation for the softening non-associated von Mises/Hill model (with tilt angle $\alpha = 60^{\circ }$)

Finally, let us consider softening plasticity. Figures 19 and 20 show the discontinuity bands obtained for the non-associated von Mises/Hill model, for tilting angles (a) $\alpha = 0^{\circ }$, (b) $\alpha = 60^{\circ }$, respectively. The adopted softening properties are the same as in Sect. 4.2.5. The resemblance with the corresponding results for perfect plasticity, Figs. 15d and 17d, respectively, is evident.

5.2 A plane strain punch test: elasto- and rigid-plastic models

The second example is the punch indentation test by a flat rigid die shown in Fig. 21. This is a well-known 2-D plane strain problem often used in the literature to test the ability of plastic models in capturing the failure modes. The problem was first studied by [42] for rigid-plastic bodies and then by [24] and [45] for elastoplastic materials.

Fig. 21

Indentation by a flat rigid die: Dimensions and loading. The bottom edge is fixed in both direction, while the left and right edges are constrained horizontally

As the non-associated models have been discussed in the previous sections, only the associated von Mises and Hill models are considered. The reference material parameters adopted in the simulations are: Young’s modulus $E_{0} = 10$ MPa, Poisson’s ratio $\nu _{0} = 0.2$, and the yield strength $\sigma _{Y} = 10$ kPa for isotropic plasticity and $\sigma _{Y,11} = 15$ KPa with all the others equal to 10 kPa for orthotropic ones (a tilt angle $60^{\circ }$ is assumed for the material axes). Perfect plasticity is used.

Fig. 22

Indentation by a flat rigid die: directions of principal stresses around the rigid footing

Note that the material right under the rigid die is almost under uniaxial vertical loading in the global axes, i.e., $\sigma _{xy} = 0$; similarly, the material around the top surface (not under the die) is subjected to uniaxial horizontal stresses; see Fig. 22. Therefore, the analytical results given in (5.1) apply here, with the localization angle depending only on the tilt of the material axes and the potential function.

5.2.1 Rough punch: Prandtl’s solution

A rough punch is first studied; that is, the material directly under the punch is not allowed to move horizontally, corresponding to so-called Prandtl’s solution.

We first consider the associated elastoplastic models. As shown in Fig. 23, the localization angle under the footing and close to the free surface is fixed $\theta ^{\text {cr}} = \pm \, 45^{\circ }$ with respect to the material axes, whatever the plastic yield function is. It is worth noting that the failure modes correspond to the claimed Prandtl’s solution for rigid-plastic models. This coincidence confirms the analytical prediction that rigid-plastic and elastoplastic failure follow similar mechanics.

Fig. 23

Indentation by a flat rigid die (rough punch): Localization angles for the associated von Mises and Hill models with tilting angle $\alpha = 60^{\circ }$

As demonstrated in [24], the failure mode is completely independent from the elastic constants. In the following, independence from the magnitude of the elastic modulus is shown. To this end, the analysis are performed with various values of Young’s modulus, ranging three orders of magnitude. The computed load–displacement curves are shown in Fig. 24. As can be seen, the global response is progressively stiffer, but the failure loads are identical as the one predicted analytically for rigid-plastic material. The corresponding failure modes are exactly identical. Moreover, the stiffer the material, the shorter the transition phase appears to be.

Finally, Fig. 25 shows the discontinuity bands obtained for the associated von Mises and Hill models with the tilting angle $\alpha = 60^{\circ }$, when softening plasticity is considered. The same softening properties as in Sect. 4.2.5 are adopted. The failure mechanisms are identical to those corresponding to perfect plasticity. Figure 26 shows the computed load–displacement curves for progressively increasing Young’s moduli. As can be seen, the global response is stiffer, but failure mechanisms and the softening branches are unaffected.

Fig. 24

Indentation by a flat rigid die: load–displacement curves for the associated von Mises and Hill models with tilting angle $\alpha = 60^{\circ }$

Fig. 25

Indentation by a flat rigid die (rough punch): localization angles for the softening associated von Mises and Hill models with tilting angle $\alpha = 60^{\circ }$

Fig. 26

Indentation by a flat rigid die: load–displacement curves for the softening associated von Mises and Hill models with tilting angle $\alpha = 60^{\circ }$

Remark 11

For the von Mises rigid-plastic model, the limit load is given by [24]

$$\begin{aligned} F = 2 a \dfrac{\sigma _{Y}}{\sqrt{3}} \big (\pi + 2 \big ) = 59370 \; \text {N} \end{aligned}$$

(5.2)

for $a = 1$ m here, coincident with the numerical predictions. $\square$

5.2.2 Smooth punch: Hill’s solution

A smooth punch is now investigated; that is, the material points located directly under the punch are allowed to move horizontally. The only difference from the previous rough case is the boundary conditions at the base of the punch.

The corresponding failure patterns for the associated von Mises and the Hill models are shown in Fig. 27. The former one corresponds to so-called Hill’s solution for the punch problem [24].

Fig. 27

Indentation by a flat rigid die (smooth punch): Localization angles for the associated von Mises and Hill models with tilting angle $\alpha = 60^{\circ }$

It can be seen that in these new solutions, the localization angles under the footing and close to the free surface are also fixed as $\theta ^{\text {cr}} = \pm \, 45^{\circ }$ with respect to the material axes.

Remarkably, the analytical and numerical load capacities of these solutions are exactly the same as those obtained for the rough punch. Additionally, the failure modes and load are independent from the elastic moduli and apply to both elastoplastic and rigid-plastic materials.

This last example illustrates that the localization condition applies locally, but the formation of global failure modes depends crucially on the global equilibrium and the kinematic boundary conditions. These are the basis of classical plastic limit analyses.

6 Conclusions

In this work, the mechanics of strain localization is addressed both analytically and numerically for isotropic and orthotropic, elasto- and rigid-plastic solids with associated or non-associated flow laws. More specifically, we postulate the stress (rate) objectivity (i.e., independent of the discontinuity bandwidth) as the necessary condition for the occurrence of strain localization, in addition to Maxwell’s kinematics and continuity of the traction (rate) for strain bifurcation. Consequently, strain localization is more demanding than the classical continuous/discontinuous strain bifurcation, though both accounts for the plastic loading/unloading and loading/loading scenarios. For the plane strain condition, there generally exists a transition stage between plastic yielding/strain bifurcation and strain localization. Moreover, regarding the stress (rate) within the discontinuity band, the boundedness condition [13, 36, 37] and the continuity condition [57,58,59], both assuming plastic loading/unloading with associated evolution laws in strain softening solids, are recovered as particular cases of strong discontinuities with a vanishing bandwidth and of regularized ones with a finite bandwidth, respectively. The concept of “slip line” or “zero rate of extension” is also incorporated for rigid-plastic solids [24] and soils [48].

The kinematic and static constraints upon strain localization are then derived analytically. In particular, the localization angles of the discontinuity band (surface) depend only on the specific stress state and the plastic flow tensor, irrespective from the elastic material constants and the plastic yield function. During the transition stage the orientation of the discontinuity band (surface) rotates progressively to the localization angle. For the plane strain condition, the yield function affects the evolution process upon which the out-of-plane stress for strain localization is achieved and consequently the transition stage, but not the localization angle.

The above strain localization condition and analytical results for the localization angle are validated numerically by several benchmark examples. The stabilized mixed finite element formulation is adopted to deal with the quasi-incompressible deformations resulting from the von Mises and Hill potential functions. It is found that for perfectly and softening plastic solids with either associated or non-associated evolution laws, upon strain localization and thereafter the stresses inside the discontinuity band are indeed independent of the bandwidth, validating the postulated assumption. Moreover, similarly to our previous work on plastic or damaging solids, the numerically predicted localization angles are coincident with those given by the analytical results, further justifying the proposed strain localization condition.

As it applies to isotropic and orthotropic rigid-/elastoplastic solids with associated or non-associated flow rules, the proposed strain localization condition can be used to determine the discontinuity orientation in the numerical modeling of localized failure in solids. In particular, it would be very helpful to track crack propagation paths, which is a challenging and open issue in the discontinuous approach like extended or enriched finite element methods [54, 61, 62]; see [3, 65, 66]. This will be explored in forthcoming jobs.