A mesh-independent framework for crack tracking in elastodamaging materials through the regularized extended finite element method

Abstract

We propose a formulation for tracking general crack paths in elastodamaging materials without mesh adaptivity and broadening of the damage band. The idea is to treat in a unified way both the damaging process and the development of displacement discontinuities by means of the regularized finite element method. With respect to previous authors’ contributions, a novel damage evolution law and an original crack tracking framework are proposed. We face the issue of mesh objectivity through several two-dimensional tests, obtaining smooth crack paths and reliable structural results.

1 Introduction

We devise a methodology where mesh and crack geometry are unrelated, for the crack path is embedded within the finite elements through the extended finite element method, so that neither strict mesh refinement in the crack front nor coarsening behind the crack tip are required. The present crack tracking approach captures the onset of diffused damage and its subsequent transition to a crack through a unified approach in the framework of the regularized extended finite element technology that has been developed by the authors for the last decade. Both the concepts of damage band and discontinuity are already inherent in the structure of the approach. We thoroughly assess the robustness of the method with respect to size, type and bias of the mesh in terms of load–displacement profiles and crack paths.

State-of-the-art models for brittle fracture have been grouped into two main categories: discrete models, such as interface and cohesive zone models [38, 50, 78], extended and generalized finite elements [8, 39], and continuum models, including smeared crack [34, 53, 72], nonlocal [17, 18, 69, 70], and phase-field models [26, 59]. However, recently, a great deal of effort has been spent in providing a bridge between continuum and discrete formulations. In this introduction, we mainly consider the phase-field method and the extended finite element method for their relevance to the present developments.

In computational fracture mechanics, the variational formulation of phase-field models mainly descends from the theory of free-discontinuity problems and, particularly, from Ambrosio and Tortorelli’s regularized energy functional, whose key role in computational fracture mechanics was first recognized by Francfort and Marigo [42] and then numerically assessed by Bourdin et al. [25] and Miehe et al. [59, 60]. Phase-field models outperform nonlocal integral and gradient models, as they rule out the marked broadening tendency of the process zone during the late stages of the cracking process. In fact, phase-field models can be regarded as smart versions of damage gradient models [58], the only difference lying in that the damage driving force vanishes for increasing values of the damage [36]. Furthermore, it has been shown [57] that, using certain gradient damage degradation functions [56], phase-field models can be constructed that consistently approximate the structural results. Another advantage is that cracking patterns naturally emerge from energy minimization and, thus, crack tracking algorithms are not necessary [2, 47, 55]. However, phase-field models usually require severe mesh refinement to satisfactorily converge, unless mesh adaptivity is used [64]. Among the most relevant transitioning approaches sharing some similarities with phase field models, we mention the thick level set method, where the undamaged zone is separated from the damaged zone by means of levels sets and the damage growth is driven by a nonlocal configurational force [24, 62].

The extended finite element method allows to capture cracks and discontinuities without mesh adaptivity. Like the generalized finite element method [39], the extended finite element method is a Partition of Unity Method [5] that enriches the space of standard partition-of-unity shape functions with functions featuring the exact or the expected mathematical structure of the searched solution [8, 61, 74]. Well known examples are the Heaviside function to reproduce displacement discontinuities, and Westergaard’s solution to capture crack-tip singularities, while material discontinuities are captured by means of appropriate $\mathcal {C}^0$ functions [10, 44]. The extended finite element method has significantly progressed in the field of crack propagation [75]. Moreover, several authors have devised successful procedures for transitioning to a discontinuous description of the cracking process based on the extended finite element method [45, 76, 77, 81]. For instance, Geelen et al. [46] have proposed an optimization-based approach to bridge phase-field models and the extended finite element method. The use of crack tracking algorithms in extended finite element models is a rather natural choice and has been thoroughly assessed [32, 40, 79].

The problem of how to perform a proper continuous-discontinuous transition in elastodamaging materials is long-standing in computational mechanics, the earliest contributions being traceable back to twenty years ago [53, 54]. Noteworthy, the finite element modelling of the continuous-discontinuous transition in elastodamaging materials is affected by pathological effects, such as mesh-size dependence and proneness to produce biased crack paths [52, 63]. In particular, the connection between mesh directionality bias and crack tracking approaches has been assessed by several research groups [29,30,31]. In brief, crack-path uniqueness and objectivity with respect to mesh bias and size are key to devise reliable crack tracking approaches for elastodamaging materials.

Unlike the aforementioned models transitioning from continuous to discontinuous settings, the current regularized extended finite element model tackles the diffused damage stage and the discontinuous regime through a unified computational framework [12, 14, 16, 19]. Particularly, the transition to the discontinuous formulation is activated at the early stages of the damaging process, while local constitutive laws are used up to the transition. The use of a regularized kinematics in the extended finite element method was originally proposed by Patzák and Jirásek [68] and later originally elaborated by the authors [12, 14, 15]. The early crack tracking strategy, however, worked only for predetermined crack paths [13, 16]. Moreover, it was not possible to transition from a process zone several finite elements wide to a process zone as wide as one finite element.

The present contribution proposes a reliable regularized extended finite element approach for tracking general crack patterns that overcomes the limitations of the previous approach [16]. In light of the structure of the displacement field, for the construction of the energy functional, we draw inspiration from the theory of free-discontinuity problems [4, 27]. For the sake of simplicity, we omit crack tip enrichment and bimaterial cracks, and focus on cases where crack branching does not occur. Interestingly, the present variational formulation incorporates some aspects of phase-field models, such as a crack density function evolving with the damage, and shares with nonlocal models the use of a regularization length that acts as a strain localization limiter. Furthermore, the present formulation lacks of the damage broadening effect typical of nonlocal models. The proposed crack tracking strategy revisits the procedures for smeared cracks proposed by Cervera [30], Cervera et al. [29], and makes use of the concept of nonlocal stress criterion [82]. However, besides the obvious differences inherent in the kinematics and the variational formulation, the resulting framework can be regarded as a unique and original contribution owing to the flexible handling of the width of the process zone based on the damage level.

The remainder of the paper is organized as follows. In Sect. 2, we borrow some mathematical arguments from the theory of free-discontinuity problems applied to fields with jumps. In Sect. 3, a regularized kinematics is formulated. We accordingly introduce the energy functional, derive the constitutive laws, and formulate the variational formulation. In Sect. 4, we present the crack tracking algorithm and describe various strategies for the choice of the crack direction and inception. Section 5 illustrates the performance of the proposed technique in terms of mesh independence, accuracy of the load–displacement results and crack paths. Finally, we critically review the obtained results in Sect. 6.

2 Basic statements of the formulation

In this section, we show the mathematical aspects typical of a discontinuous discrete kinematics. The final goal is to develop an extended finite element method, where the displacement field is approximated as the sum of a continuous term plus a jump. For this purpose, we will make a step back with respect to the usual starting point of extended finite element methods, namely the discrete expression of the displacement field [8, 9].

We first introduce the problem in Sect. 2.1 and provide the main mathematical preliminaries in Sect. 2.1.1.

Functionals are indicated with a thin notation, while a bold notation is used for vectors and tensors. Application of a tensor $\varvec{A}$ to a vector $\varvec{a}$ is indicated by $\varvec{A} \varvec{a}$, and $\varvec{a} \cdot \varvec{b}$ denotes the scalar product between vectors $\varvec{a}$ and $\varvec{b}$ [51].

Fig. 1

Problem to be solved

2.1 The problem of a cracked body

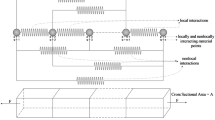
We define the displacement field u over the domain $\varOmega \subset \mathbb {R}_3$ with boundary $\partial \varOmega$. Let $\bar{u}$ be the displacement on $\partial \varOmega _d\subset \partial \varOmega$. Furthermore, u exhibits a jump $\llbracket u \rrbracket =u^+- u^-$across the crack $\varGamma$, $u^+$ and $u^-$ being the traces of u on the opposite sides of $\varGamma$. We postulate the existence of a stress field $\sigma$ and allow the exchange of cohesive forces $\sigma n = f_s$ across a certain portion $\varGamma _s$ in front of the crack line $\varGamma$, while tractions are not transmitted across $\varGamma _c$, being $\varGamma =\varGamma _c \cup \varGamma _s$. Here, n denotes the field of the relevant normal versor. We aim to solve the problem of the equilibrium of the cracked body $\varOmega$ subjected to appropriate boundary conditions and write the equations representative of the problem at hand as:

$$\begin{aligned}&\text {div}\sigma = 0&\qquad \text {in}\; \varOmega {\setminus } \varGamma , \end{aligned}$$

(1a)

$$\begin{aligned}&\sigma n = \bar{p}&\qquad \text {in}\; \partial \varOmega _p {\setminus } \varGamma ,\end{aligned}$$

(1b)

$$\begin{aligned}&\sigma n = f_s&\qquad \text {on} \;\varGamma _s,\end{aligned}$$

(1c)

$$\begin{aligned}&\sigma n = 0&\qquad \text {on} \;\varGamma _c,\end{aligned}$$

(1d)

$$\begin{aligned}&u = \bar{u}&\qquad \text {on}\; \partial \varOmega _u{\setminus } \varGamma . \end{aligned}$$

(1e)

A qualitative representation of the problem to be solved is in Fig. 1.

We reckon that the variational space such a discontinuous displacement field belongs to should be carefully chosen and that the appropriate variational formulation should descend from the theory of free-discontinuity problems formulated for fields with jumps [3].

2.1.1 Energies for fields with jumps

An extensive and erudite study about variational formulations for solids with cracks can be found in the essay [26]. We provide hereafter a synthetic description of the concepts relevant to the developments that will be presented in the next sections.

We focus the attention on a class of problems that require the formulation of energy functionals depending both on a field u that displays a jump $\llbracket u \rrbracket$ across the surface $\varGamma \subset \mathbb {R}^{m-1}$ of normal n, and on $\varGamma$ itself [42]. Free-discontinuity problems are based on the minimization of functionals of the type [3]

$$\begin{aligned} \begin{aligned} \mathcal {F}(u,\varGamma ) =&\int _{\varOmega {\setminus } \varGamma } F(x,u,\nabla u) dx + \\&\int _\varGamma F_s (x,\llbracket u \rrbracket ,n) d\mathcal {H}^{m-1}(x), \end{aligned} \end{aligned}$$

(2)

where $\varOmega \subset \mathbb {R}^m$ is an open bounded set, $\mathcal {H}^{m-1}(x)$ is the Hausdorff $m-1$-dimensional measure, $\varGamma$ varies in a class of sufficiently regular closed sets of $\varOmega$, u varies in $W^{1,2}(\varOmega {\setminus } \varGamma )$. Problems that involve the minimization of the class of functionals (2) are referred to as free discontinuity problems. The most known example is the minimization problem of the Mumford-Shah functional for image segmentation [65]

$$\begin{aligned} \mathcal {G}(u, \varGamma ) = \int _{\varOmega {\setminus } \varGamma } \bigl [ |\nabla u|^2 +\beta (u-g)^2\bigr ] dx + \alpha \mathcal {H}^{m-1} (\varGamma ),\nonumber \\ \end{aligned}$$

(3)

where $u\in W^{1,2}(\varOmega {\setminus } \varGamma )$, $\varGamma$ closed in $\varOmega$, $\alpha$ and $\beta$ are fixed positive parameters, and $g \in L^\infty (\varOmega )$ [4, 27, 35]. The existence of minimizers for the Mumford-Shah functional has been proved by De Giorgi et al. [37] through the definition of the functional

$$\begin{aligned} \bar{\mathcal {G}}(u, \varGamma ) = \int _{\varOmega } \bigl [ |\nabla u|^2 +\beta (u-g)^2\bigr ] dx + \alpha \mathcal {H}^{m-1} (\varGamma ), \end{aligned}$$

(4)

where $\varGamma$ stands for the discontinuity set of u in an approximate sense, and u varies in a special class of functions of bounded variation, denoted by SBV. SBV consists of all functions of bounded variation such that the distributional derivative is absolutely continuous with respect to Lebesgue measure plus a $m-1$-dimensional measure. In other words, a function u belongs to SBV if and only if its distributional derivative Du is a bounded measure that can be split into a bulk and a surface term, i.e. the Cantor part of the derivative vanishes. In particular, a function u belongs to SBV if the approximate gradient $\nabla u$ exists a.e. on $\varOmega$, and its distributional derivative Du can be defined as [27]

$$\begin{aligned} Du = \varepsilon + (\llbracket u \rrbracket \otimes n) \mathcal {H}^{m-1}(\varGamma ). \end{aligned}$$

(5)

Noteworthy, in Eq. (5)$, \varepsilon$ denotes the approximate gradient of u with respect to the Lebesgue measure. It could be regarded as the total variation without the term with the jump.

In fracture mechanics, worth noting results have been achieved by using regularized functionals that have the property of $\varGamma -$converging to the Mumford-Shah functional. Perhaps the most known regularized energy functional of this kind is the Ambrosio-Tortorelli functional [4, 25, 48]

$$\begin{aligned} \begin{aligned} G_\epsilon (u, v)=&\int _\varOmega v^2 |\nabla u |^2 dx + \\&\frac{1}{2} \int _\varOmega \bigl [\epsilon | \nabla v|^2 + \frac{1}{\epsilon } (1-v)^2 \bigr ] dx, \end{aligned} \end{aligned}$$

(6)

defined on functions u, v such that $(u, v) \in (H^1(\varOmega ,\mathbb {R}^m)\times H^1(\varOmega ))$, and $\epsilon \le v \le 1$ [41]. Here, the variable v is chosen to tend to take the value 1 almost everywhere and the value 0 on $\varGamma$. Noteworthy, the second integral converges to a surface energy concentrating on the jump set $\varGamma$. It is this property that allows the development of consistent variational formulations for fractured bodies based on functional (6).

Remark

It can be observed [33] that the proper functional space for linear elasticity is not SBV but SBD, the set of special functions of bounded deformation characterized by the fact that the symmetric part of the distributional gradient $Eu = \frac{1}{2}(Du + Du^T)$ is a bounded Radon measure in the space of bounded deformation (BD). SBD constitutes the natural setting for the study of plasticity, damage and fracture models in a geometrically linear framework. However, is was shown that SBD$\supset$ SBV [33], and, usually, the specialized literature restricts to SBV.

3 Regularized formulation of the problem of a cracked body

We reformulate here problem (1) starting from a regularized version of the kinematics. In the forthcoming developments, we adopt a bold vector notation to mark the change from the analytical view point adopted in the previous section to the current approximated computational approach, where the relevant fields are approximated with vector valued quantities.

3.1 A regularised approximation of cracks within an elastodamaging body

One aspect of free discontinuity functionals that is particularly useful for the present developments is that they treat in a different way the bounded and the singular parts of the deformation function. Based on this distinction, we are allowed to define a displacement field whose total variation contains a bounded and a singular term. For this reason, we seek a discontinuous solution of problem (1) among the set of vector functions of the type:

$$\begin{aligned} {\varvec{u}}= {\varvec{v}} + H \llbracket \varvec{u} \rrbracket , \end{aligned}$$

(7)

where H is the Heaviside function defined as:

$$\begin{aligned} H(s(\varvec{x})) = {\left\{ \begin{array}{ll} 1 &{} x\in \varGamma ,\\ 0 &{} x\ne \varGamma \end{array}\right. }. \end{aligned}$$

(8)

The signed distance function of ${\varvec{x}}$ with respect to the crack line $\varGamma$ is computed as

$$\begin{aligned} s(\varvec{x}) = \Vert \varvec{x}- \bar{\varvec{x}}\Vert S(\varvec{x}- \bar{\varvec{x}}), \end{aligned}$$

(9)

where $\bar{\varvec{x}}$ is the closest point projection of $\varvec{x}$ onto $\varGamma$ and S is a Boolean that takes values $\pm 1$.

We can recognize that $\varvec{u}$ in Eq. (7) descends from the fields belonging to space SBV, as its first variation can be cast as

$$\begin{aligned} D\varvec{u} = \nabla \varvec{v}+ H \nabla \llbracket \varvec{u} \rrbracket + \delta _\varGamma \bigl (\llbracket \varvec{u} \rrbracket \otimes _s \varvec{n}\bigr ), \end{aligned}$$

(10)

where the derivative of H is a distributional function, the Dirac delta function $\delta _\varGamma$. To overcome numerical issues induced by the presence of singular fields, we approximate $\varvec{u}$ through a regularized differentiable function $\varvec{u}_\rho$ that converges to $\varvec{u}$ for vanishing $\rho$. For this purpose, we replace the Heaviside function H with a regularized Heaviside function $H_{\rho }$. Thus the regularised displacement field $\varvec{u}_\rho$ takes the form

$$\begin{aligned} \varvec{u}_\rho (u, v) = {\varvec{v}} + {H}_{\rho }{\varvec{\jmath }},\qquad \; \lim _{\rho \rightarrow 0} \varvec{u}_\rho = \varvec{u}. \end{aligned}$$

(11)

For instance, ${H}_{\rho }$ can be expressed as

$$\begin{aligned} {H}_{\rho }(s(\varvec{x})) = \frac{1}{V_\rho }\int _{0}^{s(\varvec{x})} \mathcal {W}_\rho (\xi ) d \xi , \end{aligned}$$

(12)

where $\mathcal {W}_\rho$ represents a weight function centered at $\varGamma$ and $V_\rho = \int _\varOmega \mathcal {W}_\rho (\xi ) d \xi$. In particular, we have adopted the following weight function [12]

$$\begin{aligned} \mathcal {W}_\rho (\xi ) = e ^{-\frac{|\xi |}{\rho }}. \end{aligned}$$

(13)

The process zone resulting from the assumed displacement field is illustrated in Fig. 2a; the displacement profile tends to a jump in the back of $\varGamma$, where a strong discontinuity, or a macro-crack, is expected, and to a regularised profile in the frontal portion of $\varGamma$, denoting the emergence of a cohesive zone.

The variation of $\varvec{u}_\rho$ is

$$\begin{aligned} D \varvec{u}_\rho = \nabla \varvec{v}+ {H}_{\rho }\nabla \varvec{\jmath }+ {\delta }_{\rho }(\varvec{n}\otimes _s \varvec{\jmath }), \end{aligned}$$

(14)

where the term ${\delta }_{\rho }=\Vert \nabla {H}_{\rho }\Vert$ denotes the norm of the derivative of $H_\rho$. ${\delta }_{\rho }$ is localized within a crack band whose width corresponds to the support of the regularization. Since we consider linear elasticity, in the previous equation, we restrict the approximate gradients to their symmetric part. For this reason, $\varvec{n}\otimes _s \varvec{\jmath }$ denotes the symmetric part of tensor $\varvec{n}\otimes \varvec{\jmath }$.

Fig. 2

The regularized displacement jump (a) and the crack-density (b) evolve along the fracture process zone depending on the advancement of the damage localization process and on the value of the regularization length $\rho$

Function ${\delta }_{\rho }$ can be recognized as the crack field density and plays a role analogous to the crack density of phase-field models [49]. Hence, it will also be referred to as the crack density function in the following sections. A pictorial view of ${\delta }_{\rho }$ for variable $\rho$ is shown in Fig. 2b.

Width of the regularized damage band The crack-density ${\delta }_{\rho }$ has a support whose width is expected to shrink as the damaging process advances [16]. This effect is reached by modulating the regularization length according to the damage level as follows.

We define two regularization lengths, $\rho _m$ and $\rho _M$, which represent the minumum and the maximum value that $\rho$ can take, respectively. The value of $\rho$ is assumed being a function decreasing with the value of the damage $d_\rho$ according to the following law:

$$\begin{aligned} \rho = {\left\{ \begin{array}{ll} \rho _M &{} \;d_\rho = d_m,\\ \alpha d_\rho + \beta &{} d_m \le d \le d_M,\\ \rho _m &{} \;d_\rho \ge d_M, \end{array}\right. } \end{aligned}$$

(15)

where

$$\begin{aligned} \alpha = \dfrac{\rho _m -\rho _M}{d_M - d_m},\qquad \beta = \dfrac{d_M \rho _M-d_m\rho _m}{d_M-d_m}. \end{aligned}$$

(16)

Remarkably, law (15) describes a three-stage evolution of $\rho$, starting from a maximal value $\rho _M$, linearly decreasing between $d_m$ and $d_M$, with $d_m \le d_M$, up to assuming the minimum value $\rho _m$ for $d > d_M$.

Being the support of ${\delta }_{\rho }$ noncompact, it is necessary to introduce a truncation length beyond which ${\delta }_{\rho }$ is not evaluated. The approximation issues related to the choice of the truncation length were investigated in [20]. In particular, it was found that a truncated support length of $40\rho$ provides a satisfying compromise between computational burden and accuracy, at least for the present $H_\rho$. In the following developments, the lengths $\ell _{\rho ,M}$ and $\ell _{\rho ,m}$ indicate the width of the truncated supports of ${\delta }_{\rho }$ for $\rho =\rho _M$ and $\rho =\rho _m$, respectively.

3.2 Constitutive equations

We express $D \varvec{u}_\rho$ (14) as the sum of a bounded bulk term $\varvec{\varepsilon }$ and a localized terms $\varvec{\varepsilon }_\rho$ defined as:

$$\begin{aligned}&\varvec{\varepsilon }= \nabla \varvec{v}+H_\rho \nabla \varvec{\jmath }, \end{aligned}$$

(17a)

$$\begin{aligned}&\varvec{\varepsilon }_\rho = {\delta }_{\rho }(\varvec{n}\otimes _s \varvec{\jmath }), \end{aligned}$$

(17b)

in the following way:

$$\begin{aligned} D \varvec{u}_\rho = \varvec{\varepsilon }+ \varvec{\varepsilon }_\rho . \end{aligned}$$

(18)

Let the material associated with the bulk and the zone around the crack display an isotropic elastodamaging behavior. The set of the state variables includes the strain fields $\varepsilon$ and $\varepsilon _\rho$, and the scalar damage variables d and $d_\rho$, that take any value in the range [0, 1] from sound to completely damaged materials.

The idea we pursue here is that the expression of the free energy functional should be reminiscent of the structure of regularised free discontinuity energy (6), in particular, it should contain a bulk contribution and a distinct $\rho -$regularized energy term that tends to a surface energy for vanishing $\rho$. We previously referred to this latter term to as a cohesive-like term [12]. In particular, we define the following energy density:

$$\begin{aligned} \psi (\varvec{\varepsilon }, \varvec{\varepsilon }_\rho , d, d_\rho ) = \hat{\psi }(\varvec{\varepsilon },d) + \psi _{c}(\varvec{\varepsilon }_\rho ,d_\rho ). \end{aligned}$$

(19)

At the r.h.s of Eq. (19), the first term is written as

$$\begin{aligned} \hat{\psi }(\varvec{\varepsilon },d) = \frac{1}{2} \varvec{\varepsilon }\cdot (1-d) \varvec{C}\,\varvec{\varepsilon }. \end{aligned}$$

(20)

It denotes the energy associated with the standard elastodamaging energy of a bulk whose elasticity matrix is $\varvec{C}$. The second term related to the cohesive-like contribution is set as

$$\begin{aligned} \begin{aligned}&\psi _{c}(\varvec{\varepsilon }_\rho ,d_\rho ) = \frac{1}{2} {\delta }_{\rho }(1-d_\rho ) (\varvec{n} \otimes _s \varvec{\jmath })\cdot \bar{\varvec{C}} (\varvec{n} \otimes _s \varvec{\jmath }), \end{aligned} \end{aligned}$$

(21)

where $\bar{\varvec{C}}$ indicates $\varvec{C}/t$, t being a unit length to be introduced for dimensional consistency [14]. Finally, the following regularized energy functional is defined:

$$\begin{aligned} \begin{aligned}&\mathcal {E}_\rho (\varvec{\varepsilon },\varvec{\varepsilon }_\rho ,d,d_\rho ) = \\&\int _\varOmega \hat{\psi }(\varvec{\varepsilon },d) dV + \int _\varOmega {\psi }_c(\varvec{\varepsilon }_\rho ,d_\rho ) dV. \end{aligned} \end{aligned}$$

(22)

Remark on the fracture energy recovery The model is naturally endowed with a crack density function ${\delta }_{\rho }$ analogous to the crack density potential of phase-field models [60]. It is ${\delta }_{\rho }$ that makes it possible to spread the cracking process over a zone whose width shrinks for increasing damage through a smooth continuous-discontinuous transition.

While in phase-field models the fracture energy density $g_c$ is a model parameter, here, we recover the total surface energy $G_c$ in the limit. More precisely, in phase-field models, the global constitutive dissipation functional for a rate-independent fracture process is defined through an expression of the type [60]:

$$\begin{aligned} \mathcal {D} (d,\dot{d}) = \int _\varOmega g_c f(d,\nabla d) dV \end{aligned}$$

(23)

contains $g_c$ a parameter related to the fracture energy density.

In the present case, it has been proved that [19] $\int _\varOmega 2\psi _{c} dV$ converges to the surface work carried out by the traction $\varvec{t}$ across $\varGamma$ to open a discontinuity $\llbracket \varvec{u} \rrbracket$, namely to the critical cohesive fracture energy $\mathcal {G}_c$ as follows:

$$\begin{aligned} \lim _{\rho \rightarrow 0} \int _\varOmega 2 \psi _{c} dV = \int _{\varGamma } \varvec{t}\cdot \llbracket \varvec{u} \rrbracket dS = \mathcal {G}_c. \end{aligned}$$

(24)

Therefore, the two-terms structure of function $\mathcal {E}_\rho$ (22) mirrors the form of the regularized free-energy functionals for phase-field models based on Ambrosio and Tortorelli functional (6).

3.3 Constitutive laws

The first thermodynamics principle

$$\begin{aligned} \varvec{\sigma }\cdot \dot{\varvec{\varepsilon }} + \varvec{\sigma }_\rho \cdot \dot{\varvec{\varepsilon }}_\rho - \dot{\psi } \ge 0 \end{aligned}$$

(25)

makes it possible to deduce the constitutive equations

$$\begin{aligned}&\varvec{\sigma }= \frac{\partial \hat{\psi }}{\partial \varvec{\varepsilon }} = (1-d) {\varvec{C}} (\nabla \varvec{v}+ {H}_{\rho }\nabla \varvec{\jmath }), \end{aligned}$$

(26a)

$$\begin{aligned}&\varvec{\sigma }_\rho = \frac{\partial \psi _c}{\partial \varvec{\varepsilon }_\rho } = (1-d_\rho ) \bar{\varvec{C}} (\varvec{n}\otimes _s \varvec{\jmath }). \end{aligned}$$

(26b)

Here, $\varvec{\sigma }$ and $\varvec{\sigma }_\rho$ are the stress fields that are work-conjugated to $\varvec{\varepsilon }$ and $\varvec{\varepsilon }_\rho$, respectively.

3.3.1 Damage evolution

First, we define an appropriate effective stress $\tilde{\varvec{\sigma }}$ for the evolution of d and associate another one with the evolution $d_\rho$ as

$$\begin{aligned} \tilde{\varvec{\sigma }} = \varvec{C}\nabla \varvec{v}, \end{aligned}$$

(27)

and

$$\begin{aligned} \tilde{\varvec{\sigma }}_\rho = w_\rho (s(\varvec{x})) \bar{\varvec{C}}(\varvec{n}\otimes _s \varvec{\jmath }), \end{aligned}$$

(28)

respectively. In Eq. (28), $w_\rho$ plays the role of a weight function of the signed distance $s(\varvec{x})$ and is cast as

$$\begin{aligned} w_\rho (s(\varvec{x})) = {\left\{ \begin{array}{ll}1 &{} s(\varvec{x})\le \ell _{\rho ,{m}}/2,\\ {\delta }_{\rho }&{} s(\varvec{x}) > \ell _{\rho ,{m}}/2, \end{array}\right. } \end{aligned}$$

(29)

where $\ell _{\rho ,m}$ denotes the truncated support of $\delta _{\rho ,m}$. The adoption of $w_\rho$ makes it possible to carry out the transition from a thick to a thin process zone, and overcomes a previous limitation [16]. A plot of $w_\rho$ for variable values of $\rho$ is shown in Fig. 3b.

We assume an isotropic damage Rankine model and define the following damage activation functions

$$\begin{aligned} g = {\tau } - \kappa ,\qquad g_\rho = {\tau }_\rho - \kappa , \end{aligned}$$

(30)

$\tau$ and $\tau _\rho$ being equivalent stress scalars defined as:

$$\begin{aligned} {\tau }= \langle \text {max}(\text {eig}(\tilde{\varvec{\sigma }})\rangle , \qquad {\tau }_\rho = \langle \text {max}(\text {eig}(\tilde{\varvec{\sigma }}_\rho )\rangle , \end{aligned}$$

(31)

where the Macaulay brackets $\langle \cdot \rangle$ are such that $\langle x \rangle$ is the ramp function.

Fig. 3

Plot of the crack density function ${\delta }_{\rho }$ (a) and the weight function $w_\rho$ (b) for variable $\rho$; the continuous line has been obtained with $\rho _M$, the dashed line refers to $\rho _m< \rho < \rho _M$, and the dotted line to $\rho = \rho _m$

The evolution of the damage variable d and $d_\rho$ stems from the loading–unloading conditions

$$\begin{aligned} \begin{aligned}&g\le 0, \qquad \dot{d}{g} = 0,\qquad \dot{d} \ge 0,\\&\dot{d} > 0 \qquad \text {if}\;\;\;g = 0, \end{aligned} \end{aligned}$$

(32)

and

$$\begin{aligned} \begin{aligned}&g_\rho \le 0, \qquad \dot{d}_\rho {g}_\rho = 0,\qquad \dot{d}_\rho \ge 0,\\&\dot{d} _\rho > 0 \qquad \text {if}\;\;\;g _\rho = 0, \end{aligned} \end{aligned}$$

(33)

respectively. The damage variables increase monotonically with the equivalent stress, and thus, with the current damage threshold $\kappa$ and $\kappa _\rho$. In particular, given the values computed at the previous instant $\hat{d}$ and $\hat{d}_{\rho }$, the damage variables evolve as non-decreasing functions of the associated damage thresholds through the relationships [11]

$$\begin{aligned} d =\max \{\hat{d},G(\kappa )\}, \;\; d_\rho = \max \{\hat{d}_{\rho }, G(\kappa _\rho )\}. \end{aligned}$$

(34)

We adopt the following exponential law [28]

$$\begin{aligned} G(\tilde{\kappa }) = 1- \frac{\tilde{\kappa }_0}{\tilde{\kappa }} e^{h(\tilde{\kappa })},\; h(\tilde{\kappa })= -2H \dfrac{\tilde{\kappa }-\tilde{\kappa }_0}{\tilde{\kappa }_0}, \end{aligned}$$

(35)

where H is a hardening modulus, $\tilde{\kappa }$ is the current threshold and $\tilde{\kappa }_0$ is an initial threshold that is a material parameter.

Because the laws of damage evolution are non-associative, their deduction from an energy-based variational principle is not as straightforward as in the case of associative damage. For this purpose, we deduce the rate form of the variational principle following the strain-driven damage approach described in [11]. Basically, the thresholds $\kappa$ and $\kappa _\rho$ turn out being non decreasing functions of the strain field, and, therefore, the damage variables too can be regarded as non decreasing functions of the current strain of the type

$$\begin{aligned} d = \tilde{G}(\varvec{\varepsilon }), \qquad d_\rho = \tilde{G}(\varvec{\varepsilon }_\rho ). \end{aligned}$$

(36)

The strain-driven damage assumption will be exploited in the forthcoming section.

3.4 Variational formulation

We compute the rate form of the energy functional as

$$\begin{aligned} \begin{aligned}&\dot{\mathcal {E}}_\rho (\dot{\varvec{\varepsilon }},\dot{\varvec{\varepsilon }}_\rho ,\dot{d},\dot{d_\rho }) = \\&\int _{\varOmega } \bigl (\varvec{\sigma }\cdot \dot{\varvec{\varepsilon }} + \varvec{\sigma }_\rho \cdot \dot{\varvec{\varepsilon }} _\rho - Y\dot{d} -Y_\rho \dot{d}_\rho \bigr ) dV, \end{aligned} \end{aligned}$$

(37)

where the constitutive laws (26) have been replaced.

For the present strain-driven damage process, after assuming the dissipation potential [11]

$$\begin{aligned} \begin{aligned}&\mathcal {D} (\dot{\varvec{\varepsilon }}, \dot{\varvec{\varepsilon }}_\rho ) = \\&\int _{\varOmega } \biggl [\bigl (\frac{1}{2} \frac{\partial d}{\partial \varvec{\varepsilon }} \otimes \varvec{C}\varvec{\varepsilon }\bigr ) \dot{\varvec{\varepsilon }}+ \bigl (\frac{1}{2} \frac{\partial d_\rho }{\partial \varvec{\varepsilon }_\rho } \otimes \varvec{C}\varvec{\varepsilon }_\rho \bigr ) \dot{\varvec{\varepsilon }}_\rho \biggr ] dV, \end{aligned} \end{aligned}$$

(38)

the rate form of the total potential is cast as:

$$\begin{aligned} \begin{aligned}&\mathcal {P}(\dot{\varvec{v}},\dot{\varvec{\varepsilon }},\dot{\varvec{\varepsilon }}_\rho ,\dot{d},\dot{d_\rho })=\\&\dot{\mathcal {E}}_\rho (\dot{\varvec{\varepsilon }},\dot{\varvec{\varepsilon }}_\rho , \dot{d},\dot{d_\rho }) + \mathcal {D} (\dot{\varvec{\varepsilon }}, \dot{\varvec{\varepsilon }}_\rho ) - \mathcal {P}_{ext}(\dot{\varvec{v}}), \end{aligned} \end{aligned}$$

(39)

where $\mathcal {P}_{ext}(\dot{\varvec{v}})$ denotes the external work contributed by the surface forces applied on the boundary $\partial \varOmega _p$. Finally, the following variational principle governs the problem at hand:

Find $\{ \dot{v},\dot{\varvec{\varepsilon }}, \dot{\varvec{\varepsilon }}_\rho , \dot{d},\dot{d_\rho }\}$ that make functional $\mathcal {P}(\dot{\varvec{v}},\dot{\varvec{\varepsilon }},\dot{\varvec{\varepsilon }}_\rho , \dot{d}, \dot{d}_\rho )$ stationary, given the assumptions $d = \tilde{G}(\varvec{\varepsilon })$, $d_\rho = \tilde{G}(\varvec{\varepsilon }_\rho )$ and the boundary condition $\varvec{\sigma }\cdot \varvec{n}= \bar{\varvec{p}}$ on $\partial \varOmega _p {\setminus } \varGamma$.

We consider the first variation of functional $\mathcal {P}$ with respect to any admissible variation of $\varvec{\varepsilon }$, $\varvec{\varepsilon }_\rho$ and $\varvec{v}$ such that $\delta \dot{\varvec{v}}$ satisfies homogeneous boundary conditions on $\partial \varOmega _u$. The condition that the first variation vanishes for any admissible variation of the field variables is equivalent to impose that

$$\begin{aligned} \int _\varOmega \varvec{\sigma }\cdot \delta \dot{\varvec{\varepsilon }} dV + \int _\varOmega \varvec{\sigma }_\rho \cdot \delta \dot{\varvec{\varepsilon }}_\rho dV - \int _{\partial \varOmega _p {\setminus } \varGamma } \bar{\varvec{p}} \cdot \delta \dot{\varvec{v}} dS = 0\nonumber \\ \end{aligned}$$

(40)

for abitrary $\delta \dot{\varvec{\varepsilon }}$, $\delta \dot{\varvec{\varepsilon }}_\rho$ and $\delta \dot{v}$.

After replacing the strain expressions into the rate form of the variational principle (40), we write the first variation of $\mathcal {P}$ with respect to $\delta \dot{\varvec{v}}$ and $\delta \dot{\varvec{\jmath }}$ as:

$$\begin{aligned} \begin{aligned}&\int _\varOmega \varvec{\sigma }\cdot (\nabla _s \delta \dot{\varvec{v}} + H_\rho \nabla _s \delta \dot{\varvec{\jmath }}) dV + \\&\int _\varOmega \varvec{\sigma }_\rho \cdot {\delta }_{\rho }(\varvec{n}\otimes _s \delta \dot{\varvec{\jmath }}) dV - \int _{\partial \varOmega _p {\setminus } \varGamma } \varvec{\bar{p}} \cdot \delta \dot{\varvec{v}} dS = 0, \end{aligned} \end{aligned}$$

(41)

for any admissible variation $\delta \dot{\varvec{v}}$ and $\delta \dot{\varvec{\jmath }}$. To preserve the convergence of the regularized formulation to the cohesive-like formulation for vanishing regularization [12, 19], the stress $\varvec{\sigma }$ is mechanically decoupled from the Dirac-like term containing ${\delta }_{\rho }$, while the stress $\varvec{\sigma }_\rho$ is not work-conjugated with $\varvec{\varepsilon }$, the standard part of the strain. Consequently, the following Euler-Lagrange equations are obtained [12]

$$\begin{aligned}&\int _\varOmega \text {div}\varvec{\sigma }\cdot \delta \dot{\varvec{v}} dV = 0, \end{aligned}$$

(42a)

$$\begin{aligned}&\int _\varOmega \bigl ( \varvec{\sigma }\cdot \nabla _s\delta \dot{\varvec{\jmath }}+ \varvec{\sigma }_\rho \cdot {\delta }_{\rho }(\varvec{n}\otimes _s \delta \dot{\varvec{\jmath }}) \bigr ) dV = 0, \end{aligned}$$

(42b)

$$\begin{aligned}&\int _{\partial \varOmega _p} (\varvec{\sigma }\varvec{n}- \bar{\varvec{p}})\cdot \delta \dot{\varvec{v}} dV = 0, \end{aligned}$$

(42c)

for any admissible virtual variation $\delta \dot{\varvec{v}}$ and $\delta \dot{\varvec{\jmath }}$.

3.5 Space discretization

We adopt the extended finite element method [8, 61], and approximate the displacement in the enriched elements by means of the shifted basis approach as [80]:

$$\begin{aligned} \begin{aligned} \varvec{u}_h (\varvec{x})&= \sum _{I \in \mathcal {N}} N_I(\varvec{x}) \varvec{v}_I \\&\quad +\sum _{I\in \mathcal {N}_{enr}} N_I(\varvec{x})\bigl ( H_{\rho }(s(\varvec{x}))-H_{\rho ,I} \bigr ) \varvec{\jmath }_I, \end{aligned} \end{aligned}$$

(43)

where $\mathcal {N}_{enr}$ denotes the number of enriched nodes, $H_{\rho ,I} = {H}_{\rho }(s({\varvec{x}}_I))$, and $\varvec{v}_I$ and $\varvec{\jmath }_I$ are the nodal vector variables of the standard part of the displacement and the enrichment, respectively. For the sake of simplicity, we have here chosen the same shape functions N for both the standard degrees of freedom in $\mathcal {N}$ and the enriched degrees of freedom associated with $\mathcal {N}_{enr}$. In general, any partition of unity could be used as enrichment function [5]. The final picture emerging from the approximation (43) displays a set of enriched elements that are crossed by the crack line, and another set of enriched elements whose distance from the crack line is smaller or equal to the semi-diameter $\ell _\rho /2$ but are not crossed by the crack line. The remaining elements are not enriched and are governed by a standard finite element approximation.

Let $\varvec{V}$ and $\varvec{J}$ be the vectors collecting the nodal degrees of freedom, and $\varvec{B}$ and $\bar{\varvec{N}}$ denote the compatibility matrices. Then the discrete form of the strain and stress fields can be written in the compact form

$$\begin{aligned}&\varvec{\varepsilon }_h (\varvec{x}) = \varvec{B}(\varvec{x}) \varvec{V}+ \tilde{{H}_{\rho }}(s(\varvec{x}))\varvec{B}(\varvec{x}) \varvec{J},\end{aligned}$$

(44a)

$$\begin{aligned}&\varvec{\varepsilon }_{\rho ,h} (\varvec{x}) = {\delta }_{\rho }(\varvec{x})\tilde{\varvec{N}}(\varvec{x}) \varvec{J}, \end{aligned}$$

(44b)

and

$$\begin{aligned}&\varvec{\sigma }_h(\varvec{x}) = \varvec{B}(\varvec{x})\varvec{C}_d \bigl (\varvec{V}+ \tilde{{H}_{\rho }}(s(\varvec{x}))\varvec{J}\bigr ),\end{aligned}$$

(45a)

$$\begin{aligned}&\varvec{\sigma }_{\rho ,h}(\varvec{x}) = \varvec{C}_\rho \bar{\varvec{N}}(\varvec{x}) \varvec{J}, \end{aligned}$$

(45b)

where the positions

$$\begin{aligned} \varvec{C}_d = (1-d)\varvec{C},\qquad \varvec{C}_\rho =(1-d_\rho )\bar{\varvec{C}} \end{aligned}$$

(46)

have been set for the sake of conciseness of notation. Finally, the solving equations can be obtained after replacement of the previous expressions in the Euler-Lagrange equations (42) [12].

3.6 Time discrete formulation

Let the loading history from instant $t^0$ to instant $t^N$ be subdivided into N non-overlapping intervals, $[t^0, t^N] = \bigcup _{n=1, N} [t^{n-1}, t^{n}]$. Given $\varvec{\varepsilon }^{n-1}$ and $\varvec{\varepsilon }_{\rho }^{n-1}$ at instant $t^{n-1}$, so that $d^{n-1}$ and $d_\rho ^{n-1}$ are known, after a new load step during the interval $[t^{n-1}, t^n]$, we compute $\varvec{V}^{n}$ and $\varvec{J}^{n}$ and update the values of the damage, $d^{n}$ and $d_\rho ^{n}$, following the classic Backward Euler integration scheme [73]. In particular, at each Gauß point, the loading functions at the current instant $t^n$ read

$$\begin{aligned} g^{n}= \tau (\varvec{\varepsilon }^{n})- \kappa ^{n}, \qquad g_\rho ^{n}= \tau _\rho (\varvec{\varepsilon }_\rho ^{n})- \kappa _\rho ^{n}, \end{aligned}$$

(47)

where thresholds $\kappa ^{n}$ and $\kappa _\rho ^{n}$ are the maximum values that equivalent stress scalars have ever reached during the loading history up to the current instant $t^{n}$ as follows

$$\begin{aligned} \kappa ^{n}(\varvec{\varepsilon }^{n}) = \sup _{i \in [0, {n}]}\{\tau (\varvec{\varepsilon }^{i})\}, \;\kappa _\rho ^{n}(\varvec{\varepsilon }_\rho ^{n}) = \sup _{i \in [0, {n}]} \{\tau _\rho (\varvec{\varepsilon }_\rho ^{i})\}. \end{aligned}$$

(48)

Since $\kappa$ and $\kappa _\rho$ are non-decreasing functions of the strain fields, the rate form of the loading unloading conditions can be integrated over the time.

We formulate the following damage evolution laws

$$\begin{aligned} d^{n} = \left\{ \begin{array}{ll} d^{n-1} &{} \text {if} \;\kappa ^{n} < \kappa ^{n-1}, \\ G(\kappa ^{n}) &{} \text {if} \;\kappa ^{n} \ge \kappa ^{n-1} \; \text {and} \; G(\kappa ^{n}) \le d_m, \\ d_m &{} \text {if}\; G(\kappa ^{n}) > d_m, \end{array}\right. \end{aligned}$$

(49)

and

$$\begin{aligned} d_\rho ^{n} = \left\{ \begin{array}{ll} d_m &{} \text {if}\; G(\kappa _\rho ^{n})< d_m,\\ d_\rho ^{n-1} &{} \text {if}\;\kappa _\rho ^{n} < \kappa _\rho ^{n-1}, \\ G(\kappa _\rho ^{n}) &{} \text {if}\;\kappa ^{n} \ge \kappa _\rho ^{n-1}. \\ \end{array}\right. \end{aligned}$$

(50)

Whenever $d = d_m$, the transition from the continuous to the discontinuous setting becomes possible, though not automatic as it will be clarified in the next sections.

Finally, the space-time discrete form of the work principle is cast as [12]:

$$\begin{aligned}&\int _\varOmega \varvec{C}_d^n \varvec{B}( \varvec{V}^n + H_\rho \varvec{J}^n) \cdot \varvec{B}( \tilde{\varvec{V}}^n + H_\rho \tilde{\varvec{J}}^n) dV + \nonumber \\&+ \int _\varOmega \delta _\rho \bar{\varvec{N}} \varvec{J}^n \cdot \varvec{C}_\rho ^n \bar{\varvec{N}} \tilde{\varvec{J}}^n dV = \int _{\partial \varOmega _p {\setminus } \varGamma } \varvec{F}^n \cdot \varvec{N}\tilde{\varvec{V}}^n dS, \end{aligned}$$

(51)

where $\tilde{\varvec{V}}^n$ and $\tilde{\varvec{J}}^n$ are arbitrary and the damage variables are computed by means of the loading-unloading conditions (50). In virtue of the arbitrariness of $\tilde{\varvec{V}}^n$ and $\tilde{\varvec{J}}^n$, a solving system of equations is obtained and subsequently solved through a Newton-Raphson procedure, the loading increments being applied via an arc-length algorithm with indirect control of purposely selected monotonically increasing degrees of freedom.

4 Crack tracking algorithm

The level set method is the traditional tool that allows the extended finite element to track the surfaces of discontinuities and singularities [67], but it has been also exploited to develop continuous-discontinuous models where the damage is an explicit function of the level set [62]. In the present case, the crack surface evolves by incrementally adding crack segments to the crack path crystallized at the previous time step. Hence, the crack level set and the geometry of the consolidated crack path have to be stored in the crossed elements. The vector level set method [80] allows to easily store the geometric data describing the evolution of the crack line in two-dimensions as a $3\times 1$ vector consisting of the sign of the signed distance from the crack line and the coordinates of the closest point projection vector. In particular, the vector level set $\tilde{\varvec{s}}_\rho$ is defined as a compound object $\tilde{s}(\varvec{x})$ made of $\varvec{s}$ and the boolean S:

$$\begin{aligned} \tilde{\varvec{s}}_\rho (\varvec{x}) = \left\{ {\varvec{x}}- \bar{\varvec{x}}, S({\varvec{x}}- \bar{{\varvec{x}}})\right\} , \end{aligned}$$

(52)

to be defined at the Gauß points that belong to the enriched elements that are either crossed by the regularized crack axis $\varGamma _\rho$ or located within the regularized domain $\varOmega _\rho$.

4.1 Crack evolution

At instant $t^{n-1}$, let $\varGamma _\rho ^{n-1}$ and $\varOmega _\rho ^{n-1}$ be the crack line and the associated regularised crack domain, respectively. After a time interval $\Delta t = t^{n-1} - t^n$, the set of the enriched nodes will change, as new elements are being enriched and new crack segments are going to stem. In addition, the process zone width will change according to the $\rho -$evolution laws.

For each critical element e, the set of the enriched elements is updated based on three actions: verify the existence of pre-consolidated cracks within a certain radius from the barycenter of e, check whether some of them are adjacent to the current critical element, and compute the crack direction. In the following section, time dependence is dropped out for the sake of brevity of notation.

Fig. 4

The picture shows how the function ${\delta }_{\rho }$ is used as weight function in the nonlocal direction tracking criterion

Fig. 5

The element in yellow satisfies the crack tracking condition, thus it is enriched and a new crack segment is added, in red in the figure. The green element is not enriched; however, there, the damage of the bulk is frozen. Here, the nodes marked with a blue square are the enriched nodes of the elements crossed by the crack line; the nodes marked with a red circle are enriched either and belong to the enriched elements that are within the regularization volume but are not crossed by the crack line. (Color figure online)

4.1.1 Critical damage condition

The criterion of initiation is based on the evaluation of the damage variable d at the Gauß points of the finite element. As soon as the damage exceeds a critical damage value $d_m$ in an element, the element is a candidate for being enriched as a master element crossed by the crack line. Let $\mathcal {I}_\rho$ denote the set of elements where at least one of the Gauß points exceeds the first critical damage threshold $d_m$. The initiation criterion is not sufficient to decide which of the finite elements in $\mathcal {I}_\rho$ will be newly enriched. This aspect pertains to the updating stage addressed in Sect. 4.1.3.

4.1.2 Direction-tracking strategy

A threefold strategy is adopted to compute the direction of the crack: a local strategy, a nonlocal one and a local-nonlocal switch direction strategy.

• Local criterion For each finite element e, we compute the principal direction of the maximum tensile principal stress of the averaged elemental stress

  $$\begin{aligned} \bar{\varvec{\sigma }}_e= \frac{1}{N_{g}^e}\sum _{i \in \mathcal {N}_{g}^e}\varvec{\sigma }_e (\varvec{x}^e_{g,i}), \end{aligned}$$

  (53)

  where $\mathcal {N}_{g}^e$ is the set of Gauß points $\varvec{x}^e_{g,i}$ of element e.

• Nonlocal criterion The nonlocal criterion is adopted to eliminate pathological dependence of the results on mesh directionality and to smooth the crack path. It essentially eliminates the unwanted deviations of the direction of the crack path induced by zero average fluctuations of the stress components within the damaged zone. The direction of the new crack segment is computed as the principal direction of the following maximum principal nonlocal stress:

  $$\begin{aligned} \bar{\varvec{\sigma }}_{NL}(\varvec{x})= \int _{V} \delta _{\rho ,M} (\varvec{x}, \varvec{y})\varvec{\sigma }(\varvec{y}) dV(\varvec{y}). \end{aligned}$$

  (54)

  In Eq. (54), the crack-density function $\delta _{\rho ,M}$ plays the role of weighting function as shown in Fig. 4.

• Local-nonlocal switch. First, we compute the direction with the local and the nonlocal direction tracking criterion. Then, we require that the direction of the new crack segment is the one that ensures the least deviation with respect to the path of the existing crack line. Hence, the algorithm switches from the local to the nonlocal direction tracking criterion at each load step, so to minimize the deviation w.r.t the crack path consolidated at the previous load step.

Remarks on the direction tracking criterion In Eq. (54), $\delta _{\rho ,M}$ is computed in terms of $\rho _M$, so that the interaction radius equals $\ell _{\rho ,M}/2$, corresponding to averaging over a volume of width $40 \rho _{M}$. We have heuristically verified that $\rho _M$ provides a satisfying compromise between computational burden and accuracy [20]. Remarkably, both the local stress (53) and the nonlocal stress (54) are computable in any element whether enriched or not, and this is useful when the element under consideration has not yet been enriched.

The choice of the direction tracking criterion depends on the stress state. Relevant aspects are deemed to be the presence of symmetry axes, the type of loading and which of the components of the stress state are involved in crack propagation. In particular, the nonlocal direction tracking strategy is useful in those cases where the strain localization band develops as a consequence of the establishment of a stress state clearly dominated by a specific stress component, such as in pure mode I and pure mode II. Examples are the double edge notched (DEN) specimen under tensile loading, that will be considered in Sect. 5.1.1, and the single edge notched (SEN) specimen under tensile and shearing loading, whose results will be illustrated in Sects. 5.1.3 and 5.1.4. On the other hand, the local-nonlocal switch strategy is helpful when we expect the deviation of the new crack line with respect to the previous one not to exceed a certain amount of degrees and, furthermore, we do not want to give up to the nonlocal stress direction tracking criterion in certain stages of the cracking process. This is the case of the three point bending test, where the crack first develops within a zone beneath the neutral axis with dominant tensile stresses, and eventually proceeds towards the beam’s top where a compressive stress state emerges.

4.1.3 Update

We decide which of the candidate elements in $\mathcal {I}_\rho$ should host the new crack line increment. For each element $e\in \mathcal {I}_\rho$, we perform the following steps.

• Check of crack proximity For each candidate element that has met the critical damage condition, we check whether there are cracked elements in the circle of diameter $\ell _{\rho ,M}$ around element e.

• If there are cracked elements in the circle of diameter $\ell _{\rho ,M}$, the algorithm verifies whether the crack tip belongs to the set $E^e$ of the edges of element e.

• The crack tip belongs to $E^e$. Element e transitions from the continuous to the discontinuous setting and is enriched. A new crack segment is added by imposition of the crack line continuity, so that the new crack segment starts at the intersection point of the previous crack line with the relevant edge of e. This is the case of the element in yellow in Fig. 5, where the newly formed segment is highlighted in red.

• The crack tip does not belong to $E^e$. This is the case of the element in green in Fig. 5. The element is not enriched; however, the value of the damage d in e is frozen at $d = d_m$. Usually, such an element may be integrated within the influence zone of an adjacent crack segment centered at an element distinct from e but close to it.

• No cracked elements in the circle of diameter $\ell _{\rho ,M}$. Element e is enriched and a new crack line nucleates there; e hosts the first crack segment of the newly formed independent crack. The transition of e from the standard continuum setting to the status of enriched element is activated.

• End of the check of crack proximity The loop finishes as soon as each element $e\in \mathcal {I}_\rho$ has been scrutinized to assess whether it can nucleate a new crack or it just orbits within the influence area of an existing one.

Box 1 displays a synthesis of the steps undertaken in the present crack tracking procedure. The direction of the crack results from the direction tracking criterion.

The width of support $\ell _{\rho ,M}$ of the crack density function $\delta _{\rho ,M}$ for $\rho =\rho _M$ plays a duplex role of the diameter of the nonlocal zone for the nonlocal direction tracking criterion, and the minimal distance between two adjacent cracks.

The set of enriched nodes There are two types of enriched nodes. In Fig. 5, the nodes marked with blue squares belong to the elements crossed by the crack line, while red circles indicate the enriched nodes that belong to the elements that are not cut by the crack line. All the elements in the regularized discontinuity zone are fully enriched. We emphasize that the use of the regularized Heaviside and delta functions allows to automatically handle blending between fully enriched and non enriched finite elements. While sign and Heaviside functions do not raise issues, other types of enrichment functions, such as crack-tip enrichment functions, preclude the partition of unity property in partially enriched elements, unless the enrichment functions are properly modified, for instance by multiplying them by the ramp function [43]. In the present formulation, the actual blending elements are made of elements that are not crossed from the crack line though they are fully enriched, such as the elements having red and blue nodes in Fig. 5. The final effect of using the regularized functions ${H}_{\rho }$ and $\delta _\rho$ is the same as that of ramp functions to handle blending elements in standard extended finite element method. The regularized delta function is such that it is almost zero in the standard elements, except for the truncation error [20], and satisfies the partition of unit finite element property in fully enriched elements, while decaying continuously to zero in the blending elements. Analogously, the regularized Heaviside tends to a constant profile in the blending elements. Usually, the presence of a constant enrichment function can imply the ill-conditioning of the solving system of equations. In the present case, the presence of the additional stiffness term containing the regularized crack density $\delta _\rho$ makes it possible to rule out this type of ill conditioning.

5 Numerical results

In Sect. 5.1, we present the results computed by means of the crack tracking algorithm presented in Sect. 4 with a focus on mesh size and type objectivity. Moreover, in Sect. 5.2, the sensitivity of the results to the regularization length $\rho$ and to the damage parameters is assessed, while, in Sect. 5.3, we show the evolution of the crack-density function ${\delta }_{\rho }$.

5.1 Mesh independence

We aim to point out the sensitivity of the proposed regularized-crack tracking algorithm with respect to directional mesh bias, and the objectivity with respect to mesh type and size. In all the examples discussed hereafter, three-noded triangles and four-noded quadrilaterals have been used.

5.1.1 The tensile double edge notched specimen

In the present section, we discuss the case of the double edge notched specimen, denoted as DEN hereafter. The geometry is indicated in Fig. 6. Here, mesh bias sensitivity is expected [28], that makes the DEN test particularly troublesome from the computational point of view despite the fact that the plate is symmetric and a horizontal crack is expected.

Following [28], we have set the Young modulus $E= 2000$ MPa, the Poisson coefficient $\nu = 0.2$, while the hardening modulus $H =0.002$ MPa and threshold stress $\kappa _0 = 1$ MPa have been used. For comparison purpose with available numerical results, we have adopted the regularization length parameters $\rho _m = 0.08$ mm and $\rho _M =1$ mm. Finally, the damage parameters $d_m = 0.6$ and $d_M = 0.9$ trigger the transition from the diffused damage band to the localized one.

Fig. 6

Geometry and loading of the double edge notched specimen (DEN); dimensions are in mm

We have considered the four meshes in Fig. 7, the first and second meshes are structured and are made of triangles (a) and squares (b), respectively; the third triangular mesh (c) is affected from directional bias; the fourth mesh is random triangular (d).

Fig. 7

DEN: three type of meshes have been adopted, in particular, the structured triangular mesh (a), the structured quad mesh (b), the biased mesh (c) and the random triangular mesh (d)

The load versus displacement results obtained with the meshes in Fig. 7 are displayed in Fig. 8. Here, we show the results obtained with the nonlocal direction tracking criterion. However, we had previously verified that the load–displacement results were not influenced by the choice of the direction tracking criterion.

The performance of the local direction tracking algorithm has been assessed in terms of the computed damage profiles for the considered meshes. Figure 9 shows that, whereas the structured meshes capture the proper cracking patterns, the map of $d_\rho$ in mesh c) is not reliable, as expected. Here, the crack path has been indicated with a green dashed line.

On the other hand, Fig. 10 shows that the use of the nonlocal direction tracking criterion allows to recover the expected cracking pattern in the biased mesh and further improves such a pattern in both the structured and unstructured meshes. The impact of the choice of the direction tracking strategy can be appreciated in Fig. 11 displaying the full opening at failure of the plate.

5.1.2 The three-point bending test

We study mesh-directionality bias in a three-point bending test [29, 57]. In this case, a vertical crack line along the symmetry axis is expected. The test geometry has been taken from [71] and is shown in Fig. 12; the beam is made of a material whose elastic constants are the Young modulus $E= 20{,}000$ MPa and the Poisson coefficients $\nu = 0.2$, while the hardening modulus $H = 0.0013$ MPa and the threshold stress $\kappa _0 = 2.4$ MPa. Finally, we have set the regularization length parameters $\rho _m = 0.1$ mm and $\rho _M =1$ mm, and the damage parameters $d_m = 0.6$ and $d_M = 0.8$. The rationale behind this choice of $\rho _M$ is that it leads to a process zone of 4 cm, that is consistent with the width of the fracture process zone expected in a concrete like material such as the one used in the current three point bending test. On the other hand, $\rho _m = 0.1$ mm is the smallest possible value that could be resolved with the current coarsest mesh. The meshes shown in Fig. 13 have been used. Particularly, we have adopted unstructured meshes made of triangles such as the one shown in Fig. 13a, triangular meshes with structured quadrilateral elements along the symmetry axis like the one shown in Fig. 13b, and, finally, the fine biased mesh made of triangles in Fig. 13c. In all the meshes displayed in Fig. 13, the minimal mesh size is $h = 1.66$ mm, these being the finest meshes ever considered in the present case. The load–displacement results displayed in Fig. 14 satisfactorily fit with the experimental data [71]. They have been obtained for triangular and quadrilateral meshes of variable size, h being the size of the finest element. In particular, the mesh-types shown in Fig. 13 have been adopted. Both the peaks and post-peak profiles are mesh-size and mesh-type independent. Figure 15 displays the contour plots of the damage $d_\rho$ plotted in the deformed meshes shown in Fig. 13 using the local direction tracking and the local-nonlocal switch criteria. In particular, the case of the biased mesh is illustrated in Fig. 15c, d, showing the superior performance of the local-nonlocal switch criterion in the present three point bending test.

Fig. 8

DEN: Load–displacement results obtained for the meshes of Fig. 7 with the nonlocal direction tracking criterion; $\rho _M = 1.0$ mm, $\rho _m = 0.1$ mm

These results are confirmed in Fig. 16 by the corresponding crack paths obtained with the aforementioned direction tracking criteria.

5.1.3 The single edge notched plate under tensile loading

The single edge plate subjected to tensile and shearing loading is a typical benchmark for phase-field models [2, 46, 47, 60]. The geometry of the single edge specimen and the corresponding boundary conditions are shown in Fig. 17a. Following [60], the set of material parameters includes the Young modulus $E= 210000$ MPa, the Poisson coefficients $\nu = 0.2$, the hardening modulus $H = 0.0026$ MPa and the threshold stress $\kappa _0 = 17$ MPa. Additionally, the regularization length parameters $\rho _m = 0.007$ mm and $\rho _M =0.03$ mm, and the damage parameters $d_m = 0.6$ and $d_M = 0.95$ have been adopted. In the lack of analytical and experimental results, these parameters allow us to obtain results comparable with those of the available numerical solutions. Nevertheless, the adopted values of $\rho _m$ and $\rho _M$ are adequate to a material with a very brittle behavior.

Fig. 9

DEN: damage evolution in the enriched zone obtained with the local criterion for the three meshes of Fig. 7 at step C in Fig. 8

Fig. 10

DEN: damage evolution in the enriched zone obtained with the nonlocal criterion for the meshes of Fig. 7 at step C in Fig. 8

Fig. 11

DEN: Final damage pattern and deformed shape obtained in the biased mesh with the local direction tracking criterion (a) and with the nonlocal direction tracking criterion (b); the magnification factor of the deformed shape is 300

To investigate mesh type and mesh size independence, we have performed an intensive set of tests using triangular and quadrilateral finite elements for decreasing the mesh size. In particular, we have considered meshes whose characteristic size is 1/25, 1/50 and 1/100 of the specimen edge $L = 1$ mm, these meshes being quite coarse when compared to the degree of refinement necessary in phase field models. Furthermore, both the local and the nonlocal direction tracking algorithms have been used to compare the homologous results.

The load versus displacement profiles obtained with the local and the nonlocal direction tracking criterion in Figs. 18 and 19, respectively. It can be drawn that we get fully objective results with respect to both mesh-type and -size, irrespective of the adopted crack direction tracking algorithm. The damage evolution along the crack direction is displayed for both the local direction tracking criterion, in Fig. 20, and the nonlocal direction tracking algorithm, in Fig. 21. The profiles of both crack and process zone are smoother and less sensitive to the geometry of the triangular elements in the latter case.

5.1.4 The single edge notched plate under shear loading

Let the single edge notched plate studied in the previous section be subjected to a shearing displacement on the top, as shown in Fig. 17b. The same set of material and length parameters used for the tensile SEN plate have been adopted. We have also used the same meshes. The structural results shown in Figs. 22 and 23 have been obtained exploiting the local and the nonlocal direction tracking criterion, respectively, and making use of triangular and quadrilateral meshes.

Analogously to the case of tensile loading, we report in Figs. 24 and 25 the contour plots of the damage $d_\rho$ obtained with both the local and nonlocal direction tracking algorithms, respectively. We can infer from Fig. 26 that the crack paths obtained by means of triangles and quads are close each other. Moreover, the crack paths obtained with the nonlocal direction tracking criterion are smoother.

Fig. 12

Geometry of the three point bending test [28]; dimensions are in mm

Remarks on the choice of the direction tracking criterion From the obtained results for the tensile and shearing SEN, the load–displacement results do not depend on mesh type and size irrespective of the crack direction tracking criterion. However, in the shearing SEN, we can observe a discrepancy of the $7\%$ between the peaks and a different slope of the rising post-peak paths computed with the local and the nonlocal direction tracking algorithms. An accurate check of the crack paths reveals that the adoption of the nonlocal direction cracking strategy smooths the crack paths and makes the regularized zone surrounding the final part of the crack path larger than the local one, and this eventually interferes with the boundary effect induced the constraint at the right-bottom corner of the plate. It should be precised that certain phase field formulations do not even capture the aforementioned rising post-peak branch [6, 46] and that no experimental data or analytical solutions are available for the sake of a comparison. Therefore, it is not possible to establish which one of the local and the nonlocal direction strategy criterion is more physically consistent for the shearing SEN test. Nevertheless, the nonlocal one seems to lead to smoother crack patterns.

Fig. 13

Three point bending. Plot of the finest considered meshes: triangular unstructured (a), structured with quads at the center (b), and triangular biased (c)

Fig. 14

Three point bending: Load versus displacement results obtained with triangles (a) and quads (b) for variable mesh size

Fig. 15

Three point bending: Deformed shape and damage $d_\rho$ at step D in Fig. 14 for the non-structured triangles mesh (a), the structured (b) and the biased mesh with the local (c) and the local-nonlocal switch direction tracking criterion (d). A magnification factor 5 has been used

Fig. 16

Three point bending: Crack path obtained with the local direction tracking criterion in mesh 3PA with $h= 1.66$ mm (blue continuous line), and mesh 3PB with $h = 1.66$ mm (green dashed line) and the local-nonlocal switch direction tracking criterion for the biased mesh 3PC with $h = 1.66$ mm (red dotted line). (Color figure online)

Fig. 17

Geometries of the SEN under tensile (a) and shearing loading (b); dimensions are in mm

Fig. 18

Tensile SEN: Load–displacement results obtained with the local direction tracking criterion

Fig. 19

Tensile SEN: Load–displacement results obtained with the nonlocal direction tracking criterion

Fig. 20

Tensile SEN: Contour plots of the enriched damage $d_\rho$ plotted at steps A, B, C, D of Fig. 18 in the deformed mesh of quads with representative size $h= L/100$, $L = 1$ mm, using the local direction tracking criterion; the magnification factor of the deformed shape is 300

Fig. 21

Tensile SEN: Contour plots of the enriched damage $d_\rho$ plotted at the load levels A, B, C, D indicated in Fig. 19 in the deformed mesh of triangles with representative size $h= L/100$, $L = 1$ mm, using the nonlocal crack tracking criterion; the magnification factor of the deformed shape is 300

Fig. 22

SEN under shear: load–displacement results obtained with the local direction tracking criterion and with meshes made of three-noded triangles (a) and four-noded squares (b)

Fig. 23

SEN under shear: load–displacement results obtained with the nonlocal direction tracking criterion and with meshes made of three-noded triangles (a) and four-noded squares (b)

Fig. 24

SEN under shear: Contour plots of the enriched damage $d_\rho$ plotted at the load steps A, B, C, D indicated in Fig. 22 in the deformed mesh of 4-noded elements with representative size $h=L/100, L =1$ mm, using the local criterion; the magnification factor of the deformed shape is 300

Fig. 25

SEN under shear: Contour plots of the enriched damage $d_\rho$ plotted plotted at the load steps A, B, C, D indicated in Fig. 23 in the deformed mesh of quads with representative size $h= L/100, L = 1$ mm, using the principal direction of the maximum eigenvalue of the nonlocal stress; the magnification factor of the deformed shape is 300

Fig. 26

SEN under shear: Crack path obtained for variable mesh size by tracking the path with the local direction tracking criterion with triangle and quads using the local (a, b) and the nonlocal (c, d) crack-direction algorithm; the black continuous, red dashed and blue dotted lines refer to $h = 0.04$, 0.02, 0.01 mm, corresponding to $L/25,\,L/50, \, L/100$, respectively. (Color figure online)

Fig. 27

3P bending: load–displacement results obtained with the local criterion for variable values of $\rho _{m}$ (a) and $\rho _{M}$ (b). Quads with minimum mesh size $h=1.66$ mm have been used. We have set in Fig. a) $\rho _M = 0.6$ mm, $d_m = 0.6$, $d_M = 0.8$, while, in Fig. b), $\rho _m = 0.04$ mm, $d_m = 0.6$, and $d_M = 0.8$

Fig. 28

3P bending: load–displacement results obtained for the structured quads with h 1.66 mm with the local criterion for variable values of $d_{m}$ (a) and $d_{M}$ (b). In figure (a), we have set $d_M = 0.8$ mm, $\rho _m = 0.04$ mm and $\rho _M = 0.6$ mm; in figure (b), we have used $d_m = 0.6$ mm, $\rho _m = 0.04$ mm and $\rho _M = 0.6$ mm

5.2 Sensitivity to $\rho$ and damage parameters

In this section, we present a sensitivity analysis for variable regularization length and damage parameters. We recall that the transition from the continuous to the discontinuous description occurs at $d_m$ with a regularization length $\rho _M$. On the other hand, the final transition to a discontinuous kinematics is activated at $d_M$ and is governed by $\rho _m$. For instance, we report hereafter the results obtained for the 3P bending test using quadrilateral elements with $h=1.66$ mm. The reason is that they ensure the smoothest crack paths. Figure 27 displays the influence on the structural results associated with a change of the minimum value of the regularization length $\rho _{m}$ (a) and the maximum value of the regularization length $\rho _{M}$ (b). The larger $\rho _m$ and $\rho _M$ and the higher the peak of the load–displacement profiles. The effect induced by decreasing $d_m$ is that the transition is anticipated and the structural profiles are more brittle but do not change their shape. On the contrary, larger values of $d_M$ posticipate the transition and lead to higher peaks and more brittle post-peak laws. Analogously, Fig. 28 shows that a change of both the minimum and maximum values of the critical damage $d_{m}$ (a) and $d_{M}$ (b) influences the peak load and the post-peak branch. In synthesis, we can observe that the effects of $\rho _m$ and $d_M$ on the structural response are similar. The same applies to $\rho _M$ and $d_m$.

Choice of the regularization lengths The appropriate values of $\rho _m$ and $\rho _M$, the minimum and maximum values of $\rho$, are chosen as follows. The value of $\rho _M$ is in primis dictated by the width of the process zone typical of the material degradation process to be simulated, while the value taken by $\rho _m$ depends on the degree of resolution that the mesh allows. The connection between the accuracy of the results, the choice of the minimum $\rho _m$ and the adoption of Gauß quadrature was assessed in previous contributions [13, 20]. As for $\rho _M$, it strictly depends on the expected width of the process zone accompanying the early stages of the dissipation process.

From this standpoint, the regularized extended finite element method is a very versatile tool in several circumstances. For instance, it makes it possible to capture cracking processes in concrete-like materials [16], and delamination processes in FRP-reinforced beams [15, 21]. In the former case, the process zone is almost three times the width of the grain with maximum diameter [7], and the width of the support of $\rho _M$ equals the width of the process zone. In the latter case, $\rho _M$ and $\rho _m$ coincide and their support-width turns out being equal to the few millimeters thickness of the adhesive layer bonding the reinforcement plates and the beam.

In brief, the user can control the values of the regularization lengths depending on the physical phenomenon to be modeled. However, in the SEN and DEN tests, due to a lack of experimental data, the values of $\rho _M$ and $\rho _m$ have been obtained based on the numerical data available from simulations performed by other researchers with different formulations.

5.3 Evolution of the crack density function

A remarkable feature of the proposed formulation is that the crack density function closely follows the evolution of the cracking process and realistically reproduces inception, development and eventual coalescence into a macrocrack of the diffused-damage zone. In particular, we show here the evolution of ${\delta }_{\rho }$ obtained with triangular meshes in the tensile SEN test in both the cases of local direction tracking criterion and nonlocal direction tracking criterion in Fig. 29 and Fig. 30, respectively. We also report the homologous figures for the SEN test under shearing displacement in Fig. 31 and 32. In the latter case, quadrilateral meshes have been used.

It can be drawn that, in the case of pure tension and pure shear, the use of the nonlocal direction cracking criterion smooths the profiles of ${\delta }_{\rho }$ with respect to the homologous results obtained with the local direction tracking algorithm. The cohesive zone in front of the crack line is also better resolved with the nonlocal direction tracking criterion.

Fig. 29

Tensile SEN: Evolution of the crack density function ${\delta }_{\rho }$ with the local direction tracking algorithm and using a triangular mesh

Fig. 30

Tensile SEN: Evolution of the crack density function ${\delta }_{\rho }$ with the nonlocal direction tracking algorithm obtained with triangular elements

Fig. 31

SEN under shear: Evolution of the crack density function ${\delta }_{\rho }$ with the local direction tracking algorithm; quad elements have been used

The same behavior can be observed in the case of the SEN plate subjected to shearing displacement. We have reported in Fig.32 only the ${\delta }_{\rho }$ contour plots obtained in the case of the nonlocal direction tracking algorithm using quads.

Evolution of the crack path during the loading history The crack path evolves smoothly during the loading history. To highlight this aspect, the length of the crack path as been detected at each load step in the case of the tensile SEN. In particular, Fig. 33 displays the length of the crack path evaluated over the elements enriched with the discontinuous kinematics. The crack path is shown for both the local direction tracking algorithm, indicated in the figure with the acronym LDT, and the nonlocal direction tracking algorithm, there referred to as NLDT. Here, the medium and fine random triangular meshes with $h = 0.02$ mm and $h = 0.01$ mm have been employed. We infer that the local and nonlocal direction tracking algorithms are comparable as for the rate of evolution of the discontinuity line. Furthermore, the obtained crack lengths are quite independent of the mesh size, as expected from the load–displacement profiles.

Fig. 32

SEN under shear: Evolution of the crack density function ${\delta }_{\rho }$ with the nonlocal direction tracking algorithm with quad elements

6 Discussion of the results

The ingredients of the proposed crack tracking strategy are a flexible direction tracking criterion, crack-continuity enforcement, and a minimal distance among cracks. The crack tracking strategy leads to results displaying mesh size and mesh type independence in all the investigated examples. In particular, the use of the nonlocal direction tracking algorithm smooths and makes reliable the crack paths in mode I and mode II cracking. On the other hand, it can lead to crack path deviations in the case of cracks induced from bending. Like in the three-point bending test, where mesh bias is neutralized by means of a newly developed local-nonlocal-switch direction tracking algorithm, that allows to switch from a local to a nonlocal direction tracking criterion based on the minimal deviation from the crack path established during the previous load step.

Fig. 33

Crack length versus load steps in the tensile SEN obtained with the local direction tracking (LDT) and the nonlocal direction tracking (NLDT) algorithms; the crack length has been computed based on the elements transitioning from the continuous to the discontinuous regime

Finally, it can be argued that, while phase-field models explicitly contain the fracture energy $G_c$ as a model parameter, in the regularized XFEM the fracture energy is recovered as the limit for vanishing $\rho$ of the traction-separation energy smeared over the regularized zone. On the other hand, the choice of the length scale of phase-field models that allows to recover the correct crack path often leads to brittle load–displacement results that, generally, do not match with the experimental profiles, unless unrealistic values of the length scale are chosen [83]. To alleviate this effect, specific types of gradient functions can be used that make it possible to capture cohesive-cracks [56,57,58]. Furthermore, although phase-field models have been recently devised for elasto-plastic [1] and anisotropic solids [66], a generalization to anisotropic damage laws seems not so straightforward. On the contrary, the regularized XFEM can accommodate any constitutive law. For instance, it has been recently applied to elastodamaging plastic constitutive laws with anisotropic damage and multi-surface failure functions [22, 23].

7 Conclusions

We have devised a new strategy to track general crack paths independently of size, type and directionality of the adopted meshes. This study should be regarded as a new development of the regularized extended finite element method. As illustrated by means of a widespread set of tests, the proposed strategy makes it possible to obtain consistent load–displacement profiles and crack paths. Our formulation naturally introduces a regularization length and a crack density function, hence suggesting certain similarities with nonlocal and phase-field models, except that damage broadening and mesh adaptivity are not an issue for the present formulation. For the sake of simplicity, crack branching has not been considered and is being left for future developments. For the assessed cases, we can draw that the proposed framework is a viable alternative to available continuous-discontinuous procedures.