Dynamics of multiple pendulum system under a translating and tilting pivot

Abstract

In this article, we study the dynamics of multiple pendulum systems under translation and tilt. The main application considered for such systems is inertial sensing for high-precision instrumentation. To emulate the translating multiple pendulum system, we attach the pivot point of the pendulum to a cart that is free to move in the horizontal plane. Similarly, the pivot point of the tilting pendulum system is attached to a platform that rotates, enabling tilting motion for the system. First, we approach the problem from a Lagrangian dynamics perspective for a double-pendulum system under translation and tilt and then extend the solutions to a system of n pendulums, each hanging one below the other. Then, the natural frequencies of the systems are derived. The behavior of the systems under translation and tilt is studied and compared with that of fixed pivot point multiple pendulum systems, using eigenvalue analysis to understand how the natural frequency fluctuates with changes in degrees of freedom, mass, length and stiffness.

1 Introduction

Mechanical pendulums have been extensively studied in the literature through the years, from simple linear pendulums to complicated nonlinear multiple pendulum and inverted pendulum systems [1, 2]. While these studies, which focus on stationary pivots, are very important for the understanding, they are insufficient for most real-world applications which require a deep understanding of much more complicated dynamical models. This paper gives an in-depth analysis of most of the characteristics of multi-pendulum systems with translating/tilting pivots. The main reference application of such systems considered in this paper is as inertial sensors for high-precision instrumentation such as gravitational wave detectors [3] and vibration isolation systems [4, 5] .

1.1 Background

In recent times, there has been an increase in using pendulous dynamical systems for various purposes including Segways, gantry cranes, robotic manipulators, and mobility of humanoid robots, etc., all of which can be modeled as dynamic pendulum systems that are not fixed pivots [6,7,8,9]. Simple pendulum system under tilt, in particular, has been studied and applied in various fields ranging from tilting systems for railway cars to tilt-meters to measure earth strain [10,11,12]. Also, a very less explored application is inertial sensing for high-precision instrumentation where pendulous architecture can be used as inertial sensing units immune to tilt horizontal coupling [5]. Multiple pendulum systems with fixed pivots have been extensively studied in the literature, and various synchronization and control strategies have been proposed for these systems [13,14,15]. The dynamics of tilting systems can be more complex than those with fixed pivots because the pivots are no longer fixed points in space. Multiple pendulum systems with fixed pivots exhibit periodic, quasi-periodic, or chaotic motion, depending on the initial conditions and system parameters. In contrast, multiple pendulum systems with translating/tilting pivots can exhibit rich and complex motion, including bifurcations, chaos, and synchronization, due to the additional degrees of freedom and nonlinearities introduced by the pivots. Also, the control of multiple pendulum systems with fixed pivots and translating/tilting pivots presents different challenges due to the increased complexity and nonlinearity of the system [16]. A similar study was conducted by [13], but it only focuses on fixed pivot systems.

1.2 Problem statement

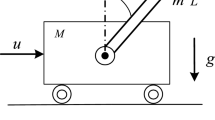
The mathematical derivation of dynamics of single and multiple pendulum systems with a fixed pivot is widely reported in the literature [1, 17,18,19,20,21,22]. But a proper derivation of the same with higher degrees of freedom ( pivot undergoing translation/tilt) is not documented well. In this paper, the authors give a deep mathematical insight into the underlying dynamics pertaining to multi-pendulum system considering Euler–Lagrangian equations of motion. The following notations are used throughout the paper. For the pendulum system under translation, the upper end of the top pendulum is fixed to a freely movable pivot point attached to a cart at point O, while the lower end of the pendulum is connected to the pendulum below. Moreover, $m_0$, $m_1$, $m_2\ldots m_n$ are the masses of the cart, top and second and nth pendulums, respectively. The length of each link of the pendulum is given by $l_1$, $l_2\ldots l_n$, and the displacement of the cart measured from the origin is given by $\theta _0$. Further, the angular displacement of the pendulums which is measured from the axes vertical down is represented by $\theta _1$, $\theta _2\ldots \theta _n$.

Fig. 1

Double-pendulum system under translation. $m_1$ and $m_2$ are the masses of the bobs, and $l_1$ and $l_2$ are the link lengths. The angles made by the top pendulum and the bottom pendulum with the vertical axis are $\theta _1$ and $\theta _2$, respectively. The initial position of the pivot point attached to the cart is given by $\theta _0$

Figure 1 shows a double-pendulum system with masses of bobs $m_1$ and $m_2$ and lengths $l_1$ and $l_2$ for the top and bottom pendulums, respectively. The angles made by the top pendulum and the bottom pendulum with the vertical axis are $\theta _1$ and $\theta _2$, respectively. This double-pendulum system has a pivot point to a cart that has a mass of “$m_0$” and can freely move in the horizontal direction. The initial position of the pivot point attached to the cart is given by $\theta _0$.

For the pendulum system under tilt (Fig. 2), the upper end of the top pendulum is attached to a platform that is able to rotate. $m_1$,$m_2\ldots m_n$ are the masses of the pendulums, and $l_1$, $l_2\ldots l_n$ are the length of the pendulum links. The angles of the pendulum system before tilting are measured from the axes vertical down as $\theta _1$, $\theta _2\ldots \theta _n$. When the platform undergoes a tilt of angle $\alpha$, the angles change to $\theta _1'$, $\theta _2'\ldots \theta _n'$, respectively.

Fig. 2

Double-pendulum system under tilt. The upper end of the top pendulum is attached to a platform that is able to rotate. $m_1$ and $m_2$ are the masses of the pendulums, and $l_1$ and $l_2$ are the length of the pendulum links. The angles of the pendulum system before tilting are measured from the axes vertical down as $\theta _1$ and $\theta _2$. When the platform undergoes a tilt of angle $\alpha$, the new angles are represented by $\theta _1'$ and $\theta _2'$, respectively

Figure 2 shows a double-pendulum system with masses $m_1$ and $m_2$ and lengths $l_1$ and $l_2$. The angle of tilt is as $\alpha$, and the resulting angles of the system are $\theta _1'$ and $\theta _2'$.

1.3 Related literature

In [23], the authors investigate the chaotic behavior of a spring pendulum system moving in a circular path subjected to an external harmonic excitation. The authors analyze the pendulum’s motion using numerical simulations and examine the bifurcation behavior of the system. Similarly, [24] examines the motion of a spring pendulum moving in an elliptic path under harmonic excitation. The authors employ numerical and analytical methods to study the pendulum’s motion near resonances, which are critical points where the system exhibits large-amplitude oscillations. In both [23] and [24], the pivot moves in a predetermined path (a circle or an ellipse) due to an external force or input. Our work investigates a system where the pivot is not externally controlled and is free to move in the horizontal plane (translating) or through tilting motion. In such a system, the behavior of the system affects the motion of the pivot as well, which in turn affects the system again. This distinction allows us to explore the unforced dynamics of multiple pendulum systems and analyze how the pivot’s motion affects the overall system behavior without the influence of external inputs. Also, [23] and [24] focus on spring pendulum systems, where the pendulum is attached to a spring. We examine normal pendulums without springs, which have different dynamic characteristics than spring pendulums. This distinction enables us to expand the understanding of pendulum systems by investigating the dynamics of multiple regular pendulums under translating and tilting pivots, providing additional insights into the behavior of these systems. In the article [25], the authors examine the planar motion of a 2DOF auto-parametric pendulum connected to a damped system. They derive the equations of motion using Lagrange’s equations and obtain approximate solutions using the method of multiple scales (MMS). By analyzing primary external and internal resonance cases, the study explores the stability and instability zones of the system. The findings reveal the system’s stable performance for certain variables and have practical applications in vibration damping across various mechanical fields, both linear and angular. In [26], the authors investigate the motion of a 3DOF automatic parametric pendulum connected to a damped system. They derive the kinematics equations using Lagrange’s equations and employ the method of multiple scales (MMS) to obtain third-order approximate solutions. The nonlinear stability approach is used to analyze the system’s stability across various parameters. The study identifies different zones of stability and instability and demonstrates that the system’s behavior is stable for numerous values of its variables. The findings have practical applications in various domains such as ship motion, transportation equipment, swaying buildings, and rotor dynamics. In terms of the mathematical approach in [23,24,25,26], the authors employ the method of multiple scales (MS) to reduce the complex nonlinear systems into reduced-order systems. This technique helps to obtain approximate solutions for the nonlinear equations of motion. Our work uses small-angle approximations to linearize the system. This simplification allows us to focus on the essential aspects of the system’s behavior, such as the natural frequencies and the impact of various parameters on the pendulum dynamics. While our approach may not capture the full complexity of the nonlinear systems, it provides valuable insights into the behavior of multiple pendulum systems under translating and tilting pivots and serves as a foundation for further investigations of more complex nonlinear effects. In [27], the authors investigate a 3 DOF dynamical system linked to an energy harvesting device, consisting of a nonlinear Duffing oscillator and a nonlinear damping spring pendulum. They utilize Lagrange’s equations and the approach of multiple scales to analyze the motion of the system and its stability. The study highlights the impact of varying parameters such as damping coefficient, excitation amplitude, and load resistance on the output power and current of the electromagnetic device.

A lot of research further extends on the study of such dynamical systems by investigating the motion, resonance cases, solvability conditions, and performing stability analysis of different systems [28,29,30,31,32]. These studies highlight the influence of various parameters on the system’s behavior and emphasize their applications in engineering fields such as swaying structures and rotor dynamics. However, the stability analysis and solvability conditions are considered out of scope for our paper due to the specific focus and objectives of our study. While stability analysis and solvability conditions are important aspects in the analysis of dynamical systems, our study primarily aims to investigate the dynamics and natural frequencies of multiple pendulum systems under translation and tilt for inertial sensing applications. We seek to understand how parameters such as degrees of freedom, mass, length, and stiffness impact the behavior of the system.

1.4 Importance of this study

This paper aims to answer questions like—how would the frequency of a multiple pendulum system changes when it is free to move or tilt and what are the parameters that affect the natural frequency of such a systems. The translating pendulum system is emulated by attaching the pivot to a freely moving cart, and the tilting is emulated by attaching the pivot to a rotating platform. The Euler–Lagrange equations are used to derive the equations of motions of the double-pendulum systems under tilt and translation, which is then extended to multiple pendulum system with “n” pendulums [33,34,35,36]. While we have mainly discussed the behavior of the pendulum system under translation and tilt, we also compared the system performance with an equivalent pendulum system with a fixed pivot point. Additionally, we discussed on how parameters like length and mass of the pendulums affect the natural frequency of the system. The paper gives an in-depth analysis on the effect of various parameters on the natural frequency of the multiple pendulum systems and an explanation for the same. This paper can be a good reference for researchers working in the area of dynamics and control of pendulous structures and systems.

1.5 Organization of the paper

The rest of the paper is organized as follows. A detailed analysis of the dynamics of multiple pendulum systems under translation is given in Sect. 2. The section starts with a single pendulum system and extends up to n-pendulum system. The derivation of the natural frequency of the above system is given in Sect. 3. Section 4 explains the dynamics of multiple pendulum systems under tilt starting from the double-pendulum system and extending up to the N-pendulum system followed by the derivation of its natural frequencies in Sect. 5. Results and discussion is given in Sect. 6. Various factors affecting the natural frequency are analyzed from simulation results. Section 7 concludes the paper followed by funding details in final section.

2 Dynamics of multiple pendulum system under translation

In this section, the dynamics equations governing the behavior of pendulum systems under translation of the pivot are presented. A single pendulum is considered initially which is extended to a double-pendulum case and is further extended to a N-pendulum system. The governing equations are derived based on Lagrangian dynamics (Fig. 3).

Fig. 3

Single pendulum system under translation

2.1 Single pendulum system

For a single pendulum system (3),

Kinetic energy of the cart:

$$\begin{aligned} K.E_\textrm{cart} = \frac{m_{0}\,{{\dot{\theta }}_{0}}^2}{2} \end{aligned}$$

(1)

Kinetic energy of the bob

$$\begin{aligned} K.E_1 = \frac{m_{1}\,\left( {\left( {\dot{\theta }}_{0}+l_{1}\,{\dot{\theta }}_{1}\,\cos \left( \theta _{1}\right) \right) }^2+{l_{1}}^2\,{{\dot{\theta }}_{1}}^2\,{\sin \left( \theta _{1}\right) }^2\right) }{2} \end{aligned}$$

(2)

Total kinetic energy of the system is

$$\begin{aligned} K.E_\textrm{total}=\frac{1}{2}m_{0}\dot{\theta }_{0}^{2}+\frac{1}{2}m_1\dot{\theta }_0^2+\frac{1}{2}m_1l_1^2\dot{\theta }_1^2+m_1l_1\dot{\theta }_0\dot{\theta }_1\cos \theta _1 \end{aligned}$$

(3)

Potential energy of cart

$$\begin{aligned} P.E_\textrm{cart}= m_0gl_0 =0 \end{aligned}$$

(4)

Potential energy of bob

$$\begin{aligned} P.E_{1}= -m_1gl_1\cos \theta _1 \end{aligned}$$

(5)

The total potential energy of the system

$$\begin{aligned} PE_\textrm{total}= -m_1gl_1\cos \theta _1 \end{aligned}$$

(6)

The Lagrangian is given by

$$\begin{aligned}{} & {} L = K.E_\textrm{total} -P.E_\textrm{total}\nonumber \\{} & {} \quad L = \frac{1}{2}m_{0}\dot{\theta }_{0}^{2}+\frac{1}{2}m_1\dot{\theta }_0^2+\frac{1}{2}m_1l_1^2\dot{\theta }_1^2+m_1l_1\dot{\theta }_0\dot{\theta }_1\cos \theta _{1}+m_1gl_1\cos \theta _1 \end{aligned}$$

(7)

The differential equation can be obtained using the Euler–Lagrange equations of the second kind.

$$\begin{aligned} \frac{d}{{dt}}\left( \frac{{\partial L}}{{\partial {{\dot{\theta }}_i}}}\right) - \frac{{\partial L}}{{\partial {\theta _i}}} = 0,\;\; i = 0,1. \end{aligned}$$

(8)

For i = 0, we get

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta }_0} \right) - \frac{\partial L}{\partial \theta _{0}}\Rightarrow m_0\ddot{\theta }_{0}+m_1\ddot{\theta }_0+m_1l_1\ddot{\theta }_1\cos \theta _1-m_1l_1\dot{\theta }_1^2\sin \theta _1=0 \end{aligned}$$

(9)

Similarly for i = 1,

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial L }{\partial \dot{\theta }_1}\right) -\frac{\partial L}{\partial \theta _{1}} \Rightarrow m_1l_1^2\ddot{\theta }_1+m_1l_1\ddot{\theta }_0\cos \theta _1+m_1gl_1\sin \theta _1=0 \end{aligned}$$

(10)

In Eqs. 9 and 10, assuming that $\theta _1$ is very small such that $\sin (\theta _i)\approx \theta _i$ and $\cos (\theta _i)\approx 1$ and neglecting higher-order terms, we can rewrite the Eqs. 9 and 10 as

$$\begin{aligned} m_0\ddot{\theta }_{0}+m_1\ddot{\theta }_0+m_1l_1\ddot{\theta }_1=0 \end{aligned}$$

(11)

$$\begin{aligned} m_1l_1^2\ddot{\theta }_1+m_1l_1\ddot{\theta }_0+m_1gl_1\theta _1=0 \end{aligned}$$

(12)

2.2 Double-pendulum system

Following similar procedure as that for a single pendulum system, the Lagrangian of the double-pendulum system can be derived as.

$$\begin{aligned} \begin{aligned} L =&\frac{m_{1}\,\left( {l_{1}}^2\,{{\dot{\theta }}_{1}}^2+2\,\cos \left( \theta _{1}\right) \,l_{1}\,{\dot{\theta }}_{0}\,{\dot{\theta }}_{1}+{{\dot{\theta }}_{0}}^2\right) }{2} \\&+ \frac{m_{2}\,\left( {\left( l_{1}\,{\dot{\theta }}_{1}\,\sin \left( \theta _{1}\right) +l_{2}\,{\dot{\theta }}_{2}\,\sin \left( \theta _{2}\right) \right) }^2+{\left( {\dot{\theta }}_{0}+l_{1}\,{\dot{\theta }}_{1}\,\cos \left( \theta _{1}\right) +l_{2}\,{\dot{\theta }}_{2}\,\cos \left( \theta _{2}\right) \right) }^2\right) }{2} \\&+\frac{m_{0}\,{{\dot{\theta }}_{0}}^2}{2}+g\,m_{2}\,\left( l_{1}\,\cos \left( \theta _{1}\right) +l_{2}\,\cos \left( \theta _{2}\right) \right) +g\,l_{1}\,m_{1}\,\cos \left( \theta _{1}\right) \end{aligned} \end{aligned}$$

(13)

Euler–Lagrange equations using

$$\begin{aligned} \frac{d}{{dt}}\left( \frac{{\partial L}}{{\partial {{\dot{\theta }}_i}}}\right) - \frac{{\partial L}}{{\partial {\theta _i}}} = 0,\;\; i = 0,1,2. \end{aligned}$$

(14)

For i=0, $\frac{d}{{dt}}\left( \frac{{\partial L}}{{\partial {{\dot{\theta }}_0}}}\right) - \frac{{\partial L}}{{\partial {\theta _0}}} = 0$

$$\begin{aligned} \begin{aligned} 0 =&-l_{2}\,m_{2}\,\sin \left( \theta _{2}\right) \,{{\dot{\theta }}_{2}}^2+{\ddot{\theta }}_{1}\,\left( l_{1}\,m_{1}\,\cos \left( \theta _{1}\right) +l_{1}\,m_{2}\,\cos \left( \theta _{1}\right) \right) \\&-{\dot{\theta }}_{1}\,\left( l_{1}\,m_{1}\,{\dot{\theta }}_{1}\,\sin \left( \theta _{1}\right) +l_{1}\,m_{2}\,{\dot{\theta }}_{1}\,\sin \left( \theta _{1}\right) \right) +{\ddot{\theta }}_{0}\,\left( m_{1}+m_{2}+m_{0}\right) \\&+l_{2}\,m_{2}\,{\ddot{\theta }}_{2}\,\cos \left( \theta _{2}\right) \end{aligned} \end{aligned}$$

(15)

For i=1, $\frac{d}{{dt}}\left( \frac{{\partial L}}{{\partial {{\dot{\theta }}_1}}}\right) - \frac{{\partial L}}{{\partial {\theta _1}}} = 0$

$$\begin{aligned} \begin{aligned} 0 =&l_{1}\,\left( l_{2}\,m_{2}\,\sin \left( \theta _{1}-\theta _{2}\right) \,{{\dot{\theta }}_{2}}^2+m_{1}\,{\ddot{\theta }}_{0}\,\cos \left( \theta _{1}\right) +m_{2}\,{\ddot{\theta }}_{0}\,\cos \left( \theta _{1}\right) +g\,m_{1}\,\sin \left( \theta _{1}\right) \right) \\&+l_{1}\left( g\,m_{2}\,\sin \left( \theta _{1}\right) +l_{1}\,m_{1}\,{\ddot{\theta }}_{1}+l_{1}\,m_{2}\,{\ddot{\theta }}_{1}+l_{2}\,m_{2}\,{\ddot{\theta }}_{2}\,\cos \left( \theta _{1}-\theta _{2}\right) \right) \end{aligned} \end{aligned}$$

(16)

For i=2, $\frac{d}{{dt}}\left( \frac{{\partial L}}{{\partial {{\dot{\theta }}_2}}}\right) - \frac{{\partial L}}{{\partial {\theta _2}}} = 0$

$$\begin{aligned} \begin{aligned} 0 = l_{2}\,m_{2}\,\left( -l_{1}\,\sin \left( \theta _{1}-\theta _{2}\right) \,{{\dot{\theta }}_{1}}^2+l_{2}\,{\ddot{\theta }}_{2}+{\ddot{\theta }}_{0}\,\cos \left( \theta _{2}\right) +g\,\sin \left( \theta _{2}\right) +l_{1}\,{\ddot{\theta }}_{1}\,\cos \left( \theta _{1}-\theta _{2}\right) \right) \end{aligned} \end{aligned}$$

(17)

Assuming that $\theta _1$ and $\theta _2$ are very small such that $\sin (\theta _i)\approx \theta _i$ and $\cos (\theta _i)\approx 1$ and neglecting higher-order terms, we can rewrite Eqs. 15, 16 and 17 as

$$\begin{aligned} 0={\ddot{\theta }}_{0}\,\left( m_{1}+m_{2}+m_{0}\right) +{\ddot{\theta }}_{1}\,\left( l_{1}\,m_{1}+l_{1}\,m_{2}\right) +l_{2}\,m_{2}\,{\ddot{\theta }}_{2} \end{aligned}$$

(18)

$$\begin{aligned} 0= l_{1}\,\left( m_{1}\,{\ddot{\theta }}_{0}+m_{2}\,{\ddot{\theta }}_{0}+g\,m_{1}\,\theta _{1}+g\,m_{2}\,\theta _{1}+l_{1}\,m_{1}\,{\ddot{\theta }}_{1}+l_{1}\,m_{2}\,{\ddot{\theta }}_{1}+l_{2}\,m_{2}\,{\ddot{\theta }}_{2}\right) \end{aligned}$$

(19)

$$\begin{aligned} 0=l_{2}\,m_{2}\,\left( {\ddot{\theta }}_{0}+g\,\theta _{2}+l_{1}\,{\ddot{\theta }}_{1}+l_{2}\,{\ddot{\theta }}_{2}\right) \end{aligned}$$

(20)

2.3 N-pendulum system

For a N-pendulum system as given in 4

Fig. 4

N-pendulum system under translation

The Cartesian position of each bob is given by

$$\begin{aligned} \begin{aligned} x_{i}= \theta _{0}+ \sum \limits _{j=1}^{i} l_{j}\sin (\theta _j)\\ y_{i} = -\sum \limits _{j=1}^{i} l_{j}\cos (\theta _j) \end{aligned} \end{aligned}$$

(21)

The velocity of the ith bob is

$$\begin{aligned} \begin{aligned} \dot{x}_{i}= \dot{\theta }_0+\sum \limits _{j=1}^il_j\dot{\theta }_j\cos (\theta _j \\ \dot{y}_j=\sum \limits _{j=1}^il_j\dot{\theta }_j\sin (\theta _j) \end{aligned} \end{aligned}$$

(22)

Kinetic energy of the system is given by

$$\begin{aligned} \begin{aligned} K.E_\textrm{Total}&= \frac{1}{2}\sum \limits _{i=0}^n m_iv_i^2 \\ K.E_\textrm{Total}&= \frac{1}{2}\sum \limits _{i=0}^{n}m_{i}\left( \left( \dot{\theta }_0+\sum \limits _{j=1}^il_j\dot{\theta }_j\cos (\theta _j)\right) ^2 + \left( \sum \limits _{j=1}^il_j\dot{\theta }_j\sin (\theta _j)\right) ^2\right) \end{aligned} \end{aligned}$$

(23)

Potential energy in the system is

$$\begin{aligned} \begin{aligned} P.E_\textrm{Total}&= -g\sum \limits _{i=0}^{n}m_iy_i \\ P.E_\textrm{Total}&= -g\sum \limits _{i=0}^{n}\sum \limits _{j=1}^{i}m_il_i\cos (\theta _j) \end{aligned} \end{aligned}$$

(24)

Lagrangian L

$$\begin{aligned}{} & {} L = K.E_\textrm{total} -P.E_\textrm{total}\nonumber \\{} & {} \quad L= \frac{1}{2}\sum \limits _{i=0}^{n}m_{i} \left( \left( \dot{\theta }_0+\sum \limits _{j=1}^il_j\dot{\theta }_j\cos (\theta _j)\right) ^2 + \left( \sum \limits _{j=1}^il_j\dot{\theta }_j\sin (\theta _j)\right) ^2\right) + g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^i m_jl_j\cos (\theta _j) \end{aligned}$$

(25)

Assume $\theta _i<< 1$ so that

$$\begin{aligned} \cos (\theta _i)\approx 1-\frac{\theta _i^2}{2} \quad \quad \sin (\theta _i)\approx \theta _i \end{aligned}$$

(26)

Then, the Lagrangian can be modified to

$$\begin{aligned} L = \frac{1}{2}\sum \limits _{i=0}^{n}m_{i} \left( \left( \dot{\theta }_0+\sum \limits _{j=1}^il_j\dot{\theta }_j\left( 1-\frac{\theta _i^2}{2}\right) \right) ^2 + \left( \sum \limits _{j=1}^il_j\dot{\theta }_j\theta _j\right) ^2\right) + g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^i m_jl_j(1-\frac{\theta _j^2}{2})) \end{aligned}$$

(27)

Neglecting higher-order terms and rearranging the terms, we get

$$\begin{aligned} \begin{aligned} L = \sum \limits _{i=0}^{n}\frac{1}{2}m_{i}\left( \dot{\theta }_0^2 +2\dot{\theta }_0\sum \limits _{j=1}^{i}l_j\dot{\theta }_j\left( 1-\frac{\theta _j^2}{2}\right) +\left( \sum \limits _{j=1}^{i}l_j\dot{\theta }_j\right) ^2 +2g\sum \limits _{j=1}^{i}l_j\left( 1-\frac{\theta _j^2}{2}\right) \right) \end{aligned} \end{aligned}$$

(28)

To compute the kth for the Lagrangian in Eq. (28), we have to find the partial derivatives of the Lagrangian with respect to $\theta _k$ and $\dot{\theta }_k$

$$\begin{aligned} \begin{aligned} \frac{\partial L}{\partial \theta _{k}}= -\frac{1}{2}\sum \limits _{i=0}^{n}m_i\dot{\theta }_0\sum \limits _{j=1}^{i}l_j\dot{\theta }_j\frac{\partial (\theta _j^2)}{\partial \theta _{k}}-\frac{1}{2}\sum \limits _{i=0}^{n}m_ig\sum \limits _{j=1}^{i}l_j\frac{\partial (\theta _j^2)}{\partial \theta _k} \end{aligned} \end{aligned}$$

(29)

which can be simplified to

$$\begin{aligned} \frac{\partial L}{\partial \theta _{k}}= -\sum \limits _{i=0}^{n}m_i\dot{\theta }_0\sum \limits _{j=1}^{i}l_k\dot{\theta }_k\theta _k\delta _{jk}-\sum \limits _{i=0}^{n}m_ig\sum \limits _{j=1}^{i}l_k\theta _k\delta _{jk} \end{aligned}$$

(30)

where $\delta {jk}$ is the Kronecker delta, defined by

$$\begin{aligned}\delta {ij}={\left\{ \begin{array}{ll}1\quad i=j\\ 0 \quad i\ne j\end{array}\right. }\end{aligned}$$

which has the effect of relabeling the summations, yielding

$$\begin{aligned} \frac{\partial L}{\partial \theta _{k}}= -l_k\theta _k\left( \dot{\theta }_0\dot{\theta }_k+g\right) \sum \limits _{i=k}^{n}m_i \end{aligned}$$

(31)

The partial derivative with respect to $\dot{\theta }_k$

$$\begin{aligned} \begin{aligned} \frac{\partial L}{\partial \dot{\theta }_k}&=\dot{\theta }_0\delta _{0k}\sum \limits _{i=0}^{n}m_i+\sum \limits _{i=0}^{n}m_i\delta _{0k}\sum \limits _{j=1}^{i}l_j\dot{\theta }_j\left( 1-\frac{\theta _j^2}{2}\right) \\&+\sum \limits _{i=0}^{n}m_i\dot{\theta }_0\sum \limits _{j=1}^{i}l_j\delta _{jk}\left( 1-\frac{\theta _j^2}{2}\right) +\sum \limits _{i=0}^{n}m_i\sum \limits _{j=1}^{i}l_j\dot{\theta }_j\sum \limits _{p=1}^{i}l_p\delta _{pk} \end{aligned} \end{aligned}$$

(32)

On relabeling the summations,

$$\begin{aligned} \begin{aligned} \frac{\partial L}{\partial \dot{\theta }_{k}}&= \dot{\theta }_0\delta _{0k}\sum \limits _{i=0}^{n}m_i+\delta _{0k}\sum \limits _{i=0}^{n}m_i\sum \limits _{j=1}^{i}l_j\dot{\theta }_j\left( 1-\frac{\theta _j^2}{2}\right) \sum \limits _{i=k}^{n}m_i\dot{\theta }_0l_k\left( 1-\frac{\theta _k^2}{2}\right) \\&+\sum \limits _{i=k}^{n}m_il_k\sum \limits _{j=1}^{i}l_j\dot{\theta }_j \end{aligned} \end{aligned}$$

(33)

Differentiating equation (33) with respect to time

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta }_k}\right)&=\ddot{\theta }_0\delta _{0k}\sum \limits _{i=0}^{n}m_i+\delta _{0k}\sum \limits _{i=0}^{n}m_i\sum \limits _{j=1}^{i}l_j\ddot{\theta }_j\left( 1-\frac{\theta _j^2}{2}\right) -\delta _{0k}\sum \limits _{i-0}^{n}m_i\sum \limits _{j=1}^{i}l_j\dot{\theta }_j^2\theta _j\\&+\sum \limits _{i=k}^{n}m_i\ddot{\theta }_0l_k\left( 1-\frac{\theta _k^2}{2}\right) -\sum \limits _{i=k}^{n}m_i\dot{\theta }_0l_k\theta _k\dot{\theta }_k+\sum \limits _{i=k}^{n}m_il_k\sum \limits _{j=1}^{i}l_j\ddot{\theta }_j \end{aligned} \end{aligned}$$

(34)

From Eqs. (34) and (31), the equations of motion is

$$\begin{aligned} \begin{aligned} 0&=\ddot{\theta }_0\delta _{0k}\sum \limits _{i=0}^{n}m_i+\delta _{0k}\sum \limits _{i=0}^{n}m_i\sum \limits _{j=1}^{i}l_j\ddot{\theta }_j\left( 1-\frac{\theta _j^2}{2}\right) -\delta _{0k}\sum \limits _{i-0}^{n}m_i\sum \limits _{j=1}^{i}l_j\dot{\theta }_j^2\theta _j\\&+\sum \limits _{i=k}^{n}m_i\ddot{\theta }_0l_k\left( 1-\frac{\theta _k^2}{2}\right) +\sum \limits _{i=k}^{n}m_il_k\sum \limits _{j=1}^{i}l_j\ddot{\theta }_j+l_k\theta _kg\sum \limits _{i=k}^{n}m_i \end{aligned} \end{aligned}$$

(35)

For $\theta _i<< 1$ and neglecting higher-order terms,

$$\begin{aligned} \boxed { \ddot{\theta }_0\delta _{0k}\sum \limits _{i=0}^{n}m_i+\delta _{0k}\sum \limits _{i=0}^{n}m_i\sum \limits _{j=1}^{i}l_j\ddot{\theta }_j +\sum \limits _{i=k}^{n}m_i\ddot{\theta }_0l_k+\sum \limits _{i=k}^{n}m_il_k\sum \limits _{j=1}^{i}l_j\ddot{\theta }_j+l_k\theta _kg\sum \limits _{i=k}^{n}m_i=0} \end{aligned}$$

(36)

Substituting $n=1$ we get 2 equations, one for $k=0$ and one for $k=1$

$$\begin{aligned}{} & {} 0 = m_0\ddot{\theta }_{0}+m_1\ddot{\theta }_0+m_1l_1\ddot{\theta }_1 \end{aligned}$$

(37)

$$\begin{aligned}{} & {} 0= m_1l_1^2\ddot{\theta }_1+m_1l_1\ddot{\theta }_0+m_1gl_1\theta _1 \end{aligned}$$

(38)

3 Natural frequencies of multiple pendulum system under translation

The natural frequencies of multiple pendulum systems under translation are derived under free condition, i.e., no external force applied on the system.

3.1 Double-pendulum system

For a double-pendulum system under translation, the linearized equations of motion can be represented in the form

$$\begin{aligned} \begin{bmatrix}M\end{bmatrix}\{\ddot{\theta }\}+\begin{bmatrix}K\end{bmatrix}\{\theta \}=0 \end{aligned}$$

(39)

where $\begin{bmatrix}M\end{bmatrix}$ is the linearized mass matrix and $\begin{bmatrix}K\end{bmatrix}$ is the linearized stiffness matrix.

For a double-pendulum system under translation

$$\begin{aligned} \begin{aligned} \begin{bmatrix}M\end{bmatrix}&= \begin{bmatrix} m_{0}+m_{1}+m_{2} &{} l_{1}\,m_{1}+l_{1}\,m_{2} &{} l_{2}\,m_{2}\\ l_{1}\,\left( m_{1}+m_{2}\right) &{} l_{1}\,\left( l_{1}\,m_{1}+l_{1}\,m_{2}\right) &{} l_{1}\,l_{2}\,m_{2}\\ l_{2}\,m_{2} &{} l_{1}\,l_{2}\,m_{2} &{} {l_{2}}^2\,m_{2} \end{bmatrix}\\ \begin{bmatrix}K\end{bmatrix}&= \begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} l_{1}\,\left( g\,m_{1}+g\,m_{2}\right) &{} 0\\ 0 &{} 0 &{} g\,l_{2}\,m_{2} \end{bmatrix} \end{aligned} \end{aligned}$$

(40)

Angular frequencies $\omega _n$ can then be evaluated using the characteristic equation

$$\begin{aligned}det\begin{vmatrix}{\begin{bmatrix}K\end{bmatrix}-\omega _n^2\begin{bmatrix}M\end{bmatrix}}\end{vmatrix}=0\end{aligned}$$

Solving for $\omega _n$ using $\begin{bmatrix}M\end{bmatrix}$ and $\begin{bmatrix}K\end{bmatrix}$ in Eq. (40) and substituting $m_0 = m_1 = m_2 = 1$, $l_1 = l_2=1$ and $g = 9.81$,

$$\begin{aligned} \omega _n=\begin{bmatrix}0\\ 3.527 \\ 6.813\end{bmatrix} \end{aligned}$$

(41)

3.2 N-pendulum system

The natural angular frequency is given by

$$\begin{aligned}det\begin{vmatrix}{\begin{bmatrix}K\end{bmatrix}-\omega _n^2\begin{bmatrix}M\end{bmatrix}}\end{vmatrix}=0\end{aligned}$$

Here, the stiffness matrix $\begin{bmatrix}K\end{bmatrix}$ can be expressed as

$$\begin{aligned} K_{(\mu +1)(\nu +1)} = \frac{\partial ^{2}(P.E_\textrm{Total})}{\partial q^{\mu }\partial q^{\nu }} \end{aligned}$$

(42)

and mass matrix $\begin{bmatrix}M\end{bmatrix}$ as

$$\begin{aligned} M_{(\mu +1)(\nu +1)}=\frac{\partial ^{2}(K.E_\textrm{Total})}{\partial \dot{q}^\mu \partial \dot{q}^{\nu }} \end{aligned}$$

(43)

Substituting values from Eqs. (23) and (24) for $K.E_\textrm{Total}$ and $P.E_\textrm{Total}$, respectively, in Eqs. (42) and (43)

$$\begin{aligned}{} & {} K_{(\mu +1)(\nu +1)}=gl_\mu \delta _{\mu \nu }\sum \limits _{i=\mu }^{n}m_i \end{aligned}$$

(44)

$$\begin{aligned}{} & {} \quad M_{(\mu +1)(\nu +1)}=\sum \limits _{i=0}^{n}m_i\delta _{0\nu }\delta _{0\mu }+\sum \limits _{i=\mu }^{n}m_il_\mu \delta _{0\nu }+\sum \limits _{i=\nu }^{n}m_il_\nu \delta _{0\mu }\nonumber \\{} & {} \quad + l_\mu l_{\nu }\sum \limits _{i=\max (\mu ,\nu )}^{n}m_i \end{aligned}$$

(45)

The natural frequency $\omega _n$ of “N”-pendulum system can be derived as,

(46)

4 Multiple pendulum system under tilt

In this section, the dynamics equations governing the behavior of pendulum systems under tilt of the pivot is presented. A single pendulum is considered initially which is extended to double-pendulum case and is further extended to a N-pendulum system. The governing equations are derived based on Lagrangian dynamics.

4.1 Double-pendulum system

For the double-pendulum system under tilt as shown in Fig. 5, the angles after tilt are $\theta _1'$ and $\theta _2'$ where

$$\begin{aligned} \theta _1' = \theta _1 +\alpha \end{aligned}$$

(47)

Fig. 5

Double-pendulum system under tilt

The kinetic energy of the top pendulum is

$$\begin{aligned} K.E_{1}=\frac{{l_{1}}^2\,m_{1}\,{\left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) }^2}{2} \end{aligned}$$

(48)

Kinetic energy of bottom pendulum

$$\begin{aligned} \begin{aligned} K.E_{2} =&\frac{1}{2} m_{2}\ {\left( l_{2}\ {\dot{{\theta }}}_{2}'\ \cos {\left( {\theta }_{2}' \right) }+l_{1}\ \cos {\left( {{\alpha }} +{{\theta }} _{1}\right) }\ \left( {\dot{\alpha }}+{\dot{{\theta }}}_{1}\right) \right) }^2\\&\quad + \frac{1}{2} m_2{\left( l_{2}\ {\dot{\theta }}_{2}'\ \sin {\left( {\theta }_{2}' \right) }+l_{1}\ \sin {\left( {\alpha } +{\theta } _{1}\right) }\ \left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) \right) }^2 \end{aligned} \end{aligned}$$

(49)

Total kinetic energy

$$\begin{aligned} \begin{aligned} K.E_\textrm{Total}=&\frac{1}{2} m_{2}\,{\left( l_{2}\,{\dot{\theta }}_{2}'\,\cos {\left( {\theta }_2'\right) }+l_{1}\,\cos {\left( {\alpha } +{\theta } _{1}\right) }\,\left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) \right) }^2\\&\quad +\frac{1}{2}m_2{\left( l_{2}\,{\dot{\theta }}_{2}'\,\sin \left( {\theta }_2'\right) +l_{1}\,\sin {\left( {\alpha } +{\theta } _{1}\right) }\,\left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) \right) }^2+\frac{{l_{1}}^2\,m_{1}\,{\left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) }^2}{2} \end{aligned} \end{aligned}$$

(50)

Potential energy due to bending of first pendulum link due to tilting pivot can be given as

$$\begin{aligned} P.E_{b1}= \frac{{kr}_{1}\,{\theta _{1}}^2}{2} \end{aligned}$$

(51)

Similarly for the bottom link,

$$\begin{aligned} P.E_{b1}= \frac{{kr}_{1}\,{\theta _{1}}^2}{2} \end{aligned}$$

(52)

Potential energy in top link due to gravity is

$$\begin{aligned} P.E_{t1}=-g\,l_{1}\,m_{1}\,\cos \left( \alpha +\theta _{1}\right) \end{aligned}$$

(53)

Potential energy in bottom link due to gravity is

$$\begin{aligned} P.E_{t2}-g\,l_{1}\,m_{2}\,\cos \left( \alpha +\theta _{1}\right) -g\,l_{2}\,m_{2}\,\cos \left( \theta _2'\right) \end{aligned}$$

(54)

Total potential energy is

$$\begin{aligned}{} & {} P.E_\textrm{Total}= P.E_{b1}+P.E_{b2}+P.E_{t1}+P.E_{t2} \nonumber \\{} & {} \quad P.E_\textrm{total} = \frac{{kr}_{2}\,{\left( \alpha +\theta _{1}-\theta _2'\right) }^2}{2}+\frac{{kr}_{1}\,{\theta _{1}}^2}{2} \nonumber \\{} & {} \quad -g\,l_{1}\,m_{1}\,\cos \left( \alpha +\theta _{1}\right) -g\,l_{1}\,m_{2}\,\cos \left( \alpha +\theta _{1}\right) -g\,l_{2}\,m_{2}\,\cos \left( \theta _2'\right) \end{aligned}$$

(55)

The Lagrangian of the system is

$$\begin{aligned} L= & {} K.E_\textrm{total}- P.E_\textrm{total}\nonumber \\{} & {} \quad L = \frac{1}{2}m_{2}\,{\left( l_{2}\,{\dot{\theta }}_{2}'\,\cos \left( \theta _2'\right) +l_{1}\,\cos \left( \alpha +\theta _{1}\right) \,\left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) \right) }^2\nonumber \\{} & {} \quad +\frac{1}{2}m_2{\left( l_{2}\,{\dot{\theta }}_{2}'\,\sin \left( \theta _2'\right) +l_{1}\,\sin \left( \alpha +\theta _{1}\right) \,\left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) \right) }^2 -\frac{{kr}_{2}\,{\left( \alpha +\theta _{1}-\theta _2'\right) }^2}{2}\nonumber \\{} & {} \quad -\frac{{kr}_{1}\,{\theta _{1}}^2}{2}+\frac{{l_{1}}^2\,m_{1}\,{\left( {\dot{\alpha }}+{\dot{\theta }}_{1}\right) }^2}{2}+g\,l_{1}\,m_{1}\,\cos \left( \alpha +\theta _{1}\right) \nonumber \\{} & {} \quad +g\,l_{1}\,m_{2}\,\cos \left( \alpha +\theta _{1}\right) +g\,l_{2}\,m_{2}\,\cos \left( \theta _2'\right) \end{aligned}$$

(56)

Euler–Lagrange equations are given by

$$\begin{aligned}\displaystyle \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta }_i}\right) -\frac{\partial L}{\partial \theta _i} = 0, i=1,2\end{aligned}$$

for $i=1$ we get

$$\begin{aligned} \begin{aligned} 0=&\;{kr}_{2}\,\alpha +{kr}_{1}\,\theta _{1}+{kr}_{2}\,\theta _{1}-{kr}_{2}\,\theta _2'+{l_{1}}^2\,m_{1}\,{\ddot{\theta }}_{1}+{l_{1}}^2\,m_{2}\,{\ddot{\theta }}_{1}+{\ddot{\alpha }}\,{l_{1}}^2\,m_{1}+{\ddot{\alpha }}\,{l_{1}}^2\,m_{2}\\&\quad +\,g\,l_{1}\,m_{1}\,\sin \left( \alpha +\theta _{1}\right) +g\,l_{1}\,m_{2}\,\sin \left( \alpha +\theta _{1}\right) +l_{1}\,l_{2}\,m_{2}\,{\ddot{\theta }}_{2}'\,\cos \left( \alpha +\theta _{1}-\theta _2'\right) \\&\quad +\,l_{1}\,l_{2}\,m_{2}\,{{\dot{\theta }}_{2}}'^2\,\sin \left( \alpha +\theta _{1}-\theta _2'\right) \end{aligned} \end{aligned}$$

(57)

for $i=2$

$$\begin{aligned} \begin{aligned} 0&={kr}_{2}\,\theta _2'-{kr}_{2}\,\theta _{1}-\textrm{kr}_{2}\,\alpha +{l_{2}}^2\,m_{2}\,{\ddot{\theta }}_{2}' +g\,l_{2}\,m_{2}\,\sin \left( \theta _2'\right) \\ {}&+{\ddot{\alpha }}\,l_{1}\,l_{2}\,m_{2}\,\cos \left( \alpha +\theta _{1}-\theta _2'\right) +l_{1}\,l_{2}\,m_{2}\,{\ddot{\theta }}_{1}\,\cos \left( \alpha +\theta _{1}-\theta _2'\right) \\ {}&-{{\dot{\alpha }}}^2\,l_{1}\,l_{2}\,m_{2}\,\sin \left( \alpha +\theta _{1}-\theta _2'\right) -l_{1}\,l_{2}\,m_{2}\,{{\dot{\theta }}_{1}}^2\,\sin \left( \alpha +\theta _{1}-\theta _2'\right) \\ {}&-2\,{\dot{\alpha }}\,l_{1}\,l_{2}\,m_{2}\,{\dot{\theta }}_{1}\,\sin \left( \alpha +\theta _{1}-\theta _2'\right) \end{aligned} \end{aligned}$$

(58)

4.2 N-pendulum system

For a N-pendulum system under tilt, if the angles made by each of the pendulum in the system before tilt is given by $\theta = {\theta _1,\theta _2,\theta _3,\theta _4,\ldots ,\theta _n }$, then the angles made by the same pendulums after tilting the platform are given by $\theta ={\theta _1',\theta _2',\theta _3',\theta _4',\ldots \theta _n'}$

where

$$\begin{aligned} \theta _1' = \theta _1 + \alpha \end{aligned}$$

(59)

After tilting, the coordinates of each bob of the pendulum system can be written as

$$\begin{aligned} \begin{aligned} x_{i}= \sum \limits _{j=1}^{i}l_j\sin \theta _{j}'\\ y_{i}= -\sum \limits _{j=1}^{i}l_j\cos \theta _j' \end{aligned} \end{aligned}$$

(60)

Then, the velocity term squared is

$$\begin{aligned} \begin{aligned} v_i^2=\dot{x}_i^2+\dot{y}_i^2 =\left( \sum \limits _{j=1}^{i}l_j\cos \theta _j'\dot{\theta }_j'\right) ^2+\left( \sum \limits _{j=1}^{i}l_j\sin \theta _j'\dot{\theta }_j'\right) ^2 \end{aligned} \end{aligned}$$

(61)

Kinetic energy of the system is

$$\begin{aligned} \begin{aligned}K.E_\textrm{Total}&= \frac{1}{2}\sum \limits _{i=1}^{n}m_iv_i^2\\ K.E_\textrm{Total}&=\frac{1}{2}\sum \limits _{i=1}^{n}m_i\left( \left( \sum \limits _{j=1}^{i}l_j\cos \theta _j'\dot{\theta }_j'\right) ^2+\left( \sum \limits _{j=1}^{i}l_j\sin \theta _j'\dot{\theta }_j'\right) ^2\right) \end{aligned} \end{aligned}$$

(62)

The potential energy is associated with bending of the rod. When the platform undergoes a very slow tilt of angle $\alpha$, the junction between the top pendulum ($n=1$) and the platform moves accordingly. We consider this junction to be a flexible hinge, due to which a slight bending appears on the pendulum link. A restoring moment caused by the stiffness of the link appears on the hinge and tends to compensate the bending moment. The resulting potential energy associated with the bending of the link is

$$\begin{aligned} P.E_{b}= \frac{1}{2}k_r\theta ^2 \end{aligned}$$

(63)

For the top link ($n=1$):

$$\begin{aligned} P.E_{b_1}=\frac{1}{2}k_{r_1}\theta _1^2 \end{aligned}$$

(64)

and the potential energy associated with the bending of the rest of the pendulum links in the system is

$$\begin{aligned} P.E_{b_{i}}=\frac{1}{2}k_{r_1}\theta _1^2+\sum \limits _{i=2}^{n} \frac{1}{2}k_{r_i}\left( \theta _i'-\theta _{(i-1)}'\right) ^2 \end{aligned}$$

(65)

Potential energy associated with gravity is

$$\begin{aligned} P.E_{g_{i}}=-g\sum \limits _{i=1}^{n}m_iy_i=-g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{i}m_il_j\cos \theta _j' \end{aligned}$$

(66)

The total potential energy is

$$\begin{aligned} P.E_\textrm{Total}= -g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{i}m_il_j\cos \theta _j'+\frac{1}{2}k_{r_1}\theta _1^2+\sum \limits _{i=2}^{n} \frac{1}{2}k_{r_i}\left( \theta _i'-\theta _{(i-1)}'\right) ^2 \end{aligned}$$

(67)

The Lagrangian L

$$\begin{aligned} \begin{aligned}L&= K.E_\textrm{Total}- P.E_\textrm{Total}\\ L&=\frac{1}{2}\sum \limits _{i=1}^{n}m_i\left( \left( \sum \limits _{j=1}^{i}l_j\cos \theta _j'\dot{\theta }_j'\right) ^2+\left( \sum \limits _{j=1}^{i}l_j\sin \theta _j'\dot{\theta }_j'\right) ^2\right) \\ {}&+g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{i}m_il_j\cos \theta _j'-\frac{1}{2}k_{r_1}\theta _1^2-\sum \limits _{i=2}^{n} \frac{1}{2}k_{r_i}\left( \theta _i'-\theta _{(i-1)}'\right) ^2\end{aligned} \end{aligned}$$

(68)

Assume $\theta _{i}<<1$ so that

$$\begin{aligned} \cos (\theta _i)\approx 1-\frac{\theta _i^2}{2}\quad \quad \sin (\theta _i)\approx \theta _i \end{aligned}$$

(69)

Then neglecting higher-order terms and rearranging, we get

$$\begin{aligned} \begin{aligned}L&= \sum \limits _{i=1}^{n}\frac{1}{2}m_i\left( \sum \limits _{j=1}^{i}l_j\dot{\theta }_j'\right) ^2+g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{i}m_il_j\left( 1-\frac{\theta _j'^2}{2}\right) \\ {}&-\frac{1}{2}k_{r_1}\theta _1^2-\sum \limits _{j=2}^{n}\frac{1}{2}k_{r_j}\left( \theta _j'-\theta _{(j-1)}'\right) ^2\end{aligned} \end{aligned}$$

(70)

Computing partial derivatives of Lagrangian with respect to $\theta _k'$ and $\dot{\theta }_k'$

$$\begin{aligned}{} & {} \frac{\partial L}{\partial \theta _k'}=-g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{i}m_il_j\theta _j'\delta _{jk}-k_{r_1}\theta _1\delta _{1k} \nonumber \\{} & {} \quad -\sum \limits _{j=2}^{n}k_{r_j}(\theta _j'-\theta _{(j-1)}')(\delta _{jk}-\delta _{(j-1)k}) \end{aligned}$$

(71)

$$\begin{aligned}{} & {} \quad \frac{\partial L}{\partial \dot{\theta }_k'}=\sum \limits _{i=1}^{n}m_i\left( \sum \limits _{j=1}^{i}l_j\dot{\theta }_j'\right) \sum \limits _{p=1}^{i}l_p\delta _{pk} \end{aligned}$$

(72)

$$\begin{aligned}{} & {} \quad \frac{\partial L}{\partial \dot{\theta }_k'}=\sum \limits _{i=1}^{n}m_i\left( \sum \limits _{j=1}^{i}l_j\dot{\theta }_j'\right) \sum \limits _{p=1}^{i}l_p\delta _{pk} \end{aligned}$$

(73)

Euler–Lagrange equations are given by

$$\begin{aligned}{} & {} \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta }_k}\right) -\frac{\partial L}{\partial \theta _k} = 0 \nonumber \\{} & {} \quad \boxed { \begin{aligned}&\quad 0=\sum \limits _{i=1}^{n}m_i\sum \limits _{j=1}^{i}l_j\ddot{\theta }_j'\sum \limits _{p=1}^{i}l_p\delta _{pk}+g\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{i}m_il_j\theta _j'\delta _{jk}+k_{r_1}\theta _1\delta _{1k} \\&\quad +\sum \limits _{j=2}^{n}k_{r_j}(\theta _j'-\theta _{(j-1)}')(\delta _{jk}-\delta _{(j-1)k}) \end{aligned} } \end{aligned}$$

(74)

5 Natural frequencies of N-pendulum system under tilt

The natural angular frequency is given by

$$\begin{aligned} det\begin{vmatrix}{\begin{bmatrix}K\end{bmatrix}-\omega _n^2\begin{bmatrix}M\end{bmatrix}}\end{vmatrix}=0\end{aligned}$$

For N-pendulum system under tilt, the stiffness matrix [K] where

$$\begin{aligned} K_{(\mu )(\nu )} = \frac{\partial ^{2}(P.E_\textrm{Total})}{\partial q^{\mu }\partial q^{\nu }} \end{aligned}$$

(75)

and mass matrix $\begin{bmatrix}M\end{bmatrix}$ as

$$\begin{aligned} M_{(\mu )(\nu )}=\frac{\partial ^{2}(K.E_\textrm{Total})}{\partial \dot{q}^\mu \partial \dot{q}^{\nu }}, \end{aligned}$$

(76)

we get

$$\begin{aligned} \begin{aligned}K_{\mu \nu }&= g l_\mu \delta _{\mu \nu } \sum \limits _{i=\mu }^{n}m_i+k_{r_1}\delta _{1\mu }\delta _{1\nu }\\ {}&+\sum \limits _{i=2}^{n}k_{r_i}(\delta _{i\mu }-\delta _{{(i-1}\mu )})(\delta _{i\nu }-\delta _{(i-1)\nu })\end{aligned} \end{aligned}$$

(77)

and

$$\begin{aligned} M_{\mu \nu }=l_{\mu }l_{\nu }\sum \limits ^{n}_{i=\max (\mu ,\nu )}m_i \end{aligned}$$

(78)

From Eqs. (77) and (76), the angular frequency $\omega _n$ can be solved using the equation

$$\begin{aligned} \boxed {0=\begin{aligned}\det \Biggl (&g l_\mu \delta _{\mu \nu } \sum \limits _{i=\mu }^{n}m_i+k_{r_1}\delta _{1\mu }\delta _{1\nu }\\ {}&+\sum \limits _{i=2}^{n}k_{r_i}(\delta _{i\mu }-\delta _{{(i-1}\mu )})(\delta _{i\nu }-\delta _{(i-1)\nu })-\omega _n^2l_{\mu }l_{\nu }\sum \limits ^{n}_{i=\max (\mu ,\nu )}m_i\Biggr ) \end{aligned}} \end{aligned}$$

(79)

6 Results and discussion

For the analysis, the natural frequency of the pendulum systems and their behavior due to changes in various parameters is presented. These results are also compared with that of other multiple pendulum systems that are not under tilt or translation. The masses of the pendulums and the cart are assumed to be equal(1 kg), and the length of each of the pendulums is taken to be 1 m. With this initial setup, the values of each of the parameters are tweaked individually to examine the effect of each of them. The results show that the frequency is dependent on the ratio of masses and not on the absolute value. The masses of the cart and the individual pendulums in the initial setup are considered to be 1 kg but can be of any absolute value as long as the ratio is the same. For the multiple pendulum system under tilt, the spiral spring stiffness is taken as $1Nm^{-1}$ unless specified, in the initial setup for studying the pendulum systems under tilt.

6.1 Effect of pendulum parameters on the natural frequency of pendulum system with translating pivot

The effect on varying parameters of pendulum systems on natural frequency is discussed in this section.

6.1.1 Number of pendulum links

For the double-pendulum system considered here, under translation, the natural frequency of the bottom pendulum is 6.813 Hz. The results indicate that if another pendulum link is added to this system, shown in Fig. 7, then the natural frequency of the selected pendulum decreases as the number of pendulums increases. For example, the natural frequency for the second pendulum in triple- and quadruple-pendulum systems is 5.694 Hz and 5.0227 Hz. This is generalized to a N-pendulum system, where the natural frequency of the selected kth pendulum decreases as more pendulums are added to the system.

Fig. 6

Adding pendulums above

Fig. 7

Adding pendulums below

Interestingly, when the pendulums are added “above” the selected pendulum, as shown in 6, then the frequency of the selected pendulums increases with an increase in the number of pendulum links added. The frequency of the bottom pendulum of the double-pendulum system is 6.813 Hz. If 3 pendulums are added above the bottom pendulum, resulting in a quintuple-pendulum system, then the natural frequency increases to 11.83 Hz as shown in Fig. 8. In Fig. 9 for a 5-pendulum system, adding 20 additional pendulums to the bottom-most pendulum converts the system to a 25-pendulum system where the “selected” pendulum to which the pendulums were added becomes the 5th pendulum with a reduced frequency compared to its initial frequency as a part of a 5-pendulum system. Here, the natural frequency of the 5th pendulum in the system starts off at 11.827 Hz for the 5-pendulum system and ends with 5.080 Hz for a 25-pendulum system.

Fig. 8

Increase in the angular frequency of the bottom pendulum as number of pendulums increases

Fig. 9

For an N-pendulum system where $n=5$, adding 20 pendulums below the bottom pendulum increasing 1 pendulum per iteration

The natural frequency of a pendulum is proportional to the square root of its effective length, which considers the length of the pendulum and the distance between the pivot point and the center of mass of the pendulum. By adding additional links to the pendulum, both the length and mass of the pendulum system increase, resulting in a decrease in the natural frequency of the system. This effect can be seen in simple pendulum clocks, which have a pendulum with a long length and a low natural frequency. By contrast, a shorter pendulum has a higher natural frequency, which makes it more suitable for use in high-precision clocks. Overall, the addition of more links below the pendulum bob will result in a longer pendulum with a lower natural frequency. But adding more links above the bob of a pendulum will decrease its effective length, which will result in an increase in the natural frequency of the pendulum. When more links are added above the bob, the distance between the pivot point and the center of mass of the pendulum decreases, which effectively shortens the length of the pendulum and increases its natural frequency. This effect can be seen in some types of clock pendulums, which have an adjustable screw near the top of the pendulum that can be used to adjust its length and natural frequency. Overall, the addition of more links above the pendulum bob will result in a shorter effective length and a higher natural frequency.

6.1.2 Mass of the system

To study the effect of mass of the cart or the pendulums in the system on the frequency, we modify each of the masses individually while keeping the rest constant. The case where the masses are changed while keeping the ratio between them constant is also studied. It is observed that the ratio between the masses in the system along with the relative position (top, middle, bottom) of these masses with each other contributes to the change in the frequency of the system. For a double-pendulum system (where all masses are equal to 1 kg and lengths are 1 m), the angular frequencies of the top and bottom pendulum are 3.527 and 6.813, respectively. If the mass of the cart is M and the mass of each of the pendulums is m, then from Fig. 10 the angular frequencies of the pendulums remain constant even when the masses of the cart or the pendulums are changed, as long as the mass ratio $\frac{M}{m}$ remains constant. The angular frequency of a simple pendulum is given by the formula $\omega = \sqrt{}$g/L where $\omega$ is the angular frequency, g is the acceleration due to gravity, and L is the length of the pendulum. When the pendulum is attached to a cart with mass M, the angular frequency of the pendulum-cart system is modified to the form $\omega = \sqrt{}[(\textrm{m}+\textrm{M})\textrm{g}/(\textrm{M}+\textrm{m})\textrm{L}]$ Since the mass ratio M/m appears in the denominator of the expression, as long as the mass ratio remains constant, the angular frequency of the system will also remain constant, regardless of the specific values of M and m.

The angular frequencies of the double-pendulum system under translation remain to be 3.527 and 6.813 for the top and bottom pendulums, respectively, when the mass of the cart and the mass of the pendulums are 10 kg. $\left( \frac{M}{m}=1\right)$. This is also true for a general “N”-pendulum system and can be seen in Fig. 11 which is the plot for a 13-pendulum system. Here, some of the frequencies of the top pendulum is 1.605 Hz, 5th pendulum is 6.999 Hz, 10th pendulum is 14.447 Hz and the bottom pendulum is 20.426 Hz and remains to be same when the mass ratio remains constant.

Fig. 10

Angular frequencies of double-pendulum system having constant mass ratios

Fig. 11

Angular frequencies for a 13-pendulum system with constant mass ratio

Now, the effect of varying the mass of the cart is studied and presented. The initial setup assumes that the mass of the cart is equal to the mass of the pendulums. This setup for a double-pendulum system under translation gives the angular frequencies of 3.527 and 6.813 of the top and bottom pendulums as discussed previously. The results show that as the mass of the cart increases, while keeping the mass of the pendulums constant, the angular frequencies of the pendulums decrease. This reduction is quite rapid for the initial increase in the mass of the cart but becomes gradual as the mass increases. Similarly, for an N-pendulum system, the n angular frequencies, all decrease for an increase in the mass of the cart.

Fig. 12

Angular frequencies of double-pendulum system under translation for an increase in the mass of cart

Fig. 13

Angular frequencies of a 10-pendulum system under translation for an increase in the mass of cart

A very interesting finding is that as the mass of cart increases, the frequencies of the system are more similar to that of a pendulum system without the translation. In the case of the double-pendulum given in Fig. 12, the initial frequencies of the top and bottom pendulums are 3.527 Hz and 6.813 Hz, respectively. However, when the mass of the cart is increased to 20 kg, the frequencies decrease to 2.40 Hz and 5.78 Hz for the top and bottom pendulums, respectively. This frequency is the same as the frequency of the double pendulum that has a fixed pivot. This phenomenon also holds true for N-pendulum systems. In Fig. 13, the change in angular frequencies of a 10-pendulum system decreases with an increase in the mass of the cart. However, this change is significantly smaller than that in the double-pendulum system. The angular frequency of the top and the bottom pendulum decreases from 1.8115 to 1.331 Hz and 17.629 to 17.1471 Hz This is because as the mass of the cart increases, the effect of the pendulums on the cart becomes increasingly negligible as the resistance to movement increases.

The top pendulum is the pendulum attached directly to the cart of the system. The results show that for an increase in the mass of the top pendulum, $m_1$, the natural frequency of the nth pendulum ($\omega _n$) has a slight initial dip after which the frequency increases rapidly. But the natural frequency of top pendulum itself ($\omega _1$) gradually decreases. The frequencies of the pendulums between the top pendulum attached to cart and the bottom pendulum ($\omega _{2},\omega _{3}\cdots \omega _{n-1}$) either increase or decrease very slightly for the initial increase in mass $m_1$ and then remain fairly constant for further increase in $m_1$.

Fig. 14

Angular frequencies for increase in the mass of top pendulum

But as the number of pendulums increases, the initial dip spreads over an increased range of mass $m_1$. Additionally, when $n\ge 7$, the dip in the of the bottom pendulum seems to be “passed on” to the next $n-1$th pendulum, i.e., the dip starts with decreasing the angular frequency of the nth pendulum for a certain range of $m_1$ after which it stagnates until the upward curve of the dip comes back from the $n-1$th pendulum, while the $n-1$th pendulum continues the dip. As n increases, the dip gets “passed on” to and also increases. In Fig. 14, the angular frequencies of a triple-pendulum system are plotted against the mass of the top pendulum. The angular frequency of the bottom pendulum represented by the yellow curve has the “initial dip” explained previously specifically when the mass of the top pendulum is around 2 units, after which the frequency of the bottom pendulum increases steadily. The frequencies of the top and middle pendulums, however, show little deviation as the mass of the top pendulum increases.

Fig. 15

Angular frequencies of a 9-pendulum system under translation for an increase in the mass of top pendulum $m_1$

Fig. 16

Angular frequencies of a 20-pendulum system under translation for an increase in the mass of top pendulum $m_1$

In Fig. 15, the bottom pendulum angular frequency, shown in red, decreases initially, after which the 8th pendulum represented by the blue line shows the curve of the dip which then continues back to the bottom pendulum after a certain mass. This can also be observed in Fig. 16, the 20 pendulum system, where the initial dip in the frequency is seen affecting all pendulums whose $n\ge 14$.

All the pendulums that are not top and bottom pendulums are considered middle pendulums. Increasing the mass of kth pendulum results in an initial dip similar to the one observed during the increase in mass of top pendulum which upon further increase in mass of kth pendulum increases the angular frequency of all pendulums from $n-k$th pendulum to nth pendulum.

Fig. 17

Angular frequencies of a 5-pendulum system under translation for an increase in the mass $m_5$

Fig. 18

Angular frequencies of a 5-pendulum system under translation for an increase in the mass $m_4$

In Fig. 17, the angular frequency of the last 2 pendulums in the system increases for an increase in the mass $m_2$. And for the same system, when the mass $m_4$ is increased as in Fig. 18, we see an increase in angular frequency of the last 4 pendulums (all pendulums except for the top pendulum in this system). Congruent with the effect of the increase in mass of the middle pendulums, where an increase in the mass of kth pendulum increases the frequency of the bottom-most k pendulums, an increase in the mass of the bottom pendulum causes an increase in the frequency of all the pendulums in the system. This increase in the angular frequency is highest for the bottom pendulum and lowest for the top pendulum, with the rate of change increasing as k increases.

Fig. 19

Angular frequencies of a 6-pendulum system under translation for an increase in the mass of bottom pendulum $m_6$

In Fig. 19, the increase in the mass of the bottom pendulum $k=6$ in a 6-pendulum system shows an increase in the angular frequency of all the pendulums involved. The increase in the angular frequency is highest for the 6th pendulum and lowest for the top pendulum. Now, let us compare the results discussed above with a standard non-translating pendulum system. The immediate difference observed between the pendulum system under translation and the pendulum system without translation is the addition of the cart. The addition of the cart of mass causes a direct increase in the angular frequencies of the system. The angular frequency of the double-pendulum system with a fixed pivot is 2.40 and 5.78, and this increases to 3.527 and 6.81 for the top and bottom pendulums, respectively, with the addition of the translating element (Fig. 20).

Fig. 20

Angular frequencies of a triple-pendulum system under translation for an increase in the mass of top pendulum $m_1$

Fig. 21

Angular frequencies of a triple-pendulum system without translation for an increase in the mass of top pendulum $m_1$

Fig. 22

Angular frequencies of a triple-pendulum system under translation for an increase in the mass of pendulum $m_2$

Fig. 23

Angular frequencies of a triple-pendulum system without translation for an increase in the mass of pendulum $m_2$

Fig. 24

Angular frequencies of a triple-pendulum system under translation for an increase in the mass of pendulum $m_3$

Fig. 25

Angular frequencies of a triple-pendulum system without translation for an increase in the mass of pendulum $m_3$

As discussed in the previous sections, an increase in the mass of the top pendulum in a translating pendulum system increases the frequency of the nth pendulum with a slight decrease in the frequency of the top pendulum. When the mass of the top pendulum is increased for a fixed pivot pendulum system, we see the exact opposite phenomenon, where the angular frequencies of the bottom decrease rapidly, while the bottom pendulum frequency increases gradually. The effect of increasing the mass of the top pendulum on the frequency of the nth pendulum is not a simple or predictable relationship and depends on the distribution of the mass in the top pendulum and the geometry of the system. In a translating pendulum system, where a series of pendulums are connected by links and are free to move in a horizontal plane, the frequency of each pendulum depends on the length of its link and the effective gravitational acceleration felt by the mass. When the top pendulum is given a small horizontal displacement, it sets the system into motion, and each pendulum begins to swing back and forth with a certain frequency. If the mass of the top pendulum is increased while keeping the length of its string constant, the frequency of the top pendulum will decrease slightly, as the effective gravitational acceleration decreases due to the increased mass. However, the effect on the frequency of the nth pendulum depends on how the mass of the top pendulum is distributed. If the mass is concentrated at the bottom of the pendulum, the effective length of the link connecting the nth pendulum to the top pendulum will decrease slightly, which will increase the frequency of the nth pendulum. On the other hand, if the mass is distributed more evenly along the length of the pendulum, the effective length of the string may not change significantly, and the frequency of the nth pendulum may not be affected much. Figures 21 and 24 represent the same, where angular frequency of the bottom pendulum (in yellow) decreases for non-translating system and increases for the translating system for the same increase in mass $m_1$. This implies that at higher values of mass of top pendulum, adding a translating element to the fixed pivot pendulum system can increase the frequency of the bottom pendulum drastically. In Figs. 22 and 23, we see that an increase in the mass of the middle pendulum, in both translating and fixed pendulum systems, results in a similar increase in the angular frequency of the bottom pendulum. But the frequency of the middle pendulum itself decreases with an increase in its mass for a fixed pendulum system, and it increases in the pendulum system with translating element. Similarly, an increase in the mass of the bottom pendulum causes an increase in the angular frequency of all pendulums with the exception of the top pendulum for the fixed pendulum system, where the frequency decreases gradually. In general, increasing the mass of the bottom pendulum in a multi-pendulum system can affect the behavior of the other pendulums. Specifically, if the system is designed so that the pendulums are coupled (i.e., connected by rigid or flexible links), then an increase in the mass of one pendulum can lead to changes in the motion and frequency of the other pendulums. For example, if the multi-pendulum system is designed so that the pendulums are connected by flexible strings or rods, then an increase in the mass of the bottom pendulum can cause changes in the tension and deformation of the strings or rods, which can affect the motion of the other pendulums. In this case, the effect on the angular frequency of the pendulums will depend on the specific geometry and stiffness of the links connecting the pendulums. However, if the multi-pendulum system is designed so that the pendulums are completely independent (i.e., not connected by any links), then an increase in the mass of one pendulum should not affect the motion or frequency of the other pendulums, since each pendulum is free to move independently. Therefore, while the statement that increasing the mass of the bottom pendulum can increase the angular frequency of all pendulums in a multi-pendulum system may be true in some specific cases, it is not a universal truth and depends on the specific geometry and parameters of the system (Fig. 25).

6.1.3 Length of the pendulum links

An increase in the length of any of the pendulums in the system causes a decrease in the angular frequency of the system. The rate of decrease in angular frequency is highest for the bottom pendulum. The change in the frequency is studied for changing lengths of each pendulum individually with the position of change(top, middle, bottom) also taken into consideration.

Fig. 26

Angular frequencies of a double-pendulum system under translation for increase in the length of top pendulum $l_1$

Fig. 27

Angular frequencies of a 12-pendulum system without translation for an increase in the mass of top pendulum $l_1$

When the length $l_1$ of the top pendulum in the translating pendulum system increases from 0.1m to 3 m, the frequencies of the system decrease from 3.8113 to 2.7746 Hz for the top pendulum and from 19.937 to 5.00 Hz. The rate of reduction is highest for the bottom pendulum. A unique observation is that the decrease in the angular frequency of the bottom pendulum seems to slow down right as it approaches the value of the angular frequency of the penultimate pendulum $(n-1)$.

Figure 26 shows the decrease in the angular frequencies of the pendulums in a double-pendulum system. The angular frequency of the bottom pendulum has a steep initial reduction that becomes gradual with a further increase in length $l_1$, creating the “L”-shaped curve. Similar behavior is shown in Fig. 27, a 12-pendulum system where angular frequencies decrease with the increasing length of the top pendulum.

The increase in the length of the middle pendulums in a translating pendulum system has a similar effect on the frequency of the pendulum when the length of the top pendulum is increased. This similarity has a divergence when the selected kth pendulum whose length is being increased has $k\ge \frac{n}{2}$ where n is the number of pendulums in the system. In this case, the rate of decrease in the angular frequency of the bottom pendulum does not slow down, rather gets “passed on” to the penultimate pendulum, after which the bottom pendulum either stagnates or shows a minimal decrease in its angular frequency. This phenomenon is where the rate of decrease in angular frequency getting passed on to the next pendulum increases as k approaches the number of pendulums n. When the length of the middle pendulum is increased, the position of the center of mass of the pendulum system is shifted upward, which can lead to changes in the motion and frequency of the other pendulums. In particular, an increase in the length of the middle pendulum will cause a decrease in the angular frequency of the bottom pendulum, as the gravitational potential energy of the system is increased. However, in a multi-pendulum system, the motion and frequency of each pendulum depends not only on its own properties but also on the motion and properties of the other pendulums in the system. When the angular frequency of the bottom pendulum decreases, this decrease can be transmitted to the penultimate pendulum through the links connecting them. This transfer of frequency from the bottom pendulum to the penultimate pendulum occurs because the energy of the system is conserved, and any decrease in the kinetic energy of the bottom pendulum must be compensated by an increase in the kinetic energy of the penultimate pendulum. As a result, after the penultimate pendulum receives the frequency decrease from the bottom pendulum, the angular frequency of the bottom pendulum either stagnates or shows a minimal decrease. This is because the kinetic energy transferred to the penultimate pendulum is not sufficient to cause a further decrease in the frequency of the bottom pendulum.

In Fig. 28, the angular frequencies of an 8- pendulum system are shown. For an increase in length $l_3$ (where $k=4$), the graph is similar to 27 with an “L”-shaped curve with maximum reduction in the angular frequency of the bottom pendulum. But when $k\ge \frac{n}{2}$ as seen in 29 and 30 where $k=7$ and $k=8$, respectively, the decrease in angular frequency can be seen being “passed on” to the next penultimate pendulum.

Fig. 28

Angular frequencies of an 8-pendulum system under translation for an increase in the length of $l_3$, ($k=4$)

Fig. 29

Angular frequencies of a 8-pendulum system under translation for an increase in the length of $l_7$, ($k=7$)

Fig. 30

Angular frequencies of an 8-pendulum system under translation for an increase in the length of $l_8$, ($k=8$)

Fig. 31

Angular frequencies of a 5-pendulum system without translation for an increase in the length of $l_1$, ($k=1$)

Fig. 32

Angular frequencies of a 5-pendulum system under translation for an increase in the length of $l_1$, ($k=1$)

Fig. 33

Angular frequencies of a 5-pendulum system without translation for an increase in the length of $l_4$, ($k=4$)

Fig. 34

Angular frequencies of a 5-pendulum system under translation for an increase in the length of $l_4$, ($k=4$)

Figures 31, 32, 33 and 34 show that the effect of changing lengths of the pendulums in an N-pendulum system is similar with or without translation. Even though the plots of angular frequencies are similar, it should be noted that the actual magnitudes of the respective plots are different for systems under translation and with a fixed pivot. For the 5-pendulum system, with translation, the angular frequency of the bottom pendulum drops from 31.652 Hz when $l_1$ is 0.1 m to 10.5898 Hz when $l_1$ is 3 m. Without translation, the angular frequency drops from 23.088 Hz when $l_1$ is 0.1 m to 10.55 Hz when $l_1$ is 3 m. When $l_4$ is increased as shown in Fig. 33, the angular frequency of the bottom pendulum starts at 20.34 Hz when $l_4$ is 0.1m, becomes stagnant around $l_4 =0.65m$ with 11.2075 Hz and gradually decreases to 11.09 Hz when $l_4$ is 3 m.

6.2 Effect of pendulum parameters on the natural frequency of pendulum system with tilting pivot

The effect of varying parameters of pendulum systems on natural frequency is discussed in this section.

6.2.1 Number of pendulum links

When extra pendulum links are added to the bottom-most pendulum link, the angular frequency decreases as the number of pendulums increases. So as the number of pendulum links increases for a pendulum system undergoing tilting, the frequency of the system decreases. Conversely, when extra pendulums are added above the bottom-most pendulum in a N-pendulum system, the frequency of the pendulum increases with the increase in the number of pendulums. This behavior is very similar to that of an N-pendulum system undergoing translation as seen in section 6.1.1. Figure 36 shows the decreasing angular frequency of the bottom pendulum of a double-pendulum system against the number of pendulums being added “below” the pendulum. Similarly, Fig. 36 shows the same for pendulums being added “above” the selected pendulum.

Fig. 35

Angular frequencies of the bottom pendulum ($n=2$) of a double-pendulum system, adding 20 pendulums below the bottom pendulum increasing 1 pendulum per iteration

Fig. 36

Angular frequencies of the bottom pendulum in a double-pendulum system when adding 20 pendulums above the bottom pendulum increasing 1 pendulum per iteration

As shown in Fig. 35, the angular frequency of the bottom pendulum of a double-pendulum system with a tilting pivot is 6.27071 Hz and decreases to 1.82474 Hz when 20 pendulums are added below it.

6.2.2 Mass of the system

The effect of the mass of the pendulums on the natural frequency of a tilting pendulum system is studied by individually changing the mass of each pendulum and observing the changes to the frequencies in the system. The angular frequencies are observed to decrease for an increase in the mass of the top pendulum, increase for an increase in the mass of the bottom pendulum, and either increase or decrease for an increase in the mass of the middle pendulums. The top pendulum is directly attached to the tilting platform of the system. The results indicate that for an increase in the mass of the top pendulum $m_1$ in a N-pendulum system under tilt, the angular frequencies of all the pendulums except the top pendulum decreases, while the angular frequency of the top pendulum itself increases with the increase in mass $m_1$. The magnitude of change in angular frequency is high for the bottom pendulum and low for the top pendulum in the system.

Figure 37 shows the angular frequencies of a triple-pendulum system for an increase in mass of top pendulum $m_1$. The angular frequencies of the bottom pendulum and middle pendulum (shown in yellow and red, respectively) decrease with an increase in mass $m_1$. The angular frequency of the bottom pendulum and middle pendulum decreases from 8.4508 and 4.9738 Hz when $m_1$ is 1 kg to 6.4165 Hz and 3.6505 Hz, respectively, when $m_1$ is 10 kg. At the same time, the angular frequency of the top pendulum (shown in blue) increases gradually with an increase in mass $m_1$.

Fig. 37

Angular frequencies of a triple-pendulum system for increase in mass of top pendulum $m_1$

The results show that for an increase in mass of kth pendulum in a N-pendulum system, where $k\ne 1$ and $k\ne n$, the angular frequencies of the bottom-most $k-1$ pendulums ($(n-(k-2))$ to n pendulums) increases along with the increase in the angular frequency of the top pendulum, whereas the angular frequencies of the remaining pendulums decrease. An exception to this phenomenon is when $k=n-1$ for $n>4$, in which case the frequency of the top pendulum decreases.

Fig. 38

Angular frequencies of a 5-pendulum system for an increase in mass $m_2$, ($k=2$)

Fig. 39

Angular frequencies of a 5-pendulum system for an increase in mass $m_4$, ($k=4$)

In the 5-pendulum system depicted in Figure 38, when the mass of a selected pendulum ($k=2$) is increased, it results in an increase in the angular frequency of only the bottom-most pendulum ($n-(k-2)=n$). Simultaneously, the frequency of the top pendulum also increases. Similarly, for the same system when the mass (m4) of the fourth pendulum ($k=4$) is increased, the angular frequency of the three pendulums below it ($k-1=3$) increases, as illustrated in Figure 39.

Increasing the mass of the bottom pendulum in a N-pendulum system under tilt increases the angular frequency of all pendulums except the angular frequency of the top pendulum which decreases with an increase in mass $m_n$

Fig. 40

Angular frequencies of a triple-pendulum system for an increase in mass of bottom pendulum $m_n$

Fig. 41

Angular frequencies of a 7-pendulum system for an increase in mass $m_7$

Fig. 42

Angular frequencies of a triple-pendulum system for increase in length of top pendulum $l_1$

In Figs. 40 and 41, the angular frequencies of all the pendulums except the top pendulum are seen increasing for an increase in mass of the bottom pendulum. The angular frequency of the bottom and middle pendulums in a triple-pendulum system in 40 increases from 8.4508 to 18.3069 Hz and 4.9738 to 10.6767 Hz, respectively, and the angular frequency of the top pendulum, on the other hand, decreases from 2.033 to 1.8473 Hz. It also shows that the magnitude of the increase is highest for the bottom pendulum.

6.2.3 Length of the pendulum links

The effect of the lengths of the pendulums on the frequency of a tilting pendulum system is studied by individually changing the length of each pendulum link. The change in frequency is similar to that in translating and fixed pivot systems with similar decrease and increase in the frequencies. The change and the values of the frequencies themselves are not equal, though similar.

When the length $l_1$ of the top pendulum in the tilting pendulum system increases, the frequencies of the system decrease. Figure 42 shows the angular frequency of a triple-pendulum system against the length of the top pendulum $l_1$, and the frequency of the bottom pendulum (in yellow) has the highest magnitude of decrease in angular frequency. Middle and top pendulums (in red and blue, respectively) show gradual decrease in the frequency for increasing length of the top pendulum. The angular frequency of the bottom pendulum is 23.1957 Hz when $l_1$ is 0.1m and decreases to 7.6285 Hz when $l_1$ increases to 3 m. The angular frequencies of the middle and the top pendulum decrease gradually from 6.1211 and 2.3774 Hz to 4.1238 and 1.5355 Hz, respectively.

The increase in the length of these pendulums causes a decrease in the angular frequency of all pendulums in the system with the rate of decrease being “passed on” when the selected pendulum k has $k\ge \frac{n}{2}$.

Fig. 43

Angular frequencies of a triple-pendulum system for an increase in length of middle pendulum $l_2$

Fig. 44

Angular frequencies of a triple-pendulum system for an increase in length of bottom pendulum $l_3$

Fig. 45

Angular frequencies of a 9-pendulum system for an increase in length of pendulum $l_7$

Figures 43 and 44 show the angular frequencies of a triple-pendulum system for an increase in the length of the middle pendulum and bottom pendulum, respectively. It is observed that the middle pendulum’s frequency (shown in red) starts off with a slightly higher frequency in 44 and has a higher deviation when compared with 43. In Fig. 45, we observe the rate of decrease in the frequency being “passed on” to the next penultimate pendulum for an increase in length of 7th pendulum.

6.2.4 Effect of stiffness

As described in Sect. 4.2, potential energy associated with the bending of the rod is $P.E_{b}= \frac{1}{2}k_{r}\theta ^2$, where $k_r$ is the equivalent spiral spring stiffness of the rod. This change in potential energy directly affects the angular frequency of the system. The effect of changing stiffness of the pendulums on the frequency of a tilting pendulum system is studied by individually changing the stiffness of each pendulums. When the stiffness of the top pendulum $k_{r_1}$ is increased in a tilting pendulum system, the angular frequency of all the pendulums in the system increases.

An interesting observation is that the rate of increase in the angular frequency decreases as the number of pendulums is increased, for the same increase in stiffness. In Fig. 46, the increase in the angular frequency for a triple-pendulum system is more drastic when compared to the increase in angular frequency in a 5-pendulum system under tilt in Fig. 47 for the same increase in stiffness of top pendulum. The angular frequencies for the top, middle and bottom pendulums in the triple-pendulum system when the stiffness $k_r=1$ are 2.033 Hz, 4.9738 Hz and 8.4508 Hz and increase to 2.1134 Hz, 5.1196 Hz and 8.8198 Hz, respectively. This observation is plausible and can be explained by considering the dynamics of the multi-pendulum system. When a force is applied to the top pendulum of a multi-pendulum system, the resulting motion of the pendulums is influenced by the stiffness and mass of each pendulum, as well as the coupling between the pendulums. For a given increase in stiffness of the top pendulum, the resulting increase in the angular frequency of the multi-pendulum system will depend on the number of pendulums in the system. Specifically, as the number of pendulums increases, the coupling between the pendulums becomes more complex, and the dynamics of the system become more sensitive to changes in the parameters. In particular, as the number of pendulums increases, the effective stiffness of the system decreases, which means that the rate of increase in the angular frequency of the system will also decrease. This can explain why the increase in the angular frequency of a triple-pendulum system is more drastic than the increase in the angular frequency of a 5-pendulum system under tilt, for the same increase in stiffness of the top pendulum. In a triple-pendulum system, the coupling between the pendulums is relatively simple, which means that the effective stiffness of the system is higher, leading to a more drastic increase in the angular frequency for a given increase in stiffness. On the other hand, in a 5-pendulum system, the coupling between the pendulums is more complex, which means that the effective stiffness of the system is lower, leading to a less drastic increase in the angular frequency for the same increase in stiffness of the top pendulum.

Fig. 46

Angular frequencies of a triple-pendulum system for an increase in stiffness of top pendulum $k_{r_1}$

Fig. 47

Angular frequencies of a 5-pendulum system for an increase in stiffness of top pendulum $k_{r_1}$

When the stiffness of any of the pendulums is increased, the angular frequencies of the system increase. The results shows a slight increase in angular frequencies when the considered pendulum for which the stiffness is increased has k closer to n, where k is the selected pendulum and n is the number of pendulums in the system. For a 5-pendulum system, as shown in Figs. 48 and 49, the angular frequency increases with increase in stiffness of the middle pendulums. The magnitude of angular frequencies is slightly higher for 49 than 48 since ($k=4$) is closer to n. For the stiffness of the bottom pendulum, Fig. 50 shows the increase in the angular frequencies for an increase in the stiffness of the bottom pendulum.

Fig. 48

Angular frequencies of a 5-pendulum system for an increase in stiffness of second pendulum $k_{r_2}$

Fig. 49

Angular frequencies of a 5-pendulum system for an increase in stiffness of fourth pendulum $k_{r_4}$

Fig. 50

Angular frequencies of a 5-pendulum system for an increase in stiffness of bottom pendulum $k_{r_5}$

6.3 Summary of contributions

The present research offers substantial contributions that differentiate it from previous studies. While prior investigations extensively covered pendulum systems with stationary pivots, this study concentrates specifically on the dynamics of pendulum systems with moving and tilting pivots. By examining the behavior of these systems during translation and tilt, the research introduces additional degrees of freedom and nonlinearities compared to systems with fixed pivots. Consequently, this inquiry yields novel insights into the dynamics of pendulum systems under various types of motion. A significant focus of this research lies in the practical implementation of multiple pendulum systems as inertial sensing elements in high-precision equipment. By investigating the dynamics of these systems and their implications for high-precision instrumentation, the study addresses a pragmatic aspect that holds relevance for researchers and engineers in the field. This emphasis on the real-world application of pendulum systems enhances the value and significance of the research. To deepen our comprehension of the dynamics of pendulum systems, this research undertakes a comprehensive parametric analysis. The study systematically varies parameters such as mass, length, and stiffness of the pendulums within the system. This analysis includes detailed plots and explanations to visually illustrate the impact of the above mentioned parameters on the natural frequency of the pendulum systems. The plots provide a clear visualization of how variations in parameters affect the behavior of the pendulums, allowing for a comprehensive understanding of the frequency changes. This meticulous exploration of the parametric space enhances our understanding of the relationships between system parameters and dynamics, thereby offering valuable insights for system design and optimization. Furthermore, this research compares the dynamics of pendulum systems with moving and tilting pivots to those with fixed pivots. By highlighting the similarities and differences between these system types, the study contributes to a deeper comprehension of the effects of translation and tilt on the behavior of multiple pendulum systems. This comparative analysis serves as a foundation for further exploration and development of control strategies tailored specifically for pendulum systems with moving and tilting pivots. In conclusion, the present research provides several noteworthy contributions to the existing literature. Its focus on pendulum systems with moving and tilting pivots yields new insights into the dynamics of such systems when compared to systems with fixed pivots. Additionally, by emphasizing the practical implementation of pendulum systems in high-precision instrumentation, the study addresses a relevant aspect for researchers and engineers in the field. The detailed parametric analysis enhances our understanding of the relationships between system parameters and dynamics, while the comparison with fixed pivot systems contributes to a deeper comprehension of the effects of translation and tilt.

7 Conclusion

This paper studies the dynamics of multiple pendulum systems that have a pivot under translation or tilt. The system for translation is considered by attaching the pivot to a movable cart. Similarly, the system for tilting is considered by connecting the pivot to a rotatable platform.

By applying the Lagrangian dynamics approach, we derived the equations of motion and the angular frequencies of the systems. Furthermore, the second derivatives of the kinetic and potential energies are used to obtain the mass matrix and the stiffness matrix, which are then used to get the angular frequency of each pendulum in the system. The equations of motion and the angular frequency of the double-pendulum system are derived first and then extended to an “n”-pendulum system. Our analysis focused on the effects of translation and tilt on the behavior of the pendulums, as well as the influences of parameters such as mass, length, and stiffness on the natural frequencies of the systems. The initial/ideal system is considered with masses of pendulums as 1 kg, lengths as 1 m and gravitational acceleration as $9.81\frac{m}{s^2}$. Additionally, for the translating system, the mass of the cart is 1 kg and the stiffness of all the pendulums in the tilting pendulum is $1Nm^{-1}$. To study the dynamics of the systems and how each parameter affects the system, the initial system is analyzed by varying a single parameter while keeping the rest constant.

From the results, it is inferred that translating or tilting a multiple pendulum system increases the angular frequency of the pendulums involved. Moreover, adding pendulums below a selected pendulum decreases the angular frequency of the pendulum, and adding pendulums above a selected pendulum increases the angular frequency of that particular pendulum. This behavior is consistent for both translating and tilting systems. The effect of mass on the natural frequency of the systems, however, is quite different for both systems. Depending on the pendulum whose mass is being varied, the behaviors of the system also change. For the translating pendulum system, when the mass of the top pendulum increases, the frequency of the bottom pendulum increases rapidly after a slight dip, while the frequency of the top pendulum itself gradually decreases. For changes in the mass of middle pendulums, we see an increase in the frequency of several pendulums depending on which pendulums mass is being varied. The increase in the mass of the bottom pendulum increases the frequency of all the pendulums in the system. Additionally, as the mass of the cart increases, the behavior of the system is more similar to that of a fixed pivot system. For tilting multiple pendulum systems, the increase in mass of the top pendulum results in a decrease in the angular frequency of all pendulums except the top pendulum itself. This behavior is completely opposite to the translating pendulum system, where the frequency of all the pendulums except the top pendulum increases. The increase in mass of the middle and bottom pendulums, however, results in an increase in the angular frequencies similar to the translating pendulum system. An increase in the lengths of the pendulums in either of the systems, translating or tilting, decreases the angular frequencies of the pendulums in the system. Moreover, when the stiffness of the pendulums is increased in the tilting pendulum system, the angular frequencies of the pendulums increase.

While our study provides valuable insights into the dynamics of multiple pendulum systems with moving and tilting pivots, there are several potential avenues for future research. Investigating the impact of damping on the system dynamics would be valuable, as damping is an important factor in real-world applications. Additionally, studying the stability of the pendulum systems under different motion conditions and exploring control strategies for stabilization would contribute to practical implementation. For translating/tilting pivots, control techniques such as model predictive control, adaptive control, and sliding mode control have been developed to stabilize the motion and achieve desired trajectories. However, control of translating/tilting pendulums is more challenging due to the increased complexity and nonlinearity of the system. Furthermore, extending the analysis to consider more complex pendulum arrangements and exploring the effects of nonlinearities in the system would provide a deeper understanding of the dynamics. Finally, examining the influence of external forces or disturbances on the system behavior could uncover important insights relevant to real-world scenarios.