1 Introduction

It is well known that many physical problems may occur in two or more places which are linked to each other, which can be called multi-place problem. To describe two-place problems, Alice–Bob systems (ABs) [1] are proposed. That is, if \(A(x,t)\) is Alice’s state and \(B(x',t')\) is Bob’s state, there is a suitable operator f̂ which can linked to the two states at the same time,

$$ B\bigl(x',t'\bigr)= \hat{f}A(x,t)=A^{\hat{f}}, \qquad A(x,t)=\hat{f}^{-1}B \bigl(x',t'\bigr)=B^{\hat{f}^{-1}}. $$
(1)

The equivalence assumption requires that the operator f̂ satisfies \(\hat{f}^{2}=1\). Usually, \((x',t')\) is far from \((x,t)\). Hence, the two-place systems or Alice–Bob systems (ABs) are nonlocal. When the operator f̂ is taken as a special case, many kinds of nonlocal integrable systems can be obtained. For example, this nonlocal nonlinear Schrödinger (NLS) equation is proposed by Ablowitz and Musslimani [2]:

$$ \begin{aligned} & iA_{t}+A_{xx} \pm A^{2}B=0, \\ &B=\hat{f}A=\hat{P}\hat{C}A=A^{*}(-x,t), \end{aligned} $$
(2)

with \(\hat{f}=\hat{P}\hat{C}\), where P̂ and Ĉ are the parity and charge conjugation operators, respectively, ∗ is for the complex conjugate. Recently, the nonlocal NLS equation was derived in a physical application of magnetics [3]. Excited by the pioneering work, the nonlocal integrable systems have attracted considerable attention in recent years. At present, the nonlocal KdV equation [4, 5], the nonlocal mKdV equation [6–8], the nonlocal discrete NLS equation [9], the nonlocal KP equation [10, 11], the nonlocal DS equation [12–14], and so on [15–17] have been studied.

Solitons represent robust nonlinear coherent structures and have been theoretically studied and observed in experiments in physical, chemical and biological science [18–20]. At present, many methods [21–40] have been developed to search for solitons of nonlinear evolution equations. Among them, the function expansion method [21–25], the bilinear method [33, 34], Darboux transformation [35, 36], the symmetry reduction method [37, 38] and the Riemann–Hilbert approach [39, 40] are very effective and widely used methods. For example, in [22], soliton solutions for a type of mKdV equation with a first local-derivative term are obtained based on the Riccati–Bernoulli sub-ordinary differential equation and a modified tanh–coth method. New solitary solutions for the Zakharov–Kuznetsov equation are worked out by a generalized exponential rational function method in [23]. The dark, bright, dark–bright, dark–singular and singular soliton of the NLS equation with quadratic–cubic nonlinearity are derived by adopting the sine-Gordon expansion method in [24]. The exact traveling wave solutions for the fractional equations and the heat transfer equations are worked out in Refs. [41–48].

With the advent of the nonlocal systems, the methods mentioned above have been developed to construct the soliton solutions of the nonlocal systems [49–57]. Meanwhile, there is few work about the soliton solutions of the nonlocal four-place systems. In this paper, new nonlocal two-place DNLS (TDNLS) and four-place DNLS (FDNLS) systems are derived based on the coupled Chen–Lee–Liu (CLL) system and the \(\hat{P}\hat{T}\hat{C}\)-symmetry group. A linear Lax pair is given which guarantees the integrability of the nonlocal TDNLS system and FDNLS system. In order to construct the group-invariant soliton solutions, we first rewrite the solutions of the DNLS equation [58] in the form expressed by hyperbolic and triangular functions. Then the \(\hat{P}\hat{T}\hat{C}\)-symmetry invariant one-soliton solution and periodic two-soliton solution of a new TDNLS system are obtained. Further, we also work out the group-invariant two-soliton solution of a FDNLS system. There is some interesting dynamics appearing in the TDNLS system and FDNLS system, different from the dynamics of the local DNLS equation.

The paper is organized as follows. In Sect. 2, we construct the coupled CLL system and its Lax pair is given. Some new nonlocal TDNLS system and FDNLS system arise from the group symmetry reductions of the coupled CLL system. In Sect. 3, the expressions of group-invariant soliton solutions for the nonlocal DNLS system are presented and the multi-soliton solutions of the TDNLS system and the FDNLS system are worked out. A conclusion is given in the last section.

2 Nonlocal multi-place derivative NLS system

The derivative NLS (DNLS) equation

$$ iq_{t}+q_{xx}+2iqq^{*}q_{x}=0 $$
(3)

can be reduced from the Chen–Lee–Liu (CLL) system [59]

$$ \begin{aligned} &q_{t}=q_{xx}+2qrq_{x}, \\ &r_{t}=-r_{xx}+2qrr_{x}, \end{aligned} $$
(4)

by setting \(r=q^{*}\) and replacing t by it and x by \(-ix\). From the coupled system (4), some different kinds of nonlocal integrable DNLS equations can be obtained by using the \(\hat{P} \hat{T}\hat{C}\)-symmetry reductions. In the following, we first find some kinds of integrable coupled CLL systems. Here is the first non-trivial coupled CLL system

$$ \begin{aligned} &q_{t}=q_{xx}+2(p+q)^{2}(r+s) (pr-qs)+2q(r+s) (p_{x}+q_{x})+2\bigl[(p+q) (qs-pr) \bigr]_{x}, \\ &p_{t}=p_{xx}-2(p+q)^{2}(r+s) (pr-qs)+2p(r+s) (p_{x}+q_{x})+2\bigl[(p+q) (pr-qs) \bigr]_{x}, \\ &r_{t}=-r_{xx}+2(p+q) (r+s)^{2}(pr-qs)+2r(p+q) (r_{x}+s_{x})+2\bigl[(r+s) (pr-qs)\bigr]_{x}, \\ &s_{t}=-s_{xx}-2(p+q) (r+s)^{2}(pr-qs)+2s(p+q) (r_{x}+s_{x})+2\bigl[(r+s) (qs-pr)\bigr]_{x}. \end{aligned} $$
(5)

It is obvious that the coupled CLL system (5) can be reduced to the standard CLL system if we take \(p=q\) and \(r=s\). The integrability of the coupled CLL system (5) can be guaranteed by the following Lax pair:

$$ \begin{aligned} &\varPsi _{x}=M\varPsi , \\ &\varPsi _{t}=N\varPsi , \qquad \varPsi =(\psi _{1}, \psi _{2})^{T}, \end{aligned} $$
(6)

with

M=[−12(λ2−(p+q)(r+s))(q+q)λ00(r+s)λ12(λ2−(p+q)(r+s))000(p−q)λ−12(λ2−(p+q)(r+s))(q+q)λ(r−s)λ0(r+s)λ12(λ2−(p+q)(r+s))],N=[n11n1200n21−n1100n31n32n11n12n41−n31n21−n11],

where

$$\begin{aligned}& n_{11}=\alpha \lambda ^{4}+(p+q) (r+s)\lambda ^{2}-\frac{1}{2}(p+q)^{2}(r+s)^{2}- \frac{1}{2}(r+s) (p_{x}+q_{x})+ \frac{1}{2}(p+q) (r_{x}+s_{x}), \\& n_{12}=(p+q)\lambda ^{3}+\bigl[-(p+q)_{x}-(p+q)^{2}(r+s) \bigr]\lambda , \\& n_{21}=(r+s) \lambda ^{3}+\bigl[(r+s)_{x}-(p+q) (r+s)^{2}\bigr]\lambda , \\& n_{31}=\beta \lambda ^{4}+2(pr-qs)\lambda ^{2}+8(p+q) (r+s) (qs-pr)-2rp _{x}+2sq_{x}+2pr_{x}-2qs_{x}, \\& n_{41}=(r-s)\lambda ^{3}+\bigl[r_{x}-s_{x}-4(r+s) (pr-qs)-(p+q) (r+s) (r-s)\bigr] \lambda . \end{aligned}$$

The full \(\hat{P}\hat{T}\hat{C}\)-symmetry group Θ possesses the form [10]

$$ \varTheta =\{1,\hat{P},\hat{T}\hat{C},\hat{P}\hat{T}\hat{C}\}\cup \hat{C}\{1, \hat{P},\hat{T}\hat{C},\hat{P}\hat{T}\hat{C}\} = \varTheta _{1} \cup \varTheta _{1}^{C}. $$

Using the sub-symmetry group \(\varTheta _{1}\) and the symmetry coset \(\varTheta _{1}^{C}\), we obtain two kinds of symmetry reductions from the coupled CLL system (5)

$$ \begin{aligned} &q_{t}=q_{xx}+2 \bigl(q^{\hat{f_{k}}}+q\bigr)^{2}\bigl(r+r^{\hat{f_{k}}}\bigr) \bigl(q^{ \hat{f_{k}}}r-qr^{\hat{f_{k}}}\bigr)+2q\bigl(r+r^{\hat{f_{k}}} \bigr) \bigl(q^{\hat{f_{k}}}+q\bigr)_{x} \\ &\hphantom{q_{t}=}{}+2\bigl[\bigl(q ^{\hat{f_{k}}}+q\bigr) \bigl(qr^{\hat{f_{k}}}-q^{\hat{f_{k}}}r\bigr)\bigr]_{x}, \\ &r_{t}=-r_{xx}+2\bigl(q^{\hat{f_{k}}}+q\bigr) \bigl(r+r^{\hat{f_{k}}}\bigr)^{2}\bigl(q^{ \hat{f_{k}}}r-qr^{\hat{f_{k}}} \bigr)+2r\bigl(q^{\hat{f_{k}}}+q\bigr) \bigl(r+r^{ \hat{f_{k}}} \bigr)_{x} \\ &\hphantom{r_{t}=}{}+2\bigl[\bigl(r+r^{\hat{f_{k}}}\bigr) \bigl(q^{\hat{f_{k}}}r-qr^{ \hat{f_{k}}}\bigr)\bigr]_{x}, \\ &\hat{f_{k}}\in \varTheta _{1}=\{1,\hat{P},\hat{T} \hat{C},\hat{P}\hat{T} \hat{C}\}, \qquad (p,s)=\hat{f_{k}}(q,r), \end{aligned} $$
(7)

and

$$ \begin{aligned} &q_{t}=q_{xx}+2(p+q)^{2} \bigl(q^{\hat{g_{j}}}+p^{\hat{g_{j}}}\bigr) \bigl(pq^{ \hat{g_{j}}}-qp^{\hat{g_{j}}} \bigr)+2q\bigl(q^{\hat{g_{j}}}+p^{\hat{g_{j}}}\bigr) (p _{x}+q_{x}) \\ &\hphantom{q_{t}=}{}+2\bigl[(p+q) \bigl(qp^{\hat{g_{j}}}-pq^{\hat{g_{j}}} \bigr)\bigr]_{x}, \\ &p_{t}=p_{xx}-2(p+q)^{2} \bigl(q^{\hat{g_{j}}}+p^{\hat{g_{j}}}\bigr) \bigl(pq^{ \hat{g_{j}}}-qp^{\hat{g_{j}}} \bigr)+2p\bigl(q^{\hat{g_{j}}}+p^{\hat{g_{j}}}\bigr) (p _{x}+q_{x}) \\ &\hphantom{p_{t}=}{}+2\bigl[(p+q) \bigl(pq^{\hat{g_{j}}}-qp^{\hat{g_{j}}} \bigr)\bigr]_{x}, \\ &\hat{g_{j}}\in \varTheta _{1}^{C}=\{ \hat{C},\hat{T},\hat{C}\hat{P}, \hat{P}\hat{T}\}, \qquad (r,s)= \hat{g_{j}}(q,p), \end{aligned} $$
(8)

respectively. Furthermore, based on the systems (7) and (8), we can work out 16 different types of DNLS systems

$$ \begin{aligned} &q_{t}=q_{xx}+2 \bigl(q^{\hat{f_{k}}}+q\bigr)^{2}\bigl(q^{\hat{g_{j}}}+q^{\hat{f_{k}} \hat{g_{j}}} \bigr) \bigl(q^{\hat{f_{k}}}q^{\hat{g_{j}}}-qq^{\hat{f_{k}} \hat{g_{j}}}\bigr) \\ &\hphantom{q_{t}=}{}+2q\bigl(q^{\hat{g_{j}}}+q^{\hat{f_{k}}\hat{g_{j}}}\bigr) \bigl(q^{ \hat{f_{k}}}+q\bigr)_{x}+2\bigl[\bigl(q^{\hat{f_{k}}}+q \bigr) \bigl(qq^{\hat{f_{k}}\hat{g_{j}}}-q ^{\hat{f_{k}}}q^{\hat{g_{j}}}\bigr) \bigr]_{x}, \\ &(p,r,s)=\bigl(q^{\hat{f_{k}}},q^{\hat{g_{j}}},q^{\hat{f_{k}}\hat{g_{j}}}\bigr), \\ & \hat{f_{k}}\in \varTheta _{1}=\{1,\hat{P},\hat{T} \hat{C},\hat{P}\hat{T} \hat{C}\}, \hat{g_{j}}\in \varTheta _{1}^{C}=\{\hat{C},\hat{T},\hat{C} \hat{P},\hat{P} \hat{T}\}. \end{aligned} $$
(9)

For example, if we take \(\hat{f_{k}}=1\), \(\hat{g_{j}}=\hat{C}\) in (9), the local DNLS equation is given by

$$ q_{t}=q_{xx}+8qq^{*}q_{x}. $$

When we take \(\hat{f_{k}}=1\), \(\hat{g_{j}}=\{\hat{T},\hat{P}\hat{C}, \hat{P}\hat{T}\}\) or \(\hat{g_{j}}=\hat{C}\), \(\hat{f_{k}}=\{\hat{P}, \hat{T}\hat{C},\hat{P}\hat{T}\hat{C}\}\), a two-place nonlocal DNLS systems can be obtained:

$$ \begin{aligned} &q_{t}=q_{xx}+2(p+q)^{2}(r+s) (pr-qs)+2q(r+s) (p_{x}+q_{x})+2\bigl[(p+q) (qs-pr) \bigr]_{x}, \\ &(p,r,s)=\bigl(q^{\hat{f_{k}}},\qquad q^{\hat{g_{j}}},q^{\hat{f_{k}}\hat{g_{j}}}\bigr). \end{aligned} $$
(10)

For instance, for \(\hat{f_{k}}=1\), \(\hat{g_{j}}=\hat{P}\hat{C}\), Eq. (10) becomes

$$ q_{t}=q_{xx}+8q q^{*}(-x,t)q_{x}. $$
(11)

For \(\hat{f_{k}}=\hat{P}\hat{T}\hat{C}\), \(\hat{g_{j}}=\hat{C}\), Eq. (10) becomes

$$\begin{aligned} &q_{t}=q_{xx}+2 \bigl[q+q^{*}(-x,-t)\bigr]^{2}\bigl[q^{*}+q(-x,-t) \bigr] \bigl[q^{*}q^{*}(-x,-t)-qq(-x,-t)\bigr] \\ &\hphantom{q_{t}=}{} +2q\bigl[q^{*}+q(-x,-t)\bigr] \bigl[q+q^{*}(-x,-t)\bigr]_{x} \\ &\hphantom{q_{t}=}{}+2\bigl[\bigl(q+q^{*}(-x,-t)\bigr) \bigl(qq(-x,-t)-q ^{*}q^{*}(-x,-t)\bigr) \bigr]_{x}. \end{aligned}$$
(12)

The systems (10) to (12) are all called two-place nonlocal DNLS equation.

If we take \(\hat{f_{k}}=\hat{P}\), \(\hat{g_{j}}=\{\hat{T},\hat{P}\hat{T} \} \), \(\hat{f_{k}}=\hat{T}\hat{C}\), \(\hat{g_{j}}=\{\hat{C}\hat{P}, \hat{P}\hat{T}\}\) or \(\hat{f_{k}}=\hat{P}\hat{T}\hat{C}\), \(\hat{g_{j}}= \{\hat{T},\hat{P}\hat{C}\} \), some four-place nonlocal DNLS equations can be obtained:

$$ \begin{aligned} &q_{t}=q_{xx}+2(p+q)^{2}(r+s) (pr-qs)+2q(r+s) (p_{x}+q_{x})+2\bigl[(p+q) (qs-pr) \bigr]_{x}, \\ &(p,r,s)=\bigl(q^{\hat{f_{k}}},q^{\hat{g_{j}}},q^{\hat{f_{k}}\hat{g_{j}}}\bigr), \\ & ( \hat{f_{k}},\hat{g_{j}})=\bigl(\hat{P},\hat{T}(1, \hat{P})\bigr),\bigl(\hat{T}\hat{C}, \hat{P}(\hat{C},\hat{T})\bigr),\bigl(\hat{P} \hat{T}\hat{C},(\hat{T}, \hat{P} \hat{C})\bigr). \end{aligned} $$
(13)

For example, for \(\hat{f_{k}}=\hat{T}\hat{C}\), \(\hat{g_{j}}=\hat{P} \hat{C}\), Eq. (13) becomes

$$\begin{aligned} q_{t}={}&q_{xx}+ 2 \bigl[q+q^{*}(x,-t)\bigr]^{2}\bigl[q(-x,t)+q^{*}(-x,t) \bigr] \bigl[q^{*}(-x,t)q ^{*}(x,-t)-qq(-x,-t)\bigr] \\ &{}+2q\bigl[q^{*}(-x,t)+q(-x,-t)\bigr] \bigl[q^{*}(x,-t)+q \bigr]_{x} \\ &{}+2\bigl[\bigl(q+q^{*}(x,-t)\bigr) \bigl(qq(-x,-t)-q ^{*}(x,-t)q^{*}(-x,t)\bigr)\bigr]_{x} . \end{aligned}$$
(14)

For \(\hat{f_{k}}=\hat{P}\hat{T}\hat{C}\), \(\hat{g_{j}}=\hat{P}\hat{C}\), Eq. (13) becomes

$$\begin{aligned} q_{t}={}&q_{xx}+ 2 \bigl[q+q^{*}(-x,-t)\bigr]^{2}\bigl[q(x,-t)+q^{*}(-x,t) \bigr] \bigl[q^{*}(-x,-t)q ^{*}(-x,t)-qq(x,-t)\bigr] \\ &{}+2q\bigl[q^{*}(-x,t)+q(x,-t)\bigr] \bigl[q^{*}(-x,-t)+q \bigr]_{x} \\ &{}+2\bigl[\bigl(q+q^{*}(-x,-t)\bigr) \bigl(qq(x,-t)-q ^{*}(-x,-t)q^{*}(-x,t)\bigr)\bigr]_{x}. \end{aligned}$$
(15)

Equations (13) to (15) are all four-place nonlocal DNLS equations.

3 \(\hat{P}\hat{T}\hat{C}\)-invariant multi-soliton solutions of the DNLS type multi-place system

In Ref. [58], the bilinear form of the generalized DNLS equation

$$ \begin{aligned} &q_{t}=q_{xx}+2qrq_{x}, \\ &r_{t}=-r_{xx}+2qrr_{x}, \end{aligned} $$
(16)

is worked out and

$$ \begin{aligned} &\bigl(D_{t}-D_{x}^{2} \bigr)g\cdot f=0, \\ &\bigl(D_{t}+D_{x}^{2}\bigr)h\cdot s=0, \\ &D_{x}^{2} f\cdot s =iD_{x} g\cdot h, \\ &D_{x} f\cdot s =gh, \end{aligned} $$
(17)

by taking the variable transformation \(q=\frac{g}{f}\), \(r=\frac{h}{s}\) and making use of some identities. As a case of reduction, taking \(r=q^{*}\), i.e. \(s=f^{*}\), \(h=g^{*}\) and replacing t by it and x by \(-ix\), the generalized DNLS equation (16) reduces to the DNLS equation (3) and the bilinear equation (17) reduces to

$$ \begin{aligned} &\bigl(iD_{t}+D_{x}^{2} \bigr)g\cdot f=0, \\ &D_{x}^{2} f\cdot f^{*} =iD_{x} g\cdot g^{*}, \\ &D_{x} f\cdot f^{*} =igg^{*}. \end{aligned} $$
(18)

Equation (18) just is the bilinear equation of the the DNLS equation (3).

Its N-soliton solutions can be uniformly written as

$$ \begin{aligned} &g_{n}=\sum _{\mu =0,1}A_{2}(\mu )\exp \Biggl[\sum _{j=1}^{2n} \mu _{j}\xi '_{j}+\sum_{1\leq j < \rho }^{2n} \mu _{j}\mu _{\rho } \theta _{j\rho }\Biggr], \\ &f_{n}=\sum_{\mu =0,1}A_{1}( \mu )\exp \Biggl[\sum_{j=1}^{2n} \mu _{j}\xi ^{\prime \prime }_{j}+\sum _{1\leq j < \rho }^{2n}\mu _{j}\mu _{ \rho }\theta _{j\rho }\Biggr], \end{aligned} $$
(19)

where

$$\begin{aligned}& \xi _{j}=ik_{j}x-ik_{j}^{2}t+ \xi _{j}^{(0)},\qquad \xi '_{j}= \xi _{j},\qquad \xi ^{\prime } _{n+j}=\xi _{j}^{*}+\log k_{j}^{*}, \\& \xi ^{\prime \prime }_{j}=\xi _{j}+\log k_{j},\qquad \xi ^{\prime \prime }_{n+j}=\xi _{j}^{*}\quad (j=1,2, \ldots , n), \\& e^{\theta _{j,n+\rho }}=\frac{1}{(k_{j}-k_{\rho }^{*})^{2}}\quad (j,\rho =1,2, \ldots , n), \\& e^{\theta _{j,\rho }}=(k_{j}-k_{\rho })^{2}, \qquad e^{\theta _{n+j,n+\rho }}=\bigl(k _{j}^{*}-k_{\rho }^{*} \bigr)^{2}\quad (j< \rho =2,3,\ldots , n), \end{aligned}$$

with arbitrary complex constants \(\xi _{j}^{(0)}\), \(j=1,2,\ldots , n\).

The summations \(A_{1}(\mu )\) and \(A_{2}(\mu )\) are taken over all possible combinations of \(\mu _{j}=0,1\) (\(j=1,2,\ldots , 2n\)) and satisfy the following conditions:

$$ \sum_{j=1}^{n}\mu _{j}= \sum_{j=1}^{n}\mu _{n+j},\qquad \sum_{j=1}^{n}\mu _{j}=\sum _{j=1}^{n}\mu _{n+j}+1, $$

respectively.

It is clear that the solution (19) is not P̂T̂Ĉ-invariant for arbitrary \(\xi _{j}^{(0)}\). So it is not the solution of the DNLS type multi-place system. In order to find P̂T̂Ĉ-invariant solutions from (19), we rewrite \(\xi _{j}\) as

$$ \begin{aligned} &\xi _{j}=ik_{j}x-ik_{j}^{2}t+ \eta _{0j}-\frac{1}{2}\sum_{\rho =1} ^{j-1}\theta _{\rho j}-\frac{1}{2}\sum _{\rho =j+1}^{2n} \theta _{j\rho }- \frac{1}{2}\log k_{j} \\ &\hphantom{\xi _{j}} =\eta _{j}-\frac{1}{2}\sum _{\rho =1}^{j-1}\theta _{\rho j}- \frac{1}{2}\sum_{\rho =j+1}^{2n} \theta _{j\rho }-\frac{1}{2}\log k _{j}, \\ &\xi _{j}^{*}=\eta _{j}^{*}- \frac{1}{2}\sum_{\rho =1}^{j-1} \theta _{\rho j}^{*}-\frac{1}{2}\sum _{\rho =j+1}^{2n}\theta _{j \rho }^{*}- \frac{1}{2}\log k_{j}^{*}. \end{aligned} $$
(20)

We can prove that the solution (19) with (20) can be written as hyperbolic and triangular functions, which guarantees the P̂T̂Ĉ-invariance when an appropriate constant is chosen. However, the general expression in terms of the hyperbolic and triangular functions is very complicated. So we only write down two examples for \(n=1\) and \(n=2\).

When \(n=1\), the one-soliton solution for the DNLS equation (3) can be rewritten as

$$ q=\frac{(k_{1}-k_{1}^{*})e^{( i\eta _{1I}+\frac{1}{4}\log k_{1}^{*}- \frac{3}{4}\log k_{1})}}{2\cosh (\eta _{1R}+\frac{1}{4}\log k_{1}- \frac{1}{4}\log k_{1}^{*})}. $$
(21)

When \(n=2\), the two-soliton solution for the DNLS equation (3) can be rewritten as

$$\begin{aligned} q =&\biggl( \vert k_{1}-k_{2} \vert \bigl\vert k_{1}-k_{2}^{*} \bigr\vert \sqrt{k_{1}^{*}k_{2}^{*}} \biggl[\frac{k _{1}-k_{1}^{*}}{\sqrt{ \vert k_{1} \vert k_{1}k_{2}}}e^{i\eta _{1I}}\cosh \biggl[\eta _{2R}+i(\alpha -\beta ) \\ &{}+\frac{1}{4}\bigl(\log k_{2}^{*}-\log k_{2}\bigr)\biggr] \\ &{}+\frac{k _{2}-k_{2}^{*}}{\sqrt{ \vert k_{2} \vert k_{1}k_{2}}}e^{i\eta _{2I}} \cosh \biggl[\eta _{1R}+i(\alpha +\beta )+\frac{1}{4}\bigl(\log k_{1}^{*}-\log k_{1}\bigr)\biggr]\biggr] \biggr) \\ &{}\Big/\biggl( \vert k _{1}-k_{2} \vert ^{2}\cosh \biggl(\eta _{1R}+\eta _{2R}+ \frac{1}{4}\log \frac{k_{1}k _{2}}{k_{1}^{*}k_{2}^{*}}\biggr) \\ &{}+ \bigl\vert k_{1}-k_{2}^{*} \bigr\vert ^{2}\cosh \biggl(\eta _{1R}-\eta _{2R}+ \frac{1}{4}\log \frac{k_{1}k_{2}^{*}}{k_{1}^{*}k_{2}}\biggr) \\ &{}-4k_{1I}k _{2I}\cos \biggl(\eta _{1I}- \eta _{2I}-\frac{i}{4}\log \frac{k_{1}k_{1}^{*}}{k _{2}k_{2}^{*}}\biggr) \biggr). \end{aligned}$$
(22)

Here

$$\begin{aligned}& k_{j}=k_{jR}+ik_{jI},\quad j=1,2 \\& \alpha =\arctan \frac{k_{1I}-k_{2I}}{k_{1R}-k_{2R}}, \qquad \beta =\arctan \frac{k _{1I}+k_{2I}}{k_{1R}-k_{2R}}, \end{aligned}$$

and \(\eta _{jR}\), \(\eta _{jI}\) are real and imaginary parts of \(\eta _{j}\), respectively,

$$\begin{aligned}& \eta _{jR}=-k_{jI}x+2k_{jR}k_{jI}t+ \eta _{j0R}, \\& \eta _{jI}=k_{jR}x-\bigl(k_{jR}^{2}-k_{jI}^{2} \bigr)t+\eta _{j0I}, \end{aligned}$$

\(\eta _{j0R}\), \(\eta _{j0I}\) are arbitrary constants.

It is straightforward to test that (21) is P̂T̂Ĉ-invariant for \(\eta _{10R}=0\), \(\eta _{10I}= \frac{1}{2} \arccos \frac{k_{1}^{\frac{3}{2}}+(k_{1}^{\frac{3}{2}})^{*}}{2(k_{1}-k _{1}^{*})^{2}\sqrt{k_{1}k_{1}^{*}}}\). Equation (22) is P̂T̂Ĉ-invariant for \(\eta _{j0R}=\frac{1}{4} \log \frac{k_{j}}{k_{j}^{*}}\), \(\eta _{10I}= -\frac{i}{2}\log \frac{\sqrt{k _{j}k_{j}^{*}}k_{1}k_{2}}{(k_{j}-k_{j}^{*})^{2}}\) (\(j=1,2\)) if \(k_{j}+k_{j}^{*}=0\). As for the solution (22), we consider the reduction of \(k_{1}=-k_{2}\). In the case of reduction, it can be tested that (22) is \(\hat{P}\hat{T}\hat{C}\)-invariant, T̂Ĉ-invariant and P̂-invariant if \(\eta _{j0R}=0\), \(\eta _{j0I}=\frac{1}{2}\arccos \frac{i\sqrt{k_{jR}^{2}+k_{jI}^{2}}k _{jR}}{2k_{jI}}\) (\(j=1,2\)).

3.1 \(\hat{P}\hat{T}\hat{C}\)-invariant solutions of a nonlocal two-place DNLS equation

In this section, we will give the \(\hat{P}\hat{T}\hat{C}\)-invariant multi-soliton solutions of a new nonlocal two-place DNLS equation. Replacing t by it, x by \(-ix\) and q by \(\frac{1}{2}q\) in Eq. (12), we obtain the following nonlocal two-place DNLS equation:

$$\begin{aligned}& iq_{t}+q_{xx}- \frac{1}{8}\bigl[q+q^{*}(-x,-t)\bigr]^{2} \bigl[q^{*}+q(-x,-t)\bigr] \bigl[q^{*}q ^{*}(-x,-t)-qq(-x,-t)\bigr] \\& \qquad {}+\frac{i}{2}q\bigl[q^{*}+q(-x,-t)\bigr] \\& \qquad {}\times \bigl[q+q^{*}(-x,-t)\bigr]_{x}+ \frac{i}{2}\bigl[\bigl(q+q^{*}(-x,-t)\bigr) \bigl(qq(-x,-t)-q^{*}q ^{*}(-x,-t)\bigr) \bigr]_{x}=0. \end{aligned}$$
(23)

Setting \(q=q^{*}(-x,-t)\), Eq. (23) can be reduced to the DNLS equation (3), so \(q \vert _{\eta _{10I}= \frac{1}{4} \arccos \frac{(k_{1R}^{2}-k_{1I}^{2})^{2}-4k _{1R}k_{1I}}{16k_{1I}^{2}(k_{1R}^{2}+k_{1I}^{2})}, \eta _{10R=0}}\) in Eq. (21) can solve the nonlocal two-place DNLS equation (23) with \(\hat{f}=\hat{P}\hat{T}\). Thus Eq. (23) has the following one-soliton solution:

$$ q=\frac{e^{ i(k_{1R}x-(k_{1R}^{2}-k_{1I}^{2})t)}}{2\cosh (-k_{1R}x+2k _{1R}k_{1I}t+\frac{i}{2}\theta )} $$
(24)

with

$$ \theta =\operatorname{arctant}\frac{k_{1I}}{k_{1R}}. $$

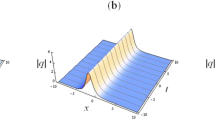
This is a traveling wave at the speed of \(2k_{1R}k_{1I}\) with an initial phase \(\frac{1}{2}\operatorname{arctant}\frac{k_{1I}}{k_{1R}}\). Figure 1 shows the shape and motion of the one-soliton case for \(t=0\) and \(t=1\).

Figure 1
figure 1

Motion of the one-soliton for the nonlocal two-place DNLS equation (23). The green one is the density distributions \(|q|^{2}\) for \(t=0\) and the red one is for \(t=1\) with \(k_{1R}=1\), \(k_{1I}=2\)

Full size image

When take \(k_{j}=ik_{jI}\) (\(j=1,2\)) in Eq. (22), we can obtain the following two-soliton solutions of Eq. (23):

$$\begin{aligned} q =&\biggl( \vert k_{1}-k_{2} \vert \bigl\vert k_{1}-k_{2}^{*} \bigr\vert \sqrt{k_{1}^{*}k_{2}^{*}} \biggl[\frac{k _{1}-k_{1}^{*}}{\sqrt{ \vert k_{1} \vert k_{1}k_{2}}}e^{i\eta _{1I}}\cosh \biggl[\eta _{2R}+i(\alpha -\beta )+\frac{1}{4}\bigl(\log k_{2}^{*}-\log k_{2}\bigr)\biggr] \\ &{}+\frac{k _{2}-k_{2}^{*}}{\sqrt{ \vert k_{2} \vert k_{1}k_{2}}}e^{i\eta _{2I}} \cosh \biggl[\eta _{1R}+i(\alpha +\beta )+\frac{1}{4}\bigl(\log k_{1}^{*}-\log k_{1}\bigr)\biggr]\biggr] \biggr) \\ &{}\Big/\biggl( \vert k _{1}-k_{2} \vert ^{2}\cosh \biggl(\eta _{1R}+\eta _{2R}+ \frac{1}{4}\log \frac{k_{1}k _{2}}{k_{1}^{*}k_{2}^{*}}\biggr) \\ &{}+ \bigl\vert k_{1}-k_{2}^{*} \bigr\vert ^{2}\cosh \biggl(\eta _{1R}-\eta _{2R}+ \frac{1}{4}\log \frac{k_{1}k_{2}^{*}}{k_{1}^{*}k_{2}}\biggr) \\ &{}-4k_{1I}k _{2I}\cos \biggl(\eta _{1I}- \eta _{2I}-\frac{i}{4}\log \frac{k_{1}k_{1}^{*}}{k _{2}k_{2}^{*}}\biggr) \biggr) \end{aligned}$$
(25)

with

$$ \eta _{jR}=-k_{jI}x,\qquad \eta _{1I}=k_{1I}^{2}t+ \frac{1}{2}\arccos (k_{2I}),\qquad \eta _{2I}=k_{2I}^{2}t+ \frac{1}{2}\arccos (k_{1I}), $$

or

$$\begin{aligned}& \eta _{jR}=-k_{jI}x+\log \frac{k_{j}}{k_{j}^{*}}\quad (j=1,2), \\& \eta _{1I}=k _{1I}^{2}t+ \frac{1}{2}\arccos (k_{2I}), \qquad \eta _{2I}=k_{2I}^{2}t+ \frac{1}{2} \arccos (k_{1I}). \end{aligned}$$

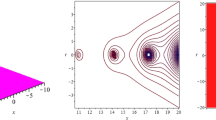
Figure 2 shows that the two-soliton solution is periodic with respect to time t and localized in the x direction. Figure 2(a) illustrates the density distributions \(|q|^{2}\) on the \((x,t)\)-plane and (b) expresses the interaction process of the two-soliton solution for \(\eta _{j0R}=0\). Figure 2(c) shows the density distributions \(|q|^{2}\) on \((x,t)\)-plane and (d) describes the profiles of the two-soliton solution for different times when the constants \(\eta _{j0R}=\log \frac{k_{j}}{k_{j}^{*}}\). It seems that the constant \(\eta _{j0R}\) influences the interaction process of the two-soliton and the two solitons with the constants \(\eta _{j0R}=\log \frac{k_{j}}{k _{j}^{*}}\) are apart from each other.

Figure 2
figure 2

Interaction of the two-soliton solution for the nonlocal two-place DNLS equation (23). Pictures (a) and (b) show the interaction of the two-soliton for \(\eta _{j0R}=0\), \(\eta _{10I}=\frac{1}{2}\arccos k_{2I}\), \(\eta _{20I}=\frac{1}{2} \arccos k_{1I}\). Pictures (c) and (d) illustrate the interaction of the two-soliton for \(\eta _{j0R}=\log \frac{k_{j}}{k_{j}^{*}}\), \(\eta _{10I}= \frac{1}{2}\arccos k_{2I}\), \(\eta _{20I}=\frac{1}{2}\arccos k_{1I}\). Here \(k_{1R}=-1\), \(k_{1I}=0.6\)

Full size image

3.2 \(\hat{P}\hat{T}\hat{C}\)-invariant multi-soliton solutions of a nonlocal four-place DNLS equation

Replacing t by it, x by \(-ix\) and q by \(\frac{1}{2}q\) in the nonlocal four-place DNLS equation (12), it becomes

$$\begin{aligned}& iq_{t}+q_{xx}- \frac{1}{8}\bigl[q+q^{*}(x,-t)\bigr]^{2} \bigl[q(-x,t)+q^{*}(-x,t)\bigr] \bigl[q ^{*}(-x,t)q^{*}(x,-t)-qq(-x,-t) \bigr] \\& \quad {}+\frac{i}{2}q\bigl[q^{*}(-x,t)+q(-x,-t)\bigr] \bigl[q^{*}(x,-t)+q\bigr]_{x} \\& \quad {}+\frac{i}{2}\bigl[\bigl(q+q ^{*}(x,-t)\bigr) \bigl(qq(-x,-t)-q^{*}(x,-t)q^{*}(-x,t)\bigr) \bigr]_{x}=0. \end{aligned}$$
(26)

In this section, we want to construct the soliton solutions of the nonlocal four-place DNLS equation (26). First, setting \(q=q^{*}(x,-t)\) in Eq. (26), it reduces to

$$ iq_{t}+q_{xx}+2iq \bigl[q^{*}(-x,t)\bigr]q_{x}=0. $$
(27)

Then setting \(q(-x,t)=q\), Eq. (27) becomes the DNLS case (3). Thus, the two-soliton solution of the nonlocal four-place DNLS equation (26) can be obtained when we take \(k_{2}=-k_{1}\) in Eq. (22),

$$\begin{aligned} q =&\biggl( \vert 2k_{1} \vert \bigl\vert k_{1}+k_{1}^{*} \bigr\vert \biggl[e^{i\eta _{1I}}\cosh \biggl[\eta _{2R}+i( \alpha -\beta )+ \frac{1}{4}\bigl(\log k_{1}^{*}-\log k_{1}\bigr)\biggr] \\ &{}+e^{i\eta _{2I}} \cosh \biggl[\eta _{1R}+i(\alpha +\beta )+ \frac{1}{4}\bigl(\log k_{1}^{*}-\log k_{1}\bigr)\biggr]\biggr]\biggr) \\ &{}\Big/\biggl( \vert 2k _{1} \vert ^{2}\cosh \biggl( \eta _{1R}+\eta _{2R}+\frac{1}{4}\log \frac{k_{1}^{2}}{k _{1}^{*2}}\biggr) \\ &{}+ \bigl\vert k_{1}+k_{1}^{*} \bigr\vert ^{2}\cosh (\eta _{1R}-\eta _{2R})+4k_{1I} ^{2}\cos (\eta _{1I}-\eta _{2I})\biggr), \end{aligned}$$
(28)

with

$$\begin{aligned}& \eta _{1R}=-k_{1I}x+2k_{1R}k_{1I}t, \qquad \eta _{2R}=k_{1I}x+2k_{1R}k_{1I}t, \\& \eta _{1I}=k_{1R}x-\bigl(k_{1R}^{2}-k_{1I}^{2} \bigr)t+\eta _{10I}, \qquad \eta _{2I}=-k _{1R}x-\bigl(k_{1R}^{2}-k_{1I}^{2} \bigr)t+\eta _{20I}, \\& \eta _{10I}=\eta _{20I}=\frac{1}{2}\arccos \frac{(k_{1I}^{2}-k_{1R}^{2})^{2}-4(k _{1I}k_{1R})^{2}}{-4k_{1I}^{2}(k_{1I}^{2}+k_{1R}^{2})^{\frac{3}{2}}}, \end{aligned}$$

and

$$ \alpha =\operatorname{arctant}\frac{k_{1I}}{k_{1R}},\qquad \beta =0. $$

The interaction of the two-soliton solution (28) is illustrated in Fig. 3. The first column show the density plots of the two-soliton solution with \(k_{1R}=1\), \(k_{1I}=1\), \(k_{1R}=3\), \(k_{1I}=1\) and \(k_{1R}=1\), \(k_{1I}=3\), respectively. Pictures (a2)–(a4), (b2)–(b4) and (c2)–(c4) reveal the interaction process of the corresponding two-soliton for different choice of the real part and imparity part. Figure 3 reveals that the real part \(k_{1R}\) and imparity \(k_{1I}\) influence the interaction of the two-soliton solution.

Figure 3
figure 3

Interaction of the two-soliton solution for the nonlocal four-place DNLS equation (26). Pictures (a1)–(a4) show the interaction of the two-soliton for \(k_{1R}=1\),\(k_{1I}=1\). Pictures (b1)–(b4) show the interaction of the two-soliton for \(k_{1R}=3\),\(k_{1I}=1\). Pictures (c1)–(c4) show the interaction of the two-soliton for \(k_{1R}=1\), \(k_{1I}=3\)

Full size image

4 Conclusions

Multi-place systems are important in both mathematical and physical fields. In this paper, we first construct the coupled CLL system and address its Lax pair which guarantees the integrability of the coupled CLL system. Then some kinds of nonlocal TDNLS equations and FDNLS equations are proposed by using the \(\hat{P}\hat{T}\hat{C}\)-symmetry.

\(\hat{P}\hat{T}\hat{C}\)-symmetry can be used not only to establish multi-place systems but also to solve the multi-place systems. With the help of the \(\hat{P}\hat{T}\hat{C}\)-symmetry, we not only obtain the one-soliton solution and periodic two-soliton solution of a nonlocal TDNLS equation but also work out the two-soliton solution of a nonlocal FDNLS equation for the first time. It is interesting to find that the arbitrary constant in the real part of \(\eta _{j}\) can influence the interaction process of the two-soliton for the TDNLS equation and new dynamical behaviors are analyzed in Fig. 2. For the FDNLS equation, it is interesting to find that the real part \(k_{jR}\) and the imparity \(k_{jI}\) of the parameter \(k_{j}\) influence the interaction process of the two-soliton and the dynamics as demonstrated in Fig. 3.

From the results of this paper, we find that there are some new interesting phenomena in the nonlocal multi-place systems. So it is significant to study the nonlocal multi-place systems.