1 Introduction

Fractional nonlinear evolution equation is one of the noticeable branches of science in recent years. Fractional calculus has a great profound physical background able to formulate many various phenomena in distinct fields such as physics, mechanical engineering, economics, chemistry, signal processing, food supplement, applied mathematics, quasi-chaotic dynamical systems, hydrodynamics, system identification, statistics, finance, fluid mechanics, solid-state biology, dynamical systems with chaotic dynamical behavior, optical fibers, electric control theory, economics, and diffusion problems. Mathematical modeling of these phenomena contains fractional derivatives, which provide a great explanation of the nonlocal property of these models since they depend on both historical and current states of the problem in contrast to the classical calculus depending on the current state only. Based on the importance of this kind of calculus, many definitions were derived such as conformable fractional, fractional Riemann–Liouville, Caputo, and Caputo–Fabrizio derivatives [7, 8, 23, 24, 41, 43, 50]. These definitions are employed to convert fractional nonlinear partial differential equations to nonlinear integer-order ordinary differential equations, and then computational and numerical schemes can be applied to get various types of solutions for these models and examples of these schemes [3, 9, 11–19, 21, 22, 25, 32, 35, 36, 39, 40, 42, 44, 45, 51–53, 57].

Recently, the mK method is formulated and applied to distinct physical models such as the complex Ginzburg–Landau model, the \((2+1)\)-dimensional KD equation and KdV equation, and the fractional \((N+1)\) sinh–Gordon, biological population, equal width, modified equal width, Duffing equations, and so on [1, 2, 6, 27–31, 38, 48].

This method depends on a new auxiliary Riccati equation [47]. The auxiliary equation of the mK method is given by

$$\begin{aligned} \mathcal{M}'(\varphi)= \frac{1}{\ln(\mathcal{Q})} { \bigl[} \delta \mathcal{Q}^{\mathcal{M}(\varphi)}+\varrho \mathcal{Q}^{-\mathcal {M}(\varphi)}+ \chi {\bigr]}, \end{aligned}$$
(1)

where \({[}\delta, \varrho , \chi, \mathcal{Q} {]}\) are arbitrary constants such that \({[}\mathcal{Q}\neq0, \mathcal {Q}\neq1 {]}\), whereas the Riccati equation is given by

$$\begin{aligned} \mathcal{R}'(\varphi)=\mathcal{E}_{0}+ \mathcal{E}_{1} \mathcal {R}(\varphi)+\mathcal{E}_{2} \mathcal{R}^{2}(\varphi), \end{aligned}$$
(2)

where \({[}\mathcal{E}_{0}, \mathcal{E}_{1}, \mathcal{E}_{2} {]}\) are arbitrary constants. So Eqs. (1) and (2) coincide when \({[}\mathcal{M}(\varphi)=\mathcal{R}(\varphi), \chi=\mathcal{E}_{1}, \varrho=\mathcal{E}_{0}, \delta=\mathcal {E}_{2} {]}\). Using this technique leads to the mK auxiliary equation, which includes many other analytical methods, but the mK method can obtain more solutions than most of them. This shows the superiority, power, and productivity of the mK method.

In this context, we employ the mK method to construct new formulas of solutions for the fractional KdV and ZKBBM equations, which are given, respectively, by [20, 26, 37, 46, 49, 54, 55]

$$\begin{aligned}& \mathcal{D}_{t} ^{\vartheta} \mathcal{K}+ \mathcal{K} \mathcal {K}_{x}+\lambda\mathcal{K}_{x x x}=0, \end{aligned}$$
(3)
$$\begin{aligned}& \mathcal{D}_{t} ^{\vartheta} \mathcal{Z}+ \mathcal{Z}_{x}-2 \nu \mathcal{Z} \mathcal{Z}_{x}-\mu \mathcal{D}_{t} ^{\vartheta} ( \mathcal{Z}_{x x} ) =0, \end{aligned}$$
(4)

where \({[} \lambda, \nu, \mu {]}\) are arbitrary constants.

The KdV model is one of the essential models in studying the shallow-water waves, and it has a strong physical impact in describing the interaction of two long waves with various dispersion relations. It is used only for the instant of time (local property); that is why the solitary wave in the soliton solutions of it may behave not very well, whereas the fractional KdV is used to estimate the effect of higher-order dispersion of the regular KdV equation to increasing the amplitude of the soliton. On the other hand, the fractional ZKBBM equation is used to investigate the gravity water waves in the long-wave regime.

In this research, we use new fractional derivative operator defined as follows.

Definition 1.1

The \(\mathcal{ABR}\) fractional operator is given by [4, 5, 10, 33, 34]

$$\begin{aligned} ^{\mathcal{ABR}} \mathcal{D}^{\alpha}_{a+} \mathcal{F}(t)=\frac {\mathcal{B}(\alpha)}{1-\alpha} \frac{d}{d t} \int_{a}^{t} \mathcal{F}(x) \mathcal{E}_{\alpha} \biggl(\frac{-\alpha (t-\alpha )^{\alpha}}{1-\alpha} \biggr) \,dx, \end{aligned}$$
(5)

where \(\mathcal{E}_{\alpha}\) is the Mittag-Leffler function define by

$$\begin{aligned} \mathcal{E}_{\alpha} \biggl(\frac{-\alpha (t-\alpha)^{\alpha }}{1-\alpha} \biggr)=\sum _{n=0}^{\infty} \frac{ (\frac {-\alpha}{1-\alpha} ) ^{n} (t-x)^{\alpha n}}{\varGamma(\alpha n+1)}, \end{aligned}$$
(6)

\(\mathcal{B}(\alpha)\) being a normalization function. Thus

$$\begin{aligned} {}^{\mathcal{ABR}} \mathcal{D}^{\alpha}_{a+} \mathcal{F}(x) =\frac {\mathcal{B}(\alpha)}{1-\alpha} \sum_{n=0}^{\infty} \biggl(\frac {-\alpha}{1-\alpha} \biggr) ^{n} {}^{R L} \mathcal{I}^{\alpha n}_{a} \mathcal{F}(x). \end{aligned}$$
(7)

Applying this definition of \(\mathcal{ABR}\) fractional operator to Eqs. (3) and (4), respectively, with the wave transformation \({[} \mathcal{K}(x,t)=\mathcal{K}(\varphi), \mathcal{Z}(x,t)=\mathcal {Z}(\varphi), \varphi=x+\frac{c (1-\alpha) t^{- \alpha n}}{B(\alpha ) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} {]}\), where k, ω are arbitrary constants, leads to conversion of Eq. (3) and (4) into the corresponding ODEs. Integration of the obtained ODEs with zero constant of integration gives

$$\begin{aligned}& 2 c \mathcal{K}+\mathcal{K}^{2}+2 \lambda \mathcal{K}''=0, \end{aligned}$$
(8)
$$\begin{aligned}& (c+1) \mathcal{Z}-\nu\mathcal{Z}^{2}-\mu c \mathcal{Z}''=0. \end{aligned}$$
(9)

Calculating the homogeneous balance value in Eqs. (8) and (9) yields \(N=1\). Thus both equations have the same general formula of solution given according to the mK method by

$$\begin{aligned} \begin{aligned} [b]\mathcal{K}(\varphi)&=\mathcal{Z}( \varphi)=\sum_{i=1}^{n} a_{i} \mathcal{Q}^{i \mathcal{M}(\varphi)}+\sum _{i=1}^{n} b_{i} \mathcal {Q}^{-i \mathcal{M}(\varphi)}+a_{0} \\ & =a_{1} \mathcal{Q}^{ \mathcal{M}(\varphi)}+a_{2} \mathcal{Q}^{2 \mathcal{M}(\varphi)}+a_{0}+b_{2} \mathcal{Q}^{-2 \mathcal{M}(\varphi )}+b_{1} \mathcal{Q}^{- \mathcal{M}(\varphi)}. \end{aligned} \end{aligned}$$
(10)

The rest of the paper is organized as follows. In Sect. 2, we apply the mK method to the nonlinear fractional Kdv and ZKBBM equations. Moreover, we give some sketches to show more physical properties of both models. In Sect. 4, we discuss the obtained computational results and compare them with those obtained in previous works. Moreover, we compare the obtained numerical results. In Sect. 5, we give the conclusion of the whole research.

2 Abundant wave solutions of the fractional KdV and ZKBBM equations

In this section, we apply an analytical scheme to the nonlinear fractional KdV and ZKBBM equations and show physical properties of the two models.

2.1 The fractional KdV equation

Applying the mK method with its auxiliary equation and the suggested general solutions of the fractional KdV equation leads to a system of algebraic equations. Using Mathematica 11.2, we find the values of the parameters in this system, which lead to two families of solutions.

Family I

$${\bigl[} a_{0}\to-12 \delta \lambda \varrho,a_{1} \to0,a_{2}\to0,b_{1}\to -12 \lambda \chi \varrho,b_{2}\to-12 \lambda \varrho^{2},c\to\lambda \bigl(4 \delta \varrho-\chi^{2} \bigr) {\bigr]}. $$

Consequently, the closed-form solutions for the fractional KdV models are given as follows.

When \([ \chi^{2}-4 \delta \varrho<0\text{ \& }\delta\neq0 ]\),

$$\begin{aligned}& \mathcal{K}_{1}(x,t)=\frac{12 \delta \lambda \varrho (\chi ^{2}-4 \delta \varrho ) \sec^{2} (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )}{ (\chi-\sqrt{4 \delta \varrho -\chi^{2}} \tan (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) ) ){}^{2}}, \end{aligned}$$
(11)
$$\begin{aligned}& \mathcal{K}_{2}(x,t)=\frac{12 \delta \lambda \varrho (\chi ^{2}-4 \delta \varrho ) \csc^{2} (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )}{ (\chi-\sqrt{4 \delta \varrho -\chi^{2}} \cot (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) ) ){}^{2}}. \end{aligned}$$
(12)

When \([ \chi^{2}-4 \delta \varrho>0\text{ \& }\delta\neq0 ]\),

$$\begin{aligned}& \mathcal{K}_{3}(x,t)=\frac{12 \delta \lambda \varrho (\chi ^{2}-4 \delta \varrho ) \text{sech}^{2} (\frac{1}{2} \sqrt {\chi^{2}-4 \delta \varrho} (x-\frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )}{ (\sqrt{\chi^{2}-4 \delta \varrho } \tanh (\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} (x-\frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho -\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac {\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) )+\chi ){}^{2}}, \end{aligned}$$
(13)
$$\begin{aligned}& \begin{aligned}[b] \mathcal{K}_{4}(x,t)={}& 12 \delta \lambda \varrho \bigl(4 \delta \varrho-\chi^{2} \bigr) \\&\Big/ { \biggl[} {\biggl(}\chi\sinh \biggl(\frac{1}{2} \sqrt{ \chi^{2}-4 \delta \varrho} \biggl(x-\frac {(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi ^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr) \\ &+\sqrt{\chi^{2}-4 \delta \varrho} \cosh \biggl( \frac{1}{2} \sqrt {\chi^{2}-4 \delta \varrho} \biggl(x- \frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} \biggr) \biggr) {\biggr)}^{2} {\biggr]}. \end{aligned} \end{aligned}$$
(14)

When \([ \delta \varrho>0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{K}_{5}(x,t)=-12 \delta \lambda \varrho \csc^{2} \biggl(\sqrt {\delta \varrho} \biggl(x-\frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac {\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr), \end{aligned}$$
(15)
$$\begin{aligned}& \mathcal{K}_{6}(x,t)=-12 \delta \lambda \varrho \sec^{2} \biggl(\sqrt {\delta \varrho} \biggl(x-\frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac {\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr). \end{aligned}$$
(16)

When \([ \delta \varrho<0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{K}_{7}(x,t)=12 \delta \lambda \varrho \text{csch}^{2} \biggl(\sqrt{-\delta \varrho} \biggl(x- \frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr), \end{aligned}$$
(17)
$$\begin{aligned}& \mathcal{K}_{8}(x,t)=-12 \delta \lambda \varrho \text{sech}^{2} \biggl(\sqrt{-\delta \varrho} \biggl(x- \frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr). \end{aligned}$$
(18)

When \([ \chi=0\text{ \& }\varrho=-\delta ] \),

$$\begin{aligned} \mathcal{K}_{9}(x,t)=12 \lambda \varrho^{2} \text{sech}^{2} \biggl(\varrho \biggl( \frac{4 (\alpha-1) \lambda \varrho^{2} t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)}+x \biggr) \biggr). \end{aligned}$$
(19)

When \([ \chi=\frac{\varrho}{2}= \kappa\text{ \& }\delta=0 ] \),

$$\begin{aligned} \mathcal{K}_{10}(x,t)=-\frac{24 \kappa^{2} \lambda \exp (\kappa (\frac{(\alpha-1) \kappa^{2} \lambda t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)}+x ) )}{ (\exp (\kappa (\frac{(\alpha-1) \kappa^{2} \lambda t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)}+x ) )-2 ){}^{2}}. \end{aligned}$$
(20)

When \([ \chi=0\text{ \& }\varrho=\delta ] \),

$$\begin{aligned} \mathcal{K}_{11}(x,t)=-12 \lambda \varrho^{2} \csc^{2} \biggl(-\frac{4 (\alpha-1) \lambda \varrho^{3} t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)}+C+x \varrho \biggr). \end{aligned}$$
(21)

When \([ \delta= 0\text{ \& }\chi\neq0\text{ \& }\varrho\neq0 ] \),

$$\begin{aligned} \mathcal{K}_{12}(x,t)=-\frac{12 \lambda \chi^{3} \varrho \exp (\chi (\frac{(\alpha-1) \lambda \chi^{2} t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)}+x ) )}{ (\varrho -\chi\exp (\chi (\frac{(\alpha-1) \lambda \chi^{2} t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)}+x ) ) ){}^{2}}. \end{aligned}$$
(22)

When \([ \chi^{2}-4 \delta \varrho=0 ] \),

$$\begin{aligned} \mathcal{K}_{13}(x,t)=3 \lambda \biggl( \frac{ ( x B(\alpha) t^{2 \alpha} \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n) )^{2}}{B(\alpha)^{2} (\chi x+2)^{2} (\sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n) ){}^{2}}-4 \delta \varrho +\frac{2 \chi^{3} x}{\chi x+2} \biggr). \end{aligned}$$
(23)

Family II

$${\bigl[} a_{0}\to-12 \delta \lambda \varrho,a_{1} \to-12 \delta \lambda \chi,a_{2}\to-12 \delta^{2} \lambda,b_{1}\to0,b_{2}\to0,c\to \lambda \bigl(4 \delta \varrho-\chi^{2} \bigr) {\bigr]}. $$

Consequently, the closed-form solutions for the fractional KdV models are given as follows.

When \([ \chi^{2}-4 \delta \varrho<0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned}& \begin{aligned}[b]\mathcal{K}_{14}(x,t)&=3 \lambda \bigl( \chi^{2}-4 \delta \varrho \bigr) \\&\quad\times\sec^{2} \biggl( \frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} \biggl(x- \frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr),\end{aligned} \end{aligned}$$
(24)
$$\begin{aligned}& \begin{aligned}[b] \mathcal{K}_{15}(x,t)&=3 \lambda \bigl( \chi^{2}-4 \delta \varrho \bigr) \\&\quad\times\csc^{2} \biggl( \frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} \biggl(x- \frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr).\end{aligned} \end{aligned}$$
(25)

When \([ \chi^{2}-4 \delta \varrho>0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned} \begin{aligned}[b] \mathcal{K}_{16}(x,t)&=3 \lambda \bigl( \chi^{2}-4 \delta \varrho \bigr) \\&\quad\times\operatorname{sech}^{2} \biggl(\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} \biggl(x-\frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr),\end{aligned} \end{aligned}$$
(26)
$$\begin{aligned} \begin{aligned}[b] \mathcal{K}_{17}(x,t)&=3 \lambda \bigl(4 \delta \varrho-\chi ^{2} \bigr) \\&\quad\times\operatorname{csch}^{2} \biggl( \frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} \biggl(x- \frac{(\alpha-1) \lambda t^{-2 \alpha} (4 \delta \varrho-\chi^{2} )}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr).\end{aligned} \end{aligned}$$
(27)

When \([ \delta \varrho>0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{K}_{18}(x,t)=-12 \delta \lambda \varrho \sec^{2} \biggl(\sqrt{\delta \varrho} \biggl(x-\frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr), \end{aligned}$$
(28)
$$\begin{aligned}& \mathcal{K}_{19}(x,t)=-12 \delta \lambda \varrho \csc^{2} \biggl(\sqrt{\delta \varrho} \biggl(x-\frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr). \end{aligned}$$
(29)

When \([ \delta \varrho<0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{K}_{20}(x,t)=-12 \delta \lambda \varrho \operatorname {sech}^{2} \biggl(\sqrt{-\delta \varrho} \biggl(x- \frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} \biggr) \biggr), \end{aligned}$$
(30)
$$\begin{aligned}& \mathcal{K}_{21}(x,t)=12 \delta \lambda \varrho \operatorname{csch}^{2} \biggl(\sqrt{-\delta \varrho} \biggl(x- \frac{4 (\alpha-1) \delta \lambda \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr). \end{aligned}$$
(31)

When \([ \chi=0\text{ \& }\varrho=-\delta ] \),

$$\begin{aligned} \mathcal{K}_{22}(x,t)=-12 \lambda \varrho^{2} \operatorname{csch}^{2} \biggl(\varrho \biggl( \frac{4 (\alpha-1) \lambda \varrho^{2} t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)}+x \biggr) \biggr). \end{aligned}$$
(32)

When \([ \chi=\delta= \kappa\text{ \& }\varrho=0 ] \),

$$\begin{aligned} \mathcal{K}_{23}(x,t)=-3 \kappa^{2} \lambda \operatorname{csch}^{2} \biggl(\frac {1}{2} \kappa \biggl(\frac{(\alpha-1) \kappa^{2} \lambda t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)}+x \biggr) \biggr). \end{aligned}$$
(33)

When \([ \varrho= 0\text{ \& }\chi\neq0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned} \mathcal{K}_{24}(x,t)=-\frac{24 \delta \lambda \chi^{2} \exp (\chi (\frac{(\alpha-1) \lambda \chi^{2} t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)}+x ) )}{ (\delta \exp (\chi (\frac{(\alpha-1) \lambda \chi^{2} t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)}+x ) )-2 ){}^{2}}. \end{aligned}$$
(34)

When \([ \chi=0\text{ \& }\varrho=\delta ] \),

$$\begin{aligned} \mathcal{K}_{25}(x,t)=-12 \lambda \varrho^{2} \sec^{2} \biggl(-\frac{4 (\alpha-1) \lambda \varrho^{3} t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)}+C+x \varrho \biggr). \end{aligned}$$
(35)

When \([ \chi^{2}-4 \delta \varrho=0 ] \),

$$\begin{aligned} \mathcal{K}_{26}(x,t)=12 \delta \lambda \varrho \biggl(-\frac{4 \delta \varrho B(\alpha)^{2} t^{4 \alpha} (\chi x+2)^{2} (\sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n) ){}^{2}}{\chi^{4} (-x B(\alpha) t^{2 \alpha} \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n) ){}^{2}}+\frac{4}{\chi x}+1 \biggr). \end{aligned}$$
(36)

2.2 The fractional ZKBBM equation

Applying the mK method with its auxiliary equation and the suggested general solutions for the fractional ZKBBM equation leads to a system of algebraic equations. Using Mathematica 11.2, we find the values of the parameters in this system, which lead to the following families of solutions.

Family I

$$\begin{gathered} {\biggl[} a_{0}\to-\frac{3 c \mu \chi^{2}+c+1}{2 \nu},a_{1} \to0,a_{2}\to 0,b_{1}\to-\frac{6 c \mu \chi\varrho}{\nu},b_{2} \to-\frac{6 c \mu \varrho^{2}}{\nu},\\\quad c\to\frac{1}{4 \delta \mu \varrho-\mu \chi^{2}-1}, \text{where } 4 \delta \mu \varrho-\mu \chi^{2}\neq1, \nu\neq 0 {\biggr]}. \end{gathered}$$

Consequently, the closed-form solutions for the fractional ZKBBM models are given as follows.

When \([ \chi^{2}-4 \delta \varrho<0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned}& \begin{aligned}[b] \mathcal{Z}_{1}(x,t)={}& \biggl[ c {\biggl(}-\frac{3 \mu (\chi \sqrt{4 \delta \varrho-\chi^{2}} \tan (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+4 \delta \varrho -\chi^{2} ){}^{2}}{ (\chi-\sqrt{4 \delta \varrho-\chi^{2}} \tan (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty } (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) ) ){}^{2}}\hspace{-12pt} \\ &-1 {\biggr)}-1 {\biggr]} \times\frac{1}{2 \nu}, \end{aligned} \end{aligned}$$
(37)
$$\begin{aligned}& \begin{aligned}[b] \mathcal{Z}_{2}(x,t)={}& { \biggl[} c {\biggl(}-\frac{3 \mu (\chi \sqrt{4 \delta \varrho-\chi^{2}} \cot (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+4 \delta \varrho -\chi^{2} ){}^{2}}{ (\chi-\sqrt{4 \delta \varrho-\chi^{2}} \cot (\frac{1}{2} \sqrt{4 \delta \varrho-\chi^{2}} (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty } (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) ) ){}^{2}}\hspace{-12pt} \\ &-1 {\biggr)}-1 {\biggr]} \times\frac{1}{2 \nu}. \end{aligned} \end{aligned}$$
(38)

When \([ \chi^{2}-4 \delta \varrho>0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned}& \mathcal{Z}_{3}(x,t)=\frac{c (-\frac{3 \mu (\chi\sqrt {\chi^{2}-4 \delta \varrho} \tanh (\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )-4 \delta \varrho +\chi^{2} ){}^{2}}{ (\sqrt{\chi^{2}-4 \delta \varrho} \tanh (\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} (x-\frac {(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) )+\chi ){}^{2}}-1 )-1}{2 \nu}, \end{aligned}$$
(39)
$$\begin{aligned}& \mathcal{Z}_{4}(x,t)=\frac{c (-\frac{3 \mu (\chi\sqrt {\chi^{2}-4 \delta \varrho} \coth (\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )-4 \delta \varrho +\chi^{2} ){}^{2}}{ (\sqrt{\chi^{2}-4 \delta \varrho} \coth (\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} (x-\frac {(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) )+\chi ){}^{2}}-1 )-1}{2 \nu}. \end{aligned}$$
(40)

When \([ \delta \varrho>0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{Z}_{5}(x,t)=-\frac{12 c \delta \mu \varrho \cot^{2} (\sqrt{\delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}, \end{aligned}$$
(41)
$$\begin{aligned}& \mathcal{Z}_{6}(x,t)=-\frac{12 c \delta \mu \varrho \tan^{2} (\sqrt{\delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}. \end{aligned}$$
(42)

When \([ \delta \varrho<0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{Z}_{7}(x,t)=-\frac{12 c \delta \mu \varrho \coth^{2} (\sqrt{-\delta\varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}, \end{aligned}$$
(43)
$$\begin{aligned}& \mathcal{Z}_{8}(x,t)=-\frac{12 c \delta \mu \varrho \tanh^{2} (\sqrt{-\delta\varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}. \end{aligned}$$
(44)

When \([ \chi=0\text{ \& }\varrho=-\delta ] \),

$$\begin{aligned} \begin{aligned} [b]\mathcal{Z}_{9}(x,t)={}& \frac{1}{2 \nu} {\biggl[} c \biggl(12 \mu \varrho^{2} \biggl(1- \frac{4}{ (\exp (2 \varrho (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty } (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) )+1 ){}^{2}} \biggr)-1 \biggr) \\ &-24 c \mu \varrho^{2} \tanh \biggl(\varrho \biggl(x- \frac{(\alpha -1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac {\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} \biggr) \biggr)-1 {\biggr]}. \end{aligned} \end{aligned}$$
(45)

When \([ \chi=\frac{\varrho}{2}= \kappa\text{ \& }\delta=0 ] \),

$$\begin{aligned} \mathcal{Z}_{10}(x,t)=\frac{c (-\frac{3 \kappa^{2} \mu (\exp (\kappa (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+2 ){}^{2}}{ (\exp (\kappa (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) )-2 ){}^{2}}-1 )-1}{2 \nu}. \end{aligned}$$
(46)

When \([ \chi=\delta=0\text{ \& }\varrho\neq0 ] \),

$$\begin{aligned} \mathcal{Z}_{11}(x,t)=-\frac{\frac{12 c \mu B(\alpha)^{2} t^{4 \alpha} (\sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n) ){}^{2}}{ (x B(\alpha) t^{2 \alpha} (\sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n) )-\alpha c+c ){}^{2}}+c+1}{2 \nu}. \end{aligned}$$
(47)

When \([ \chi=0\text{ \& }\varrho=\delta ] \),

$$\begin{aligned} \mathcal{Z}_{12}(x,t)=-\frac{12 c \mu \varrho^{2} \cot^{2} (-\frac{(\alpha-1) c \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)}+C+x \varrho )+c+1}{2 \nu}. \end{aligned}$$
(48)

When \([ \delta= 0\text{ \& }\chi\neq0\text{ \& }\varrho\neq0 ] \),

$$\begin{aligned} \mathcal{Z}_{13}(x,t)=\frac{c (-\frac{3 \mu \chi^{2} (\chi\exp (\chi (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+\varrho ){}^{2}}{ (\varrho-\chi\exp (\chi (x-\frac{(\alpha -1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac {\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) ) ){}^{2}}-1 )-1}{2 \nu}. \end{aligned}$$
(49)

When \([ \chi^{2}-4 \delta \varrho=0 ] \),

$$\begin{aligned} \begin{aligned} [b]\mathcal{Z}_{14}(x,t)={}&{-} \frac{1}{2 \nu} {\biggl[} \frac{3 c \mu \chi^{4} (x B(\alpha) t^{2 \alpha} (\sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n) )-\alpha c+c ){}^{2}}{ ((\alpha-1) c \chi-B(\alpha ) t^{2 \alpha} (\chi x+2) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n) ){}^{2}} \\ &+\frac{6 \mu \chi^{3} x}{\frac{2-2 \alpha}{x B(\alpha) t^{2 \alpha } (\sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n) )-\alpha c+c}-\frac{\chi x+2}{c}}+3 c \mu \chi^{2}+c+1 {\biggr]}. \end{aligned} \end{aligned}$$
(50)

Family II

$$\begin{gathered} {\biggl[} a_{0}\to-\frac{3 c \mu \chi^{2}+c+1}{2 \nu},a_{1}\to- \frac{6 c \delta \mu \chi}{\nu},a_{2}\to-\frac{6 c \delta^{2} \mu}{\nu },b_{1} \to0,b_{2}\to0, \\ \quad c\to\frac{1}{4 \delta \mu \varrho-\mu \chi^{2}-1},\text{where } 4 \delta \mu \varrho-\mu \chi^{2}\neq1, \nu\neq 0 {\biggr]}.\end{gathered} $$

Consequently, the closed-form solutions for the fractional ZKBBM models are given as follows.

When \([ \chi^{2}-4 \delta \varrho<0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned}& \mathcal{Z}_{15}(x,t)=-\frac{3 c \mu (4 \delta \varrho-\chi ^{2} ) \tan^{2} (\frac{1}{2} \sqrt{4 \delta \varrho-\chi ^{2}} (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )+c+1}{2 \nu}, \end{aligned}$$
(51)
$$\begin{aligned}& \mathcal{Z}_{16}(x,t)=-\frac{3 c \mu (4 \delta \varrho-\chi ^{2} ) \cot^{2} (\frac{1}{2} \sqrt{4 \delta \varrho-\chi ^{2}} (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )+c+1}{2 \nu}. \end{aligned}$$
(52)

When \([ \chi^{2}-4 \delta \varrho>0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned}& \mathcal{Z}_{17}(x,t)=-\frac{3 c \mu (\chi^{2}-4 \delta \varrho ) \tanh^{2} (\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )+c+1}{2 \nu},\hspace{-12pt} \end{aligned}$$
(53)
$$\begin{aligned}& \mathcal{Z}_{18}(x,t)=-\frac{3 c \mu (\chi^{2}-4 \delta \varrho ) \coth^{2} (\frac{1}{2} \sqrt{\chi^{2}-4 \delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )+c+1}{2 \nu}.\hspace{-12pt} \end{aligned}$$
(54)

When \([ \delta \varrho>0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{Z}_{19}(x,t)=-\frac{12 c \delta \mu \varrho \tan^{2} (\sqrt{\delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}, \end{aligned}$$
(55)
$$\begin{aligned}& \mathcal{Z}_{20}(x,t)=-\frac{12 c \delta \mu \varrho \cot^{2} (\sqrt{\delta \varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}. \end{aligned}$$
(56)

When \([ \delta \varrho<0\text{ \& }\varrho\neq0\text{ \& }\delta\neq0\text{ \& } \chi=0 ] \),

$$\begin{aligned}& \mathcal{Z}_{21}(x,t)=-\frac{12 c \delta \mu \varrho \tanh^{2} (\sqrt{-\delta\varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}, \end{aligned}$$
(57)
$$\begin{aligned}& \mathcal{Z}_{22}(x,t)=-\frac{12 c \delta \mu \varrho \coth^{2} (\sqrt{-\delta\varrho} (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}. \end{aligned}$$
(58)

When \([ \chi=0\text{ \& }\varrho=-\delta ] \),

$$\begin{aligned} \mathcal{Z}_{23}(x,t)=-\frac{12 c \mu \varrho^{2} \text{csch}^{2} (\varrho (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)} ) )+12 c \mu \varrho^{2}+c+1}{2 \nu}. \end{aligned}$$
(59)

When \([ \chi=\delta= \kappa\text{ \& }\varrho=0 ] \),

$$\begin{aligned} \mathcal{Z}_{24}(x,t)=-\frac{3 c \kappa^{2} \mu \coth^{2} (\frac {1}{2} \kappa (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) )+c+1}{2 \nu}. \end{aligned}$$
(60)

When \([ \varrho= 0\text{ \& }\chi\neq0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned} \mathcal{Z}_{25}(x,t)=-\frac{c (\frac{3 \mu \chi^{2} (\delta \exp (\chi (x-\frac{(\alpha-1) c t^{-2 \alpha }}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n)} ) )+2 ){}^{2}}{ (\delta \exp (\chi (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)} ) )-2 ){}^{2}}+1 )+1}{2 \nu}. \end{aligned}$$
(61)

When \([ \chi=\varrho=0\text{ \& }\delta\neq0 ] \),

$$\begin{aligned} \mathcal{Z}_{26}(x,t)=-\frac{\frac{12 c \mu B(\alpha)^{2} t^{4 \alpha} (\sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n) ){}^{2}}{ (x B(\alpha) t^{2 \alpha} (\sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n) )-\alpha c+c ){}^{2}}+c+1}{2 \nu}. \end{aligned}$$
(62)

When \([ \chi=0\text{ \& }\varrho=\delta ] \),

$$\begin{aligned} \mathcal{Z}_{27}(x,t)=-\frac{12 c \mu \varrho^{2} \tan^{2} (-\frac{(\alpha-1) c \varrho t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha} )^{n} \varGamma (1-\alpha n)}+C+x \varrho )+c+1}{2 \nu}. \end{aligned}$$
(63)

When \([ \chi^{2}-4 \delta \varrho=0 ] \),

$$\begin{aligned} \begin{aligned} [b]\mathcal{Z}_{28}(x,t)={}&{-} \frac{1}{2 \nu} {\biggl[} \frac{48 c \delta ^{2} \mu \varrho^{2} ((\alpha-1) c \chi-B(\alpha) t^{2 \alpha} (\chi x+2) \sum_{n=0}^{\infty} (-\frac{\alpha}{1-\alpha } )^{n} \varGamma(1-\alpha n) ){}^{2}}{\chi^{4} (x B(\alpha) t^{2 \alpha} (\sum_{n=0}^{\infty} (-\frac {\alpha}{1-\alpha} )^{n} \varGamma(1-\alpha n) )-\alpha c+c ){}^{2}} \\ &-\frac{48 c \delta \mu \varrho}{\chi (x-\frac{(\alpha-1) c t^{-2 \alpha}}{B(\alpha) \sum_{n=0}^{\infty} (-\frac{\alpha }{1-\alpha} )^{n} \varGamma(1-\alpha n)} )}-24 c \delta \mu \varrho+3 c \mu \chi^{2}+c+1 {\biggr]}. \end{aligned} \end{aligned}$$
(64)

3 Interpretation of figures

In this section, we give a physical interpretation of the shown figures. All our obtained solutions are considered as traveling wave solutions. We further give a physical interpretation of the shown figures:

  1. 1.

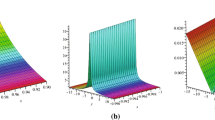
    Fig. 1 shows the bright cone wave solution (13) in the three-dimensional plot (a) to explain the perspective view of the solution, the two-dimensional plot (b) to explain the wave propagation pattern of the wave along the x-axis, and the contour plot (c) to explain the overhead view of the solution when \({[} \alpha=\frac{1}{2}, \delta=6, \lambda=3, m=1, n=1, \chi=5, \varrho =1 {]}\).

    Figure 1
    figure 1

    Numerical simulation of Eq. (13) in three distinct types of plots

    Full size image
  2. 2.

    Fig. 2 shows the dark cone wave solution (14) in the three-dimensional plot (a) to explain the perspective view of the solution, the two-dimensional plot (b) to explain the wave propagation pattern of the wave along the x-axis, and the contour plot (c) to explain the overhead view of the solution when \({[} \alpha=\frac {1}{2}, \delta=6, \lambda=3, m=1, n=1, \chi=5, \varrho=1 {]}\).

    Figure 2
    figure 2

    Numerical simulation of Eq. (14) in three distinct types of plots

    Full size image
  3. 3.

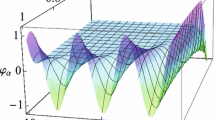
    Fig. 3 shows the periodic bright cone-wave solution (40) in the three-dimensional plot (a) to explain the perspective view of the solution, the two-dimensional plot (b) to explain the wave propagation pattern of the wave along the x-axis, and the contour plot (c) to explain the overhead view of the solution when \({[} \alpha=\frac{1}{2}, \delta=6, \lambda=3, m=1, n=1, \chi=5, \varrho=1 {]}\).

    Figure 3
    figure 3

    Numerical simulation of Eq. (40) in three distinct types of plots

    Full size image
  4. 4.

    Fig. 4 shows the cone-wave solution (43) in the three-dimensional plot (a) to explain the perspective view of the solution, the two-dimensional plot (b) to explain the wave propagation pattern of the wave along the x-axis, and the contour plot (c) to explain the overhead view of the solution when \({[} \alpha=\frac {1}{2}, \delta=-9, \lambda=3, m=1, n=1, \chi=0, \varrho=1 {]}\).

    Figure 4
    figure 4

    Numerical simulation of Eq. (43) in three distinct types of plots

    Full size image

4 Results and discussion

This section is divided into two main parts. In the first part, we studyg the obtained computational solutions for the two fractional suggested models. whereas in the second part, we compare them with the other obtained results in previous works.

  1. 1.

    The shown solutions in our paper.

    • In this paper, we investigate the fractional KdV and ZKBBM equation by the employment of the mK method and a new fractional definition (\(\mathcal{ABR}\)). Abundant explicit closed-form solutions are obtained for each fractional model. Receptive twenty-six and twenty-eight solutions are obtained for each mentioned fractional model.

  2. 2.

    The solutions obtained in previous works.

    • In [56], two analytical methods are applied to three different models involving two our models. However, they use two schemes, but a very few special solutions are obtained.

    • Two analytical schemes in [56] are just particular cases of the mK method when \({[} \mathcal{Q}^{\mathcal{M}(\varphi )}= ( \frac{G'}{G} ), \varrho=-\mu, \chi=-\lambda, \delta=1 {]}\).

    • Eq. (27) is equal to Eq. (3.9) in [56] when \({[} e_{0}=-12 \delta(\mu+d (d-\lambda)), -3(\lambda^{2}-4 \mu )=\delta\lambda\varrho {]}\).

    • Eq. (43) is equal to Eq. (3.30) in [56] when \({[} B=0, a=v, c=2 b v \lambda^{2}-8 b V \mu+V, b V (\lambda^{2}-4 \mu)=-4 c \delta\mu\varrho {]}\).

    • All other solutions obtained in this paper are new when compared with those obtained in [56].

5 Conclusion

In our paper, we solved the flaws and disadvantages of the \(( \frac{G'}{G} ) \)-expansion method that is used by Ali Akbar et al. [56] because, as shown in the previous section, it is just a particular case of our method. Moreover, we use a new definition of fractional derivative, which successfully converts the fractional-order differential equations from our models to integer-order ordinary differential equations. Abundant new solutions for both models were obtained, and to further clarify the physical meaning of these solutions, some plots are sketched in three- and two-dimensional and contour plots (Figs. 1, 2, 3, 4).