1 Introduction

The aim of this paper is to investigate the dynamic behaviors of the following Lotka–Volterra predator–prey system incorporating fear effect of the prey and the predator having other food resource:

$$ \begin{aligned} &\frac{du}{dt} = \frac{r_{0}u}{1+kv}-du-au^{2}-puv, \\ &\frac{dv}{dt} = cpuv+m v-d_{1}v^{2}, \end{aligned} $$
(1.1)

where u and v are the density of prey species and the predator species at time t, respectively. \(r_{0}\) is the birth rate of the prey species, d is the death rate of the prey species, a is the intraspecific competition of the prey species, m is the intrinsic grow rate of the predator species; p denotes the strength of interspecific between prey and predator; c is the conversion efficiency of ingested prey into new predators; \(d_{1}\) is the intraspecific competition of the predator species; k is the level of fear, which is due to anti-predator behaviors of the prey. Here we make the assumption that without the prey species, the predator species satisfies the logistic equation

$$ \frac{dv}{dt} = m v-d_{1}v^{2}. $$
(1.2)

It is well known that the logistic equation admits a unique positive equilibrium which is globally attractive. Therefore, here we assume that the predator species could be permanent without the affordable of the prey species. Such an assumption means that the predator species takes other species as food resources.

The predator–prey relationship has been highly valued by scholars because of its widespread existence [1–24]. Wang, Zanette and Zou [1] proposed the following Lotka–Volterra predator–prey system incorporating the fear effect of the prey:

$$ \begin{aligned} &\frac{du}{dt}=r_{0}uf(k,v)-du-au^{2}-puv, \\ &\frac{dv}{dt}=cpuv-m v. \end{aligned} $$
(1.3)

The system admits three nonnegative equilibria, \(E_{0}(0,0)\), \(E_{1}(\frac{r_{0}-d}{a},0)\) and \(E_{2}(\overline{u},\overline{v})\), where \(\overline{u}=\frac{m}{cp}\), and v̅ satisfies

$$ r_{0}f(k,\overline{v})-d-a\overline{u}-p\overline{v}=0. $$
(1.4)

Concerned with the dynamic behaviors of the system (1.3), the authors obtained the following result (see Theorems 3.1 and 3.2 in [1]).

Theorem A

Assume that\(r_{0}< d\), then\(E_{0}\)is globally asymptotically stable; The boundary equilibrium\(E_{1}\)is globally asymptotically stable if\(r_{0}\in(d, d+\frac{am}{cp})\), and the unique positive equilibrium\(E_{2}\)is globally asymptotically stable if\(r_{0}> d+\frac{am}{cp}\).

One could easily see that in Theorem A, all the conditions are independent of k, which means that the fear effect of the prey species has no influence to the dynamic behaviors of the system. It brings to our attention that in system (1.3), without the prey species, the predator species satisfies the equation

$$ \frac{dv}{dt} = -m v. $$
(1.5)

Hence,

$$ v(t)=v(0)\exp\{-mt\}\rightarrow0 \quad \mbox{as } t \rightarrow+\infty. $$
(1.6)

This indicates that in system (1.3), the predator species has prey as its unique food resource. Now, it is well known that in the nature, predator species often take many species as its food resource, such that if one resource is scarce, it could take other food resource to maintain its life. This leads us to propose the system (1.1).

The aim of this paper is to investigate the dynamic behaviors of the system (1.1), and to find the influence of the fear effect on the prey species.

The rest of the paper is arranged as follows. We will investigate the local and global stability property of the equilibria of the system (1.1) in Sects. 2 and 3, respectively, and then discuss the influence of fear effect in Sect. 4. Numeric simulations are presented in Sect. 5 to show the feasibility of the main results. We end this paper with a brief discussion.

2 The existence and local stability of the equilibria of system (1.1)

Concerned with the existence of the equilibria of system (1.1), we have the following results.

Theorem 2.1

System (1.1) always admits the trivial boundary equilibrium\(E_{0}(0,0)\)and prey free equilibrium\(E_{1}(0,\frac{m}{d_{1}})\), if\(r_{0}>d \)holds, then the predator free equilibrium\(E_{2} (\frac{r_{0}-d }{a},0 )\)exists. Also, there exists a unique positive equilibrium\(E_{3}(u^{*},v^{*})\), if

$$ r_{0}>d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}} $$
(2.1)

holds, where\(v^{*}=\frac{m+cpu^{*}}{d_{1}}\)and\(u^{*}\)is the unique positive solution of the equation

$$ A_{1}u^{2}+A_{2}u+A_{3}=0, $$
(2.2)

where

$$ \begin{aligned} &A_{1} = {c}^{2}k{p}^{3}+ac d_{1}kp, \\ &A_{2} = cd d_{1} kp+2 ckm{p}^{2}+a d_{1} km+c d_{1} {p}^{2}+ad_{1}^{2}, \\ &A_{3} = d d_{1}km+k{m}^{2}p+d d_{1}^{2}- d_{1}^{2} r_{0}+ d_{1}mp. \end{aligned} $$
(2.3)

Proof

The equilibrium of system (1.1) satisfies the equation

$$ \begin{aligned} &\frac{r_{0}u}{1+kv}-du-au^{2}-puv=0, \\ &cpuv+m v-d_{1}v^{2}=0. \end{aligned} $$
(2.4)

From the second equation of (2.4), one has \(v=0\) or \(v =\frac{cpu+m}{d_{1}}\). Substituting \(v=0\) to the first equation of (2.4) leads to

$$ r_{0}u -du-au^{2} = 0. $$
(2.5)

Equation (2.5) has solutions \(u_{1}=0 \) and \(u_{2}=\frac{r_{0}-d }{a}\). Hence, system (1.1) admits the trivial equilibrium \(E_{0}(0,0)\), and if \(r_{0}>d\) holds, the predator free equilibrium \(E_{2} (\frac{r_{0}-d}{a},0 )\) exists.

Next, substituting \(v =\frac{cpu+m}{d_{1}}\) to the first equation of (2.4) and simplify, then we obtain

$$ A_{1}u^{2}+A_{2}u+A_{3}=0, $$
(2.6)

Under the assumption of (2.1), one could easily see that \(A_{3}<0\), hence, (2.6) admits a unique positive solution \(u^{*}\), consequently, system (1.1) admits a unique positive equilibrium \(E_{3}(u^{*},v^{*})\).

The first equation of (2.4) has solution \(u=0\), substituting this to second equation of (2.4) leads to

$$ m v-d_{1}v^{2} = 0. $$
(2.7)

Hence, system (1.1) admits the prey free equilibrium \(E_{2}(0,\frac{m}{d_{1}})\).

This ends the proof of Theorem 2.1. □

Remark 2.1

One may curiously, whether the system could exist two, one or none positive equilibrium, since this may lead to the saddle-node bifurcation, however, this is impossible. Indeed, if \(A_{3}\geq0\), let us consider the function

$$ F(u)=A_{1}u^{2}+A_{2}u+A_{3}, $$
(2.8)

since the symmetry axis of quadratic function \(F(u)\) is \(u=-\frac{A_{2}}{2A_{1}}<0\), \(F(u)\) should intersect with the negative half part of the u-axis, which means that the other one solution of Eq. (2.6) should be negative. Therefore, it is enough for us to consider the situation of (2.1) and need not to investigate the case

$$ r_{0}< d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}}. $$
(2.9)

Theorem 2.2

The trivial equilibrium\(E_{0}(0,0)\)is unstable, if

$$ r_{0}>d $$
(2.10)

holds, the predator free equilibrium\(E_{2} (\frac{r_{0}-d }{a},0 )\)is unstable, and the prey free equilibrium\(E_{1}(0, \frac{m}{d_{1}})\)is locally asymptotically stable if

$$ r_{0}< d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}} $$
(2.11)

holds; the positive equilibrium\(E_{3}(u^{*},v^{*}) \)is locally asymptotically stable if

$$ r_{0}>d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}} $$
(2.12)

holds, i.e., the positive equilibrium is locally asymptotically stable as long as it exists.

Proof

The Jacobian matrix of the system (1.1) is calculated as

$$ J = \begin{pmatrix} J_{11}& J_{12} \\ J_{21}& J_{22}\end{pmatrix} , $$
(2.13)

where

$$ \begin{aligned} &J_{11} = \frac{ r_{0}}{kv+1} -d-2au-pv, \\ &J_{12} = -\frac{r_{0}uk}{(kv+1)^{2}}-pu, \\ &J_{21} = cpv, \\ &J_{22} = cpu+m-2d_{1}v.\end{aligned} $$
(2.14)

Then the Jacobian matrix of the system (1.1) about the trivial equilibrium \(E_{0}(0,0)\) is

$$ J \bigl(E_{0}(0,0) \bigr) = \begin{pmatrix} r_{0}-d & 0 \\ 0 & m\end{pmatrix} . $$
(2.15)

The eigenvalues of \(J(E_{0})\) are \(\lambda_{1}=r_{0}-d \), \(\lambda_{2}=m>0\). Thus, the trivial equilibrium \(E_{0}(0,0)\) is unstable since one of the eigenvalues is positive.

It follows from (2.3) that the Jacobian matrix of the system (1.1) about the predator free equilibrium \(E_{2} (\overline{u},0 )\), where \(\overline{u}=\frac{r_{0}-d }{a}\), is

$$\begin{aligned}& J \bigl( E_{2} (\overline{u},0 ) \bigr) \\& \quad= \begin{pmatrix} r_{0}-d -2a\overline{u}&-r_{0}\overline{u}k-p\overline{u} \\ 0 & cp\overline{u}+m\end{pmatrix} . \end{aligned}$$
(2.16)

Under the assumption (2.11) holds, the eigenvalues of \(J(E_{2})\) are \(\lambda_{1}=r_{0}-d -2a\overline{u}\), \(\lambda_{2}= cp\overline{u}+m>0\). Thus, \(E_{2}(\overline{u},0)\) is unstable if (2.11) holds, since \(\lambda_{2}>0\).

The Jacobian matrix of the system (1.1) about the equilibrium \(E_{1}(0,\frac{m}{d_{1}})\) is

$$\begin{aligned}& J \biggl(E_{1} \biggl(0,\frac{m}{d_{1}} \biggr) \biggr) \\& \quad= \begin{pmatrix} -{ \frac{d{ d_{1}} km+k{m}^{2}p+d{{ d_{1}}}^{2}-{ r_{0}} {{d_{1}}}^{2}+{ d_{1}} mp}{ ( km+{ d_{1}} ) { d_{1}}}} &0 \\ \frac{mcp}{d_{1}}& -m \end{pmatrix} . \end{aligned}$$
(2.17)

Then we have

$$ \lambda_{1}=-m< 0 $$

and

$$ \lambda_{2}= -{ \frac{d{ d_{1}} km+k{m}^{2}p+d{{ d_{1}}}^{2}-{ r_{0}} {{d_{1}}}^{2}+{ d_{1}} mp}{ ( km+{ d_{1}} ) { d_{1}}}}< 0 $$

if (2.11) holds, consequently, \(E_{1}(0,\frac{m}{d_{1}})\) is locally asymptotically stable. Also, \(E_{1}\) is unstable if (2.12) holds, since in this case \(\lambda_{2}>0\).

Noting that \((u^{*},v^{*})\) satisfies the equation

$$ \begin{aligned} &\frac{r_{0}}{1+kv^{*}}-d-au^{*}-pv^{*} = 0, \\ &cpu^{*}+m -d_{1}v^{*} = 0. \end{aligned} $$
(2.18)

Then the Jacobian matrix of the system (1.1) about the positive equilibrium \(E_{3}(u^{*},v^{*})\) is

$$\begin{aligned}& J \bigl(E_{3} \bigl(u^{*},v^{*} \bigr) \bigr) \\& \quad= \begin{pmatrix} \frac{ r_{0}}{kv^{*}+1} -d-2au^{*}-pv^{*} &-\frac{r_{0}u^{*}k}{(kv^{*}+1)^{2}}-pu^{*} \\ cpv^{*}& cpu^{*}+m-2d_{1}v^{*} \end{pmatrix} \\& \quad= \begin{pmatrix} -au^{*} &-\frac{r_{0}u^{*}k}{(kv^{*}+1)^{2}}-pu^{*} \\ cpv^{*}& -d_{1}v^{*} \end{pmatrix} . \end{aligned}$$
(2.19)

Then we have

$$ DetJ \bigl(E_{3} \bigl(u^{*},v^{*} \bigr) \bigr)=ad_{1}u^{*}v^{*}-cpv^{*}u^{*} \biggl(- \frac{r_{0} k}{(kv^{*}+1)^{2}}-p \biggr)>0 $$

and

$$ TrJ \bigl(E_{3} \bigl(u^{*},v^{*} \bigr) \bigr)= -au^{*}-d_{1}v^{*} < 0. $$

So both eigenvalues of \(J (E_{3}(u^{*},v^{*}))\) have negative real parts, consequently, \(E_{3}(u^{*},v^{*})\) is locally asymptotically stable.

This ends the proof of Theorem 2.2. □

Remark 2.2

Theorem A shows that under some suitable assumption, the trivial equilibrium \(E_{0}\) and the predator free equilibrium \(E_{1}\) of system (1.3) are globally asymptotically stable, however, Theorem 2.2 shows that \(E_{0}\) and \(E_{1}\) of system (1.1) are unstable. Thus, the dynamic behaviors of system (1.3) are quite different to system (1.1). Also, system (1.3) has no prey free equilibrium, while under some assumption, system (1.1) admits a prey free equilibrium, which is locally asymptotically stable.

3 Global asymptotical stability

The aim of this section is to investigate the global stability property of the prey free equilibrium \(E_{2}(0,\frac{m}{d_{1}})\) and the positive equilibrium \(E_{3}(u^{*},v^{*})\) of system (1.1). Indeed, we have the following result.

Theorem 3.1

  1. (i)

    The prey free equilibrium\(E_{1}(0, \frac{m}{d_{1}})\)is globally asymptotically stable if

    $$ r_{0}< d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}} $$
    (3.1)

    holds;

  2. (ii)

    the positive equilibrium\(E_{3}(u^{*},v^{*}) \)of system (1.1) is globally asymptotically stable if

    $$ r_{0}>d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}} $$
    (3.2)

    holds, i.e., the positive equilibrium is globally asymptotically stable as long as it exists.

Proof

(i) We will prove (i) by constructing some suitable Lyapunov function.

Let us define a Lyapunov function

$$ V_{1}(u, v)= c u +v- \overline{v}-\overline{v}\ln \frac{v}{\overline{v}}, $$
(3.3)

where \(\overline{v} =\frac{m}{d_{1}}\).

Then the time derivative of \(V_{1}\) along the trajectories of (1.1) is

$$ \begin{aligned}[b] D^{+}V_{1}(t) &= c \biggl( \frac{r_{0}u}{1+kv}-du-au^{2}-puv \biggr) \\ &\quad{} +(v-\overline{v}) (cpu+m -d_{1}v) \\ &= c \biggl( \frac{r_{0}u}{1+kv}-du-au^{2}-puv \biggr) \\ &\quad{} +(v-\overline{v}) \bigl(cpu+d_{1}v^{*} -d_{1}v \bigr) \\ &\leq c (r_{0}-d )u-cau^{2}-cp\overline{v}u-d_{1} \bigl(v-v^{*} \bigr)^{2} \\ &< 0. \end{aligned} $$
(3.4)

Thus, \(V_{1}(x, y)\) satisfies the Lyapunov asymptotic stability theorem, and the boundary equilibrium \(E_{1}(0, \frac{m}{d_{1}})\) of system (1.1) is globally asymptotically stable.

(ii) Under the assumption of (3.2), it follows from Theorem 2.2 that system (1.1) admits a unique positive equilibrium, which is locally asymptotically stable, and the prey free equilibrium is unstable. To show that \(E_{3}(u^{*}, v^{*})\) is globally asymptotically stable, it is enough to show that the system admits no limit cycle in the first quadrant (see [25–34]). Let us consider the Dulac function \(B(u,v)=\frac{1}{uv}\), then

$$ \begin{aligned}[b] &\frac{\partial(PB)}{\partial{u}}+\frac{\partial(QB)}{\partial{v}} \\ &\quad={\frac{1}{uv} \biggl( {\frac{{ r_{0}}}{kv+1}}-d-2 au-pv \biggr) } \\ &\qquad{}-{ \frac{1}{{u}^{2}v} \biggl( {\frac{{ r_{0}} u}{kv+1}}-du-a{u}^{2}-puv \biggr) } \\ &\qquad{}+{\frac{cpu-2 { d_{1}} v+m}{uv}}-{ \frac{cpuv-{ d_{1}} { v}^{2}+mv}{u{v}^{2}}} \\ &\quad= -\frac{au+d_{1}v}{uv}< 0, \end{aligned} $$
(3.5)

where

$$ \begin{aligned} &P(u,v) = \frac{r_{0}u}{1+kv}-du-au^{2}-puv, \\ &Q(u,v) = cpuv+m v-d_{1}v^{2}. \end{aligned} $$
(3.6)

By the Dulac theorem [34], there is no closed orbit in the first quadrant. Consequently, \(E_{3}(u^{*}, v^{*})\) is globally asymptotically stable.

The proof of Theorem 3.1 is finished. □

4 The influence of fear effect

In the following we will discuss the effect of the fear effect.

Denote

$$ \begin{aligned} &F \bigl(u^{*},v^{*},k \bigr) = \frac{r_{0} }{1+kv^{*}}-d -au^{*} -p v^{*}, \\ &G \bigl(u^{*},v^{*},k \bigr) = cpu^{*} +m -d_{1}v^{*}. \end{aligned} $$
(4.1)

Then the positive equilibrium \(E_{3}(u^{*},v^{*})\) satisfies

$$ \textstyle\begin{cases} F(u^{*},v^{*},k)=0, \\ G(u^{*},v^{*},k)=0. \end{cases} $$
(4.2)

By simple computation, we have

$$\begin{aligned} J =& \frac{D(F,G)}{D(u^{*},v^{*})} \\ =& \begin{vmatrix} F_{u^{*}}& F_{v^{*}} \\ G_{u^{*}}& G_{v^{*}} \end{vmatrix} \\ =& \begin{vmatrix} -a &-\frac{r_{0}k}{(1+kv^{*})^{2}}-p \\ cp &-d_{1} \end{vmatrix} \\ =&ad_{1}+ cp \biggl(\frac{r_{0}k}{(1+kv^{*})^{2}}+p \biggr)>0 \end{aligned}$$

for all \(u^{*}>0\), \(v^{*}>0\), \(k>0\). Thus, Eqs. (4.2) satisfy the conditions of the existence theorem for implicit functions, then Eqs. (4.2) determine the two implicit functions of

$$ u^{*}=u^{*}(k),\qquad v^{*}=v^{*}(k) $$

for all \(k>0\). Also,

$$ \frac{d u^{*}}{d k}=-\frac{1}{J}\frac{D(F,G)}{D(k,v^{*})},\qquad \frac{d v^{*}}{d k}=-\frac{1}{J}\frac{D(F,G)}{D(u^{*},k)}. $$

By computation, we have

$$\begin{aligned}& \frac{D(F,G)}{D(k,v^{*})}= \begin{vmatrix} -\frac{r_{0}v^{*}}{(1+kv^{*})^{2}}&-\frac{r_{0}k}{(1+kv^{*})^{2}}-p \\ 0&-d_{1}\end{vmatrix} =\frac{r_{0}d_{1}v^{*}}{(1+kv^{*})^{2}}>0, \\& \frac{D(F,G)}{D(u^{*},k)}= \begin{vmatrix} -a&-\frac{r_{0}v^{*}}{(1+kv^{*})^{2}} \\ cp&0\end{vmatrix} =\frac{cpr_{0}v^{*}}{(1+kv^{*})^{2}}>0, \end{aligned}$$

and so \(\frac{d u^{*}}{d k}<0\), \(\frac{d v^{*}}{d k} <0\), that is, both the prey and predator density are a decreasing function of k.

5 Numeric simulations

We will introduce two examples to show the feasibility of the main results.

Example 5.1

Let us consider the following model:

$$ \begin{aligned} &\frac{du}{dt} = \frac{2u}{1+v} u-u^{2}-uv, \\ &\frac{dv}{dt} = \frac{1}{2}uv+ v- v^{2}. \end{aligned} $$
(5.1)

Here, corresponding to system (1.1), we take \(r_{0}=2\), \(d=k=a=p=m=d_{1} =1\), \(c=0.5\). then one could see that

$$ r_{0}=2< 4=d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}}. $$
(5.2)

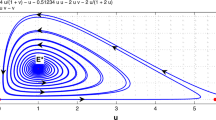
Hence, it follows from Theorem 3.1 that the prey free equilibrium \(E_{2}(0,1)\) of system (5.1) is globally asymptotically stable. Numeric simulation (Fig. 1) also supports this assertion.

Figure 1
figure 1

Dynamic behaviors of the system (5.1), the initial condition \((u(0), v(0))=(2,2), (2, 1), (2, 0.2)\) and \((2, 0.5)\), respectively

Full size image

Example 5.2

Let us consider the following model:

$$ \begin{aligned} &\frac{du}{dt} = \frac{5u}{1+v} u-u^{2}-uv, \\ &\frac{dv}{dt} = \frac{1}{2}uv+ v- v^{2}. \end{aligned} $$
(5.3)

Here, corresponding to system (1.1), we take \(r_{0}=5\), \(d=1\), \(k=a=p=q_{1}=m= q_{2}=1\), \(c=0.5 \), then one could see that

$$ r_{0}=5>4=d+\frac{d d_{1} km+k{m}^{2}p+ { d_{1}} mp}{d_{1}^{2}}. $$
(5.4)

Hence, it follows from Theorem 3.1 that system (5.3) admits a unique positive equilibrium which is globally asymptotically stable. Numeric simulations (Figs. 2 and 3) also support this assertion.

Figure 2
figure 2

Dynamic behaviors of the prey species in system (5.3), the initial condition \((u(0), v(0))=(0.1,0.5), (0.6, 2), (0.5, 0.2)\) and \((1.2, 2)\), respectively

Full size image
Figure 3
figure 3

Dynamic behaviors of the predator species in system (5.3), the initial condition \((u(0), v(0))=(0.1,0.5), (0.6, 2), (0.5, 0.2)\) and \((1.2, 2)\), respectively

Full size image

Now, based on system (5.3), let us furthermore consider the system

$$ \begin{aligned} &\frac{du}{dt} = \frac{5u}{1+kv} u-u^{2}-uv, \\ &\frac{dv}{dt} = \frac{1}{2}uv+ v- v^{2}. \end{aligned} $$
(5.5)

Obviously, the positive equilibrium \(E_{3}(u^{*},v^{*})\) satisfies the equation

$$ \begin{aligned} &\frac{5}{1+kv^{*}}- 1-u^{*}-v^{*} = 0, \\ &\frac{1}{2}u^{*}+ 1- v^{*} = 0. \end{aligned} $$
(5.6)

Solving (5.6) we obtain

$$ u^{*} = \frac{-5k-3+\sqrt{k^{2}+66k+9}}{3k}, \qquad v^{*} = \frac{1}{2}u^{*}+1. $$
(5.7)

From Fig. 4, one could see that \(u^{*}\) is the decreasing function of k. This is in coincidence with the analysis result of the previous section. Also, from the relationship of \(v^{*}\) and \(u^{*}\), one could easily see that \(v^{*}\) is a decreasing function of k.

Figure 4
figure 4

Relationship of \(u^{*}\) and k

Full size image

6 Conclusion

Wang, Zanette and Zou [6] proposed a Lotka–Volterra predator–prey system incorporating the fear effect of prey species, i.e., system (1.3). Their result (Theorem A) indicates that the fear effect has no influence to the existence and stability of the equilibria. That is, if for the system without fear effect there exists a positive equilibrium, then the system with fear effect also admits a unique positive equilibrium, which is globally asymptotically stable. Hence, the fear effect of prey species has no influence on the persistent property of the system.

Stimulated by the fact that the predator species generally speaking is omnivorous, and if a particular kind of food source die out, they will feed on other food resources, we propose the system (1.1). One may conjecture that system (1.1) has similar dynamic behaviors to that of system (1.3). However, our study shows that the trivial equilibrium and the predator free equilibrium are both unstable, while the prey free equilibrium may be globally asymptotically stable. This affirms the fact that the predator species may still be permanent, despite the extinction of the prey species.

There are also some similarities between the system (1.1) and (1.3), indeed, if the positive equilibrium of system (1.1) exists, it is globally asymptotically stable, this is similar to the property of system (1.1).

From the numeric simulation (Fig. 4) of Example 5.2, one could see that with increasing fear effect, the final density of the prey species may approach zero, which means that the prey species will finally be driven to extinction. That is, the fear phenomenon has a negative effect on the survival of the prey species, it may be one of the essential factor that leads to the extinction of prey species. Such a finding is quite different from the result of Wang, Zanette and Zou [6].