1 Introduction

Throughout this paper, for a bounded continuous function g defined on R, let \(g^{L}\) and \(g^{M}\) be defined as

$$g^{L}=\inf_{t\in R}g(t),\qquad g^{M}=\sup _{t\in R}g(t). $$

During the last two decades, the study of dynamic behaviors of predator-prey system incorporating a prey refuge become one of the most important research topic, see [1–45] and the references cited therein. In [1], Yue proposed and studied the following modified Leslie-Gower predator-prey model with Holling-type II schemes and a prey refuge:

$$\begin{aligned}& \begin{aligned} & \dot{x}(t)=x \biggl(r_{1}-b_{1}x- \frac{a_{1}(1-m)y}{(1-m)x+k_{1}} \biggr), \\ & \dot{y}(t)=y \biggl(r_{2}- \frac{a_{2} y}{(1-m)x+k_{2}} \biggr), \end{aligned} \end{aligned}$$
(1.1)

where \(x(t)\) and \(y(t)\) denote the densities of the predator and prey species at time t, respectively, and all the coefficients are all positive constants, \(0\leq m<1\). Such a topic as the global stability property of the positive equilibrium was investigated.

Many authors [2, 4, 5, 8, 9] argued that with the biological and environmental change of the circumstance, it is reasonable to propose and study the nonautonomous system, the success of [2, 4, 5, 8, 9] motivates us to propose the corresponding nonautonomous case of system (1.1), i.e., the following system:

$$\begin{aligned}& \begin{aligned} & \dot{x}(t)=x \biggl(r_{1}(t)-b_{1}(t)x- \frac {a_{1}(t)(1-m(t))y}{(1-m(t))x+k_{1}(t)} \biggr), \\ & \dot{y}(t)=y \biggl(r_{2}(t)- \frac{a_{2}(t) y}{(1-m(t))x+k_{2}(t)} \biggr), \end{aligned} \end{aligned}$$
(1.2)

where \(x(t)\) and \(y(t)\) denote the densities of the predator and prey species at time t, respectively; One could refer to [1] for the biological meaning of the coefficients. Throughout this paper, we assume that

(\(H_{1}\)):

\(r_{i}(t)\), \(k_{i}(t)\), \(a_{i}(t)\), \(i=1,2\), \(m(t)\), \(b_{1}(t)\) are continuous and strictly positive functions, which satisfy

$$\begin{aligned}& \min \bigl\{ r_{i}^{L}, k_{i}^{L}, a_{i}^{L}, m^{L}, b_{1}^{L} \bigr\} >0, \\& \max \bigl\{ r_{i}^{M}, k_{i}^{M}, a_{i}^{M}, m^{M}, b_{1}^{M} \bigr\} < +\infty. \end{aligned}$$

We consider (1.2) together with the following initial conditions:

$$ x(0)> 0,\qquad y(0)> 0. $$
(1.3)

It is not difficult to see that solutions of (1.2)-(1.3) are well defined for all \(t\geq0\) and satisfy

$$ x(t)>0,\qquad y(t)>0 \quad \mbox{for all } t\geq0. $$
(1.4)

The paper is arranged as follows: In Section 2, we obtain sufficient conditions which guarantee the permanence of the system (1.2). In Section 3, we obtain sufficient conditions which ensure the global attractivity of the system (1.2). In Section 4, an example together with its numeric simulations illustrates the feasibility of the main results. We end this paper by a brief discussion.

2 Permanence

Lemma 2.1

Let \((x(t),y(t))^{T}\) be any solution of system (1.2) with the initial conditions (1.3), then

$$\begin{aligned}& \begin{aligned} &\limsup_{t\rightarrow+\infty} x(t)\leq \frac {r_{1}^{M}}{b_{1}^{L}} \stackrel{\mathrm{def}}{=}M_{1}, \\ &\limsup_{t\rightarrow+\infty} y(t)\leq \frac {r_{2}^{M} ((1-m^{L})M_{1}+k_{2}^{M} )}{a_{2}^{L}}\stackrel{ \mathrm{def}}{=}M_{2}. \end{aligned} \end{aligned}$$
(2.1)

Proof

Let \((x(t),y(t))^{T}\) be any solution of system (1.2) with the initial conditions (1.3). From the first equation of system (1.2), it follows that

$$\begin{aligned} \dot{x}(t) =&x \biggl(r_{1}(t)-b_{1}(t)x- \frac {a_{1}(t)(1-m(t))y}{(1-m(t))x+k_{1}(t)} \biggr) \\ \leq&x\bigl(r_{1}^{M}- b_{1}^{L}x \bigr). \end{aligned}$$
(2.2)

Applying Lemma 2.3 in [46] to (2.2), it immediately follows that

$$ \limsup_{t\rightarrow+\infty} x(t)\leq\frac {r_{1}^{M}}{b_{1}^{L}}\stackrel{\mathrm{def}}{=}M_{1}. $$
(2.3)

For any positive constant \(\varepsilon>0\) small enough, it follows from (2.3) that there exists a \(T_{1}>0\) such that

$$ x(t)< M_{1}+\varepsilon\quad \mbox{for all } t\geq T_{1}. $$
(2.4)

For \(t>T_{1}\), (2.4) together with the second equation of system (1.2) leads to

$$\begin{aligned} \dot{y}(t) =&y \biggl(r_{2}(t)- \frac{a_{2}(t) y}{(1-m(t))x+k_{2}(t)} \biggr) \\ \leq& y \biggl(r_{2}^{M}- \frac{a_{2}^{L} }{(1-m^{L})(M_{1}+\varepsilon)+k_{2}^{M}}y \biggr). \end{aligned}$$
(2.5)

Applying Lemma 2.3 in [46] to (2.5), it immediately follows that

$$ \limsup_{t\rightarrow+\infty} y(t)\leq \frac {r_{2}^{M}((1-m^{L})(M_{1}+\varepsilon)+k_{2}^{M})}{a_{2}^{L}}. $$
(2.6)

Setting \(\varepsilon\rightarrow0\), then

$$ \limsup_{t\rightarrow+\infty} y(t)\leq \frac{r_{2}^{M} ((1-m^{L})M_{1}+k_{2}^{M} )}{a_{2}^{L}}\stackrel{ \mathrm{def}}{=}M_{2}. $$
(2.7)

 □

Lemma 2.2

Let \((x(t),y(t))^{T}\) be any solution of system (1.2) with the initial conditions (1.3), assume that

$$ r_{1}^{L}> \frac{a_{1}^{M}(1-m^{L})M_{2}}{k_{1}^{L}} $$
(2.8)

holds, then

$$\begin{aligned}& \liminf_{t\rightarrow+\infty} x(t)\geq \frac {r_{1}^{L}k_{1}^{L}-a_{1}^{M}(1-m^{L})M_{2}}{k_{1}^{L}b_{1}^{M}}\stackrel{\mathrm {def}}{=}m_{1}, \end{aligned}$$
(2.9)
$$\begin{aligned}& \liminf_{t\rightarrow+\infty} y(t)\geq\frac{r_{2}^{L} ((1-m^{M})m_{1}+k_{2}^{L} )}{a_{2}^{M}}\stackrel{ \mathrm{def}}{=}m_{2}. \end{aligned}$$
(2.10)

Proof

Condition (2.8) implies that one could choose \(\varepsilon>0\) small enough such that

$$ r_{1}^{L}> \frac{a_{1}^{M}(1-m^{L})(M_{2}+\varepsilon)}{k_{1}^{L}} $$
(2.11)

holds. For this ε, it follows from (2.7) that there exists a \(T_{2}>T_{1}\) such that

$$ y(t)< M_{2}+\varepsilon \quad \mbox{for all } t\geq T_{2}. $$
(2.12)

Let \((x(t),y(t))^{T}\) be any solution of system (1.2) with the initial conditions (1.3). For \(t>T_{2}\), (2.12) together with the first equation of system (1.2) leads to

$$\begin{aligned} \dot{x}(t) =&x \biggl(r_{1}(t)-b_{1}(t)x- \frac {a_{1}(t)(1-m(t))y}{(1-m(t))x+k_{1}(t)} \biggr) \\ \geq& x \biggl(r_{1}^{L}- \frac{a_{1}^{M}(1-m^{L})(M_{2}-\varepsilon) }{ k_{1}^{L}}-b_{1}^{M}x \biggr). \end{aligned}$$
(2.13)

Applying Lemma 2.3 in [46] to (2.13), it immediately follows that

$$ \liminf_{t\rightarrow+\infty} x(t)\geq \frac{r_{1}^{L}- \frac{a_{1}^{M}(1-m^{L})(M_{2}-\varepsilon) }{ k_{1}^{L}}}{b_{1}^{M}}. $$
(2.14)

Setting \(\varepsilon\rightarrow0\), then

$$ \liminf_{t\rightarrow+\infty} x(t)\geq \frac {r_{1}^{L}k_{1}^{L}-a_{1}^{M}(1-m^{L})M_{2}}{k_{1}^{L}b_{1}^{M}}\stackrel{\mathrm {def}}{=}m_{1}. $$
(2.15)

Let \(\varepsilon>0\) be any positive constant small enough such that \(\varepsilon<\frac{1}{2}m_{1}\). It then follows from (2.15) that there exists a \(T_{3}>T_{2}\), such that

$$ x(t)>m_{1}-\varepsilon \quad \mbox{for all } t\geq T_{3}. $$
(2.16)

From the second equation of system (1.2), it follows that

$$\begin{aligned} \dot{y}(t) =&y \biggl(r_{2}(t)- \frac{a_{2}(t) y}{(1-m(t))x+k_{2}(t)} \biggr) \\ \geq&y(t) \biggl[r_{2}^{L}- \frac{a_{2}^{M}y(t)}{(1-m^{M})(m_{1}-\varepsilon)+k_{2}^{L}} \biggr]. \end{aligned}$$
(2.17)

Applying Lemma 2.3 in [46] to (2.17), it immediately follows that

$$ \liminf_{t\rightarrow+\infty} y(t)\geq\frac{r_{2}^{L} ((1-m^{M})(m_{1}-\varepsilon)+k_{2}^{L} )}{a_{2}^{M}}. $$
(2.18)

Setting \(\varepsilon\rightarrow0\), then

$$ \liminf_{t\rightarrow+\infty} y(t)\geq\frac{r_{2}^{L} ((1-m^{M})m_{1}+k_{2}^{L} )}{a_{2}^{M}}\stackrel{ \mathrm{def}}{=}m_{2}. $$
(2.19)

 □

As a direct corollary of Lemma 2.1 and 2.2, we have the following.

Theorem 2.1

Assume that (2.8) holds, then system (1.2)-(1.3) is permanent.

3 Global attractivity

Before we state the main result of this section, we introduce some notations. Set

$$\begin{aligned}& \Delta_{1}(m_{1})\stackrel{\mathrm{def}}{=}\bigl( \bigl(1-m(t)\bigr)m_{1}+k_{1}(t) \bigr)^{2}, \\& \Delta_{2}(m_{1})\stackrel{\mathrm{def}}{=} \bigl(\bigl(1-m(t)\bigr)m_{1} +k_{2}(t) \bigr)^{2}, \\& \Delta_{2}(M_{1})\stackrel{\mathrm{def}}{=}\bigl( \bigl(1-m(t)\bigr)M_{1} +k_{2}(t) \bigr)^{2}, \end{aligned}$$
(3.1)

and

$$\begin{aligned}& \Gamma_{1}(t)\stackrel{\mathrm{def}}{=}b_{1}(t)- \frac {a_{1}(t)(1-m(t))^{2}M_{2}}{\Delta_{1}(m_{1})} - \frac{a_{2}(t)(1-m(t))M_{2}}{\Delta_{2}(m_{1})}, \\& \Gamma_{2}(t)\stackrel{\mathrm{def}}{=} \frac{ a_{2}(t)k_{2}(t)}{\Delta_{2}(M_{1})}+ \frac{a_{2}(t)(1-m(t))m_{1}}{\Delta _{2}(M_{1})} \\& \hphantom{\Gamma_{2}(t)\stackrel{\mathrm{def}}{=}}{}- \frac{a_{1}(t)(1-m(t))k_{1}(t)}{\Delta_{1}(m_{1})}- \frac {a_{1}(t)(1-m(t))^{2}M_{1}}{\Delta_{1}(m_{1})}. \end{aligned}$$
(3.2)

Theorem 3.1

Assume that all the conditions of Theorem 2.1 hold, assume further that

$$ \liminf_{t\rightarrow+\infty} \bigl\{ \Gamma_{1}(t), \Gamma_{2}(t) \bigr\} >0, $$
(3.3)

then for any positive solutions \((x(t),y(t))^{T}\) and \((x_{1}(t),y_{1}(t))^{T} \) of system (1.2), one has

$$\lim_{t\rightarrow+\infty }\bigl(\bigl\vert x(t)-x_{1}(t)\bigr\vert +\bigl\vert y(t)-y_{1}(t)\bigr\vert \bigr)=0. $$

Proof

Condition (3.3) implies that there exists a small enough positive constant ε (without loss of generality, we may assume that \(\varepsilon<\frac{1}{2}\{m_{1}, m_{2}\}\)) such that

$$\begin{aligned}& \Gamma_{1}(\varepsilon,t)=b_{1}(t)- \frac {a_{1}(t)(1-m(t))^{2}(M_{2}+\varepsilon)}{\Delta_{1}(m_{1}^{\varepsilon})} \\& \hphantom{\Gamma_{1}(\varepsilon,t)=}{} - \frac{a_{2}(t)(1-m(t))(M_{2}+\varepsilon)}{\Delta _{2}(m_{1}^{\varepsilon})}\geq\varepsilon, \\ & \\ & \Gamma_{2}(\varepsilon,t)= \frac{ a_{2}(t)k_{2}(t)}{\Delta _{2}(M_{1}^{\varepsilon})}+ \frac{a_{2}(t)(1-m(t))(m_{1}-\varepsilon)}{\Delta_{2}(M_{1}^{\varepsilon})} \\& \hphantom{\Gamma_{2}(\varepsilon,t)=}{}- \frac{a_{1}(t)(1-m(t))k_{1}(t)}{\Delta_{1}(m_{1}^{\varepsilon})}- \frac{a_{1}(t)(1-m(t))^{2}(M_{1}+\varepsilon)}{\Delta_{1}(m_{1}^{\varepsilon})}\geq\varepsilon, \end{aligned}$$
(3.4)

where

$$\begin{aligned}& \Delta_{1}\bigl(m_{1}^{\varepsilon}\bigr)=\bigl( \bigl(1-m(t)\bigr) (m_{1}-\varepsilon) +k_{1}(t) \bigr)^{2}, \\& \Delta_{2}\bigl(m_{1}^{\varepsilon}\bigr)= \bigl(\bigl(1-m(t)\bigr) (m_{1}-\varepsilon) +k_{2}(t) \bigr)^{2}, \\& \Delta_{2}\bigl(M_{1}^{\varepsilon}\bigr)=\bigl( \bigl(1-m(t)\bigr) (M_{1}+\varepsilon) +k_{2}(t) \bigr)^{2}. \end{aligned}$$
(3.5)

For two arbitrary positive solutions \((x(t),y(t))^{T}\) and \((x_{1}(t),y_{1}(t))^{T}\) of system (1.2), for the above \(\varepsilon>0\), it then follows from (2.1), (2.15), and (2.19) that there exists a \(T>T_{3}\), such that for all \(t\geq T\),

$$\begin{aligned}& \begin{aligned} & x(t),x_{1}(t)< M_{1}+ \varepsilon, \qquad y(t), y_{1}(t)< M_{2}+\varepsilon, \\ & x(t), x_{1}(t)>m_{1}-\varepsilon, \qquad y(t), y_{1}(t)>m_{2}-\varepsilon. \end{aligned} \end{aligned}$$
(3.6)

Set

$$\begin{aligned}& \begin{aligned} &\Delta_{1}\bigl(x(t),x_{1}(t)\bigr)= \bigl(\bigl(1-m(t)\bigr)x_{1}(t)+k_{1}(t) \bigr) \bigl( \bigl(1-m(t)\bigr)x(t)+k_{1}(t) \bigr), \\ &\Delta_{2}\bigl(x(t),x_{1}(t)\bigr)= \bigl(\bigl(1-m(t) \bigr)x_{1}(t)+k_{2}(t) \bigr) \bigl(\bigl(1-m(t) \bigr)x(t)+k_{2}(t) \bigr). \end{aligned} \end{aligned}$$
(3.7)

Now we let

$$\begin{aligned}& V_{1}(t)= \bigl\vert \ln x(t)-\ln x_{1}(t) \bigr\vert , \end{aligned}$$
(3.8)
$$\begin{aligned}& V_{2}(t)= \bigl\vert \ln y(t)-\ln y_{1}(t) \bigr\vert . \end{aligned}$$
(3.9)

Then for \(t>T\), we have

$$\begin{aligned} &D^{+}V_{1}(t) \\ &\quad \leq \operatorname{sgn}\bigl(x(t)-x_{1}(t)\bigr) \biggl( -b_{1}(t)x(t)- \frac {a_{1}(t)(1-m(t))y(t)}{(1-m(t))x(t)+k_{1}(t)} \\ &\qquad {}+b_{1}(t)x_{1}(t)+ \frac {a_{1}(t)(1-m(t))y_{1}(t)}{(1-m(t))x_{1}(t)+k_{1}(t)} \biggr) \\ &\quad \leq -b_{1}(t)\bigl\vert x(t)-x_{1}(t)\bigr\vert \\ &\qquad {}+a_{1}(t) \bigl(1-m(t)\bigr) \biggl\vert \frac{y_{1}(t)}{(1-m(t))x_{1}(t)+k_{1}(t)}- \frac{y(t)}{(1-m(t))x(t)+k_{1}(t)} \biggr\vert \\ &\quad = -b_{1}(t)\bigl\vert x(t)-x_{1}(t)\bigr\vert + \frac{a_{1}(t)(1-m(t))}{\Delta _{1}(x(t),x_{1}(t))} \\ &\qquad {} \times\bigl\vert y_{1}(t) \bigl(\bigl(1-m(t) \bigr)x(t)+k_{1}(t)\bigr)-y(t) \bigl( \bigl(1-m(t)\bigr)x_{1}(t)+k_{1}(t) \bigr) \bigr\vert \\ &\quad = -b_{1}(t)\bigl\vert x(t)-x_{1}(t)\bigr\vert + \frac{a_{1}(t)(1-m(t))k_{1}(t)}{\Delta _{1}(x(t),x_{1}(t))}\bigl\vert y(t)-y_{1}(t)\bigr\vert \\ &\qquad {}+ \frac{a_{1}(t)(1-m(t))^{2}}{\Delta_{1}(x(t),x_{1}(t))} \bigl\vert y_{1}(t)x(t) -y(t) x_{1}(t) \bigr\vert \\ &\quad = -b_{1}(t)\bigl\vert x(t)-x_{1}(t)\bigr\vert + \frac{a_{1}(t)(1-m(t))k_{1}(t)}{\Delta _{1}(x(t),x_{1}(t))}\bigl\vert y(t)-y_{1}(t)\bigr\vert \\ &\qquad {}+ \frac{a_{1}(t)(1-m(t))^{2}}{\Delta_{1}(x(t),x_{1}(t))} \bigl\vert y_{1}(t) x(t)-y_{1}(t)x_{1}(t)+y_{1}(t)x_{1}(t) -y(t) x_{1}(t) \bigr\vert \\ &\quad = -b_{1}(t)\bigl\vert x(t)-x_{1}(t)\bigr\vert + \frac{a_{1}(t)(1-m(t))k_{1}(t)}{\Delta _{1}(x(t),x_{1}(t))}\bigl\vert y(t)-y_{1}(t)\bigr\vert \\ &\qquad {}+ \frac{a_{1}(t)(1-m(t))^{2}y_{1}(t)}{\Delta_{1}(x(t),x_{1}(t))} \bigl\vert x(t)- x_{1}(t) \bigr\vert \\ &\qquad {}+ \frac{a_{1}(t)(1-m(t))^{2}x_{1}(t)}{\Delta_{1}(x(t),x_{1}(t))} \bigl\vert y_{1}(t)- y(t) \bigr\vert \\ &\quad \leq -b_{1}(t)\bigl\vert x(t)-x_{1}(t)\bigr\vert + \frac{a_{1}(t)(1-m(t))k_{1}(t)}{\Delta _{1}(m_{1}^{\varepsilon})}\bigl\vert y(t)-y_{1}(t)\bigr\vert \\ &\qquad {}+ \frac{a_{1}(t)(1-m(t))^{2}(M_{2}+\varepsilon)}{\Delta _{1}(m_{1}^{\varepsilon})} \bigl\vert x(t)- x_{1}(t) \bigr\vert \\ &\qquad {}+ \frac{a_{1}(t)(1-m(t))^{2}(M_{1}+\varepsilon)}{\Delta _{1}(m_{1}^{\varepsilon})} \bigl\vert y_{1}(t)- y(t) \bigr\vert \end{aligned}$$

and

$$\begin{aligned} &D^{+}V_{2}(t) \\ &\quad =\operatorname{sgn}\bigl(y(t)-y_{1}(t)\bigr) \biggl( - \frac{a_{2}(t) y(t)}{(1-m(t))x(t)+k_{2}(t)}+ \frac{a_{2}(t) y_{1}(t)}{(1-m(t))x_{1}(t)+k_{2}(t)} \biggr) \\ &\quad = \frac{\operatorname{sgn}(y(t)-y_{1}(t))}{\Delta(x(t),x_{1}(t))} \bigl( - a_{2}(t) y(t) \bigl( \bigl(1-m(t)\bigr)x_{1}(t)+k_{2}(t) \bigr) \\ &\qquad {}+ a_{2}(t) y_{1}(t) \bigl(\bigl(1-m(t) \bigr)x(t)+k_{2}(t) \bigr) \bigr) \\ &\quad = \frac{\operatorname{sgn}(y(t)-y_{1}(t))}{\Delta_{2}(x(t),x_{1}(t))} \bigl( - a_{2}(t)k_{2}(t) \bigl(y(t)-y_{1}(t)\bigr) \bigr) \\ &\qquad {}+ \frac{\operatorname{sgn}(y(t)-y_{1}(t))}{\Delta_{2}(x(t),x_{1}(t))} \bigl(-a_{2}(t) \bigl(1-m(t)\bigr) \bigl(y(t)x_{1}(t)-y_{1}(t)x(t)\bigr) \bigr) \\ &\quad \leq \frac{- a_{2}(t)k_{2}(t)}{\Delta_{2}(M_{1}^{\varepsilon })}\bigl\vert y(t)-y_{1}(t)\bigr\vert + \frac{\operatorname{sgn}(y(t)-y_{1}(t))}{\Delta _{2}(x(t),x_{1}(t))} \\ &\qquad {}\times \bigl(-a_{2}(t) \bigl(1-m(t)\bigr) \bigl(y(t)x_{1}(t)-y_{1}(t)x_{1}(t)+y_{1}(t)x_{1}(t)-y_{1}(t)x(t) \bigr) \bigr) \\ &\quad \leq - \frac{ a_{2}(t)k_{2}(t)}{\Delta_{2}(M_{1}^{\varepsilon })}\bigl\vert y(t)-y_{1}(t)\bigr\vert - \frac{a_{2}(t)(1-m(t))(m_{1}-\varepsilon)}{\Delta _{2}(M_{1}^{\varepsilon})}\bigl\vert y(t)-y_{1}(t)\bigr\vert \\ &\qquad {} + \frac{a_{2}(t)(1-m(t))(M_{2}+\varepsilon)}{\Delta _{2}(m_{1}^{\varepsilon})}\bigl\vert x(t)-x_{1}(t)\bigr\vert . \end{aligned}$$

Now let us set

$$V(t)=V_{1}(t)+V_{2}(t). $$

Then

$$ D^{+}V(t)\leq -\Gamma_{1}(\varepsilon,t)\bigl\vert x(t)-x_{1}(t)\bigr\vert -\Gamma _{2}(\varepsilon,t)\bigl\vert y(t)-y_{1}(t)\bigr\vert . $$
(3.10)

Integrating both sides of (3.10) on the interval \([T,t)\),

$$ V(t)-V(T)\leq \int_{T}^{t} \bigl[- \Gamma_{1}( \varepsilon,s) \bigl\vert x(s)-x_{1}(s) \bigr\vert - \Gamma_{2}(\varepsilon,s) \bigl\vert y(s)-y_{1}(s) \bigr\vert \bigr]\,ds \quad \mbox{for } t\geq T. $$
(3.11)

It follows from (3.4) that

$$ V(t)+\varepsilon \int_{T}^{t} \bigl[ \bigl\vert x(s)-x_{1}(s) \bigr\vert + \bigl\vert y(s)-y_{1}(s) \bigr\vert \bigr]\,ds\leq V(T) \quad \mbox{for } t\geq T. $$
(3.12)

Therefore, \(V(t)\) is bounded on \([T,+\infty)\) and also

$$ \int_{T}^{t} \bigl[ \bigl\vert x(s)-x_{1}(s) \bigr\vert + \bigl\vert y(s)-y_{1}(s) \bigr\vert \bigr]\,ds< +\infty. $$
(3.13)

By Lemma 2.1, 2.2, and Theorem 2.1, \(\vert x(t)-x_{1}(t)\vert \), \(\vert y(t)-y_{1}(t)\vert \) are bounded on \([T,+\infty)\). On the other hand, it is easy to see that \(\dot{x}(t)\), \(\dot{y}(t)\), \(\dot{x}_{1}(t)\), and \(\dot{y}_{1}(t)\) are bounded for \(t\geq T\). Therefore, \(\vert x(t)-x_{1}(t)\vert \), \(\vert y(t)-y_{1}(t)\vert \) are uniformly continuous on \([T,+\infty)\). By the Barbălat lemma [47], one can conclude that

$$\lim_{t\rightarrow+\infty} \bigl[ \bigl\vert x(t)-x_{1}(t) \bigr\vert + \bigl\vert y(t)-y_{1}(t) \bigr\vert \bigr]=0. $$

This ends the proof of Theorem 3.1. □

4 Numeric example

Now let us consider the following example.

Example 4.1

$$\begin{aligned}& \begin{aligned} & \dot{x}(t)=x \biggl(11+\cos t -6x- \frac{(1.5+0.5\sin t)(1-0.1)y}{(1-0.1)x+1} \biggr), \\ & \dot{y}(t)=y \biggl(2- \frac{2 y}{(1-0.1)x+2} \biggr). \end{aligned} \end{aligned}$$
(4.1)

Corresponding to system (1.2), one has

$$\begin{aligned}& r_{1}(t)=11+\cos t,\qquad b_{1}(t)=6,\qquad a_{1}(t)=1.5+0.5 \sin t,\qquad m(t)=0.1, \\& k_{1}(t)=1,\qquad r_{2}(t)=2,\qquad a_{2}(t)=2, \qquad k_{2}(t)=2. \end{aligned}$$

And so,

$$\begin{aligned}& M_{1}= \frac{r_{1}^{M}}{b_{1}^{L}}=2,\qquad M_{2}= \frac{r_{2}^{M} ((1-m^{L})M_{1}+k_{2}^{M} )}{a_{2}^{L}}= \frac{2(0.9\times 2+2)}{2}=3.8. \end{aligned}$$
(4.2)

Consequently

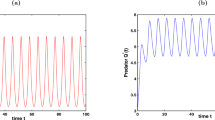
$$ r_{1}^{L}- \frac{a_{1}^{M}(1-m^{L})M_{2}}{k_{1}^{L}}=10- \frac{2\times 0.9\times3.9}{1}=2.98>0. $$
(4.3)

Equation (4.3) shows that (2.8) holds, thus, it follows from Theorem 2.1 that system (4.1) is permanent, and numeric simulations (Figures 1, 2) also support these findings.

Figure 1
figure 1

Dynamic behavior of the first component \(\pmb{x(t)}\) of the solution \(\pmb{(x(t),y(t))}\) of system ( 4.1 ) with the initial condition \(\pmb{(x(0), y(0))=(0.2,5), (0.4, 1), (0.6,3),\mbox{and } (4, 2)}\) , respectively.

Full size image
Figure 2
figure 2

Dynamic behavior of the second component \(\pmb{y(t)}\) of the solution \(\pmb{(x(t),y(t))}\) of system ( 4.1 ) with the initial condition \(\pmb{(x(0), y(0))=(0.2,5), (0.4, 1), (0.6,3),\mbox{and } (4, 2)}\) , respectively.

Full size image

5 Discussion

In this paper, we propose and study a nonautonomous modified Leslie-Gower predator-prey model with Holling-type II schemes and a prey refuge. We first obtain a set of sufficient conditions which ensure the permanence of the system, after that, by constructing a suitable Lyapunov function, we also investigate the stability property of the system.

Condition (2.8) implies that the prey refuge has a positive effect on the persistence property of the system, indeed, with the increasing of prey refuge, the predators have difficulty in catching the prey species, this directly increasing the survival possibility of the prey species.

We mention here that in condition (\(H_{1}\)) we make the assumption that the intrinsic growth rate of the prey species is a positive function, however, in some cases, the growth rate may be negative (see [48–50]) and the references therein), we leave this for future investigation.