Abstract
In this paper, we investigate a delayed differential algebraic prey–predator system, where commercial harvesting on predator and additive Allee effect on prey are considered. A discrete time delay is utilized to represent gestation delay of the predator population. Positivity of solutions and uniform persistence of system are discussed. In the absence of time delay, by taking economic interest as a bifurcation parameter, some sufficient conditions associated with additive Allee effect and economic interest are derived to show that the proposed system undergoes singularity-induced bifurcation around the interior equilibrium. In the presence of time delay, combined dynamic effects of time delay and additive Allee effect on population dynamics are discussed in the case of positive economic interest of commercial harvesting. Existence of Hopf bifurcation and local stability switch around the interior equilibrium are studied as gestation delay crosses the critical value. Furthermore, properties of Hopf bifurcation are investigated based on the center manifold theorem and the norm form of a delayed singular system. Existence of global continuation of periodic solutions bifurcating from interior equilibrium is discussed by using a global Hopf bifurcation theorem. Numerical simulations are provided to show consistency with theoretical analysis.
Similar content being viewed by others
1 Introduction
In the 1930s, W.C. Allee proposed the concept of Allee effect from experimental studies and extensively investigated ecological significance of animal aggregations [1]. It is well known that Allee effect is highly relevant to reduction in mating success, reduced inbreeding efficiency, suppressed social thermoregulation [2, 3], and some other biological or ecological reasons which can be found in [4, 5] and the references therein. It may cause a positive feedback between a component of individual fitness and either number or density of conspecifics. From ecological perspective, Allee effect can be categorized as strong Allee effect and weak Allee effect, respectively. If some population undergoes the strong Allee effect, then the population must surpass certain threshold to sustainable survival. However, the population threshold does not exist for the population with weak Allee effect.
Generally, a prey–predator system plays a significant role in bioeconomics, which depicts the basic interspecies relationships among various populations within an ecological system. In 1960, P.H. Leslie and J.C. Gower [6] introduced a dynamical model in which the environmental carrying capacity of the predator population is proportional to the population density of the prey population. In recent decades, the prey–predator system with Leslie–Gower functional response has attracted research attentions from both biologists and mathematicians [7–12]. Complex dynamics and stability analysis of the proposed model around corresponding equilibria are investigated in [7, 8, 10]. Some diffusive prey–predator model with modified Leslie–Gower schemes and additive Allee effect on prey are proposed in [9, 11], and local and global asymptotical stability of the unique positive constant equilibrium point of the system are analyzed in [9, 11]. In [12], authors establish the following dynamical prey–predator model with Leslie–Gower functional response:
where \(N(t)\) and \(P(t)\) represent the population density of prey and predator, respectively. \(1-N(t)-\frac{m}{N(t)+a}\) represents the additive Allee effect term, which was first introduced in [13]. The term \(\frac{m}{N(t)+a}\) can cause weak or strong Allee effect without predator. The additive Allee effect in [12] can be categorized as follows:
-
if \(0< m< a\), then the Allee effect in (1) is weak Allee effect,
-
if \(m>a\), then the Allee effect in (1) is strong Allee effect,
where m and a are Allee effect constants, a denotes the population size at which fitness is half its maximum value [12], all the parameters mentioned above are positive constants. By utilizing system (1), authors investigate complex dynamics of a Leslie–Gower predation model with additive Allee effect on prey, which reveals that Allee effect can increase the risk of ecological extinction [12].
Generally, commercial harvesting may be affected by various factors such as market demand, seasonality, revenue, cost, and other factors in a market economy. Based on the economic theory proposed in [14], an algebraic equation is constructed to study economic interest of commercial harvesting:
We will extend the work in [12] by incorporating commercial harvesting on predator into system (1). \(E(t)\) represents the commercial harvesting effort on predator at time t, w represents the harvesting reward coefficients, c represents the cost per unit harvesting effort for unit weight of predator. v is the economic interest of commercial harvesting on predator. Based on system (1) TR and TC in Eq. (2), it is easy to show that \(\mathrm{TR}=w E(t)P(t)\) and \(\mathrm{TC}=cE(t)\).
Remark 1.1
Recently, it has been shown that commercial harvesting on a prey–predator system with Allee effect has a strong impact on population dynamics (see [7, 10, 15–19] and the references therein). However, dynamical behavior due to variation of economic interest of commercial harvesting is not discussed in [7, 10, 15–18]. Only dynamic effects of strong Allee effect on population dynamics are considered in [19], the weak Allee effect case is not investigated in [19]. On the other hand, the reproduction of predator after predating prey is not instantaneous but will be mediated by some time lag required for gestation of the predator population. Hence, it is necessary to investigate combined dynamics of time delay and additive Allee effect on population dynamics of a harvested prey–predator system with commercial harvesting. Although the harvested prey–predator system with Allee effect has attracted a great deal of attention, to authors’ best knowledge, little work has been done on combined dynamic effects of time delay and additive Allee effect on population dynamics of the harvested prey–predator system with commercial harvesting.
In this paper, keeping all these aspects in mind, we extend the work in [12] by incorporating commercial harvesting on predator and gestation delay for predator into system (1), where predator is assumed to be delayed by gestation delay τ. A singular system with additive Allee effect and time delay is established as follows:
interpretations for parameters and state variables share the same interpretations introduced in systems (1) and (2). Furthermore, the initial conditions for system (3) take the following form:
System (3) can be rewritten in the matrix form as follows:
Remark 1.2
Since the algebraic equation in (3) includes no differentiated variables, the third row in matrix \(\Xi(t)=\left [ {\scriptsize\begin{matrix}{}1& 0 & 0 \cr 0& 1 &0\cr 0&0&0 \end{matrix}} \right ] \) has a corresponding zero row.
The remaining sections of this paper are organized as follows. Positivity of solutions and uniform persistence of system (3) are investigated in the second section. In the third section, in the absence of time delay, the existence of singularity-induced bifurcation is investigated under the case of additive Allee effect on prey. In the absence of time delay, combined dynamic effects of time delay and additive Allee effect on population dynamics are discussed, local stability switch around interior equilibrium and the existence of Hopf bifurcation are also discussed. In the fourth section, properties of Hopf bifurcation are investigated. Existence of global continuation of periodic solutions bifurcating from interior equilibrium is discussed by using a global Hopf bifurcation theorem. In the fifth section, numerical simulations are provided to support theoretical findings. Finally, this paper ends with a conclusion.
Remark 1.3
The dynamical model proposed in [12] is composed of ordinary differential equations, and it is utilized to study interaction mechanism of a prey–predator system with additive Allee effect. Compared with the system established in [12], an algebraic equation is introduced into system (3), which concentrates on dynamic effect of economic interest of commercial harvesting on population dynamics and provides a straightforward way to investigate complex dynamics due to variation of economic interest. Furthermore, a discrete time delay, which represents gestation delay of the predator population, is incorporated into system (3). Consequently, compared with the work done in [12], we can investigate combined dynamic effects of time delay and additive Allee effect on population dynamics by analyzing the local stability and bifurcation phenomenon of system (3) in this paper.
2 Positivity and uniform persistence
In this section, positivity of solutions and uniform persistence of system (3) with initial conditions (4) will be studied.
Theorem 2.1
All solutions of system (3) with initial conditions (4) are positive for all \(t\geq0\).
Proof
For solutions of system (3), it is easy to show that \(F_{i}:R^{3+1}_{+}\rightarrow R^{3}\) is locally Lipschitz and satisfies the condition \(F_{i}>0\), where \(F_{i}\) (\(i=1,2,3\)) can be found in (5). Due to the lemma in [20] and Theorem A.4 in [21], all solutions of system (3) with initial conditions (4) exist uniquely, and each component of solution remains within the interval \([0, U_{0})\) for some \(U_{0}>0\). Standard and simple arguments show that any solution of system (3) always exists and stays positive. □
Lemma 2.2
([22])
Consider the following equation:
where \(a_{1}\), \(a_{2}\), \(a_{3}\), and σ are positive constants, \(u(t)>0\) for \(t\in[-\sigma,0]\),
-
(i)
if \(a_{1}>a_{2}\), then \(\lim_{t\rightarrow\infty}u(t)=\frac {a_{1}-a_{2}}{a_{3}}\),
-
(ii)
if \(a_{1}< a_{2}\), then \(\lim_{t\rightarrow\infty}u(t)=0\).
Theorem 2.3
If τ is bounded, \(e^{\frac{b\tau}{k_{1}}}< k_{1}\) and \(we^{2(\tau+k_{2}\tau)}>c\) hold, then system (3) with initial conditions (4) is uniformly persistent.
Proof
By taking the Taylor series expansion in [23], for \(N(t)\), \(P(t)\), and \(\tau>0\), we have
Hence, it follows that
where τ is defined in system (3). Based on the first equation of system (3), it follows from Theorem 2.1 and (6) that \(\dot{N}(t)< N(t-\tau)\leq N(t)\), so we derive that \(N(t)\leq N(t-\tau)e^{\tau}\) for \(t>\tau\), which is equivalent to \(N(t-\tau )\geq N(t)e^{-\tau}\), since for \(t>\tau\), we have
It follows from standard comparison arguments that
If τ is bounded, then \(N_{1}\) is bounded and \(N(t)\leq N_{1}\) holds for \(t>T_{1}+\tau\), where \(T_{1}>0\). On the other hand, from the first equation of system (3), it follows from Theorem 2.1 and (6) that
Hence, there exists \(T_{2}>T_{1}\) such that \(N(t)\geq N(t-\tau )e^{-\frac{b\tau}{k_{1}}}\) holds for \(t>T_{2}+\tau\), which is equivalent to \(N(t-\tau)\leq N(t)e^{\frac{b\tau}{k_{1}}}\), for \(t>T_{2}+\tau\), we have
By using Lemma 2.2, if \(e^{\frac{b\tau}{k_{1}}}< k_{1}\), then
which gives that there exists \(T_{3}>T_{2}\) such that \(N(t)>M_{1}>0\) for \(t>T_{3}+\tau\).
Based on the second equation of system (3), if follows from Theorem 2.1 and (6) that \(\dot{P}(t)\leq k_{2}P(t)\).
Hence there exists \(T_{4}>T_{3}\) such that \(P(t)\leq P(t-\tau )e^{k_{2}\tau}\) for \(t>T_{4}+\tau\), which is equivalent to \(P(t-\tau )\geq P(t)e^{-k_{2}\tau}\). Consequently, for \(t>T_{4}+\tau\),
By using standard comparison arguments, we can obtain that
If τ is bounded, then it shows that \(N_{2}>0\) is bounded, and there exists \(T_{5}>T_{4}\) such that \(P(t)< N_{2}\) holds for \(t>T_{5}+\tau\). When \(v>0\), by solving the third equation of system (3), we easily obtain that
By virtue of (9), it follows that there exists \(T_{6}>T_{5}+\tau\), for \(t>T_{6}\), we have
If \(w e^{2(\tau+k_{2}\tau)}>c\) and τ are bounded, then it is easy to show that \(M_{3}>0\) is bounded, and then there exists \(T_{7}>T_{6}\) such that \(E(t)\geq M_{3}\) holds for \(t>T_{7}\).
According to practical biological interpretations, it follows from the second equation of system (3) that
According to the third equation of system (3), it follows from Theorem 2.1 that \(wP(t)>c\) holds for \(v>0\), which gives that
Hence, if τ is bounded, \(v>0\), \(e^{\frac{b\tau}{k_{1}}}< k_{1}\), and \(we^{2(\tau+k_{2}\tau)}>c\) hold, then it is obtained that \(N_{i}>0\) and \(M_{i}>0\) (\(i=1,2,3\)) are bounded. Therefore
which derives that system (3) with initial conditions (4) is uniformly persistent. □
3 Local stability analysis
According to common property resource economic theory in [14, 24], when \(v=0\), there is a phenomenon of equilibrium state. An interior equilibrium is as follows: \(S^{*}(N^{*}, P^{*}, E^{*})= ( N^{*}, \frac{c}{w}, k_{2}(1-\frac{c}{w (N^{*}+k_{3})}) ) \), and \(N^{*}\) satisfies the following equation:
where \(\xi_{1}=\frac{a+k_{1}-1}{3}\), \(\xi_{2}=\frac{1}{3} [ m-a+k_{1}(a-1)+\frac{bc}{w} ] \), \(\xi_{3}=k_{1}(m-a)+\frac{abc}{w}\).
By using the transformation \(x=N+\xi_{1}\), the above equation can be transformed as follows:
where \(\eta_{1}=\xi_{2}-\xi^{2}_{1}\), \(\eta_{2}=\xi_{3}-3\xi_{1}\xi _{2}+2\xi^{3}\).
Furthermore, we will investigate the existence of positive roots of Eq. (13).
Lemma 3.1
Existence conditions of positive roots of Eq. (13) are as follows:
-
(i)
If \(\eta_{2}<0\), then Eq. (13) has a single positive root.
-
(ii)
Assuming that \(\eta_{2}>0\) and \(\eta_{1}<0\),
-
(iii)
If \(\eta_{2}=0\) and \(\eta_{1}<0\), then Eq. (13) has a unique positive root.
Proof
By simple computations, it is easy to show that the maximum and minimum values of function \(h(x)\) are \(L_{1}=\eta_{2}+2\sqrt{ \vert \eta_{1} \vert ^{3}}\) and \(l_{1}=\eta_{2}-2\sqrt{ \vert \eta_{1} \vert ^{3}}\), respectively.
When \(\eta_{3}<0\) and \(\eta_{1}\geq0\), by virtue of \(\dot {h}(x)=3(x^{2}+\eta_{1})\geq0\), we have \(h(x)\) is strictly increasing and continuous in \([0,+\infty)\), which yields \(h(x)\geq h(0)=\eta _{2}\). Consequently, \(h(x)\) has a positive root.
When \(\eta_{3}<0\) and \(\eta_{1}\leq0\), it is easy to show that Eq. (13) has a positive root.
When \(\eta_{2}>0\), it is easy to derive that \(\eta_{1}<0\), otherwise \(h(x)=x^{3}+3\eta_{1}x+\eta_{2}\) may not be equal to zero.
If \(\eta_{2}^{2}+4\eta^{3}_{1}=0\), then Eq. (13) has a positive root of multiplicity two. Furthermore, if \(\eta_{2}^{2}+4\eta^{3}_{1}<0\), then Eq. (13) has two positive roots.
When \(\eta_{2}=0\), we have that \(\eta_{1}<0\), otherwise \(h(x)=x^{3}+3\eta_{1}x+\eta_{2}\) may not be equal to zero. Hence, Eq. (13) has a unique positive root. □
Moreover, simple algebraic computations show that Eq. (13) has two positive roots, which are given as follows:
It should be noted that if the cubic equation (13) has one positive root, it must be
By considering \(\eta_{1}=0\) and \(\eta_{2}=0\), one can determine \(m=m_{1}^{*}\), \(m=m_{2}^{*}\), where
Based on the above analysis, sufficient conditions associated with the existence of interior equilibria of system (3) with strong Allee effect and weak Allee effect can be concluded in Lemma 3.2 and Lemma 3.3, respectively.
Lemma 3.2
Existence conditions of interior equilibria of system (3) with strong Allee effect are as follows:
-
(i)
If either of the following inequalities holds:
$$ \textstyle\begin{cases} 2k_{1}+1-a-b>0,\quad 0< a< m< m^{*}_{2}, \\ 2k_{1}+1-a-b< 0,\quad 0< \max\{a,m^{*}_{2}\}< m, \end{cases} $$(14)then system (3) has a unique interior equilibrium
$$ S_{s}^{*}= \bigl(N_{s}^{*},P_{s}^{*},E_{s}^{*} \bigr)= \biggl( x_{1}-\xi_{1}, \frac{c}{w}, k_{2} \biggl(1-\frac{c}{w(x_{1}-\xi_{1}+k_{3})} \biggr) \biggr) . $$ -
(ii)
If either of the following inequalities holds:
$$ \textstyle\begin{cases} 2k_{1}+1-a-b>0, \quad 0< \max\{a,m^{*}_{2}\}< m< m^{*}_{1}, \\ 2k_{1}+1-a-b< 0,\quad 0< b< m< \min\{m^{*}_{1},m^{*}_{2}\}, \end{cases} $$(15)then the following conclusions associated with the existence of interior equilibria of system (3) hold:
-
system (3) has two interior equilibria:
$$\begin{aligned}& S_{s1}^{*}= \bigl(N_{s1}^{*},P_{s1}^{*},E_{s1}^{*} \bigr)= \biggl( x_{1}-\xi_{1}, \frac{c}{w}, k_{2} \biggl(1-\frac{c}{w(x_{1}-\xi_{1}+k_{3})} \biggr) \biggr) , \\& S_{s2}^{*}=(N_{s2}^{*},P_{s2}^{*},E_{s2}^{*})= \biggl( x_{2}-\xi_{1}, \frac{c}{w}, k_{2}\biggl(1-\frac{c}{w(x_{2}-\xi_{1}+k_{3})}\biggr) \biggr) ; \end{aligned}$$ -
system (3) has a unique interior equilibrium
$$ {S}_{s3}^{*}= \bigl({N}_{s3}^{*},{P}_{s3}^{*},{E}_{s3}^{*} \bigr)= \biggl( \sqrt{-\eta_{1}}, \frac{c}{w}, k_{2} \biggl(1-\frac{c}{w(\sqrt{-\eta_{1}}+k_{3})} \biggr) \biggr) $$with \(\eta_{2}^{2}+4\eta_{1}^{3}=0\).
-
-
(iii)
If \(a< m< m_{1}^{*}\), system (3) has a unique interior equilibrium
$$ {S}_{s}^{*}= \bigl({N}_{s}^{*},{P}_{s}^{*},{E}_{s}^{*} \bigr)= \biggl( \sqrt{-3\eta_{1}},\frac{c}{w},k_{2} \biggl(1-\frac{c}{w(\sqrt{-3\eta_{1}+k_{3}})} \biggr) \biggr) . $$
Lemma 3.3
Existence conditions of interior equilibria of system (3) with weak Allee effect are as follows:
-
(i)
If either of the following inequalities holds:
$$ \textstyle\begin{cases} 2k_{1}+1-a-b>0,\quad 0< m< \min\{a,m_{2}^{*}\}, \\ 2k_{1}+1-a-b< 0,\quad 0< m_{2}^{*}< m< a, \end{cases} $$(16)then system (3) has a unique interior equilibrium
$$ S_{w}^{*}= \bigl(N_{w}^{*},P_{w}^{*},E_{w}^{*} \bigr)= \biggl( x_{1}-\xi_{1},\frac{c}{w},k_{2} \biggl(1-\frac{c}{w(x_{1}-\xi_{1}+k_{3})} \biggr) \biggr) . $$ -
(ii)
If either of the following inequalities holds:
$$ \textstyle\begin{cases} 2k_{1}+1-a-b>0,\quad 0< m_{2}^{*}< m< \min\{a,m^{*}_{1}\}, \\ 2k_{1}+1-a-b< 0,\quad 0< m< \max\{a,m^{*}_{1},m_{2}^{*}\}, \end{cases} $$(17)then the following conclusions associated with the existence of interior equilibria of system (3) hold:
-
system (3) has two interior equilibria as follows:
$$\begin{aligned}& S_{w1}^{*}= \bigl(N_{w1}^{*},P_{w1}^{*},E_{w1}^{*} \bigr)= \biggl( x_{1}-\xi_{1},\frac{c}{w},k_{2} \biggl(1-\frac{c}{w(x_{1}-\xi_{1}+k_{3})} \biggr) \biggr) , \\& S_{w2}^{*}= \bigl(N_{w2}^{*},P_{w2}^{*},E_{w2}^{*} \bigr)= \biggl( x_{2}-\xi_{1},\frac{c}{w},k_{2} \biggl(1-\frac{c}{w(x_{2}-\xi_{1}+k_{3})} \biggr) \biggr) ; \end{aligned}$$ -
system (3) has a unique interior equilibrium
$$ S_{w3}^{*}= \bigl(N_{w3}^{*},P_{w3}^{*},E_{w3}^{*} \bigr)= \biggl( \sqrt{-\eta_{1}},\frac{c}{w},k_{2} \biggl(1-\frac{c}{w(\sqrt{-\eta_{1}+k_{3}})} \biggr) \biggr) , $$where \(\eta_{2}^{2}+4\eta_{1}^{3}=0\).
-
-
(iii)
If \(0< m<\max\{a,m^{*}_{1}\}\), then system (3) has a unique interior equilibrium
$$ S_{w}^{*}= \bigl(N_{w}^{*},P_{w}^{*},E_{w}^{*} \bigr)= \biggl( \sqrt{-3\eta_{1}},\frac{c}{w},k_{2} \biggl(1-\frac{c}{w(\sqrt{-3\eta_{1}+k_{3}})} \biggr) \biggr) . $$
In the case of positive economic interest \(v>0\) and \(m>a\), interior equilibrium can be obtained as follows: \(\tilde{S}^{*}_{s}=(\tilde {N}^{*}_{s},\tilde{P}^{*}_{s},\tilde{E}^{*}_{s})= ( \frac{k_{2}\tilde {P}^{*}_{s}(w \tilde{P}^{*}_{s}-c)}{k_{2}w \tilde {P}^{*}_{s}-ck_{2}-v}-k_{3},\tilde{P}^{*}_{s},\frac{v}{w \tilde {P}^{*}_{s}-c} ) \) and \(\tilde{P}_{s}^{*}\) satisfies the following equation:
where \(\zeta_{is}\), \(i=1,2,\ldots,6\), are defined as follows:
Based on the Routh–Hurwitz criterion [23], if a simple sufficient condition \(\zeta_{6s}<0\) holds, then Eq. (18) will have at least one positive root, which derives that
On the other hand, it follows from practical interpretations and mathematical formulations of \(\tilde{S}^{*}_{s}=(\tilde {N}^{*}_{s},\tilde{P}^{*}_{s},\tilde{E}^{*}_{s})\) that \(\tilde {N}^{*}_{s}>0\), \(\tilde{P}^{*}_{s}>0\), \(\tilde{E}^{*}_{s}>0\), which derives that
By using Viete theorem [23], the above inequalities can be derived as follows:
According to the above analysis, the existence conditions for interior equilibrium in the case of strong Allee effect are concluded in Lemma 3.4.
Lemma 3.4
When \(v>0\) and \(m>a\), interior equilibrium \(\tilde {S}^{*}_{s}\) exists provided the following inequalities hold:
Similarly, in the case of positive economic interest \(v>0\) and \(0< m< a\), interior equilibrium is as follows: \(\tilde{S}^{*}_{w}=(\tilde {N}^{*}_{w},\tilde{P}^{*}_{w},\tilde{E}^{*}_{w})= ( \frac{k_{2}\tilde {P}^{*}_{w}(w \tilde{P}^{*}_{w}-c)}{k_{2}w \tilde {P}^{*}_{w}-ck_{2}-v}-k_{3},\tilde{P}^{*}_{w},\frac{v}{w \tilde {P}^{*}_{w}-c} ) \) and \(\tilde{P}_{w}^{*}\) satisfies the following equation:
where \(\zeta_{iw}\), \(i=1,2,\ldots,6\), are defined as follows:
Based on the Routh–Hurwitz criterion [23], if a simple sufficient condition \(\zeta_{6w}<0\) holds, then Eq. (20) will have at least one positive root, which derives that
On the other hand, it follows from practical interpretations and mathematical formulations of \(\tilde{S}^{*}_{w}=(\tilde {N}^{*}_{w},\tilde{P}^{*}_{w},\tilde{E}^{*}_{w})\) that \(\tilde {N}^{*}_{w}>0\), \(\tilde{P}^{*}_{w}>0\), \(\tilde{E}^{*}_{w}>0\), which derives
According to the above analysis, the existence conditions for interior equilibrium in the case of weak Allee effect are concluded in Lemma 3.5.
Lemma 3.5
When \(v>0\) and \(0< m< a\), interior equilibrium \(\tilde {S}^{*}_{w}\) exists provided the following inequalities hold:
3.1 Case I: system (3) with strong Allee effect
When \(\tau=0\), system (3) takes the following form:
By taking v as a bifurcation parameter, the existence of singularity-induced bifurcation and local stability switch around \(S^{*}_{s}\) and \(\tilde{S}^{*}_{s}\) will be investigated due to variation of v in Theorem 3.6.
Theorem 3.6
When \(\tau=0\) and \(m>a\), system (22) undergoes singularity-induced bifurcation around \(S^{*}_{s}\), \(v=0\) is a bifurcation value. When v increases though 0, system (22) is unstable around \(S^{*}_{s}\) and \(\tilde{S}^{*}_{s}\) in the case of zero and positive economic interest, respectively.
Proof
Let v be a bifurcation parameter, \(X_{1}(t)=(N(t),P(t))\), \(X_{2}(t)=E(t)\), and D be a differential operator:
It follows from simple computations that
It follows from (19) that
By defining \(g_{3}(X_{1}(t),X_{2}(t),v)=D_{X_{2}}g_{2}(X_{1}(t),X_{2}(t),v)=w P(t)-c\).
By using (19) and simple computations, we can obtain that
Based on three items (23), (24), and (25) computed above, the existence theorem of singularity-induced bifurcation (Theorem in [25]) holds, hence system (22) undergoes singularity-induced bifurcation around \(S^{*}_{s}\) and the bifurcation value is \(v=0\).
Along the line of the above computation, it can be obtained that
By using similar arguments, it can be obtained that
By virtue of (7), (8), and (19) and simple computations, it can be obtained that \(\frac{{G}_{1}}{{G}_{2}}>0\), \(\frac{\tilde{G}_{1}}{\tilde {G}_{2}}>0\). Based on Theorem 3 in [25], when v increases through 0, one eigenvalue of system (22) moves from \(\mathbb{C}^{-}\) to \(\mathbb{C}^{+}\) along the real axis by diverging through ∞. Hence, when v increases through 0, system (22) is unstable around \(S^{*}_{s}\) and \(\tilde{S}^{*}_{s}\) in the case of zero and positive economic interest, respectively. □
When \(\tau>0\) and \(m>a\), according to the Jacobian of system (3) evaluated around \(\tilde{S}_{s}^{*}\) and the leading matrix \(\Xi (t)\) in Remark 1.1, the characteristic equation of system (3) around \(\tilde{S}_{s}^{*}\) is as follows:
where \(n_{is}\), \(i=1,2,3,4\), are defined as follows:
Substituting \(\lambda=i\sigma_{s}\), where \(\sigma_{s}\) is a positive real number, into Eq. (26) and separating real and imaginary parts gives
which derives that
Theorem 3.7
If \(a>k_{3}\), \(k_{1}>k_{3}\), \(c\leq1\), \(0< v< v_{1}\) hold, then system (3) is locally stable around \(S^{*}_{s}\) when \(0<\tau<\tau_{1c}^{*}\). System (3) undergoes Hopf bifurcation around \(\tilde{S}^{*}_{s}\) when \(\tau=\tau_{1c}^{*}\), where \(v_{1}\) and \(\tau_{1c}^{*}\) are defined as follows:
Proof
If \(2-k_{1}< a<\min\{m, \frac{k_{1}-m}{k_{1}-1}\}\), \(0< v< w k_{3}(k_{2}+1+\sqrt{k_{2}+1})\) hold, then system (3) has at least an interior equilibrium \(\tilde{S}^{*}_{s}\). Furthermore, if \(a>k_{3}\), \(k_{1}>k_{3}\), \(c\leq1\), and \(0< v<(1-c)k_{2}+ck_{2}-k_{2}w -w \tilde {P}^{*}_{s}\) hold, then it is obtained that \(n_{2s}^{2}-n_{1s}^{2}<0\), which guarantees that Eq. (27) has a pair of purely imaginary roots of the form \(\pm i\sigma^{*2}_{s}\).
By eliminating \(\sin(\sigma_{s} \tau)\) from the transcendental equation, it can be obtained that \(\tau_{1c}^{*}\) corresponding to \(\sigma^{*}_{s}\) is as follows:
By using Butler’s lemma [26], system (3) is locally asymptotically stable around \(\tilde{P}^{*}_{s}\) when \(0<\tau<\tau_{1c}^{*}\).
Let \(\lambda=i\sigma^{*}_{s}\) represent a purely imaginary root of Eq. (26), we will determine the direction of motion of λ as τ varied, namely we determine
Further computations show that
By differentiating Eq. (26) with respect to τ, it can be obtained that
If \(0< v<\min\{k_{2}-w \tilde{P}^{*}_{s}-ck_{2}, (1-c)k_{2}+ck_{2}-k_{2}w -w \tilde{P}^{*}_{s}\}\), then it follows from simple computations that \(\Theta>0\). Consequently, if \(0< v< v_{1}\) holds, where \(v_{1}\) is defined in Theorem 3.7, then the transversality condition holds and system (3) undergoes Hopf bifurcation around \(\tilde{S}^{*}_{s}\) when \(\tau=\tau_{1c}^{*}\). □
3.2 Case II: system (3) with weak Allee effect
When \(\tau=0\) and \(0< m< a\), by taking v as a bifurcation parameter, the existence of singularity-induced bifurcation and local stability switch around \(S^{*}_{w}\) and \(\tilde{S}^{*}_{w}\) will be investigated due to variation of v in Theorem 3.8.
Theorem 3.8
When \(\tau=0\) and \(0< m< a\), system (22) undergoes singularity-induced bifurcation around \(S^{*}_{w}\), \(v=0\) is a bifurcation value. When v increases though 0, system (22) is unstable around \(S^{*}_{w}\) and \(\tilde{S}^{*}_{w}\) in the case of zero and positive economic interest, respectively.
Proof
By using a proof similar to that in Theorem 3.6, it is easy to show Theorem 3.8. □
When \(\tau>0\) and \(0< m< a\), according to the Jacobian of system (3) evaluated around \(\tilde{S}_{w}^{*}\) and the leading matrix \(\Xi (t)\) in Remark 1.1, the characteristic equation of system (3) around \(\tilde{P}_{w}^{*}\) is as follows:
where \(n_{iw}\), \(i=1,2,3,4\), are defined as follows:
Theorem 3.9
If \(2-a-k^{3}_{3}< m< a\), \(\max\{2-k_{1}, m\}< a<1\), \(k^{3}_{3}< k_{1}\), \(0< v< v_{2}\) hold, then system (3) is locally stable around \(\tilde{S}^{*}_{w}\) when \(0<\tau<\tau_{1d}^{*}\). System (3) undergoes Hopf bifurcation around \(\tilde{S}^{*}_{w}\) when \(\tau=\tau_{1d}^{*}\), where \(v_{2}\) and \(\tau_{1d}^{*}\) are defined as follows:
and \(\sigma_{w}^{*}\) satisfies the following equation:
Proof
By using a proof similar to that in Theorem 3.7, it is easy to show Theorem 3.9. □
4 Properties of Hopf bifurcation
In this section, τ is regarded as a bifurcation parameter. Properties of Hopf bifurcation around interior equilibrium \(\tilde {S}^{*}_{w}\) in the case of weak Allee effect are discussed. By using the similar analysis, symmetric analysis about the properties of Hopf bifurcation around interior equilibrium \(\tilde{S}^{*}_{s}\) in the case of strong Allee effect can be also obtained, which is omitted in this section.
Bars of variables are dropped for simplicity of notation, system (3) is transformed to the following functional delayed differential equation in the Banach space of continuous functions mapping \(\mathbb{C}=\mathbb {C}([-{\tau}, 0], \mathbb{R})\). Based on \(E(t)=\frac{v}{w P-c}\) and a normal form of delayed differential-algebraic system [19], by using the following transformations:
system (3) can be rewritten as follows:
where \(b_{ij}\) (\(i=1,2\), \(j=1,2,\ldots,8\)) are as follows:
According to the Riesz representation theorem [27], there exists a \(2\times2\) matrix function \(\eta(\vartheta, \mu)\) of bounded variation for \(\vartheta\in[-{\tau}, 0]\) such that
where \(\varphi(\vartheta)=(\varphi_{1}(\vartheta), \varphi _{2}(\vartheta))\in\mathbb{C}([-{\tau}, 0], \mathbb{R}^{2})\), \(\eta : [-{\tau}, 0]\rightarrow\mathbb{R}^{2}\times\mathbb{R}^{2}\) is a real-valued bounded function in \([-{\tau}, 0]\) with Dirac delta function δ,
If φ is a given function in \(C([-{\tau}, 0],\mathbb{R}^{2})\) and \(Y(\varphi)\) is the unique solution of linearized equation \(\dot {Y}(t)=L_{\upsilon}(Y_{t})\) of Eq. (29) with initial function φ at zero, then the solution operator \(\tilde{T}(t): \mathbb {C}\rightarrow\mathbb{C}\) is defined as \(\tilde{T}(t)\varphi =Y_{t}(\varphi)\), \(t\geq0\).
It follows from Lemma 7.11 in [23] that \(\tilde{T}(t)\), \(t\geq0\) is a strongly continuous semigroup of linear transformation on \([0, +\infty)\) and the infinitesimal generator \(B_{\upsilon}\) of \(\tilde {T}(t)\), \(t\geq0\), is as follows:
for \(\varphi\in\mathbb{C}^{1}([-{\tau}, 0],\mathbb{R}^{2})\), the space of a function mapping the interval \([-{\tau}, 0]\) into \(\mathbb {R}^{2}\) which has a continuous first derivative, and also define
where \(V(\upsilon,\varphi)=(V_{1}(\upsilon,\varphi), V_{2}(\upsilon ,\varphi))^{T}\), and
Hence, system (29) is equivalent to
For \(\phi\in\mathbb{C}^{1}([-{\tau}, 0],(\mathbb{R}^{2})^{*})\), the space of functions mapping interval \([-{\tau}, 0]\) into two-dimensional row vectors which have continuous first derivative, let
and a bilinear inner product
where \(\eta(\vartheta)=\eta(\vartheta, 0)\). It is easy to show that \(B(0)\) and \(B^{*}\) are adjoint operators, and \(\pm i\sigma_{w}^{*} \tau_{1d}^{*}\) are eigenvalues of \(B(0)\) and \(B^{*}\).
Suppose that \(r(\vartheta)=(1,\beta)^{T}e^{i\sigma_{w}^{*} \tau _{1d}^{*} \vartheta}\) is an eigenvector of \(B(0)\) corresponding to \(i\sigma_{w}^{*} \tau_{1d}^{*}\), which derives \(B(0)r(0)=i\sigma _{w}^{*} \tau_{1d}^{*} r(\vartheta)\). By virtue of \(B(0)\), (30), (31), and (32), it follows from \(r(-1)=r(0)e^{-i\sigma_{w}^{*}\tau _{1d}^{*}}\) that \(\beta=\frac{i\sigma_{w}^{*} -(b_{11}+b_{13})e^{-i\sigma_{w}^{*} \tau_{1d}^{*}}}{b_{12}}\).
Similarly, it follows from simple computations that the eigenvector of \(B^{*}\) corresponds to \(-i\sigma_{w}^{*}\tau_{1d}^{*} \vartheta\), which gives that \(\beta^{*}=\frac{i\sigma_{w}^{*}}{b_{22}}\).
In order to assume \(\langle r^{*}(s), r(\vartheta) \rangle=1\), we need to determine the value of H in the following part. By virtue of (35), it is obtained that
Hence, we can choose \(\bar{H}=\frac{1}{1+\beta\bar{\beta}^{*}+\tau _{1d}^{*} e^{-i\sigma_{w}^{*} \tau _{1d}^{*}}(b_{13}+b_{14}+b_{22}\beta\bar{\beta}^{*})}\). Next, we will compute the coordinate to describe the center manifold \(C_{0}\) at \(\upsilon=0\). Let \(Y_{t}\) be the solution of Eq. (34) when \(\upsilon =0\). We define
On the center manifold \(C_{0}\), it derives that \(U(t, \vartheta )=U(\varsigma(t), \bar{\varsigma}(t), \vartheta)\), and
ς and ς̄ are local coordinates for \(C_{0}\) in the direction of \(r^{*}\) and \(\bar{r}^{*}\).
It is noted that U is real if \(Y_{t}\) is real, and we only consider real solutions. For solution \(Y_{t}\in C_{0}\) of Eq. (34), since \(\upsilon=0\), it derives that
Equation (38) can be rewritten as \(\dot{\varsigma}(t)=i\sigma _{w}^{*}\tau_{1d}^{*}\varsigma(t)+f(\varsigma, \bar{\varsigma})\), where
By virtue of (29), (30), and (31), it derives that
and the detailed form of \(f(\varsigma, \bar{\varsigma})\) can be found in Appendix A of this paper.
By comparing the coefficients with (39) and (44), we have that
Since \(f_{21}\) is associated with \(U_{20}(\vartheta)\) and \(U_{11}(\vartheta)\), which can be found in Appendix B of this paper, hence the following values can be computed as follows:
Theorem 4.1
Properties of a bifurcating periodic solution in the center manifold at the critical value \(\tau_{1d}^{*}\) are determined based on the values computed in Eq. (41):
-
(i)
If \(\gamma_{2}>0\) (\(\gamma_{2}<0\)), then Hopf bifurcation is supercritical (subcritical), and the bifurcating periodic solutions exist for \(\tau>\tau_{1d}^{*}\) (\(\tau>\tau_{1d}^{*}\));
-
(ii)
Bifurcating periodic solutions are stable (unstable) if \(\iota_{2}<0\) (\(\iota_{2}>0\));
-
(iii)
Period increases (decreases) if \(T>0\) (\(T<0\)).
By using the global Hopf bifurcation theorem for general functional delayed differential equations introduced in [28], the existence of global continuation of periodic solutions bifurcating from interior equilibrium \(\tilde{S}^{*}_{w}\) will be discussed in the following part. In order to facilitate the following analysis, system (29) is rewritten as the following functional delayed differential system:
where \(Z_{t}=(z_{1}(t), z_{2}(t))^{T}\), \(Z_{t}(\theta)\in Y\triangleq C([-\tau_{1d}^{*}, 0], \mathbb{R}^{2})\).
Following the work done in [28], some definitions are given as follows. Let \(\Gamma=Cl\{(Z_{t}, \tau, \mu)\in Y\times\mathbb {R}\times\mathbb{R}^{+}\}\), \(\mathcal{N}\{(\bar{Z}_{t}, \tau, \mu)\mid F(\bar{Z}_{t}, \tau, \mu )=0\}\), where Z̄ and Z denote an interior equilibrium and a nonconstant periodic solution of (42), respectively. The characteristic matrix of system (42) around Z̄ is as follows:
where I denotes the identity matrix and \(\mathrm{D}F(\bar{Z}, \tau, \mu)\) represents the Fréchet derivative of F with respect to \(Z_{t}\) evaluated at \((\bar{Z}, \tau, \mu)\).
We define \((\bar{Z}, \tau, \mu)\) as a center provided that \((\bar{Z}, \tau, \mu)\in\mathcal{N}\) and \(\Delta(\bar{Z}, \tau, \mu)=0\). The center \(\Delta(\bar{Z}, \tau, \mu)\) is relevant to be isolated when it is the only center in some neighborhood of it. The global Hopf bifurcation theorem for general functional delayed differential equations introduced in [28] is stated as follows.
Lemma 4.2
If \((\bar{Z}, \tau, \mu)\) is an isolated center satisfying assumptions (A1–A4) in [28], let \(\mathcal{L}_{(\bar {Z}, \tau_{1}, \mu)}\) be a connected component of \((\bar{Z}, \tau _{1}, \mu)\) in Γ, then either item (i) or (ii) holds:
-
(i)
\(\mathcal{L}_{(\bar{Z}, \tau, \mu)}\) is unbounded,
-
(ii)
\(\mathcal{L}_{(\bar{Z}, \tau, \mu)}\), \(\mathcal{L}_{(\bar {Z}, \tau, \mu)}\cap\Gamma\) is finite and \(\sum_{(\bar{Z}, \tau , \mu)\in\mathcal{L}(\bar{Z}, \tau, \mu)\cap\mathcal{N}}\gamma _{m}(\bar{Z}, \tau, \mu)=0\) for \(m=1,2,\ldots\) , \(\gamma_{m}(\bar{Z}, \tau, \mu)\) is the mth crossing number of \((\bar{Z}, \tau, \mu)\).
It is easy to show that if (ii) of Lemma 4.2 is not true, then \(\mathcal {L}\) is unbounded. Hence, if the projections of \(\mathcal{L}_{(\bar{Z}, \tau, \mu)}\) onto z-space and onto μ-space are bounded, then the projection of \(\mathcal{L}_{(\bar{Z}, \tau, \mu)}\) is unbounded. Furthermore, if we can show that the projection of \(\mathcal{L}_{(\bar {Z}, \tau, \mu)}\) onto τ-space is away from zero, then the projection of τ-space must include \([\tau, \infty)\).
Theorem 4.3
If \(2-a-k^{3}_{3}< m< a\), \(\max\{2-k_{1}, m\}< a<1\), \(k^{3}_{3}< k_{1}\), \(0< v< v_{2}\) hold (\(v_{2}\) has been defined in Theorem 3.9), then for \(\tau_{1}>\tau_{1d}^{*}\) and \(\sigma_{w}^{*}\) defined in Theorem 3.9, system (29) has at least one periodic solution.
Proof
It is easy to show that \((\tilde{S}^{*}_{w}, \tau, \frac {2\pi}{\sigma_{w}^{*}})\) is an isolated center of system (29). Let \(\mathcal{L}_{(\tilde{S}^{*}_{w}, \tau, \frac{2\pi}{\sigma _{w}^{*}})}\) denote a connected component passing through \((\tilde {S}^{*}_{w}, \tau, \frac{2\pi}{\sigma_{w}^{*}})\) in Γ. It follows from Theorem 3.9 of this paper that \(\mathcal{L}_{(\tilde {S}^{*}_{w}, \tau, \frac{2\pi}{\sigma_{w}^{*}})}\) is nonempty.
Let \(\Delta(\tilde{S}^{*}_{w}, \tau, \rho)(\lambda)\) represent the characteristic matrix of system (29) around \(\tilde{S}^{*}_{w}\). Based on the discussion in Sect. 3.2 of this paper, it can be verified that \((\tilde{S}^{*}_{w}, \tau, \frac{2\pi}{\sigma_{w}^{*}})\) is an isolated center, and there exist \(\epsilon>0\), \(\delta_{1}>0\), a smooth curve \(\lambda: (\tau-\delta_{1}, \tau+\delta _{1})\rightarrow\mathbb{C}\) such that \(\vert \Delta(\tilde {s}^{*}_{w}, \tau, \mu)(\lambda) \vert =0\), \(\vert \lambda (\tau)-i\sigma_{w}^{*} \vert <\epsilon\) for all \(\tau\in[\tau _{1d}^{*}-\delta_{1}, \tau_{1d}^{*}+\delta_{1}]\).
Let
It is easy to show that \(\vert \Delta(\tilde{S}^{*}_{w}, \tau _{1}, \mu)(\eta+\frac{2\pi i}{\mu}) \vert =0\) if and only if \(\eta=0\), \(\tau_{1}=\tau_{1d}^{*}\), \(\mu=\frac{2\pi}{\sigma_{w}^{*}}\).
Hence, assumptions (A1–A4) in [28] all hold. Moreover, if we define
then a crossing number of the isolated center \((\tilde{S}^{*}_{w}, \tau _{1d}^{*}\pm\delta_{1}, \mu)\) is as follows:
By using Theorem 2.1 in [28], it can be concluded that \(\mathcal {L}_{(\tilde{S}^{*}_{w}, \tau_{1d}^{*}, \frac{2\pi}{\sigma _{w}^{*}})}\) passing through \((\tilde{S}^{*}, \tau_{1d}^{*}, \frac {2\pi}{\sigma_{w}^{*}})\) in Γ is nonempty. Consequently, we have
It follows from Lemma 4.2 of this paper that the connected component \(\mathcal{L}_{(\tilde{S}^{*}, \tau_{1d}^{*}, \frac{2\pi}{\sigma _{w}^{*}})}\) passing through \((\tilde{S}^{*}, \tau_{1d}^{*}, \frac {2\pi}{\sigma_{w}^{*}})\) in Γ is unbounded.
Next, we will show that the projection \(\mathcal{L}_{(\tilde{S}^{*}, \tau_{1d}^{*}, \frac{2\pi}{\sigma_{w}^{*}})}\) onto τ-space is \([\bar{\tau}, \infty)\), where \(\bar{\tau}<\tau_{1d}^{*}\). If \(2-a-k^{3}_{3}< m< a\), \(\max\{2-k_{1}, m\}< a<1\), \(k^{3}_{3}< k_{1}\), \(0< v< v_{2}\), then system (29) without time delay has no nontrivial periodic solution. Hence, the projection of \(\mathcal {L}_{(\tilde{S}^{*}, \tau_{1d}^{*}, \frac{2\pi}{\sigma_{w}^{*}})}\) onto τ-space is away from 0.
It is assumed that the projection of \(\mathcal{L}_{(\tilde{S}^{*}, \tau _{1d}^{*}, \frac{2\pi}{\sigma_{w}^{*}})}\) onto τ-space is bounded, which implies the projection of \(\mathcal{L}_{(\tilde{S}^{*}, \tau_{1d}^{*}, \frac{2\pi}{\sigma_{w}^{*}})}\) onto τ-space is included in a bounded interval \((0, \tau_{1d}^{*})\). By using \(\frac {2\pi}{\sigma_{w}^{*}}<\tau_{1d}^{*}\), we have \(\mu<\tau_{1d}^{*}\) for \((Z, \tau, \mu)\) belonging to \(\mathcal{L}_{(\tilde{S}^{*}, \tau _{1d}^{*}, \frac{2\pi}{\sigma_{w}^{*}})}\), which implies that the projection of connected component \(\mathcal{L}_{(\tilde{S}^{*}, \tau _{1d}^{*}, \frac{2\pi}{\sigma_{w}^{*}})}\) onto μ-space is bounded. Hence, it leads to a contradiction, which means that the projection of \(\mathcal{L}_{(\tilde{S}^{*}, \tau_{1d}^{*}, \frac{2\pi }{\sigma_{w}^{*}})}\) onto τ-space is \([\tau_{1d}^{*}, \infty )\), where \(\bar{\tau}\leq\tau_{1d}^{*}\). □
5 Numerical simulation
Numerical simulations are carried out to show combined dynamic effects of time delay and additive Allee effect on population dynamics. Parameters are partially taken from the numerical simulations in [12].
Numerical simulation I: strong Allee effect. Parameters are taken as follows: \(a=0.25\), \(b=0.1\), \(k_{1}=0.035\), \(k_{2}=0.1\), \(k_{3}=0.2\), \(w=4\), \(c=1\), and \(m=0.3\) with appropriate units. By simple computations, it can be obtained that there exists a unique interior equilibrium provided that \(0< v<0.0264\). In the following numerical simulation, \(v=0.01\) is arbitrarily selected within \((0, 0.0264)\) which is enough to merit theoretical analysis in this paper. By using given parameters and simple computations, the unique interior equilibrium of system (3) with strong Allee effect is as follows: \(\tilde{S}_{s}^{*}=(0.6029,0.2891,0.0640)\).
When \(v=-0.01\), the eigenvalues of system (3) are −0.314, −7.687; when \(v=0.01\), the eigenvalues of system (3) are −0.314, 570.2. Obviously, one eigenvalue remains almost constant and another moves from \(\mathbb{C}^{-}\) to \(\mathbb {C}^{+}\) along the real axis by diverging through ∞. It follows from Theorem 3.7 that system (3) is locally stable around \(\tilde {S}_{s}^{*}=(0.6029,0.2891,0.0640)\) when \(0<\tau<\tau _{1c}^{*}=1.3657\). In the case of strong Allee effect, dynamical variations of prey, predator biomass, and harvest amount with the increasing time with \(\tau=0.5\) and \(\tau=1.3657\), which are indicated in Fig. 1(i) and Fig. 1(ii), respectively. The limit cycle around \(\tilde{S}_{s}^{*}=(0.6029,0.2891,0.0640)\) corresponding to Fig. 1(ii) is plotted in Fig. 1(iii). The bifurcation diagram of system (3) with respect to τ is also provided in Fig. 2.
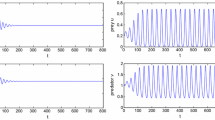
In the case of strong Allee effect, dynamical variations of prey, predator biomass, and harvest amount with the increasing time with \(\tau=0.5\) and \(\tau=1.3657\), which are indicated in Fig. 1(i) and Fig. 1(ii), respectively. The limit cycle around \(\tilde {S}_{s}^{*}=(0.6029,0.2891,0.0640)\) corresponding to Fig. 1(ii) is plotted in Fig. 1(iii)
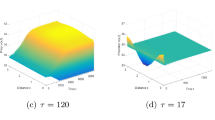
In the case of strong Allee effect, bifurcation diagram of system (3) with respect to τ
Numerical simulation II: weak Allee effect. Parameters are taken as follows: \(a=0.4\), \(b=0.5\), \(k_{1}=0.3\), \(k_{2}=0.125\), \(k_{3}=0.2\), \(w=5\), \(c=1\), and \(m=0.24\) with appropriate units. By simple computations, it can be obtained that there exists a unique interior equilibrium provided that \(0< v<0.0194\). In the following numerical simulation, \(v=0.01\) is arbitrarily selected within \((0, 0.0194)\) which is enough to merit theoretical analysis in this paper. By using given parameters and simple computations, the unique interior equilibrium of system (3) with weak Allee effect is as follows: \(\tilde{S}_{w}^{*}=(0.2643,0.4226,0.0089)\).
When \(v=-0.005\), the eigenvalues of system (3) are −0.529, −14.591; when \(v=0.005\), the eigenvalues of system (3) are −0.529, 375.8. Obviously, one eigenvalue remains almost constant and another moves from \(\mathbb{C}^{-}\) to \(\mathbb {C}^{+}\) along the real axis by diverging through ∞. It follows from Theorem 3.9 that system (3) is locally stable around \(\tilde {S}_{w}^{*}=(0.2643,0.4226,0.0089)\) when \(0<\tau<\tau _{1d}^{*}=1.6429\). In the case of weak Allee effect, dynamical variations of prey, predator biomass, and harvest amount with the increasing time with \(\tau=0.8\) and \(\tau=1.6429\), which are indicated in Fig. 3(i) and Fig. 3(ii), respectively. The limit cycle around \(\tilde{S}_{w}^{*}=(0.2643,0.4226,0.0089)\) corresponding to Fig. 3(ii) is plotted in Fig. 3(iii). The bifurcation diagram of system (3) with respect to τ is also provided in Fig. 4. Further computations show that \(\gamma_{2}=1.0329>0\), \(\iota_{2}=-0.4127<0\), and \(T=1.4193>0\), it follows from Theorem 4.1 that the Hopf bifurcation is supercritical, the direction of the Hopf bifurcation is \(\tau>\tau _{1d}^{*}\) and these bifurcating periodic solutions from the interior equilibrium \(\tilde{S}^{*}_{w}\) at \(\tau_{1d}^{*}\) are stable.
In the case of weak Allee effect, dynamical variations of prey, predator biomass, and harvest amount with the increasing time with \(\tau=0.8\) and \(\tau=1.6429\), which are indicated in Fig. 3(i) and Fig. 3(ii), respectively. The limit cycle around \(\tilde {S}_{w}^{*}=(0.2643,0.4226,0.0089)\) corresponding to Fig. 3(ii) is plotted in Fig. 3(iii)
In the case of weak Allee effect, bifurcation diagram of system (3) with respect to τ
6 Conclusion
In this paper, a delayed singular biological system with additive Allee effect and commercial harvesting is established, which extends the work done in [12] by incorporating gestation delay for the predator population. Positivity of solutions and uniform persistence of the proposed system are discussed in Theorem 2.1 and Theorem 2.3, respectively. Some sufficient conditions for the existence of interior equilibrium in the case of strong and weak Allee effect are investigated in Lemma 3.2 to Lemma 3.5. In the absence of time delay, on account of variation of economic interest of commercial harvesting, we reveal that system (3) undergoes singularity-induced bifurcation around interior equilibrium, and the proposed system is unstable when economic interest increases through zero, which can be found in Theorem 3.6 and Theorem 3.8 in the case of strong Allee effect and weak Allee effect, respectively. In the presence of time delay, by analyzing the associated characteristic equation of system (3), we reveal that when gestation delay crosses the corresponding critical value, the interior equilibrium of the system loses local stability, and system (3) undergoes Hopf bifurcation, which can be found in Theorem 3.7 and Theorem 3.9 in the case of strong Allee effect and weak Allee effect, respectively. By using the center manifold theorem and the norm form of a delayed singular system, we investigate the properties of Hopf bifurcation in Theorem 4.1. The global continuation of Hopf bifurcation is investigated in Theorem 4.3. Finally, numerical simulations are provided to validate theoretical analysis obtained in this paper.
It follows from the analytical findings in Theorem 3.6 and Theorem 3.8 that a singularity-induced bifurcation occurs and local stability switches when economic interest increases through zero, and it can be practically interpreted that the population density dramatically increases beyond environment capacity during a short time period. It follows from the analytical findings in Theorem 3.7 and Theorem 3.9 that local stability will switch when time delay crosses critical value. It can be practically interpreted that commercially harvested population density shows periodic fluctuation and may even arrive at a very low population density during some time, which is disadvantageous to sustainable survival of each population and sustainable exploitation of certain economic population.
The dynamical model proposed in [12], composed of ordinary differential equations, is utilized to study the interaction mechanism of a prey–predator system with additive Allee effect. Compared with the system established in [12], an algebraic equation is introduced into system (3), which concentrates on dynamic effect of economic interest of commercial harvesting on population dynamics and provides a straightforward way to investigate complex dynamics due to variation of economic interest. Furthermore, a discrete time delay, which represents gestation delay of the predator population, is incorporated into system (3). Consequently, compared with the work done in [12], we can investigate combined dynamic effects of time delay and additive Allee effect on population dynamics by analyzing the local stability and bifurcation phenomenon of system (3) in this paper, which makes this paper have some new and positive features.
References
Allee, W.C.: Animal Aggregations: A Study in General Sociology. University of Chicago Press, Chicago (1931)
Courchamp, F., Brock, T.C., Grenfell, B.: Inverse density dependence and the Allee effect. Trends Ecol. Evol. 14, 405–410 (1999)
Stephens, P.A., Sutherland, W.J., Freckleton, R.: What is the Allee effect? Oikos 87, 185–190 (1999)
Berec, L., Angulo, E., Courchamp, F.: Multiple Allee effects and population management. Trends Ecol. Evol. 22, 185–191 (2006)
Courchamp, F., Berec, L., Gascoigne, J.: Allee Effect in Ecology and Conservation. Oxford University Press, New York (2009)
Leslie, P.H., Gower, J.C.: The properties of a stochastic model for the predator–prey type of interaction between two species. Biometrika 47, 219–234 (1960)
Lenhart, S., Workman, J.T.: Optimal Control Applied to Biological Models. Chapman and Hall/CRC Mathematical and Computational Biology. Chapman & Hall/CRC, Boca Raton (2007)
Zhang, G.D., Shen, Y., Chen, B.S.: Hopf bifurcation of a predator–prey system with predator harvesting and two delays. Nonlinear Dyn. 73, 2119–2131 (2013)
Wang, W.M., Zhu, Y.N., Cai, Y.L., Wang, W.J.: Dynamical complexity induced by Allee effect in a predator prey model. Nonlinear Anal., Real World Appl. 16, 103–119 (2014)
Pal, D., Mahapatra, G.S.: A bioeconomic modeling of two prey and one predator fishery model with optimal harvesting policy through hybridization approach. Appl. Math. Comput. 242, 748–763 (2014)
Liu, Y., Zhong, S.M.: Dynamics of a diffusive predator prey model with modified Leslie Gower schemes and additive Allee effect. Comput. Appl. Math. 34, 671–690 (2015)
Cai, Y.L., Zhao, C.D., Wang, W.M.: Dynamics of a Leslie Gower predator–prey model with additive Allee effect. Appl. Math. Model. 39, 2092–2106 (2015)
Dennis, B.: Allee effect: population growth, critical density, and the chance of extinction. Nat. Resour. Model. 3(4), 481–538 (1989)
Gordon, H.S.: Economic theory of a common property resource: the fishery. J. Polit. Econ. 62, 124–142 (1954)
Srinivasu, P.D.N., Kumar, G.K.: Bioeconomics of a renewable resource subjected to strong Allee effect. Comput. Appl. Math. 34, 671–690 (2015)
Bouguima, S.M., Benzerdjeb, S.: An age structured fishery model: dynamics and optimal management with perfect elastic demand. Appl. Math. Model. 40, 218–232 (2016)
Biswas, S., Sasmal, S.K., Samanta, S., Saifuddin, M.D., Pal, N., Chattopadhyay, J.: Optimal harvesting and complex dynamics in a delayed eco-epidemiological model with weak Allee effects. Nonlinear Dyn. 87, 1553–1573 (2017)
Sasmal, S.K., Mandal, D.S., Chattopadhyay, J.: A predator–pest model with Allee effect and pest culling and additional food provision to the predator application to pest control. J. Biol. Syst. 25, 295–326 (2017)
Liu, C., Lu, N., Zhang, Q.L.: Dynamical analysis in a hybrid bioeconomic system with multiple time delays and strong Allee effect. Math. Comput. Simul. 136, 104–131 (2017)
Yang, X., Chen, L.S., Chen, J.E.: Permanence and positive periodic solution for single species semiautonomous delay diffusive model. Comput. Math. Appl. 32, 106–116 (1996)
Thieme, H.R.: Mathematics in Population Biology. Princeton University Press, Princeton (2003)
Song, X., Chen, L.S.: Optimal harvesting and stability for a two-species competitive system with stage structure. Math. Biosci. 170, 173–186 (2001)
Hale, J.K.: Theory of Functional Differential Equations. Springer, New York (1997)
Liu, C., Lu, N., Zhang, Q.L., Li, J.N., Liu, P.Y.: Modelling and analysis in a prey–predator system with commercial harvesting and double time delays. Appl. Math. Comput. 281, 77–101 (2016)
Venkastasubramanian, V., Schaettler, H., Zaborszky, J.: Local bifurcations and feasibility regions in differential-algebraic systems. IEEE Trans. Autom. Control 40, 1992–2013 (1995)
Zhou, S.R., Liu, Y.E., Wang, G.: The stability of predator–prey systems subject to Allee effects. Theor. Popul. Biol. 67, 23–31 (2005)
Hassard, B., Kazarinoff, H., Wan, Y.H.: Theory and Applications of Hopf Bifurcation. London Mathematical Society Lecture Note Series, vol. 41. Cambridge University Press, Cambridge (1981)
Wu, J.: Symmetric functional differential equations and neural networks with memory. Trans. Am. Math. Soc. 350, 4799–4838 (1998)
Acknowledgements
Authors would like to express their gratitude to the editor and anonymous reviewers for valuable comments and suggestions, and for the time and efforts they have spent in the review. Without the expert comments made by the editor and anonymous reviewers, the paper would not be of this quality.
Availability of data and materials
All authors of this article declare that all parameter values and data utilized in the numerical simulation section of this paper are taken from the numerical simulation section in Ref. [12], and interested readers can access all parameter values and data in the the numerical simulation section in Ref. [12].
Authors’ information
All email addresses of authors are as follows: (Chao Liu), (Luping Wang), (Na Lu), (Longfei Yu).
Funding
This work is supported by the National Natural Science Foundation of China, grant No. 61673099, Research Program for Liaoning Excellent Talents in University, grant No. LJQ2014027, Hebei Province Natural Science Foundation, grant No. F2015501047, and Fundamental Research Funds for the Central Universities, grant No. N162304006.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests. All authors of this article declare that there is no conflict of interests regarding the publication of this article. We have no proprietary, financial, professional, or other personal interest of any nature or kind in any product, service, and/or company that could be construed as influencing the position presented in, or review of this article.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Appendix 2
By virtue of (34) and (36), we have
where
Substituting the corresponding series into (45) and comparing coefficients, we have
It follows from (45) that for \(\vartheta\in[-{\tau}_{1d}^{*},0)\),
By comparing coefficients in (46) with those in (40), we derive that
Based on the definition of B, (47) and (49), it can obtained that
where \(Q_{1}=(Q_{1}^{(1)}, Q_{1}^{(2)})\) is a constant vector, and \(r(\vartheta)=(1, \beta)^{T}e^{i\sigma_{w}^{*}\tau _{1d}^{*}\vartheta}\).
Similarly, it follows from (47) and (50) that
where \(Q_{2}=(Q^{(1)}_{2}, Q^{(2)}_{2})\) is a constant vector, and \(r(\vartheta)=(1, \beta)^{T}e^{i\sigma_{w}^{*}\tau _{1d}^{*}\vartheta}\).
By using the definition of B and (45), we have
where \(\eta(\vartheta)=\eta(0, \vartheta)\). Based on (45), it derives that in the case of \(\vartheta=0\),
from which it follows that
By virtue of (29) and (36), it can be obtained that
then we have
According to (55) and (56), we have
Since \(i\sigma_{w}^{*}\tau_{1d}^{*}\) is the eigenvalue of \(B(0)\) and \(r(0)\) is the corresponding eigenvector, for I is the identity matrix, we obtain that
By substituting (51) and (57) into (53), \(Q_{1}^{(1)}\) and \(Q_{1}^{(2)}\) are as follows:
By substituting (52) and (58) into (54), \(Q_{2}^{(1)}\) and \(Q_{2}^{(2)}\) are as follows:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, C., Wang, L., Lu, N. et al. Modelling and bifurcation analysis in a hybrid bioeconomic system with gestation delay and additive Allee effect. Adv Differ Equ 2018, 278 (2018). https://doi.org/10.1186/s13662-018-1738-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1738-0