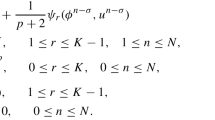Abstract
In this paper, we propose an efficient numerical scheme for the approximate solution of a time fractional diffusion-wave equation with reaction term based on cubic trigonometric basis functions. The time fractional derivative is approximated by the usual finite difference formulation, and the derivative in space is discretized using cubic trigonometric B-spline functions. A stability analysis of the scheme is conducted to confirm that the scheme does not amplify errors. Computational experiments are also performed to further establish the accuracy and validity of the proposed scheme. The results obtained are compared with finite difference schemes based on the Hermite formula and radial basis functions. It is found that our numerical approach performs superior to the existing methods due to its simple implementation, straightforward interpolation and very low computational cost. A convergence analysis of the scheme is also discussed.
Similar content being viewed by others
1 Introduction
1.1 Problem description
For \(T>0\) and \(\Omega=[a,b]\), we consider the following model of the time fractional diffusion-wave equation with reaction term:
with initial conditions
and the following boundary conditions:
where a, b, \(\phi_{1}(x)\), \(\phi_{2}(x)\), \(\psi_{1}(t)\) and \(\psi_{2}(t)\) are given, \(\alpha>0\) is the reaction coefficient and \(\frac{\partial ^{\gamma}}{\partial t^{\gamma}}u(x,t)\) represents the Caputo fractional derivative of order γ given by [1]
To obtain the time fractional diffusion-wave equation from the standard diffusion or wave equation, we replace the ordinary first or second time derivative by a fractional derivative of order γ, where \(0<\gamma<1\) or \(1<\gamma<2\). As γ changes from 0 to 2, the process transforms from slow diffusion to classical diffusion and from diffusion-wave to classical wave phenomenon. We consider, in this paper, the case of diffusion-wave, i.e., \(1 < \gamma< 2\). It can be used to deal with viscoelastic problems and disordered media to examine structures, semiconductors and dielectrics.
1.2 Applications and literature review
The subject of fractional calculus [1–4] in its modern form has a history of at least three decades and has developed rapidly due to its wide range of applications in fluid mechanics, plasma physics, biology, chemistry, mechanics of material science and so on [3, 5]. Other applications include system control [1], viscoelastic flow [6], hydrology [7, 8], tumor development [9] and finance [10–12]. Since the fractional models in certain situations tend to behave more appropriately than the conventional integer order models, several techniques have been developed to study these models. These techniques have been continuously improved and modified to achieve more and more accuracy.
Since exact analytical solutions of only a few fractional differential equations exist, the search for approximate solutions is a concern of many recently published articles. Many research publications have been devoted to numerical techniques for solving time fractional diffusion-wave equations. Zeng [13] proposed two second order stable and one conditionally stable finite difference schemes for the time fractional diffusion-wave model. Using a class of finite difference methods based on the Hermite formula, Khader and Adel [14] obtained numerical solutions of a fractional diffusion-wave equation. Avazzadeh et al. [15] obtained numerical solutions of a fractional diffusion-wave equation by using the radial basis function method. Pskhu [16] obtained fundamental solutions of a fractional order diffusion-wave equation. It has been shown that this fundamental solution gives the corresponding solutions for diffusion and wave equations when the fractional order is equal to one or approaches two. Povstenko [17] discussed Neumann boundary-value problems for a time-fractional diffusion-wave equation in a half-plane. Numerical solutions to the fractional diffusion-wave equation under Dirichlet and Neumann boundary conditions were obtained by Povstenko. Liemert and Kienle [18] discussed a time fractional wave-diffusion equation in an inhomogeneous half-space. Ren and Sun [19] obtained efficient numerical solutions of the multi-term time fractional diffusion-wave equation by using a compact finite difference scheme with fourth-order accuracy. Jin et al. [20] utilized a Galerkin finite element method to find approximate solution for a multi-term time-fractional diffusion equation. Jianfei et al. [21] presented two efficient finite difference schemes to approximate solutions of time fractional diffusion equations. A second order BDF alternating direction implicit difference scheme for the two-dimensional fractional evolution equation was discussed in [22].
An efficient numerical scheme based on trigonometric cubic B spline functions is presented in this paper to find the approximate solutions of a time fractional diffusion-wave equation with reaction term. First, we discretize the Caputo time fractional derivative by the usual finite difference formula and then use trigonometric cubic B-spline basis to approximate derivatives in space. Trigonometric cubic B-spline functions provide better accuracy than the usual finite difference schemes due to their minimal support and \(C^{2}\) continuity. Numerical experiments are carried out, and the obtained results are compared with those of [14] and [15]. The comparison shows that the presented scheme has accuracy up to 10−11, whereas the scheme discussed in [14] has accuracy of 10−5. The scheme is shown to be unconditionally stable using a procedure similar to Von-Neumann stability analysis, whereas the scheme of [14] is conditionally stable. Convergence analysis of the presented scheme is also discussed. Numerical experiments confirm the validity and efficiency of the algorithm.
The outline of this paper is as follows. In Section 2, we give temporal discretization using a forward finite difference scheme of Eq. (1). In Section 3, we present the derivation of the scheme for the fractional diffusion-wave equation using the trigonometric cubic B-spline functions. The stability analysis of the proposed scheme is given in Section 4. Section 5 discusses convergence analysis of the scheme. Computational experiments are conducted to check the efficiency and validity of the scheme, and the numerical results are reported in Section 6. The last section is devoted to the concluding remarks of the study.
2 Temporal discretization
To find time discretization of Eq. (1), we discretize the Caputo time fractional derivative \(\frac{\partial^{\gamma }u(x,t)}{\partial t^{\gamma}}\) appearing in the equation using the usual finite difference method. Following the standard notations, we let \(t_{n}=n \Delta t\), \(n=0,1,\ldots M\), where \(\Delta t=\frac{T}{M}\) is the time step. First we approximate the second order differential operators using a forward finite difference method as follows:
where \(s \in[t_{n},t_{n+1}]\). Using (5), we can obtain an efficient approximation to the fractional derivative \(\frac{\partial^{\gamma}u(x,t)}{\partial t^{\gamma}}\) as follows:
where \(e_{\Delta t}^{n+1}\) is the truncation error, \(r=(t_{n+1}-s)\) and \(b_{j}=(j+1)^{2-\gamma}-j^{2-\gamma}\). The reader may verify that
-
\(b_{j} >0\), \(j=0,1,2,\ldots,n\),
-
\(1=b_{0}>b_{1}>b_{2}>\cdots>b_{n}\) and \(b_{n}\rightarrow0\) as \(n \rightarrow\infty\),
-
\(\sum_{j=0}^{n} (b_{j}-b_{j+1})=(1-b_{1})+\sum_{j=1}^{n-1} (b_{j}-b_{j+1})+b_{n}=1\).
Substituting (6) into (1), we obtain the following temporal discretization:
Letting \(\alpha_{0}=\frac{1}{(\Delta t)^{\gamma}\Gamma(3-\gamma)}\), \(u^{n+1}=u(x,t_{n+1})\), the last equation can be rewritten as
where \(n=0,1,\ldots M\). It is observed that the term \(u^{-1}\) will appear when \(n=0\) or \(j=n\). To eliminate \(u^{-1}\), we utilize the initial condition to obtain
It follows then that \(u^{-1}=u^{1}-2 \Delta t u_{t}^{0}\) or \(u^{-1}=u^{1}-2 \Delta t \phi_{2}(x)\).
3 Description of the numerical scheme
In this section, we derive the cubic trigonometric B-spline collocation method (CuTBSM) for finding the numerical solution of time fractional diffusion-wave equation problem (1). The solution domain \(a\leq x\leq b\) is uniformly partitioned by knots \(x_{i}\) into N subintervals \([x_{i}, x_{i+1}]\) of equal length \(h=\frac{b-a}{N}\), \(i=0,1,2,\ldots,N-1\), where \(a=x_{0}< x_{1}<\cdots<x_{n-1}<x_{N}=b\). Our numerical approach for solving (1) using trigonometric cubic B-splines is to seek an approximate solution \(U(x,t)\) to the exact solution \(u(x,t)\) in the following form [23, 24]:
where \(c_{i}(t)\) are to be required for the approximate solution \(U(x,t)\) to the exact solution \(u(x,t)\). The twice differentiable trigonometric basis functions \(TB^{4}_{i} (x)\) [25] at the knots \(x_{i}\) are given by
where
Since there are three non-zero terms at each knot, notably \(TB^{4}_{j-1}(x)\), \(TB^{4}_{j}(x)\) and \(TB^{4}_{j+1}(x)\), therefore the approximation \(u_{j}^{n}\) at the grid point \((x_{j},t_{n})\) to the exact solution at nth time level is given as
The time dependent unknowns \(c_{j}^{n}(t)\) are to be determined by making use of the initial and boundary conditions, and the collocation conditions on \(TB^{4}_{i} (x)\). As a result, we obtain the approximations \(u_{j}^{n}\) together with their necessary derivatives as given below:
where
To obtain full discretization which relates the successive time levels and the unknowns \(c_{j}^{n+1}\), we plug in the approximations \(u_{j}^{n}\) and their derivatives (13) into Eq. (8). After some simplifications, we arrive at the following recurrence relation:
System (14) contains \((N+1)\) linear equations in \((N+3)\) unknowns. To obtain two additional equations, the boundary conditions (3) are utilized to obtain a unique solution of the problem. Consequently, a matrix system of dimension \((N + 3)\times(N + 3)\), which is a tri-diagonal system, is obtained. The Thomas algorithm [26] is then used to uniquely solve this system.
3.1 Initial vector \(c^{0}\)
In order to commence the iteration process, it is required to find the initial solution vector \(c^{0}=[c_{-1}^{0},c_{0}^{0}, \ldots, c_{N+1}^{0}]^{T}\). The process of finding the initial vector involves the computation of initial condition and its derivatives at the two boundaries as explained below [25]:
-
(i)
\((u_{j}^{0})_{x}=\frac{d}{dx}\phi_{1}(x_{j})\), \(j=0\),
-
(ii)
\(u_{j}^{0}=\phi_{1}(x_{j})\), \(j=0,1,\ldots N\),
-
(iii)
\((u_{j}^{0})_{x}=\frac{d}{dx}\phi_{1}(x_{j})\), \(j=N\).
The above tri-diagonal system consists of \((N+3)\) linear equations in \((N+3)\) unknowns whose matrix form is given as
where
and \(b=[\phi_{1}'(x_{0}), \phi_{1}(x_{0}), \ldots, \phi_{1}(x_{N}), \phi_{1}'(x_{N})]^{T}\).
4 Stability analysis
By Duhamel’s principle [27], it follows that the solution to an inhomogeneous problem is the superposition of the solutions to homogeneous problems. As a consequence, a scheme is stable for the inhomogeneous problem if it is stable for the homogeneous one. It is sufficient to present the stability analysis for scheme (14) for the force-free case (\(f=0\)) only. The growth factor of a Fourier mode is assumed to be \(\rho_{j}^{n}\), and let \(\tilde{\rho}_{j}^{n}\) be its approximation. Define \(E_{j}^{n}=\rho _{j}^{n}-\tilde{\rho}_{j}^{n}\) which on substitution in (14) gives the following roundoff error equation:
The error equation satisfies the boundary conditions
and the initial conditions
Define the grid function
Note that the Fourier expansion of \(E^{K}(x)\) is
where \(a^{k}(m)=\frac{1}{(b-a)}\int_{a}^{b} E^{k}(x)e^{\frac{-i 2 \pi m x}{(b-a)}} \,dx\). Let
and introduce the norm
By Parseval’s equality, it is observed that
so that the following relation is obtained:
Suppose that Eqs. (16)-(18) have a solution of the form \(E_{j}^{n}=\xi_{n} e^{i \beta j h}\), where \(i=\sqrt{-1}\) and β is real. Substituting this expression in Eq. (16) and dividing by \(e^{i \beta j h}\), we obtain
Using the relation \(e^{-i \beta h}+e^{i \beta h}=2\cos(\beta h)\) and grouping like terms, we obtain the following relation:
where \(\nu=1+\frac{2(a_{1}\alpha-a_{4})\cos(\beta h)+(a_{2}\alpha -a_{5})}{\alpha_{0}(2 a_{1} \cos(\beta h)+a_{5})}\). Obviously, \(\nu\geq1\).
Proposition 1
If \(\xi_{n}\) is the solution of Eq. (21), then \(\vert \xi _{n} \vert \leq2 \vert \xi_{0} \vert \), \(n=0,1,\ldots, T \times M\).
Proof
Mathematical induction is used to prove the result. For \(n=0\), we have from Eq. (21) that \(\xi_{1}=\frac{2}{\nu} \xi_{0}\). Since \(\nu\geq1\), we have
Now suppose that \(\vert \xi_{n} \vert \leq2 \vert \xi _{0} \vert \), \(n=1,\ldots,T \times M-1 \), so that from (21) we obtain
□
Theorem 1
The collocation scheme (14) is unconditionally stable.
Proof
Using formula (19) and Proposition 1, we obtain
which establishes that the scheme is unconditionally stable. □
5 Convergence analysis
First we introduce some usual notations and a lemma due to Lopez-Marcos [28] that play a crucial role in convergence analysis of the scheme.
Let \(\Omega_{h}=\{x_{j}\vert0 \leq i \leq N\}\) and \(\Omega_{\tau}=\{ t_{n}\vert0 \leq n \leq M\}\) be uniform partitions of the intervals \([a,b]\) and \([0,L]\), respectively, where \(x_{i}=ih\) and \(t_{n}=n \tau\) with \(\tau=\frac {T}{M}\). Let \(u_{j}^{n}\) be approximation to exact solution at the point \((x_{j},t_{n})\) and \(V=\{v_{j}\vert0\leq j\leq M\}\) and \(W=\{w_{j}\vert0\leq j\leq M\}\) be two grid functions defined on \(\Omega_{h} \). Introduce
From [28], we have the following important lemma regarding the nonnegative nature of some real quadratic forms possessing a convolution structure.
Lemma 5.1
Let \(\{w_{n}\}_{n=0}^{\infty}\) be a monotonically decreasing sequence of nonnegative real numbers with the property \(a_{n+1}+a_{n-1}\geq2 a_{n}\) (\(n\geq1\)), then for any positive integer K and real vector \((V_{1},v_{2},\ldots, V_{K})\in R^{K}\), we have
Let C be a positive number which assumes different values at different locations and is independent of i, n, h and τ such that
Then, for scheme (7), we have
and
where \(u(x_{j},t_{n})\) is exact and \(u_{j}^{n}\) is approximate solution at the point \((x_{j},t_{n})\) and \(f_{j}^{n+1}=f(x_{j},t_{n})\).
Theorem 2
Let \(u(x,t)\) and \(u_{i}^{n}\) be solutions of (1) and (24), respectively, and \(u(x,t)\) satisfies the smoothness condition (23), then for sufficiently small h and τ, it holds that
where \(e_{i}^{n+1}=u(x_{i},t^{n+1})-u_{i}^{n+1}\).
Proof
To obtain the error equation, we subtract (24) from (25) to get
where \(r_{j}^{n+1}=O(\tau^{2}+\tau h^{2})\).
Multiplying both sides of (26) by \(he_{j}^{n+1}\) and summing up for j from 1 to M, we obtain
Rearranging terms, we obtain
Since \(\frac{1}{\alpha} \Vert (e^{n+1})_{x} \Vert ^{2} \geq 0\), therefore
Then
Adding up all the above inequalities gives
Using Lemma (5.1), it follows that \(\sum_{p=0}^{n}\sum_{k=0}^{p} b_{k} ( \delta^{2}e^{p+1-k}, e^{p+1})\geq0\) so that we obtain from the last inequality
So
By the Cauchy-Schwarz inequality, we obtain
Then
from where (26) can be very easily deduced. □
6 Numerical results and discussion
In this section, numerical experiments are carried out for the time fractional diffusion-wave equation (1) with initial (2) and boundary conditions (3). The efficiency and accuracy of the method are checked by calculating the error norms \(L_{2}\) and \(L_{\infty}\) given by
and
respectively. We compare the numerical solutions obtained by CuTBSM for one-dimensional fractional diffusion equations (1) with known exact solutions. Numerical calculations are carried out by using Mathematica 9 on an Intel®Core™ i5-2410M CPU @2.30 GHz with 8 GB RAM and 64-bit operating system (Windows 7).
Example 1
As a first experiment, we consider the following fractional diffusion-wave equation for \(\alpha=0\):
where the source term is \(f(x,t)=\frac{2 t^{2-\gamma}\sin(\pi x)}{\Gamma[3-\gamma]}+(t^{2}-t)\sin(\pi x)\pi^{2}\). The exact solution of the problem is \(u(x,t)=\sin(\pi x)(t^{2}-t)\) [14].
Figure 1 compares the graphs of the exact and approximate solutions with different values of γ, h and Δt at different time levels. The graphs show excellent agrement between the solutions. In Figure 2, we exhibit the absolute error profiles at different time levels from where high accuracy of the method can be observed. Figure 3 compares the graphs of the exact and approximate solutions using our scheme with those obtained in [14] at time \(t=2\). It is observed that our scheme gives much better accuracy. Figure 4 shows a very close comparison of 3D plots of the exact and approximate solutions at time \(t=0.1\). In Tables 1-2, the maximum errors obtained are compared with those of Hermite formula (HF) [14] for different values of γ to demonstrate that our scheme is more accurate and gives accuracy of 10−7. In Tables 3-4, error norms are computed for various values of parameters to further confirm the accuracy and efficiency of the presented scheme.
The comparison of exact (solid lines) and numerical solutions (stars, bullets and triangles) for Example 1 when \(\pmb{h=\frac{1}{80}}\) , \(\pmb{\Delta t=\frac{1}{100}}\) and \(\pmb{\gamma=1.75}\) at different time levels.
Error profiles for \(\pmb{\gamma=1.5}\) , \(\pmb{h=\frac {1}{150}}\) , \(\pmb{\Delta t=\frac{1}{120}}\) at different time levels for Example 1 .
Behavior of numerical solutions for Example 1 when \(\pmb{h=\frac{1}{150}}\) , \(\pmb{\Delta t=\frac{1}{120}}\) and \(\pmb{t=2}\) .
A 3D comparison of exact (left) and numerical solutions (right) for Example 1 when \(\pmb{h=\frac{1}{64}}\) , \(\pmb{\Delta t=\frac {1}{100}}\) and \(\pmb{\gamma=1.5}\) at \(\pmb{t=1}\) .
Example 2
As a second experiment, consider the time fractional diffusion-wave equation
where the forcing term \(f(x,t)\) is supposed to be
The exact solution of problem (29) is \(u(x,t)=t^{2} x (1-x)\).
The proposed scheme is applied to solve this problem. Figure 5 shows the graphs of the exact and approximate solutions at different time levels with \(\gamma=1.5\), \(\Delta t=0.01\) and \(t=1\) for \(N=80\). An excellent agrement between the exact and approximate solutions can be observed. To exhibit the accuracy of the scheme, the absolute error profile is plotted at different time levels in Figure 6 (with \(N=60\), \(\Delta t=0.001\)). The 3D plot approximate and exact solutions are shown in Figure 7 by fixing values of different parameters. A tremendous similarity can be seen between the solutions. The absolute errors at different points \((x_{j},t_{j})\in[0,1]\times [0,1]\) for different values of γ chosen in the range \(1<\gamma \leq2\) are tabulated in Table 5. From Figure 7 and Table 5, it is clear that the proposed scheme is very accurate and efficient. It is worthwhile to note that the numerical solutions are in excellent agreement with the exact solutions for many values of γ.
The comparison of exact (lines) and approximate solutions for Example 2 when \(\pmb{\gamma=0.5}\) , at \(\pmb{t=0.5}\) (triangles), \(\pmb{t=0.75}\) (circles) and \(\pmb{t=1}\) (stars) with \(\pmb{N=80}\) , \(\pmb{\Delta t=0.01}\) .
Error profiles for Example 2 at different time levels when \(\pmb{N=60}\) , \(\pmb{\Delta t=0.01}\) .
3D space-time graphs of exact (right) and numerical solutions (left) for Example 2 .
Example 3
As the last example, consider the time fractional diffusion-wave equation
where the source term is
The exact solution of problem (30) is \(u(x,t)=t^{2} \sinh(x)\) [15].
The above problem is solved by using the proposed scheme. Figure 8 exhibits the graphs of the exact and approximate solutions at different time levels with \(\gamma=1.5\), \(\Delta t=0.01\) and \(t=1\) for \(N=80\). By taking \(N=40\), \(\Delta t=0.001\), the absolute error profile is plotted at different time levels in Figure 9. Figures 8 and 9 show a very close comparison between the exact and approximate solutions. The 3D exact and numerical solutions are shown in Figure 10 by fixing values of different parameters. In Table 6, we present the absolute errors at different points \((x_{j},t_{j})\in[0,1]\times[0,1]\) for different values of γ chosen in the range \(1<\gamma\leq2\). The comparison between the obtained results and those of radial basis functions (RBF) [15] is given in Tables 7-9. From Figure 10 and Tables 6-9, it is clear that the proposed scheme is very accurate and efficient. It is noticed that the numerical solutions are in close agreement with the exact solutions for many values of γ.
The comparison of exact (lines) and approximate solutions for Example 3 when \(\pmb{\gamma=0.5}\) , at \(\pmb{t=0.5}\) (triangles), \(\pmb{t=0.75}\) (circles) and \(\pmb{t=1}\) (stars) with \(\pmb{N=80}\) , \(\pmb{\Delta t=0.01}\) .
Error profiles for Example 3 at different time levels when \(\pmb{N=60}\) , \(\pmb{\Delta t=0.01}\) .
3D space-time graphs of exact and numerical solutions for Example 3 .
7 Concluding remarks
This study presents a finite difference scheme with a combination of cubic trigonometric B-spline basis for the time fractional fractional diffusion-wave equation with reaction term. This algorithm is based on a discretization using finite difference formulation for the Caputo sense. The cubic trigonometric B-spline basis functions have been used to approximate derivatives in space. The scheme provides accuracy of 10−11, and the obtained numerical results are in superconformity with the exact solutions. A special attention has been given to study the stability of the scheme by using a procedure similar to Von Neumann stability analysis. The scheme is shown to be unconditionally stable, whereas the scheme of [14] is conditionally stable. A convergence analysis of the scheme is also presented.
References
Podlubny, I: Fractional Differential Equations. Academic Press, San Diego (1999)
Mainardi, F: In: Fractals and Fractional Calculus Continuum Mechanics, pp. 291-348. Springer, Berlin (1997)
Hilfer, R: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Kilbas, AA, Srivastava, HM, Trujillo, JJ: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Sokolov, IM, Klafter, J, Blumen, A: Fractional kinetics. Phys. Today 55, 48-54 (2002)
Diethelm, K, Freed, AD: On solution of nonlinear fractional order differential equations used in modelling of viscoplasticity. In: Scientific Computing in Chemical Engineering II: Computational Fluid Dynamics, Reaction Engineering and Molecular Properties, pp. 217-224. Springer, Heidelberg (1999)
Beker-Keren, P, Meerschaert, MM, Scheffler, HP: Limit theorem for continuous-time random walks with two time scales. J. Appl. Probab. 41, 455-466 (2004)
Meerschaert, MM, Zhang, Y, Baeumerc, B: Particle tracking for fractional diffusion with two time scales. Comput. Math. Appl. 59, 1078-1086 (2010)
Iomin, A, Dorfman, S, Dorfman, L: On tumor development: fractional transport approach. http://arxiv.org/abs/qbio/0406001
Gorenflo, R, Mainradi, F, Scalas E, Raberto M: Fractional calculus and continuous-time finance. III, The diffusion limit. In: Mathematical Finance. Trends in Math., 171-180 (2001)
Meerschaert, MM, Scalas, E, Mainradi, F: Coupled continuous time random walks in finance. Physica A 370, 114-118 (2006)
Raberto, M, Scalas, E, Mainradi, F: Waiting-times and returns in high-frequency financial data: an empirical study. Physica A 314, 749-755 (2002)
Zeng, F: Second-order stable finite difference schemes for the time-fractional diffusion-wave equation. J. Sci. Comput. 65(1) 411-430 (2015)
Khader, MM, Adel, MH: Numerical solutions of fractional wave equations using an efficient class of FDM based on the Hermite formula. Adv. Differ. Equ. 2016, 34 (2016)
Avazzadeh, Z, Hosseini, VR, Chen, W: Radial basis functions and FDM for solving fractional diffusion-wave equation. Iran. J. Sci. Technol. 38(A3), 205-212 (2014)
Pskhu, AV: The fundamental solution of a diffusion-wave equation of fractional order. Izv. Math. 73(2), 351-392 (2009)
Povstenko, Y: Neumann boundary-value problems for a time-fractional diffusion-wave equation in a half plane. Comput. Math. Appl. 64, 3183-3192 (2012)
Liemert, A, Kienle, A: Time-fractional wave-diffusion equation in an inhomogeneous half-space. J. Phys. A, Math. Theor. 48, 1-19 (2015)
Ren, J, Sun, Z: Efficient numerical solution of the multi-term time fractional diffusion-wave equation. East Asian J. Appl. Math. 5(1), 1-28 (2015)
Jin, B, Lazarov, R, Liu, Y, Zhou, Z: The Galerkin finite element method for a multi-term time-fractional diffusion equation. J. Comput. Phys. 281, 825-843 (2015)
Huang, J, Tang, Y, Vázques, L, Yang, J: Two finite difference schemes for time fractional diffusion-wave equation. Numer. Algorithms 64, 707-720 (2013)
Chen, H, Xu, D, Pang, Y: A second order BDF alternating direction implicit difference scheme for the two-dimensional fractional evolution. Appl. Math. Model. 41, 54-67 (2017)
Prenter, PM: Splines and Variational Methods. Wiley, New York (1989)
Boor, C: A Practical Guide to Splines. Springer, Berlin (1978)
Abbas, M, Majid, AA, Ismail, AIM, Rashid, A: The application of cubic trigonometric B-spline to the numerical solution of the hyperbolic problems. Appl. Math. Comput. 239, 74-88 (2014)
Burdern, RL, Faires, JD: Numerical Analysis, 8th edn. Brooks Cole (2004)
Strikwerda, JC: Finite Difference Schemes and Partial Differential Equations, 2nd edn. Society for Industrial and Applied Mathematics, Philadelphia (2004)
Lopez-Marcos, JC: A difference scheme for a nonlinear partial integrodifferential equation. SIAM J. Numer. Anal. 27(1), 20-31 (1990)
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
All authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to writing of this paper. All authors read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yaseen, M., Abbas, M., Nazir, T. et al. A finite difference scheme based on cubic trigonometric B-splines for a time fractional diffusion-wave equation. Adv Differ Equ 2017, 274 (2017). https://doi.org/10.1186/s13662-017-1330-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1330-z