Temporal Second-Order Fast Finite Difference/Compact Difference Schemes for Time-Fractional Generalized Burgers’ Equations

Abstract

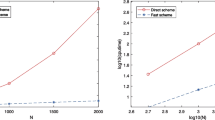
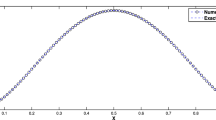
Two kinds of numerical schemes are investigated for time-fractional generalized Burgers’ equations (TFGBE). The first kind is obtained by the temporal second-order fast finite difference approach for the TFGBE with Dirichlet boundary conditions, and the second kind is obtained by the temporal second-order fast finite compact difference approach for TFGBE with periodic boundary conditions. In the time direction, both schemes employ nonuniform meshes to overcome the initial singularity, where the nonuniform Alikhanov formula with the sum-of-exponentials is used to approximate the time-fractional derivative. As a result, this allows the time direction to achieve second-order accuracy and saves a lot of computational costs. In the space direction, the classical second-order difference formulae are used to discretize the spatial derivatives in the finite difference scheme, which can arrive at second-order accuracy. The developed compact difference formulae are employed to approach the spatial derivatives in the compact difference scheme, which can allow the space direction to achieve fourth-order accuracy. For the two difference schemes, we carry out detailed theoretical analysis, including solvability, boundedness, and convergence analysis. In addition, we provide several numerical examples to test the effectiveness of the proposed fast difference/compact difference schemes and to verify the correctness of the theoretical analysis.

Appendix: The Proof of Uniqueness for the Proposed Fast Difference Scheme (17)–(20)

To obtain the uniqueness result, we first invoke the following two lemmas.

Lemma A1

[33] For any grid function $\phi \in \mathring{{\mathcal {V}}}_h$, there exists inverse estimate

$$\begin{aligned} |\phi |_1\le \frac{2}{h}\Vert \phi \Vert . \end{aligned}$$

In addition, by combing the third inequality of Lemma 2, we also have

$$\begin{aligned} \Vert \phi \Vert _\infty \le \sqrt{L}h^{-1}\Vert \phi \Vert . \end{aligned}$$

(A1)

Lemma A2

Suppose that $\{ u_r^n, \phi _r^n\}$ is the solution of the fast difference scheme (17)–(20). Based on the conditions of Theorem 4, and if $\rho \alpha \ge 2$, the spatial step $h \le 1$ and the maximum temporal step $\tau$ satisfies

$$\begin{aligned} \tau \le \min \{{1}/{\root \eta \of {2{\mathfrak {P}}_A\varGamma (2-\eta )c_3}},\sqrt{h}\}, \end{aligned}$$

then for any $0\le n \le N$, we have

$$\begin{aligned} |u^n|_1\le C, \quad \Vert u^n\Vert _\infty \le C. \end{aligned}$$

(A2)

Proof

When $\rho \alpha \ge 2$, then the inequality (44) becomes

$$\begin{aligned} \Vert e^n\Vert \le C(\tau ^2+h^2), \quad 0\le n \le N, \end{aligned}$$

and combing the inverse estimate and (A1), we have

$$\begin{aligned} \begin{aligned}&|e^n|_1 \le 2h^{-1}\Vert e^n\Vert \le 2Ch^{-1}(\tau ^2+h^2),\quad 0\le n \le N,\\&\Vert e^n\Vert _\infty \le \sqrt{L}h^{-1}\Vert e^n\Vert \le \sqrt{L}Ch^{-1}(\tau ^2+h^2), \quad 0\le n \le N. \end{aligned} \end{aligned}$$

When $h\le 1$ and $\frac{\tau ^2}{h}\le 1$ i.e., $\tau \le \sqrt{h}$, we can get

$$\begin{aligned} | e^n|_1 \le C, \quad \Vert e^n\Vert _\infty \le C. \end{aligned}$$

Finally, we can obtain

$$\begin{aligned} \begin{aligned}&|u^n|_1 \le |U^n|_1+|e^n|_1 \le c_0+C\le C,\\&\Vert u^n\Vert _\infty \le \Vert U^n\Vert _\infty +\Vert e^n\Vert _\infty \le c_0+C\le C. \end{aligned} \end{aligned}$$

This accomplished the proof. $\square$

Remark 4

It is worth noting that the assumption of $\rho \alpha \ge 2$ is intended to be concise and easy to understand. Although $\rho \alpha < 2$, we only need to adjust the restriction condition of the maximum temporal step $\tau \le \root \rho \alpha \of {h}$, the conclusion of Lemma A2 also holds.

Proof of Theorem 2

Let $\{ \tilde{u}^n,\;\tilde{\phi }^n \in \mathring{{\mathcal {V}}}_h \}$ and $\{ \hat{u}^n,\;\hat{\phi }^n \in \mathring{{\mathcal {V}}}_h \}$ be the solutions of the fast difference scheme (17)–(20), respectively, then we have

and

For convenience, let

$$\begin{aligned} \bar{u}_r^n=\tilde{u}_r^{n}-\hat{u}_r^n,\quad \bar{\phi }_r^n=\tilde{\phi }_r^{n}-\hat{\phi }_r^n,\quad 0\le r\le K, \quad 0\le n\le N. \end{aligned}$$

Now, subtracting (A7)–(A10) from (A3)–(A6), respectively. Then we get

where the definition of function g is same as (37). According to the differential mean value theorem, from (A12), we have

$$\begin{aligned} |\bar{\phi }_r^{n}|=|g(\tilde{u}_r^{n})-g(\hat{u}_r^{n})|\le \tilde{c}_2|\bar{u}_r^{n}|,\quad 0\le r\le K, \quad 0\le n\le N. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \Vert \bar{\phi }^{n}\Vert \le \tilde{c}_2\Vert \bar{u}^{n}\Vert , \quad 0\le n\le N. \end{aligned}$$

(A15)

Then, taking the inner product of (A11) with $\bar{u}^{n-\sigma }$, we obtain

$$\begin{aligned} \begin{aligned} \left\langle \left( {\mathcal {D}}_{\tau }^{\eta }\bar{u}\right) ^{n-\sigma },\bar{u}^{n-\sigma }\right\rangle&+\frac{1}{p+2}\left\langle \psi (\tilde{\phi }^{n-\sigma },\tilde{u}^{n-\sigma }) -\psi (\hat{\phi }^{n-\sigma },\hat{u}^{n-\sigma }),\bar{u}^{n-\sigma } \right\rangle \\&-\mu \left\langle \delta _x^2\bar{u}^{n-\sigma },\bar{u}^{n-\sigma } \right\rangle =0. \end{aligned} \end{aligned}$$

(A16)

Now, we shall analyze the above equation term by term. Using the Lemma 5, we have

$$\begin{aligned} \left\langle \left( {\mathcal {D}}_{\tau }^{\eta }\bar{u}\right) ^{n-\sigma },\bar{u}^{n-\sigma } \right\rangle \ge \frac{1}{2} \sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _\tau (\Vert \bar{u}^k\Vert ^2). \end{aligned}$$

(A17)

According to (A2), let $\tilde{c}_0:=\max \limits _{0\le n \le N}\Vert \tilde{u}^n\Vert _\infty$. Using Lemmas 1–3 and Cauchy-Schwarz inequality, Young inequality, then we have

$$\begin{aligned} \begin{aligned}&-\frac{1}{p+2}\left\langle \psi (\tilde{\phi }^{n-\sigma },\tilde{u}^{n-\sigma })-\psi (\hat{\phi }^{n-\sigma }, \hat{u}^{n-\sigma }),\bar{u}^{n-\sigma } \right\rangle \\&\quad = -\frac{1}{p+2}\left\langle \psi (\bar{\phi }^{n-\sigma },\tilde{u}^{n-\sigma })+\psi (\tilde{\phi }^{n-\sigma }, \bar{u}^{n-\sigma })-\psi (\bar{\phi }^{n-\sigma },\bar{u}^{n-\sigma }),\bar{u}^{n-\sigma } \right\rangle \\&\quad =-\frac{1}{p+2}\left\langle \psi (\bar{\phi }^{n-\sigma },\tilde{u}^{n-\sigma }),\bar{u}^{n-\sigma } \right\rangle \\&\quad =-\frac{h}{p+2}\sum _{r=1}^{K-1}\left[ \bar{\phi }_r^{n-\sigma }\varDelta _x\tilde{u}_r^{n-\sigma } +\varDelta _x(\bar{\phi }_r^{n-\sigma }\tilde{u}_r^{n-\sigma })\right] \bar{u}_r^{n-\sigma }\\&\quad =-\frac{h}{p+2}\sum _{r=1}^{K-1}\left[ \bar{\phi }_r^{n-\sigma }\varDelta _x\tilde{u}_r^{n-\sigma }\bar{u}_r^{n-\sigma } -\bar{\phi }_r^{n-\sigma }\tilde{u}_r^{n-\sigma }\varDelta _x\bar{u}_r^{n-\sigma }\right] \\&\quad \le \frac{c^\star }{p+2} \Vert \bar{\phi }^{n-\sigma }\Vert \Vert \bar{u}^{n-\sigma }\Vert +\frac{\tilde{c}_0}{p+2} \Vert \bar{\phi }^{n-\sigma }\Vert |\bar{u}^{n-\sigma }|_1\\&\quad \le \frac{c^\star \tilde{c}_2}{p+2} \Vert \bar{u}^{n-\sigma }\Vert ^2+\frac{\tilde{c}_0\tilde{c}_2}{p+2} \Vert \bar{u}^{n-\sigma }\Vert |\bar{u}^{n-\sigma }|_1 \\&\quad \le \frac{c^\star \tilde{c}_2}{p+2} \Vert \bar{u}^{n-\sigma }\Vert ^2+\frac{\tilde{c}_0^2\tilde{c}_2^2}{4\mu (p+2)^2} \Vert \bar{u}^{n-\sigma }\Vert ^2+\mu |\bar{u}^{n-\sigma }|_1^2, \end{aligned} \end{aligned}$$

(A18)

where $c^\star$ is a positive constant, from which we use the fact, for any $1\le r \le K-1$ and $1\le n \le N$ that

$$\begin{aligned} \begin{aligned} |\varDelta _x\tilde{u}_r^{n-\sigma }|&=\left| \frac{\tilde{u}_{r+1}^{n-\sigma }-U_{r+1}^{n-\sigma }+U_{r+1}^{n-\sigma } -U_{r-1}^{n-\sigma }+U_{r-1}^{n-\sigma }-\tilde{u}_{r-1}^{n-\sigma }}{2h} \right| \\&\le \frac{1}{2h}\Vert e^{n-\sigma }\Vert _\infty +|u_x(\xi _r,t_{n-\sigma })|+\frac{1}{2h}\Vert e^{n-\sigma }\Vert _\infty \\&\le \sqrt{L}h^{-2}\Vert e^{n-\sigma }\Vert +c_0 \le \sqrt{L}C(\frac{\tau ^2}{h^2}+1)+c_0, \end{aligned} \end{aligned}$$

in which, we only need to limit $\tau /h \le 1$, i.e., $\tau \le h$ we have $|\varDelta _x\tilde{u}_r^{n-\sigma }|\le c^\star$. In addition,

$$\begin{aligned} -\mu \left\langle \delta _x^2\bar{u}^{n-\sigma },\bar{u}^{n-\sigma } \right\rangle =\mu |\bar{u}^{n-\sigma }|_1^2. \end{aligned}$$

(A19)

Substituting the results of (A17)–(A19) into (A16), we have

$$\begin{aligned} \begin{aligned} \frac{1}{2} \sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _\tau (\Vert \bar{u}^k\Vert ^2) \le \left( \frac{c^\star \tilde{c}_2}{p+2}+\frac{\tilde{c}_0^2\tilde{c}_2^2}{4\mu (p+2)^2}\right) \Vert \bar{u}^{n-\sigma }\Vert ^2. \end{aligned} \end{aligned}$$

Denote $\tilde{c}_3:=\frac{2c^\star \tilde{c}_2}{p+2}+\frac{\tilde{c}_0^2\tilde{c}_2^2}{2\mu (p+2)^2}$, we have

$$\begin{aligned} \sum _{k=1}^{n}A_{n-k}^{(n)}\nabla _\tau (\Vert \bar{u}^k\Vert ^2) \le \tilde{c}_3 \Vert \bar{u}^{n-\sigma }\Vert ^2. \end{aligned}$$

(A20)

We observe that the above inequality satisfies the conditions of Lemma 6, that is, $v ^k=\Vert \bar{u}^k\Vert ,~\lambda _0=\tilde{c}_3$, $\lambda _l=0$ for $l\ge 1$, and $\xi ^n=0$. Therefore, we can obtain by Lemma 6 that

$$\begin{aligned} \Vert \bar{u}^n\Vert \le 2E_\eta \Big (\frac{7}{2}{\mathfrak {P}}_A \tilde{c}_3t_n^\eta \Big )\Vert \bar{u}^0\Vert =0, \quad 1\le n\le N. \end{aligned}$$

However, $\Vert \bar{u}^n\Vert \ge 0$. Thus, $\Vert \tilde{u}^n-\hat{u}^n\Vert =0$. $\square$