Abstract
In this paper, we study an inverse initial value problem for the fractional diffusion equation with discrete noise. This problem is ill-posed in the sense of Hadamard. We apply the trigonometric method in a nonparametric regression associated with the quasi-boundary value regularization method to deal with this ill-posed problem. The corresponding convergence estimate for this method is obtained. The numerical results show that this regularization method is flexible and stable.
Similar content being viewed by others
1 Introduction
In recent years, fractional differential equations have attracted worldwide attention due to their wide applications in different research areas and engineering, such as physical [1, 2], chemical [3], biology [4], signal processing [5], mechanical engineering [6] and systems identification [7], electrical and fractional dynamics [8–10]. However, for some practical situations, the part of the diffusion coefficient, or initial data, or boundary data, or source term may not be known, we need to find them using some additional measurement data, which will lead to the inverse problem of the fractional diffusion equation, such as [11–13]. Recently, many researchers have presented results of the initial value problem and boundary value problem on fractional differential equations, such as [14–16]. In [17], the authors used the monotone iterative method to consider the existence and uniqueness of solution of the initial value problem for a fractional differential equation. In [18], the authors used quasi-reversible method to consider initial value problem for a time-fractional diffusion equation. In [19], the authors used a modified quasi-boundary value method to determine the initial data from a noisy final data in a time-fractional diffusion equation. Above these references on identifying the initial value of fractional diffusion equations, the measurable data is selected as a continuous function. However, in practice, the measure data is always discrete. The discrete random data is closer to practice. To the best of our knowledge, there were few papers for identifying the initial value of fractional diffusion equations with the discrete random data. In [20], the authors once used the truncation regularization method to identify the unknown source for a time-fractional equation with the discrete random noise, but we consider the inverse initial value problem with this special type of noise in the data.
In this paper, we consider an inverse initial value problem for the time-fractional diffusion equation as follows:
where the time-fractional derivative \(D_{t}^{\alpha}\) is the Caputo fractional derivative with respect to t, x and t are the space and time variables. The Caputo fractional derivative of order α (\(0<\alpha\leq1\)) defined by [21]
where \(\Gamma(x)\) denotes the standard Gamma function.
In this problem (1.1), the source function \(F(x,t)\) and the final value data \(u(x,T)=g(x)\) are known in advance. Our purpose is to obtain the initial function \(u(x,0)=p(x)\) from some additional data. In practical applications, the additional data \(g(x)\) used in this study is observed at a final moment \(t=T\), which may contain measurement errors. We assume the measured data are given at a discrete set of points and contain errors. Therefore, we put
and set \(H=(\tilde{g}(x_{1}),\tilde{g}(x_{2}),\ldots,\tilde{g}(x_{M}))\), which is the measure of \((g(x_{1}),g(x_{2}),\ldots,g(x_{M}))\).
We assume the random noise data H satisfies the nonparametric regression model
where \(\varepsilon_{k}\) is unknown independent random errors. Moreover, \(\varepsilon_{k} \sim N(0,1)\), and \(\sigma_{k}\) are unknown positive constants, bounded by a positive constant \(R_{\mathrm{max}}\) i.e., \(0<\sigma _{k}<R_{\mathrm{max}}\) for all \(k=1,2,\ldots,M\). The noises \(\varepsilon_{k}\) are mutually independent.
In this paper, we extend this discrete random noise to identify the initial value problem by the quasi-boundary value regularization method. In [22], the quasi-boundary value method was first called non-local boundary value problem method and was used to solve the backward heat conduction problem. Wei and Wang in [19] used the quasi-boundary value regularization method to deal with the backward problem. Now, this method is also studied for solving various types of inverse problems, such as parabolic equations [22–24], hyper-parabolic equations [25], and elliptic equations [26].
The general structure of this paper is as follows: we first present some preliminary results in Sect. 2. In Sect. 3 we develop the trigonometric method in nonparametric regression associated with quasi-boundary value regularization method to construct the regularized solution. Section 4 contains the convergence estimate under an a priori assumption for the exact solution. Some numerical results are presented in Sect. 5. Section 6 is a brief conclusion.
2 Preliminaries
In this section, we introduce some useful definitions and preliminary results.
Definition 2.1
([27])
The generalized Mittag–Leffler function is defined as
where \(\alpha>0\) and \(\beta\in\mathbb{R}\) are arbitrary constants.
Lemma 2.1
([27])
Let \(\lambda>0\), then we have
where \({E_{\gamma,\beta}}^{(k)}(y):=\frac{d^{k}}{dy^{k}}E_{\gamma,\beta}(y)\).
Lemma 2.2
([28])
Let \(0<\alpha_{0}<\alpha_{1}<1\), then, for all \(\alpha\in[\alpha_{0},\alpha_{1}]\), there exists a constant \(C_{\pm}>0\) depending on \(\alpha_{0}\), \(\alpha_{1}\) such that
Lemma 2.3
([29])
For any \(\lambda_{n}\) satisfying \(\lambda_{n}\geq\lambda_{1}>0\), there exist positive constants \(C_{1}\), \(C_{2}\) depending on α, T, \(\lambda_{1}\) such that
Lemma 2.4
([30], page 144)
Let \(n=1,2,\ldots,M-1\), and \(m=1,2,\ldots \) , with \(x_{k}=\frac{2k-1}{2M}\) and \(\varphi_{n}(x_{k})=\sqrt{2}\sin(n\pi x_{k})\), then we have
If \(m=1,2,\ldots,M-1\), then
and
Lemma 2.5
Let \(n,M\in\mathbb{N}\) such that \(1\leq n\leq M-1\). Assume that g is piecewise \(C^{1}\) on \([0,1]\). Then
where
Proof
Using the complete orthonormal basis \(\{\varphi_{m}\}^{\infty }_{m=1}\), we can infer the expansion of g as follows:
where \(g_{m}=(g(x), \varphi_{m}(x))\). From Lemma 2.4, we get
So the conclusion is completed. □
Now, we will need the solution of the direct problem (1.1). Applying the separation of variables and Laplace transform of Mittag–Leffler function [Lemma 2.1], we can get the solution of problem (1.1) as follows:
where
is an orthogonal basis in \(L^{2}(0,1)\), and
Making use of the supplementary condition \(u(x,T)=g(x)\), we can obtain
where \(p_{n}=(p(x),\varphi_{n}(x))\), \(F_{n}(t)=(F(x,t),\varphi_{n}(x))\). Using (2.13), we can get
and
From Lemma 2.5, we deduce that
3 Regularized solutions for backward problem for time-fractional diffusion equation
In this section, we introduce the trigonometric method in nonparametric regression associated with quasi-boundary value regularization method to solve the inverse initial value problem of a time-fractional diffusion equation. We will do a modification of Eq. (1.1), where a term of \(u(x,0)\) is added as follows:
We can obtain the regularization solution of problem (1.1) from the solution of the following problem:
where μ plays the role of regularization parameter.
Using the separation of variables and Laplace transform of Mittag–Leffler function [Lemma 2.1], we can infer the solution \(p_{\mu}(x)\) of problem (3.2) which is the regularization solution of problem (1.1) with the exact measurable data as follows:
From Lemma 2.5, we can get the regularization solution \(\tilde {p}_{\mu,M}(x)\) of problem (1.1) with noise measurable data as follows:
4 Estimators and convergence results
In this section, we will give the error estimate of the quasi-boundary value regularization method under the a priori parameter choice rule. For \(\gamma>0\), let \(D^{\gamma}(\Omega)\) be the set of all function \(\psi\in L^{2}(\Omega)\) defined by
Lemma 4.1
For any \(q>0\), \(0<\mu<1\), and \(n\geq1 >0\), we have the following inequality:
Proof
For \(0< q<2\), we can easily see
then we infer
where \(n^{*}\) is the root of \(A'(n)=0\), and \(n^{*}=\sqrt{\frac {(2-q)C_{1}}{\mu\pi^{2}q}}\).
So
For \(q\geq2\) and \(1< n<\frac{1}{\mu}\), we have
For \(q\geq2\) and \(n\geq\frac{1}{\mu}\), we get
□
Lemma 4.2
For any \(0<\mu<1\), and \(n\geq1\), we have the following inequality:
The proof is very easy and we omit it here.
The main result of this section is the following.
Theorem 4.1
Assume an a priori bound is imposed as follows:
where \(q>0\) and \(E>0\) are two constants. Suppose the a priori condition (4.4) and the noises data assumption (1.3) hold. We have an estimate as follows:
As \(0<\mu<1\) and \(\lim_{M\rightarrow+\infty} \frac{1}{M \mu^{2}}=0\), we obtain
Proof
Applying (2.16) and (3.4), we can get
Using Parseval’s equality, we obtain
We use \(\mathbb{E}(\varepsilon_{j}\varepsilon_{l})=0\) (\(j\neq l\)), and \(\mathbb{E}\varepsilon_{j}^{2}=1\), \(j=1,2,\ldots,M\). Then we obtain
From Lemma 2.3, we know that
Since \(\sigma_{k}< R_{\mathrm{max}}\) and Lemma 4.2, we estimate \(M_{1}\) as follows:
By (2.14), (4.4), (4.9) and Lemma 4.1, we obtain
Combining (4.10) and (4.11) , we can easy get the conclusion. □
Remark 4.1
By choosing \(\mu=(\frac{1}{M})^{\frac {1}{q+2}}\), and by (4.6), in the case \(0< q<2\), we can conclude that
Remark 4.2
By choosing \(\mu=(\frac{1}{M})^{\frac{1}{4}}\), and by (4.6), in the case \(q\geq2\), \(1< n<\frac{1}{\mu}\), we can conclude that
Remark 4.3
By choosing \(\mu=(\frac{1}{M})^{\frac {1}{2q}}\), and by (4.6), in the case \(q\geq2\), \(n\geq\frac{1}{\mu }\), we can conclude that
5 Numerical results
In this section, we present a numerical experiment in the MATLAB programs to show the validity of our scheme. First we display the discrete data with and without noise in Fig. 1. Comparing with two picture in Fig. 1, we can observe the non-smoothness of curve data in the case of random noise. And the measured data is very chaotic.
Since the analytic solution of problem (1.1) is difficult to obtain, we construct the final data \(g(x)\) by solving the following forward problem:
We construct the final data \(g(x)\) by solving the forward problem with the give data \(F(x,t)\) and \(p(x)\) by a finite difference method. Let the sequence \(\{g_{k}\}_{k=1}^{M}\) represent samples from the function \(g(x)\) on an equidistant grid. Choosing \(M=31\), \(\sigma_{k}^{2}=\sigma^{2}=10^{-i}\), \(i=4,5\), we have the following nonparametric regression model of data:
where \(\varepsilon_{k} \sim N(0,1)\).
The relative error level is computed by
Example
Choose
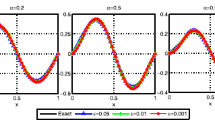
Figures 2 and 3 show the comparison between the exact solution and its regularized solution for various noise levels \(\sigma ^{2}=10^{-4},10^{-5}\) in the case of \(\alpha=0.2,0.8\). According to these figures, we can find that the smaller σ and α, the fitting effect between the exact solution and regularized solution is also better. In addition, we see that the relative errors (for various noise levels \(\sigma^{2}=10^{-4},10^{-5}\) in the case of \(\alpha=0.8\)) are decreased when M are increased (see Fig. 4). The results of this experiment have demonstrated the convergence results in Remarks 4.1–4.3 and the effectiveness of our method. Tables 1 and 2 show the numerical results of the example for different \(\sigma^{2}=10^{-4},10^{-5}\) with different α.
6 Conclusion
In this paper, we solve the inverse initial value problem for a time-fractional diffusion equation. The trigonometric method in nonparametric regression associated with the quasi-boundary value regularization method is applied to solve the ill-posed problem. Specially, the problem is dealt with the discrete random noise. The convergence estimate is presented under an a priori regularization parameter choice rule. In numerical experiments, the computational cost is within 10 seconds and the convergence results is proved, so this work is good. In future work, we will continue to research the other inverse problems of this special type of noise in the data, such as identifying the source of the space-fractional diffusion equation.
References
Metzler, R., Klafter, J.: Boundary value problems for fractional diffusion equations. Phys. A, Stat. Mech. Appl. 278(1), 107–125 (2000)
Autuori, G., Cluni, F., Gusella, V., Pucci, P.: Mathematical models for nonlocal elastic composite materials. Adv. Nonlinear Anal. 6(4), 355–382 (2017)
Ghergu, M., Radulescu, V.D.: Nonlinear PDEs. Mathematical Models in Biology, Chemistry and Population Genetics. Springer Monographs in Mathematics, Springer, Heidelberg (2012)
Yuste, S.B., Lindenberg, K.: Subdiffusion-limited reactions. Chem. Phys. 284(1), 169–180 (2002)
Kumar, S., Kumar, D., Singh, J.: Fractional modelling arising in unidirectional propagation of long waves in dispersive media. Adv. Nonlinear Anal. 5(4), 383–394 (2016)
Magin, R., Feng, X., Baleanu, D.: Solving the fractional order Bloch equation. Concepts Magn. Reson., Part A, Bridg. Educ. Res. 34(1), 16–23 (2009)
Duncan, T.E., Pasik-Duncan, B.: A direct approach to linear-quadratic stochastic control. Opusc. Math. 37(6), 821–827 (2017)
Jin, B.T., Rundell, W.: A tutorial on inverse problems for anomalous diffusion processes. Inverse Probl. 31(3), 035003 (2015)
Marin, M., Dumitru, B.: On vibrations in thermoelasticity without energy dissipation for micropolar bodies. Bound. Value Probl. 2016, 111 (2016)
Radulescu, V.D., Repovš, D.D.: Partial Differential Equations with Variable Exponents. Variational Methods and Qualitative Analysis. Monographs and Research Notes in Mathematics. CRC Press, Boca Raton (2015)
Wang, J.G., Zhou, Y.B., Wei, T.: Two regularization methods to identify a space-dependent source for the time-fractional diffusion equation. Appl. Numer. Math. 68, 39–57 (2013)
Yang, F., Fu, C.L.: The quasi-reversibility regularization method for identifying the unknown source for time-fractional diffusion equation. Appl. Math. Model. 39, 1500–1512 (2015)
Sakamoto, K., Yamamoto, M.: Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 382(1), 426–447 (2011)
Bachar, I., Mâagli, H., Radulescu, V.D.: Fractional Navier boundary value problems. Bound. Value Probl. 79, 14 (2016)
Bachar, I., Mâagli, H., Radulescu, V.D.: Positive solutions for superlinear Riemann–Liouville fractional boundary-value problems. Electron. J. Differ. Equ. 240, 16 (2017)
Denton, Z., Ramírez, J.D.: Existence of minimal and maximal solutions to RL fractional integro-differential initial value problems. Opusc. Math. 37(5), 705–724 (2017)
Wei, Z.L., Li, Q.D., Che, J.L.: Initial value problems for fractional differential equations involving Riemann–Liouville sequential fractional derivative. J. Math. Anal. Appl. 367, 260–272 (2010)
Yang, M., Liu, J.J.: Solving a final value fractional diffusion problem by boundary condition regularization. Appl. Numer. Math. 66, 45–58 (2013)
Wei, Y., Wang, J.G.: A modified quasi-boundary value method for the backward time-fractional diffusion problem. Math. Model. Numer. Anal. 48, 603–621 (2014)
Tuan, N.H., Nane, E.R.: Inverse source problem for time fractional diffusion with discrete random noise. Stat. Probab. Lett. 120, 126–134 (2017)
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Academic Press, San Diego (1999)
Hao, D.N., Duc, N.V., Lesnic, D.: Regularization of parabolic equations backward in time by a non-lacal boundary value problem method. Appl. Math. (Irvine) 75, 291–315 (2010)
Denche, M., Bessila, K.: A modified quasi-boundary value method for ill-posed problems. J. Math. Anal. Appl. 301, 419–426 (2005)
Hao, D.N., Duc, N.V., Sahli, H.: A non-local boundary value problem method for parabolic equations backward in time. J. Math. Anal. Appl. 345, 805–815 (2008)
Showalter, R.E.: Cauchy problem for hyper-partial differential equations. North-Holl. Math. Stud. 110, 421–425 (1985)
Feng, X.L., Elden, L., Fu, C.L.: A quasi-boundary-value method for the Cauchy problem for elliptic equations with nonhomogeneous Neumann data. J. Inverse Ill-Posed Probl. 18, 617–645 (2010)
Podlubny, I.: Fractional Differential Equation. Academic Press, San Diego (1999)
Liu, J.J., Yamamoto, M.: A backward problem for the time-fractional diffusion equation. Appl. Anal. 89(11), 1769–1788 (2010)
Wang, J.G., Zhou, Y.B., Wei, T.: A posteriori regularization parameter choice rule for the quasi-boundary value method for the backward time-fractional diffusion problem. Appl. Math. Lett. 26(7), 741–747 (2013)
Eubank, R.L.: Nonparametric Regression and Spline Smoothing, 2nd edn. Statistics: Textbooks and Monographs, vol. 157. Dekker, New York (1999)
Acknowledgements
The authors would like to thanks the editor and the referees for their valuable comments and suggestions that improve the quality of our paper.
Availability of data and materials
Not applicable.
Funding
The work is supported by the National Natural Science Foundation of China (11561045,11501272) and the Doctor Fund of Lan Zhou University of Technology.
Author information
Authors and Affiliations
Contributions
The main idea of this paper was proposed by FY and YZ prepared the manuscript initially and performed all the steps of the proofs in this research. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Abbreviations
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yang, F., Zhang, Y., Li, XX. et al. The quasi-boundary value regularization method for identifying the initial value with discrete random noise. Bound Value Probl 2018, 108 (2018). https://doi.org/10.1186/s13661-018-1030-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-018-1030-y