Abstract
We study periodic solutions of the suspension bridge model proposed by Lazer and McKenna with a periodic damping term. Under the Dolph-type condition and a small periodic damping term condition, the existence and the uniqueness of a periodic solution have been proved by a constructive method. Two numerical examples are presented to illustrate the effect of the periodic damping term.
MSC: 34B15, 34C15, 34C25.
Similar content being viewed by others
1 Introduction
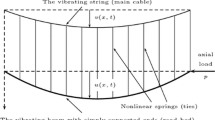
Many people pay close attention to oscillations in suspension bridges after the collapse of the Tacoma Narrows suspension bridge. In the late 1980s and early 1990s, Lazer and McKenna [1]–[3] have studied the suspension bridge model
where , , satisfies the boundary conditions
, , are constant, and . System (1)-(2) describes the transverse vibrations of a beam hinged at both ends with length L and external force . The term takes into account the fact that the cables’ restoring force exists only in the situation of stretching. Here represents the damping term.
In this paper, we consider problem (1) with 2π-periodic damping term
where is the 2π-periodic external force as same as the assumption in [2]. Looking for a standing-wave solution of (3) and (2), we have
which leads to an equivalent ordinary differential equation
in which and .
In the past years, the jumping nonlinearity has been discussed by many authors [1]–[9]. However, to our knowledge, there is no result about periodic damping term. In the early 1990s, Li [10] obtained an ingenious method to discuss the existence and uniqueness of nonlinear two-point boundary value problems with variable coefficient. Recently, the second author of this paper extended this method to the periodic situation [11]. In this paper we refine this method to solve problem (4) and take some numerical simulations to illustrate the effect of periodic damping term.
The rest of this paper is organized as follows. In Section 2, we briefly state the main results. In Section 3, we study the properties of the homogeneous equation by a constructive method. In Section 4, we prove our main results by Leray-Schauder degree theory. In Section 5, we present some numerical experiments. In Section 6, we give the conclusion.
2 Main results
We denote by N a positive integer and . To study the existence of periodic solutions of (4), we need the following assumptions:
(H1): Dolph-type condition:
(H2): Small periodic damping term condition:
Theorem 1
Let (H1) and (H2) hold. Then problem (4) has a unique 2π-periodic solution.
The more general form of the suspension bridge model is
Here and are positive 2π-periodic functions satisfying
where is the variational coefficient of cables’ restoring force. Denote , , , . Then
To study the existence of periodic solutions of (5), we make the following assumptions:
(H3): Dolph-type condition:
(H4): Small periodic damping term condition:
Theorem 2
Let (H3) and (H4) hold. Then problem (5) has a unique 2π-periodic solution.
Remark 1
Problem (4) with (H1) and (H2) is a particular case of problem (5) with (H3) and (H4). So we shall only give the proof of Theorem 2.
3 Homogeneous equation
The following lemmas will be used in this section.
Lemma 3
(see [12])
Let, , with
Then
and the constantis optimal.
Lemma 4
(see [12])
Let, , with the boundary value conditions. Then
Consider the periodic boundary value problem
We will prove the following proposition by similar methods to [11].
Proposition 5
Suppose that, , are-integrable 2π-periodic functions satisfying (6), (H3) and (H4), then (7) has only the trivial 2π-periodic solution.
Proof
We assume that (7) has a nonzero 2π-periodic solution . A contradiction will be proved in six steps.
Step 1. We will prove that has at least one zero in . Otherwise, we may we assume , . Then we have in . Consider the following equivalent equation:
where is undetermined. By Rolle’s theorem, there exists a with . Then
which leads to a contradiction.
Without loss of generality, we assume , .
Step 2. We construct two auxiliary equations. Consider the initial value problem
The first auxiliary equation is
Obviously,
is the solution of (8) and
where with . Since
holds under the assumptions of (H3), there is a such that
Thus, we have
Since and sint is decreasing in , we have
By (H4), we have
and . Therefore
We also consider the initial value problem
Clearly,
is the solution of (13), where θ is the same as the previous one, and
Hence there exists a with , such that
Then . From (10) and (14), it follows that
Since sint is decreasing on , we have , and
Step 3. We will prove that has a zero point in . Assume, on the contrary, for .
Let on . Since , , on , we have
which implies
Notice that , we have
By (12), we know that .
Let on . Since , , we have
Since , , on , we have
which implies
i.e.,
But and imply that
which is a contradiction to on . Therefore has at least one zero in with .
Step 4. We will prove that has at least zeros on . Let be the first zero point in such that , . We claim that there must exist a zero point in . Otherwise, we consider . With a similar argument to Step 3, we have a such that there must be a zero in and . Step by step, we find that has at least zeros on .
Step 5. We will prove that has at least zeros on . On the contrary, we assume has exactly zeros on . We write them as
Obviously,
Without loss of generality, we may assume . Since
we obtain , which contradicts . Therefore has at least zeros on .
Step 6. Since has at least zeros on , there are two zeros and with . Integrating from to , we have
Assume that there are k zeros in denoted by , . By Lemma 3,
By Lemma 4, we have
Since , we have
Hence
which implies for . Due to the uniqueness of the solution for the initial value problem, we get for , a contradiction. □
4 Non-homogeneous equation
In this section, we will give the complete proof of Theorem 2.
4.1 Uniqueness
Proof
Let and be two 2π-periodic solutions of (5). Denote , then v is a solution of the following problem:
where is defined in (6). Since
there exists a such that
Then (18) equals
If ,
Equation (18) satisfies (H3) and (H4). Otherwise, −v as a solution satisfies (H3) and (H4). By Proposition 5, we have . □
4.2 Boundedness
We consider the homotopy equation
where . Denote by the usual normal in , i.e., . We assert there exists such that every possible periodic solution of (19) satisfies . If not, there exists and the solution with (). Let , we have and . Obviously, (). It satisfies the following problem:
in which we have
Since
, are uniformly bounded and equicontinuous. By the Ascoli lemma, there exists a continuous function , , and a subsequence of (denote it again by ) such that
As a consequence (20) weakly converges to the following equation in :
which satisfy (H3) and (H4). By Proposition 5, we have for , which contradicts . Thus, the possible periodic solution is bounded.
4.3 Existence
Proof
Assume is the fundamental solution matrix of with . Obviously, it is nonresonant by (H3). Equation (19) can be transformed into the integral equation
Because is a 2π-periodic solution of (22), then
Obviously, is invertible,
Define an operator
such that
Since the right-hand side of is continuous (non-smooth), it is easy to see that is a completely continuous operator in . Denote
and
Because for , by Leray-Schauder degree theory, we have
So we conclude that has at least one fixed point in Ω, that is, (5) has a unique solution. □
5 Numerical experiment
5.1 Example 1
Let us consider
By Theorem 2, there is a unique 2π-periodic solution.
In Figure 1, we make a 10-fold Newton iteration to get an approximate solution of (27), displayed by a blue line. It is obvious that the solution here is locally stable and unique. The error here is about 10−10. The red line in Figure 1 is the approximate solution of (27) without periodic damping term. Our simulation illustrates that the effect of the small periodic damping term is limited.
The approximate solution of ( 27 ) with and without periodic damping term.
In Figure 2, we consider the effect of the cables’ restoring force . If there is no cables’ restoring force, we have the following system:
The blue line in Figure 2 is the approximate solution of (27) and the red line in Figure 2 is the approximate solution of (28). The latter one is a particular case that can be tackled by [11].
5.2 Example 2
Let us consider
By Theorem 1, there is a unique 2π-periodic solution.
The blue line in Figure 3 is the approximate solution of (29). The red line in Figure 3 is the approximate solution of (29) without periodic damping term. Our simulation illustrates that the effect of the small periodic damping term is limited. The method we applied is a 10-fold Newton iteration and the error here is about 10−10.
The approximate solution of ( 29 ) with and without periodic damping term.
In Figure 4, we consider the effect of the cables’ restoring force . If there is no cables’ restoring force, we have the following system:
The blue line in Figure 4 is the approximate solution of (29) and the red line in Figure 4 is the approximate solution of (30).
6 Conclusions
Periodic solutions of the suspension bridge model with a periodic damping term have been studied. After transforming this system into an equivalent ordinary differential equation, we get the existence and the uniqueness of a periodic solution by the Dolph-type condition and a small periodic damping term condition. Our constructive method is very adaptable to this kind of non-smooth problem. Two numerical examples have been presented to simulate our main results. By the numerical experiment, we know that the effect of the small periodic damping term is limited. Furthermore, we compare the approximate solution of our system to the suspension bridge model without the cables’ restoring force, the latter one is a particular case of [11].
References
Lazer AC, McKenna PJ: Large scale oscillatory behaviour in loaded asymmetric systems. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 1987, 4: 243-274.
Lazer AC, McKenna PJ: Existence, uniqueness, and stability of oscillations in differential equations with asymmetric nonlinearities. Trans. Am. Math. Soc. 1989, 315: 721-739. 10.1090/S0002-9947-1989-0979963-1
Lazer AC, McKenna PJ: Large-amplitude periodic oscillations in suspension bridges: some new connections with nonlinear analysis. SIAM Rev. 1990, 32: 537-578. 10.1137/1032120
Dancer EN: On the Dirichlet problem for weakly non-linear elliptic partial differential equations. Proc. R. Soc. Edinb., Sect. A 1976/77, 76: 283-300.
Agarwal RP, Perera K, O’Regan D: A variational approach to singular quasilinear elliptic problems with sign changing nonlinearities. Appl. Anal. 2006, 85: 1201-1206. 10.1080/00036810500474655
Ding ZH: Traveling waves in a suspension bridge system. SIAM J. Math. Anal. 2003, 35: 160-171. 10.1137/S0036141002412690
Fabry C: Large-amplitude oscillations of a nonlinear asymmetric oscillator with damping. Nonlinear Anal. TMA 2001, 44: 613-626. 10.1016/S0362-546X(99)00295-3
Fučík S: Boundary value problems with jumping nonlinearities. Čas. Pěst. Mat. 1976, 101: 69-87.
Li X, Zhang ZH: Unbounded solutions and periodic solutions for second order differential equations with asymmetric nonlinearity. Proc. Am. Math. Soc. 2007, 135: 2769-2777. 10.1090/S0002-9939-07-08928-9
Li Y: Boundary value problems for nonlinear ordinary differential equations. Northeast. Math. J. 1990, 6: 297-302.
Zu J: Existence and uniqueness of periodic solution for nonlinear second-order ordinary differential equations. Bound. Value Probl. 2011., 2011: 10.1155/2011/192156
Mitrinović DS: Analytic Inequalities. Springer, Berlin; 1970.
Acknowledgements
The authors express deep gratitude to the anonymous referees for their useful suggestions and comments, especially for pointing out the flaws in Step 3 of Section 3. The authors also thank Professor Yong Li for his useful discussion.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, L., Zu, J. Periodic oscillation in suspension bridge model with a periodic damping term. Bound Value Probl 2014, 231 (2014). https://doi.org/10.1186/s13661-014-0231-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-014-0231-2