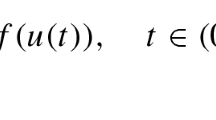Abstract
In this paper, we consider some types of scalar equations and systems of generalized one-dimensional Minkowski-curvature problems. Using an inequality technique, we establish several new Lyapunov-type inequalities for the problems considered. Our results extend the existing work in the literature.
Similar content being viewed by others
1 Introduction
In [1], Russian mathematician Lyapunov proved the following result: If \(y(t)\) is a solution of
satisfying \(y(a)=y(b)=0\) (\(a< b\)) and \(y(t)\neq 0\) for \(t\in (a,b)\), then
The above result is known as the Lyapunov inequality.
This result plays an important role in the study of various properties of solutions of Eq. (1) such as oscillation theory, disconjugacy and eigenvalue problems. After this seminal paper, the Lyapunov inequality and many of its generalizations have been studied by many researchers; see [2–42] and the references therein.
For example, Yang [43] obtained a Lyapunov-type inequality for the second order half-linear equation
where \(q,r\in C([a,b],\mathbb{R})\) such that \(r(t)>0\) for \(t\in [a,b]\), and \(p>0\) is a constant.
Theorem 1.1
([43])
Assume Eq. (3) has a solution\(y(t)\), then the inequality
holds, where\(q_{+}(t):=\max \{q(t),0\}\).
Recently, Yang et al. [44] investigated a Lyapunov-type inequality for one-dimensional Minkowski-curvature problem with singular weight
They presented the following result.
Theorem 1.2
([44])
If the problem (6) has a positive solution, then one has
where\(k(t)\geq 0\)for all\(t\in (a,b)\), \(k\not \equiv 0\)in any compact subinterval of\([a,b]\)and\(k\in U=\{k\in L^{1}_{\mathrm{loc}}((a,b),[0,\infty )):\int _{a}^{b}(t-a)(b-t)k(t) \,\mathrm{d}t<\infty \}\).
Motivated by this work, in this paper, we will establish Lyapunov-type inequalities for the generalized one-dimensional Minkowski-curvature problems with singular weight function
and
and the cycled systems of a generalized one-dimensional Minkowski-curvature problem with singular weight functions
and
where \(p>1\), \(1< p<\alpha <\beta \) or \(1<\beta <\alpha <p\), \(r, r_{i}\in C([a,b],(0,+\infty ))\), \(q(t), q_{i}(t)\geq 0\) for all \(t\in (a,b)\), \(q, q_{i}\not \equiv 0\) in any compact subinterval of \([a,b]\) and
\(i=1,2,\ldots ,n\). \(l(t), h(t), l_{i}(t), h_{i}(t)> 0\) for all \(t\in (a,b)\) such that
satisfy \(A, A_{i}\in \mathfrak{D}\), \(i=1,2,\ldots , n\). Class \(\mathfrak{D}\) admits rather stronger singular functions at the boundary. For example, \(q(t)=t^{-(2p-1)/p}\in \mathfrak{D}\) with \(a=0\), \(b=1\) but not in \(L^{1}(0,1)\).
Our results not only extend the existing work in the literature, but also give necessary conditions for the existence of positive solutions for scalar equations and systems of generalized one-dimensional Minkowski-curvature problems with singular weight functions.
2 Preliminaries
In this section, we give some definitions and lemmas which are needed in the sequel.
Definition 2.1
We say y is a solution of problem (9)–(10) (or (11)–(12)) if \(y\in C^{1}[a,b]\), \(\|y'\|_{\infty }<1\), and \(\frac{r(\cdot )|y'(\cdot )|^{p-2}y'(\cdot )}{\sqrt{1-|y'(\cdot )|^{p}}}\) is absolutely continuous in any compact subinterval of \((a,b)\), and y satisfies the equation and the boundary conditions in problem (9)–(10) (or (11)–(12)).
Definition 2.2
We say \((y_{1},y_{2}, \ldots , y_{n})\) is a solution of problem (13)–(14) (or (15)–(16)) if \(y_{i}\in C^{1}[a,b]\), \(\|y'_{i}\|_{\infty }<1\), and \(\frac{r(\cdot )|y'_{i}(\cdot )|^{p-2}y'_{i}(\cdot )}{\sqrt{1-|y'_{i}(\cdot )|^{p}}}\) is absolutely continuous in any compact subinterval of (a,b), and \(y_{i}\) satisfies the equations and the boundary conditions in problem (13)–(14) (or (15)–(16)).
Lemma 2.1
([12])
Suppose that\(a, b\in \mathbb{R}\), \(\gamma >0\). Then
where
Lemma 2.2
If\(y\in C^{1}[a,b]\), \(y(a)=y(b)=0\)and\(p>1\), then we have
where
Proof
From Hölder’s inequality, we get \(\forall t\in [a,b]\),
where \(p^{*}=\frac{p}{p-1}\). In view of \((b-t)/(b-a)\geq 0\), we obtain
Thus
Similarly, from \((t-a)/(b-a)\geq 0\), and
we obtain
Thus
According to \(\frac{p}{p^{*}}=p-1\), we get
On the other hand, from Lemma 2.1 we obtain
Therefore, by (21) and (22), we get
The proof is complete. □
Lemma 2.3
([45])
Letm, n, p, αandβbe positive constants, then, for each\(x\geq 0\),
holds for the cases when\(0< p<\alpha <\beta \)or\(0<\beta <\alpha <p\).
3 Main results
Theorem 3.1
If\(y(t)\)is a positive solution of problem (9)–(10), then
where\(K(p)\)is defined as in (18).
Proof
Multiplying (9) by \(y(t)\) and integrating from a to b by parts yield
By Lemma 2.2, we get
On the other hand,
It follows from (26)–(28) and \(\|y'\|_{\infty }<1\) that
Now, we claim that
In fact, if the above inequality is not true, then we have
Then \(y'(t)=0\) for \(t\in [a, b]\). By condition (10), we obtain \(y(t)=0\) for \(t\in [a, b]\), which contradicts to \(y(t)\not \equiv 0\), \(t\in [a, b]\). Thus dividing both sides of (29) by
we obtain
from which (25) is obtained. The proof is complete. □
Remark 3.1
If we take \(p=2\) and \(r(t)\equiv 1\), then Theorem 3.1 reduces to [44, Theorem 2.1].
Theorem 3.2
If\(y(t)\)is a positive solution of problem (11)–(12), then
where
and\(K(p)\)is defined as in (18).
Proof
Multiplying (11) by \(y(t)\) and integrating from a to b by parts yield
By Lemma 2.3, the right side of (32) satisfies
From Lemma 2.2, we have
On the other hand,
It follows from (32)–(35) and \(\|y'\|_{\infty }<1\) that
The rest of the proof is similar to that of Theorem 3.1, and therefore is omitted. The proof is complete. □
Theorem 3.3
If\((y_{1}(t),y_{2}(t), \ldots , y_{n}(t))\)is a positive solution of problem (13)–(14), then
where\(K(p)\)is defined as in (18).
Proof
From Lemma 2.2, we get
i.e.,
Multiplying (13) by \(y_{1}(t)\) and integrating from a to b by parts, we have
Together with (39), we obtain
Repeating this procedure to each equation in problem (13)–(14), for \(i=2,3,\ldots ,n\), we have
where \(y_{n+1}(t)=y_{1}(t)\). Multiplying all inequalities, and from the fact \(\int _{a}^{b}|y'_{i}(t)|^{p}\,\mathrm{d}t>0\), \(i=1,2,\ldots ,n\), we obtain (37). The proof is complete. □
Remark 3.2
If we take \(p=2\) and \(r_{i}(t)\equiv 1\), \(i=1,2,\ldots ,n\), then Theorem 3.3 reduces to [44, Theorem 4.1].
Theorem 3.4
If\((y_{1}(t),y_{2}(t), \ldots , y_{n}(t))\)is a positive solution of problem (15)–(16), then
where
and\(K(p)\)is defined as in (18).
Proof
Multiplying (15) by \(y_{1}(t)\) and integrating from a to b by parts, we have
The rest of the proof is similar to that of Theorem 3.3, and therefore is omitted. The proof is complete. □
References
Lyapunov, A.M.: Probleme général de la stabilité du mouvement (French translation of a Russian paper dated 1893). Ann. Fac. Sci. Univ. Toulouse Sci. Math. Sci. Phys. 2, 27–247 (1907) Reprinted as Ann. Math. Studies, No. 17, Princeton (1947)
Pinasco, J.: Lower bounds for eigenvalues of the one-dimensional p-Laplacian. Abstr. Appl. Anal. 2, 147–153 (2004)
Lee, C.F., Yeh, C.C., Hong, C.H., Agarwal, R.P.: Lyapunov and Wirtinger inequalities. Appl. Math. Lett. 17, 847–853 (2004)
Agarwal, R.P., Özbekler, A.: Disconjugacy via Lyapunov and Vallée–Poussin type inequalities for forced differential equations. Appl. Math. Comput. 265, 456–468 (2015)
Çakmak, D.: Lyapunov-type integral inequalities for certain higher order differential equations. Appl. Math. Comput. 216, 368–373 (2010)
Liu, H.D.: Lyapunov-type inequalities for certain higher-order half-linear differential equations. J. Math. Inequal. 13(4), 1159–1170 (2019)
Dhar, S., Kong, Q.K.: Lyapunov-type inequalities for α-th order fractional differential equations with \(2<\alpha \leq 3\) and fractional boundary conditions. Electron. J. Differ. Equ. 2017, 203 (2017)
Eliason, S.B.: Lyapunov inequalities and bounds on solutions of certain second order equations. Can. Math. Bull. 17(4), 499–504 (1974)
Liu, X.G., Tang, M.L.: Lyapunov-type inequality for higher order difference equations. Appl. Math. Comput. 232, 666–669 (2014)
Liu, H.D.: Half-linear Volterra–Fredholm type integral inequalities on time scales and their applications. J. Appl. Anal. Comput. 10(1), 234–248 (2020)
Zhang, Q.M., Tang, X.H.: Lyapunov-type inequalities for even order difference equations. Appl. Math. Lett. 25, 1830–1834 (2012)
Shao, J., Meng, F.W.: Nonlinear impulsive differential and integral inequalities with integral jump conditions. Adv. Differ. Equ. 2016, 112 (2016)
Yang, X.J., Lo, K.M.: Lyapunov-type inequalities for a class of higher-order linear differential equations with anti-periodic boundary conditions. Appl. Math. Lett. 34, 33–36 (2014)
Liu, H.D., Meng, F.W.: Some new generalized Volterra–Fredholm type discrete fractional sum inequalities and their applications. J. High Energy Phys. 2016, 213 (2016)
Zhao, D.L., Yuan, S.L., Liu, H.D.: Stochastic dynamics of the delayed chemostat with Lévy noises. Int. J. Biomath. 12(5), 1950056 (2019)
Jleli, M., Samet, B.: On Lyapunov-type inequalities for (p,q)-Laplacian systems. J. Inequal. Appl. 2017, 100 (2017)
Liu, H.D.: Some new integral inequalities with mixed nonlinearities for discontinuous functions. Adv. Differ. Equ. 2018, 22 (2018)
Zou, C., Xia, Y., Pinto, M., Shi, J., Bai, Y.: Boundness and linearisation of a class of differential equations with piecewise constant argument. Qual. Theory Dyn. Syst. 18(2), 495–531 (2019)
Liu, H.D.: Lyapunov-type inequalities for second-order boundary value problems with a parameter. Discrete Dyn. Nat. Soc. 2020, Article ID 1209260 (2020)
Zhang, B., Zhuang, J.S., Liu, H.D., Cao, J.D., Xia, Y.H.: Master-slave synchronization of a class of fractional-order Takagi–Sugeno fuzzy neural networks. Adv. Differ. Equ. 2018, 473 (2018)
Liu, H.D., Yin, C.C.: Some generalized Volterra–Fredholm type dynamical integral inequalities in two independent variables on time scale pairs. Adv. Differ. Equ. 2020, Article ID 31 (2020)
Guseinov, G.S., Kaymakcalan, B.: Lyapunov inequalities for discrete linear Hamiltonian systems. Comput. Math. Appl. 45, 1399–1416 (2003)
Liu, H.D., Meng, F.W., Liu, P.C.: Oscillation and asymptotic analysis on a new generalized Emden–Fowler equation. Appl. Math. Comput. 219(5), 2739–2748 (2012)
Zhao, D.L.: Study on the threshold of a stochastic SIR epidemic model and its extensions. Commun. Nonlinear Sci. Numer. Simul. 38, 172–177 (2016)
Tang, X.H., Zhang, M.: Lyapunov inequalities and stability for linear Hamiltonian systems. J. Differ. Equ. 252, 358–381 (2012)
Liu, H.D.: Some new half-linear integral inequalities on time scales and applications. Discrete Dyn. Nat. Soc. 2019, Article ID 9860302 (2019)
Unal, M., Çakmak, D., Tiryaki, A.: A discrete analogue of Lyapunov-type inequalities for nonlinear systems. Comput. Math. Appl. 55, 2631–2642 (2008)
Liu, H.D., Meng, F.W.: Existence of positive periodic solutions for a predator-prey system of Holling type IV function response with mutual interference and impulsive effects. Discrete Dyn. Nat. Soc. 2015, 138984 (2015)
Zhao, D.L., Liu, H.D.: Coexistence in a two species chemostat model with Markov switchings. Appl. Math. Lett. 94, 266–271 (2019)
Liu, H.D.: An improvement of the Lyapunov inequality for certain higher order differential equations. J. Inequal. Appl. 2018, 215 (2018)
Cheng, S.S.: Lyapunov inequalities for differential and difference equations. Fasc. Math. 23, 25–41 (1991)
Zhao, D.L., Yuan, S.L., Liu, H.D.: Random periodic solution for a stochastic SIS epidemic model with constant population size. Adv. Differ. Equ. 2018, 64 (2018)
Liu, H.D., Li, C.Y., Shen, F.C.: A class of new nonlinear dynamic integral inequalities containing integration on infinite interval on time scales. Adv. Differ. Equ. 2019, 311 (2019)
Tunç, E., Liu, H.D.: Oscillatory behavior for second-order damped differential equation with nonlinearities including Riemann–Stieltjes integrals. Electron. J. Differ. Equ. 2018, 54 (2018)
Liu, H.D.: A class of retarded Volterra–Fredholm type integral inequalities on time scales and their applications. J. Inequal. Appl. 2017, 293 (2017)
Feng, Q.H., Meng, F.W., Zheng, B.: Gronwall–Bellman type nonlinear delay integral inequalities on time scale. J. Math. Anal. Appl. 382, 772–784 (2011)
Liu, H.D., Meng, F.W.: Interval oscillation criteria for second-order nonlinear forced differential equations involving variable exponent. Adv. Differ. Equ. 2016, 291 (2016)
Xia, Y.H., Chen, L., Kou, K.I.: Holder regularity of Grobman–Hartman theorem for dynamic equations on measure chains. Bull. Malays. Math. Sci. Soc. 41(3), 1153–1180 (2018)
Liu, H.D., Meng, F.W.: Nonlinear retarded integral inequalities on time scales and their applications. J. Math. Inequal. 12(1), 219–234 (2018)
Tiryaki, A., Çakmak, D., Aktas, M.F.: Lyapunov-type inequalities for a certain class of nonlinear systems. Comput. Math. Appl. 64, 1804–1811 (2012)
Liu, H.D.: Lyapunov-type inequalities for certain higher-order difference equations with mixed non-linearities. Adv. Differ. Equ. 2018, 229 (2018)
Zhang, Q.M., Tang, X.H.: Lyapunov inequalities and stability for discrete linear Hamiltonian system. Appl. Math. Comput. 218, 574–582 (2011)
Yang, X.J.: On inequalities of Lyapunov type. Appl. Math. Comput. 134(2–3), 293–300 (2003)
Yang, R., Sim, I., Lee, Y.-H.: Lyapunov-type inequalities for one-dimensional Minkowski-curvature problems. Appl. Math. Lett. 91, 188–193 (2019)
Liu, H.D.: Lyapunov-type inequalities for higher-order half-linear difference equations. J. Inequal. Appl. 2020, Article ID 80 (2020)
Acknowledgements
The author is indebted to the anonymous referees for their valuable suggestions and helpful comments which helped improve the paper significantly.
Availability of data and materials
Not applicable.
Funding
This research was supported by the Natural Science Foundation of Shandong Province (China) (No.: ZR2018MA018), and the National Natural Science Foundation of China (No.: 61873144).
Author information
Authors and Affiliations
Contributions
The author carried out the results, and read and approved the current version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that there is no conflict of interests regarding the publication of this paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, H. Lyapunov-type inequalities for generalized one-dimensional Minkowski-curvature problems. J Inequal Appl 2020, 169 (2020). https://doi.org/10.1186/s13660-020-02431-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-020-02431-8