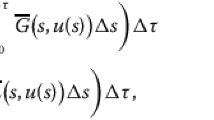Abstract
In this paper, we investigate some new nonlinear dynamic integral inequalities containing integration on infinite interval on time scales, which provide explicit bounds on unknown functions. Our results not only generalize some dynamic inequalities in related literature, but also are new even for the continuous and discrete time cases. Two examples are given to illustrate the present results.
Similar content being viewed by others
1 Introduction
The theory of time scales, as a unification of the continuous and discrete analysis, was initiated by Stefan Hilger [1] in 1988. Since then, more and more authors have been interested in this area. Along with the in-depth research into the theory, researchers find it not only can be used in pure mathematics but also is an important tool in many branches of science and engineering such as 3D tracking of shape [2], DNA dynamics [3], and so on.
As one of the most fundamental topics, the analysis of dynamic equations on time scales has been extensively investigated in recent years, see [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Because dynamic inequalities play an important role in qualitative analysis of dynamic equations on time scales, there have been plenty of results focused on them, we refer the readers to [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. Among these inequalities, the well-known Gronwall type inequalities have been intensively investigated due to their wide applications. However, to the best of our knowledge, Gronwall type inequalities containing integration on infinite interval have received less attention. Recent results in this direction include the works of [32, 33]. For instance, Meng et al. [33] investigated some integral inequalities on time scales containing integration on infinite interval
where p is a real constant, \(u, a, f, g, h: \mathbb{T}^{\kappa } \rightarrow \mathbb{R}_{+}\) are rd-continuous functions.
In this paper, we establish some new nonlinear dynamic inequalities containing integration on infinite interval on time scales. Our results not only generalize some dynamic inequalities that have been studied in [33], but also are new even for the continuous and discrete time cases.
2 Preliminaries
In what follows, we always assume that \(\mathbb{R}\) denotes the set of real numbers, \(\mathbb{R}_{+}=[0,\infty )\), \(\mathbb{T}\) is an arbitrary time scale (nonempty closed subset of \(\mathbb{R}\)), \(\mathbb{T}^{ \kappa }\) is defined as follows: If \(\mathbb{T}\) has a maximum m and m is left-scattered, then \(\mathbb{T}^{\kappa }=\mathbb{T}-\{m\}\), otherwise \(\mathbb{T}^{\kappa }=\mathbb{T}\). \(\mathcal{R}\) denotes the set of all regressive and rd-continuous functions, \(\mathcal{R}^{+}= \{p\in \mathcal{R}:1+\mu (t)p(t)>0 \text{ for all } t\in \mathbb{T}\}\). The “circle minus” addition ⊖ defined by \((p\ominus q)(t):=\frac{p(t)-q(t)}{1+\mu (t)q(t)}\) for all \(t\in \mathbb{T}^{\kappa }\).
The following lemmas are useful in the proof of the main results of this paper.
Lemma 2.1
Let \(m>0\), \(n>0\), \(p>0\), \(\alpha >0\), and \(\beta >0\) be given, then for each \(x\geq 0\),
holds for the cases when \(0< p<\alpha <\beta \) or \(0<\beta <\alpha <p\).
Proof
If \(x=0\), then it is easy to see that inequality (2) holds. So we only prove that inequality (2) holds when \(x>0\). For the case \(0< p<\alpha <\beta \), set \(F(x)=mx^{\alpha -p}-nx^{\beta -p}\), \(x>0\), where \(m>0\) and \(n>0\). Let \(F'(x)=0\), we get \(x_{0}= (\frac{m(\alpha -p)}{n(\beta -p)} )^{1/( \beta -\alpha )}\). Since \(\forall x\in (0,x_{0})\), \(F'(x)>0\); \(\forall x\in (x_{0},+\infty )\), \(F'(x)<0\), F attains its maximum at \(x_{0}= (\frac{m(\alpha -p)}{n(\beta -p)} )^{1/( \beta -\alpha )}\) and \(F_{\max }=F(x_{0})=\frac{m(\beta -\alpha )}{ \beta -p} (\frac{(\beta -p)n}{(\alpha -p)m} )^{(\alpha -p)/( \alpha -\beta )}\). Thus, (2) holds. For the case when \(0<\beta <\alpha <p\), by a similar argument with the case \(p<\alpha <\beta \), we can get (2) holds. The proof is complete. □
Lemma 2.2
([54])
Assume that \(x\geq 0\), \(p\geq q\geq 0\), and \(p\neq 0\), then for any \(K>0\),
Lemma 2.3
([4, Theorem 6.1])
Suppose that \(\sup_{t\in \mathbb{T}^{\kappa }}t=\infty \), \(x, q\in C_{rd}( \mathbb{T}^{\kappa },\mathbb{R}_{+})\), \(p\in \mathcal{R}^{+}\), and x is delta differential at \(t\in \mathbb{T}^{\kappa }\), then
implies
3 Main results
In this section, we deal with some nonlinear inequalities on time scales. For convenience, we always assume that \(t\geq t_{0}\), \(t\in \mathbb{T}^{\kappa }\).
Theorem 3.1
Assume that \(x, f, g, h, a, b, c, m, n\in C_{rd}( \mathbb{T}^{\kappa }, \mathbb{R}_{+})\), \(k, l\in C_{rd}(\mathbb{T} ^{\kappa },(0,\infty ))\), \(\mu (t)F(t)<1\), \(e_{G\ominus (-F) }(\infty ,t)<\infty \) for \(t\in \mathbb{T}^{\kappa }\), p, q, r, α, and β are constants satisfying
-
(i)
\(0\leq q\leq p\), \(0\leq r\leq p\), \(p<\alpha <\beta \); or
-
(ii)
\(0\leq q\leq p\), \(0\leq r\leq p\), \(0<\beta <\alpha <p\).
Suppose that x satisfies
then, for any \(K_{1}>0\) and \(K_{2}>0\),
where
Proof
where \(B(t)\) is defined as in (8). Denote
From the assumptions on x, a, b, c, m, n, h, B, (10), and (11), we obtain z is nonincreasing and
In view of (11) and (12), we have
Using Lemma 2.2 on the right-hand side of (13), for any \(K_{1}>0\) and \(K_{2}>0\), we obtain
where \(F(t)\), \(G(t)\), and \(A(t)\) are defined as in (5), (6), and (7). From (14) we have
which yields
that is,
where \(C(t)\) is defined as in (9). Note that z is rd-continuous, and from the assumption \(\mu (t)F(t)<1\), \(t\in \mathbb{T}^{\kappa }\), we get \((-F)\ominus G\in \mathcal{R}^{+}\). Then, by Lemma 2.3 and (15), we obtain
From \(e_{G\ominus (-F) }(\infty ,t)<\infty \) and \(\ominus ((-F)\ominus G)=(G\ominus (-F))\), we have \(e_{\ominus ((-F)\ominus G)}(\infty ,t)< \infty \). According to \(z(\infty )=0\) and (16), we obtain
Combining (12), we get the desired inequality (4). This completes the proof. □
If we let \(h(t)\equiv 0\) in Theorem 3.1, then we obtain the following corollary.
Corollary 3.1
Assume that x, f, g, a, b, c, m, n, p, q, r, and F are defined the same as in Theorem 3.1, \(e_{\ominus (-F) }( \infty ,t)<\infty \) for \(t\in \mathbb{T}^{\kappa }\),
then, for any \(K_{1}>0\) and \(K_{2}>0\),
where
Remark 3.1
If \(g(t)\equiv 1\), \(m(t)\equiv 0\), and \(q=1\), then Corollary 3.1 reduces to Theorem 3.3 in [33].
Theorem 3.2
Assume that x, f, g, h, a, b, c, k, l, p, q, α, β, B, and G are defined the same as in Theorem 3.1, \(\mu (t)\widetilde{F}(t)<1\) and \(e_{G\ominus (-\widetilde{F}) }( \infty ,t)<\infty \) for \(t\in \mathbb{T}^{\kappa }\). Suppose that x satisfies
then, for any \(K_{1}>0\),
where
Proof
Denote
In view of Lemma 2.1, (23), and (24), we have
Using Lemma 2.2 on the right-hand side of (25), for any \(K_{1}>0\), we obtain
where \(\widetilde{F}(t)\), \(G(t)\), and \(\widetilde{A}(t)\) are defined as in (20), (6), and (21). By a similar argument with Theorem 3.1 in the rest of the proof, one can prove that (19). This completes the proof. □
Theorem 3.3
Assume that x, f, g, h, a, b, c, p, q, and r are defined the same as in Theorem 3.1, \(k, l\in C_{rd}( \mathbb{T}^{\kappa }, \mathbb{R}_{+})\), and \(\mu (t)P(t)<1\), \(e_{Q\ominus (-P) }(\infty ,t)<\infty \) for \(t\in \mathbb{T}^{\kappa }\). Suppose that x satisfies
then, for any \(K_{1}>0\) and \(K_{2}>0\),
where
Proof
Denote
In view of (33) and (34), we have
Using Lemma 2.2 on the right-hand side of (35), we obtain
where \(P(t)\), \(Q(t)\), and \(R(t)\) are defined as in (29), (30), and (31). By a similar argument with Theorem 3.1 in the rest of the proof, one can prove that (28). This completes the proof. □
4 Applications
In this section, we apply our results to study the boundedness of the solutions of two dynamic equations on time scales.
Example 4.1
Consider the following dynamic equation on time scales:
where \(p>0\) and \(x_{0}\) are constants, \(W\in C(\mathbb{T}^{\kappa } \times \mathbb{R}\times \mathbb{R}\times \mathbb{R},\mathbb{R})\), and \(V\in C(\mathbb{T}^{\kappa }\times \mathbb{R},\mathbb{R})\).
Theorem 4.1
Suppose that the functions W and V in (37) satisfy the conditions
where \(a, b, c, m, n\in C_{rd}(\mathbb{T}^{\kappa }, \mathbb{R}_{+})\), and \(k,l\in C_{rd}(\mathbb{T}^{\kappa },(0,\infty ))\), q, r, α, and β are constants satisfying
-
(i)
\(0\leq q\leq p\), \(0\leq r\leq p\), \(p<\alpha <\beta \); or
-
(ii)
\(0\leq q\leq p\), \(0\leq r\leq p\), \(0<\beta <\alpha <p\).
If x is a solution of Eq. (37) satisfying (38), \(\mu (t)A(t)<1\) and \(e_{B\ominus (-F) }(\infty ,t)< \infty \) for \(t\in \mathbb{T}^{\kappa }\), then, for any \(K_{1}>0\) and \(K_{2}>0\),
where
Proof
Considering (38), then the equivalent integral equation of Eq. (37) is denoted by
Using assumptions (37)–(40) and (42), we have
Then a suitable application of Theorem 3.1 to (43) yields (41). □
Example 4.2
Consider the following dynamic integral equation on time scales:
where x, a, b, c, h, k, and l are defined the same as in Theorem 3.1, \(f\in C_{rd}(\mathbb{T}^{\kappa }, \mathbb{R})\), \(\mu (t)\times \widetilde{F}(t)<1\), and \(e_{G\ominus (-\widetilde{F}) }(\infty ,t)< \infty \) for \(t\in \mathbb{T}^{\kappa }\), then, for any \(K_{1}>0\),
where
In fact, from (44), we have
Then a suitable application of Theorem 3.2 to (46) yields (45).
5 Conclusions
In this paper, we have established some new nonlinear dynamic integral inequalities containing integration on infinite interval on time scales which can be used as tools in the qualitative theory of certain classes of dynamic equations on time scales. Our results complement the results established in the literature.
References
Hilger, S.: Ein Maßkettenkalkül mit Anwendung auf Zentrumsmanningfaltigkeiten. PhD thesis, Universität Würzburg (1988)
Metaxas, D., Tsechpenakis, G.: Dynamic data driven coupling of continuous and discrete methods for 3D tracking. In: Computational Science-ICCS, vol. 712, Springer, Berlin (2005)
Klapper, I., Qian, H.: Remarks on discrete and continuous large-scale models of DNA dynamics. Biophys. J. 74(5), 2504–2514 (1998)
Bohner, M., Peterson, A.: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston (2001)
Bohner, M., Peterson, A.: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston (2003)
Adivar, M., Raffoul, Y.N.: Existence results for periodic solutions of integro-dynamic equations on time scales. Ann. Mat. Pura Appl. 188, 543–559 (2009)
Atici, F.M., Biles, D.C., Lebedinsky, A.: An application of time scales to economics. Math. Comput. Model. 43, 718–726 (2006)
Bi, L., Bohner, M., Fan, M.: Periodic solutions of functional dynamic equations with infinite delay. Nonlinear Anal. 68, 170–174 (2008)
Liu, H.D., Meng, F.W., Liu, P.C.: Oscillation and asymptotic analysis on a new generalized Emden-Fowler equation. Appl. Math. Comput. 219(5), 2739–2748 (2012)
Chen, D., Kou, K.I., Xia, Y.H.: Linear quaternion-valued dynamic equations on time scales. J. Appl. Anal. Comput. 8, 172–201 (2018)
Dogan, A.: Positive solutions of the p-Laplacian dynamic equations on time scales with sign changing nonlinearity. Electron. J. Differ. Equ. 2018, 39 (2018)
Tunç, E., Liu, H.D.: Oscillatory behavior for second-order damped differential equation with nonlinearities including Riemann-Stieltjes integrals. Electron. J. Differ. Equ. 2018, 54 (2018)
Liu, H.D., Meng, F.W.: Existence of positive periodic solutions for a predator-prey system of Holling type IV function response with mutual interference and impulsive effects. Discrete Dyn. Nat. Soc. 2015, 138984 (2015)
Zhao, D.L., Liu, H.D.: Coexistence in a two species chemostat model with Markov switchings. Appl. Math. Lett. 94, 266–271 (2019)
Erbe, L., Jia, B.G., Peterson, A.: On the asymptotic behavior of solutions of Emden-Fowler equations on time scales. Ann. Mat. Pura Appl. 191, 205–217 (2012)
Liu, H.D., Meng, F.W.: Some new generalized Volterra–Fredholm type discrete fractional sum inequalities and their applications. J. High Energy Phys. 2016, 213 (2016)
Federson, M., Mesquita, J.G., Slavik, A.: Measure functional differential equations and functional dynamic equations on time scales. J. Differ. Equ. 252, 3816–3847 (2012)
Zhao, D.L.: Study on the threshold of a stochastic SIR epidemic model and its extensions. Commun. Nonlinear Sci. Numer. Simul. 38, 172–177 (2016)
Zhang, B., Zhuang, J.S., Liu, H.D., Cao, J.D., Xia, Y.H.: Master-slave synchronization of a class of fractional-order Takagi-Sugeno fuzzy neural networks. Adv. Differ. Equ. 2018, 473 (2018)
Zhao, D.L., Yuan, S.L., Liu, H.D.: Random periodic solution for a stochastic SIS epidemic model with constant population size. Adv. Differ. Equ. 2018, 64 (2018)
Erbe, L., Jia, B.G., Peterson, A.: Belohorec-type oscillation theorem for second order sublinear dynamic equations on time scales. Math. Nachr. 284, 1658–1668 (2011)
Liu, H.D., Liu, P.C.: Oscillation and asymptotic analysis on a new generalized Emden-Fowler equation. Abstr. Appl. Anal. 2013, Article ID 962590 (2013)
Zhao, D.L., Yuan, S.L., Liu, H.D.: Stochastic Dynamics of the delayed chemostat with Lévy noises. Int. J. Biomath. (2019). https://doi.org/10.1142/S1793524519500566
Liu, H.D.: Lyapunov-type inequalities for certain higher-order difference equations with mixed non-linearities. Adv. Differ. Equ. 2018, 229 (2018)
Feng, Q.H., Meng, F.W.: Oscillation results for a fractional order dynamic equation on time scales with conformable fractional derivative. Adv. Differ. Equ. 2018, 193 (2018)
Liu, H.D., Ma, C.Q.: Oscillation criteria for second-order neutral delay dynamic equations with nonlinearities given by Riemann-Stieltjes integrals. Abstr. Appl. Anal. 2013, Article ID 530457 (2013)
Liu, H.D., Meng, F.W.: Interval oscillation criteria for second-order nonlinear forced differential equations involving variable exponent. Adv. Differ. Equ. 2016, 291 (2016)
Karpuz, B.: Volterra theory on time scales. Results Math. 65, 263–292 (2014)
Liu, H.D.: Some new integral inequalities with mixed nonlinearities for discontinuous functions. Adv. Differ. Equ. 2018, 22 (2018)
Slavik, A.: Averaging dynamic equations on time scales. J. Math. Anal. Appl. 388, 996–1012 (2012)
Liu, H.D., Ma, C.Q.: Oscillation criteria of even order delay dynamic equations with nonlinearities given by Riemann-Stieltjes integrals. Abstr. Appl. Anal. 2014, Article ID 395381 (2014)
Zheng, B., Feng, Q.H., Meng, F.W., Zhang, Y.M.: Some new Gronwall-Bellman type nonlinear dynamic inequalities containing integration on infinite intervals on time scales. J. Inequal. Appl. 2012, 201 (2012)
Meng, Z.W., Zheng, B., Wen, C.B.: Some new integral inequalities on time scales containing integration on infinite intervals. J. Inequal. Appl. 2013, 245 (2013)
Agarwal, R.P., Bohner, M., Peterson, A.: Inequalities on time scales: a survey. Math. Inequal. Appl. 4, 535–557 (2001)
Anderson, D.R.: Nonlinear dynamic integral inequalities in two independent variables on time scale pairs. Adv. Dyn. Syst. Appl. 3, 1–13 (2008)
Bohner, E.A., Bohner, M., Akin, F.: Pachpatte inequalities on time scale. JIPAM. J. Inequal. Pure Appl. Math. 6(1), Article ID 6 (2005)
Liu, H.D.: Some new half-linear integral inequalities on time scales and applications. Discrete Dyn. Nat. Soc. 2019, 9860302 (2019)
Meng, F.W., Shao, J.: Some new Volterra–Fredholm type dynamic integral inequalities on time scales. Appl. Math. Comput. 223, 444–451 (2013)
Xia, Y.H., Li, J.B., Wong, P.J.Y.: On the topological classification of dynamic equations on time scales. Nonlinear Anal., Real World Appl. 14(6), 2231–2248 (2013)
Liu, H.D.: An improvement of the Lyapunov inequality for certain higher order differential equations. J. Inequal. Appl. 2018, 215 (2018)
Saker, S.H.: Some nonlinear dynamic inequalities on time scales. Math. Inequal. Appl. 14, 633–645 (2011)
Sun, Y.G., Hassan, T.S.: Some nonlinear dynamic integral inequalities on time scales. Appl. Math. Comput. 220, 221–225 (2013)
Xia, Y.H., Chen, L., Kou, K.I.: Holder regularity of Grobman-Hartman theorem for dynamic equations on measure chains. Bull. Malays. Math. Sci. Soc. 41(3), 1153–1180 (2018)
Feng, Q.H., Meng, F.W., Zheng, B.: Gronwall-Bellman type nonlinear delay integral inequalities on time scale. J. Math. Anal. Appl. 382, 772–784 (2011)
Pachpatte, D.B.: Explicit estimates on integral inequalities with time scale. J. Inequal. Pure Appl. Math. 7, Article ID 143 (2006)
Liu, H.D.: On some nonlinear retarded Volterra–Fredholm type integral inequalities on time scales and their applications. J. Inequal. Appl. 2018, 211 (2018)
Li, L.Z., Meng, F.W., Ju, P.J.: Some new integral inequalities and their applications in studying the stability of nonlinear integro-differential equations with time delay. J. Math. Anal. Appl. 377(2), 853–862 (2011)
Liu, H.D.: A class of retarded Volterra–Fredholm type integral inequalities on time scales and their applications. J. Inequal. Appl. 2017, 293 (2017)
Tian, Y.Z., Cai, Y.L., Li, L.Z., Li, T.X.: Some dynamic integral inequalities with mixed nonlinearities on time scales. J. Inequal. Appl. 2015, 12 (2015)
Liu, H.D., Meng, F.W.: Nonlinear retarded integral inequalities on time scales and their applications. J. Math. Inequal. 12(1), 219–234 (2018)
Wang, J.F., Meng, F.W., Gu, J.: Estimates on some power nonlinear Volterra–Fredholm type dynamic integral inequalities on time scales. Adv. Differ. Equ. 2017, 257 (2017)
Gu, J., Meng, F.W.: Some new nonlinear Volterra–Fredholm type dynamic integral inequalities on time scales. Appl. Math. Comput. 245, 235–242 (2014)
Li, W.N., Sheng, W.H.: Some Gronwall type inequalities on time scales. J. Math. Inequal. 4(1), 67–76 (2010)
Jiang, F.C., Meng, F.W.: Explicit bounds on some new nonlinear integral inequalities with delay. J. Comput. Appl. Math. 205, 479–486 (2007)
Acknowledgements
The authors are indebted to the anonymous referees for their valuable suggestions and helpful comments which helped improve the paper significantly.
Funding
This research was supported by the Natural Science Foundation of Shandong Province (China) (No.: ZR2018MA018) and the National Natural Science Foundations of China (Nos.: 11671227, 61873144).
Author information
Authors and Affiliations
Contributions
HDL carried out the main part of this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, H., Li, C. & Shen, F. A class of new nonlinear dynamic integral inequalities containing integration on infinite interval on time scales. Adv Differ Equ 2019, 311 (2019). https://doi.org/10.1186/s13662-019-2236-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2236-8