1 Introduction

The Standard Model (SM) of particle physics predicted the existence of a neutral scalar particle, the Higgs boson, with an unknown mass. After decades of technological and experimental developments since the prediction, eventually such a particle with mass near 125 GeV was discovered at the Large Hadron Collider (LHC) [1, 2]. This discovery completed the SM as a successful quantum field theory description of the electroweak and strong interactions. However, to date, there remained observations and theoretical indications of physics beyond the SM (BSM).

Supersymmetry(SUSY)-based BSM, such as the Next-to-Minimal Supersymmetric Standard Model (NMSSM) [3,4,5], have spectra with multiple neutral scalar particles. A lot of theoretical and phenomenological work within the NMSSM framework have been done by various groups. To mention a non-exhaustive selection, these include global fits of the model’s sub-spaces along experimental constraints [6,7,8,9,10], studies on its relation to baryogenesis [11,12,13,14], phenomenological comparisons [15,16,17,18] and vacuum stability analyses [19,20,21]. In this article we analyse, for the first time, a weak-scale NMSSM with many free parameters in contrast to the analogue at the grand unification theory scale which have been typically studied the most. We call this scenario the “phenomenological NMSSM” (pNMSSM), as it is constructed with similar motivations to the well-studied pMSSM [22,23,24,25,26].

Within the pNMSSM, various Higgs sector scenarios can be considered depending on how the observed 125 GeV scalar at the LHC, which we shall label as \(h_{125}\), is identified and on how the other Higgs boson masses are restricted. Within the literature, the scenario studied the most is the ordinary case for which the lightest CP-even scalar, \(h_1\), is identified as \(h_{125}\). Here we consider three scenarios, \(\mathcal{H}_0\), \(\mathcal{H}_1\), and \(\mathcal{H}_2\), which are defined as follows:

  • \(\mathcal{H}_0\): \(h_1 \equiv h_{125}\). pNMSSM points were discarded if \(m_{h_1} \notin [122, 128] \,\text {GeV}\). To make \(\mathcal{H}_0\) mutually exclusive to \(\mathcal{H}_{1,2}\), \(m_{h_2} \notin [122, 128] \,\text {GeV}\) is required for this scenario. No restrictions on the other Higgs bosons were imposed.

  • \(\mathcal{H}_1\): \(h_1 \equiv h_{125}\) with \(m_{h_2} \in @@[122, 128] \,\text {GeV}\).

  • \(\mathcal{H}_2\): \(h_2 \equiv h_{125}\). To make \(\mathcal{H}_2\) mutually exclusive to \(\mathcal{H}_{0,1}\), \(m_{h_1} \notin [122, 128] \,\text {GeV}\) is required. No restrictions on the other Higgs boson masses were imposed.

  • \(\mathcal{H}_3\): \(h_1 \equiv h_{125}\) with the restriction that \(m_{h_2} \sim m_{h_3} \sim m_{h_1}\). This and other potentially interesting further possibilities will not be addressed in this article.

Here \(h_i\), with \(i = 1,2,3\), represent the three mass-ordered CP-even Higgs bosons. Our proposal is that by using Bayesian models comparison technique, one can find out which of the alternative hypotheses is supported most and, from another perspective, one can assess the status of the pNMSSM in light of the experimental data used. This method has been successfully applied in various particle physics phenomenology [26,27,28,29,30,31,32,33,34,35,36,37] and to greater extent in cosmology and astro-particles research. For instance, see [38,39,40,41] and their citations. For our analyses, we use the PolyChord [41, 42] “next-generation” (to MultiNest [40]) nested sampling implementation for making the comparisons.

The aim of this article is to determine which of the scenarios, \(\mathcal{H}_0\) , \(\mathcal{H}_1\) and \(\mathcal{H}_2\), is supported most by current data. Performing such a comparison analyses will add new directions to previous studies concerning quasi-degenerate Higgs boson scenarios such as in [9, 16, 43,44,45,46]. Likewise, the strength of the data in constraining the pNMSSM can be quantified. New benchmarks and perhaps experimentally unexplored pNMSSM regions can be extracted for future investigations along the searches for BSM physics. In the sections that follow, we first describe the Bayesian models comparison technique which makes the base for our analyses. This will be followed by a description of the weak-scale parametrisation, the procedure for fitting the parameters to data, and then the results of the comparisons made. The article ends with a Conclusions section.

2 Bayesian model selection

Using the nested sampling algorithm, the Bayesian evidence based on a given set of data can be readily computed and thereafter used for comparing alternative physics scenarios. With this algorithm, the parameters estimation is a by-product of the evidence computation. This is a unique advantage of nested sampling in contrast to traditional Monte Carlo techniques.

There are various possibilities for performing Bayesian models comparison. One can perform a comparison between two completely different physics models based on a common set of data. For example in [28] various SUSY-breaking mediation mechanisms were compared. Another possibility is the comparison of alternative physics scenarios within a single model. Examples of this can be found in [27, 29]. In [29], the comparison was between the MSSM scenario whereby the neutralino lightest sparticle (LSP) is considered to make all of the observed cold dark matter relic density compared to the alternative for which the LSP accounts for only part, not all, of the observed relic density. Along this line of thought, the pNMSSM scenarios \(\mathcal{H}_0\), \(\mathcal{H}_1\) and \(\mathcal{H}_2\), can be compared among one another based on a common set of experimental data. In the subsections that follow we briefly describe Bayes’ theorem, the Bayes factors which were used for the comparisons, and the similarities/differences between PolyChord and MultiNest.

2.1 Bayes theorem and Bayes factors

For a given context, \(\mathcal {H}\), based on a model with a set of N parameters, \( \theta \), the a priori assumed values which the parameters can take is encoded in the prior probability density distribution, \(p( \theta )\). The support a given hypothesis could draw from a data set is quantified by the probability density of observing the data set given the hypothesis,

$$\begin{aligned} \mathcal {Z} \equiv p( d|\mathcal{{H}}) = \int {p( d| \theta ,\mathcal{{H}}) \, p( \theta )}\ d \theta . \end{aligned}$$
(1)

This can be obtained directly from Bayes’ theorem,

$$\begin{aligned} p( \theta | d, \mathcal{{H}}) = \frac{p( d| \theta ,\mathcal{{H}}) \, p( \theta )}{p( d|\mathcal{{H}})}. \end{aligned}$$
(2)

Here \(p( d| \theta , \mathcal{{H}})\) is the likelihood, a measure of the probability for obtaining the data set d from a given set of the model parameters. To compare between say, \(\mathcal{{H}}_{0}\) and \(\mathcal{{H}}_{1}\) the Bayes factor, \(K = \frac{\mathcal {Z}_1}{\mathcal {Z}_0}\), should be computed. This could be done via the the posterior odd ratios:

$$\begin{aligned} \frac{p(\mathcal{{H}}_{1}| d)}{p(\mathcal{{H}}_{0}| d)} =\frac{p( d|\mathcal{{H}}_{1})p(\mathcal{{H}}_{1})}{p( d| \mathcal{{H}}_{0})p(\mathcal{{H}}_{0})} =\frac{\mathcal {Z}_1}{\mathcal {Z}_0}\frac{p(\mathcal{{H}}_{1})}{p(\mathcal{{H}}_{0})}. \end{aligned}$$
(3)

For the case where the two hypotheses are a priori equally likely, \(p(\mathcal{{H}}_{1})/p(\mathcal{{H}}_{0}) = 1\), then the logarithm of the Bayes factor can be obtained as the logarithm of the posterior odd factors:

$$\begin{aligned} \Delta \log _e \mathcal {Z} = \log _e \left[ \frac{p(\mathcal{{H}}_{1}|d)}{p(\mathcal{{H}}_{0}| d)}\right] = \log _e \left[ \frac{\mathcal {Z}_1}{\mathcal {Z}_0}\right] . \end{aligned}$$
(4)

Getting \(\mathcal {Z}_1/\mathcal {Z}_0 > 1\) will infer that the data supports \(\mathcal{{H}}_1\) more compared to \(\mathcal{{H}}_0\) and vice versa if the ratio is less than one. The Jeffrey’s scale shown in Table 1 calibrates the significance of the Bayes factors. Next we are going to explain what the Bayes factors describe within the context of the pNMSSM global fits to data.

Table 1 Jeffreys’ scale [47] (see also the work in Ref. [48]) for the interpretation of the Bayes factors. The Bayes factors, as explained below, could also quantify the relative posterior probability masses for the scenarios compared which are a priori equally likely
Full size table

From a point of view, the Bayes factor encodes information about the scenarios’ posterior masses as measured by the chosen priors. It can tell which scenario is more plausible based on a given set of data. To see this, let the pNMSSM posterior without restricting to any of the \(\mathcal{H}_{0}\), \(\mathcal{H}_{1}\), or \(\mathcal{H}_{2}\) scenarios be

$$\begin{aligned} p( \theta | d) = \frac{p( d| \theta )\,p( \theta )}{\mathcal{Z}}. \end{aligned}$$
(5)

Assuming that the scenarios represent mutually exclusive volumes, \(\Omega _0, \Omega _1\) and \(\Omega _2\) respectively, in the “full” \(\theta \)-space then the corresponding posterior probability masses can be computed. For instance,

$$\begin{aligned} \mathcal{Z}_0^{'} = \int _{\Omega _0} \, p(\theta | d) \, d\theta = \int _{\Omega _0} \, \frac{p( d| \theta )p( \theta )}{\mathcal{Z}} \, d\theta = \frac{\mathcal{Z}_0}{\mathcal{Z}}. \end{aligned}$$
(6)

The global evidence, \(\mathcal{Z}\), will cancel out when computing the ratios, such as \(\frac{\mathcal{Z}_0^{'}}{\mathcal{Z}_1^{'}} = \frac{\mathcal{Z}_0}{\mathcal{Z}_1}\). So the evidence and posterior mass ratios are equivalent. As such, the priors for scenarios \(\mathcal{H}_{0,1,2}\) are not free to be chosen arbitrarily. They are rather set by the prior distribution \(p(\theta )\), with the relative priors such as \(\frac{p(\mathcal{H}_0)}{p(\mathcal{H}_1)}\) constrained to match the corresponding integrations of \(p(\theta |\mathcal{H}_{0,1})\) over the domains \(\Omega _{1,2}\). The prior ratios can be estimated by scanning over the pNMSSM parameters without imposing the likelihoods or scenario requirements and then find the number of survived points after imposing the Higgs boson(s) mass restrictions. Thus \(p(\mathcal{H}_i)\), \(i = 0, 1, 2\) can be considered to be the fraction of the survived points.

For the nested sampling implementation in PolyChord, parameter points were sampled from a flat prior distribution, \(p( \theta )\), which integrates to 1 over the “full” pNMSSM \(\theta \)-space. This “global” prior is used for each of the three scenarios considered. So PolyChord is run once for each of the scenarios. From the sampled parameter points, the \(\mathcal{H}_0\), \(\mathcal{H}_1\), or \(\mathcal{H}_2\) cuts on the Higgs boson masses were applied. For instance, in the case of the PolyChord run for \(\mathcal{H}_0\) the sampled pNMSSM points were discarded if \(m_{h_1} \notin [122, 128] \,\text {GeV}\) and \(\mathcal{H}_{1,2}\), \(m_{h_2} \notin [122, 128] \,\text {GeV}\). As such the evidence value returned by PolyChord will be

$$\begin{aligned} \mathcal{Z}_0^{''}= & {} \int _{\Omega _0} \, p(d | \theta ) \, p(\theta ) \, d\theta \nonumber \\= & {} \int _{\Omega _0} \, p(d | \theta ) \, p(\theta | \mathcal{H}_0) \, p(\mathcal{H}_0) \, d\theta \end{aligned}$$
(7)

with \(\int \, p(\theta ) \, d\theta = 1\), since in principle \(p(\theta )\) can be expanded as \(p(\theta ) = p(\theta | \mathcal{H}_0) \, p(\mathcal{H}_0) + p(\theta | \mathcal{H}_1) \, p(\mathcal{H}_1) + p(\theta | \mathcal{H}_2) \, p(\mathcal{H}_2)\). This way, the ratios such as \(\frac{\mathcal{Z}_0^{''}}{\mathcal{Z}_1^{''}} = \frac{\mathcal{Z}_0}{\mathcal{Z}_1} \,\, \frac{p(\mathcal{H}_0)}{p(\mathcal{H}_1)}\) represents the full posterior mass ratio as in Eq. (3). Thus the Bayes factor, K can be obtained from what PolyChord returns (the \(\mathcal{Z}^{''}\)s) as

$$\begin{aligned} K = \frac{\mathcal{Z}_0}{\mathcal{Z}_1} = \frac{\mathcal{Z}_0^{''}}{\mathcal{Z}_1^{''}} \,\, \frac{p(\mathcal{H}_1)}{p(\mathcal{H}_0)}. \end{aligned}$$
(8)

2.2 PolyChord versus MultiNest

Here we briefly describe the similarities and contrast between the relatively new PolyChord [41, 42] and the MultiNest algorithm [40, 49] which we have used in the past for similar analyses. Both MultiNest and PolyChord are effective Bayesian evidence calculators that perform as excellent multi-modal posterior samplers. At their core, “nested sampling” algorithm [38] is implemented. They differ on how a new set of model parameters is generated over sampling iterations. MultiNest is based on rejection sampling or, alternatively, importance sampling. On the other hand, PolyChord is based on slice sampling method.

We used PolyChord because of its improved scaling with dimensionality, D, as illustrated in [42]. For the multi-dimensional Gaussian problem analysed in [42], the number of likelihood calculations needed for the run to converge scales as \(\mathcal{O}(D^3)\) at worst using PolyChord instead of the approximately exponential scaling that emerges for higher dimensions (greater than around 20) as is expected for the rejection sampling method (see Sect. 29.3 of [50]). The 26-dimensional pNMSSM considered for the analysis presented in this article is more complicated in comparison to the toy Gaussian problem.

There are two tuning parameters for running PolyChord, namely the number of live points maintained throughout the nested sampling implementation, \(n_{live}\), and the length of the slice sampling chain, \(n_{repeats}\), used for generating new live points. With \(n_{live} = 200\) and \(n_{repeats} = 26\), running PolyChord on the pNMSSM parameters space finished with 700208 likelihood calculations using 96 core-hours of computing time. This compares to 11344428 likelihood calculations for the same pNMSSM model with MultiNest tuning parameters \(n_{live} = 5000\) and \(efr = 0.1\) using 4480 core-hours. Making \(n_{live} = 1000\) instead of \(n_{live} = 200\), the amount of time and likelihood calculations needed to finish the PolyChord run increased drastically but ends up with similar results for the Bayesian evidence. It took 6272 core-hours and 3492331 likelihood calculations. Setting \(n_{repeats} = 2 \times 26\) instead of \(n_{repeats} = 26\), PolyChord finished with 1632936 likelihood calculations and 512 core-hours. These basic comparison between PolyChord and MultiNest are summarised in Table 2. Given the experience in using MultiNest for large parameter models (order 20 to 30), especially the difficulties in getting runs to finish over tightly constrained or models with high number of parameters, we decide to use PolyChord.Footnote 1

Table 2 An example of basic quantitative comparison of the relative performance between PolyChord and MultiNest for the 26 parameters pNMSSM. Here N, efr, r, \(\log \mathcal {Z}\), \(t_{CPU}\) and \(N_l\) are respectively the nested sampling number live points, MultiNest algorithm tuning parameter, PolyChord tuning parameter (\(n_{repeats}\)), the logarithm of the Bayesian factor obtained in a run, the CPU core-hours taken and the number of likelihood calculations done before finishing a run
Full size table

3 The phenomenological NMSSM

The NMSSM, for reviews see e.g. [3,4,5], has phenomenological advantages over the MSSM. These include the solution of the \(\mu \)-problem [51]. The vacuum expectation value of an additional gauge-singlet (S) can generate superpotential \(\mu \)-term dynamically. It also has a richer Higgs-sector. There are three CP-even Higgs bosons, \(h_{1,2,3}\), and two CP-odd Higgs bosons \(a_{1,2}\) which are mixtures of the MSSM-like Higgs doublet fields and respectively the real or imaginary part of S. For our analyses, we shall consider an R-parity conserving NMSSM with minimal CP and flavour violating free parameters and superpotential,

$$\begin{aligned} W_{NMSSM} = W_{MSSM'} - \epsilon _{ab}\lambda {S} {H}^a_1 {H}^b_2 + \frac{1}{3} \kappa {S}^3 \ , \end{aligned}$$
(9)

where \(W_{MSSM'}\) is the MSSM-like superpotential without the \(\mu \)-term,

$$\begin{aligned} W_{MSSM'}= & {} \epsilon _{ab} \left[ (Y_E)_{ij} H_1^a L_i^b {\bar{E}}_j + (Y_D)_{ij} H_1^a Q_i^{b} {\bar{D}}_{j} \right. \nonumber \\&\left. + (Y_U)_{ij} H_2^b Q_i^{a} {\bar{U}}_{j} \right] . \end{aligned}$$
(10)

Here, the chiral superfields have the following \(SU(3)_C\otimes SU(2)_L\otimes U(1)_Y\) quantum numbers,

$$\begin{aligned}&L:\left( 1,2,-\frac{1}{2}\right) ,\quad {\bar{E}}:(1,1,1),\quad \, Q:\,\left( 3,2,\frac{1}{6}\right) ,\nonumber \\&\quad {\bar{U}}:\,\left( \bar{3},1,-\frac{2}{3}\right) , {\bar{D}}:\left( \bar{3},1,\frac{1}{3}\right) ,\quad H_1:\left( 1,2,-\frac{1}{2}\right) ,\nonumber \\&\quad H_2:\,\left( 1,2,\frac{1}{2}\right) . \end{aligned}$$
(11)

The corresponding soft SUSY-breaking terms are

$$\begin{aligned} V_\mathrm {soft}= & {} V_2 + V_3 + m_\mathrm {S}^2 | S |^2 \nonumber \\&+ (-\epsilon _{ab}\lambda A_\lambda {S} {H}^a_1 {H}^b_2 + \frac{1}{3} \kappa A_\kappa {S}^3 + \mathrm {H.c.}), \end{aligned}$$
(12)

with the trilinear and bilinear contributions given by

$$\begin{aligned} V_2= & {} m_{H_1}^2 {{H^*_1}_a} {H_1^a} + m_{H_2}^2 {{H^*_2}_a} {H_2^a} + {\tilde{Q}^*}_{i_La} (m_{\tilde{Q}}^2)_{ij} \tilde{Q}_{j_L}^{a} \nonumber \\&+ {\tilde{L}^*}_{i_La} (m_{\tilde{L}}^2)_{ij} \tilde{L}_{j_L}^{a} \nonumber \\&+ \tilde{u}_{i_R} (m_{\tilde{u}}^2)_{ij} {\tilde{u}^*}_{j_R} + \tilde{d}_{i_R} (m_{\tilde{d}}^2)_{ij} {\tilde{d}^*}_{j_R} + \tilde{e}_{i_R} (m_{\tilde{e}}^2)_{ij} {\tilde{e}^*}_{j_R},\nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned} V_3= & {} \epsilon _{ab} \sum _{ij} \left[ (T_E)_{ij} H_1^a \tilde{L}_{i_L}^{b} \tilde{e}_{j_R}^* \right. \nonumber \\&\left. + (T_D)_{ij} H_1^a \tilde{Q}_{i_L}^{b} \tilde{d}_{j_R}^* + (T_U)_{ij} H_2^b \tilde{Q}_{i_L}^{a} \tilde{u}_{j_R}^* \right] + \mathrm {H.c.}.\nonumber \\ \end{aligned}$$
(14)

A tilde-sign over the superfield symbol represents the scalar component. However, an asterisk over the superfields as in, for example, \(\tilde{u}_R^*\) represents the scalar component of \(\bar{U}\). The \(SU(2)_L\) fundamental representation indices are donated by \(a,b=1,2\) while the generation indices by \(i,j=1,2,3\). \(\epsilon _{12}=\epsilon ^{12}=1\) is a totally antisymmetric tensor. In a similar approach to the pMSSM [22, 24,25,26] construction, the pNMSSM parameters are defined at the weak scale. For suppressing sources of unobserved CP-violation and flavour-changing neutral currents, the sfermion mass and trilinear scalar coupling parameters were chosen to be real and diagonal. For the same motivation, the first and second generation sfermion mass parameters were set to be degenerate. The gaugino mass parameters were reduced to be real by neglecting CP-violating phases. These lead to a non-Higgs sector set of parameters

$$\begin{aligned} M_{1,2,3};\;\; m^{3rd \, gen}_{\tilde{f}_{Q,U,D,L,E}},\;\; m^{1st/2nd \, gen}_{\tilde{f}_{Q,U,D,L,E}}; \;\;A_{t,b,\tau }. \end{aligned}$$
(15)

Here, \(M_{1,2,3}\) and \(m_{\tilde{f}}\) are respectively the gaugino and the sfermion mass parameters. \(A_{t,b,\tau }\) represent the trilinear scalar couplings, with \(T_{ij} \equiv A_{ij} Y_{ij}\) (no summation over i, j). So \(A_{t,b,\tau }\) is equivalent to the \(A_{33}\) corresponding, respectively, to the diagonalised matrices \(T_{U}\), \(T_{D}\), and \(T_{L}\). Here Y represent the Yukawa matrices. After electroweak symmetry breaking, the vacuum expectation value (vev) of S, \(v_s\), develops an effective \(\mu \)-term, \(\mu _\mathrm {eff} = \lambda \, v_s\). This and the ratio of the MSSM-like Higgs doublet vevs, \(\tan \beta =\left<H_2\right>/\left<H_1\right>\), are free parameters which together with mass of the Z-boson, \(m_Z\), can be used for computing \(m^2_{H_{1,2},S}\) via minimisation of the scalar potential. With these, the tree-level Higgs sector parameters are

$$\begin{aligned} \tan \beta , \lambda , \kappa , A_{\lambda }, A_{\kappa }, \lambda \, v_s. \end{aligned}$$
(16)

Adding to the list of parameters in Eqs. (15) and (16), four SM nuisance parameters, namely, the top and bottom quarks \(m_{t,b}\), \(m_Z\) and the strong coupling constant, \(\alpha _s\), makes the 26 free parameters of the pNMSSM:

$$\begin{aligned} \theta= & {} \{ M_{1,2,3};\;\; m^{3rd \, gen}_{\tilde{f}_{Q,U,D,L,E}},\;\; m^{1st/2nd \, gen}_{\tilde{f}_{Q,U,D,L,E}}; \;\;A_{t,b,\tau ,\lambda , \kappa }; \nonumber \\&\tan \beta , \lambda , \kappa , \mu _\mathrm {eff}; \;\; m_{t,Z,b}, \alpha _s \}. \end{aligned}$$
(17)

\(M_{1,2}\) strongly affect the electroweak gaugino masses for which a wide range of values, GeV to TeV, is possible. We let \(M_1 \in [-4, 4] \,\text {TeV}\) and same for \(M_2\) but fixed to be positive without loss of generality (see e.g. [52]). A strong sensitivity of the pNMSSM Higgs sector on the gluino and the 1st/2nd generation squark mass parameters is not anticipated. However we choose to let them vary since the limits from searches for SUSY will be part of the experimental data to be used. As such, following the work in [24, 26] we let the gluino and squark mass parameters vary within \([100 \,\text {GeV}, 4 \,\text {TeV}]\) and the trilinear scalar couplings within \([-8 \,\text {TeV}, 8 \,\text {TeV}]\). \(\tan \beta \) is allowed to vary between 2 and 60. With the aim of minimising fine-tuning, we subjectively choose to vary the effective \(\mu \)-parameter, \(\mu _\mathrm {eff} = \lambda \, v_s\), to be within 100 to 400 GeV and not (orders of magnitude) far away from the \(m_Z\). The remaining Higgs-sector parameters were allowed in ranges as summarised in Table 3. For all the parameters, except the SM ones, flat prior probability density distribution was assumed. For the experimentally measured SM nuisance parameters, Gaussian distributions around the measured values were used.

Table 3 The 26 pNMSSM parameters and their corresponding flat prior probability density distribution ranges. The SM parameters were varied according to Gaussian distributions with the shown central values and standard deviations
Full size table

Checking the prior-dependence of results is useful for assessing the strength of the data in constraining the model in an unambiguous manner. The priors can be chosen to be flat or logarithmic with the latter favouring lower regions of the parameter ranges. There are two bottle-necks concerning our attempts for sampling the pNMSSM parameters with logarithmic priors. On one hand, the absence of signatures for SUSY at the LHC pushes sparticle mass lower bounds towards or well into the multi-TeV regions. Therefore, sampling the phenomenologically viable parameters according to a logarithmic prior will be difficult and computationally expensive. For the attempted log-prior fits, only parameters that do not cross zero were sampled logarithmically. Those that have the possibility of being zero were sampled uniformly. On the other hand, for the nested sampling algorithm in PolyChord to get started, a 200-points sample of the 26-parameters pNMSSM is required. By using logarithmic priors, it was not possible to generate the 200 model points within the maximal possibility of 3072 CPU core-hours per run at our disposal.Footnote 2 Thus we restrict our analyses to the flat priors only. The conclusions presented in this article are valid only within this context.

Another issue concerning our pNMSSM parametrisation is related to “naturalness” or the avoidance of excessive fine-tuning associated with obtaining the correct weak-scale (\(m_Z\)). With the naturalness prior parametrisation [53], the fine-tuning can be avoided by directly scanning the parameters \(m_Z\) and \(\tan \beta \) rather than \(m_{H_1}\) an \(m_{H_2}\). Moreover it was shown [37] that naturalness prior parametrisation could significantly affect the Bayesian evidence values. For the analyses presented in this article, such parametrisation was not considered. Rather, a Gaussian prior for \(m_Z\) centred on the measured value was used. Doing this injects information about what the weak scale is into the prior. In addition, \(\mu _{eff}\) were chosen to be near the electroweak symmetry breaking scale, between 100 to 400 GeV, since one of our aims is to show that there are still vast regions in parameter space with low mass gauginos and BSM Higgs bosons which are not ruled out by current data. It is accepted that fine-tuning penalisation manifests implicitly and automatically within Bayesian global fits as presented in [33, 54, 55]. The same applies to the fact that fine-tuning limits could be imposed during fits by using the various fine-tuning measures [53, 56,57,58,59,60,61]. Using any of these is not within the scope of our present analyses given the deliberate target to regions with low mass electroweak gauginos.

Now, coming back to the Higgs sector potential, the details concerning the NMSSM Higgs mass matrices and couplings can be found in the literature, for example see [4, 62,63,64,65,66]. The \(\mathbb {Z}_3\)-invariant NMSSM Higgs potential can be obtained from the SUSY gauge interactions, soft-breaking and F- terms as

$$\begin{aligned} V_\mathrm {Higgs}= & {} \left| \lambda H_2.H_1 + \kappa S^2 \right| ^2\nonumber \\&+ \left( m_{H_2}^2 + \left| \lambda S\right| ^2\right) \left( \left| H_2^0\right| ^2 + \left| H_2^+\right| ^2\right) \nonumber \\&+\left( m_{H_1}^2 + \left| \lambda S\right| ^2\right) \left( \left| H_1^0\right| ^2 + \left| H_1^-\right| ^2\right) \nonumber \\&+\frac{g_1^2+g_2^2}{8}\left( \left| H_2^0\right| ^2 + \left| H_2^+\right| ^2 - \left| H_1^0\right| ^2 - \left| H_1^-\right| ^2\right) ^2 \nonumber \\&+\frac{g_2^2}{2}\left| H_2^+ H_1^{0*} +H_2^0 H_1^{-*}\right| ^2\nonumber \\&+m_{S}^2 |S|^2 +\big ( \lambda A_\lambda H_2.H_1 S \nonumber \\&\quad + \frac{1}{3} \kappa A_\kappa \, S^3 + \mathrm {H.c.}\big ), \text { with } \nonumber \\&H_1 = \left( \begin{array}{c} H_1^0 \\ H_1^- \end{array} \right) , \text { and } H_2 = \left( \begin{array}{c} H_2^+ \\ H_2^0 \end{array} \right) . \end{aligned}$$
(18)

Here \(g_1\) and \(g_2\) denotes the \(U(1)_Y\) and SU(2) gauge couplings, respectively. Out of the 22 non-SM pNMSSM parameters, six, compared to two for the pMSSM, are directly from the Higgs sector. After electroweak symmetry breaking, replacement of the Higgs sector fields with corresponding fluctuations on top of the vevs,

$$\begin{aligned} H_2^0= & {} \left<H_2\right> + \frac{H_{2R} + iH_{2I}}{\sqrt{2}}, \nonumber \\ H_1^0= & {} \left<H_1\right> + \frac{H_{1R} + iH_{1I}}{\sqrt{2}}, \quad S = s + \frac{S_R + iS_I}{\sqrt{2}}\;, \end{aligned}$$
(19)

leads to the realisation of CP-even Higgs boson mixing matrix

$$\begin{aligned} h_i^{\text {mass}} = O_{ij} h_j^{\text {weak}}. \end{aligned}$$
(20)

Here the physical Higgs fields have indices R for the CP-even, and indices I for the CP-odd states. \(h_i^{\text {weak}} = (H_{1R}, H_{2R}, S_R)\) represents the interaction, and \(h_i^{\text {mass}}\), the mass-ordered, eigenstates. The mixing of the SU(2) doublets with the singlet state affects the phenomenology of the Higgs bosons. For instance, the reduced couplings (see, e.g. [66])

$$\begin{aligned} \xi _i = \sin \beta \, O_{i2} + \cos \beta \, O_{i1} \end{aligned}$$
(21)

of the 3 CP-even mass-eigenstates \(h_i\) to the electroweak gauge bosons can be very small in some regions of parameter space. The sum rule \(\sum _{i=1}^3 \xi _i^2 = 1\) is always satisfied. The reduced couplings are inputs to the Lilith [67] program for comparing the pNMSSM signal strengths to the experimentally measured values.

4 Experimental constraints and fit procedure

During the global fits, the experimental constraints used were those implemented in NMSSMTools [68,69,70,71,72,73], Lilith [67], and MicrOMEGAs [74,75,76,77,78,79,80,81,82,83]. The set of experimental constraints, d, shown in Table 4 were used to associate each pNMSSM point, \(\{ \theta , \mathcal{{H}}\}\), with a likelihood \(p( d| \theta , \mathcal{{H}})\). The likelihood as a function of the parameters is explained as follows.

Table 4 Summary of the data used for the pNMSSM global fits. Theoretical uncertainties have been added in quadrature to the experimental uncertainties quoted. The Higgs signal strengths are those implemented in Lilith which returns a log-likelihood value for each model point. The cold dark matter direct detection limits implemented are shown in Fig. 4. Finally, the HiggsBounds and SmodelS constraints impose the 95% C.L. bounds on collider pseudo-observables such as \(\sigma .Br\) for specific Higgs and SUSY processes respectively
Full size table

In modelling the likelihood, the set of constraints used during the global fits are divided into the three groups:

  • Constraints on the Higgs boson mass \(m_h\), the neutralino cold dark matter (CDM) relic density \(\Omega _{CDM} h^2\), anomalous magnetic moment of the muon \(\delta a_\mu \) and B-physics related limits summarised in the upper part of Table 4 form the first part of the data set, d. The likelihood is computed from the pNMSSM predictions, \(O_i\), corresponding to the constraints i, with experimental central values \(\mu _i\) and uncertainties \(\sigma _i\), as

    $$\begin{aligned} p( d| \theta , \mathcal{{H}}) = \prod _i \, \frac{ \exp \left[ - (O_i - \mu _i)^2/2 \sigma _i^2\right] }{\sqrt{2\pi \sigma _i^2}}. \end{aligned}$$
    (22)

    Here the index i runs over the relevant experimental constraints in Table 4.

  • Signal strength measurements from Tevatron [103], ATLAS [98, 100, 104,105,106,107,108,109,110,111,112] and CMS [99, 101, 102, 113,114,115,116,117,118,119] as implemented in Lilith v1.1 (with data version 15.09) [67] represent the second part of the data set. For each pNMSSM point, the returned likelihood from Lilith is combined with the product in Eq. (22). The likelihood can be computed via either the Higgs boson signal strengths or their reduced couplings with respect to the SM. For the first case, a pNMSSM point with corresponding signal strength \(\mu _i\) is associated with the likelihood

    $$\begin{aligned}&-2L_{lilith}( \theta ) = - 2 \sum _i \log L(\mu _i) \nonumber \\&\quad = \sum _{i} \left( \frac{\mu _i(\theta ) - \hat{\mu }_i}{\Delta \mu _i}\right) ^2. \end{aligned}$$
    (23)

    Here i runs over the various categories of Higgs boson production and decay modes combinations. \(\hat{\mu }_i \pm \Delta \hat{\mu }_i\) represents the experimentally determined signal strengths. Theoretically, the signal strength associated to a model point can be computed, for a given production mode X and decay mode Y as

    $$\begin{aligned} \mu = \sum _{X,Y} \epsilon _{X,Y} \frac{ \sigma (X) \, BR(H \rightarrow Y)}{\left[ \sigma (X) \, BR(H \rightarrow Y) \right] ^{SM}}. \end{aligned}$$
    (24)

    Here \(\epsilon _{X,Y}\) are the experimental efficiencies, \(X \in \{ ggH, VH, VBF, ttH\}\) and \(Y \in \{ \gamma \gamma , VV^{(*)}, b \bar{b}, \tau \tau , ttH\}\). For a proton-proton collider, the elements in X represent: the gluon-gluon fusion (ggH), associated production with a boson (VH), vector boson fusion (VBF) or associated production with top quarks (ttH). The elements in Y represent the Higgs diphoton (\(\gamma \gamma \)), W or Z bosons (VV), bottom quarks (bb) or tau leptons (\(\tau \tau \)) decay modes.

    Now, computing \(\mu \) as in Eq. (24) could be impractical since for a meaningful theory versus experiment comparison, the non-SM predictions in the numerator should be computed using the same prescriptions such as the order in perturbation, implementation of parton distribution functions etc. The second approach, whereby the input to Lilith are the reduced couplings does not suffer from this problem. BSM physics effects can be parametrised in terms of the reduced couplings. The cross section (or partial decay width) for each production process X (or decay mode Y) can be scaled [158] with a factor of \(C_X^2\) and \(C_Y^2\) respectively such that

    $$\begin{aligned} \sigma (X) = C_X^2 \, \sigma (X)^{SM} \quad \text { and } \quad \Gamma (Y) = C_Y^2 \, \Gamma (Y)^{SM}. \end{aligned}$$
    (25)

    The reduced couplings computed from the NMSSMTools together with their invisible and undetectable decay branching ratios can then be passed to Lilith for computing the likelihood based on

    $$\begin{aligned} \mu= & {} ( 1 - BR(H \rightarrow \, undetected) \nonumber \\&- BR(H \rightarrow \, invisible) ) \frac{ \sum _{X,Y} \epsilon _{X,Y} C_X^2 \, C_Y^2}{\sum _Y \, C_Y^2 \, BR(H \rightarrow Y)^{SM}}\nonumber \\ \end{aligned}$$
    (26)

    and the table of likelihood values as a function of \(\mu \) within the Lilith database of experimental results. This procedure is valid only for Higgs bosons with mass between 123 to 128 GeV. For the multi-Higgs case with masses within this range, such as for \(\mathcal{H}_1\), the combined [159] signal strengths were used.

  • The third set of constraints in d is the CDM direct detection limits. These are from searches for the elastic scattering of CDM with nucleons. The recoil energy deposited on nuclei in a detector can be measured. In the absence of discovery, upper limits on the scattering cross section can be determined. The cross sections can be either spin-independent (SI) or spin-dependent (SD) depending on whether the LSP-nucleon coupling is via scalar or axial-vector interaction. For the fits with the direct detection limits imposed, only parameter points that pass the SI [120,121,122] and SD [123,124,125,126] limits were accepted.

Another set of limits were used for fitting the pNMSSM. These were not included during the global fit samplings. Instead, the limits implemented in SModelS [136,137,138,139,140,141,142,143,144,145,146] and HiggsBounds [127, 128] were applied to the posterior samples from the pNMSSM fits to the data on the upper section of Table 4. The inclusion of SModelS constraints during the fits will slow the exploration of the pNMSSM space beyond tolerance. For this reason, the “post-processing” procedure was used. The “post-processing” means passing the posterior sample points, in SLHA[160] format, to SModelS and HiggsBounds for imposing the experimental 95% confidence limits from ATLAS and CMS SUSY bounds [147,148,149,150,151,152,153,154,155,156,157] and the Tevatron and LHC Higgs physics bounds [98,99,100,101,102, 127,128,129,130,131,132,133,134,135] respectively. The ruled out points were taken out of the samples and the evidence values re-weighted accordingly. The impact of SModelS and HiggsBounds on the evidence values is rather insignificant since the ruled-out points do not saturate the likelihood space.

5 Results

5.1 Bayesian evidences

Table 5 Here \(\mathcal {Z}\) represents the evidence returned by PolyChord. There are three set of results demarcated by the double horizontal lines. The first set is for the pNMSSM global fits to the observables shown in Table 4 but without the CDM direct detection (DD), \(Br(B_s \rightarrow \mu ^+ \mu ^-)\), \(Br(B_u \rightarrow \tau \nu )\) and \(\delta a_{\mu }\) limits. For the second and third sets, the limits from CDM DD searches were added. The third set is done with all the observables included. The inclusion of all the limits significantly changed the discriminating power of the data
Full size table

The results for the Bayesian comparisons between the hypotheses considered are shown in Table 5. There are three sets of results demarcated by the double horizontal lines. In the first set, the CDM direct detection (DD), \(Br(B_s \rightarrow \mu ^+ \mu ^-)\), \(Br(B_u \rightarrow \tau \nu )\) and \(\delta a_{\mu }\) limits were not included during the fits. For the third set, all the observables were included. The Bayesian evidence (\(\log _e \mathcal{Z}\)) values returned by PolyChord for each of the scenarios are shown in the second column. The Bayes factors, K, for the comparisons between \(\mathcal{H}_i\) and \(\mathcal{H}_j\) scenarios are shown on the third column while the corresponding remarks are displayed on the fourth column. The priors \(p(\mathcal{H}_i)\), \(i = 0, 1, 2\) were estimated via a random scan of 2156295 pNMSSM points without any of the \(\mathcal{H}_i\) constraints imposed. Out of these, 1867739, 128, and 7646 points respectively survived the \(\mathcal{H}_0\), \(\mathcal{H}_1\), and \(\mathcal{H}_2\) requirements. This way, \(p(\mathcal{H}_0) = 8.6618 \times 10^{-1}\), \(p(\mathcal{H}_1) = 5.9361 \times 10^{-5}\), and \(p(\mathcal{H}_2) = 3.5459 \times 10^{-3}\). As expected, the stronger the data set is, the better the discrimination between the scenarios becomes. But this depends on whether all the elements in the set pull the posterior mass towards a common region. The addition of two sets of data with tendencies for pulling the posterior in opposite directions will dilute the discrimination strength of the combined set. This characteristic behaviour can be seen in going from the second to the third set of results shown in Table 5. the \(Br(B_s \rightarrow \mu ^+ \mu ^-)\), \(Br(B_u \rightarrow \tau \nu )\) and \(\delta a_{\mu }\) set tends to prefer lighter SUSY states. The inclusion of this set diluted the discrimination power of the combined data set. Without the \(Br(B_s \rightarrow \mu ^+ \mu ^-)\), \(Br(B_u \rightarrow \tau \nu )\) and \(\delta a_{\mu }\) limits, the conclusions drawn are Moderate or Strong. These changed to Inconclusive or Moderate when the mentioned set of data are included as can be seen for the third set of results in Table 5. For the third set of the results, we discuss the comparisons between the scenarios as follows.

  • The data shows an inconclusive result for the comparison between \(\mathcal{H}_0\) against \(\mathcal{H}_1\). This an indication that the CDM DD limits on one hand, versus the \(Br(B_s \rightarrow \mu ^+ \mu ^-)\), \(Br(B_u \rightarrow \tau \nu )\) and \(\delta a_{\mu }\) set of limits on another are sensitive to these scenarios but in opposite directions. This can be seen by noting that the support for \(\mathcal{H}_1\) against \(\mathcal{H}_0\) changed from Strong to Moderate and then to Inconclusive in going from the first to the second and then third set of results shown in Table 5.

  • Similarly, the data demonstrates a moderate evidence in support of \(\mathcal{H}_2\) against \(\mathcal{H}_1\). For the \(\mathcal{H}_2\) versus \(\mathcal{H}_1\) comparison the evidence changes from Moderate to Strong upon the inclusion of CDM direct detection limits. This can be understood as being due to the presence of relatively much lighter \(h_1\) in the \(\mathcal{H}_2\) scenario (see Fig. 1, first-row left plot). Lighter \(h_1\) leads to bigger LSP-nucleon cross sections and thus more likely to be ruled out by the direct detection limits.

  • The data has a Moderate support for \(\mathcal{H}_2\) relative to \(\mathcal{H}_0\). Over the first two sets of results, the support for \(\mathcal{H}_2\) against \(\mathcal{H}_0\) is Strong. The inclusion of the \(Br(B_s \rightarrow \mu ^+ \mu ^-)\), \(Br(B_u \rightarrow \tau \nu )\) and \(\delta a_{\mu }\) limits diluted the conclusion to a Moderate one.

All together, there is a Moderate support for \(\mathcal{H}_2\) against \(\mathcal{H}_0\) and the latter may be considered as being ranked first in comparison to \(\mathcal{H}_0\) or \(\mathcal{H}_1\) which can be simultaneously ranked second. The hypothesis with a single Higgs boson around \(125 \,\text {GeV}\) is not decisively supported. The data has a tendency towards preferring the \(\mathcal{H}_2\) scenario which permits the possibility of having an additional but much lighter (than \(125 \,\text {GeV}\)) scalar.

5.2 Posterior distributions related to CP-even Higgs bosons

Fig. 1
figure 1

Marginalised one- (top) and two-dimensional (bottom) posterior distributions for the first-two lightest CP-even Higgs bosons. The dashed/green (H0), dash-dotted/red (H1) and solid/black (H2) lines represent respectively the hypotheses \(\mathcal{{H}}_0\), \(\mathcal{{H}}_1\) and \(\mathcal{{H}}_2\). The top-right plot shows the \(m_{h_2}\) distribution for \(\mathcal{{H}}_0\) which is not visible on the top-left plot. For the plot on the bottom, \(m_{h_2}\) for \(\mathcal{{H}}_0\) scenario (H0, on the legend) is re-scaled

Full size image

To complement the Bayes’ factors reported on Table 5, in this subsection we describe the posterior distributions of the first two light Higgs boson masses and couplings. The plots Footnote 3 in Fig. 1 show respectively the one- and two-dimensional mass distributions within each of the scenarios considered. For \(\mathcal{{H}}_2\), \(m_{h_1}\) distribution is peaked at a value much less than 125 GeV. This is because of the interplay between the large electron-positron (LEP) and LHC constraints. With respect to the position of the peak, the lower mass region is suppressed by LEP constraints such as upper limits on the cross section of \(e^- \, + \, e^+ \rightarrow h_1 \, Z\) [161, 162]. The heavier mass region beyond the peak gets ruled out by the upper limits on the reduced production cross sections, at the LHC, such as for \(p\,p \rightarrow h_1 \rightarrow a_1 a_1\) [163], \(ggF \rightarrow h_1 \rightarrow \gamma \, \gamma \) [164], and \(ggF \rightarrow h_1 \rightarrow \tau \, \tau \) [165, 166] processes.

The nature of the two lightest CP-even Higgs bosons in each of the three scenarios can be determined by considering their reduced couplings to fermions (up-type, u and down-type, d) and gauge bosons (W, Z, and \(\gamma \)). As shown in Fig. 2, for \(\mathcal{{H}}_0\) (dashed/green line), \(h_1\) is completely SM-like. For \(\mathcal{{H}}_1\) (dash-dotted/red line), \(h_2\) is mostly SM-like when \(h_1\) is not and vice versa. This due to the so-called “sharing of couplings” effect. \(h_1\) is almost completely non SM-like within \(\mathcal{{H}}_2\) (solid/black line) for which \(h_2\) is identified as \(h_{125}\). These features stem from the combined effects of the various limits imposed on the pNMSSM parameter space. The most pronounced of these for \(h_1\) are the LHC limits on the signal strengths which are directly proportional to the reduced couplings, and subsequently to the elements of the Higgs mixing matrix.

Fig. 2
figure 2

Marginalised posterior distributions for the first-two lightest CP-even Higgs bosons (\(h_j\), \(j = 1\) or 2) reduced couplings, \(C_i^{h_j}\), to matter and gauge particles \(i = u, d, V, \gamma \) (respectively up-type, and down-type matter particles, W, Z, and photon). The dashed/green line (H0), dash-dotted/red line (H1) and solid/black (H2) lines represent respectively the hypotheses \(\mathcal{{H}}_0\), \(\mathcal{{H}}_1\) and \(\mathcal{{H}}_2\)

Full size image
Fig. 3
figure 3

Marginalised posterior distributions for the neutralino LSP content. Here \(p_1 = N_{11}^2 + N_{12}^2\), \(p_2 = N_{13}^2 + N_{14}^2\), and \(p_3 = N_{15}^2\) quantifies the gaugino, Higgsino, and singlino content of the LSP. The dashed/green (H0), dash-dotted/red (H1) and solid/black (H2) lines represent the hypotheses \(\mathcal{{H}}_0\), \(\mathcal{{H}}_1\) and \(\mathcal{{H}}_2\) respectively

Full size image

5.3 Posterior distributions related to neutralino CDM candidate

The LSP is identified as a candidate for explaining the observed CDM relic density. Here we show the posterior distributions for the neutralino composition and direct detection cross sections are presented. The nature of the LSP is one of the most important factors affecting its relic density and scattering cross sections. The relevant part of the Lagrangian for the neutralino is

$$\begin{aligned} \mathcal{L} = \frac{1}{2} M_1 \lambda _1 \lambda _1 + \frac{1}{2} M_2 \lambda _2^i \lambda _2^i + \frac{1}{2} M_3 \lambda _3^a \lambda _3^a\, . \end{aligned}$$
(27)

Here \(\lambda _1\), \(\lambda _2^i\) (with \(i=1, 2, 3\)), and \(\lambda _3^a\) (with \(a=1, \dots , 8\)) represents respectively the \(U(1)_Y\), \(SU(2)_L\) and \(SU(3)_c\) gaugino fields. \(\lambda _1\) and \(\lambda _2^3\) mix with the neutral Higgsinos \(H_1^0, H_2^0, S\) to form a symmetric \(5 \times 5\) mass matrix \(\mathcal{M}_0\). With \(\psi ^0 = (-i\lambda _1 , -i\lambda _2^3, H_1^0, H_2^0, S)\), the neutralino mass term takes the form \(\mathcal{L} = - \frac{1}{2} (\psi ^0)^T \mathcal{M}_0 (\psi ^0) + \mathrm {H.c.}\). \(\mathcal{M}_0\) can be diagonalised by an orthonormal matrix \(N_{ij}\) such that the five mass-ordered eigenstates are superpositions of \(\psi ^0_j\):

$$\begin{aligned} \chi _i^0 = N_{ij} \, \psi ^0_j \, . \end{aligned}$$
(28)

The neutralino LSP is considered to be gaugino-, Higgsino- or singlino-like when \(p_1 = N_{11}^2 + N_{12}^2\), \(p_2 = N_{13}^2 + N_{14}^2\), or \(p_3 = N_{15}^2\) dominates respectively. The posterior distributions for these are shown in Fig. 3. It resulted in the fact that for \(\mathcal{{H}}_0\) (dashed/green line), the LSP is mixed gaugino-Higgsino with approximately zero singlino content. The case is different for \(\mathcal{{H}}_2\), for which the LSP is mixed Higgsino-singlino but with dominantly singlino and zero gaugino content. Instead, in the case for \(\mathcal{{H}}_1\) the LSP is dominantly Higgsino.

The nature of the neutralino LSP composition determines what leading role the annihilation and co-annihilation processes (see, e.g., Ref. [4]) play for getting the relic density around the experimental value, \(\Omega _{CDM} h^2 = 0.12\) [97]. It also determines the processes that could be involved for the direct detection of the dark matter candidate. Concerning the latter, the dominant processes are the t-channel Z or Higgs boson exchange for spin dependent or independent interactions, respectively. For instance, highly singlino-like LSP leads to small spin dependent cross section. The application of the dark matter direct detection limit will therefore lead to a posterior distribution with dominantly singlino LSP as is the case within \(\mathcal{{H}}_2\).

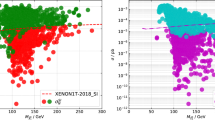
In Fig. 4 (first-row) the posterior distributions of the spin-independent and spin-dependent LSP-proton scattering cross sections compatible with all the considered collider, astrophysical, including the CDM direct detection bounds reported in [120,121,122,123,124,125,126], and flavour physics constraints are shown. The sudden suppressions in the direct detection cross sections occur at points for which there are cancellations from the neutralino-neutralino-Higgs interaction terms [167].

Fig. 4
figure 4

Marginalised two-dimensional posterior distributions for the neutralino LSP mass versus its spin-independent (1st-row left) and spin-dependent (1st-row right) scattering cross-section with proton. The green (H0), red (H1) and black (H2) regions represent \(\mathcal{{H}}_1\), \(\mathcal{{H}}_1\) and \(\mathcal{{H}}_2\) scenarios respectively. Inner and outer contours respectively enclose \(68\%\) and \(98\%\) Bayesian credibility regions of the posteriors. The blue/dotted contour lines on the left- and right-hand side plots show respectively the XENON1T [121] and PICO-2L [124] which represents the most constraining of the CDM direct detection limits used. The XENONnT and PICO-500 black/dotted contours show possible sensitivity of future upgrades of the experiments. The posterior distributions of the neutralino relic densities for each of the three pNMSSM scenarios are shown on the last plot (3rd-row). The dashed/green, dash-dotted/red and solid/black lines respectively represent the \(\mathcal{H}_0\), \(\mathcal{H}_1\) and \(\mathcal{H}_2\) scenarios. For parameter points with relic densities (in logarithmic scale) to the left of the mark near \(-1.0\), the direct detection constraints were rescaled to account for the neutralino dark matter under-production

Full size image
Fig. 5
figure 5

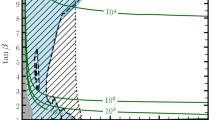
Marginalised posterior distribution for the NMSSM parameters \(\lambda \) and \(\kappa \). The green (H0), red (H1) and black (H2) regions represent the hypotheses \(\mathcal{{H}}_1\), \(\mathcal{{H}}_1\) and \(\mathcal{{H}}_2\), respectively. Inner and outer contours respectively enclose \(68\%\) and \(98\%\) Bayesian credibility regions

Full size image

The second-row of plots in Fig. 4 show the DM direct detection limits used for the global fits. Regions above the contour lines are excluded at 95% C.L.. Possible sensitivity of the experiments’ future upgrades are also shown (XENONnT and PICO-500). These should probe better the pNMSSM parameter space, although the situation depends very much on the neutralino CDM relic density. Under-production of the relic density makes the direct detection limits less constraining. For instance the regions above the blue/dots line in Fig. 4 (first-row left) would have been excluded. They were not excluded because the relic densities at those points are much less than the experimentally measured central value around 0.1 as shown in Fig. 4 (third/last plot).

6 Conclusions

The nested sampling technique [38] implementation in PolyChord [41, 42] has been applied for computing the Bayesian evidence within a 26-parameters pNMSSM. The evidence values are based on limits from collider, astrophysical bounds on dark matter relic density and direct detection cross sections, and low-energy observables such as muon anomalous magnetic moment and flavour physics observables. These were used for comparing between three pNMSSM hypotheses:

  • \(\mathcal{H}_0\): The scenario for which the observed scalar around \(125 \,\text {GeV}\) is identified as the lightest CP-even Higgs boson, \(h_1\). \(m_{h_1}\) were allowed according to a Gaussian distribution with \(3 \,\text {GeV}\) standard deviation.

  • \(\mathcal{H}_1\): This is the same as \(\mathcal{H}_0\) but with the restriction that \(m_{h_2}\) be within 122–\(128 \,\text {GeV}\).

  • \(\mathcal{H}_2\): The scenario for which the observed scalar around \(125 \,\text {GeV}\) is identified as the second lightest Higgs boson, \(h_2\).

Using the Jeffreys’ scale for interpreting the evidence values (see Table 1), the analyses indicate that \(\mathcal{H}_2\) could be considered as being ranked first, with a Moderate support, amongst the three hypotheses. \(\mathcal{H}_0\) and \(\mathcal{H}_1\) can be considered as ranked second at the same time. That is, the current data used for the Bayesian comparisons favours the hypothesis with the possibility of having an additional but much lighter (than \(125 \,\text {GeV}\)) scalar. The lightest scalar within \(\mathcal{H}_2\) turned out to have mass distribution centred below the W-boson mass as shown in Fig. 1. Due to the “sharing of couplings” effect, \(h_2\) is SM-like while \(h_1\) is dominantly singlet-like.

From the posterior distributions presented, pNMSSM benchmark points could be constructed for further analyses with regards to non SM-like Higgs bosons. For instance, consider the two-dimensional posterior distribution on the (\(\lambda \), \(\kappa \)) plane shown in Fig. 5. For the \(\mathcal{H}_2\) hypothesis, the plane is well constrained and approximately reduced to a line. The model points along the line could be excellent benchmarks for testing non-SM Higgs scenarios.

Other possible directions for further investigations can be described as follows. In this article, the composition of the LSP was not fixed. The only requirement was that the relic density and the elastic cross section with nucleons be within the experimentally allowed range. One can go beyond this by demanding, a priori, a particular LSP composition. That is, one could require, in addition to what the masses of the light CP-even Higgs bosons could be, that only a specific LSP composition be allowed during the pNMSSM parameter space explorations. Next, there are experimental measurements which could possibly probe, in a better way, the pseudo-degenerate Higgs scenario. These include the precise determination of the Higgs boson’s total decay width. An update of the analyses presented here to include these ideas could shed more light about the pseudo-degenerate Higgs scenario.

There are caveats within our analyses. One is concerning the uncertainty of the Higgs mass prediction. Here we have used the traditional, and possibly too optimistic uncertainty of \(3 \,\text {GeV}\). A more careful analysis and systematic treatment of the uncertainties, see e.g. [168, 169], could significantly impact the Bayesian evidence values. This is also the case should naturalness priors be used for the analyses. In [37], it was shown that imposing naturalness requirements significantly affect the evidence. The correlations among the various observables were not included. Whenever available, the inclusion of correlations could possibly alter the pNMSSM posteriors. For instance, the measurements of the Higgs boson mass and couplings could come from a single experiment and therefore likely to be correlated. Finally, the inclusion of SUSY limits, such as in SmodelS, during the fits and using logarithmic priors should lead to more robust conclusions about the pNMSSM.