1 Introduction

Since the seminal work by Hawking and Bekenstein on the radiation of black holes, the exploration of thermodynamic properties of black holes has received a wide range of attention [1,2,3] and also acquired great progress [4,5,6,7]. Of more particular interest is the thermodynamics of anti-de Sitter (AdS) black holes [8, 9] where the AdS/CFT duality plays a pivotal role in recent developments of theoretical physics [10, 11]. In the context of AdS/CFT correspondence [12,13,14], the Hawking–Page phase transition [15] of five-dimensional AdS black holes can be explained as the phenomenon of the confinement/deconfinement transition in the four-dimensional Yang–Mills gauge field theory [16]. Another archetypal example of the AdS/CFT correspondence is the holographic superconductor, which can be regarded as the scalar field condensation around a four-dimensional charged AdS black hole [17].

With the cosmological constant \(\Lambda \) being treated as a thermodynamic pressure variable [18,19,20,21,22,23] and its conjugate variable being considered as the thermodynamic volume, the thermodynamics in the extended phase space has been getting more and more attentions. In this paradigm, the mass of black holes is identified as the enthalpy rather than the internal energy. This idea has also been applied to other known parameters, such as the Born–Infeld parameter [24, 25], the Gauss–Bonnet coupling constant [26], the noncommutative parameter [27], and the Horndeski non-minimal kinetic coupling strength [28], etc. All the parameters just mentioned can be regarded as a kind of thermodynamic pressure. Furthermore, there exists a similar situation in the exploration of charged AdS hairy black holes [29] of Einstein–Maxwell theory conformally coupled to a scalar field in five dimensions. The model’s action has been given by [30,31,32,33]

$$\begin{aligned} I=\frac{1}{\kappa }\int \text {d}^5 x\sqrt{-g}\left( R-2\Lambda -\frac{1}{4} F^2+\kappa {L}_{m}(\phi , \nabla \phi )\right) ,\nonumber \\ \end{aligned}$$
(1.1)

where \(\kappa = 16\pi \), R is the scalar curvature, F the electromagnetic field strength, \(g_{\mu \nu }\) the metric with mostly plus signatures, and \(g=\text {det}(g_{\mu \nu })\). In addition, the Lagrangian matter \({L}_{m}(\phi , \nabla \phi )\) takes the following form in five dimensions:

$$\begin{aligned} L_{m}(\phi , \nabla \phi )= & {} b_0 \phi ^{15}+b_1 \phi ^7 {S_{\mu \nu }}^{\mu \nu }+b_2\phi ^{-1}({S_{\mu \lambda }}^{\mu \lambda } {S_{\nu \delta }}^{\nu \delta }\nonumber \\&-\,4{S_{\mu \lambda }}^{\nu \lambda }{S_{\nu \delta }}^{\mu \delta }+ {S_{\mu \nu }}^{\lambda \delta }{S^{\nu \mu }}_{\lambda \delta }), \end{aligned}$$
(1.2)

where \(b_0\), \(b_1\), and \(b_2\) are coupling constants and the four-rank tensor

$$\begin{aligned} {S_{\mu \nu }}^{\lambda \delta }= & {} \phi ^2{R_{\mu \nu }}^{\lambda \delta } -12\delta _{[\mu }^{[\lambda }\delta _{\nu ]}^{\delta ]}\nabla _{\rho }\phi \nabla ^{\rho }\phi \nonumber \\&-\,48\phi \delta _{[\mu }^{[\lambda }\nabla _{\nu ]} \nabla ^{\delta ]}\phi +18\delta _{[\mu }^{[\lambda }\nabla _{\nu ]}\phi \nabla ^{\delta ]}\phi \end{aligned}$$
(1.3)

has been shown [31,32,33,34] to transform covariantly, \({S_{\mu \nu }}^{\lambda \delta }\rightarrow \Omega ^{-8/3}{S_{\mu \nu }}^{\lambda \delta }\), under the Weyl transformation, \(g_{\mu \nu }\rightarrow \Omega ^2 g_{\mu \nu }\) and \(\phi \rightarrow \Omega ^{-1/3}\phi \).

In fact, one can see that the above model is the most general scalar field/gravity coupling formulation whose field equations are of second order for both gravity and matter. Hence, we can say that this formulation is a generalization of the Horndeski theory [35] whose action contains a non-minimal kinetic coupling of a massless real scalar field and the Einstein tensor. Even more importantly, being a simple and tractable model, it provides a significant advantage for studying the phase transition of hairy black holes on the AdS spacetime where the back-reaction of the scalar field on the metric can be solved analytically in five dimensions. In the paradigm where there exists a complete physical analogy between the four-dimensional Reissner–Nordström AdS black hole and the real van der Waals fluid [20] in the phase transition, the recent research [29] shows that this charged AdS hairy black hole also exhibits the van der Waals-type thermodynamic behavior; moreover, such a black hole undergoes a reentrant phase transition which usually occurs in higher curvature gravity theory. We note that all the interesting results just mentioned are available by making the coupling parameter dynamical, i.e. treating the coupling parameter as a certain thermodynamic variable.

Based on the results pointed out above, we take advantage of the well-established Maxwell equal area law [36,37,38,39,40,41] to make a further investigation of the van der Waals-type phase transition, of the co-existence curve, and of the \(P{-}V\) critical phenomenon for this charged AdS hairy black hole. We give analytically the critical values of the charged hairy black hole and show in detail the behavior of the phase transition from a small black hole to a large one. We also give the distribution of the critical points in the parameter space of q (the coupling constant of the scalar field) and e (the electric charge of the black hole), and we obtain for the uncharged case the fitting formula of the co-existence curve. More importantly, we analyze the validity and invalidity of the Maxwell equal area law for the five-dimensional charged AdS hairy black hole and determine the conditions for the law to hold. Meanwhile, the latent heat is calculated, which gives the energy released or absorbed between the small and large black hole phases in the isothermal–isobaric procedure.

The paper is organized as follows. In Sect. 2, we review the analytic solution of the charged AdS hairy black hole in \(D=5\) dimensions and some relevant thermodynamic quantities. In Sect. 3, we calculate the \(P{-}V\) critical values and investigate the Maxwell equal area law for this five-dimensional charged AdS hairy black hole. This section contains two subsections, which correspond to the scenarios without and with charges, respectively. Finally, Sect. 4 is devoted to drawing our conclusion.

2 Analytic solution in \(D=5\) dimensions

The model described by Eqs. (1.1) and (1.2) admits [29, 32] an exactly electrically charged solution in five dimensions,

$$\begin{aligned} \text {d}s^2=-f \text {d}t^2+\frac{\text {d}r^2}{f}+r^2 \text {d}\Omega ^2_{3(k)}, \end{aligned}$$
(2.1)

where the function f takes the form

$$\begin{aligned} f(r)=k-\frac{m}{r^2}-\frac{q}{r^3}+\frac{e^2}{r^4}+\frac{r^2}{l^2}, \end{aligned}$$
(2.2)

\(\text {d}\Omega ^2_{3(k)}\) is the metric of the three-dimensional surface with a constant curvature, the curvature is positive for \(k=1\), zero for \(k=0\), and negative for \(k=-1\), and m and e are two integration constants corresponding to the mass and the electric charge of the black hole, respectively. Here the parameter l represents the curvature radius of the AdS spacetime, which is associated with the cosmological constant \(\Lambda \), whose role is analogous to the thermodynamic pressure,

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }=\frac{3}{4\pi l^2}. \end{aligned}$$
(2.3)

Moreover, the parameter q is characterized as the coupling constant of the scalar field,

$$\begin{aligned} q=\frac{64\pi }{5}\varepsilon k b_1\left( -\frac{18kb_1}{5b_0}\right) ^{3/2}, \end{aligned}$$
(2.4)

where \(\varepsilon =-1,0,1\) and there exists an additional constraint: \(10b_0 b_2=9b_1^2\), to ensure the existence of this black hole solution. These conditions imply that q only takes values \(0, \pm |q|\). Meanwhile, the scalar field configuration takes the form

$$\begin{aligned} \phi (r)=\frac{n}{r^{1/3}}, \quad n=\varepsilon \left( -\frac{18kb_1}{5b_0}\right) ^{1/6}, \end{aligned}$$
(2.5)

and the Maxwell gauge potential reads

$$\begin{aligned} A=\frac{\sqrt{3}e}{r^2}, \end{aligned}$$
(2.6)

where the field strength still takes the standard form: \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\).

The location of this hairy black hole horizon is denoted by \(r_h\), which is taken to be the largest real positive root of \(f(r)=0\). That is, the horizon radius \(r_h\) satisfies the following polynomial equation [32]:

$$\begin{aligned} r_h^6+k l^2 r_h^4-ml^2 r_h^2-ql^2 r_h+e^2 l^2=0. \end{aligned}$$
(2.7)

For the horizon thermodynamic properties of this hairy black hole, some thermodynamic quantities have been calculated in Refs. [29, 32] and are listed below for later use. The thermodynamic enthalpy M, temperature T, entropy S, and charge Q take the following forms:

$$\begin{aligned} M= & {} \frac{3\omega _{3(k)}}{16\pi }m=\frac{3\omega _{3(k)}}{16\pi }\left( kr_h^2-\frac{q}{r_h}+\frac{e^2}{r_h^2}+\frac{r_h^4}{l^2}\right) , \end{aligned}$$
(2.8)
$$\begin{aligned} T= & {} \frac{k}{2\pi r_h}+\frac{q}{4\pi r_h^4}-\frac{e^2}{2\pi r_h^5}+\frac{r_h}{\pi l^2}, \end{aligned}$$
(2.9)
$$\begin{aligned} S= & {} \frac{\omega _{3(k)}}{4}\left( r_h^3-\frac{5}{2}q\right) , \end{aligned}$$
(2.10)
$$\begin{aligned} Q= & {} -\frac{\omega _{3(k)}\sqrt{3}}{16\pi }e, \end{aligned}$$
(2.11)

where \(\omega _{3(k)}\) denotes the area of the compact three-dimensional manifold with the metric \({\text{ d }}\Omega ^2_{3(k)}\). In order to develop the first law and the Smarr relation, the coupling parameter is dealt with [29] as a dynamical variable, which means that q is extended to be a continuous and real parameter. Thus, q should appear in the Smarr relation and its variation should be included in the first law of thermodynamics to make the first law of black hole thermodynamics be consistent with the Smarr relation.

Overall, the extended first law of thermodynamics can be written in terms of the thermodynamic quantities mentioned above as follows:

$$\begin{aligned} \text {d}M=T \text {d}S+V\text {d}P+\Phi \text {d}Q+K \text {d}q, \end{aligned}$$
(2.12)

where the thermodynamic volume V, the electric potential \(\Phi \), and the extensive variable K conjugate to the coupling parameter q have the forms

$$\begin{aligned} V\equiv \left( \frac{\partial M}{\partial P}\right) _{S,Q,q}= & {} \frac{\omega _{3(k)}}{4}r_h^4, \end{aligned}$$
(2.13)
$$\begin{aligned} \Phi \equiv \left( \frac{\partial M}{\partial Q}\right) _{S,P,q}= & {} -\frac{2\sqrt{3}}{r_h^2}e, \end{aligned}$$
(2.14)
$$\begin{aligned} K\equiv \left( \frac{\partial M}{\partial q}\right) _{S,P,Q}= & {} \frac{\omega _{3(k)}}{32 l^2 r_h^5}[20r_h^6+2r_h^4 l^2(5k-3)\nonumber \\&+\,5qr_h l^2-10e^2 l^2]. \end{aligned}$$
(2.15)

Correspondingly, the extended Smarr relation can be deduced [29],

$$\begin{aligned} 2M=3T S-2PV+2\Phi Q+3qK. \end{aligned}$$
(2.16)

Meanwhile, the Gibbs free energy and the equation of state for this hairy black hole can be written in terms of Eqs. (2.8)–(2.10) as follows:

$$\begin{aligned}&G\equiv M-TS \nonumber \\&=\frac{\omega _{3(k)}}{16\pi }\left\{ kr_h^2-\frac{r_h^4}{l^2}+\frac{5q^2}{2r_h^4} \left( \frac{10r_h}{l^2}+\frac{5k-4}{r_h}\right) q\right. \nonumber \\&\left. +\left( \frac{5}{r_h^2}-\frac{5q}{r_h^5}\right) e^2\right\} , \end{aligned}$$
(2.17)
$$\begin{aligned}&P(r_h, T)=\frac{3T}{4r_h}-\frac{3k}{8\pi r_h^2}-\frac{3q}{16\pi r_h^5}+\frac{3e^2}{8\pi r_h^6}. \end{aligned}$$
(2.18)

Next, we shall discuss the Maxwell equal area law for this hairy black hole in order to investigate its critical behavior and the co-existence curve of two phases resorting to Eqs. (2.13) and (2.18) in the (P, V) plane. Note that, in the planar case, i.e. \(k=0\), according to Eq. (2.4), we see \(q=0\). It implies that there are no hairs. In addition, for the hyperbolic case, i.e. \(k=-1\), there are no physically critical values as pointed out in Ref. [29]. Hence, we shall focus only on the spherical case, i.e. \(k=1\), in the following context.

3 Maxwell equal area law

The thermodynamic behavior of black holes in the AdS background is analogous to that of the real van der Waals fluid. As was known, the critical behavior of the van der Waals fluid occurs at the critical isotherm \(T=T_c\) when the \(P{-}V\) diagram has an inflection point,

$$\begin{aligned} \frac{\partial P}{\partial r_h}=0,\quad \frac{\partial ^2 P}{\partial r_h^2}=0. \end{aligned}$$
(3.1)

When \(T<T_c\), there is an oscillating part in the \(P{-}V\) diagram. We have to replace this oscillating part by an isobar in order to describe it in such a way that the areas above and below the isobar are equal to each other. This treatment is based on the Maxwell equal area law. Thus, by making an analogy between the black hole in the AdS background and the real van der Waals fluid, we find that there also exists an oscillating part below the critical temperature \(T_c\) in the \(P{-}V\) diagram, which indicates that the first order phase transition occurs from a small black hole to a large one. This isobar, which satisfies the Maxwell equal area law, represents the co-existence curve of small and large black holes [41].

Normally, the Maxwell equal area law is constructed in the (P, V) plane for a constant temperature, and it can also be made in the (T, S) or \((\Phi , Q)\) plane. These constructions are equivalent. Theoretically, the law can be established from the variation of the Gibbs free energy defined by Eq. (2.17),

$$\begin{aligned} \text {d} G=\text {d} M-T \text {d}S-S \text {d}T. \end{aligned}$$
(3.2)

On resorting to the first law of thermodynamics (2.12) and keeping in mind that the co-existing phases have the same Gibbs free energy, one thus arrives at the Maxwell equal area law in the (P, V) plane by integrating Eq. (3.2) at constant T, Q, and q,

$$\begin{aligned}&P(r_1, T)=P(r_2, T)=P^{*},\nonumber \\&P^{*}\cdot (V_2-V_1)=\int _{r_1}^{r_2}P(r_h, T)\,\text {d}V, \end{aligned}$$
(3.3)

where \(P^{*}\) stands for an isobar, and \(V_1\) and \(V_2\) denote the thermodynamic volume defined by Eq. (2.13) for the small and large black holes with the horizon radii \(r_1\) and \(r_2\), respectively. Thanks to the Maxwell equal area law Eq. (3.3), we also obtain the latent heat which represents the amount of energy released or absorbed from one phase to the other in the isothermal–isobaric condition,

$$\begin{aligned} L=T[S_2-S_1], \end{aligned}$$
(3.4)

where \(S_1\) and \(S_2\) denote the entropy defined by Eq. (2.10) for the small and large black holes with the horizon radii \(r_1\) and \(r_2\), respectively. It is worth mentioning that the co-existence curve of the two phases, i.e. the small and large black holes that are described by an isobar in the Maxwell equal area law, is governed by the Clausius–Clapeyron equation,

$$\begin{aligned} \left( \frac{\text {d}P}{\text {d}T}\right) _{Q,q}=\frac{S_2-S_1}{V_2-V_1}. \end{aligned}$$
(3.5)

In the following we specialize to the Maxwell equal area law, the critical values, and the co-existing phases for this AdS hairy black hole.

3.1 Uncharged case: \(e=0\)

For this hairy black hole with the spherical symmetry in the absence of a Maxwell field, according to Eqs. (2.18) and (2.17), we see that the equation of state reduces to

$$\begin{aligned} P(r_h, T)=\frac{3T}{4r_h}-\frac{3}{8\pi r_h^2}-\frac{3q}{16\pi r_h^5}, \end{aligned}$$
(3.6)

and that the Gibbs free energy becomesFootnote 1

$$\begin{aligned} G=\frac{\pi }{8}\left\{ r_h^2-\frac{r_h^4}{l^2}+\frac{5q^2}{2r_h^4}+\left( \frac{10r_h}{l^2}+\frac{1}{r_h}\right) q\right\} . \end{aligned}$$
(3.7)

3.1.1 Critical values

The critical values defined by Eq. (3.1) have been obtained in Ref. [29],

$$\begin{aligned} r_c= & {} (-5q)^{1/3}, \nonumber \\ T_c= & {} -\frac{3}{20}\cdot \frac{(-5q)^{2/3}}{\pi q}, \nonumber \\ P_c= & {} \frac{9}{200\pi }\left( -\frac{\sqrt{5}}{q}\right) ^{2/3}, \end{aligned}$$
(3.8)

which exist only for \(q<0\), and the relevant ratio reads

$$\begin{aligned} \frac{P_c r_c}{T_c}=\frac{3}{10}. \end{aligned}$$
(3.9)

We observe that this ratio is a constant that does not depend on the parameter q, and that it is different from that of the real van der Waals fluid or the five-dimensional Reissner–Nordström AdS black hole [20].

3.1.2 Maxwell equal area law

Inserting Eqs. (3.6) and (2.13) into Eq. (3.3), we giveFootnote 2 the Maxwell equal area law,

$$\begin{aligned}&2r_1^3 r_2^3 (r_1+r_2)+q[(r_1+r_2)^4+4r_1^2 r_2^2]=0, \nonumber \\&4\pi T r_1^3 r_2^3(r_1^2+r_1 r_2+r_2^2)+3q[(r_1+r_2)^4-r_1^2 r_2^2]=0.\nonumber \\ \end{aligned}$$
(3.10)

When taking the critical limit \(r_1=r_2=r_c\), we see that Eq. (3.10) turns back to Eq. (3.8). Moreover, with the help of Eqs. (2.10) and (3.10) we obtain the latent heat L between the small and large black hole phases,

$$\begin{aligned} L=\frac{\pi ^2 T}{2}(r_2^3-r_1^3). \end{aligned}$$
(3.11)
Fig. 1
figure 1

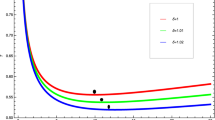
\(P{-}V\) diagrams described by Eqs. (3.6) and (2.13) and \(P{-}G\) diagram described by Eq. (3.7) at \(q=-2\). Left The temperature takes the values of \(T=0.12000\) (black), \(T=T_c=0.11081\) (blue dotted), \(T=0.09500\) (orange), \(T=0.07520\) (purple), and \(T=0.05500\) (green), respectively. Middle The temperature takes the value of \(T=0.11000\), and for the isobar \(P^{*}=0.01515\), \(V_1\) and \(V_2\) correspond to \(r_1=1.94812\) and \(r_2=2.40186\), respectively. Corresponding to the middle diagram, the Gibbs free energy is depicted in the right diagram, showing the characteristic swallowtail behavior

Full size image

In order to highlight the outstanding thermodynamic properties of the uncharged case, the numerical calculations as regards the Maxwell equal area law, Eq. (3.10), in the (P, V) plane, are displayed in Table 1, meanwhile the \(P{-}V\) critical behavior and the Gibbs free energy described by Eqs. (3.6), (3.7), and (2.13) are portrayed in Fig. 1 for the specific value of \(q=-2\). From Table 1, we see clearly that the horizon radii of the small and large black holes, \(r_1\) and \(r_2\), shrink into the critical horizon radius \(r_c=2.15443\) when the isotherm condition \(T=T_c=0.11081\) is taken. It implies that no phase transitions occur and correspondingly the latent heat L is of course equal to zero. At this moment, the isobar \(P^{*}\) becomes the critical pressure \(P_c=0.01543\). With gradually decreasing of the temperature T from the critical value \(T_c=0.11081\), it is clear that \(r_1\) decreases while \(r_2\) increases, and the Maxwell equal area law is always valid. Furthermore, the small black hole with the radius \(r_1\) and the large one with the radius \(r_2\) have the same Gibbs free energy, where the values of the Gibbs free energy are listed in the fifth column of Table 1. Quantitatively, the latent heat L between the two phases takes a sharp increase with the temperature decreasing. Qualitatively, our analysis is given below. As we have known, \(r_1\) decreases while \(r_2\) increases when T decreases. Combining Eq. (3.10) with Eq. (3.11), we get \(L \sim \frac{3\pi }{4}r_2^2\) when T is decreasing. Due to \(r_2\) increasing, the latent heat L increases in the quadratic form of \(r_2\). As a result, the qualitative analysis coincides with the quantitative one shown in Table 1.

Table 1 The numerical results of the Maxwell equal area law Eqs. (3.3) and (3.10), the Gibbs free energy Eq. (3.7), and the latent heat Eq. (3.11) for the hairy black hole with the spherical symmetry in the absence of a Maxwell field
Full size table
Fig. 2
figure 2

Left The co-existence curve for the five-dimensional AdS hairy black hole without charges, the blue points for the numerical values, and the red solid curve for the fitting formula. Right The co-existence curve in the parameter q space. Each blue dotted curve indicates a co-existence curve at a fixed q and the red curve at the boundary corresponds to the critical points

Full size image

Next, we take a close look at Fig. 1 which portrays the critical behavior of the uncharged case. The left diagram demonstrates the representative \(P{-}V\) critical curves. When the temperature T exceeds the critical temperature \(T_c\), see the black curve, there is no criticality at all. The middle diagram illustrates the typical equal area law, where we indeed observe a van der Waals-type oscillation shown in the red curve. By analogy with the real van der Waals fluid, this oscillating part must be replaced by an isobar in the \(P{-}V\) diagram. Adopting the Maxwell equal area law, i.e., the areas of the regions surrounded by an oscillation (red dashed curve) and an isobar (black solid line) are equal to each other, we find this isobar \(P^{*}\) and correspondingly the thermodynamic volumes \(V_1\) and \(V_2\). In other words, the phase transition from the small black hole to the large one occurs in this situation, and these two types of black holes have the same Gibbs free energy, displayed by the crossing point A in the right diagram.

With the aid of the Clausius–Clapeyron equation Eq. (3.5) and the Maxwell equal area law Eq. (3.3), we obtain the co-existence curve of two phases. Considering that the co-existence curve for the real van der Waals fluid has a positive slope everywhere and terminates at the critical point, we try to fit it using a polynomial. Thanks to the simple forms of the critical point Eq. (3.8), such a treatment can be realized. By introducing the reduced parameters,

$$\begin{aligned} t\equiv \frac{T}{T_c},\quad p\equiv \frac{P}{P_c}, \end{aligned}$$
(3.12)

we eventually obtain the parametrization form of the co-existence curve,

$$\begin{aligned} p= & {} 0.828355 t^2+0.096202 t^3-0.558203 t^4\nonumber \\&+\,2.43626 t^5-4.74242 t^6 +5.05509 t^7-2.53495 t^8\nonumber \\&+\,0.241581 t^9+0.178083 t^{10}, \end{aligned}$$
(3.13)

where \(t\in (0,1)\). Then we plot the numerical values governed by the Clausius–Clapeyron equation Eq. (3.5) and the Maxwell equal area law Eq. (3.3), and also plot the fitting formula Eq. (3.13) of the co-existence curve of the small and large black holes in Fig. 2. We can see clearly that the numerical values and the fitting formula match well with each other. Both of them terminate at the critical point, i.e. the point C(1, 1). With the increasing of q, the critical values, see Eq. (3.8), take an increasing trend shown in the right diagram of Fig. 2.

At last, we make a brief summary of this subsection. For the AdS hairy black hole with the spherical symmetry in the absence of a Maxwell field, the \(P{-}V\) critical behavior is available only under the condition of \(q<0\), and the Maxwell equal area law always holds under this condition. Meanwhile, we take the specific value of \(q=-2\) as an example to highlight the salient features of this black hole in Table 1 and Fig. 1. Furthermore, because the critical point Eq. (3.8) has a simple form, we obtain the fitting formula (3.13) of the co-existence curve; see Fig. 2 for the illustration. As to the charged case, it shows complications, as exhibited in the following subsection.

3.2 Charged case: \(e\ne 0\)

For the spherically symmetric AdS hairy black hole with the Maxwell field, the equation of state takes the form

$$\begin{aligned} P(r_h, T)=\frac{3T}{4r_h}-\frac{3}{8\pi r_h^2}-\frac{3q}{16\pi r_h^5}+\frac{3e^2}{8\pi r_h^6}, \end{aligned}$$
(3.14)

and the Gibbs free energy reads

$$\begin{aligned} G= & {} \frac{\pi }{8}\left\{ r_h^2-\frac{r_h^4}{l^2}+\frac{5q^2}{2r_h^4}+ \left( \frac{10r_h}{l^2}+\frac{1}{r_h}\right) q\right. \nonumber \\&\left. +\left( \frac{5}{r_h^2}-\frac{5q}{r_h^5}\right) e^2\right\} . \end{aligned}$$
(3.15)

3.2.1 Critical values

Substituting Eq. (3.14) into Eq. (3.1), we obtain the critical radius, which satisfies the following equation:

$$\begin{aligned} r_c^4+5q r_c-15e^2=0, \end{aligned}$$
(3.16)

and derive the critical temperature,

$$\begin{aligned} T_c=\frac{3(16e^2-5q r_c)}{4\pi r_c^5}, \end{aligned}$$
(3.17)

and the critical pressure,

$$\begin{aligned} P_c=\frac{3(10e^2-3q r_c)}{8\pi r_c^6}. \end{aligned}$$
(3.18)

Then, using Eqs. (3.16)–(3.18), we give the ratio of three critical values,

$$\begin{aligned} \frac{P_c r_c}{T_c}=\frac{10e^2-3q r_c}{2(16e^2-5qr_c)}, \end{aligned}$$
(3.19)

which leads us back to Eq. (3.9), i.e. the uncharged case, when \(e=0\). Moreover, if \(q=0\), this ratio equals 5 / 16, which coincides with the ratio of the five-dimensional Reissner–Nordström AdS black hole [20]. Nonetheless, this ratio depends in general on the values of the parameters e and q.

Let us try to solve Eq. (3.16). At first, we set \(w(r_c)\equiv r_c^4+5q r_c-15e^2\) and take a look at its asymptotic behavior. When \(r_c \rightarrow 0\), we get a negative value, \(w(r_c)\rightarrow -15e^2\). When \(r_c \rightarrow +\infty \), we see \(w(r_c)\rightarrow +\infty \). In addition, we notice that for \(q>0\) the function \(w(r_c)\) is monotone increasing at the interval \([0, +\infty )\), and for \(q<0\) it is monotone increasing at the interval \([(-5q/4)^{1/3}, +\infty )\) but monotone decreasing at the interval \([0,(-5q/4)^{1/3}]\). Hence, we conclude that the equation \(w(r_c)=0\) must have one and only one positive root,Footnote 3

$$\begin{aligned} r_c=\frac{1}{2}\left\{ \left( \frac{10|q|}{\sqrt{t_c}}-t_c\right) ^{1/2}\pm \sqrt{t_c}\right\} , \end{aligned}$$
(3.20)

where the plus sign corresponds to the case of \(q<0\) and the minus sign to the case of \(q>0\), and the newly introduced parameter \(t_c\) is defined as

$$\begin{aligned} t_c \equiv 4\sqrt{5}e \sinh \left\{ \frac{1}{3} \sinh ^{-1}\left( \frac{\sqrt{5} q^2}{16e^3}\right) \right\} . \end{aligned}$$

3.2.2 Maxwell equal area law

Substituting Eqs. (3.14) and (2.13) into Eq. (3.3), we giveFootnote 4 the Maxwell equal area law,

$$\begin{aligned}&2r_1^4 r_2^4 (r_1+r_2)+qr_1 r_2[(r_1+r_2)^4+4r_1^2 r_2^2]\nonumber \\&\quad -\,2e^2[(r_1+r_2)^5-r_1r_2(r_1^3+r_2^3)]=0,\nonumber \\&4\pi T r_1^4 r_2^4(r_1^2+r_1 r_2+r_2^2)+3qr_1 r_2[(r_1+r_2)^4-r_1^2r_2^2]\nonumber \\&\quad -\,6e^2(r_1+r_2)^3(r_1^2+r_1 r_2+r_2^2)=0. \end{aligned}$$
(3.21)

If \(e=0\), i.e. for the uncharged case, the above set of equations turns back to Eq. (3.10). When taking the critical limit, \(r_1=r_2=r_c\), we see that Eq. (3.21) reduces to Eqs. (3.16) and (3.17), that is, it coincides with the critical behavior. It is remarkable for the charged case that the entropy defined by Eq. (2.10) probably becomes negative in the case of \(q>0\), which brings about an extra constraint on the \(P{-}V\) criticality and the equal area law.

3.2.3 The case of \(q<0\)

In this situation, the entropy of the hairy black hole with the Maxwell field, Eq. (2.10), is always positive. There are no additional restrictive conditions for investigating the Maxwell equal area law and the phase transition. The treatment is the same as that of the scenario without charges. We can directly write down the condition under which the van der Waals-type phase transition exists and the Maxwell equal area law holds, i.e., the temperature takes the values \(T <T_c\), where \(T_c\) is given by Eq. (3.17) together with the constraint \(q<0\).

Table 2 displays the numerical results of the Maxwell equal area law (Eq. (3.21)), and Fig. 3 depicts the critical behavior of the equation of state (Eqs. (3.14) and (2.13)) and the Gibbs free energy (Eq. (3.15)) for an example of the charged hairy black hole at \(q=-2\) and \(e=2\). We can see a similar critical behavior to that of the uncharged case. When \(T>T_c\), there is no criticality; when \(T <T_c\), there exists a representative van der Waals-type oscillation in the \(P{-}V\) diagram. By using the Maxwell equal area law and replacing the oscillating part by an isobar, we observe the phase transition from the small black hole to the large one in the middle diagram of Fig. 3, and find that the two phases have the same Gibbs free energy displayed by the crossing point A in the right diagram. Moreover, when T is decreasing, the horizon radius of the small black hole, \(r_1\), decreases while that of the large black hole, \(r_2\), increases, and the latent heat L between the two phases presents a sharp increasing tendency. This observation means that the phase transition needs more energy at the lower temperature of the isothermal–isobaric procedure.

Table 2 The numerical results of the Maxwell equal area law Eqs. (3.3) and (3.21), the Gibbs free energy Eq. (3.15), and the latent heat Eq. (3.4) for the spherically symmetric AdS hairy black hole with the Maxwell field
Full size table
Fig. 3
figure 3

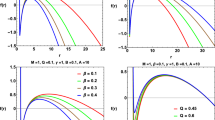
\(P{-}V\) diagrams described by Eqs. (3.14) and (2.13) at \(q=-2\) and \(e=2\). Left The temperature takes the values of \(T=0.08800\) (black), \(T=T_c=0.08072\) (blue dotted), \(T=0.06650\) (orange), \(T=0.05364\) (purple dashed), and \(T=0.04800\) (green), respectively. Middle The temperature takes the value of \(T=0.07520\), and for the isobar \(P^{*}=0.00681\), \(V_1\) and \(V_2\) correspond to \(r_1=2.38204\) and \(r_2=4.32768\), respectively. Corresponding to the middle diagram, the Gibbs free energy described by Eq. (3.15) is depicted in the right diagram, showing the characteristic swallowtail behavior

Full size image
Fig. 4
figure 4

\(P{-}V\) diagrams (Eqs. (3.14) and (2.13)) and the corresponding Gibbs free energy (Eq. (3.15)) at \(q=2\) and \(e=1.5\). Left The temperature takes the value of \(T=0.14000\). For the isobar \(P^{*}=0.02311\), \(V_s\), \(V_1\), and \(V_2\) correspond to \(r_s=1.70998\), \(r_1=1.73921\), and \(r_2=2.20835\), respectively. Note that \(r_1 > r_s\). Right The temperature takes the value of \(T=0.13800\). For the isobar \(P^{*}=0.02237\), \(V_s\), \(V_1\), and \(V_2\) correspond to \(r_s=1.70998\), \(r_1=1.66931\), and \(r_2=2.33574\), respectively. Note that \(r_1 < r_s\)

Full size image

3.2.4 The case of \(q>0\)

In the situation of a positive parameter q, the analysis becomes complicated. Due to the entropy described by Eq. (2.10) being probably negative, we have to impose an extra constraint to the horizon radius,

$$\begin{aligned} r_h \ge r_s \equiv \left( \frac{5q}{2}\right) ^{1/3}. \end{aligned}$$
(3.22)

The purpose is to avoid the negative entropy that appears if \(r_h < r_s\), where the negative entropy is regarded as an unphysical variable at present.

The Maxwell equal area law holds under the condition \(T <T_c\) together with the constraint Eq. (3.22), where \(T_c\) is given by Eq. (3.17) under the condition \(q>0\).

Now we consider an extreme situation, i.e., \(r_c=r_s\), which leads to the critical value of the electric charge,

$$\begin{aligned} |e_s|=\frac{\sqrt{5}}{5}\left( \frac{5q}{2}\right) ^{2/3}=\frac{r_s^2}{\sqrt{5}}. \end{aligned}$$
(3.23)

This critical value (\(r_s\) or \(e_s\)) gives the boundary of violating or maintaining the \(P{-}V\) criticality and the Maxwell equal area law. That is, if \(|e|<|e_s|\), we have \(r_c<r_s\), resulting in the violation of the \(P{-}V\) criticality (Eqs. (3.16)–(3.18)) and of the Maxwell equal area law (Eq. (3.21)); if \(|e|>|e_s|\), we have \(r_c>r_s\), maintaining the validity of the \(P{-}V\) critical values, but we have to add the condition \(r_1>r_s\) in order to establish the Maxwell equal area law. A sample of the latter situation is depicted in Fig. 4 for the specific fixing of \(q=2\) and \(e=1.5\). In this sample, we have \(e>e_s=1.30766\) and figure out \(r_s=1.70998\) and \(r_c=1.94471\). Hence, the validity of the Maxwell equal area law depends on the temperature with the range of \(T <T_c\), where \(T_c=0.14207\). The left two diagrams of Fig. 4 correspond to \(T=0.14000 < T_c=0.14207\), which leads to \(r_1>r_s\) and illustrates the equal area law and the characteristic swallowtail behavior. The red dashed curve corresponds to a negative entropy, which is unphysical, but it does not affect the application for the equal area law and the characteristic swallowtail structure owing to \(r_1>r_s\). On the contrary, if \(r_1<r_s\), see the right two diagrams of Fig. 4, the red dashed curve corresponding to the negative entropy indeed violates the equal area law and the characteristic swallowtail structure. Let us take a close look at this kind of violation. We can still determine the isobar \(P^{*}\) because the initial point at \(r_1\) (or \(V_1\)) and the terminal one at \(r_2\) (or \(V_2\)) are independent of Eq. (3.22). However, when \(T=0.13800\), that brings about \(r_1<r_s\), i.e. the breaking of Eq. (3.22), and we find that the branch of negative entropy terminates at \(r_s\) (or \(V_s\)), which is larger than \(r_1\), which evidently leads to a violation of the Maxwell equal area law and the characteristic swallowtail structure.

Fig. 5
figure 5

The distribution of the critical points described by Eqs. (3.17) and (3.18) for different values of e and q. The left diagram corresponds to \(e=1.90\), 2.05, 2.20, and 2.35, respectively, from top to bottom, the green dotted curve for \(q<0\), the purple dotted curve for \(q>0\), and the red dots for \(q=0\). The middle diagram depicts the case of \(q \ge 0\) with discrete values of \(q=0\) (red), 0.3 (green), 0.6 (blue), and 1.2 (purple), and the right diagram depicts the case of \(q \le 0\) with discrete values of \(q=0\) (red), \(-0.2\) (green), \(-0.3\) (blue), and \(-0.5\) (purple)

Full size image

In addition, we take a look at the co-existence curve governed by the Clausius–Clapeyron equation, Eq. (3.5), and the Maxwell equal area law, Eq. (3.21), for the five-dimensional AdS hairy black hole with charges. As the formulas of the critical values, Eqs. (3.17) and (3.18), are much more complicated than Eq. (3.8), it is hard to give a perfect fitting formula of the co-existence curve of the small and large black holes. Nonetheless, we know through the above analysis that the thermodynamic behavior for the case with charges is the same as that of the case without charges within the scope of validity of the Maxwell equal area law, and that the co-existence curve always has a positive slope and terminates at the critical point. Figure 5 shows the critical points for different values of e and q, from which we see that the critical values \(T_c\) and \(P_c\) show an increasing trend with an increasing q but a fixed e, while they show a decreasing trend with an increasing e but a fixed q.

Before the end of this section, let us take a look at the physical meaning of the appearance of a negative entropy in the charged case with positive q. We illustrate this situation by setting \(q=2\) and \(e=1.5\), where the behavior of the Gibbs free energy (Eq. (3.15)) can be classified into three types, which are shown in Fig. 6 and the lower-left and lower-right diagrams of Fig. 4. We know that the stable black hole is thermodynamically favorable to the lower Gibbs free energy.

Fig. 6
figure 6

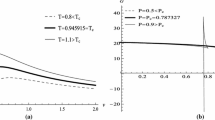
The Gibbs free energy (Eq. (3.15)) at \(q=2\), \(e=1.5\), and \(T=0.13960\). \(P^{*}\) corresponds to the pressure of the intersection (point d), \(P_{t}\) corresponds to the pressure of the cusp (point a), and \(P_{s}\) corresponds to the pressure of point c with zero entropy. The red dashed curve corresponds to the negative entropy. A black arrow indicates an increasing trend of the horizon radius \(r_h\)

Full size image

  • If \(P^{*}<P_s<P_t\), see Fig. 6, one can see that the global minimum of the Gibbs free energy emerges as a discontinuous characteristic due to the negative entropy (see the red dashed curve). More precisely, when \(P_s<P<P_t\), the global minimum is located on the curve \(a\rightarrow b\). When \(P^{*}<P<P_s\), the global minimum is located on the curve \(c\rightarrow d\). When \(P<P^{*}\), the global minimum is located on the curve \(d\rightarrow e\). At \(P=P_s\), the Gibbs free energy has a discontinuous global minimum, which means the occurrence of the zeroth order phase transition as reported in Ref. [29]. At \(P=P^{*}\), the global minimum of the Gibbs free energy has an inflection point, which implies a standard first order small/large black hole phase transition, i.e. a van der Waals-type phase transition, and the Maxwell equal area law holds.

  • If \(P_s > P_t\), see the lower-left diagram of Fig. 4, the global minimum of the Gibbs free energy is continuous and also has an inflection point (corresponding to the pressure \(P^{*}\)), indicating the existence of a van der Waals-type phase transition.

  • If \(P_s< P^{*}\), see the lower-right diagram of Fig. 4, the global minimum of the Gibbs free energy is continuous but has no inflection points, which indicates nonexistence of phase transitions and results in invalidity of the Maxwell equal area law.

All in all, it is the positivity/negativity of the entropy that affects the behavior of the global minimum of the Gibbs free energy. The discontinuity of the Gibbs free energy causes a zeroth order phase transition at the pressure \(P_s\in [P^{*},P_t]\) under a certain temperature. Moreover, if \(P_s<P^{*}\), the disappearance of inflection points leads to the failure of the Maxwell equal area law, so that no real physical isobar exists for phase transitions, as shown in the upper-right diagram of Fig. 4.

4 Conclusion

In this paper, we investigate the \(P{-}V\) criticality, the Maxwell equal area law, and the co-existence curve for the spherically symmetric AdS black hole with a scalar hair [29, 32] both in the absence of and in the presence of a Maxwell field, respectively. Especially in the charged case, we give the exactly analytical \(P{-}V\) critical values; see Eqs. (3.16)–(3.18), and (3.20). Meanwhile, we provide the conditions of validity of the Maxwell equal area law for the hairy black hole without and with charges, respectively. Our results can be summarized as follows:

  • The case of \(q<0\)

    • Scenario without charges: the Maxwell equal area law holds under the conditions \(T<T_c\) and Eq. (3.8).

    • Scenario with charges: the Maxwell equal area law holds under the conditions \(T<T_c\) and Eq. (3.17).

  • The case of \(q>0\)

    • Scenario without charges: the Maxwell equal area law is violated.

    • Scenario with charges: besides the conditions \(T<T_c\) and Eq. (3.17) together with the extra constraint Eq. (3.22), whether the Maxwell equal area law holds or not depends on the charge and the relation between the temperature and the horizon radius, which can be classified into the following two situations:

    • \({*}\) when \(|e|<|e_s|\), the law does not hold.

    • \({*}\) when \(|e|>|e_s|\), the law holds if \(r_1 > r_s\), but fails if \(r_1 < r_s\), where \(r_1\) depends on the temperature T shown in Fig. 4.

Within the scope in which the Maxwell equal area law holds, we point out that there exists a representative van der Waals-type oscillation in the \(P{-}V\) diagram. This oscillating part that indicates the phase transition from a small black hole to a large one can be replaced by an isobar and the small and large black holes have the same Gibbs free energy. These salient features have been illustrated in Tables 1 and 2, and Figs. 1 and 3, from which we conclude that when the temperature T is decreasing, the horizon radius of the small black hole \(r_1\) decreases, while that of the large black hole \(r_2\) increases; moreover, the latent heat L between the two phases presents a sharp increasing tendency. This observation means that the phase transition needs more energy at the lower temperature of the isothermal–isobaric procedure. Furthermore, for the uncharged case we obtain the fitting formula (3.13) of the co-existence curve depicted in Fig. 2 due to the simple form of the critical point equation (3.8). For the charged case, we give the distribution of the critical points described by Eqs. (3.17) and (3.18) in the parameter space of q and e in Fig. 5. Finally, we point out that the positivity/negativity of the entropy has effect on the global minimum of the Gibbs free energy. The inflection point of the Gibbs free energy leads to the van der Waals-type phase transition, but the Maxwell equal area law does not hold and the real physical isobar does not exist for phase transitions if no inflection points exist as shown in Fig. 4. The discontinuity of the Gibbs free energy causes a zeroth order phase transition as shown in Fig. 6.