A Generalized Discrete Morse–Floer Theory

Abstract

Forman has developed a version of discrete Morse theory that can be understood in terms of arrow patterns on a (simplicial, polyhedral or cellular) complex without closed orbits, where each cell may either have no arrows, receive a single arrow from one of its facets, or conversely, send a single arrow into a cell of which it is a facet. By following arrows, one can then construct a natural Floer-type boundary operator. Here, we develop such a construction for arrow patterns where each cell may support several outgoing or incoming arrows (but not both), again in the absence of closed orbits. Our main technical achievement is the construction of a boundary operator that squares to 0 and therefore recovers the homology of the underlying complex.

1 Introduction

Morse theory, introduced by Morse in 1925 [23], is an important tool for the study of the topology of differentiable manifolds. It recovers the homology groups of the manifold from the critical points of a Morse function and the relations between them. The Morse inequalities are inequalities between the Betti numbers (these are the dimensions of the homology groups) of the manifold and the numbers of critical points of fixed indices of the function. To get the homology groups, one attaches a k-dimensional cell for each critical point of index k, and gluing relations between those cells then yield the homological boundary operator. Floer [9] discovered a more direct way to achieve this. He directly constructed the boundary operator from the critical points by counting the gradient lines between critical points with index difference one. Floer’s direct construction of the boundary operator in terms of critical points and gradient lines, without having to invoke the local geometry of the manifold in question, made spectacular applications to symplectic geometry possible. In fact, Floer’s theory needs only index differences, but no absolute indices, and it therefore also applies in certain infinite- dimensional situations, with functionals like the Dirac functional where each critical point would have an infinite index. Floer homology was fully developed in [25]. For a presentation in the context of Riemannian geometry, see also [17].

In a rather different direction, Forman [10] developed a discrete version of Morse theory for CW complexes. This is also the setting of the present paper, and we therefore recall the setting. The topological boundary elements of a cell are called its faces. If a cell $\sigma ^{(k)}$ of dimension k is a face of another cell $\tau$, we write $\sigma < \tau$ if $\,\dim \sigma =\dim \tau -1$, in which case $\sigma$ is called a facet of $\tau$. Further concepts, in particular those of a regular facet, will be defined in Sect. 2.

A discrete Morse function, according to Forman, is a real-valued function defined on the set of cells such that it locally increases in dimension, except possibly in one direction. More formally, we have:

Definition 1.1

(Discrete Morse function) For all cells $\sigma ^{(k)}$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {for all}\,\, \tau \,\,\text {s.t.}\,\,\sigma \,\,\,\text {is an irregular face of}\,\, \tau , \,\,\, f(\sigma )< f(\tau );\\ Un(\sigma ):=\sharp \{\tau ^{(k+1)}\,|\, \sigma \,\,\text {is a regular facet of}\,\, \tau \,\text {and}\, f(\tau ) \le f(\sigma )\} \le 1; \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {for all}\,\, \nu \,\,\text {s.t.}\,\,\nu \,\,\,\text {is an irregular face of}\,\, \sigma , \,\,\, f(\nu )< f(\sigma );\\ Dn(\sigma ):=\sharp \{\nu ^{(k-1)}\,|\, \nu \,\,\text {is a regular facet of}\,\, \sigma \,\text {and}\, f(\nu ) \ge f(\sigma )\} \le 1. \end{array}\right. } \end{aligned}$$

($\sharp A$ is the cardinality of A). The cell $\sigma$ is called critical if it is not a regular facet of some other cell, or in the regular case, if both $Dn(\sigma )$ and $Un(\sigma )$ are 0.

Although the definition works in full generality, here we assume that the underlying CW complex is regular (the definition will be recalled below). In fact, on a regular CW complex, one easily sees that at most one of $Dn(\sigma )$ and $Un(\sigma )$ can be 1; the other then has to be 0.

A pair $\{\sigma ,\tau \}$ with $\sigma <\tau$ and $f(\sigma )\ge f(\tau )$ is called a noncritical pair. If we draw an arrow from $\sigma$ to $\tau$ whenever $\sigma <\tau$ but $f(\sigma )\ge f(\tau )$, then we get a vector field associated with this function, and each noncritical cell has precisely one arrow which is either incoming or outgoing. Therefore, for the Euler number, we only need to count the critical cells with appropriate signs according to their dimensions, since the noncritical cells cancel in pairs. This is illustrated in Fig. 1, where the 0-cells are the nodes, the 1-cells are the edges and the 2-cells are the interiors of triangles. Moreover the noncritical pairs are the pairs of cells between which there is an arrow, while the critical cells are those without arrows.

In [12], a combinatorial vector field on a CW complex $\mathbb {K}$ is defined as follows.

Definition 1.2

A combinatorial vector field on a CW complex $\mathbb {K}$ is a map $V :\mathbb {K}\rightarrow \mathbb {K}\,\cup \, \{ 0\}$ satisfying:

• (i) if $V(\sigma )\ne 0$, then $\dim V(\sigma )\,=\,\dim (\sigma )+1$ and $\sigma < V(\sigma );$

• (ii) if $V(\sigma )\,=\,\tau \ne 0$, then $V(\tau )=0;$

• (iii) for any $\tau$, there is at most one $\sigma$ s.t. $V(\sigma )=\tau$;

• (iv) for each $\sigma$, either $V(\sigma )=0$ or $\sigma$ is a regular face of $V(\sigma )$.

Thus, if we draw an arrow from $\sigma$ to $\tau$ whenever $\tau =V(\sigma )$, one sees that a cell cannot be at the same time the head and the tail of an arrow, and each cell has a unique incoming or outgoing arrow but never both.

We write $\sigma \rightarrow \tau$ to indicate that there is an arrow from $\sigma$ to $\tau$.

In contrast to a general combinatorial vector field, the vector field extracted from a discrete Morse function admits no closed orbits, where by a closed orbit we mean a path of the form

$$\begin{aligned} \sigma _0 \rightarrow \tau _0> \sigma _1 \rightarrow \tau _1> \cdots \sigma _m \rightarrow \tau _m > \sigma _0. \end{aligned}$$

Conversely, one can always construct a discrete Morse function from a combinatorial vector field that admits no closed orbits.

Fig. 1

Vector field of a Morse function

In [11], Forman defined a boundary operator using the vector field generated from this discrete Morse function. See Definition 2.1 for the reformulation for CW complexes. In [12], he developed some discrete analogue of Conley theory for CW complexes. For a combinatorial vector field, as isolated invariant sets, he considers the rest points (which are the critical cells) and the closed orbits. The isolating neighborhoods here are the unions of all the cells in the isolated invariant sets together with those in their boundaries; the exit set is just the collections of cells in the isolating neighborhood that are not in the isolated invariant sets.

Thus, a general picture emerges. Given a combinatorial vector field, satisfying suitable restrictions, one can flow along the arrows to retract the underlying complex onto something simpler or smaller, while preserving the topological information. From that perspective, the restrictions in Forman’s work on the combinatorial vector field are rather strong. Each cell can support at most one arrow, incoming or outgoing. We want to generalize this. What we shall achieve in the present paper is a version of discrete Morse–Floer–Conley theory for vector fields on complexes where each cell may support more than one incoming or outgoing arrow, but still not both types simultaneously. Also, we still exclude closed orbits.

In any case, the construction of the combinatorial flow, that is, of the boundary operator, will be much more difficult, because from a cell, we may have to flow into several directions simultaneously, or conversely, a cell may receive flows from several of its facets.

The motivation behind this is that Conley theory for dynamical systems on manifolds can work with arbitrary flows, more general than the gradient flows derived from a Morse function, to extract the topological invariants of the manifold under consideration. Also, in the smooth setting, Morse–Bott theory is a generalization of Morse theory. In a different direction, there is the Morse theory for not necessarily smooth continuous functions by Corvellec [7].

As already indicated, we shall define a boundary operator from which we can derive the Betti numbers of the CW complex under consideration. We shall also derive some Morse-related inequalities.

More specifically, on a finite CW complex $\mathbb {K}$, in which each cell is given an orientation, we consider arrow configurations of the following type.

Definition 1.3

(Arrow configuration) An arrow configuration assigns to each k-cell $\sigma$ a collection of $(k+1)$-cells that have $\sigma$ as a facet. We draw an arrow from $\sigma$ to each cell in that collection. The cardinality of that collection is denoted by $n_\mathrm{ou}(\sigma )$. Conversely, for each k-cell $\sigma$, we let $n_\mathrm{in}(\sigma )$ be the number of arrows that it receives from its facets. Thus, $n_\mathrm{ou}(\sigma )$ is the number of outgoing arrows of $\sigma$ while $n_\mathrm{in}(\sigma )$ is the number of incoming arrows of $\sigma$.

We require that at most one of $n_\mathrm{ou}(\sigma )$ and $n_\mathrm{in}(\sigma )$ be different from zero and that there should not be any closed orbit.

When $n_\mathrm{in}(\sigma )\ge 2$ (resp. $n_\mathrm{ou}(\sigma )\ge 2$), we say the corresponding cell $\sigma$ is abnormally downward (resp. abnormally upward) noncritical.

We recall that if $\mathbb {K}$ is a CW complex (in which every cell is endowed with an orientation called initial orientation), and R is any principal ideal domain, $C_k(\mathbb {K};R)$ is the free R-module generated by the (oriented) k-cells of $\mathbb {K}$. The cellular boundary operator $\,\partial ^c:C_{k+1}(\mathbb {K};R)\rightarrow C_{k}(\mathbb {K};R)$ is given by

$$\begin{aligned} \partial ^c(\tau ^{(k+1)})=\sum _{\sigma <\tau }[\tau ^{(k+1)}:\sigma ^{(k)}]\sigma ^{(k)}, \end{aligned}$$

where $[\tau :\sigma ]$ is the incidence number of $\tau$ and $\sigma$. That is, the number of times that $\tau$ (along its boundary) is wrapped around $\sigma$. (Taking the induced orientation from $\tau$ onto $\sigma$ into account: for $\sigma$ a regular facet of $\tau$, if the induced orientation on $\sigma$ coincides with the initial orientation of $\sigma$, $[\tau : \sigma ]=+1$; if not, then it is $-1$.)

In order to develop a version of Floer’s theory in this setup, we start with a finite CW complex, in which each cell is given an orientation and whose Betti numbers can be computed using cellular homology. We define a boundary operator, using all the arrows, which is based on some probabilistic and averaging technique. This boundary operator is the composition of some systematically well-defined “flow map” with the cellular boundary operator. We then need to take care of various types of cells that we call defective. These comprise the critical cells, that is, those with no incoming and outgoing arrow; the abnormally downward noncritical cells; the cells having an outgoing arrow pointing to an abnormally downward noncritical cell; the abnormally upward noncritical cells; and the cells having an incoming arrow from an abnormally upward noncritical cell. By carefully handling those defective cells, we shall construct a boundary operator from which we can read off the topological Betti numbers.

In Sect. 2, we state our assumptions and make precise what type of cells we encounter in our framework that were not present in Forman’s framework. We recall Forman’s boundary operator and show that the arrow configuration that we consider is generated by some discrete function. We also observe that we can compute the Euler number of a CW complex using the arrow configuration, but without invoking any boundary operator. The story is different for the Betti numbers, however.

In Sect. 3, we construct our boundary operator and state and prove the main theorems; in particular, that the square of this boundary operator is zero and that we can recover the Betti numbers of the CW complex from it. We obtain some Morse-type inequalities as well.

In Sect. 4, we develop some Conley-type analysis from an arrow configuration as considered in Sect. 3.

2 Notations

Let $\mathbb {K}$ be a finite CW complex in which each cell is endowed with an orientation (called initial orientation). We recall that the topological boundary elements of a cell are called its faces and the co-dimension one faces are called facets. A reference for CW complexes is [26], for instance.

A CW complex consists of cells $\tau$; for each such $\tau$ of dimension p, there is a continuous map $h:B^p \rightarrow \mathbb {K}$ (considered as a topological space) from the closed unit ball $B^p$ of dimension p that maps the interior of $B^p$ homeomorphically onto $\tau$. A facet $\sigma$ of $\tau$ is called regular if $h:h^{-1}(\sigma ) \rightarrow \sigma$ is also a homeomorphism and $\overline{h^{-1}(\sigma )}$ is a closed ball of dimension $p-1$. For a regular CW complex, all faces are regular. The incidence property of regular CW complexes states that if $\nu< \sigma <\tau$ in a regular CW complex, then there exists $\widetilde{\sigma } \ne \sigma$ s.t. $\nu< \widetilde{\sigma }<\tau$. The same holds for CW complexes provided $\nu$ is a regular facet of $\sigma$ and $\sigma$ is a regular facet of $\tau$.

We let f be a discrete Morse function on a finite CW complex $\mathbb {K}$. Then, for a noncritical cell $\sigma$, either

$$\begin{aligned} \sharp \{\,\tau \,> \,\sigma \, | \, f(\tau ) \,\le \,f(\sigma )\,\}=1,\,\, \hbox {in which case we say that} \, \sigma \hbox {is} \, \mathbf{upward~noncritical } \end{aligned}$$

or

$$\begin{aligned} \sharp \{ \nu < \sigma | f(\nu )\, \ge \,f(\sigma )\,\}=1, \,\, \hbox {in which case} \, \sigma \, \hbox {is said to be} \, \mathbf{downward~noncritical }. \end{aligned}$$

Indeed, if $\sigma$ is such that $\nu<\sigma < \tau$ and $f(\nu )\ge f(\sigma )\ge f(\tau )$, then in particular, by Definition 1.1$\nu$ must be a regular facet of $\sigma$ and $\sigma$ is a regular facet of $\tau$. Then, there exists a cell $\widetilde{\sigma }\ne \sigma$, $\,\widetilde{\sigma }< \tau$ s.t. $f(\widetilde{\sigma })<f(\tau )$. Choose $\widetilde{\sigma }$ s.t. $\nu <\widetilde{\sigma }$. This is always possible from the incidence of $\nu$ and $\tau$, as just noted. Then, $f(\nu )< f(\widetilde{\sigma })$, as otherwise the discrete Morse conditions are violated. Hence,

$$\begin{aligned} f(\nu ) \ge f(\sigma ) \ge f(\tau )> f(\widetilde{\sigma }) > f(\nu ), \end{aligned}$$

which is a contradiction. Thus, a cell cannot be downward and upward noncritical at the same time.

We recall that whenever we have a discrete Morse function f, we draw an arrow from $\,\,\sigma \,\,$ to $\,\,\tau \,\,$ if $\,\,\sigma < \tau \,\,$ but $\,\,f(\sigma )\ge f(\tau )$. In this way, we get a vector field. A boundary operator can also be computed using a combinatorial vector field extracted from a discrete Morse function; see [11].

Since not every CW complex is orientable, we look at local orientations: We assume that every cell in $\mathbb {K}$ is endowed with an orientation called its initial orientation. The orientations on the higher dimensional cells will induce orientations on the lower dimensional ones; see [14]. If the induced orientation on a cell coincides with its initial one, the cell will be counted with a $+$ sign; if not, then a − sign. We recall that the incidence number between two critical cells $\tau ^{(k+1)}$ and $\sigma ^{(k)}$, denoted $[\tau :\sigma ]$, is the number of times that $\tau$ is wrapped (along its boundary) around $\sigma$. When orientations are taken into account and $\sigma$ is a regular facet of $\tau$, $[\tau :\sigma ]$ is equal to $+1$ if the induced orientation from $\tau$ to $\sigma$ coincides with the initial orientation of $\sigma$, and is $-1$ otherwise. See [14] for the precise formulation.

Remark 2.1

For a regular CW complex, if a cell $\sigma ^{(k)}$ is a face of another cell $\omega ^{(k+2)}$, then there exist $\tau ^{(k+1)}_1$ and $\tau ^{(k+1)}_2$ s.t. $\sigma<\tau _i<\omega$. Looking at the orientations, see [14], $\omega$ will induce some orientations on $\tau _1$ and $\tau _2$. The orientation on $\tau _1$ (induced from $\omega$) will induce an orientation on $\sigma$ that will be different from the one induced from $\tau _2$. However, when the CW complex is not regular, and $\sigma$ is an irregular facet of $\tau < \omega$), then we cannot induce a consistent orientation on $\sigma$ from $\tau$.

More generally, even if $\sigma$ is not a face of $\omega$, in the regular case, the orientation on $\omega$ will induce an orientation on $\sigma$ along each path from $\omega$ to $\sigma$.

Let $C_k(\mathbb {K};\mathbb {Z})$ ($C_k(\mathbb {K};\mathbb {Z}_2)$) be the free $\mathbb {Z}$-module ($\mathbb {Z}_2$-module) generated by the critical oriented k-cells of $\mathbb {K}$. We now define Forman’s boundary operator $\partial ^F$ [10, 11]. The idea is to construct a discrete flow by iterating the cellular boundary operator $\partial ^c$ until hitting a critical cell. We define $\,v^F:\mathbb {K}\cup \{0\} \rightarrow \mathbb {K}\cup \{0\}\,$ by:

$$\begin{aligned} v^F(\sigma )=&{\left\{ \begin{array}{ll} \sigma &{} \text {if}\,\,\sigma \,\,\text {is critical},\\ \displaystyle \sum _{ \widetilde{\sigma }<\tau ,\,\widetilde{\sigma }\ne \sigma } v^F(\widetilde{\sigma })&{} \text {if}\,\,\sigma \text { is upward noncritical, with an arrow}\,\, \sigma \rightarrow \tau ,\\ 0 &{} \text {else}.\\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.1)

The crucial point for us is that those simplices that receive an arrow are put to 0, and they will therefore drop out of the boundary operator. To compensate for that and to preserve the fundamental relation that the square of the boundary be 0, we then need to flow in the direction of outgoing arrows. Working in $\mathbb {Z}$, we use the following orientation convention: The initial orientation of a facet $\widetilde{\sigma }< \tau$ is taken in such a way that it is induced from the orientation of $\tau$ inducing an orientation of $\sigma < \tau$ opposite to the initial orientation of $\sigma$.

The preceding definition is recursive so we have to argue that it terminates. Indeed, for a discrete Morse function f, the cells $\sigma$ and $\widetilde{\sigma }$ in (2.1) satisfy: $\,f(\sigma )>f(\widetilde{\sigma })$. The finiteness of the CW complex then ensures that we shall stop at some point.

Definition 2.1

(Definition of the boundary operator $\partial ^F$) The boundary operator $\partial ^F: C_k \rightarrow C_{k-1}$ is given by:

$$\begin{aligned} \partial ^F(\tau ):=v^F\circ \partial ^c \tau = \sum _{\sigma <\tau }[\tau :\sigma ]v^F(\sigma ). \end{aligned}$$

Fig. 2

Definition of Forman’s boundary operator

Example 2.1

In Fig. 2, the arrows are drawn between the critical cells of index difference one (going downward), and the sign of each arrow between two critical cells represents the incidence number. The left subfigure specifies the initial orientations of the cells. That is,

$$\begin{aligned} \sigma _0= & {} [\nu _1,\nu _0],\,\,\sigma _1=[\nu _0,\nu _2],\,\,\sigma _2=[\nu _1,\nu _2], \,\,\sigma _3=[\nu _2,\nu _3],\,\,\sigma _4=[\nu _3,\nu _1], \\ \tau _1= & {} [\nu _0,\nu _2,\nu _1],\,\,\tau _2=[\nu _1,\nu _2,\nu _3]. \end{aligned}$$

Now, using the initial orientations of each cell, we have:

$\partial ^F_2 (\tau _2)= \sigma _2 +\sigma _3$; the edge $\sigma _4$ is downward noncritical so we ignore it.

$\partial ^F_2 (\tau _1)= -\sigma _2 + \sigma _1$; the edge $\sigma _0$ is downward noncritical so we ignore it.

$\partial ^F_1 (\sigma _3)= \nu _1-\nu _2$, since the other vertex $\nu _3$ is upward noncritical with the edge $\sigma _4$ which in turn has the vertex $\nu _1$ as critical.

$\partial ^F_1(\sigma _1)= \nu _2-\nu _1$, since the other vertex $\nu _0$ is upward noncritical with the edge $\sigma _0$ which in turn has the vertex $\nu _1$ as critical.

$$\begin{aligned} \partial ^F_1 (\sigma _2)= & {} \nu _2-\nu _1. \\ \partial ^F_0(\nu _i)= & {} 0\, \hbox { for } \,\,i=1,2. \end{aligned}$$

Then, one can easily check that $\partial ^F_{k-1}\circ \partial ^F_{k}=0$ for all $k=1,2$, and for $b_k:=\ker \partial ^F_k / {{\,\mathrm{im}\,}}\partial ^F_{k+1}$, we get the desired Betti numbers, that is $b_0=1,\,\, b_1=0,\,\,b_2=0$.

Fig. 3

A collapse/deformation retraction

Remark 2.2

Topologically, Definition 2.1 means that we apply a collapse to each cell with an outgoing arrow with the cell that receives that arrow, and then take the cellular boundary operator of the new complex obtained after all the collapses have been carried out. Each such collapse is a strong deformation retraction and therefore homotopy preserving. See Fig. 3 for an illustration.

Our aim is to extend such a definition to arrow configurations on $\mathbb {K}$. For such arrow configurations, each cell may have finitely many outgoing or incoming arrows. We shall need to require, however, that we do not have both incoming and outgoing arrows together at any cell and also that the arrow configuration does not have closed orbits.

Definition 2.2

(Closed orbit) A closed orbit (of dimension k) is a closed path of arrows, that is,

$$\begin{aligned} \sigma ^{(k)}_1\rightarrow \tau ^{(k+1)}_1>\sigma ^{(k)}_2 \rightarrow \tau ^{(k+1)}_2 \cdots \tau ^{(k+1)}_{l-1}>\sigma ^{(k)}_l \rightarrow \tau ^{(k+1)}_l >\sigma ^{(k)}_{1} \quad (P). \end{aligned}$$

Figure 4 shows an example of a closed orbit.

Definition 2.3

(Arrow configuration) An arrow configuration assigns to each k-cell $\sigma$ a collection of cardinality denoted by $n_\mathrm{ou}(\sigma )$ of $(k+1)$-cells that have $\sigma$ as a facet. We draw an arrow from $\sigma$ to each cell in that collection. Conversely, we let $n_\mathrm{in}(\sigma )$ be the number of arrows that $\sigma$ receives from its facets. Thus, $n_\mathrm{ou}(\sigma )$ is the number of outgoing arrows while $n_\mathrm{in}(\sigma )$ is the number of incoming arrows of $\sigma$. We denote these collections by

$$\begin{aligned} ADn(\sigma ):=\{ \nu \in \mathbb {K}\, |\,\nu <\sigma ,\, \exists \, \nu \rightarrow \sigma \}, \quad AUn(\sigma ):=\{\tau \in \mathbb {K}\,|\, \tau >\sigma ,\,\exists \, \sigma \rightarrow \tau \}. \end{aligned}$$

We require that at most one of $n_\mathrm{ou}(\sigma )$ and $n_\mathrm{in}(\sigma )$ be different from zero and that there should not be any closed orbit.

Fig. 4

A vector field not originating from a discrete function

Fig. 5

A discrete function whose vector field is not our arrow configuration

An arrow configuration with a closed orbit and where each cell carries at most one arrow cannot be generated by a discrete function. Also, if in the arrow configuration a cell $\sigma$ has both an incoming arrow $\nu \rightarrow \sigma$ and an outgoing $\sigma \rightarrow \tau$ and if there exists $\rho \ne \sigma ,\,\, \nu<\rho <\tau$, for which there is no arrow from $\rho$ to $\tau$, then again there can be no generating function f, as we would have the contradiction $f(\nu )\ge f(\sigma ) \ge f(\tau )> f(\rho )> f(\nu )$ for some $\rho \ne \sigma ,\,\, \nu<\rho <\tau$. However,

Lemma 2.1

An arrow configuration as in Definition 2.3 is generated by some discrete function.

Fig. 6

A function with a closed orbit

Proof

Under our assumptions, we can construct a function $f:\mathbb {K}\rightarrow \mathbb {R}$ that satisfies for every $\sigma \in \mathbb {K}$

$$\begin{aligned}&f(\sigma ) \,\le \, \min \{f(\nu )\,|\,\nu \in ADn(\sigma )\} \quad \text {if} \quad n_\mathrm{in}(\sigma )\ge 1, \\&f(\sigma ) \,\ge \, \max \{f(\tau )\,|\,\tau \in AUn(\sigma )\} \quad \text {if} \quad n_\mathrm{ou}(\sigma )\ge 1, \\&f(\sigma )\,> \,\max \{f(\nu )\,|\,\nu<\sigma , \, \nu \notin ADn(\sigma )\}, \\&f(\sigma )\,<\, \min \{f(\tau )\,|\,\tau >\sigma , \, \tau \notin AUn(\sigma )\}. \end{aligned}$$

$\square$

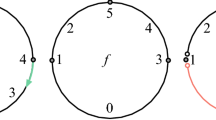
The converse of Lemma 2.1 is not true. Indeed, Fig. 5 shows an example of a function whose extracted vector field allows for a cell to have at the same time an incoming and an outgoing arrow. Also, in Fig. 6 we have a discrete function whose extracted vector field has a closed orbit. In this case, the edge with value 6 has more than one outgoing arrow, one of which points to the 2-cell with value 2 which has more than one incoming arrow.

In Forman’s framework, the downward noncritical cells have only one incoming arrow, the upward noncritical cells have only one outgoing arrow and the critical cells have no arrows. We call the first two types: Forman type or normally noncritical cells.

Definition 2.4

(Abnormally noncritical cell) A cell $\,\,\tau \,\,$ is abnormally downward noncritical if $n_\mathrm{in}(\tau )>1$, that is, the number of incoming arrows of $\,\,\tau \,\,$ is greater than $\,\,1.$ A cell $\,\,\tau \,\,$ is abnormally upward noncritical if $n_\mathrm{ou}(\tau )>1$, that is, the number of outgoing arrows of $\,\,\tau \,\,$ is greater than $\,\,1.$

Fig. 7

Different types of defective cells

For our examples, in which we mostly use simplicial complexes, we write $[\nu _1,\nu _2,\ldots ,\nu _k]$ to denote the oriented cell with vertices $\nu _1,\ldots ,\nu _k$.

Example 2.2

(a):

In Fig. 7a, the vertex $\nu _2$ is abnormally upward noncritical.

(b):

In Fig. 7b, the 2-cell $\tau =[\nu _1,\nu _2,\nu _3]$ is abnormally downward noncritical.

Definition 2.5

(Defective cell) A cell $\sigma$ with its arrow pattern is said to be defective if it satisfies any one of the following:

• (a) $n_\mathrm{in}(\sigma )=0$ and $n_\mathrm{ou}(\sigma )=0$ ($\sigma$ is critical in the standard sense);

• (b) $n_\mathrm{in}(\sigma )>1$ ($\sigma$ is abnormally downward noncritical);

• (c) $\sigma \in ADn(\tau )$ for some $\tau$ satisfying $n_\mathrm{in}(\tau )>1$ ($\sigma$ has an arrow into an abnormally downward noncritical cell);

• (d) $n_\mathrm{ou}(\sigma )>1$ ($\sigma$ is abnormally upward noncritical);

• (e) $\sigma \in AUn(\nu )$ for some $\nu$ satisfying $n_\mathrm{ou}(\nu )>1$ ($\sigma$ receives an arrow from an abnormally upward noncritical cell).

We now observe that the Euler number can be computed by using the contribution only from those cells that are either critical or support or receive more than one arrow.

Definition 2.6

(Contribution function) The contribution $C :\mathbb {K}\rightarrow \mathbb {Z},\,\,$ of a cell $\sigma ^{(k)} \in \mathbb {K},$ is

$$\begin{aligned} C( \sigma ^{(k)})= (-1)^k + (-1)^{k-1}n_\mathrm{in}(\sigma ^{(k)}) + (-1)^{k+1}n_\mathrm{ou}(\sigma ^{(k)}). \end{aligned}$$

In particular, $C( \sigma )=0$ if $\sigma$ has only a single (incoming or outgoing) arrow.

Proposition 2.2

The Euler number of the cell complex $\mathbb {K}$ is given by:

$$\begin{aligned} \chi (\mathbb {K})= \sum _{\sigma \in \mathbb {K}} C(\sigma ). \end{aligned}$$

(2.2)

Proof

An outgoing (resp. incoming) arrow of a k-cell is an incoming arrow of a $(k+1)$-cell (resp. outgoing arrow of a $(k-1)$-cell). Therefore, the contributions cancel in (2.2).$\square$

We want to refine this simple observation and construct a boundary operator from our arrow configuration that also passes over those cells that have only a single arrow and recovers not only the Euler number, but also the Betti numbers of our complex. In order to yield homology, the square of such a boundary operator has to be 0.

We shall assume that each cell is oriented.

3 A Generalized Boundary Operator

We are now in a position to generalize Forman’s discrete Morse–Floer theory. The data for our construction consist of a finite CW complex $\mathbb {K}$ (with cellular boundary operator $\partial ^c$), where each cell is given an orientation and an arrow configuration as in Definition 2.3, that is, a cell can have more than one outgoing or incoming arrow, but not both, and there are no closed orbits.

Let $\sigma \, \in \mathbb {K}$ be a cell, and recall that $n_\mathrm{in}(\sigma )$ (resp. $n_\mathrm{ou}(\sigma )$) denotes the number of incoming arrows (resp. outgoing arrows) of $\sigma$.

We first define suitable collections of cells.

$$ \begin{aligned} A^u:= & {} \{\sigma \in \mathbb {K}\,|\,n_\mathrm{ou}(\sigma )\ge 1\}\\ \bar{C}^{(k)}_o:= & {} \{ \sigma ^{(k)} \in \mathbb {K}\,|\, n_\mathrm{in}(\sigma )=0\,\, \& \,\,n_\mathrm{ou}(\sigma )=0\} \\ \bar{C}^{(k)}_{in}:= & {} \{ \sigma ^{(k)} \in \mathbb {K}\,|\, n_\mathrm{ou}(\sigma )=0\,\, \& \,\,n_\mathrm{in}(\sigma )>1\}\\ \bar{C}^{(k)}_\mathrm{ou}:= & {} \{ \sigma ^{(k)} \in \mathbb {K}\,|\, n_\mathrm{ou}(\sigma )>1\,\, \& \,\,n_\mathrm{in}(\sigma )=0\}\\ \bar{C}^{(k)}_{sin}:= & {} \{ \sigma ^{(k)} \in \mathbb {K}\,|\, \sigma \in ADn(\tau )\,\, \text {with} \,\,n_\mathrm{in}(\tau )>1,\,\,\text {for some}\,\tau \}\\ \bar{C}^{(k)}_{sou}:= & {} \{ \sigma ^{(k)} \in \mathbb {K}\,|\, \sigma \in AUn(\nu )\,\, \text {with} \,\,n_\mathrm{ou}(\nu )>1,\,\,\text {for some}\,\nu \}\\ \bar{C}^{(k)}:= & {} \bar{C}^{(k)}_o\cup \bar{C}^{(k)}_\mathrm{ou} \cup \bar{C}^{(k)}_{in}\cup \bar{C}^{(k)}_{sin}\cup \bar{C}^{(k)}_{sou}, \end{aligned}$$

and let $\bar{C}_k$ be the free $\mathbb {R}$-module generated by the (oriented) cells in $\bar{C}^{(k)}$.

Let $\beta (l)=0$ for $l=1$ and choose some value $0<\beta (l)<1$ for $l>1$, for instance $\beta (l)=1/2$.

3.1 Definition of the Boundary Operator

Here, we develop our definition of the boundary operator, using the above arrow configuration.

The idea is the following. In the topological boundary of a cell $\tau$, we want to ignore those cells $\sigma$ that receive a single arrow from a noncritical facet $\rho$, that is, $\rho$ has only a single outgoing arrow, and that arrow points into $\sigma$. In order to compensate for that when we compute the square of the boundary operator, we need to let $\rho$ flow along $\sigma$ into its other boundary components. When we compute the square of the topological boundary operator of $\tau$, $\rho$ cancels, because it occurs in the boundary of $\sigma$ and also, but with opposite orientation, in the boundary of another facet $\sigma '$ of $\tau$ (that is, $\sigma$ and $\sigma '$ meet at $\rho$). Now, when $\sigma$ is no longer accounted for in the boundary of $\tau$, we need to compensate for that by letting $\rho$ flow along $\sigma$ into the latter’s other boundary components, to achieve the cancelation. For instance, when $\sigma$ is an edge, it has another boundary vertex $\rho '$ that is also a boundary vertex, again with opposite orientation, of another edge $\sigma ''$ of $\tau$. Letting $\rho$ thus flow into $\rho '$ achieves the cancelation with that boundary vertex of $\sigma ''$.

Since simplices may carry several arrows, either incoming or outgoing, we only need to account for those in our flow, but since simplices with more than one arrow will not put to 0 in our boundary operator, we have some flexibility here. We might simply keep them and not let them flow. That would mean that we only take those simplices with precisely one arrow, received from a facet with only one outgoing arrow, into account. That would essentially be the situation considered by Forman. We could also let them flow and divide the contributions among the different arrows. As some examples show, that might change the Betti numbers (but not the Euler number). Or we can let them partially flow and keep a fraction fixed. That is what we shall do, because we want to put all arrows to work in some kind of diffusion process on our complex.

We now formally define the generalized “flow” map v that will be composed with the topological boundary operator to construct our flow boundary operator. We put

$$\begin{aligned} v(\sigma ):={\left\{ \begin{array}{ll} \sigma &{}\text {if } \sigma \in \bar{C}_o \cup \bar{C}_{in} \cup \bar{C}_{sou},\\ \text {to be defined}&{} \text {if } \sigma \in A^u,\\ 0 &{} \text {else}. \end{array}\right. } \end{aligned}$$

(3.1)

Thus, we have handled the cases when $\sigma$ has no outgoing arrows. It does not move, unless it is noncritical and does not receive an arrow from a noncritical cell, in which case we simply put $v(\sigma )=0$. When a cell $\sigma$ has some outgoing arrows, that is, $\sigma \in A^u$, $v(\sigma )$ will be a linear combination of the cells of the same dimension that are in the cellular boundary operator of the cells to which the arrows of $\sigma$ point. However, some of those cells in the boundary of some $\tau \in AUn(\sigma )$ might have arrows themselves, and some of them may even point back into $\tau$. Therefore, the definition needs to proceed recursively. Here are the details.

To define v for a cell $\sigma \in A^u$, we consider the set $AUn(\sigma )=\{\tau ^{\sigma }_1,\ldots ,\tau ^{\sigma }_{{m}}\}$ of the target cells of arrows coming from $\sigma$. The first step of the definition then is

$$\begin{aligned} v(\sigma ):=\beta (m)\,\sigma +\frac{1-\beta (m)}{m}\sum _{r=1}^{m} v(\sigma \rightarrow \tau ^{\sigma }_r). \end{aligned}$$

(3.2)

Thus, when $m>1$, since then $\beta (m)>0$, some part of $\sigma$ is retained and does not flow. The rest, or all of $\sigma$ when $m=1$, flows into the boundaries of the cells into which the arrows from $\sigma$ point. We now define $v(\sigma \rightarrow \tau )$ for an arrow $\sigma \rightarrow \tau$. We write $ADn(\tau )=\{\sigma _1,\sigma _2,\ldots ,\sigma _l\}$, with $\sigma =\sigma _1$. When $l=1$, $\tau$ receives no other arrows. When $l \ge 1$, for each $i=1,\ldots ,l$, $AUn(\sigma _i)=\{\tau ^{\sigma _i}_1,\ldots ,\,\tau ^{\sigma _i}_{m_{i}}\}$ with $\tau ^{\sigma _i}_1=\tau$. We put

$$\begin{aligned} \,\,A^{\sigma _1}=A^{\sigma }:=\{\tau \}\times AUn(\sigma _2) \times \cdots \times AUn(\sigma _{l}). \end{aligned}$$

Note that possible other outgoing cells of $\sigma$ itself are not included in this product.

For an element $E\in A^{\sigma }$, define

$$\begin{aligned} \,P_{\tau }(E)=\{\sigma _i\in ADn(\tau )\,| \, {{\,\mathrm{Proj}\,}}_i(E)=\tau \,\,\text {for some}\,\,i\}\,\quad \text {and set }\quad \eta _E:=|P_\tau (E)|. \end{aligned}$$

As an example for the definition of $P_{\tau }$, take $E=(\tau ,\tau ,\tau ,E_4,\dots , E_l)$, with $E_4, \ldots , E_l \ne \tau$, then $P_\tau (E)=\{\sigma ,\sigma _2,\sigma _3\}$.

We write $E\cap AUn(\sigma _j)$ to denote the projection of E, as an element of the product set $\{\tau \}\times AUn(\sigma _2) \times \cdots \times AUn(\sigma _{l})$, onto the component $AUn(\sigma _j)$.

We can now define

$$\begin{aligned} v(\sigma \rightarrow \tau ):=\frac{1}{|A^{\sigma }|}\displaystyle \sum _{E\in A^{\sigma }}v(\sigma ,E) \quad \quad \left( |A^{\sigma }|=\prod _{j\ge 2} m_j\right) \end{aligned}$$

with, for $E \in A^{\sigma },$

$$\begin{aligned} v(\sigma ,E):= & {} \beta (\eta _E)\,\sigma +\frac{1-\beta (\eta _E)}{\eta _E}\Bigg ( (\eta _E-1)\sigma + \sum _{\begin{array}{c} h\ge 2\\ \sigma _h\in P_\tau (E) \end{array}} \sigma _h \nonumber \\&+\, \sum _{\begin{array}{c} \sigma ' < \tau \\ \sigma ' \notin ADn(\tau ) \end{array}} v(\sigma ') + \sum _{\begin{array}{c} \tau ^{\sigma _j} \ne \tau \\ \tau ^{\sigma _j}\in E\cap AUn(\sigma _j) \end{array}} v(\sigma _j\rightarrow \tau ^{\sigma _j})\Bigg ). \end{aligned}$$

(3.3)

Thus, we keep a fraction of $\sigma$ itself (first term) and some fraction of those other boundary facets of $\tau$ that have an arrow pointing back into $\tau$ (second term), flow from those boundary facets that do not have an arrow into $\tau$ into other simplices into which they point (third term) and finally flow into other simplices from boundary facets of $\tau$ that have arrows pointing into $\tau$ and arrows pointing into other simplices (fourth term). We assume for simplicity that the initial orientation of a facet $\widetilde{\sigma }< \tau$ is taken in such a way that it is induced from the orientation of $\tau$ inducing an orientation of $\sigma < \tau$ opposite to the initial orientation of $\sigma$. Note that $v(-\sigma \rightarrow \tau )= -v(\sigma \rightarrow \tau )$ where $-\sigma$ is the cell $\sigma$ with the opposite orientation.

This recursive definition above terminates after finitely many steps. In fact, by Lemma 2.1 there is a discrete function f that generates the given arrow configuration. From the proof of Lemma 2.1, $f(\sigma )\ge f(\tau )>f(\sigma ')$. That is, the arguments of $v(\sigma ')$ in (3.3) have strictly smaller value for the function f than the value $f(\sigma )$. However, $f(\sigma )$ need not be greater than $f(\sigma _j)$. But the absence of closed orbits in our arrow configuration ensures that the flow map v cannot return to $\sigma$ after leaving $\tau$. So, the absence of closed orbits and the finiteness of $\mathbb {K}$ together imply that we stop at some point.

Definition 3.1

(Boundary operator) We define $\,\, \bar{C}_k \xrightarrow {\bar{\partial }_{k}} \bar{C}_{k-1}\,\,$ by

$$\begin{aligned} \bar{\partial }\tau =v\circ \partial ^c \tau =\sum _{\sigma <\tau }v(\sigma ). \end{aligned}$$

(3.4)

We now want to see how Definition 3.1 simplifies when the arrow configuration is restricted to the specific cases of merging and forking.

Fig. 8

A forking case

3.1.1 The Forking Case

In this part, we restrict the boundary operator given by Definition 3.1 in the case where a cell can have many outgoing arrows or at most one incoming arrow, and there are no closed orbits.

Suppose that on $\mathbb {K}$ we have the arrow configuration given by Definition 2.3 with the assumption that for each cell $\sigma$,

$$\begin{aligned} n_\mathrm{in}(\sigma )\le 1. \end{aligned}$$

Let the set of all defective k-cells be given by

$$\begin{aligned} \bar{C}^{(k)}:=\bar{C}^{(k)}_o \cup \bar{C}^{(k)}_\mathrm{ou} \cup \bar{C}^{(k)}_{sou}, \end{aligned}$$

and $\bar{C}_k$ be the free $\mathbb {R}$-module generated by the oriented cells in $\bar{C}^{(k)}$.

Let us denote in this case the “flow” map by $v^\mathrm{up}$.

The map $v^\mathrm{up} :\mathbb {K}\cup \{0\} \rightarrow \mathbb {K}\cup \{0\}$ is given by:

$$\begin{aligned} v^\mathrm{up}(\sigma )= & {} {\left\{ \begin{array}{ll} \sigma &{} \text {if} \quad \sigma \in \bar{C}_o \cup \bar{C}_{sou},\\ V^\mathrm{up}(\sigma ) &{} \text {if}\quad \sigma \in A^u,\\ 0 &{} \text {else,} \\ \end{array}\right. } \end{aligned}$$

where, if $AUn(\sigma )=\{\tau _1,\tau _2,\ldots ,\tau _m \}$,

$$\begin{aligned} V^\mathrm{up}(\sigma )=\beta (m)\,\sigma +(1-\beta (m))\frac{1}{m}\sum _{i=1}^m v^\mathrm{up}(\sigma \rightarrow \tau _i), \end{aligned}$$

with

$$\begin{aligned} v^\mathrm{up}(\sigma \rightarrow \tau _i) = \sum _{\rho <\tau _i, \rho \ne \sigma } v^\mathrm{up}(\rho ). \end{aligned}$$

(3.5)

In this situation however, the arrow configuration cannot have closed orbits. Indeed, Lemma 2.1 ensures there is a discrete function f that generates the given arrow configuration. Also, the argument of $v^\mathrm{up}(\rho )$ in (3.5) has strictly smaller value for the function f than the value $f(\sigma )$. Indeed, from the proof of Lemma 2.1, $f(\sigma ) \ge f(\tau _i)$ for each i. We are in the forking case so each $\tau _i$ has only one arrow coming from $\sigma$. Thus, $f(\tau _i)>f(\rho )$, since there is no arrow from $\rho$ to $\tau _i$. Hence, $f(\sigma )>f(\rho )$. This tells us that the flow map $v^\mathrm{up}$ cannot return to $\sigma$. Since $\mathbb {K}$ is finite, it implies we stop at some point.

Remark 3.1

The crucial fact about the definition of $v^\mathrm{up}$ above is that the coefficient $\beta (m)$ is not zero whenever $m>1$. Consider for example Fig. 8 with the orientations:

$$\begin{aligned} \sigma _1=[\nu _2,\nu _1],\,\sigma _2=[\nu _2,\nu _3],\,\sigma _3=[\nu _4,\nu _2]. \end{aligned}$$

If we suppose that $\beta (m)=0$ for all m, we obtain

$$\begin{aligned} \bar{\partial }\sigma _1= & {} \nu _1-\frac{1}{2}(\nu _3+\nu _4), \, \bar{\partial }\sigma _2=\nu _3-\frac{1}{2}(\nu _3+\nu _4)=\frac{1}{2}(\nu _3-\nu _4), \, \hbox {and} \\ \bar{\partial }\sigma _3= & {} \nu _4-\frac{1}{2}(\nu _4+\nu _3)=\frac{1}{2}(\nu _4-\nu _3). \end{aligned}$$

Then, one immediately sees that

$$\begin{aligned} \ker \bar{\partial }_0=\langle \nu _1,\nu _2,\nu _3,\nu _4\rangle ,\,\,\,{{\,\mathrm{im}\,}}\bar{\partial }_1= \langle \bar{\partial }\sigma _1,\bar{\partial }\sigma _3\rangle , \,\,\,\ker \bar{\partial }_1=\langle \sigma _3-\sigma _2\rangle ,\,\,\, {{\,\mathrm{im}\,}}\bar{\partial }_2=0. \end{aligned}$$

This does not give the right Betti numbers since we obtain

$$\begin{aligned} \bar{b}_0=dim \big (\ker \bar{\partial }_0/{{\,\mathrm{im}\,}}\bar{\partial }_{1}\big )=2\ne 1=b_0, \, \hbox { and } \, \bar{b}_1=\dim \big (\ker \bar{\partial }_1/{{\,\mathrm{im}\,}}\bar{\partial }_{2}\big )=1\ne 0=b_1. \end{aligned}$$

Fig. 9

Example in the forking case

Example 3.1

In Fig. 9, the initial orientation of each cell is given in the right subfigure, that is:

$$\begin{aligned} \tau _1= & {} [\nu _1,\nu _2,\nu _3];\quad \tau _2=[\nu _1,\nu _3,\nu _0];\quad \tau _3=[\nu _0,\nu _3,\nu _4]; \quad \sigma _0=[\nu _4,\nu _0];\quad \\ \sigma _1= & {} [\nu _0,\nu _1]; \\ \sigma _2= & {} [\nu _1,\nu _2];\quad \sigma _3=[\nu _2,\nu _3];\quad \sigma _4=[\nu _3,\nu _4];\quad \sigma _5=[\nu _1,\nu _3];\quad \sigma _6=[\nu _3,\nu _0]. \end{aligned}$$

The cell $\nu _3$ is abnormally upward noncritical with the cells $\sigma _4,\,\sigma _5$ and $\sigma _6$. We have the following:

$$\begin{aligned} \bar{C}^{(0)}_o= & {} \{\nu _0\,,\,\nu _1\},\quad \bar{C}^{(1)}_o=\{\sigma _2\}, \quad \bar{C}^{(2)}_o=\{\tau _1,\tau _3\}; \\ \bar{C}^{(0)}_\mathrm{ou}= & {} \{\nu _3\}, \quad \bar{C}^{(1)}_{sou}=AUn(\nu _3)=\{\sigma _4\,,\,\sigma _5\,,\,\sigma _6\}; \\ v^\mathrm{up}(\nu _3)= & {} \beta (3)\nu _3+(1-\beta (3))\frac{1}{3}\Big (v^\mathrm{up}(\nu _3 \rightarrow \sigma _5) + v^\mathrm{up}(\nu _3 \rightarrow \sigma _6)+v^\mathrm{up}(\nu _3 \rightarrow \sigma _4)\Big ) \nonumber \\= & {} \beta (3)\nu _3+(1-\beta (3))\frac{1}{3}(\nu _1+2\nu _0); \\ \bar{\partial }\tau _1= & {} -\sigma _5 + \sigma _2 ,\quad \bar{\partial }\tau _3=(-\sigma _6+\sigma _4), \end{aligned}$$

since the induced orientation from $\tau _1$ (resp. $\tau _3$) onto $\sigma _5$ (resp. $\sigma _6$) does not coincide with the initial orientation of $\sigma _5$ (resp. $\sigma _6$);

$$\begin{aligned} \bar{\partial }\sigma _2 =-\nu _1+v^\mathrm{up}(\nu _3), \end{aligned}$$

since the induced orientation from $\sigma _2$ (also $\sigma _5$) onto $\nu _3$ coincides with the initial orientation of $\nu _3$, whereas the one induced by $\sigma _4$ (or $\sigma _6$) does not coincide with the initial orientation. Also, the initial orientation of $\nu _1$ does not coincide with its induced orientation from $\sigma _2$. We therefore have:

$$\begin{aligned} \bar{\partial }\sigma _2= & {} -\nu _1+v^\mathrm{up}(\nu _3), \quad \bar{\partial }\sigma _5=-\nu _1+v^\mathrm{up}(\nu _3), \quad \bar{\partial }\sigma _4=\nu _0-v^\mathrm{up}(\nu _3), \\ \bar{\partial }\sigma _6= & {} \nu _0-v^\mathrm{up}(\nu _3). \end{aligned}$$

One easily checks that $\bar{\partial }\circ \bar{\partial }=0$.

3.1.2 The Merging Case

In this case, we restrict the Definition 3.1 to situation where a cell can have at most one outgoing arrow but as much incoming arrows as possible. Let $\mathbb {K}$ be a finite CW complex in which each cell is endowed with an orientation, together with the arrow configuration given by Definition 2.3.

Fig. 10

A merging case

Suppose that for each cell $\sigma$,

$$\begin{aligned} n_\mathrm{ou}(\sigma )\le 1. \end{aligned}$$

Set

$$\begin{aligned} \bar{C}^{(k)}=\bar{C}^{(k)}_o \cup \bar{C}^{(k)}_{in}\cup \bar{C}^{(k)}_{sin}, \end{aligned}$$

and $\bar{C}_k$ the free $\mathbb {R}$-module generated by the oriented cells in $\bar{C}^{(k)}$.

We denote the “flow” map by $\,v^\mathrm{do}:\mathbb {K}\cup \{0\}\rightarrow \mathbb {K}\cup \{0\}$, and it is given by:

$$\begin{aligned} v^\mathrm{do}(\sigma )&= {\left\{ \begin{array}{ll} \sigma &{} \text {if} \quad \sigma \in \bar{C}_o \cup \bar{C}_{in},\\ V^\mathrm{do}(\sigma ) &{} \text {if} \quad \sigma \in A^u,\\ 0 &{} \text {else}, \end{array}\right. } \end{aligned}$$

where, for $\sigma \in A^u,$ there exists a $\,\,\tau \, \,\,\text {s.t.}\, \,ADn(\tau )=\{\sigma _1,\ldots ,\sigma _l\}\,\, \text {with} \,\,\sigma =\sigma _1$, and $\,\,V^\mathrm{do}(\sigma )$ is given by

$$\begin{aligned} V^\mathrm{do}(\sigma ):=\beta (l)\, \sigma +\frac{1-\beta (l)}{l}\left( (l-1)\sigma +\sum _{j\ne 1} \sigma _j + \sum _{\widetilde{\sigma }< \tau , \widetilde{\sigma } \notin ADn(\tau )} v^\mathrm{do}(\widetilde{\sigma })\right) .\nonumber \\ \end{aligned}$$

(3.6)

In this case, to argue that the recursive definition above terminates after finitely many steps only follows from Lemma 2.1. Indeed, assuming there is a discrete function f that generates the given arrow configuration, for such a function f, because there is an arrow from $\sigma$ to $\tau$, we have $f(\sigma )\ge f(\tau )$. In turn, $f(\tau )>f(\widetilde{\sigma })$ since there is no arrow from $\widetilde{\sigma }$ to $\tau$. Hence, $f(\sigma )>f(\widetilde{\sigma })$. That is, the argument of $v^\mathrm{do}(\widetilde{\sigma })$ in (3.6) has strictly smaller value, for the function f, than the value $f(\sigma )$. Hence, the flow map $v^\mathrm{do}$ cannot return to $\sigma$. Since $\mathbb {K}$ is finite, it implies we stop at some point.

Remark 3.2

What is crucial about the definition above is the fact that $\beta (l)\ne 0$ for $l>1$. Consider for example Fig. 10, with the initial orientations given by:

$$\begin{aligned} \tau =[\nu _1,\nu _2,\nu _3],\quad \sigma _1=[\nu _1,\nu _3],\quad \sigma _2=[\nu _3,\nu _2],\quad \sigma _3=[\nu _1,\nu _2]. \end{aligned}$$

Assuming $\beta (l)=0$ for all l, we get:

$$\begin{aligned} \bar{\partial }\sigma _1= & {} \nu _3-\frac{1}{2}(\nu _1+\nu _2), \bar{\partial }\sigma _2=-\nu _3+\frac{1}{2}(\nu _1+\nu _2), \bar{\partial }\sigma _3=0,\\&\,\hbox {and} \, \bar{\partial }\tau =-\sigma _1-\sigma _2+\sigma _3. \end{aligned}$$

Then, one immediately sees that $\sigma _3$ adds an additional element in $\ker \bar{\partial }_1$. Indeed,

$$\begin{aligned} \ker \bar{\partial }_0= & {} \langle \nu _1,\nu _2,\nu _3\rangle ,\quad {{\,\mathrm{im}\,}}\bar{\partial }_1=\langle \bar{\partial }\sigma _1\rangle ,\\ \ker \bar{\partial }_1= & {} \langle \sigma _1+\sigma _2, \sigma _3\rangle , \quad {{\,\mathrm{im}\,}}\bar{\partial }_2=\langle -\sigma _1-\sigma _2+\sigma _3\rangle . \end{aligned}$$

This then does not give the right Betti numbers since we get

$$\begin{aligned} \bar{b}_0=\dim \big (\ker \bar{\partial }_0/{{\,\mathrm{im}\,}}\bar{\partial }_{1}\big )=2\ne b_0=1, \, \hbox {and} \, \bar{b}_1=\dim \big (\ker \bar{\partial }_1/{{\,\mathrm{im}\,}}\bar{\partial }_{2}\big )=1\ne 0=b_1. \end{aligned}$$

Fig. 11

Another example of a merging case

Example 3.2

Using Fig. 11, the initial orientations given by the right subfigure are such that:

$$\begin{aligned}&\tau _1=[\nu _1,\nu _2,\nu _3];\quad \tau _2=[\nu _0,\nu _1,\nu _3];\quad \tau _3=[\nu _1,\nu _0,\nu _2];\quad \tau _4=[\nu _2,\nu _0,\nu _3]; \\&\sigma _0=[\nu _0,\nu _2];\quad \sigma _1=[\nu _3,\nu _0];\quad \sigma _2=[\nu _3,\nu _1];\quad \sigma _3=[\nu _1,\nu _2];\quad \sigma _4=[\nu _0,\nu _1]; \\&\sigma _5=[\nu _2,\nu _3]. \end{aligned}$$

The cell $\sigma _4$ is upward noncritical with the cell $\tau _3$, and the cell $\tau _1$ is abnormally downward noncritical with the cells $\sigma _2$, $\,\sigma _3$ and $\sigma _5$. We then have:

$$\begin{aligned} v^\mathrm{do}(\sigma _3)= & {} \beta (3)\sigma _3+\frac{1-\beta (3)}{3}(2\sigma _3 -\sigma _2-\sigma _5); \\ v^\mathrm{do}(\sigma _2)= & {} \beta (3)\sigma _2+\frac{1-\beta (3)}{3}(2\sigma _2 -\sigma _3-\sigma _5); \\ v^\mathrm{do}(\sigma _5)= & {} \beta (3)\sigma _5+\frac{1-\beta (3)}{3}(2\sigma _5 -\sigma _2-\sigma _3). \\ \bar{\partial }\tau _4= & {} -\sigma _0-\sigma _1-v^\mathrm{do}(\sigma _5) \\= & {} -\beta (3)(\sigma _0+\sigma _1+\sigma _5) \\&-\,\frac{(1-\beta (3))}{3}\Big (2(\sigma _0+\sigma _1+\sigma _5)+ (\sigma _0+\sigma _1-\sigma _2-\sigma _3)\Big ). \end{aligned}$$

Also,

$$\begin{aligned} \bar{\partial }\tau _2= & {} \sigma _1-v^\mathrm{do}(\sigma _2)+ \sigma _0-v^\mathrm{do}(\sigma _3)\\= & {} \sigma _1+\sigma _0 +2\frac{(1-\beta (3))}{3}\sigma _5-\frac{1+2 \beta (3)}{3}(\sigma _2+\sigma _3).\\= & {} 2\frac{(1-\beta (3))}{3}(\sigma _1+\sigma _0+\sigma _5)+ \frac{1+2\beta (3)}{3}(\sigma _1+\sigma _0-\sigma _2-\sigma _3). \end{aligned}$$

Similarly, one gets

$$\begin{aligned} \bar{\partial }\tau _1= & {} v^\mathrm{do}(\sigma _3)+v^\mathrm{do}(\sigma _2)+v^\mathrm{do}(\sigma _5) \\= & {} \beta (3)\sigma _3+\frac{1-\beta (3)}{3}(2\sigma _3 -\sigma _2-\sigma _5)+ \beta (3)\sigma _2+\frac{1-\beta (3)}{3}(2\sigma _2 -\sigma _3-\sigma _5)\\&+\, \beta (3)\sigma _5+\frac{1-\beta (3)}{3}(2\sigma _5 -\sigma _2-\sigma _3)=\beta (3)(\sigma _5+\sigma _3+\sigma _2). \end{aligned}$$

Each term in brackets is the cellular boundary of some linear combination of cells. One then checks by direct computation that $\bar{\partial }\circ \bar{\partial }=0$.

3.2 Generalized Morse Inequalities

We now come to the main theorems of this paper, the first of which establishes the fact that the square of the boundary operator $\bar{\partial }$ is zero.

Theorem 3.1

$$\begin{aligned} \bar{\partial } \circ \bar{\partial }=0. \end{aligned}$$

(3.7)

Proof

This follows from the argument given at the beginning of Sect. 3.1. Those boundary components that are put to 0 in the boundary of $\tau$ compensate by letting their own boundary components flow into others. Topologically, this simply means that we contract them to points. Such a contraction does not affect the square of the boundary operator. This argument shows (3.7). For an algebraic computation, we refer to [28]. $\square$

With Theorem 3.1, we can use the boundary operator $\bar{\partial }$ to define homology groups. Let $\bar{b_i}:=\dim \big ( \ker \bar{\partial }_i/{{\,\mathrm{im}\,}}\bar{\partial }_{i+1}\big )$ be the corresponding Betti numbers.

Lemma 3.2

$\bar{b_i}=b_i$, where the $b_i$ are the ordinary Betti numbers of our complex.

Proof

We assume for simplicity that the CW complex $\mathbb {K}$ has no noncritical cells that belong to Forman’s framework, since the Forman-type noncritical cells can be collapsed, preserving the homotopy type of the CW complex in the process. Indeed, when we put $\beta (s)=0$ that is $s=1$ in (3.2) and (3.3), we have the setting of Forman’s theory, and it follows from that theory that the Betti numbers are equal.

Suppose that $0<\beta (s)\le 1$. Under this assumption, $C_k=\bar{C}_k$, and by definition, see (3.4),

$$\begin{aligned} \ker \partial ^c \subset \ker \bar{\partial }. \end{aligned}$$

(3.8)

When we put $\beta (s)=1$, nothing flows out and we have the setting of the cellular boundary operator, and it follows that the kernels are equal. When we perturb $\beta$, the dimension of the kernel can at most decrease, but that cannot happen by (3.8). Therefore, for $\beta (s)$, $s>1$ close to 1, the kernels still agree. For fractional $\beta$, no further cancelations are possible that could increase the dimension of the kernel. That could happen at most for $\beta (s)=0$, but we do not allow that for $s>1$. $\square$

Again, a more detailed algebraic computation can be found in [28].

Let $\overline{m}_k:=\dim \bar{C}_k.$ We then have the following Morse-type inequalities.

Theorem 3.3

(Generalized Morse inequalities) There exists R(t), a polynomial in t with nonnegative integer coefficients such that

$$\begin{aligned} \sum _{i=0}^{\dim \mathbb {K}} \overline{m}_i t^i = \sum _{i=0}^{\dim \mathbb {K}}b_i t^i + (1+t)R(t). \end{aligned}$$

Proof

Since $b_i=\bar{b}_i$ by Lemma 3.2, we can use the following standard argument:

$$\begin{aligned} \sum _{k=0}^n \bar{m}_kt^k - \sum _{k=0}^n\bar{b}_kt^k= & {} \sum _{k=0}^n (\dim \ker \bar{\partial }_k + \dim {{\,\mathrm{im}\,}}\bar{\partial }_k)t^k \\&-\sum _{k=0}^n(\dim \ker \bar{\partial }_k- \dim {{\,\mathrm{im}\,}}\bar{\partial }_{k+1})t^k \\= & {} \sum _{k=0}^n (\dim {{\,\mathrm{im}\,}}\bar{\partial }_k+ \dim {{\,\mathrm{im}\,}}\bar{\partial }_{k+1})t^k \\= & {} \sum _{k=0}^n(\bar{m}_k-\dim \ker \bar{\partial }_k)t^k +\sum _{k=0}^n(\bar{m}_{k+1}-\dim \ker \bar{\partial }_{k+1})t^k \\= & {} (t+1)\sum _{k=1}^n(\bar{m}_k-\dim \ker \bar{\partial }_k)t^{k-1}, \end{aligned}$$

since $\bar{m}_0= \dim \ker \bar{\partial }_0$ and $\bar{m}_{n+1}=0=\dim \ker \bar{\partial }_{n+1}$.

The proof ends by using the fact that $\,\dim \ker \bar{\partial }_k \le \bar{m}_k\,$ for all $\,k=1,2,\ldots ,n$. $\square$

Fig. 12

Initial orientations

Fig. 13

A general example

Example 3.3

Using Figs. 12 and 13, we have the following:

$$\begin{aligned}&\omega ^{(3)}_1=[\nu _1,\nu _2,\nu _3,\nu _4]; \quad \omega ^{(3)}_2=[\nu _0,\nu _1,\nu _3,\nu _2]; \\&\tau _0=[\nu _0,\nu _1,\nu _2];\quad \tau _1=[\nu _0,\nu _2,\nu _3];\quad \tau _2=[\nu _0,\nu _3,\nu _1];\quad \tau _4=[\nu _1,\nu _3,\nu _2]; \\&\tau _3=[\nu _1,\nu _2,\nu _4];\quad \tau _5=[\nu _1,\nu _4,\nu _3];\quad \tau _6=[\nu _2,\nu _3,\nu _4]; \\&\sigma _0=[\nu _0,\nu _2];\quad \sigma _1=[\nu _1,\nu _0];\quad \sigma _2=[\nu _3,\nu _0];\quad \sigma _3=[\nu _1,\nu _2];\quad \sigma _4=[\nu _4,\nu _2]; \\&\sigma _5=[\nu _2,\nu _3];\quad \sigma _6=[\nu _3,\nu _1];\quad \sigma _7=[\nu _3,\nu _4];\quad \sigma _8=[\nu _4,\nu _1]; \end{aligned}$$

The cell $w^{(3)}_2$ is abnormally downward noncritical with the cells $\tau _0$ and $\tau _4$.

The cell $\tau _5$ is abnormally downward noncritical with the cells $\sigma _8$ and $\sigma _6$.

The edge $\sigma _6$ is abnormally upward noncritical with the cells $\tau _5$ and $\tau _2$.

The vertex $\nu _4$ is abnormally upward noncritical with the edges $\sigma _7$ and $\sigma _4$.

We then get the following sets:

$$\begin{aligned} \bar{C}_o^{(0)}= & {} \{\nu _2,\nu _3\},\,\,\bar{C}_o^{(1)}= \{\sigma _5,\sigma _2,\sigma _3\},\,\,\bar{C}_o^{(2)}=\{\tau _6,\tau _3, \tau _1\},\,\,\bar{C}_o^{(3)}=\{\omega ^{(3)}_1\}; \\ \bar{C}_{in}^{(2)}= & {} \{\tau _5\},\,\,\bar{C}_{in}^{(3)}= \{\omega _2^{(3)}\},\,\,\bar{C}_\mathrm{ou}^{(0)}=\{\nu _4\},\,\, \bar{C}_\mathrm{ou}^{(1)}=\{\sigma _6\}; \\ \bar{C}_{sin}^{(1)}= & {} \{\sigma _8,\sigma _6\},\,\,\bar{C}_{sin}^{(2)} =\{\tau _4,\tau _0\},\,\,\bar{C}_{sou}^{(1)}=\{\sigma _4,\sigma _7\},\,\, \bar{C}_{sou}^{(2)}=\{\tau _5,\tau _2\}; \end{aligned}$$

We obtain

$$\begin{aligned} \bar{\partial }\omega ^{(3)}_1= \tau _6+\tau _3+ \tau _5+v(\tau _4), \end{aligned}$$

since we take all the cells in $\,\, \bar{C}_o \cup \bar{C}_{in}\cup \bar{C}_{sou}\,\,$ and $\tau _4 \in \bar{C}_{sin}$. We also take induced orientations into account. Following the outgoing arrow from $\tau _4$, the cell $\omega ^{(3)}_2 \,\,$ has $\, \,\tau _0 \,\,s.t.\, \,AUn(\tau _0)=\{\omega ^{(3)}_2\};$ thus,

$$\begin{aligned} A=\{(\omega ^{(3)}_2,\omega ^{(3)}_2)\}\,\, \hbox {and} \,\,P_{\omega ^{(3)}_2}((\omega ^{(3)}_2,\omega ^{(3)}_2))=\{\tau _4,\tau _0\}. \end{aligned}$$

We then have

$$\begin{aligned} v(\tau _4\rightarrow \omega ^{(3)}_2)= v(\tau _4,(\omega ^{(3)}_2,\omega ^{(3)}_2)) =\beta (2)\tau _4 +\frac{1-\beta (2)}{2}(\tau _4-\tau _0 -\tau _1 -\tau _2), \end{aligned}$$

since the arrow from $\tau _4$ meets the incoming one from $\tau _0$. Hence,

$$\begin{aligned} \bar{\partial }\omega ^{(3)}_1= & {} \tau _6+\tau _3+\tau _5+\beta (2) \tau _4+\frac{1-\beta (2) }{2}(\tau _4-\tau _0-\tau _1-\tau _2)\\= & {} \big (\beta (2) +\frac{1-\beta (2)}{2}\big )(\tau _6+\tau _3+\tau _5+\tau _4) \\&+\, \frac{1-\beta (2)}{2}(\tau _6+\tau _3+\tau _5-\tau _0-\tau _1-\tau _2); \\ \bar{\partial }\omega ^{(3)}_2= & {} \tau _1+\tau _2+\beta (2)\tau _4+ \frac{1-\beta (2)}{2}(\tau _4-\tau _0-\tau _1-\tau _2)\\&+\, \beta (2)\tau _0+\frac{1-\beta (2)}{2}(\tau _0-\tau _4-\tau _1-\tau _2)\\= & {} \beta (2)(\tau _1+\tau _2+\tau _0+\tau _4); \\ \bar{\partial }\tau _3= & {} \sigma _3-\sigma _4 +v(\sigma _8), \end{aligned}$$

and following the arrow $\sigma _8 \rightarrow \tau _5$, the cell $\tau _5\,\,$ has $\,\,\sigma _6\,\, s.t. \,\,AUn(\sigma _6)=\{\tau _5,\tau _2\}.$ Thus, $\,\, A^{\sigma _8}=\{(\tau _5,\tau _5),(\tau _5,\tau _2)\},\,\,$ and we need to take the average over the possibilities that we have at the edge $\sigma _6$. We have

$$\begin{aligned} v(\sigma _8\rightarrow \tau _5)=\frac{1}{2}(v(\sigma _8,(\tau _5,\tau _5))+ v(\sigma _8,(\tau _5,\tau _2))). \end{aligned}$$

Also,

$$\begin{aligned} P_{\tau _5}((\tau _5,\tau _5))= & {} \{\sigma _8,\sigma _6\} \Rightarrow v(\sigma _8,(\tau _5,\tau _5)) =\beta (2) \sigma _8 + \frac{1-\beta (2)}{2}(\sigma _8+\sigma _6-\sigma _7),\,\, \\ P_{\tau _5}((\tau _5,\tau _2))= & {} \{\sigma _8\}\Rightarrow v(\sigma _8, (\tau _5,\tau _2))=-\sigma _7 + v(\sigma _6\rightarrow \tau _2)=-\sigma _7 +\sigma _2, \end{aligned}$$

where $\,\,\tau _2\in AUn(\sigma _6)\cap E$, and $\,\,\tau _2 \ne \tau _5.$ This yields

$$\begin{aligned} \bar{\partial }\tau _3= & {} \sigma _3-\sigma _4+\frac{1}{2} \Big ( \beta (2) \sigma _8 +\frac{1-\beta (2)}{2}\big (\sigma _8-\sigma _7+\sigma _6\big )+(-\sigma _7+\sigma _2) \Big ) \\= & {} \left( \frac{\beta (2)}{2}+\frac{1-\beta (2)}{4}\right) (\sigma _3-\sigma _4+\sigma _8) + \frac{1-\beta (2)}{4}(\sigma _3-\sigma _4-\sigma _7+\sigma _6) \\&+\,\frac{1}{2}(\sigma _3-\sigma _4-\sigma _7+\sigma _2); \end{aligned}$$

Similarly, one gets

$$\begin{aligned} \bar{\partial }\tau _4= & {} -\sigma _5-\sigma _3-v(\sigma _6)\\= & {} -\sigma _5-\sigma _3-\beta (2)\sigma _6-\frac{1-\beta (2)}{2}\big (v(\sigma _6 \rightarrow \tau _5)+v(\sigma _6 \rightarrow \tau _2)\big )\\= & {} -\sigma _5-\sigma _3-\beta (2)\sigma _6-\frac{1-\beta (2)}{2}\Big (\beta (2)\sigma _6+\frac{1-\beta (2)}{2}(\sigma _6+\sigma _8+\sigma _7) +\sigma _2\Big )\\= & {} -\big (\beta (2)(1+\frac{1-\beta (2)}{2})+\frac{(1-\beta (2))^2}{4}\big )(\sigma _5+\sigma _3+\sigma _6)\\&-\,\frac{(1-\beta (2))^2}{4}(\sigma _5+\sigma _3+\sigma _8+\sigma _7) - \frac{1-\beta (2)}{2}(\sigma _5+\sigma _3+\sigma _2); \\ \bar{\partial }\tau _2= & {} -\sigma _2+v(\sigma _6)\\= & {} -\sigma _2+ \beta (2)\sigma _6+\frac{1-\beta (2)}{2}\Big (\beta (2) \sigma _6+\frac{1-\beta (2)}{2}(\sigma _6+\sigma _8+\sigma _7) +\sigma _2\Big )\\= & {} -\Big (\beta (2)\big (1+\frac{1-\beta (2)}{2}\big )+\frac{(1-\beta (2))^2}{4}\Big )\big (\sigma _2-\sigma _6\big ) \\&-\,\frac{(1-\beta (2))^2}{4}(\sigma _2-\sigma _8-\sigma _7); \\ \bar{\partial }\tau _5= & {} -\sigma _7+v(\sigma _6)-v(\sigma _8)\\= & {} -\sigma _7+ \beta (2)\sigma _6+\frac{1-\beta (2)}{2}\Big (\beta (2)\sigma _6 +\frac{1-\beta (2)}{2}(\sigma _6+\sigma _8+\sigma _7) +\sigma _2\Big )\\&-\,\frac{1}{2} \Big ( \beta (2) \sigma _8 +\frac{1-\beta (2)}{2} \big (\sigma _8-\sigma _7+\sigma _6\big )+(-\sigma _7+\sigma _2) \Big )\\= & {} \big (\beta (2)(1+\frac{1-\beta (2)}{4})\big )(\sigma _6-\sigma _8-\sigma _7) -\frac{\beta (2)}{2}(\sigma _2-\sigma _8-\sigma _7); \\ \bar{\partial }\tau _0= & {} \sigma _3; \quad \bar{\partial }\tau _6=(\sigma _7+\sigma _4)+\sigma _5; \quad \bar{\partial }\tau _1=\sigma _2+\sigma _5; \\ \bar{\partial }\sigma _2= & {} \nu _2-\nu _3=\bar{\partial }\sigma _6; \quad \bar{\partial }\sigma _5=\nu _3-\nu _2; \quad \bar{\partial }\sigma _3=0; \\ \bar{\partial }\sigma _8= & {} \nu _2-\beta (2)\nu _4-\frac{1-\beta (2)}{2}(\nu _3+\nu _2);\quad \bar{\partial }\sigma _4= \nu _2- \beta (2)\nu _4-\frac{1-\beta (2)}{2}(\nu _3+\nu _2); \\ \bar{\partial }\sigma _7= & {} -\nu _3+\beta (2)\nu _4+\frac{1-\beta (2)}{2}(\nu _3+\nu _2). \end{aligned}$$

One checks by direct computation that $\bar{\partial } \circ \bar{\partial }=0$.

$$\begin{aligned} \ker \bar{\partial }_0= & {} \langle \nu _2\,,\,\nu _3\,,\,\nu _4\rangle , \quad {{\,\mathrm{im}\,}}\bar{\partial }_1= \left\langle \nu _2-\nu _3\,,\,\nu _2-\beta (2)\nu _4+\frac{1-\beta (2)}{2}(\nu _3+\nu _2)) \right\rangle ; \\ \ker \bar{\partial }_1= & {} \langle \sigma _3\,,\,\sigma _2+\sigma _5\,,\,\sigma _5+\sigma _6\,,\,\sigma _4-\sigma _8\,,\,\sigma _7+\sigma _4+\sigma _5 \rangle = {{\,\mathrm{im}\,}}\bar{\partial }_2; \\ \ker \bar{\partial }_2= & {} \langle \tau _0+\tau _1+\tau _4+\tau _2\,,\,\tau _3+\tau _4+\tau _5+\tau _6\rangle , \\ {{\,\mathrm{im}\,}}\bar{\partial }_3= & {} \langle \beta (2)(\tau _1+\tau _2+\tau _0+\tau _4)\,,\, \bar{\partial } \omega ^{(3)}_1\rangle ; \\ \ker \bar{\partial }_3= & {} 0= {{\,\mathrm{im}\,}}\bar{\partial }_4. \end{aligned}$$

This yields

$$\begin{aligned} \bar{b}_0=1=b_0,\,\,\bar{b}_1=0=b_1,\,\,\bar{b}_2=0=b_2,\,\,\bar{b}_3=0=b_2. \end{aligned}$$

Also, we have

$$\begin{aligned} \overline{m}_0=3,\,\, \overline{m}_1=7,\,\,\overline{m}_2=7,\,\,\overline{m}_3=2, \end{aligned}$$

and we obtain

$$\begin{aligned}&\sum _k \overline{m}_kt^k=3+7t+7t^2+2t^3=1+ (1+t)(2+5t+2t^2),\quad \text {that is} \\&R(t)=2+5t+2t^2. \end{aligned}$$

We now move to the last section of this paper which shows how we can retrieve the Poincaré polynomial of our CW complex using some systematically defined isolated invariant sets.

4 Conley Theory

In this section, we shall show how to retrieve the Poincaré polynomial of our CW complex from isolated invariant sets in the sense of Conley.

From the arrow configuration, we have

• The singletons consisting of the cells without arrows,

• The collections $\{\tau \}\cup ADn(\tau ),\,\,\,\text { for}\,\,\, n_\mathrm{in}(\tau )>1$ and

• The collections $\{\sigma \}\cup AUn(\sigma ),\,\,\,\text { for}\,\,\, n_\mathrm{ou}(\sigma )>1$.

By iteratively merging $\{\sigma \}\cup AUn(\sigma )$ for $n_\mathrm{ou}(\sigma )>1$ and $\{\tau \}\cup ADn(\tau )$ for $n_\mathrm{in}(\tau )>1$, whenever $\sigma \in ADn(\tau )$ (equivalently $\tau \in AUn(\sigma )$), we obtain disjoint collections $C_i$ of subcells such that any critical cell, any abnormally downward noncritical cell together with all those cells from which arrows point into it and any abnormally upward noncritical cell together with all cells into which its arrows point are contained in one of the $C_i$. An important observation is that because no cell is allowed to possess both incoming and outgoing arrows, each $C_i$ consists either of a single critical cell, or its members are of two adjacent dimensions.

By construction, there is no path (following the arrows) that moves from a cell in $C_i$ to another cell outside of $C_i$. Therefore, each $C_i$ is invariant. Since they constitute the building blocks for computing the Poincaré polynomial of the CW complex, we may formulate

Definition 4.1

• (i) The isolated invariant sets are the collections $I_i=C_i$;

• (ii) The isolating neighborhood N(I) of I is $N(I)=\cup _{\sigma \in I} \bar{\sigma }$;

• (iii) The exit set E(I) for each such I is $E(I)=N(I)\setminus I$.

To proceed, we show that we can find a discrete Morse–Bott function f such that the extracted vector field of f is exactly our arrow configuration.

Proposition 4.1

Suppose we have a CW complex $\mathbb {K}$ together with the arrow configuration given by Definition 2.3. Then, there exists a discrete Morse–Bott function whose extracted vector field coincides with this arrow configuration.

Proof

We already know that it is always possible, from Lemma 2.1, to find a discrete function f such that the vector field extracted from f yields the given arrow configuration. We get a discrete Morse–Bott function f, see [30, Definition 2.2], by requiring that for every isolated invariant set I:

• for every $\sigma ,\,\,\tau \,\in \,I,$$\,\,f(\sigma )=f(\tau )$,

• for every cell $\sigma \in I$,

  • (i) $f(\sigma ) \,\, >\,\,\max \{f(\nu ),\,\nu <\sigma ,\,\nu \,\notin \,I\}$,

  • (ii) $f(\sigma )\,\,<\,\,\min \{f(\tau ),\,\tau >\sigma ,\,\tau \,\notin \,I\}$.

• The remaining cells in the CW complex are those that belong to noncritical pairs, and we require

  • (iii) $f(\sigma ) \,\,<\,\,f(\nu )$, for $\nu <\sigma \,\,$ s.t.    $n_\mathrm{in}(\sigma )=1,\,\,n_\mathrm{ou}(\nu )=1$ and $\, \,\nu \rightarrow \sigma ,$

  • (iv) $f(\sigma ) \,\, >\,\,f(\tau )$, for $\tau >\sigma$ s.t.    $n_\mathrm{ou}(\sigma )=1,\,\,n_\mathrm{in}(\tau )=1$ and $\, \,\sigma \rightarrow \tau$.

Such a function f is discrete Morse–Bott, and each isolated invariant set is exactly a reduced collection (that is not a noncritical pair); see [30, Definition 2.5]. $\square$

Before stating the main result, we shall prove some auxiliary results.

Lemma 4.2

The set $N(I)\setminus I$ is a subcomplex.

Proof

Although this follows from [30, Theorem 3.2], we provide a proof that does not use the discrete Morse–Bott function, but only the arrow pattern.

If $\sigma \in N(I)\setminus I$, then $\sigma$ is the face of an element in I but it is not in I. Since N(I) is a subcomplex, we only need to show that any $\nu <\sigma$ is not in I.

$\nu \in I$ is not possible, however, because, as observed above, the cells in I are at most of two adjacent dimensions $k, k+1$. And then $\sigma$ has to be of dimension k or $k-1$, and $\nu$ consequently of dimension $k-1$ or $k-2$, and thus cannot be in I. $\square$

Definition 4.2

For an isolated invariant set I, the boundary operator $\,\partial ^{I}_k:C_k(I,\mathbb {Z})\rightarrow C_{k-1}(I,\mathbb {Z})$ is given by:

$$\begin{aligned} \partial ^I_k\tau ^{(k)}=\sum _{\sigma \in I,\sigma <\tau }[\tau :\sigma ] \sigma ^{(k-1)}. \end{aligned}$$

Lemma 4.2 implies that the boundary operator $\partial ^{I}$, see also [30, Definition 2.7], is a well-defined relative boundary operator of the pair (N(I), E(I)).

Recall that $\bar{m}_k:=\dim \bar{C}_k$, and let

$$\begin{aligned} n_k^{I}:=\sharp \{\sigma ^{(k)}\in I\}; \end{aligned}$$

then, we have the following.

Lemma 4.3

$\sum _k \overline{m}_k t^k = \sum _i \sum _k n_k^{I_i} t^k$.

Proof

It follows easily from the definitions of $\overline{m}_k$ and the $I_i$’s, since the $I_i$’s are disjoint and $\cup _i I^{(k)}_i= \bar{C}_k$, where $I^{(k)}$ denotes the set of k-cells of I. $\square$

Let us recall that for an isolated invariant set I,

$$\begin{aligned} P_t(I):= \sum _{k=0}^{\dim \mathbb {K}} \dim \big (\ker \partial ^I_k/ {{\,\mathrm{im}\,}}\partial ^I_{k+1}\big ) t^k. \end{aligned}$$

Lemma 4.4

For each i, there exist $r_i(t)$, a polynomial in t with nonnegative integer coefficients, such that

$$\begin{aligned} \sum _k n^{I_i}_k t^k = P_t(I_i)+ (1+t)r_i(t). \end{aligned}$$

Proof

From [30, Proposition 2.6], each $r_i(t)=\sum _{k=1} (n_k^{I_i}-\dim \ker \partial _k^{I_i})t^{k-1}$, where $\partial _k^{I_i}$ is also the relative boundary operator of $(N(I_i),E(I_i))$ since both $N(I_i)$ and $E(I_i)$ are subcomplexes. $\square$

The main result in this section now states that we can retrieve the Poincaré polynomial of the CW complex from those of the isolated invariant sets, or from those of the index pairs of the isolated invariant sets.

Theorem 4.5

Let $I_i$ be the isolated invariant sets of Definition 4.1 obtained from an arrow configuration as in Definition 2.3. Then, there exists $\bar{R}(t)$, a polynomial in t with nonnegative integer coefficients, such that

$$\begin{aligned} \sum _i P_t(N(I_i), E(I_i))=\sum _i P_t(I_i)= P_t(\mathbb {K}) + (1+t)\bar{R}(t). \end{aligned}$$

Proof

The first equality follows from the fact that $\partial _k^{I}$ is the relative boundary operator of the pair (N(I), E(I)). Now, using Proposition 4.1, the fact that $\sum _i P_t(I_i)= P_t(\mathbb {K}) + (1+t)\bar{R}(t)$ follows from [30, Theorem 2.7] and the fact that $\sum _i P_t(N(I_i), E(I_i))= P_t(\mathbb {K}) + (1+t)\bar{R}(t)$ follows from [30, Theorem 3.2]. $\square$

Example 4.1

In Fig. 14,

$$\begin{aligned}&\tau _1=(\nu _1,\nu _2,\nu _4), \tau _2=(\nu _2,\nu _3,\nu _4),\\&\tau _3=(\nu _1,\nu _3,\nu _4), \tau _4=(\nu _1,\nu _2,\nu _3).\\&\sigma _1=(\nu _1,\nu _4), \sigma _2=(\nu _1,\nu _2), \sigma _3=(\nu _2,\nu _4), \\&\sigma _4=(\nu _2,\nu _3), \sigma _5=(\nu _3,\nu _4), \sigma _6=(\nu _1,\nu _3). \end{aligned}$$

We get $I_i=\{\nu _i\}$, for $i=1,\ldots ,4$,

$$\begin{aligned}&I_5=\{\tau _1, \sigma _1,\sigma _2\}, I_6=\{\tau _4,\sigma _4,\sigma _6\}, \\&I_7=\{\tau _3\}, I_8=\{\sigma _5\}. \end{aligned}$$

For $i=1,\ldots ,4$, $P_t(I_i)=1$, $P_t(I_5)=t$, $P_t(I_6)=t$, $P_t(I_7)=t^2$, $P_t(I_8)=t$.

$$\begin{aligned} {\sum }_i P_t(I_i)=4+3t+t^2=1+t^2 +3(1+t), \end{aligned}$$

so $\bar{R}(t)=3$, since $P_t(\mathbb {K})=1+t^2$.

Fig. 14

A vector field as in Definition 2.3

Fig. 15

Isolating neighborhood and exit set for $I_5$ in Example 4.1

Remark 4.1

In Example 4.1, one also looks at the exit set and isolating neighborhoods for each $I_i$. For example, Fig. 15 shows what is the exit set denoted by E and the isolating neighborhood denoted by N, for the isolated invariant set $I_5$. Geometrically, one looks at N / E by identifying the exit set E and using $P_t(N,E)=P_t(N/E)-1=t.$ One gets a similar result for $I_6$.