Introduction

The main object of water flooding in high-watercut oilfield has changed from homogeneous reservoirs with good physical property to heterogeneous reservoirs with low permeability or ultra-low permeability. The overall utilization of heterogeneous low-permeability reservoirs under current development conditions remains to be improved. Therefore, the seepage flow patterns in heterogeneous low-permeability reservoirs are basic problems to be further studied on. Qualitative description and quantitative characterization of seepage flow patterns in low-permeability reservoirs in different heterogeneous conditions offer certain guidance in further study of seepage mechanism and oilfield production practice.

At present, there are many researches on fluid percolation characteristics in porous media, but the research of seepage flow patterns and relevant mechanism in heterogeneous low-permeability reservoirs is not systematic and perfect, and experiments are limited to relationship between pressure difference and fluid volume (Kortekaas 1985; Mala and Li 1999; Qu and Kong 2002) or experimental determination of relative permeability curves of natural cores (Zhang et al. 2004; Li et al. 2008). Relevant research of pressure gradient distribution for characterizing seepage flow patterns on plane is rarely studied. The conventional one-dimensional physical models are well used and widely developed because of low cost and easy test, but it cannot simulate the influence of heterogeneity condition and injection–production relationship (Yan et al. 1990; Wu et al. 2012; Liu et al. 2013). Three-dimensional heterogeneous low-permeability artificial core plate models can simulate reservoirs with poor physical property and characterize the influence of injection–production and heterogeneity (Xue 2011; Xu et al. 2012), so as to study on seepage flow patterns in heterogeneous low-permeability reservoirs.

Background

Similarity theory is the basic principle of experiments, and the experimental conditions such as geometric, physical and institutional and time proportion should be reduced to reasonable scale (Geertsma et al. 1956; Kong 1997; Teng et al. 2013). The corresponding proportion of physical quantity is brought into the oil–water two-phase control equation, and simplified physical quantities similar scale can be obtained.

$$\frac{{P_{\text{m}} t_{\text{m}} }}{{L_{\text{m}}^{2} \mu_{\text{m}} }} = \frac{{P_{\text{r}} t_{\text{r}} }}{{L_{\text{r}}^{2} \mu_{\text{r}} }}$$
(1)
$$\frac{{P_{\text{m}} }}{{L_{\text{m}} }} = \frac{{P_{\text{r}} }}{{L_{\text{r}} }}$$
(2)
$$\frac{{P_{\text{m}} }}{{\rho_{\text{m}} gL_{\text{m}} }} = \frac{{P_{\text{r}} }}{{\rho_{\text{r}} gL_{\text{r}} }}$$
(3)
$$\frac{{P_{\text{m}} }}{{\sigma_{\text{m}} \cos \theta_{\text{m}} }} = \frac{{P_{\text{r}} }}{{\sigma_{\text{r}} \cos \theta_{\text{r}} }}$$
(4)

\(\frac{Pt}{{\mu L^{2} }}\), \(\frac{P}{L}\), \(\frac{P}{\rho gL}\) and \(\frac{P}{\sigma \cos \theta }\) these four combined physical quantities should remain unchanged at corresponding time points and positions, where P m is pressure in plate model; P r is pressure in reservoir; t m is simulation of production time in plate model; t r is production time in reservoir; L m is geometry dimension of plate model; L r is geometry dimension of reservoir; μ m is fluid viscosity in plate model; μ r is fluid viscosity in reservoir; ρ m is fluid density in plate model; ρ r is fluid density in reservoir; σ m is interfacial tension between fluid and medium in plate model; σ r is interfacial tension between fluid and medium in reservoir; θ m is wetting angle in plate model; θ r is wetting angle in reservoir.

Heterogeneous artificial core plate models with low permeability are designed and made based on permeability and porosity characteristics. Sand packing method is carried out to simulate greatly varied sedimentary facies between injection and production points, permeability is controlled by particle size, and porosity is controlled by cement content and packing pressure (Pi 2010).

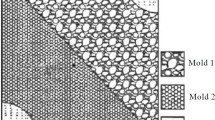
Twelve pressure transducers are symmetrically arranged on plane in the vertical middle position of artificial core plate models to design of heterogeneous artificial core plate models (Fig.1). Pressure transducers cannot be set too many to influence the fluid seepage flow patterns and the pressure bearing performance of plate models, and not too few to get enough pressure eigenvalues.

Fig. 1
figure 1

Design of heterogeneous artificial core plate models

Full size image

Figure 2 shows the top view and front view of certain heterogeneous artificial core plate model; its appearance, size and seal meet the design standards and laboratory simulation requirements.

Fig. 2
figure 2

Top view and front view of some artificial core plate model

Full size image

The similar variation trend of permeability with pressure can ensure the accuracy of simulation, the permeability of low-permeability reservoirs change under different pressure conditions. Equivalent permeability derived from the formula of Darcy flow in five-point well patterns (Hubbert 1956) is used to characterize the ability of plate models to allow fluid to seepage flow.

$$\bar{K} = \frac{{Q\mu \left[ {{ \ln }\frac{d}{{r_{\text{w}} }} - 0.619} \right]}}{4\pi h\Delta P}$$
(5)

where \(\bar{K}\) is equivalent permeability of plate model; Q is flow rate; h is formation thickness; ∆P is pressure difference of injection and production wells; μ is fluid viscosity; d is well spacing of injection and production wells; r w is wellbore radius.

Relation curves between equivalent permeability of heterogeneous artificial core plate models with low permeability and pressure difference show that the equivalent permeability increases with the increase in pressure difference due to the influence of starting pressure gradient when the permeability of cores or plate models is at a low level. Equivalent permeability changes more significantly when the pressure difference is low. The variation trend of permeability with pressure difference in artificial core plate models and low-permeability reservoir cores with the same permeability is similar (Fig. 3).

Fig. 3
figure 3

Relationship between pressure difference and equivalent permeability of artificial core plate model and cores from low-permeability reservoir

Full size image

Experiments

The self-designed physical simulation equipments of artificial core plate models consist of four parts: injection and control system, artificial core plate model auxiliary system, pressure measurement and recording system, and production and measurement system.

Different heterogeneous artificial core plate models with low permeability are designed, made and evaluated in order to study on the seepage flow patterns of low-permeability reservoirs with different heterogeneity conditions (Fig. 4). Physical simulation experiments were carried out using four groups of plate models named 10–10, 10–20, 10–50 and 10–100 mD to characterize four types of plane heterogeneity. The permeability of injection point zone is set to 10 × 10−3 μm2, and the permeability of production point zone is set between 10 × 10−3 μm2 and 100 × 10−3 μm2. The analysis focuses on four cases of permeability contrast of 1, 2, 5 and 10. Filtered formation water is injected under constant pressure difference of 0.35 MPa to simulate production under constant pressure. The pressure value at each measurement point on plane is obtained after the flow rate of production point is stable, and pressure gradient data can be filled with pressure data with extrapolation interpolation algorithm processing after planar mesh generation. Pressure gradient distribution map and seepage flow patterns map of different plate models can be drew to analyze seepage flow patterns of heterogeneous low-permeability reservoirs with different properties.

Fig. 4
figure 4

Self-designed physical simulation equipments of artificial core plate models. 1 Injection and controlling system; 2 Artificial core plate model auxiliary system; 3 Pressure measurement and recording system; 4 Production and measurement system; 5 High-pressure pump; 6 Pressure stabilizing device; 7 Injection fluid tank; 8 Micro-flowmeter; 9 Electronic balance; 10 Pressure inspection instrument; 11 Recording system

Full size image

Results and discussion

Fluid seepage flow in reservoirs is the process of fluid flow by consuming pressure, and pressure gradient represents the pressure change in unit length along the pressure and fluid flow direction, so pressure gradient distribution of heterogeneous artificial core plate models with low permeability can reflect seepage flow patterns of heterogeneous low-permeability reservoirs. The same color metric scale is used to facilitate contrastive analysis.

Pressure gradient distribution maps of artificial core plate models (Fig. 5) show that the pressure gradient contours are approximately elliptical with the well points as the center of the ellipse and connection line of injection and production points as long axis, and the integral form of pressure gradient contours of different plate models are similar. The pressure gradient is very high around well points, and the pressure gradient of diagonal corner is very low.

Fig. 5
figure 5

Pressure gradient distribution maps of artificial core plate models

Full size image

The variation of pressure gradient around wellbore increases as increased heterogeneity degree determined by different permeability of different plate models. The area of high pressure gradient around the wellbore is decreased due to the increasing of permeability of production zone, the distribution of contours is more sparse, the pressure drop of the same distance becomes smaller, and the propagation distance of the same pressure becomes larger. At the same time, low pressure gradient region of plate models becomes smaller.

The distribution of pressure gradient of connection line of injection and production points in heterogeneous artificial core plate models with low permeability is shown in Fig. 6. The horizontal axis is the dimensionless length expressed as L refers to the ratio of distance from the injection point and well spacing. Pressure gradient distribution map shows that pressure gradient around well points is very high, and the pressure gradient of the midpoint of the connection line is the lowest. The pressure gradient of connection line of injection and production points showed a trend of decreasing first and then rising (Table 1).

Fig. 6
figure 6

Pressure gradient distribution map of connection line of injection and production points

Full size image
Table 1 Pressure gradient of connection line of injection and production points
Full size table

The pressure gradient around injection and production points in different heterogeneous artificial core plate models changes greatly, and the pressure gradient of the midpoint of the connection line of injection and production points has little change. For injection point, the minimum pressure gradient of 10–10 mD plate model is 0.8669 MPa/m, and pressure gradient of 10–100 mD plate model increases to 0.9352 MPa/m, and the change extent is 9.95%. For production point, the maximum pressure gradient of 10–10 mD plate model is 0.8664 MPa/m and decreases to 0.8258, 0.7562, 0.6936 MPa/m as permeability decreases.

The heterogeneity of plate models is determined by change of permeability, and heterogeneity and permeability both influence pressure gradient distribution. The heterogeneity of plate model is stronger as the permeability of production point is higher when overall physical property of plate models is poor. The pressure gradient decreases and the propagation distance increases, and strong heterogeneity has a negative effect on pressure propagation at the same time. The energy attenuation of fluid flow becomes larger and the pressure gradient around wellbores increases, and pressure drop of the same distance increases.

Typical relation curves of seepage velocity and pressure gradient in low-permeability reservoir (Fig. 7) shows that the seepage velocity is zero when the pressure gradient is less than G s, the seepage velocity increases nonlinearly as concave curve when the pressure gradient is between G s and G c, the seepage velocity increases linearly when pressure gradient is more than G c.

$$V = \left\{ {\begin{array}{*{20}l} 0 \hfill & {G < G_{\text{s}} } \hfill \\ {a\frac{K}{\mu }G^{b} } \hfill & {G_{\text{s}} < G < G_{\text{c}} } \hfill \\ {\frac{K}{\mu }\left( {G - G_{\text{q}} } \right)} \hfill & {G > G_{\text{c}} } \hfill \\ \end{array} } \right.$$
(6)
Fig. 7
figure 7

Typical relation curves of seepage velocity and pressure gradient in low-permeability reservoir

Full size image

Typical relation curves of seepage velocity and pressure gradient can be divided into three sections, i.e., the non-seepage flow section, the nonlinear seepage flow section and the quasi-linear seepage flow section by G s and G c, where K is permeability; V is velocity of fluid flow; G s is starting pressure gradient; G c is critical starting pressure gradient; G q is quasi-starting pressure gradient; a and b are fitting coefficients.

The typical seepage flow pattern chart of low-permeability reservoir (Fig. 8) shows that there are three types of seepage flow for fluid in low-permeability reservoirs, which are non-flow, nonlinear flow and quasi-linear flow (Prada and Civan 1999; Lu et al. 2002; Shi 2006), and plate models can be divided into three sections by types of seepage flow for fluid flowing through, i.e., the non-seepage flow section, the nonlinear seepage flow section and the quasi-linear seepage flow section as pressure gradient change.

Fig. 8
figure 8

Typical seepage flow pattern chart of low-permeability reservoir

Full size image

Sketch map of seepage flow section of heterogeneous low-permeability plate models (Fig. 9) shows that there is non-seepage flow section in the diagonal corner, the ratio of non-seepage flow section is the smallest, and the ratio of nonlinear seepage flow section is the largest in plate model. Form and ratio of different seepage flow sections change as heterogeneity of plate models enhance caused by permeability of production points increasing.

Fig. 9
figure 9

Sketch map of seepage flow section of heterogeneous low-permeability plate models

Full size image

Ratio of non-seepage flow section in 10–10 mD plate model is up to 15.749%, and it is the biggest of all four models, and ratio of non-seepage flow section gradually decreases as permeability of production points increases. Ratio of non-seepage flow section in 10–100 mD plate model is 14.361%, change extent is 8.813% compared with 10–10 mD plate model, and it is the smallest of all four models. On the contrary, ratio of seepage flow section included nonlinear seepage flow section and quasi-linear seepage flow section overall increases. Ratio of nonlinear seepage flow section reduces from 50.707 to 50.292, 49.668 and 49.504%, and ratio of quasi-linear seepage flow section which is more conducive to fluid flow increases gradually from 33.544 to 36.135%.

Seepage flow capacity of plate models increases with the increase in permeability, but the enhancement of heterogeneity has a negative effect on pressure transmission at the same time. Seepage flow section of heterogeneous low-permeability plate models shows that the effect of permeability is greater than the negative impact of heterogeneous when the overall permeability of the plate model is at a very low level.

Conclusions

Heterogeneous artificial core plate models with low permeability are designed, made and evaluated based on similarity theory of heterogeneous reservoir with low-permeability physical simulation by artificial core plate model; then, simulative experiments for seepage flow patterns can be carried out. Pressure data can be obtained by pressure transducers symmetrically arranged in artificial core plate models to study on the seepage flow patterns in heterogeneous reservoir with low permeability.

The pressure gradient contours are approximately elliptical with the well points as the center of the ellipse and connection line of injection and production points as long axis. The pressure gradient is very high around well points, and the pressure gradient of diagonal corner is very low. The variation of pressure gradient around wellbore increases as increased heterogeneity degree determined by different permeability of different plate models.

Plate models can be divided into three sections by types of seepage flow for fluid flowing through, i.e., the non-seepage flow section, the nonlinear seepage flow section and the quasi-linear seepage flow section as pressure gradient change. There is non-seepage flow section in the diagonal corner, and the form and ratio of different seepage flow sections change as heterogeneity of plate models enhances (Table 2).

Table 2 Seepage flow sections of heterogeneous low-permeability plate models
Full size table

Seepage flow capacity of plate models increases with the increase in permeability, but the enhancement of heterogeneity has a negative effect on pressure transmission at the same time. Seepage flow section of heterogeneous low-permeability plate models shows that the effect of permeability is greater than the negative impact of heterogeneous when the overall permeability of the plate model is at a very low level.