Similar construction method for non-Newtonian power-law fluid seepage models with elastic outer boundary conditions

Abstract

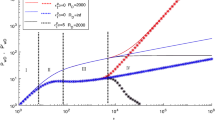
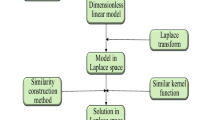
In oil and gas engineering, non-Newtonian fluids are universal. Thus, studies on the seepage laws of non-Newtonian power-law fluids are of great importance and significance. In this paper, we introduced the definition of elastic coefficient based on the establishing elastic outer boundary conditions. We then set up a homogeneous well test model for non-Newtonian power-law fluids under elastic outer boundary conditions, considering wellbore reservoir and skin effect. The Laplace space solution of the bottom hole pressure was obtained using the similar structure method, and the double logarithmic characteristic curve was drawn using the Stehfest numerical inversion technique. Furthermore, the main parameters affecting the characteristic curve were analyzed. The experimental results showed that the early phase of the homogeneous well test curve can be affected by the wellbore storage coefficient. In addition, the mid-term seepage is greatly influenced by the power-law flow exponent and the skin factor, while the elastic coefficient predominantly acts on the later phase of fluid flow. We concluded that the introduction of the elastic outer boundary expands the traditional fixed form of ideal outer boundary conditions, enabling a more general representation of the seepage model. This approach provides a more effective theoretical basis for further exploration of the seepage law of the reservoir. Meanwhile, we simplify the calculation process of the solution model by the use of the similar structure method of the solution and point out a new research direction for solving the more complex seepage model.

Appendices

Appendix A: The process of solving the boundary value problem

For the boundary value problem of the second-order linear homogeneous ordinary differential equation

$$\begin{aligned} \left\{ \begin{aligned}&{{x}^{2}}y''+Axy'-B{{x}^{d}}y=0 \\&{{\left[ Ey+\left( 1+EF \right) y' \right] }_{x=a}}=D \\&{{\left[ {{\varepsilon }_{b}}y+xy' \right] }_{x=b}}=0 \\ \end{aligned} \right. , \end{aligned}$$

(A1)

where A, B, D, E, F, a, b, d are all real constants, and $D \ne 0$, $0< a < b$.

Assuming that there exists a unique solution to the boundary value problem Eq. (A1), the solution can be described in the following continuous fractional form

$$\begin{aligned} y\left( x \right) = D \cdot \frac{1}{{E + \frac{1}{{F + \Phi \left( a \right) }}}} \cdot \frac{1}{{F + \Phi \left( a \right) }} \cdot \Phi \left( x \right) . \end{aligned}$$

(A2)

Derivation: the definite solution equation in the boundary value problem Eq. (A1) is made variable replacement

$$\begin{aligned} h = {x^m}y,s = \kappa {x^l}, \end{aligned}$$

(A3)

then it is reduced to the following modified Bessel equation that can be shown as follows

$$\begin{aligned} \frac{{{d^2}h}}{{d{s^2}}} + \frac{1}{s}\frac{{dh}}{{ds}} - \left( {1 + \frac{{{v^2}}}{{{s^2}}}} \right) h = 0, \end{aligned}$$

(A4)

where $m = \frac{{A - 1}}{2}$, $l = \frac{d}{2}$, $\kappa \mathrm{{ = }}\frac{{2\sqrt{B} }}{d}$, $v = \frac{{1 - A}}{d}$.

Then, the general solution of the modified Bessel equation Eq. (A4) is

$$\begin{aligned} h = {C_1}{K_v}\left( {\kappa {x^l}} \right) + {C_2}{I_v}\left( {\kappa {x^l}} \right) , \end{aligned}$$

(A5)

where ${C_1}$, ${C_2}$ are arbitrary constants and ${I_v}\left( \cdot \right)$, ${K_v}\left( \cdot \right)$ are the first and second type of modified Bessel functions of order v, respectively. Bringing Eq. (A5) into the variable substitution Eq. (A3), the general solution of the definite solution equation in the boundary value problem Eq. (A1) can be shown as:

$$\begin{aligned} y\left( x \right) = {x^m}\left[ {{C_1}{K_v}\left( {\kappa {x^l}} \right) + {C_2}{I_v}\left( {\kappa {x^l}} \right) } \right] . \end{aligned}$$

(A6)

Bringing Eq. (A6) into the second and third equations in the boundary value problem Eq. (A1), we obtain

$$\begin{aligned}{} & {} \begin{array}{llll} \left\{ {E{a^m}{K_v}\left( {\kappa {a^l}} \right) + \left( {1 + EF} \right) \left[ {\left( {m + lv} \right) {a^{m - 1}}{K_v}\left( {\kappa {a^l}} \right) - \kappa l{a^{m + l - 1}}{K_{v + 1}}\left( {\kappa {a^l}} \right) } \right] } \right\} {C_1}\\ + \left\{ {E{a^m}{I_v}\left( {\kappa {a^l}} \right) + \left( {1 + EF} \right) \left[ {\left( {m + lv} \right) {a^{m - 1}}{I_v}\left( {\kappa {a^l}} \right) + \kappa l{a^{m + l - 1}}{I_{v + 1}}\left( {\kappa {a^l}} \right) } \right] } \right\} {C_2} = 0, \end{array} \end{aligned}$$

(A7)

$$\begin{aligned}{} & {} \begin{array}{llll} \left[ {\left( {{\varepsilon _b} + m + lv} \right) {b^m}{K_v}\left( {\kappa {b^n}} \right) - \kappa l{b^{m + l}}{K_{v + 1}}\left( {\kappa {b^l}} \right) } \right] {C_1} + \big [ \left( {{\varepsilon _b} + m + lv} \right) {b^m}{I_v}\left( {\kappa {b^n}} \right) \\ + \kappa l{b^{m + l}}{I_{v + 1}}\left( {\kappa {b^l}} \right) \big ]{C_2} = 0. \end{array} \end{aligned}$$

(A8)

Combining Eqs. (4)–(8), we obtain the coefficient matrices of Eqs. (A7) and (A8)

$$\begin{aligned} \Delta \mathrm{{ = }}E{\varepsilon _b}{\varphi _{0,0}}\left( {a,b} \right) + Eb{\varphi _{0,1}}\left( {a,b} \right) + \left( {1 + EF} \right) {\varepsilon _b}{\varphi _{1,0}}\left( {a,b} \right) + \left( {1 + EF} \right) b{\varphi _{1,1}}\left( {a,b} \right) . \end{aligned}$$

(A9)

Because $\Delta \ne 0$ and $D \ne 0$, so applying Cramer’s rule, we can find ${C_1}$, ${C_2}$,

$$\begin{aligned} {C_1} = \frac{D}{\Delta }\left[ {\left( {{\varepsilon _b} + m + nv} \right) {b^m}{I_v}\left( {\kappa {b^l}} \right) + \kappa l{b^{m + l}}{I_{v + 1}}\left( {\kappa {b^l}} \right) } \right] , \end{aligned}$$

(A10)

$$\begin{aligned} {C_2} = - \frac{D}{\Delta }\left[ {\left( {{\varepsilon _b} + m + nv} \right) {b^m}{K_v}\left( {\kappa {b^l}} \right) - \kappa l{b^{m + l}}{K_{v + 1}}\left( {\kappa {b^l}} \right) } \right] . \end{aligned}$$

(A11)

Bring Eqs. (A10) and (A11) into Eq. (A6) and collate to get

$$\begin{aligned} y\left( x \right) = \frac{{{\varepsilon _b}{\varphi _{0,0}}\left( {x,b} \right) + b{\varphi _{0,1}}\left( {x,b} \right) }}{{E{\varepsilon _b}{\varphi _{0,0}}\left( {a,b} \right) + Eb{\varphi _{0,1}}\left( {a,b} \right) + \left( {1 + EF} \right) {\varepsilon _b}{\varphi _{1,0}}\left( {a,b} \right) + \left( {1 + EF} \right) b{\varphi _{1,1}}\left( {a,b} \right) }}. \end{aligned}$$

(A12)

Define the similar kernel function $\Phi \left( x \right)$ as Eq. (3), then Eq. (A12) can be reduced to Eq. (2).

Appendix B Nomenclature

Subscript:

D = Dimensionless

w = Well

Symbol	Meaning	Unit
p	Pressure	MPa
${p_0}$	Initial pressure	MPa
${p_w}$	Wellbore pressure	MPa
r	Radial distance	m
${r_w}$	Wellbore distance	m
${\mu _{eff}}$	Effective viscosity for power-law fluids	Mpa s
${\mu ^ * }$	Characteristic viscosity for power-law fluids	Mpa s
q	Flow rate, stock-tank	$\mathrm{m^3}/\textrm{d}$
${q_{sf}}$	Sand-face flow rate, stock-tank	$\mathrm{m^3}/\textrm{d}$
k	Permeability	$\mu \mathrm{m^2}$
${C_t}$	Total compressibility	$\textrm{MP}\mathrm{a^{ - 1}}$
${C_L}$	Fluid compressibility	$\textrm{MP}\mathrm{a^{ - 1}}$
${C_f}$	Rock compressibility	$\textrm{MP}\mathrm{a^{ - 1}}$
C	Wellbore storage coefficient	$\mathrm{m^3}/\textrm{MPa}$
h	Reservoir thichness	m
t	Production time	h
n	Flow behavior index(power law paeameter)	Dimensionless
${\varepsilon _r}$	Elastic coefficient	Dimensionless
$\phi$	Porosity	Dimensionless
S	Skin factor	Dimensionless