Abstract
Where are we to look for the unique hues? Out in the world? In the eye? In more central processing? 1. There are difficulties looking for the structure of the unique hues in simple combinations of cone-response functions like (L − M) and (S − (L + M)): such functions may fit pretty well the early physiological processing, but they don’t correspond to the structure of unique hues. It may seem more promising to look to, e.g., Hurvich & Jameson’s ‘chromatic response functions’; but these report on psychophysical behaviour, not on underlying physiology. So ‘opponent processing’ isn’t any particular help on the unique hues—and even physiology in general seems not to have come up with any good correlate or explanation. 2. Wright (Review of Philosophy and Psychology 2: 1–17, 2011) looks in a different place: to (a) magnitude of total visual response that a stimulus light provokes, the maxima and minima of which, he thinks, give us the boundaries of the main hue categories (Wright connects these with Thornton’s ‘prime’ and ‘antiprime’ colours in an illuminant: Journal of the Optical Society of America 61 (1971): 1155–1163); and (b) the ratio of chromatic to achromatic response, the maxima and minima of which, he suggests, give us the focal points of the unique hues. The suggestions are extremely interesting; but the desired correspondences have some counterexamples; and where they hold, one could wonder how much they depend upon the particular choice of functions to measure (a) and (b); and one could hope for more of an explanatory linkage between the sets of items in question. 3. Could the unique hues come from, so to speak, the external world? White and black can easily be defined as particular kinds of reflectance. What of the standard four unique hues? Variation in kinds of sunlight and skylight coincides well with variation along a line from unique yellow to unique blue (cf. Shepard 1992, Mollon 2006). If we wanted something to calibrate our standards for unique yellow and blue as the lens of the eye changes with age, and despite interpersonal cone differences, this would be a good basis—and there are several ways this can be extended to surface colours. But is there any essential connection between these things: is there any rationale why the light of the sun and the sky should be counted as unique hued? An answer may be: because in our environment, these illuminants are as close to white (or the natural illuminant colour) as you can get—to see things tinged with sunlight or skylight should be to see them minimally tinged with any alien colour. Whereas other hues in an illuminant would be treated as tinging with a more alien colour the thing seen.










Similar content being viewed by others
Notes
I shall later be talking of the functions used in the 1931 colorimetric system of the CIE (Commission Internationale de l’Éclairage). The functions \( \overline x \left( \lambda \right) \), \( \overline y \left( \lambda \right) \) and \( \overline z \left( \lambda \right) \) yield X, Y and Z values for a stimulus wavelength λ: they can be thought of as colour-matching functions giving the amounts of supersaturated red, green and blue lights that would be needed to match 1 unit of spectral light of wavelength λ presented in a 2° field. They are linear transformations of RGB functions that gave the amounts of real red, green and blue primaries in similar matching; for various technical reasons, the transformed functions have been found more useful than the original RGB functions relating to real primaries. For further details, see Wright 1944/1969, ch. 4; Hunt 1987 & 1998, ch. 2. There are weaknesses with the functions, some of which are corrected in the CIE 1964 colour matching functions for 10° fields, and there are now the improved cone-fundamentals of Stockman and Sharpe 1999. But the CIE 1931 system remains a standard one and useful if its limitations are recognized. The chromaticity of a stimulus may be specified by giving the proportions of X, Y, and Z needed to match it, which can be specified by x, y and z, where \( x = X/\left( {X + Y + Z} \right) \), \( y = Y/\left( {X + Y + Z} \right) \) and \( z = Z/\left( {X + Y + Z} \right) \). And since \( x + y + z = {1} \), one needs to specify only the x and y values for any given stimulus: as illustrated in the CIE x, y chromaticity diagram, e.g., as used in Figs. 5 and 8 below. For further details, see, e.g., Hunt 1987 & 1998, ch. 3.
The point is not new and should have been kept in mind even in the 1960s. Judd 1949 presents (as a development of G. E. Müller’s theory, with similarities also to Schrödinger 1925) an extraordinarily clear-sighted development of a ‘zone’ theory: the three photosensitive substances of the Young-Helmholtz theory feed into a second stage of ‘retinal sensory processes’, characterized by functions of the form a 1 L − a 2 M and b 1 L + b 2 M − b 3 S (1949, 4), much as in Fig. 1 above; which in turn feed into a third ‘optic-nerve fiber’ stage, characterized by functions equivalent (except for scaling factors) to those that became famous as Hurvich and Jameson’s ‘chromatic response functions’. (Judd (1949, 10) has an RG function equivalent to 1.0X − 1.0Y, and a YB function equivalent to 0.3168Y − 0.3168Z, whereas Hurvich and Jameson have 1.0X − 1.0Y and 0.4Y − 0.4Z (1955, 602, acknowledging their use of Judd 1951).) There are ideas in Judd’s paper that have not stood the test of time, such as Müller’s conception of deuteranopia as involving a failure of the RG-sense of the optic nerve, and his talk of these processes as (presumably chemical) changes in various ‘substances’ rather a matter of electrical firing rates in cells. But it is impressive work—and it is interesting that Judd has no tendency to talk of the second-stage retinal processes as relating to ‘red-green’ and ‘yellow-blue’ variation; rather he thinks of the a 1 L − a 2 M process as involving ‘yellowish red’ vs. ‘bluish green’, and the b 1 L + b 2 M − b 3 S process as giving ‘greenish yellow’ vs. ‘reddish blue’.
‘At several spectral loci, one or the other of the opponent curves crosses the zero line. This means that the corresponding opponent system is in neutral balance at that point. From left to right, the first of these … occurs where the red-green curve crosses the axis at 475 nm. At 475 nm, the yellow-blue system is negative and, hence, signals blue. So here redness, greenness, and yellowness are all zero. What the subject sees is a blue without any other chromatic component—a unique blue …’ (Hardin 1988, 37, my emphasis, except on ‘unique’.) This looks very much like a reference to an underlying physiological mechanism (‘the corresponding opponent system’) which is supposedly giving rise to the phenomenal character of the experience. (In general, Hardin believes, ‘The resemblances and differences of the colors are grounded not just in the physical properties of objects but even more in the biological makeup of the animal that perceives them.’ 1988, 7.) But graphs like these are reports of cancellation experiments (or of theoretical modelling of ‘cancellation’ on the basis of CIE 1931 colorimetric functions), not of discovered physiological processes. Hurvich & Jameson, and Hardin, of course knew perfectly well that such graphs as Fig. 2 are, in the first instance, graphs of psychophysical performance: their belief was that that psychophysical performance could be taken as an indication of corresponding physiological mechanisms that could then be cited as ‘explanations’ of the behaviour. But it was entirely speculative in their day, and it remains entirely speculative today, that there are physiological mechanisms of the kind they have in mind. It is no doubt true that character of brain and eye are, in some sense and some ways, responsible for the character of our colour experience; but that there is for each region in the visual field some particular channel representing degree of redness in line with positive values of a function defined as 1.6645L − 2.2301M − 0.3676S, is not something we are told by the physiologists, and not something we need to believe for a priori reasons about mind-brain type correspondence either. This is the basis of the general response I have to Byrne and Hilbert’s 2003 argument in favour of taking redness to be definable as (approximately) the external cause of some particular type of physiological response: they take it that, even if the (L − M) function doesn’t quite work, there will be a better function, physiologically realized, to plug into their theory instead. But it is, I think, entirely unnecessary, and quite possibly false, to assume there will be a single type of physiological response that is a measure, quite generally, of degree of redness (present when looking at a reddish yellow, a reddish blue, a pure red,. etc., and with a metric suitably corresponding to degree of experienced redness) and that it is the core of what underlies all our experiences of different shades and degrees of red. See also Broackes 2003 on Byrne and Hilbert 2003.
It might seem that functions with simple definitions like X − Y − Z at least have a simple naturalness to recommend them. But of course the X, Y and Z functions of the CIE are themselves defined functions, defined originally as linear transformations of certain colour-matching functions. Reexpressed in terms of hypothesized L, M and S fundamentals (the König fundamentals in Wyszecki & Stiles 1967/1982, 606), the simple-looking X − Y − Z, −X + Y − Z, and −X − Y + Z emerge with a little linear algebra as equivalent to: (1.6645L − 2.2301M − 1.4149S), (−1.6645L + 2.2301M − 2.1501S) and (−3.3695L + 1.9225M + 1.4149S). Is it plausible that functions with these coefficients have any physiological realization in the visual system? In the absence of any physiological realization, what explanatory power are we entitled to think they have?
The ‘zero-crossings from Fig. 8 will be used for prime and anti-prime colors’ (Wright 2011, 10): i.e. the values of λ for which d(|| e 1(λ), e 2(λ), e 3(λ) ||) / dλ = 0, which will be the values of λ for which || e 1(λ), e 2(λ), e 3(λ) || is at a maximum or a minimum. In the printed paper, Wright (working to the nearest 5 nm) gives these values as 445, 535, and 605 nm (for primes) and 490 and 570 nm (for anti-primes), and in an earlier version he gave 440 nm as the value of the first prime. By my own calculation (following the definitions he has supplied me with for the e-functions), the maxima and minima of his norm function are at 442, 539, and 604 nm and at 490 and 571 nm (working in 1 nm steps)—so in the main text I hope my talk of Wright placing his first prime in the ‘440–445 nm region’ is accurate enough for present purposes.
I thank Wright for pointing this out to me. Thornton’s sensitivity functions are to be understood as giving the sensitivities not of cones, but of three channels ‘deep in the normal human visual system’ (1999, 153). Whether there actually are any such ‘cortical signal’ channels meeting Thornton’s specifications deep in the visual system seems to me rather doubtful, and I am not sure that they are in any way needed to explain the colour-matching phenomena that fascinate him. A TV camera with sensors having maxima at 442, 543 and 570 nm and a sensitivity profile like the cones would also show just the same patterns of colour-matching (with, e.g., 1 unit of R600–610 light being much more efficient as a primary than R645 or YG565): there was no need for any appeal to processes with a special maximum at 600–610 nm ‘deeper’ in the visual system.
Wright tells us (Wright 2011, 5; citing Romney and Chiao 2009, 10378) that his e 1 function correlates well with the CIE Y (or V(λ)) function: the correlation between the e 1 function and the CIE L* function as applied to Munsell chips is as high as 0.9992 (where L* is defined in terms of Y/Y n, and Y n is the Y for a reference white). This may be true, but it is far from being a sign that the e 1 function is a good measure of luminance. I have done a quick back-of-an-envelope type calculation of the values of the e 1 and the CIE Y function for 15 pigments varying through the colour wheel, as illuminated in D55. (I have used the same pigments as in §12.6 of Broackes 2010, sampling the relevant functions at 20 nm intervals between 400 and 700 nm.) I have normalized the two functions to have an output of 100 for an ideal white. The correlation is indeed high (r = 0.9924); but the proportionate discrepancy between the two functions can in many cases still be very large:
 And the discrepancies between the two functions are even higher if the illuminant is a bit bluer, e.g. D75. (The correlation falls to 0.9874, and the values of the e
1 function for these pigments in D75 are in two cases 64% and 32% higher than the Y value.) The obvious conclusion is that we should not be misled by the ‘correlation’ of these two functions being above 0.99 (for some domains of application): that is perfectly compatible with the two functions having obvious and important discrepancies over significant parts of even those same domains. Of course, the Y(λ) function has its own problems as a measure of luminance and the Stockman & Sharpe V*(λ) function is surely an improvement on it. But the e
1(λ) function diverges dramatically from the V*(λ) function too in application to real-world yellows and blues: e.g., the e
1 value for Cobalt Blue in D55 is 43% above its V* value. There is no reason why, if one is making a free choice of orthogonal basis functions in terms of which to decompose the L, M and S functions, one should expect any of the functions to correspond particularly closely with luminance or brightness; conversely, since brightness is something with a fair degree of salience in the visual system, we have at least some reason to think that other functions than these e-functions are realized in the human visual system, and functions like the e
1, e
2, e
3 functions may well not be.
And the discrepancies between the two functions are even higher if the illuminant is a bit bluer, e.g. D75. (The correlation falls to 0.9874, and the values of the e
1 function for these pigments in D75 are in two cases 64% and 32% higher than the Y value.) The obvious conclusion is that we should not be misled by the ‘correlation’ of these two functions being above 0.99 (for some domains of application): that is perfectly compatible with the two functions having obvious and important discrepancies over significant parts of even those same domains. Of course, the Y(λ) function has its own problems as a measure of luminance and the Stockman & Sharpe V*(λ) function is surely an improvement on it. But the e
1(λ) function diverges dramatically from the V*(λ) function too in application to real-world yellows and blues: e.g., the e
1 value for Cobalt Blue in D55 is 43% above its V* value. There is no reason why, if one is making a free choice of orthogonal basis functions in terms of which to decompose the L, M and S functions, one should expect any of the functions to correspond particularly closely with luminance or brightness; conversely, since brightness is something with a fair degree of salience in the visual system, we have at least some reason to think that other functions than these e-functions are realized in the human visual system, and functions like the e
1, e
2, e
3 functions may well not be.
References
Abramov, I., and J. Gordon. 1994. Color appearance: On seeing red—or yellow, or green, or blue. Annual Review of Psychology 45: 451–485.
Abramov, I., and J. Gordon. 2005. Seeing unique hues. Journal of the Optical Society of America A 22: 2143–2153.
Boynton, R. 1979. Human Color Vision. New York: Holt, Rinehart & Winston.
Broackes, J. 1997. Could we take lime, purple, orange and teal as unique hues? Behavioral and Brain Sciences 20: 183–184.
Broackes, J. 2003. Do opponent process theories help physicalism about color? Behavioral and Brain Sciences 26(6): 786–788.
Broackes, J. 2010. What do the Color-Blind see? In Color ontology and color science, eds. J. Cohen & M. Matthen, 291–405. MIT Press.
Byrne, A., and D.R. Hilbert. 2003. Color realism and color science. Behavioral & Brain Sciences 26: 3–21. With subsequent Commentaries and Replies.
Cohen, J. 2001. Visual color and color mixture. Chicago: University of Illinois.
Conway, B.R., S. Moeller, and D.Y. Tsao. 2007. Specialized color modules in macaque extrastriate cortex. Neuron 56: 560–573.
Dacey, D.M., and O.S. Packer. 2003. Colour coding in the primate retina: Diverse cell types and cone-specific circuitry. Current Opinion in Neurobiology 13: 421–427.
De Valois, L.R., I. Abramov, and G.H. Jacobs. 1966. Analysis of response patterns of LGN cells. Journal of the Optical Society of America 56: 966–977.
De Valois, R.L., and K.K. De Valois. 1975. Neural coding of color. In Handbook of perception. Vol. V: Seeing, ed. E.C. Carterette and M.P. Friedman, 117–166. New York: Academic.
Derrington, A.M., J. Krauskopf, and P. Lennie. 1984. Chromatic mechanisms in lateral geniculate nucleus of macaque. The Journal of Physiology 357: 241–265.
Golz, J., and D. MacLeod. 2002. Influence of scene statistics on colour constancy. Nature 415: 637–640.
Hardin, C.L. 1988. Color for philosophers: Unweaving the rainbow. Expanded edn., 1993. Indianapolis: Hackett.
Hering, Ewald. 1878. Zur Lehre vom Lichtsinne: Sechs Mitteilungen an die Kaiserl. Akademie der Wissenschaften in Wien. 2. unveränd. Abdr. Wien: Carl Gerold’s Sohn.
Hunt, R.W.G. 1987. Measuring colour. Chichester, G.B./New York: Ellis Horwood. (2nd Edition, 1991. 3rd ed., 1998.)
Hurvich, L.M., and D. Jameson. 1955. Some quantitative aspects of an opponent-colors theory: II. Brightness, saturation, and hue in normal and dichromatic vision. Journal of the Optical Society of America 45: 602–616.
Hurvich, L.M., and D. Jameson. 1957. An opponent-process theory of color vision. Psychological Review 64: 384–404.
Jameson, D., and L.M. Hurvich. 1955. Some quantitative aspects of an opponent-colors theory: I. Chromatic responses and spectral saturation. Journal of the Optical Society of America 45: 546–552.
Jameson, K., and R. D’Andrade. 1997. It’s not really red, green, yellow, blue: An inquiry into perceptual color space. In Color categories in thought and language, eds. C.L. Hardin and L. Maffi, 295–319. Cambridge/New York: Cambridge University Press.
Johnson, K., and W. Wright. 2008. Reply to Philipona and O’Regan. Visual Neuroscience 25: 221–224.
Jordan, G., and J.D. Mollon. 1995. Rayleigh matches and unique green. Vision Research 35: 613–620.
Jordan, G., and J.D. Mollon. 1997. Unique hues in heterozygotes for protan and deutan deficiencies. In Colour vision deficiencies XIII, ed. C.R. Cavonius, 67–76. Dordrecht: Kluwer.
Judd, D.B. 1949. Response functions for types of vision according to the Müller theory. Journal of Research of the National Bureau of Standards (U.S.) 42: 1–16. Repr. in D. B. Judd, Contributions to Color Science, ed. D. L. MacAdam (Washington, DC: US Dept. of Commerce, 1979), 355–371.
Judd, D.B. 1951. Basic correlates of the visual stimulus. In Handbook of experimental psychology, ed. S.S. Stevens, 811–867. New York: Wiley.
Judd, D.B. 1952. Color in business, science, and industry. New York: Wiley.
Judd, D.B., D.L. MacAdam, and G. Wyszecki. 1964. Spectral distribution of typical daylight as a function of correlated color temperature. Journal of the Optical Society of America 54: 1031–1040.
Kuehni, R.G. 2004. Variability in unique hue selection: A surprising phenomenon. Color Research & Application 29(2): 158–162.
Kuehni, R.G., R. Shamey, M. Matthews, and B. Keene. 2010. Perceptual prominence of Hering’s perceptual primaries. Journal of the Optical Society of America A 27: 159–165.
MacLeod, Donald. 2010. Into the Neural Maze. In Color ontology and color science, ed. J. Cohen & M. Matthen, 151–178. MIT Press
Mollon, J. 2006. Monge: The Verriest lecture, Lyon, July 2005. Visual Neuroscience 23: 297–309.
Mollon, J. 2009. A neural basis for unique hues? Current Biology 19: R441–R442.
Mollon, J., and O. Estévez. 1988. Tyndall’s paradox of hue discrimination. Journal of the Optical Society of America A 5: 151–159.
Mollon, J.D., and G. Jordan. 1997. On the nature of unique hues. In John Dalton’s colour vision legacy, ed. C. Dickinson, I. Murray, and D. Carden, 391–403. London: Taylor and Francis.
Palmer, S.E. 1999. Vision science: Photons to phenomenology. Cambridge: MIT.
Philipona, D.L., and J.K. O’Regan. 2006. Color naming, unique hues, and hue cancellation predicted from singularities in reflection properties. Visual Neuroscience 23: 331–339.
Philipona, D.L., and J.K. O’Regan. 2008. Reply to Johnson and Wright. Visual Neuroscience 25: 225–226.
Regan, B.C., C. Julliot, B. Simmen, F. Viénot, P. Charles-Dominique, and J.D. Mollon. 2001. Fruits, foliage and the evolution of primate colour vision. Philosophical Transactions of the Royal Society B 356: 229–283.
Romney, A.K., and C.C. Chiao. 2009. Functional computational model for optimal color coding. Proceedings of the National Academy of Sciences 106: 10376–10381.
Saunders, B.A.C., and J. van Brakel. 1997. Are there non-trivial constraints on colour categorization? Behavioral and Brain Sciences 20: 167–228.
Schefrin, B.E., and J.S. Werner. 1990. Loci of spectral unique hues throughout the life span. Journal of the Optical Society of America A 7: 305–317.
Schrödinger, E. 1925. Über das Verhältnis der Vierfarben- zur Dreifarbentheorie. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften (Wien), Abteilung IIa (Mathematik, Astronomie, Physik …) 134: 471.
Shepard, R.N. 1992. The perceptual organization of colors: An adaptation to regularities of the terrestrial world. In The adapted mind: Evolutionary psychology and the generation of culture, ed. J.H. Barkow, L. Cosmides, and J. Tooby. Oxford: Oxford University Press.
Stockman, A., and L.T. Sharpe. 1999. Cone spectral sensitivities and color matching. In Color vision: From genes to perception, ed. K.R. Gegenfurtner and L.T. Sharpe, 53–87. New York: Cambridge University Press.
Stoughton, C., and B.R. Conway. 2008. Neural basis for unique hues. Current Biology 18: R698–R699.
Thornton, W.A. 1971. Luminosity and color-rendering capability of white light. Journal of the Optical Society of America 61: 1155–1163.
Thornton, W.A. 1999. Spectral sensitivities of the normal human visual system, color-matching functions and their principles, and how and why the two sets should coincide. Color Research & Application 24: 139–156.
Volbrecht, V.J., J.L. Nerger, and C.E. Harlow. 1997. The bimodality of unique green revisited. Vision Research 37: 404–416.
Webster, M.A., E. Miyahara, G. Malkoc, and V.E. Raker. 2000a. Variations in normal color vision. I. Cone-opponent axes. Journal of the Optical Society of America A 17(9): 1535–1544.
Webster, M.A., E. Miyahara, G. Malkoc, and V.E. Raker. 2000b. Variations in normal color vision. II. Unique hues. Journal of the Optical Society of America A 17(9): 1545–1555.
Webster, M.A., S.M. Webster, S. Bharadwaj, R. Verma, J. Jaikuma, G. Mada, and E. Vaithilingham. 2002. Variations in normal color vision. III. Unique hues in Indian and United States observers. Journal of the Optical Society of America A 19: 1951–1962.
Werner, J.S., and B.E. Schefrin. 1993. Loci of achromatic points throughout the life span. Journal of the Optical Society of America A 10: 1509–1516.
Wright, W. 2011. On the retinal origins of the Hering primaries. Review of Philosophy and Psychology 2: 1–17.
Wright, William D. 1944/1969. The measurement of colour, 4th ed. London: Adam Hilger.
Wyszecki, G. and W.S. Stiles. 1967/1982. Color science: Concepts and methods, quantitative data and formulas. 2nd edition. New York: Wiley.
Acknowledgments
Many thanks to Wayne Wright for his original paper and for continuing exchange of views on these points. I have benefited from his paper in revising the paper for publication. I am grateful to Steven Yamamoto for comments on an earlier draft and to the editors of this journal for encouraging a debate on this contentious issue.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Broackes, J. Where Do the Unique Hues Come from?. Rev.Phil.Psych. 2, 601–628 (2011). https://doi.org/10.1007/s13164-011-0050-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13164-011-0050-7


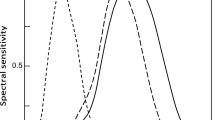

 And the discrepancies between the two functions are even higher if the illuminant is a bit bluer, e.g. D75. (The correlation falls to 0.9874, and the values of the e
1 function for these pigments in D75 are in two cases 64% and 32% higher than the Y value.) The obvious conclusion is that we should not be misled by the ‘correlation’ of these two functions being above 0.99 (for some domains of application): that is perfectly compatible with the two functions having obvious and important discrepancies over significant parts of even those same domains. Of course, the Y(λ) function has its own problems as a measure of luminance and the Stockman & Sharpe V*(λ) function is surely an improvement on it. But the e
1(λ) function diverges dramatically from the V*(λ) function too in application to real-world yellows and blues: e.g., the e
1 value for Cobalt Blue in D55 is 43% above its V* value. There is no reason why, if one is making a free choice of orthogonal basis functions in terms of which to decompose the L, M and S functions, one should expect any of the functions to correspond particularly closely with luminance or brightness; conversely, since brightness is something with a fair degree of salience in the visual system, we have at least some reason to think that other functions than these e-functions are realized in the human visual system, and functions like the e
1, e
2, e
3 functions may well not be.
And the discrepancies between the two functions are even higher if the illuminant is a bit bluer, e.g. D75. (The correlation falls to 0.9874, and the values of the e
1 function for these pigments in D75 are in two cases 64% and 32% higher than the Y value.) The obvious conclusion is that we should not be misled by the ‘correlation’ of these two functions being above 0.99 (for some domains of application): that is perfectly compatible with the two functions having obvious and important discrepancies over significant parts of even those same domains. Of course, the Y(λ) function has its own problems as a measure of luminance and the Stockman & Sharpe V*(λ) function is surely an improvement on it. But the e
1(λ) function diverges dramatically from the V*(λ) function too in application to real-world yellows and blues: e.g., the e
1 value for Cobalt Blue in D55 is 43% above its V* value. There is no reason why, if one is making a free choice of orthogonal basis functions in terms of which to decompose the L, M and S functions, one should expect any of the functions to correspond particularly closely with luminance or brightness; conversely, since brightness is something with a fair degree of salience in the visual system, we have at least some reason to think that other functions than these e-functions are realized in the human visual system, and functions like the e
1, e
2, e
3 functions may well not be.