Resource-constrained project scheduling problem with uncertain durations and renewable resources

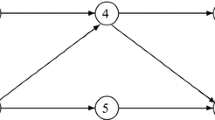
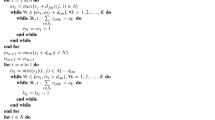Abstract

Resource-constrained project scheduling problem is to make a schedule for minimization of the makespan subject to precedence and resource constraints. In this paper, we consider an uncertain resource-constrained project scheduling problem (URCPSP) in which the activity durations, with no historical data generally, are estimated by experts. In order to deal with these estimations, an uncertainty-theory-based project scheduling model is proposed. Furthermore, a genetic algorithm integrating a 99-method based uncertain simulation is designed to search the quasi-optimal schedule. Numerical examples are also provided to illustrate the effectiveness of the model and the algorithm.

Appendix

In this section, some concepts and theorems of uncertainty theory are introduced to lay the foundation for the URCPSP modeling. Uncertainty theory is a branch of axiomatic mathematics for subjective uncertainty modeling, which has been well developed and applied in a wide variety of real problems.

Let $\Gamma$ be a nonempty set, $\fancyscript{ L }$ a $\sigma$-algebra over $\Gamma$, and each element $\Lambda$ in $\fancyscript{L}$ is called an event. Uncertain measure is defined as a function from $\fancyscript{L}$ to [0, 1]. In detail, the concept of uncertain measure is pioneered by [19] and redefined by [20]. Uncertain measure $\fancyscript{M}$ is a set function defined over the following four axioms.

Axiom 1

(Normality Axiom) $\fancyscript{M}\{\Gamma \}=1$.

Axiom 2

(Duality Axiom) $\fancyscript{M}\{\Lambda \}+\fancyscript{M}\{\Lambda ^{c}\}=1$ for any event $\Lambda$.

Axiom 3

(Subadditivity Axiom) For every countable sequence of events $\{\Lambda _{i}\}$, we have:

$${\fancyscript{M}}\left\{{\bigcup\limits_{{i = 1}}^{\infty } {\Lambda _{i} }}\right\} \le \sum\limits_{{i = 1}}^{\infty } M \{ \Lambda _{i} \} .$$

Axiom 4

(Product Measure Axiom) Let $(\Gamma _k, \fancyscript{L}_{k}, \fancyscript{M}_{k})$ be uncertainty spaces for $k=1,2,\ldots$, the product uncertain measure $\fancyscript{M}$ is an uncertain measure satisfying

$$\begin{aligned} \fancyscript{M}\left\{ \prod \limits _{k=1}^\infty A_{k}\right\} =\bigwedge _{k=1}^\infty \fancyscript{M}_{k}\{A_{k}\} \end{aligned}$$

where $A_{k}$ are arbitrarily chosen events from $\fancyscript{ L }_{k}$ for $k=1,2,\ldots$, respectively.

Definition 1

[19] An uncertain variable is a measurable function $\xi$ from an uncertainty space $(\Gamma , \fancyscript{ L }, \fancyscript{M})$ to the set of real numbers, i.e., for any Borel set B of real numbers, the set

$$\begin{aligned} \{\xi \in B\}=\{\gamma \in \Gamma \ \big |\ \xi (\gamma )\in B\} \end{aligned}$$

is an event.

The uncertainty distribution is indispensable to establish the practical uncertain optimization problems model.

Definition 2

[19] The uncertainty distribution $\Phi$ of an uncertain variable $\xi$ is defined by

$$\begin{aligned} \Phi (x)=\fancyscript{M}\{\xi \le x\} \end{aligned}$$

for any real number x.

An uncertainty distribution $\Phi$ is confirmed to be regular if its inverse function $\Phi ^{-1}(\alpha )$ exists uniquely for each $\alpha \in [0,1]$.

Definition 3

[19] Let $\xi$ be an uncertain variable. The expected value of $\xi$ is defined by

$$\begin{aligned} E[\xi ]=\int _0^{+\infty }\fancyscript{M}\{\xi \ge r\}\mathrm{d}r-\int _{-\infty }^{0}\fancyscript{M}\{\xi \le r\}\mathrm{d}r \end{aligned}$$

provided that at least one of the above two integrals is finite.

Lemma 1

[20] Let $\xi$ be an uncertain variable with uncertainty distribution $\Phi$. If the expected value exists, then

$$\begin{aligned} E[\xi ]=\int _{0}^{+\infty } (1-\Phi (x))\mathrm{d}x-\int _{-\infty }^{0} \Phi (x)\mathrm{d}x. \end{aligned}$$

Lemma 2

([20]) Let $\xi$ be an uncertain variable with regular uncertainty distribution $\Phi$. If the expected value exists, then

$$\begin{aligned} E[\xi ]=\int _0^1 \Phi ^{-1}(\alpha )d \alpha . \end{aligned}$$

Example 1

The expected value of the zigzag uncertain variable $\xi =\fancyscript{ Z }(a,b,c)$ is:

$$\begin{aligned} E[\xi ]=&\int _{0}^{0.5}((1-2\alpha )a + 2\alpha b)\mathrm {d}\alpha +\int _{0.5}^{1}((2-2\alpha )b + (1-2\alpha ) c)\mathrm{d}\alpha \\ =&\frac{a+2b+c}{4}.\nonumber \end{aligned}$$

(4)

Lemma 3

[20] Let $\xi _{1}, \xi _{2}, \ldots ,\xi _{n}$ be independent uncertain variables with regular uncertainty distributions $\Phi _{1},\Phi _{2},\ldots ,\Phi _{n}$, respectively. A function $f(x_{1},x_{2},\ldots ,x_{n})$ which is strictly increasing with respect to $x_{1},x_{2},\ldots ,x_{m}$ and strictly decreasing with respect to $x_{m+1},x_{m+2},\ldots ,x_{n}$. Then the $\xi =f(\xi _{1},\xi _{2},\ldots , \xi _{n})$ is an uncertain variable with inverse uncertainty distribution

$$\begin{aligned} \Psi ^{-1}(\alpha )= f(\Phi _{1}^{-1}(\alpha ),\ldots ,\Phi _{m}^{-1}(\alpha ),\Phi _{m+1}^{-1}(1-\alpha ),\ldots ,\Phi _{n}^{-1}(1-\alpha )). \end{aligned}$$

(5)

Lemma 4

[36] Let $\xi _{i}(i = 1, 2, . . . , n)$ be independent uncertain variables with regular uncertainty distributions $\Phi _{1},\Phi _{2},\ldots ,\Phi _{n}$ respectively. If a function $f(x_{1},x_{2},\ldots ,x_{n})$ is strictly increasing with respect to $x_{1},x_{2},\ldots ,x_{m}$ and strictly decreasing with respect to $x_{m+1},x_{m+2},\ldots ,x_{n}$ , respectively, then the expected value of uncertain variables $\xi =f(\xi _{1},\xi _{2},\ldots , \xi _{n})$ has an expected value as follows:

$$\begin{aligned} E [\xi ]&=\int _{0}^{1}f(\Phi _{1}^{-1}(\alpha ),\ldots ,\Phi _{m}^{-1}(\alpha ),\Phi _{m+1}^{-1}(1-\alpha ),\Phi _{n}^{-1}(1-\alpha ))\mathrm{d}\alpha \end{aligned}$$

(6)

provided that the expected value $E[\xi ]$ exists.