A Model for Dissolution of Lime in Steelmaking Slags

Abstract

In a previous study by Sarkar et al. (Metall. Mater. Trans. B 46B:961 2015), a dynamic model of the LD steelmaking was developed. The prediction of the previous model (Sarkar et al. in Metall. Mater. Trans. B 46B:961 2015) for the bath (metal) composition matched well with the plant data (Cicutti et al. in Proceedings of 6th International Conference on Molten Slags, Fluxes and Salts, Stockholm City, 2000). However, with respect to the slag composition, the prediction was not satisfactory. The current study aims to improve upon the previous model Sarkar et al. (Metall. Mater. Trans. B 46B:961 2015) by incorporating a lime dissolution submodel into the earlier one. From the industrial point of view, the understanding of the lime dissolution kinetics is important to meet the ever-increasing demand of producing low-P steel at a low basicity. In the current study, three-step kinetics for the lime dissolution is hypothesized on the assumption that a solid layer of 2CaO·SiO₂ should form around the unreacted core of the lime. From the available experimental data, it seems improbable that the observed kinetics should be controlled singly by any one kinetic step. Accordingly, a general, mixed control model has been proposed to calculate the dissolution rate of the lime under varying slag compositions and temperatures. First, the rate equation for each of the three rate-controlling steps has been derived, for three different lime geometries. Next, the rate equation for the mixed control kinetics has been derived and solved to find the dissolution rate. The model predictions have been validated by means of the experimental data available in the literature. In addition, the effects of the process conditions on the dissolution rate have been studied, and compared with the experimental results wherever possible. Incorporation of this submodel into the earlier global model (Sarkar et al. in Metall. Mater. Trans. B 46B:961 2015) enables the prediction of the lime dissolution rate in the dynamic system of LD steelmaking. In addition, with the inclusion of this submodel, significant improvement in the prediction of the slag composition during the main blow period has been observed.

Introduction

In their recent publication,[1] the authors developed a dynamic model for predicting the bath and slag compositions during blowing in a 160-ton LD converter. While model predictions for bath compositions appeared to be in relatively good agreement with measurements in an actual LD converter by Cicutti et al.,[2] those for the slag compositions did not correspond well to the actual values. Predictions for percent CaO in slag were too high and consequently those for percent FeO were too low. Among the assumptions made in the model,[1] one was the uniform dissolution of lime during the blowing period. The model thus lacked a proper submodel for lime dissolution which might have resulted in the observed incongruity with the real values. The current study aims to develop a submodel for lime dissolution in steelmaking slags and study the effects of different process variables on dissolution rates. Finally, this submodel would be incorporated into the global model for dynamically calculating lime dissolution rates with the aim of improving upon the predictions for slag compositions.

In the context of LD steelmaking, understanding dissolution kinetics of lime is imperative for several reasons. Lime constitutes a significant part of the total expenses for raw materials, and cutting down on lime consumption would considerably reduce the overall cost of steelmaking. A far more important reason is to get rid of free lime which is a perennial problem for operating steel plants. For conditions pertinent to Tata Steel, the amount of free lime in slags varies in the range from 5 to 10 pct,[3] and this limits its usage as a suitable building material. Another key motivation to study lime dissolution is to produce low-P steels with low-basicity slags. LD shops in Tata Steel typically operate in the basicity range from 3.2 to 3.8, and recently, there has been an increasing drive to reduce the basicity of LD slags without compromising on turndown phosphorus. Process conditions, sequence of lime addition, lime particle size, etc. may be controlled within permissible limits to achieve this goal, but first, the effects of these parameters on turndown slag conditions must be understood. A fundamental study on lime dissolution in steelmaking slags is necessary because it plays a very important role in achieving the desired slag composition at turndown.

Model Formulation

Reaction between solid CaO and SiO₂ (as SiO₄ ⁴⁻ ions) in slags results in the formation of calcium silicates, the experimental evidence for which may be found in the studies of several researchers.[4–7] The type of silicates formed depends on slag conditions (primarily slag basicity and FeO content). In the current study, it is assumed that the reaction between solid CaO and SiO₂ in slags results only in the formation of solid 2CaO·SiO₂ which forms a layer around the unreacted core of CaO. Under such conditions, further reaction between CaO and SiO₂ would require the diffusion of SiO₂ from the slag through the solid 2CaO·SiO₂ layer to the interface between the unreacted CaO and 2CaO·SiO₂. The kinetic steps involved in the dissolution process may then be summarized as:

• 1. Slag-film diffusion This step involves the diffusion of SiO₂ from the bulk slag through the slag-film boundary layer formed around solid 2CaO·SiO₂

• 2. Product-layer diffusion This involves the diffusion of SiO₂ through the 2CaO·SiO₂ layer formed around the unreacted core of CaO.

• 3. Interfacial reaction It involves the reaction between solid CaO and SiO₂ at the interface between unreacted CaO and the solid 2CaO·SiO₂. A schematic representation of these steps for a spherical CaO particle is shown in Figure 1.

  Fig. 1

  

  Schematic representation of a CaO particle in slag and the hypothetical kinetic steps in the dissolution process

Experimental study on lime dissolution in steelmaking slags have been done by several researchers.[4–10] Modeling studies on lime dissolution have been relatively less but still available.[11–13] While several insights about the dissolution of lime in slags are available from these studies, none of them provide a definite conclusion about the rate-controlling step. A majority of the experimental and modeling studies on cylindrical lime particles assumes diffusion through the slag film as rate-controlling, referring to the study by Matsushima et al.[4] However, Matsushima et al.’s[4] conclusion that slag-film diffusion is rate-controlling is not corroborated by their experimental data. They argued that an increase in dissolution rates with the increasing speeds of revolution (of the rotating lime cylinder) confirms that slag-film diffusion is rate-controlling but even in case of mixed control rates would increase with increase in the speed of revolution. Furthermore, plots of $f$ ($X$) vs $t$ for their experimental data do not confirm that slag-film diffusion is rate-controlling. Guo et al.’s[10] experimental results for dissolution of spherical lime particles in blast furnace slags clearly show three regimes in which three different mechanisms control the rate. For rectangular specimens, Deng et al.’s[7] experiments indicate that diffusion through the product layer may be rate-controlling. However, the number of data points reported by Deng et al.[7] is too less to conclude anything decisive about the rate-controlling step.

In view of the above, the current authors debunk the hypothesis made in several previous investigations (especially those on cylindrical lime specimens) that slag-film diffusion controls the overall kinetics of lime dissolution in steelmaking slags. It is further argued that in a real steelmaking process where slag conditions like basicity, FeO content, temperature etc. are continually varying during the blow it seems unlikely that a single mechanism will be rate-controlling throughout. Rather, a mixed control model that takes into account contributions from the all the three (hypothetical) kinetic steps would be more appropriate. Thus in the current study, mixed control models have been developed for calculating dissolution rates of lime.

Model Assumptions

Apart from the basic assumption about the formation of solid 2CaO·SiO₂, the following are the main assumptions of the model:

• 1. At the interface between the unreacted lime and the solid 2CaO·SiO₂ layer, equilibrium conditions are attained.

• 2. Steady-state conditions are assumed to prevail, except in some cases where a pseudo-steady-state approximation has been made.

• 3. Diffusion of only SiO₂ is considered. Diffusion of other slag constituents like FeO, P₂O₅, etc. is not considered.

• 4. Diffusion is primarily considered to be taking placing along one principal direction.

• 5. Different geometries of lime specimen have been considered, but it has been assumed that lime particles of a particular geometry retain their original shape.

Governing Equations

The initial part of the model development involves the derivation of rate equations for each of the three rate–controlling steps for three different lime geometries. After that rate equations for mixed control kinetics have been derived for each of these geometries.

Cylindrical specimen

Slag-film diffusion control

Figure 2 gives a schematic representation of a cylindrical lime specimen in slag and the concentration profiles for slag-film diffusion control. A shell mass balance for the species SiO₂ over a cylindrical shell in the slag-film of radius $r$, thickness $\Delta r$, and length $L$ gives (when $\Delta r \rightarrow 0$):

Fig. 2

Shell mass balance for a cylindrical CaO particle in slag and schematic concentration profiles for slag-film diffusion control

$$ \frac{\text{d}}{{{\text{d}}r}}\left( {rN_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right) = 0. $$

(1)

Integrating Eq. [1] and using the relationship between $J^{*}_{{{\text{SiO}}_{2} ( - r)}}$ and $N_{{{\text{SiO}}_{2} \left( { - r} \right)}}$ as[14]

$$ \frac{{J^{*}_{{{\text{SiO}}_{2} \left( { - r} \right)}} }}{{(1 - x_{{{\text{SiO}}_{2} }} )}} = N_{{{\text{SiO}}_{2} \left( { - r} \right)}}. $$

(2)

we get

$$ \frac{{J^{*}_{{{\text{SiO}}_{2} \left( { - r} \right)}} }}{{(1 - x_{{{\text{SiO}}_{2} }} )}} = \frac{{C_{1} }}{r}. $$

(3)

Using Fick’s first law,[8] the relation between $x_{{{\text{SiO}}_{2} }}$and $C_{{{\text{SiO}}_{2} }}$and substituting in Eq. [3], we get

$$ \frac{1}{{(\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} )}} \cdot \frac{{{\text{d}}C_{{{\text{SiO}}_{2} }} }}{{{\text{d}}r}} = \frac{{C_{2} }}{r}. $$

(4)

Integrating Eq. [4] with the boundary conditions

$$ \left. {\begin{array}{ll} {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{e} \quad {\text{at}} \quad r = r_{\text{CaO}}^{0} } \\ {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{b} \quad {\text{at}} \quad r = r_{\text{CaO}}^{0} + \delta_{C} } \\ \end{array} } \right\}. $$

(5)

we obtain the concentration profile for SiO₂ as

$$ \ln \left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} }}} \right) = { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right) \cdot \frac{{\ln \left( {\frac{r}{{r_{\text{CaO}}^{0} }}} \right)}}{{\ln \left( {\frac{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}{{r_{\text{CaO}}^{0} }}} \right)}}. $$

(6)

The molar rate of diffusion $\left. {W_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{r}$ is given as

$$ \left. {W_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{r} = 2\pi rL \cdot \left. {N_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{r} = \frac{{2\pi L\rho_{s} D_{s} { \ln }\left( {\frac{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\ln \left( {\frac{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}{{r_{\text{CaO}}^{0} }}} \right)}}. $$

(7)

Since all the kinetic steps are in series, and using the stoichiometry of the reaction

$$ 2{\text{CaO}}({\text{s}}) + ({\text{SiO}}_{2} ) = 2{\text{CaO}} \cdot {\text{SiO}}_{2} ({\text{s}}) $$

we get

$$ \left. {W_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{r} = \left. {W_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{{r_{\text{CaO}} }} = \left. { - \frac{{{\text{d}}n_{{{\text{SiO}}_{2} }} }}{{{\text{d}}t}}} \right|_{{r_{\text{CaO}} }} = \left. { - \frac{1}{2}\frac{{{\text{d}}n_{\text{CaO}} }}{{{\text{d}}t}}} \right|_{{r_{\text{CaO}} }}. $$

(8)

Substituting $\left. {W_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{r}$ in Eq. [8] and rewriting $n_{\text{CaO}}$ in terms of $r_{\text{CaO}}$we get

$$ - r_{\text{CaO}} \frac{{{\text{d}}r_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{2\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} \ln \left( {\frac{{r_{\text{CaO}}^{0} + \delta_{C} }}{{r_{\text{CaO}}^{0} }}} \right)}} $$

(9)

Integrating Eq. [9] within proper limits and replacing $r_{\text{CaO}}$ in terms of $X$ we get

$$ X = \frac{{4\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} {r_{\text{CaO}}^{0}}{^{2}} { \ln }\left( {\frac{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}{{r_{\text{CaO}}^{0} }}} \right)}}t. $$

(10)

Equation [10] is the integrated rate equation for slag-film diffusion for cylindrical geometry.

Product-layer diffusion control

Figure 3 gives a schematic representation of the concentration profile for a cylindrical lime specimen when the diffusion through the product (2CaO·SiO₂(s)) layer controls the overall rate. Proceeding in the same way as above and integrating using the pseudo steady-state assumption[15] for the boundary conditions,

Fig. 3

Shell mass balance for a cylindrical CaO particle in slag and schematic concentration profiles for product-layer diffusion control

$$ \left. {\begin{array}{*{20}c} {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{e} \quad {\text{at}} \quad r = r_{\text{CaO}} } \\ {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{b} \quad {\text{at}} \quad r = r_{\text{CaO}}^{0} } \\ \end{array} } \right\}. $$

(11)

The concentration profile for $C_{{{\text{SiO}}_{2} }}$is obtained as

$$ \ln \left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} }}} \right) = { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right).\frac{{\ln \left( {\frac{r}{{r_{\text{CaO}} }}} \right)}}{{\ln \left( {\frac{{r_{\text{CaO}}^{0} }}{{r_{\text{CaO}} }}} \right)}}. $$

(12)

Following the same procedure, the differential equation for the variation of $r_{\text{CaO}}$ with $t$ comes as

$$ - r_{\text{CaO}} { \ln }\left( {\frac{{r_{\text{CaO}}^{0} }}{{r_{\text{CaO}} }}} \right)\frac{{{\text{d}}r_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{2\rho_{\text{s}} D_{\text{p}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} }}. $$

(13)

The integrated rate equation for product-layer diffusion control is then obtained as

$$ X + \left( {1 - X} \right)\ln \left( {1 - X} \right) = \frac{{8\rho_{\text{s}} D_{\text{p}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} {r_{\text{CaO}}^{0}}{^{2}} }}t. $$

(14)

Interfacial reaction control

For the reaction,

$$ 2{\text{CaO}}({\text{s}}) + ({\text{SiO}}_{2} ) = 2{\text{CaO}} \cdot {\text{SiO}}_{2} ({\text{s}}) $$

assuming that the concentration of solids remain unchanged, the rate of reaction of CaO per unit area ($- v_{\text{CaO}}$) is given by

$$ - v_{\text{CaO}} = k_{\text{f}}^{'} C_{{{\text{SiO}}_{2} }}^{b} - k_{\text{b}}^{'} \;({\text{where }}k_{\text{f}}^{'} = k_{\text{f}} C_{\text{CaO}}^{2} \;{\text{and}}\;k_{b}^{'} = k_{b} C_{{2{\text{CaO}} \cdot {\text{SiO}}_{2} }} ). $$

(15)

At equilibrium, $- v_{\text{CaO}} = 0$ which gives

$$ \frac{{k_{\text{f}}^{'} }}{{ k_{\text{b}}^{'} }} = \frac{1}{{C_{{{\text{SiO}}_{2} }}^{e} }}. $$

(16)

Substituting this in Eq. [15], we get

$$ - v_{\text{CaO}} = k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{b} - C_{{{\text{SiO}}_{2} }}^{e} } \right]. $$

(17)

Substituting $- v_{{\text{CaO}}}$ with $n_{\text{CaO}}$ and rewriting $n_{\text{CaO}}$ in terms of $r_{\text{CaO}},$ we get

$$ - \frac{{{\text{d}}r_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{b} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}{{\rho_{\text{CaO}} }}. $$

(18)

The integrated rate equation for interfacial reaction control is then obtained as

$$ 1 - \left( {1 - X} \right)^{{\frac{1}{2}}} = \frac{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{b} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}{{\rho_{\text{CaO}} r_{\text{CaO}}^{0} }}t. $$

(19)

Spherical specimen

Slag-film diffusion control

Figure 4 gives a schematic representation of a spherical lime specimen in slag and the concentration profiles for slag-film diffusion control. A shell mass balance for SiO₂ over a spherical shell of radius $r$ and thickness $\Delta r$ yields (when $\Delta r \rightarrow 0$):

Fig. 4

Shell mass balance for a spherical CaO particle in slag and schematic concentration profiles for slag-film diffusion control

$$ \frac{\text{d}}{{{\text{d}}r}}\left( {r^{2} N_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right) = 0. $$

(20)

Integrating Eq. [20] and following the same procedure as for a cylinder, we get

$$ \frac{1}{{(\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} )}}.\frac{{{\text{d}}C_{{{\text{SiO}}_{2} }} }}{{{\text{d}}r}} = \frac{{C_{3} }}{{r^{2} }}. $$

(21)

Integrating Eq. [21] with the same boundary conditions as Eq. [5], we get

$$ \ln \left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} }}} \right) = { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right) \cdot { \ln }\left( {\frac{{\frac{1}{{r_{\text{CaO}}^{0} }} - \frac{1}{r}}}{{\frac{1}{{r_{\text{CaO}}^{0} }} - \frac{1}{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}}}} \right). $$

(22)

$$ \left. {W_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{r} = 4\pi r^{2} \cdot \left. {N_{{{\text{SiO}}_{2} \left( { - r} \right)}} } \right|_{r} = \frac{{4\pi \rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\left( {\frac{1}{{r_{\text{CaO}}^{0} }} - \frac{1}{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}} \right)}}. $$

(23)

The equation for the variation of $r_{\text{CaO}}$ with $t$ as is obtained using the same method as

$$ - r_{\text{CaO}}^{2} \frac{{{\text{d}}r_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{2\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} \left( {\frac{1}{{r_{\text{CaO}}^{0} }} - \frac{1}{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}} \right)}}. $$

(24)

The integrated form of rate equation for slag-film diffusion control is then obtained as

$$ X = \frac{{6\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} \left( {\frac{1}{{r_{\text{CaO}}^{0} }} - \frac{1}{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}} \right){{r_{\text{CaO}}^{0}}}}{^3}}t. $$

(25)

Product-layer diffusion control

Figure 5 gives a schematic representation of the concentration profile for a spherical lime specimen when the diffusion through the product (2CaO·SiO₂) layer is rate controlling. Performing a shell mass balance in the product layer and integrating with the boundary conditions of Eq. [11], the concentration profile for $C_{{{\text{SiO}}_{2} }}$ is obtained as

Fig. 5

Shell mass balance for a spherical CaO particle in slag and schematic concentration profiles for product-layer diffusion control

$$ \ln \left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} }}} \right) = { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right) \cdot { \ln }\left( {\frac{{\frac{1}{{r_{\text{CaO}} }} - \frac{1}{r}}}{{\frac{1}{{r_{\text{CaO}} }} - \frac{1}{{r_{\text{CaO}}^{0} }}}}} \right). $$

(26)

The differential equation for the variation of $r_{\text{CaO}}$with $t$ and the integrated rate equation are then obtained, respectively, as

$$ - r_{\text{CaO}}^{2} \frac{{{\text{d}}r_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{2\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} \left( {\frac{1}{{r_{\text{CaO}} }} - \frac{1}{{r_{\text{CaO}}^{0} }}} \right)}}. $$

(27)

$$ 1 - \frac{2}{3}X - \left( {1 - X} \right)^{{\frac{2}{3}}} = \frac{{4\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} {r_{\text{CaO}}^{0}}{^{2}} }}t. $$

(28)

Interfacial reaction control

To obtain the rate equations for interfacial reaction control, we make use of Eq. [17] and then replace $- v_{\text{CaO}}$ in terms of $r_{\text{CaO}}$ for a spherical geometry. Using the same method as before, the differential form of rate equation obtained is the same as Eq. [18], and the integrated rate equation is derived as

$$ 1 - \left( {1 - X} \right)^{{\frac{1}{3}}} = \frac{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{b} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}{{\rho_{\text{CaO}} r_{\text{CaO}}^{0} }}t. $$

(29)

Rectangular specimen

Slag-film diffusion control

Considering a rectangular shell having dimensions $\Delta l$, $w$ and $b$ (Figure 6) and a performing shell mass balance for the species SiO₂ over this rectangular shell, we get

Fig. 6

Shell mass balance for a rectangular CaO particle in slag and schematic concentration profiles for slag-film diffusion control

$$ \frac{\text{d}}{{{\text{d}}l}}\left( {N_{{{\text{SiO}}_{2} \left( { - l} \right)}} } \right) = 0. $$

(30)

The differential equation for the variation of $C_{{{\text{SiO}}_{2} }}$with l is then obtained as

$$ \frac{1}{{(\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} )}} \cdot \frac{{{\text{d}}C_{{{\text{SiO}}_{2} }} }}{{{\text{d}}l}} = C_{6}. $$

(31)

Integrating Eq. [31] with the boundary conditions

$$ \left. {\begin{array}{ll} {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{e} \quad {\text{at}} \quad l = l_{\text{CaO}}^{0} } \\ {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{b} \quad {\text{at }} \quad l = l_{\text{CaO}}^{0} + \delta_{\text{C}} } \\ \end{array} } \right\}. $$

(32)

The concentration profile for $C_{{{\text{SiO}}_{2} }}$ is obtained as

$$ \ln \left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} }}} \right) = { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right) \cdot \left( {\frac{{l - l_{\text{CaO}}^{0} }}{{\delta_{\text{C}} }}} \right). $$

(33)

The molar rate of diffusion at is given by

$$ \left. {W_{{{\text{SiO}}_{2} \left( { - l} \right)}} } \right|_{l} = \left. {wbN_{{{\text{SiO}}_{2} \left( { - l} \right)}} } \right|_{l} = \frac{{wb\rho_{\text{s}} D_{\text{s}} }}{{\delta_{\text{C}} }} \cdot { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right). $$

(34)

The differential form of the rate equation is obtained likewise as

$$ - \frac{{{\text{d}}l_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{2\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} \delta_{\text{C}} }}, $$

(35)

and the integrated rate equation for slag-film diffusion control is given by

$$ X = \frac{{2\rho_{\text{s}} D_{\text{s}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} \delta_{\text{C}} l_{\text{CaO}}^{0} }}t. $$

(36)

Product-layer diffusion control

Considering a shell having dimensions $\Delta l$, $w$ and $b$ in the product layer (Figure 7) and following the same procedure as above, an equation similar to Eq. [31] is obtained. Now integrating with the boundary conditions

Fig. 7

Shell mass balance for a rectangular CaO particle in slag and schematic concentration profiles for product-layer diffusion control

$$ \left. {\begin{array}{*{20}c} {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{e} \quad {\text{at}} \quad l = l_{\text{CaO}} } \\ {C_{{{\text{SiO}}_{2} }} = C_{{{\text{SiO}}_{2} }}^{b} \quad {\text{at}} \quad l = l_{\text{CaO}}^{0} } \\ \end{array} } \right\}. $$

(37)

The concentration profile for SiO₂ is obtained as

$$ \ln \left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }} }}} \right) = { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right) \cdot \left( {\frac{{l - l_{\text{CaO}} }}{{l_{\text{CaO}}^{0} - l_{\text{CaO}} }}} \right). $$

(38)

Following the same procedure as before, the differential and integrated forms of rate equations are obtained, respectively, as

$$ - \left( {l_{\text{CaO}}^{0} - l_{\text{CaO}} } \right)\frac{{{\text{d}}l_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{2\rho_{\text{s}} D_{\text{p}} { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} }}. $$

(39)

$$ X^{2} = \frac{{4\rho_{\text{s}} D_{\text{p}} { \ln }\left( {\frac{{\rho_{s} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} l_{\text{CaO}}^{{2_{0} }} }}t. $$

(40)

Interfacial control

Using Eq. [17] and substituting $- v_{\text{CaO}}$ in terms of $w$, $b$, $l_{\text{CaO}}$ for rectangular geometry, differential and integrated rate laws for interfacial reaction control are obtained, respectively, as

$$ - \frac{{{\text{d}}l_{\text{CaO}} }}{{{\text{d}}t}} = \frac{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{b} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}{{\rho_{\text{CaO}} }}. $$

(41)

$$ X = \frac{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{b} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}{{\rho_{\text{CaO}} l_{\text{CaO}}^{0} }}t. $$

(42)

A summary of integrated rate equations for different geometries of lime specimen and for different controlling mechanisms is given in Table I.

Table I Summary of Integrated Forms of Rate Equations for Different Geometries and Rate-Controlling Mechanisms

Mixed control model for lime dissolution

Cylindrical specimen

Using the differential and integrated forms of rate equations for the three different controls and following the general procedure used for deriving mixed control equations,[16] the differential and integrated rate equations for mixed control kinetics are obtained, respectively, as

$$ - \frac{{{\text{d}}r_{\text{CaO}} }}{{{\text{d}}t}}\left( {\frac{{r_{\text{CaO}} \ln \left( {\frac{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}{{r_{\text{CaO}}^{0} }}} \right)}}{{2\rho_{\text{s}} D_{\text{s}} }} + \frac{{r_{\text{CaO}} { \ln }\left( {\frac{{r_{\text{CaO}}^{0} }}{{r_{\text{CaO}} }}} \right)}}{{2\rho_{\text{s}} D_{\text{p}} }} + \frac{1}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right) = \frac{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} }}. $$

(43)

$$ \left( {\frac{{r_{\text{CaO}}^{0} \ln \left( {\frac{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}{{r_{\text{CaO}}^{0} }}} \right)}}{{4\rho_{\text{s}} D_{\text{s}} }}X + \frac{{r_{\text{CaO}}^{0} }}{{8\rho_{\text{s}} D_{\text{p}} }}\left( {X + \left( {1 - X} \right)\ln \left( {1 - X} \right)} \right) + \frac{{1 - (1 - X)^{{\frac{1}{2}}} }}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right) = \frac{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} r_{\text{CaO}}^{0} }}t. $$

(44)

Spherical specimen

Differential and integrated rate laws for a spherical lime specimen are obtained likewise as

$$ - \frac{{{\text{d}}r_{\text{CaO}} }}{{{\text{d}}t}}\left( {\frac{{r_{\text{CaO}}^{2} \left( {\frac{1}{{r_{\text{CaO}}^{0} }} - \frac{1}{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}} \right)}}{{2\rho_{\text{s}} D_{\text{s}} }} + \frac{{r_{\text{CaO}}^{2} \left( {\frac{1}{{r_{\text{CaO}} }} - \frac{1}{{r_{\text{CaO}}^{0} }}} \right)}}{{2\rho_{s} D_{p} }} + \frac{1}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right) = \frac{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} }}. $$

(45)

$$ \left( {\frac{{\delta_{\text{C}} }}{{6\rho_{\text{s}} D_{\text{s}} }}X + \frac{{r_{\text{CaO}}^{0} }}{{12\rho_{\text{s}} D_{\text{p}} }}\left( {3 - 3\left( {1 - X} \right)^{{\frac{2}{3}}} - 2X} \right) + \frac{{1 - \left( {1 - X} \right)^{{\frac{1}{3}}} }}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right) = \frac{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} r_{\text{CaO}}^{0} }}t. $$

(46)

Rectangular specimen

Differential and integrated rate laws for a cube lime specimen are obtained likewise as

$$ - \frac{{{\text{d}}l_{\text{CaO}} }}{{{\text{d}}t}}\left( {\frac{{\delta_{\text{C}} }}{{2\rho_{\text{s}} D_{\text{s}} }} + \frac{{\left( {l_{\text{CaO}}^{0} - l_{\text{CaO}} } \right)}}{{2\rho_{\text{s}} D_{\text{p}} }} + \frac{1}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right) = \frac{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} }}. $$

(47)

$$ \left( {\frac{{\delta_{\text{C}} }}{{2\rho_{\text{s}} D_{\text{s}} }}X + \frac{{l_{\text{CaO}}^{0} }}{{4\rho_{\text{s}} D_{\text{p}} }}X^{2} + \frac{X}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right) = \frac{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}{{\rho_{\text{CaO}} l_{\text{CaO}}^{0} }}t. $$

(48)

Calculation of concentration boundary layer thickness ($\delta_{\text{C}}$)

Rate equations developed in the preceding sections necessitate the estimation of $\delta_{\text{C}}$. Kosaka et al.[17] empirically expressed $\delta_{\text{C}}$ as a function of slag properties, and the speed of revolution for the dissolution of a rotating steel cylinder into liquid zinc or aluminum as

$$ \delta_{\text{C}} = 4.76 \cdot d_{\text{CaO}}^{1.5} \cdot {\text{Re}}^{ - 0.62} \cdot {\text{Sc}}^{ - 0.35}. $$

(49)

In the absence of any suitable correlation for calculating $\delta_{C},$ in the case of lime dissolution in steelmaking slags, Eq. [49] is used to estimate $\delta_{\text{C}}$. A correction factor $\alpha$ is then used so that reasonable agreement between the model predictions and experimental results is achieved.

Temperature dependence of diffusivity ($D_{{\text{s}}}$) and viscosity ($\eta$)

In the proposed model, effects of temperature on $D_{\text{s}}$ (and $D_{{\text{p}}}$) and $\eta$ are modeled by assuming that they exhibit an Arrhenius type of relationship with temperature, respectively, as follows:

$$ D_{\text{s}} = D_{0} \exp \left( {\frac{{ - E_{\text{S}} }}{RT}} \right). $$

(50)

$$ \eta = \eta_{0} \exp \left( {\frac{{E_{\eta } }}{RT}} \right). $$

(51)

Estimation of activity coefficient of SiO₂ ($\gamma_{{{\text{SiO}}_{2} }}$)

To estimate $\gamma_{{{\text{SiO}}_{2} }}$ as a function of slag composition and temperature, a large number of thermodynamic calculations are carried out using Equilib module of FactSage Version 6.4[18] at various slag compositions and temperatures (relevant to steelmaking operations). Finally, the thermodynamic data have been curve-fitted to obtain an equation for predicting $\gamma_{{{\text{SiO}}_{2} }}$as a function of slag composition and temperature. In the ranges studied, analyses yield

$$ {\text{log }}\gamma_{{{\text{SiO}}_{2} }} = - 1.1414 - 4.0259x_{\text{CaO}} + 10.8373x_{{{\text{SiO}}_{2} }} + 4.5569x_{\text{FeO}} - \frac{5243.4}{T}\,(R^2=0.99). $$

(52)

Solution Strategy

Computational study for the present model has been carried out using MATLAB ® Version R2009a.Algebraic and transcendental equations are solved using the Newton-Raphson method. An under-relaxation parameter ($\beta$) is used wherever necessary, and its value has been chosen by reaching a compromise between accuracy in calculations and computational speed.

For validating the model with experimental data of other researchers,[4,7,10] rate equations for different geometries are solved with input conditions similar to those mentioned in the relevant literature . When this model is applied as a submodel to the global model for LD steelmaking, the pertinent equations are solved with input conditions already published in the previous study[1] and hence not repeated here. Only, the list of new model variables used in the submodel for lime dissolution is mentioned in Table II. A new lance height practice is applied in the current study for better agreement with plant measurements[2] and has also been mentioned in Table II. The thermodynamic data required for model calculations are obtained from one of the standard data-sources.[19] Diffusivity of silica in slags is obtained from typical values reported by Dolan et al.[20] and the values of $E_{\text{S}}$ and $E_{\eta }$ are obtained from Matsushima et al.[4] In the absence of experimental data on $D_{\text{p}}$, simulation studies are carried out for different values of $\varphi$ (the ratio between $D_{\text{p}}$ and $D_{\text{s}}$). A value of $\varphi = 0.5$ gives a reasonably good agreement between model predictions and the observed values.

Table II List of Input Parameters used in the Lime Dissolution Submodel[4,20]

Results and Discussions

In this section, the results of the solutions of rate equations for mixed control (Eqs. [43] through [48]) are discussed and compared with experimental data published elsewhere.[4,7,10] In addition, the effects of process variables on lime dissolution rate have been identified and also compared with experimental results, whatsoever available.[4,9] Finally, this model is incorporated as a submodel in the global model[1] for calculating lime dissolution rates during actual blowing conditions. With the lime dissolution submodel incorporated, the predictions for slag compositions have been discussed, and improvements vis-a-vis the previous model have been analyzed.

Dissolution Rates for Different Lime Geometries

Cylindrical specimen

To calculate the rate of dissolution for a cylindrical lime specimen, Eq. [44] is solved to obtain the fractional conversion of lime ($X$) at various times. The results are plotted in Figure 8 and compared with the experimental results published by Matsushima et al.[4] for different speeds of revolution of the rotating lime specimen. As evident from Figure 8, model predictions for $r_{\text{CaO}}$ show good agreement with the experimental values. The model predicts the right trend in $X$ vs t plots for all different speeds of revolutions, and the agreement with experimental data is increasingly prominent for higher speeds of revolution. At 300 and 400 rpm, model predictions match excellently with the experimental results. At 200 and 100 rpm, predictions are relatively poor although the model still predicts the right trends. A possible reason for the relatively poor agreement at low rpms (especially for rpm = 100) might be the error involved in calculating $\delta_{\text{C}}$ using Eq. [49]. At low rpms, values of $\delta_{\text{C}}$ are expected to be very high resulting in much slower rates of diffusion through the slag-film. Under such conditions slag-film diffusion may be rate controlling. However, when $\delta_{\text{C}}$ is calculated using Eq. [49], it does not become sufficiently large at low rpms, and hence the model over-predicts the values of X at lower speeds of revolutions.

Fig. 8

Model predictions of fractional conversion of CaO ($X$) for a rotating cylindrical specimen compared with the experimental data of Matsushima et al.:[4] (a) 100 rpm, (b) 200 rpm, (c) 300 rpm, and (d) 400 rpm

Spherical specimen

Rates of dissolution for a spherical lime specimen have been calculated by solving Eq. [46] to obtain the fractional conversion of lime ($X$) at various times. The results are plotted in Figure 9 and compared with the experimental data reported by Guo et al.[10] An analysis of the experimental data published by Guo et al.[10] clearly shows three distinct regimes in $X$ vs $t$ plot. The authors argue that the formation of multisolid layer (assumed to 2CaO·SiO₂ in the current study) starts after some period, reaches a particular thickness and then the layer gets completely dissolved. Such phenomena, however, are not considered in the model (which assumes that a layer of 2CaO·SiO₂ is present always) and thus predictions do not necessary corroborate with the experimental results, especially during the initial regime. Predicted trend of $X$ vs $t$ plot shows only two distinct regimes: an initial period when $\delta_{\text{C}}$ is high (since $r_{\text{CaO}}$ is large) and slag-film diffusion is rate-controlling; and a final regime when $\delta_{\text{C}}$ is low (because of smaller $r_{\text{CaO}}$) and a mixed control mechanism of slag-film diffusion and product-layer diffusion govern the rate. In the later stages, there is a good correspondence between predicted and experimental values, although predictions for the initial periods have a greater deviation.

Fig. 9

Model predictions of fractional conversion of CaO ($X$) for a spherical specimen compared with the experimental data of Guo et al.[10]

Rectangular specimen

For rectangular specimen Eq. [48] is solved to obtain $X$ at various times ($t$). Results have been compared with the experimental data on lime dissolution for cubic specimens by Deng et al.[7] and plotted in Figure 10. As evident from the model results for $X$ vs $t$ plot, a mixed control mechanism of slag-film and product-layer diffusion determines the rate of dissolution. Experimental results also point toward such a mechanism, and a fairly good agreement is achieved between the model results and the experimental values during a major part of the time-period. Only toward the very late stages, the model predictions show some deviation from the experimental data. A possible source of error, as already explained, may be the inaccuracy in calculating $\delta_{\text{C}}$. Also, the present model assumes diffusion to be occurring only along one direction. For a rectangular geometry, such an assumption holds true only if each of the other two directions is much larger than the direction of diffusion. However, Deng et al's.[7] experimental data are for cubic specimens where all dimensions are equal and diffusion is expected to take place along all the three directions. Thus evidently, this approximation might have resulted in some errors in calculation.

Fig. 10

Model predictions of fractional conversion of CaO ($X)$ for a rectangular specimen compared with the experimental data of Deng et al.[7]

Effects of Process Variables on Dissolution Rate

Temperature

Effects of temperature on dissolution rate have been modeled by taking into account its effect on the model variables. $C_{{{\text{SiO}}_{2} }}^{e}$($a_{{{\text{SiO}}_{2} }}$ and $\gamma_{{{\text{SiO}}_{2} }}$), $k_{\text{f}}^{'}$,$\rho_{\text{s}}$,$\rho_{\text{CaO}}$,$D_{\text{s}}$ (and also $D_{\text{p}}$), $\eta$ (and hence $\delta_{\text{C}}$) are the model variables which vary with temperature. In the range of temperatures considered, $\rho_{\text{s}}$ and $\rho_{\text{CaO}}$ do not practically vary with temperature, and the effect of temperature on $k_{\text{f}}^{'},$ although significant, is of no practical importance since interfacial reaction does not have much effect on the overall rate. Both $a_{{{\text{SiO}}_{2} }}$and $\gamma_{{{\text{SiO}}_{2} }}$increase with temperature thus counteracting the effect of temperature on $C_{{{\text{SiO}}_{2} }}^{e}$ (which depends on the ratio between $a_{{{\text{SiO}}_{2} }}$and $\gamma_{{{\text{SiO}}_{2} }}$). Still $C_{{{\text{SiO}}_{2} }}^{e}$marginally increases with temperature but that practically has no effect on dissolution rate which depends on the concentration difference ($\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e}$) and $\rho_{\text{s}}$ is at least two orders of magnitude higher than $C_{{{\text{SiO}}_{2} }}^{e}$. Thus $D_{\text{s}}$ (and also $D_{\text{p}}$) and $\eta$ (and hence $\delta_{\text{C}}$) are the only variables which vary significantly with temperature. From Eq. [49], we get

$$ k_{\text{m}} \propto D_{\text{s}}^{0.7} \eta^{ - 0.32}. $$

(53)

As evident from Eqs. [50] and [51], $D_{\text{s}}$ exponentially increases and $\eta$ exponentially decreases with temperature, both of which increase $k_{\text{m}}$. $D_{\text{p}}$ (assumed to be $0.5D_{\text{s}}$) also increases exponentially with temperature, and hence lime dissolution rates increase significantly with temperature. In fact, lime dissolution rate also follow an Arrhenius relationship with temperature as illustrated in Figure 11. For an increase in temperature by 50 K (50 °C) from 1773 K to 1823 K (1500 °C to 1550 °C) the dissolution rate becomes almost twice its value at 1773 K (1500 °C). For validation, model results are compared with experimental data reported by Matsushima et al.[4] and a fairly good agreement between the two is obtained as evident from Figure 11.

Fig. 11

Model predictions of the effects of temperature on dissolution rate of CaO compared with the experimental data of Matsushima et al.[4]

Slag composition

Effects of slag composition on lime dissolution rates are modeled by considering its effects on $\gamma_{{{\text{SiO}}_{2} }}$ and $\eta$. The effects of slag composition on $\gamma_{{{\text{SiO}}_{2} }}$are studied using Eq. [52] while those on $\eta$ are investigated using the Viscosity module of FactSage version 6.4.[18] The results are analyzed by considering the effects of the two most important parameters that define the composition of LD slags:

Slag basicity

For fixed FeO content, the effects of slag basicity on dissolution rates are plotted in Figure 12 and compared with the experimental investigations of Matsushima et al.[4] and Hamano et al.[9] As evident from Eq. [52], $\gamma_{{{\text{SiO}}_{2} }}$decreases with increasing basicity, and hence $C_{{{\text{SiO}}_{2} }}^{e}$ increases. This, however, does not have a significant effect on the rate of dissolution for reasons previously discussed. Slag basicity has a much more pronounced effect on $\eta$. In the basicity range considered (0.5 to 3.0), as the slag basicity increases, $\eta$ initially increases, and then after a limiting basicity is reached, $\eta$ remains practically unchanged with basicity. Variation of $k_{\text{m}}$ with basicity follows the reverse trend, and thus with increasing basicity, dissolution rates first decreases, and then remains practically constant. Model predictions correspond well with the experimental results of both sets of investigations at low values of basicity (0.5 to 1.0).[4,9] At higher basicities, model results cannot be validated with experimental results since dissolution rates at higher basicities are not reported.[4,9]

Fig. 12

Model predictions of the effects of slag basicity on dissolution rate of CaO compared with the experimental data of Matsushima et al.[4] and Hamano et al.[9]

Slag FeO content

Figure 13 shows the effects of FeO content of slags on dissolution rates at constant basicity. As in the previous case, model predictions are compared with the experimental data published by Matsuhima et al.[4] and Hamano et al. [9] With the increasing FeO content of slags, $\gamma_{{{\text{SiO}}_{2} }}$ increases, and $C_{{{\text{SiO}}_{2} }}^{e}$decreases. This, however, has negligible effects on the rate of dissolution as previously discussed. FeO content has a much more significant effect on $\eta$. In the range currently considered (10 to 60 pct FeO), $\eta$ greatly decreases with increase in slag FeO content but after about 50 pct FeO, $\eta$ remains practically unchanged with further increase in FeO. Thus $k_{\text{m}}$ increases with the increasing FeO content till some limiting value (at around 50 pct) are reached after which it fairly remains constant. Dissolution rates follow a similar trend, as illustrated in Figure 13.

Fig. 13

Model predictions of the effects of slag FeO content on dissolution rate of CaO compared with the experimental data of Matsushima et al.[4] and Hamano et al.[9]

Experimental results published by Matsushima et al.[4] and Hamano et al.[9] indicate similar trends in the variation of dissolution rates with variation in FeO content of slags. In the case of Matsushima et al.,[4] model predictions agree very well with the experimental results in the range 20 to 40 pct FeO. In Hamano et al.’s[9] case, however, the experimental studies report a much greater increase in rates with the increasing FeO in the range 40 to 55 pct FeO, thus indicating that model predictions are not very accurate at higher FeO ranges (>40 pct). Error involved in calculating $\eta$ through FactSage calculations at higher FeO contents might be a possible reason for such deviation. For all practical purposes, however, dissolution rates at FeO content >40 pct is unimportant because FeO content in real steelmaking slags hardly becomes >40 pct. Nevertheless, further investigations on the reasons behind such deviations are necessary.

Lime particle size

To examine the effect of lime particle size on dissolution rate, the time for complete conversion of lime ($\tau$) is calculated for three different geometries currently considered (termed $\tau_{\text{c}}$, $\tau_{\text{s}}$ and $\tau_{\text{r}}$ for cylindrical, spherical, and rectangular specimens, respectively). Putting $X = 1$ in Eqs. [44], [46], and [48], we get

$$ \tau_{\text{c}} = \frac{{\rho_{\text{CaO}} r_{\text{CaO}}^{0} \left( {\frac{{r_{\text{CaO}}^{0} \ln \left( {\frac{{r_{\text{CaO}}^{0} + \delta_{\text{C}} }}{{r_{\text{CaO}}^{0} }}} \right)}}{{4\rho_{\text{s}} D_{\text{s}} }} + \frac{{r_{\text{CaO}}^{0} }}{{8\rho_{\text{s}} D_{\text{p}} }} + \frac{1}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right)}}{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}. $$

(54)

$$ \tau_{\text{s}} = \frac{{\rho_{\text{CaO}} r_{\text{CaO}}^{0} \left( {\frac{{\delta_{\text{C}} }}{{6\rho_{\text{s}} D_{\text{s}} }} + \frac{{r_{\text{CaO}}^{0} }}{{12\rho_{\text{s}} D_{\text{p}} }} + \frac{1}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right)}}{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}. $$

(55)

$$ \tau_{\text{r}} = \frac{{\rho_{\text{CaO}} l_{\text{CaO}}^{0} \left( {\frac{{\delta_{\text{C}} }}{{2\rho_{\text{s}} D_{\text{s}} }} + \frac{{l_{\text{CaO}}^{0} }}{{4\rho_{\text{s}} D_{\text{p}} }} + \frac{1}{{k_{\text{f}}^{'} \left[ {C_{{{\text{SiO}}_{2} }}^{p} - C_{{{\text{SiO}}_{2} }}^{e} } \right]}}} \right)}}{{1 + { \ln }\left( {\frac{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{e} }}{{\rho_{\text{s}} - C_{{{\text{SiO}}_{2} }}^{b} }}} \right)}}. $$

(56)

Figure 14 illustrates the effect of lime particle size on $\tau$ for the three geometries. For all three geometries, $\tau$ varies as the square of the lime particle size. This is also evident from Eqs. [54] through [56] and is characteristic of mixed control kinetics. It is also to be noted from Figure 14 that for the same particle size, $\tau_{\text{s}}$ is the least, and $\tau_{\text{r}}$ is maximum. $\tau_{\text{c}}$ is only slightly higher than $\tau_{\text{s}}$and both $\tau_{\text{c}}$ and $\tau_{\text{s}}$ are much smaller than $\tau_{r}$. An explanation for this can be sought from Eqs. [54] through [56]. With the substitution of $l_{\text{CaO}}^{0} = 2r_{\text{CaO}}^{0}$ and assuming that the contributions from interfacial reaction control is negligible, it can be seen from Eqs. [55] and [56] that $\tau_{\text{r}}$ is approximately twelve times $\tau_{\text{s}}$. Using a similar argument, $\tau_{\text{r}}$ can be found to be approximately eight times $\tau_{\text{c}}$.

Fig. 14

Effect of particle size on the time required for complete conversion of CaO ($\tau$) for different geometries

Application to a Real Steelmaking Process

In the preceding sections, a mixed control model for calculating the dissolution rate of lime in steelmaking slags has been developed. Also, the effects of process variables on dissolution rates have been examined. This model is now incorporated in the global model for LD steelmaking,[1] and in this section, the model predictions for variation in lime dissolution rates (calculated using the lime dissolution submodel) have been discussed. Finally, improvements in slag compositions (in terms of how closer they approach real-time values) with respect to the previous model have been analyzed.

Variation in lime dissolution rate during the blow

Figure 15 shows the variation in lime dissolution rate during blowing in a 160-ton LD converter. For a fixed particle size of the lime particle, dissolution rate depends on temperature, slag basicity, and FeO content. As already discussed, dissolution rates increases with the increasing temperature and FeO content and decreases with the increasing basicity. For the first 1 to 2 minutes of the blow, FeO content is very high (about 40 pct) and basicity is low (in the range 1.1 to 1.2). These factors result in high dissolution rates for the first 1 to 2 minutes even though the slag temperature is not high. As the blow proceeds, FeO content in slag starts decreasing and basicity increases. Both these factors result in a decrease in dissolution rate which reaches a minimum after about 5 minutes. After this, slag FeO content remains relatively constant for the major part of the blow. Both basicity and temperature, however, increases continually as the blow proceeds. These factors have counteracting effects on dissolution rates. As a result, lime dissolution rates remains fairly constant after about 5 minutes throughout the major part of the remaining blowing period. Slight increase in lime dissolution rate can be observed in Figure 15 because temperature has a much greater effect on dissolution rates as compared to slag basicity. Toward the very end of the blow, (after about 14 minutes from the start) FeO content starts increasing significantly. Temperatures are also very high and slag basicity slightly decreases due to the dilution effect of very high FeO content. All these factors favor the dissolution of lime in slag. Thus dissolution rates sharply increases in this period (14 to 16 minutes).

Fig. 15

Model predictions of variation in dissolution rate of CaO during blowing in a 160-ton LD converter

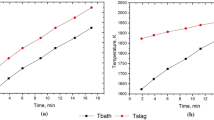
Variation in slag compositions during the blow

As previously discussed, the previous model[1] already predicted the variations in slag compositions during blowing in a 160-ton LD converter. This model aimed at improving the model predictions of slag compositions by incorporating a lime dissolution submodel into the global model. Figures 16(a) and (b) show the variations in slag compositions during the blow with and without the lime dissolution model. As evident from Figures 16(a) and (b), with the lime dissolution submodel, the global model predictions correspond much better with actual plant measurements.[2] Towards the beginning of the blow dissolution rate of CaO is high, as previously discussed. However, as the blow proceeds, it starts to decrease. Consequently, lesser amount of CaO goes into the slag, and the overestimation in percent CaO is significantly reduced. Since percent FeO in slag depends on the dilution of slag by CaO, the underestimation in FeO percent is also eliminated to a large extent. Similar to predictions of the previous model, percent CaO reaches a maximum, and percent FeO reaches a minimum after about 5 minutes from the start of the blow. However, with the lime dissolution model incorporated, the maximum in percent CaO is reached at a much lower value, and hence the minimum in percent FeO is reached at a much higher value. Afterward, the percent compositions of CaO and FeO remain practically constant, and this trend is observed in model predictions both with and without the lime dissolution model as well as in plant measurements by Cicutti et al.[2] Toward the very end of the blow, (in the period 14 to 16 minutes after the blow-start), there is not much improvement in model predictions with the incorporation of the lime dissolution model. This deviation, however, is attributed more to a demerit inherent to the global model. In the end-blow regime, the amount of hot metal in the emulsion becomes too low, and hence, the consumption of FeO due to reactions is very less, thus resulting in very high FeO content in the slag.[1] Further refinement with regard to this aspect may be necessary to obtain realistic predictions during the final stages of the blow. Very high rates of lime dissolution in these stages may compensate for the high FeO content thus bringing down the percent FeO values by dilution effects. Such high rates of dissolution, however, are not obtained using the present submodel even during the very late stages of the blow.

Fig. 16

Models predictions of variations in slag compositions during blowing in a 160-ton LD converter with and without the CaO dissolution model: (a) CaO and (b) FeO

Conclusion

The current study was aimed to develop a model for dissolution of lime in steelmaking slags based on the assumption that CaO reacts with SiO₂ in slags to form solid 2CaO·SiO₂. A three-step kinetic process for the dissolution of lime has been hypothesized. Critically analyzing experimental data published by other researchers, it has been argued that the observed kinetics cannot be suitably explained if any one of the three (hypothetical) reaction steps is rate controlling. Thus, mixed control models have been proposed in the current study for calculating lime dissolution rates. Integrated rate equations for each of the three rate-controlling mechanisms are first obtained, and then the rate laws for mixed control kinetics have been derived. Proposed mixed control models for different lime geometries are first validated using experimental data published elsewhere. Then, the effects of temperature, slag basicity, slag FeO content, and lime particle size on dissolution rates have been analyzed and validated with experimental results of other researchers. Finally, this model has been incorporated in the already existing global model for LD steelmaking. Incorporation of the submodel into the global model enabled the calculation of lime dissolution rates dynamically during blowing in a 160-ton LD steelmaking converter. More importantly, considerable improvements in predictions of slag compositions have been observed. With the inclusion of the lime-dissolution submodel, predictions for percent CaO and percent FeO corroborate much better with the industrial results for a major part of the blow. In the end-blow regime, not much improvement in model predictions can be achieved, thus indicating that further refinement of the model may be required.