Disease Emergence in Multi-Patch Stochastic Epidemic Models with Demographic and Seasonal Variability

Abstract

Factors such as seasonality and spatial connectivity affect the spread of an infectious disease. Accounting for these factors in infectious disease models provides useful information on the times and locations of greatest risk for disease outbreaks. In this investigation, stochastic multi-patch epidemic models are formulated with seasonal and demographic variability. The stochastic models are used to investigate the probability of a disease outbreak when infected individuals are introduced into one or more of the patches. Seasonal variation is included through periodic transmission and dispersal rates. Multi-type branching process approximation and application of the backward Kolmogorov differential equation lead to an estimate for the probability of a disease outbreak. This estimate is also periodic and depends on the time, the location, and the number of initial infected individuals introduced into the patch system as well as the magnitude of the transmission and dispersal rates and the connectivity between patches. Examples are given for seasonal transmission and dispersal in two and three patches.

1 Introduction

Seasonal fluctuations in disease incidence have been known since the time of Hippocrates, about 400 B.C. (Fisman 2007). Seasonal changes in temperature, humidity, and rainfall affect pathogen survival, host behavior, and host immune function, which in turn affect successful transmission (Grassly and Fraser 2006; Altizer et al. 2006). Seasonal changes also affect the movement of susceptible and infected hosts and impact the spatial spread of disease in humans and in domestic and wild animal populations (Altizer et al. 2006). Some of the many infectious diseases that are impacted by seasonal variations include seasonal influenza, avian influenza (AI), malaria, cholera, dengue, plague, foot-and-mouth disease, Ebola, Middle East respiratory syndrome (MERS), and severe acute respiratory syndrome (SARS), e.g., (Breban et al. 2009; Brown et al. 2014; Camitz and Liljeros 2006; Endo and Nishiura 2018; Fisman 2007; Gao et al. 2019; Parham and Michael 2010; Keeling 2005; McLennan-Smith and Mercer 2014; Schmidt et al. 2017; Vaidya and Wahl 2015). The emergence of the new coronavirus disease named COVID-19 and the worldwide pandemic has raised concerns about seasonal or sporadic outbreaks after the pandemic period (Kissler et al. 2020). It is the goal of the present investigation to study infectious disease outbreaks in a multi-patch setting when transmission within and movement between the patches are seasonal. Our modeling framework and methods with knowledge about travel patterns and seasonal trends will provide insight about effective methods for control or prevention of disease outbreaks.

Many modeling studies have focused on disease spread among discrete patches with no seasonal variations. These studies have been based on ordinary differential equations (ODEs), e.g., (Allen et al. 2007; Arino 2009; Arino and van den Driessche 2003b, a, 2006; Baguette et al. 2014; Cosner et al. 2009; Gao and Ruan 2012; Gao et al. 2019; Kelly Jr. et al. 2016) and on stochastic models, e.g., (Ball 1991; Ball and Clancy 1993; Clancy 1994; Breban et al. 2009; Lahodny Jr and Allen 2013; McCormack and Allen 2007; Milliken 2017; Neal 2012). The ODE multi-patch epidemic models have established upper and lower bounds on the basic reproduction number, existence and stability of an endemic equilibrium and conditions for disease persistence or extinction under various dispersal/movement assumptions. In a cholera ODE multi-patch model, Kelly Jr. et al. (2016) showed that targeting vaccination to specific patches is effective in controlling the disease. In stochastic time-homogeneous models, the effect of dispersal on epidemic final size and on probability of an outbreak has also been studied in multi-patch settings.

The effects of seasonal variation on disease dynamics have been studied in ODE models, e.g., (Bacaër and Guernaoui 2006; Bacaër 2007; Gao et al. 2014; Jin and Lin 2018; McLennan-Smith and Mercer 2014; Mitchell and Kribs 2017; Posny and Wang 2014; Schwartz and Smith 1983; Suparit et al. 2018; Vaidya and Wahl 2015; Wang et al. 2012; Wang and Zhao 2017a, b; Zhang and Zhao 2007; Wolf et al. 2006) and in stochastic models, e.g., (Bacaër and Ait Dads 2014; Billings and Forgoston 2018; Breban et al. 2009; Jin and Lin 2018; Keeling et al. 2001; Lin et al. 2015; Nipa and Allen 2020). The ODE models are nonautonomous and include seasonal variation through periodic coefficients. In these models, the existence of a basic reproduction number ${\mathscr {R}}_0$ with stability of the disease-free state has been verified for ${\mathscr {R}}_0<1$ (Bacaër 2007; Zhang and Zhao 2007). Interestingly, numerical examples have demonstrated that ${\mathscr {R}}_0$ for the nonautonomous model differs from the autonomous model when coefficients are fixed at their average values. Recently, Bacaër and Ait Dads (2014) showed that the basic reproduction number ${\mathscr {R}}_0$ from the underlying nonautonomous ODE model serves as a threshold for disease extinction in the corresponding stochastic time-nonhomogeneous model. If ${\mathscr {R}}_0<1$, the probability of disease extinction is equal to 1, but when ${\mathscr {R}}_0>1$, the probability of disease extinction is periodic with probability $<1.$ Nipa and Allen (2020) applied these results to estimate the probability of disease extinction in a stochastic vector-host epidemic model.

This investigation extends the previous research by combining multi-patch epidemic models with seasonal variation in a stochastic setting. In particular, we formulate a stochastic multi-patch epidemic model with seasonal variability in transmission and dispersal rates. Through multi-type branching process approximation and application of the backward Kolmogorov differential equation, an estimate for the probability of disease extinction is derived. It is shown that the probability of disease extinction and disease outbreak is periodic and less than 1 when ${\mathscr {R}}_0>1$. In particular, the probability of disease extinction and disease outbreak is dependent on the time, the location, and the number of initial infected individuals i introduced at time $\tau$ into the patch system:

$$\begin{aligned} 0<{\mathbb {P}}_{ext}(i,\tau )<1 \end{aligned}$$

and ${\mathbb {P}}_{outbreak}(i,\tau )=1-{\mathbb {P}}_{ext}(i,\tau )$, where $I(\tau )=i=(i_1,\ldots ,i_n)$ and $i_j$ is the number of infected individuals in patch j for $j=1,\ldots ,n$ at the initial time $\tau \in [0,\textit{T}]$ with $\textit{T}$ the total length of the seasons (generally one year) and n the total number of patches.

In the next section, a nonautonomous ODE multi-patch epidemic model is introduced which serves as a framework for the stochastic time-nonhomogeneous model in Sect. 3. Approximation of the time-nonhomogeneous process by a multi-type branching process and the backward Kolmogorov differential equation leads to estimates of the periodic probability of disease extinction. Several numerical examples with two patches in Sect. 4 illustrate the dependence of the probability of an outbreak on time, the location, and the initial number of infected individuals. Examples with three patches in Sect. 5 show the importance of patch arrangement and connectivity on the probability of a disease outbreak. In the concluding section, we summarize our results and suggest areas for further research.

2 ODE Multi-Patch Model

We consider a susceptible-infected-recovered (SIR) multi-patch epidemic model with the dispersal of individuals between patches. The term dispersal is used to represent seasonal movement or migration rather than human movement associated with daily commuter travel, e.g., (Arino and van den Driessche 2003b; Cosner et al. 2009). Before defining the stochastic process, we define the underlying nonautonomous ODE model.

Let n be the total number of patches. For patch j, susceptible individuals are denoted as $S_j$, infected individuals as $I_j$, and recovered individuals as $R_j$, $j=1,2,\ldots ,n$. We assume there are births and natural deaths as well as disease-related deaths. The total population size in each patch equals $N_j=S_j+I_j+R_j,$ $j=1, 2, \ldots , n$ and the total population size equals $N=\sum _{j=1}^nN_j$. For each patch j, parameter $\mu _j$ represents the birth and natural death rate, parameter $\alpha _j$ is the disease-related death rate, and parameter $\gamma _j$ is the recovery rate. The transmission and dispersal rates are assumed to be time-periodic functions. The disease transmission rate is frequency-dependent, $\beta _j(t)$, and the dispersal rate from patch j to patch k is $d^{\ell }_{jk}(t)$, $j, k=1, 2, \ldots , n$ and $j \ne k$. That is,

$$\begin{aligned} \beta _j(t)=\beta _j(t+{\textit{T}})\quad \mathrm{and } \quad d^{\ell }_{jk}(t)=d^{\ell }_{jk}(t+{\textit{T}}), \end{aligned}$$

(1)

where $\ell =S,I,R$ represents the dispersal rate for either susceptible, infected or recovered individuals. These functions are continuous for $t\in (-\infty ,\infty )$ with period ${\textit{T}}>0$.

The multi-patch model with a total of n patches takes the following form:

$$\begin{aligned} \hbox { Patch } j\left\{ \begin{aligned} \dot{S_j}&=-\beta _j(t)\frac{I_j}{N_j}S_j+\mu _j(N_j-S_j)+\sum _{k=1,k \ne j}^{n}\left( d_{kj}^S(t)S_k-d_{jk}^S(t)S_j\right) \\ \dot{I_j}&=\beta _j(t)\frac{I_j}{N_j}S_j-(\mu _j+\alpha _j+\gamma _j)I_j+\sum _{k=1,k \ne j}^{n}\left( d_{kj}^I(t)I_k-d_{jk}^I(t)I_j\right) \\ \dot{R_j}&=\gamma _jI_j-\mu _jR_j+\sum _{k=1,k \ne j}^{n}\left( d_{kj}^R(t)R_k-d_{jk}^R(t)R_j\right) , \end{aligned}\right. \nonumber \\ \end{aligned}$$

(2)

where $S_j(0)>0$, $I_j(0)\ge 0$, $R_j(0)=0$, $S_j(0)+I_j(0)+R_j(0)=N_j$ and with all parameters nonnegative such that $\beta _j(t)>0$ and $\mu _j+\gamma _j+\alpha _j>0$ for $j=1,\ldots ,n$. In general,

$$\begin{aligned} \dot{N}=-\sum _{j=1}^n\alpha _j I_j. \end{aligned}$$

If there are no disease-related deaths, $\alpha _j=0$, then the total population size N is constant. However, with dispersal and disease, the population size within each patch may change over time.

We make some simplifying assumptions to ensure there exists a unique disease-free equilibrium (DFE). Assume

$$\begin{aligned} d^{\ell }_{jk}(t)=d^{\ell }_{kj}(t) \end{aligned}$$

(3)

for $\ell =S,I,R$. In the absence of infection, $I_j\equiv 0$, the equilibrium population sizes within each of the patches are constant, i.e., $N_1=N_2=\cdots =N_n$. The unique DFE is ${\bar{S}}_j=N_j=N/n$, $j=1,\ldots ,n$. The simplifying assumption in Eq. (3) implies movement to and from a patch is balanced or symmetric. This assumption does not hold, for example, if there is directed movement such as asymmetric connectivity as in Chen et al. (2020). We relax this assumption for an example in Sect. 4.

Linearizing the system (2) about the DFE for the n infected states $I=(I_1,\ldots ,I_n)^T$ results in the linear system

$$\begin{aligned} \dot{I}=[F(t)-V(t)] I. \end{aligned}$$

(4)

The basic reproduction number, ${\mathscr {R}}_0$, depends on the two matrices, F(t) and V(t). Matrix F(t) represents new infections, a diagonal matrix, and matrix V(t) represents other transitions (dispersal, recovery and deaths):

$$\begin{aligned} F(t)=\begin{pmatrix} \beta _1(t) &{} 0 &{} \ldots &{} 0\\ 0 &{} \beta _2(t) &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} \beta _n(t) \end{pmatrix} \end{aligned}$$

(5)

and

$$\begin{aligned} V(t)=\begin{pmatrix} v_{11}(t) &{} -d_{21}^I(t) &{} -d_{31}^I(t) &{} \ldots &{} -d_{n1}^I(t) \\ -d_{12}^I(t) &{} v_{22}(t) &{} -d_{32}^I(t) &{} \ldots &{}-d_{n2}^I(t) \\ -d_{13}^I(t) &{} -d_{23}^I(t)&{} v_{33}(t) &{} \ldots &{} -d_{n3}^I(t) \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ -d_{1n}^I(t) &{} -d_{2n}^I(t) &{} -d_{3n}^I(t) &{} \ldots &{} v_{nn}(t) \end{pmatrix}, \end{aligned}$$

(6)

where $v_{ii}(t)=\mu _i+\alpha _i+\gamma _i+\sum _{k=1,k \ne i}^{n}d_{ik}^I(t)$. For the nonautonomous system, explicit solutions for the basic reproduction number can be calculated only in special cases, e.g., Mitchell and Kribs (2017); Wang and Zhao (2008). For example, if there is no dispersal between patches, the basic reproduction number for patch j can be computed as follows:

$$\begin{aligned} {\mathscr {R}}_{0j}=\dfrac{\int _0^{\textit{T}} \beta _j(t)\, dt}{\int _0^{\textit{T}} (\mu _j+\alpha _j+\gamma _j)\, dt}=\dfrac{\int _0^{\textit{T}} \beta _j(t)\, dt}{{\textit{T}}(\mu _j+\alpha _j+\gamma _j)}=\dfrac{\bar{\beta }_j}{\mu _j+\alpha _j+\gamma _j}. \end{aligned}$$

(7)

We refer to ${\mathscr {R}}_{0j}$ as the patch reproduction number which in this case is simply the average of the transmission rate, denoted as $\bar{\beta }_j$, multiplied by the average duration of the infection, $1/(\mu _j+\alpha _j+\gamma _j).$

In the more general case, Assumptions (A1)–(A7) (Appendix A) ensure that the basic reproduction number exists for the system (2) (Wang and Zhao 2008). Theoretically, ${\mathscr {R}}_0$ can be found from the following linear periodic system:

$$\begin{aligned} {\dot{w}}=[ F(t) /\lambda -V(t)] w. \end{aligned}$$

(8)

The spectral radius of the fundamental matrix solution of system, evaluated at $t={\textit{T}}$, equals one, then $\lambda ={\mathscr {R}}_0$ (Theorem 2.1 p. 704, (Wang and Zhao 2008)), i.e.,

$$\begin{aligned} \phi _{F(t)/\lambda -V(t)}({\textit{T}})=1. \end{aligned}$$

If an analytical solution cannot be obtained, numerical methods as well as computer algebra systems can be used to compute the spectral radius of this matrix (Klausmeier 2008; Posny and Wang 2014). In the following examples, we compute the results numerically by choosing a sequence of values $\lambda _i$, $i=1,2,\ldots$ and $0<\epsilon \ll 1$, where $|\lambda _{i+1}-\lambda _i|<\epsilon$ until a value of $\lambda _k$ is reached such that $\phi _{F(t)/\lambda _k-V(t)}({\textit{T}})\approx 1$. Then, ${\mathscr {R}}_0\approx \lambda _k$. It should be noted that the basic reproduction number does not depend on the dispersal of S or R, only the dispersal rate of I. We use the terminology that patch j is high-risk if ${\mathscr {R}}_{0j}>1$ and is low-risk if ${\mathscr {R}}_{0j}<1$ (Allen et al. 2007).

3 Time-Nonhomogeneous Stochastic Process

The ODE model serves as a framework for formulation of the time-nonhomogeneous stochastic process. For simplicity, the same notation is used for the variables as in the ODE model. The random variables are discrete and time is continuous, $t\in [0,\infty )$,

$$\begin{aligned} S_j(t),I_j(t),R_j(t) \in \{0, 1, 2, 3, \ldots , N_j\} \end{aligned}$$

for $j=1,2,\ldots ,n$. The changes in the random variables are $\pm 1$ during a small interval of time $\varDelta t$. The rates in the ODE model are used to define the infinitesimal transition probabilities. They are summarized in Table 1.

Table 1 Infinitesimal transition probabilities for the stochastic n-patch model

Fig. 1

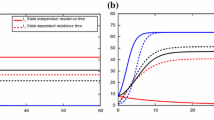
(Color Figure Online) Two sample paths are graphed with one infected individual introduced into patch 1, $(S_1(0),I_1(0),R_1(0))=(1999,1,0)$ $(S_2(0),I_1(0),R_2(0))=(2000,0,0)$. Patch 1 is high-risk with ${\mathscr {R}}_{01}=3$ and patch 2 is low-risk with ${\mathscr {R}}_0=0.2$. One sample path illustrates a major outbreak, while the second sample path illustrates rapid disease extinction. The top two panels show the dynamics of susceptible, infected, and recovered individuals in the two patches. The bottom two panels show a close-up view of the two sample paths of the infected individuals. Parameter values are $\beta _1(t)=18(1+0.8\sin (\pi t/2)),$ $\beta _2(t)=1.2(1+0.8\sin (\pi t/2)),$ $d^{\ell }_{jk}=2(1+0.8\sin (\pi t/2)),$ $\ell =S,I,R$, $\mu _1=\mu _2=0.01,$ $\gamma _1=\gamma _2=5.99,$ and $\alpha _1=\alpha _2=0$

For example, a new infection in patch j at time t results in a change in the random variables, $\varDelta S_j(t)=S_j(t+\varDelta t)-S_j(t)=-1$ and $\varDelta I_j(t)=I_j(t+\varDelta t)-I_j(t)=+1$ with probability

$$\begin{aligned} \mathbb {P}\{(\varDelta S_j(t),\varDelta I_j(t))=(-1,+1)|(S_j(t),I_j(t))=(s_j,i_j)\}=\beta _j(t)\dfrac{i_j}{n_j}s_j\varDelta t +o(\varDelta t). \end{aligned}$$

The lower case letters $s_j$, $i_j$, and $n_j$ denote the values of the random variables $S_j(t)$, $I_j(t)$, and $N_j(t)$, respectively.

A simple example of two patches illustrates the dynamics of the stochastic time-nonhomogeneous process when either a disease outbreak or disease extinction occurs. In Fig. 1, two sample paths are graphed for $(I_1(0),I_2(0))=(1,0)$. The top two panels show the dynamics of the SIR process in two patches when an outbreak occurs. In this example, susceptible, infected, and recovered individuals have the same periodic dispersal rates in both patches, but the periodic transmission rates differ in patches 1 and 2. Disease extinction is not visible in the top two panels, but a close-up view in the bottom two panels shows the infected population in each patch. In one sample path, there is no outbreak, the number of infected individuals reaches zero by time 0.25 (approximately 3 weeks), whereas in the other sample path there is a disease outbreak. It is clear that a major outbreak occurs in patch 1, where the number of infected individuals reaches a level of over 500 individuals, and a smaller outbreak is visible in patch 2. There is only a single outbreak as the susceptible populations are depleted in both patches, and the infected population sizes reach zero in both patches before a second outbreak occurs. That is, the populations in both patches become disease-free.

3.1 Branching Process Approximation

A multi-type branching process approximation is applied to the n infected states $I_j$ in the time-nonhomogeneous process near the DFE, where $S_j=N_j$. The infinitesimal transition rates in the branching process approximation during a small period of time $\varDelta t$ are summarized in Table 2.

Table 2 Infinitesimal transition probabilities for the infected states in the branching process approximation of the stochastic n-patch model

The changes in the infected states are related to the transitions that occur in the linearized ODE system, Eq. (4). Unlike the nonhomogeneous stochastic process defined in Table 1, the random variables for the branching process are not bounded above,

$$\begin{aligned} I_j(t)\in \{0,1,2,\ldots \}\quad j=1,\ldots ,n. \end{aligned}$$

Bacaër and Ait Dads (2014) applied the forward Kolmogorov differential equation to show that the basic reproduction number ${\mathscr {R}}_0$ from the ODE model serves as a threshold for the branching process approximation. In particular, they showed if ${\mathscr {R}}_0\le 1$, then the multi-type branching process with the same periodic rates has an asymptotic periodic probability of disease extinction that depends on the time of introduction $\tau$ and the number of infected individuals $i=(i_1,\ldots ,i_n)$, i.e., $I_j(\tau )=i_j\ge 0$ and $I(\tau )=i$. If ${\mathscr {R}}_0\le 1$, then the asymptotic probability of disease extinction is 1, but if ${\mathscr {R}}_0>1$, then

$$\begin{aligned} 0<{\mathbb {P}}_{ext}(i,\tau )<1,\ \ \tau \in [0,{\textit{T}}]. \end{aligned}$$

In addition, the asymptotic probability of a disease outbreak can be approximated as follows:

$$\begin{aligned} {\mathbb {P}}_{outbreak}(i,\tau )=1-{\mathbb {P}}_{ext}(i,\tau ). \end{aligned}$$

We describe another method to obtain the estimate for the probability of disease extinction via probability generating functions (pgfs) and the backward Kolmogorov differential equation (Nipa and Allen 2020). Denote the transition probability for the multi-type branching process as

$$\begin{aligned} p_{i,m}(\tau ,t)={\mathbb {P}}\{I(t)=m|I(\tau )=i\},\quad \tau <t, \end{aligned}$$

where the notation $m=(m_1, \ldots , m_n)$, $I_j(t)=m_j\ge 0$, $j=1,\ldots ,n$ is the number infected at time t and $i=(i_1,\ldots ,i_n)$, $I_j(\tau )=i_j$, $j=1,\ldots ,n$ is the number infected at time $\tau$. The backward Kolmogorov differential equation can be derived from the transitions defined in Table 2, e.g., (Athreya and Ney 2004; Harris 1963; Jagers and Nerman 1985):

$$\begin{aligned} \begin{aligned} - \frac{\partial p_{i,m}(\tau ,t)}{\partial \tau }&=\sum _{j=1}^ni_j\left[ \beta _j(\tau )p_{(i+e_j,m)}(\tau ,t)+(\mu _j+\alpha _j+\gamma _j)p_{(i_j-e_j,m}(\tau ,t)\right] \\ {}&\quad +\sum _{j=1}^n\sum _{k=1,k\ne j}^ni_j d_{jk}^{I}(\tau )p_{(i-e_j+e_k,m)}(\tau ,t)\\&\quad -\sum _{j=1}^ni_j\left[ \beta _j(\tau )+(\mu _j+\alpha _j+\gamma _j)+\sum _{k=1,k\ne j}^n d_{jk}^{I}(\tau )\right] p_{(i,m)}(\tau ,t), \end{aligned} \end{aligned}$$

(9)

where $e_j$ is the standard unit vector in ${\mathbb {R}}^n$.

Next, we define the offspring pgfs, one for each of the random variables $I_j$. The offspring pgfs for this time-continuous process are distinct from those in a discrete-time Markov chain (DTMC). The number of infections generated by $I_j$ in the time-continuous process is assumed to occur in a small period of time $\varDelta t$ rather than during the entire infectious period as in a DTMC. Given $I_j(\tau )=1$ and $I_k(\tau )=0$ for $k \ne j$, one of four events defined in Table 2, if any, occurs in a small period of time $\varDelta t$. An infected individual in patch j (1) transmits the infection to another individual in patch j or (2) dies (naturally or from the infection) or (3) recovers from the infection or (4) moves to another patch k. The pgf for $I_j$ that includes these four events is defined by

$$\begin{aligned} f_{j}(u,\tau )=\frac{\beta _j(\tau )u_j^2+\mu _j+\alpha _j+\gamma _j+\sum _{k=1,k \ne j}^{n}d_{jk}^I(\tau )u_k}{\beta _j(\tau )+\mu _j+\alpha _j+\gamma _j+\sum _{k=1,k \ne j}^{n}d_{jk}^I(\tau )}, \end{aligned}$$

(10)

where $u=(u_1,\ldots ,u_n)\in [0,1]^n$, $j=1,\ldots ,n.$ Each pgf has the property that $f_{j}(u,\tau )|_{u=\mathbf{1}}=1$ and $f_{j}$ is nonlinear in u and positive on the set $[0,1]^n$. The difference between this pgf and the pgf for the model with constant parameters (equation (12) in Lahodny Jr and Allen (2013)) is that the pgf (10) is dependent on $\tau$.

In addition to the offspring pgfs for each of the infected states, we define the generating function for the multi-type branching process consisting of all n infected states. Let

$$\begin{aligned} G_{i}(u,\tau ,t)={\mathbb {E}}\left[ \prod _{j=1}^nu_j^{I_j(t)}|I(\tau )=i\right] =\sum _m p_{i,m}(\tau ,t)\prod _j^n u_j^{m_j},\quad \tau <t, \end{aligned}$$

(11)

where $u=(u_1,\ldots ,u_n)$. In the branching process, the random variables $I_j$ are assumed to be independent, resulting in

$$\begin{aligned} G_{i}(u,\tau ,t)=\prod _{k=1}^n [G_{e_k}(u,\tau ,t)]^{i_k}. \end{aligned}$$

(12)

This is a reasonable assumption if the initial number of infected individuals is small. Let $I_j(\tau )=i_j$ and the remaining infected states $I_k(\tau )=0$, $k\ne j.$ Then, for $i=(0,\ldots ,i_j,\ldots ,0)$, differentiating Eq. (12) with respect to $\tau$, using the definition (11), applying the identity (9), and substituting the pgf (10), leads to a differential equation for $G_{e_j}$. That is,

$$\begin{aligned} \dfrac{\partial G_{e_j}}{\partial \tau }=-\omega _j(\tau )[f_{j}(G_{e_1},\ldots ,G_{e_n},\tau )-G_{e_j}], \end{aligned}$$

(13)

where

$$\begin{aligned} \omega _j(\tau )=\beta _j(\tau )+\mu _j+\alpha _j+\gamma _j+\sum _{j=1,j\ne k}^n d_{jk}^{I}(\tau ). \end{aligned}$$

(A more detailed derivation of (13) in the case of two patches is given in Appendix B.) An estimate of the probability of extinction follows from (11) and (12):

$$\begin{aligned} p_{e_j,0}(\tau ,t)= & {} G_{e_j}(0,\tau ,t)\\ p_{i,0}(\tau ,t)= & {} \prod _{j=1}^n [G_{e_j}(0,\tau ,t)]^{i_j}. \end{aligned}$$

The asymptotic probability of disease extinction is a periodic function

$$\begin{aligned} \lim _{t\rightarrow \infty } p_{i,0}(\tau ,t)={\mathbb {P}}_{ext}(i,\tau ) \end{aligned}$$

for $\tau \in [0, {\textit{T}}]$ (Bacaër and Ait Dads 2014). In particular, the probability of an outbreak given $I_j(\tau )=i_j$, $j=1,\ldots ,n$ equals

$$\begin{aligned} {\mathbb {P}}_{outbreak}(i,\tau )=1-\prod _{k=1}^n[{\mathbb {P}}_{ext}(e_k,\tau )]^{i_k}. \end{aligned}$$

(14)

3.2 Numerical Methods

In the following examples for two and three patches, we estimate the probability of an outbreak given by Eq. (14) from the differential equation (13). In particular, we make a change of variable $s=t-\tau$ in the differential equation (13) and for simplicity, we fix $t=0$, $P_j(s)=p_{e_j,0}(\tau ,0)$, so that

$$\begin{aligned} \dfrac{dP_j(s)}{ds}=\omega _j(-s)\left[ f_j(P_1,\ldots ,P_n,-s)-P_j\right] , \quad P_j(0)=0. \end{aligned}$$

The preceding differential equation is solved (backward in time) for sufficiently large $s>0$ so that there is convergence to a periodic solution,

$$\begin{aligned} P_j(s+k{\textit{T}})\rightarrow \varPhi _j(s)\quad \mathrm{as} \ k\rightarrow \infty . \end{aligned}$$

Another change of variable yields ${\mathbb {P}}_{ext}(e_j,\tau )\approx \varPhi _j(T-\tau )$.

For each numerical example, we estimate ${\mathbb {P}}_{ext}(e_j,\tau )$ and apply formula (14). This estimate is checked against the full nonlinear time-nonhomogeneous stochastic process based on the transition probabilities in Table 1. A Monte Carlo approach is used with a small time step $\varDelta t$, chosen sufficiently small, such that during each time step, only one, if any, of the events in Table 1 occurs ($\varSigma (t)\varDelta t<1$). The accuracy of the Monte Carlo approximation is tested by using a sequence of progressively smaller time steps. A total of $10^4$ sample paths are simulated for a given set of initial conditions at a specific time $\tau$. Each sample path continues until a time $t_s>\tau$ when either $\sum _jI_j(t_s)=0$ or $\sum _j I_j(t_s)=50$. If the total infected population reaches 50, then it is assumed that there is an outbreak. The proportion of sample paths q out of $10^4$ that reach zero is an estimate for the probability of extinction, and the remaining proportion $1-q$ that reach 50 is an estimate of the probability of an outbreak.

4 Two Patches

For two patches, the SIR ODE model has a simple form, illustrated in the compartmental diagram in Fig. 2.

Fig. 2

(Color Figure Online) Compartmental diagram for the two-patch model

Sinusoidal functions are assumed for the transmission and dispersal rates with period ${\textit{T}}$:

$$\begin{aligned} \begin{aligned} \beta _j(t)&=\bar{\beta }_j\left( 1+\delta _j\sin \left( \frac{2{\pi }t}{{\textit{T}}}\right) \right) ,\\ d^{\ell }_{jk}(t)&=\bar{d}^{\ell }_{jk}\left( 1+\delta ^{\ell }_{jk}\sin \left( \frac{2{\pi }t}{{\textit{T}}}\right) \right) ,\quad \ell =S,I,R, \end{aligned} \end{aligned}$$

(15)

$j,k=1,2,$ $j\ne k$. The amplitude of these rates are $|\delta _j|$ and $|\delta ^{\ell }_{jk}|$, respectively. The dispersal rates in each patch are the same, except for the value of $\delta ^{\ell }_{jk}$ which may be either positive or negative while the transmission rates differ in the magnitude of $\bar{\beta }_j$. If the values $\delta _j$ and $\delta ^{\ell }_{jk}$ have the same sign, we say the parameters for transmission and dispersal are “synchonized,” but if they have opposite signs, one positive and one negative, we say they are “desynchronized.” Synchronization of transmission and dispersal rates means that the times of the extrema for the two rates are the same, whereas desynchronization means the times of the extrema are reversed, i.e., high transmission rate corresponds to low dispersal rate and vice versa. Figure 3 shows an example when the two patches are synchronized or desynchronized with respect to dispersal and transmission.

Fig. 3

(Color Figure Online) An illustration when patches 1 and 2 are either synchronized or desynchronized with respect to dispersal and transmission

Parameter values for the two-patch model are given in Table 3. The year is divided into four seasons, and the transmission and dispersal rates in Eq. (15) have a period ${\textit{T}}=4$. The time unit 1 equals three months. We assume either all susceptible, infected, and recovered individuals disperse at the same rate or only infected individuals disperse. In addition, we let $\mu _i=0=\alpha _i$ or $\mu _i=0.01$ and $\alpha _i=0.5$ but keep ${\mathscr {R}}_{0i}$, $i=1,2$ constant, i.e., ${\mathscr {R}}_{0i}=\bar{\beta }_i/(\gamma _i+\mu _i+\alpha _i)$. Each patch has the same recovery and death rates but differs in the average transmission rates, $\bar{\beta }_i$, $i=1,2$. Patch 1 is high-risk with patch reproduction number ${\mathscr {R}}_{01}=3$ and patch 2 is low-risk with ${\mathscr {R}}_{02}=0.2$ (Fig. 4). The following examples show that the probabilities of an outbreak depend on the time and location of the first infected individual and the relation between dispersal and transmission rates.

Table 3 Baseline Parameter values for the two- and three-patch models where the units are per season

Fig. 4

(Color Figure Online) Two patches with one high-risk patch, ${\mathscr {R}}_{01}=3$, and one low-risk patch, ${\mathscr {R}}_{02}=0.2$

In Fig. 5, four different cases are considered, (A)–(D), with constant transmission or dispersal and synchronized or desynchronized transmission and dispersal. In the top two panels of each of (A)–(D), the transmission and dispersal rates are graphed for patches 1 and 2 and in the bottom two panels, the periodic probabilities of an outbreak for initial conditions $(I_1(\tau ), I_2(\tau ))=(1,0)$ and (0, 1), respectively. The branching process estimate is verified by checking thirteen different times $\tau =0, 1/3, 2/3, \ldots , 4$ with a Monte Carlo simulation of $10^4$ sample paths of the nonhomogeneous stochastic process. The results from the Monte Carlo simulations show good agreement with the branching process approximation.

Fig. 5

(Color Figure Online) Two-patch model with the periodic transmission (black solid curve) and dispersal (red dashed curve) rates, graphed in each of the top two (a)–(d), and probability of an outbreak, graphed in each of the bottom two (a)–(d) for patches 1 and 2 when $(I_1(\tau ),I_2(\tau ))=(1,0)$ or (0, 1), respectively. In a constant transmission with periodic dispersal, b constant dispersal with periodic transmission, c transmission synchronized with dispersal and d transmission desynchronized with dispersal. Thirteen different introductions of one infected individual into either patch 1 or 2 at times $t=0,1/3,2/3,\ldots ,4$ are checked using $10^4$ sample paths of the Monte Carlo simulation of the full nonhomogeneous process (Num Sim, circles). The parameter values are given in Table 3

Dispersal between the two patches allows an outbreak to occur even when an infected individual is introduced into a low-risk patch, but there is a much smaller probability of an outbreak if the infection is initiated into a low-risk patch than into a high-risk patch (Fig. 5). With desynchronized dispersal and transmission (Fig. 5D), the probability of an outbreak when the infection starts in the low-risk patch is smaller than in cases (A), (B), or (C). Also, fluctuation in the transmission rate has a greater effect on the amplitude of the periodic outbreaks than dispersal (compare Fig. 5A, B). In all cases, the time of the highest (lowest) transmission rate is closely related to the highest (lowest) probability of an outbreak. But the extrema of the probability of an outbreak are shifted slightly left of the extrema of the transmission rates. This phenomenon was also noted by Nipa and Allen (2020) in a vector-host epidemic model. When infected individuals are first introduced, they may not transmit the infection to others immediately. Whether there is a successful transmission depends on the duration of the infectious period (average duration $1/(\gamma _j+\mu _j+\alpha _j)$), the patch j, the location of the infectious individual and the value of the transmission rate $\beta _j(t)$ at the time of transmission. The largest probability of an outbreak occurs just before the peak of transmission when the transmission rate is increasing.

Table 4 records the average of the periodic probabilities of an outbreak that are displayed in Fig. 5A–D. The average is computed as follows:

$$\begin{aligned} {\bar{P}}_{outbreak}(i, j)=\dfrac{1}{{\textit{T}}}\int _0^{\textit{T}} {\mathbb {P}}_{outbreak}(i, j, \tau )\, d\tau . \end{aligned}$$

For each case (A)–(D), the threshold value ${\mathscr {R}}_0$ from the underlying nonautonomous ODE model is also calculated. For comparison purposes, the baseline case (Base) with constant transmission and dispersal rates, set at their average values, is also included. It is notable that the four cases of periodic transmission and dispersal have an overall lower average probability of an outbreak than at the baseline case. The lowest average probabilities of an outbreak occur with desynchronized transmission and dispersal. The magnitude of ${\mathscr {R}}_0$ is not a good predictor of disease severity in these cases as the largest value of ${\mathscr {R}}_0$ has the lowest average probability of an outbreak.

Table 4 Average probability of an outbreak ${\bar{P}}_{outbreak}(1,0)$ for patch 1 and ${\bar{P}}_{outbreak}(0,1)$ for patch 2 and the threshold value ${\mathscr {R}}_0$ for the two-patch system when ${\mathscr {R}}_{01}=3$ and ${\mathscr {R}}_{02}=0.2$

We show that the branching process estimate is also a good approximation when there are several infected individuals introduced into one or both patches (Fig. 6). For two patches, the probability of an outbreak in Eq. (14) equals

$$\begin{aligned} {{\mathbb {P}}}_{outbreak}(i,j,\tau )=1- [{{\mathbb {P}}}_{ext}(1,0,\tau )]^i[{{\mathbb {P}}}_{ext}(0,1,\tau )]^j. \end{aligned}$$

The probability of an outbreak is close to 1 when $I_2(\tau )=3$ and $\tau \in [0,5/3]$ but drops rapidly to $< 0.3$ for $\tau \in [7/3,3]$. The example in Fig. 6 illustrates synchronous dispersal and transmission. Additional Monte Carlo simulations showed good agreement with the branching process estimate for desynchronous dispersal and transmission and for unequal population sizes in the two patches ranging from 200 to 5000 (not shown). The branching process approximation may fail if population sizes are too small. Some other limitations of the branching process approximation are discussed in the conclusion.

Fig. 6

(Color Figure Online) For synchronous dispersal as in Fig. 5C, the probability of an outbreak for one infected individual in patch 2 and either 0, 1, 2, or 3 infected individuals in patch 1 (four graphs ordered from bottom to top, have initial conditions for the high-risk patch 1, $I_1(\tau )=0,1,2,3$, respectively ). The blue circles are the results of the Monte Carlo simulation of the nonhomogeneous stochastic process with $5\times 10^3$ sample paths at $\tau =0,1/3,2/3,1,\ldots ,4.$ The parameter values are given in Table 3

Next, we examine how an increase in the dispersal rate affects the probability of an outbreak (Fig. 7). As the average dispersal rate $\bar{d}^I_{jk}$ increases, the periodic curves for the probability of an outbreak in the two patches come closer together. That is, with a large amount of mixing of infected individuals in the two patches, whether infection is initiated into the high-risk or the low-risk patch does not matter, as the periodic probabilities of outbreaks for patches 1 and 2 are very close to each other. This phenomenon also occurs when constant dispersal rates are increased (Lahodny Jr and Allen 2013).

Fig. 7

(Color Figure Online) The probabilities of an outbreak for initial conditions $(I_1(\tau ),I_2(\tau ))=(1,0)$ (patch 1, solid curves) or (0, 1) (patch 2, dashed curves) are graphed when the average dispersal rate is increased $\bar{d}^I_{jk}=1/4,1/2,1,2,4,8$, $j,k=1,2,$ $j\ne k$, when transmission and dispersal rates in patches 1 and 2 are synchronized (Fig. 5C). The arrows indicate the direction of change in the probability of an outbreak as $\bar{d}^I_{jk}$ increases

In the final two-patch example, we relax the restriction imposed on dispersal, condition (3). We assume individuals disperse at different rates in the two patches, $d_{12}^{\ell }\ne d^{\ell }_{21}$, $\ell =S,I,R.$ The dispersal parameters for the two-patch model are

$$\begin{aligned} \bar{d}^{\ell }_{12}=2, \ \bar{d}^{\ell }_{21}=1,\ \delta _{12}^{\ell }=0.8,\ \delta _{21}^{\ell }=-0.8,\quad \ell =S,I,R \end{aligned}$$

(16)

with remaining parameters

$$\begin{aligned} \bar{\beta }_1=18,\ \bar{\beta }_2=1.2,\ \delta _i=0.8,\ \mu _i=0.2,\ \alpha _i=0.5,\ \gamma _i=6-\mu _i-\alpha _i \end{aligned}$$

(17)

for $i=1,2.$ In patch 1, transmission and dispersal are synchronized but in patch 2, they are desynchronized. The values of the patch reproduction numbers are the same as in Fig. 4. Relaxation of the condition (3) results in oscillation of the populations in the absence of infection (Fig. 8). In the Monte Carlo simulations of the time-nonhomogeneous process, the initial conditions for the population sizes are equal to the disease-free population sizes. That is, $N_j(\tau )$ takes the value of $S_j(\tau )$ in Fig. 8 for $\tau \in [0,{\textit{T}}].$ When infection is introduced, $(I_1(\tau ),I_2(\tau ))=(1,0)$ or (0, 1), then $S_j(\tau )=N_j(\tau )-I_j(\tau )$, and $R_j(\tau )=0$, $j=1,2$.

Fig. 8

(Color Figure Online) Disease-free solution of the two-patch model is graphed for the ODE two-patch model (black solid and red dashed curves) and one sample path of the stochastic time-nonhomogeneous process (green curves). Initial conditions are $S_1(0)=N_1(0)=2000$ and $S_2(0)=N_2(0)=1000$. Parameter values are summarized in the list (16)

The branching process estimate in Fig. 9 agrees well with the Monte Carlo simulations of the time-nonhomogeneous process. The reason for this agreement is due to the assumption of frequency-dependent transmission; $S_i(t)\approx N_i(t)$ at the initiation of an epidemic.

Fig. 9

(Color Figure Online) Periodic probability of a disease outbreak for two patches with oscillating population sizes. Parameter values are summarized in the lists (16) and (17)

5 Three Patches

For three patches, we consider how the connections between low- and high-risk patches affect the probability of an outbreak. For each example, we keep the same relation between transmission and dispersal rates, as in Fig. 5A–D. Three types of connection between the patches are referred to as full connection (FC), bidirectional connection (BC), and circular connection (CC).

With full connection (FC), each patch is connected to its neighbors by a one-step transition, i.e., $1\leftrightarrow 2\leftrightarrow 3\leftrightarrow 1$ (Fig. 10). Patch 1 is high-risk with ${\mathscr {R}}_{01}=5$, and patches 2 and 3 are low-risk with ${\mathscr {R}}_{02}=0.5$ and ${\mathscr {R}}_{02}=0.25$. The second type of connection is called a circular connection (CC), i.e., $1\rightarrow 2 \rightarrow 3\rightarrow 1$. The patch reproduction numbers are the same as in FC. In the third type of connection, referred to as a bidirectional connection (BC), the patches are linearly ordered and connected only to nearest neighbor, i.e., $1\leftrightarrow 2\leftrightarrow 3$. The arrangement is changed in the third case, the second patch has ${\mathscr {R}}_{02}=0.25$ and ${\mathscr {R}}_{03}=0.5$. The periodic functions for dispersal and transmission are given in Eq. (15) with parameter values in Table 3.

Fig. 10

(Color Figure Online) Three patches with either full connection (FC), circular connection (CC) or bidirectional connection (BC) containing one high-risk patch ${\mathscr {R}}_{01}=5$ and two low-risk patches, ${\mathscr {R}}_{02}=0.5$ and ${\mathscr {R}}_{03}=0.25$ (FC and CC) or ${\mathscr {R}}_{02}=0.25$ and ${\mathscr {R}}_{03}=0.5$ (BC)

The periodic probabilities of an outbreak with FC are illustrated in Fig. 11 when initial conditions $(I_1(\tau ),I_2(\tau ),I_3(\tau ))=(1,0,0),(0,1,0)$, and (0, 0, 1) for patches 1, 2, and 3, respectively. (The graphs for BC and CC are in Appendix C, Figs. 13 and 14). Similar trends are observed for three patches with FC as in two patches. The largest probability of an outbreak occurs when infected individuals are introduced into the high-risk patch 1 and the lowest when introduced into low-risk patch 3 with the smallest patch reproduction number, ${\mathscr {R}}_{03}=0.25$. Desynchronized dispersal and transmission rates in case (D) show that the peaks of an outbreak are smaller in both of the low-risk patches but larger in the high-risk patch than in cases (A), (B), or (C). The periodic transmission rate has a greater impact on the magnitude of the periodic probability of an outbreak than periodic dispersal, case (A) versus case (B).

There are similar trends in the average probabilities for cases (A)–(D) for FC as in two patches (Tables 4, 5). Case (D), desynchronized dispersal and transmission, has the largest threshold value of ${\mathscr {R}}_0$, but the average probabilities are generally lower than for constant transmission and dispersal.

Fig. 11

(Color Figure Online) The periodic probabilities of an outbreak for FC with the four cases of dispersal and transmission (a)–(d) as in Fig. 5. The initial conditions are $(I_1(\tau ),I_2(\tau ),I_3(\tau ))=(1,0,0),(0,1,0)$ and (0, 0, 1) for patches 1, 2, and 3, respectively. Patch 1 is high-risk, ${\mathscr {R}}_{01}=5$, and patches 2 and 3 are low-risk, ${\mathscr {R}}_{02}=0.5$ and ${\mathscr {R}}_{02}=0.25$. Parameter values are given in Table 3

Table 5 Average probabilities of an outbreak in three patches with FC for the four cases in Fig. 11

The most important difference between FC and the two other connections is whether a low-risk patch is directly connected to the high-risk patch. The low-risk patch directly connected to the high-risk patch (patch 3 in CC and patch 2 in BC) has a larger probability of an outbreak than the low-risk patch not directly connected. In the case of BC, infection initiated in the patch with the smallest patch reproduction number does not correspond to the lowest probability of an outbreak. More important is the direct connection to the high-risk patch (see Table 6).

Table 6 Average probabilities of an outbreak in three patches with BC and CC for the four cases (A)–(D) corresponding to Figs. 13 and 14

In a final example for three patches, we compare the probabilities of an outbreak in each of the three patches with synchronized dispersal and transmission, (case (C) in Figs. 11, 13, 14) for FC, BC, and CC. In Fig. 12, the changes in the periodic probabilities of an outbreak are shown for increasing recovery rates (i) $\gamma _i=0.5$ (top), (ii) $\gamma _i=1$, (ii) $\gamma _i=2$, (iv) $\gamma _i=4$ (bottom), $i=1,2,3$. Here, we assume natural and disease-related death rates are $\mu _i=0=\alpha _i$ so that ${\mathscr {R}}_{0i}=\bar{\beta }_i/\gamma _i$. As the recovery rate $\gamma _i$ increases from (i) to (iv), the average duration of the infection shortens, each patch reproduction number ${\mathscr {R}}_{0i}$ decreases and the probability of an outbreak decreases. The low-risk patches 2 and 3 have the lowest probability of outbreak in all three cases with a large recovery rate. It is interesting to note that the high-risk patch in BC and CC has a larger probability of an outbreak than FC, but the low-risk patches in BC and CC have lower probabilities of outbreaks than FC. This is clearly visible in case (D) with the largest recovery rate. The lowest risk of an outbreak in Figure 12 occurs when infections are introduced during $\tau \in (2,3)$ when transmission is decreasing.

Fig. 12

(Color Figure Online) Probability of an outbreak with synchronized dispersal in three patches with FC, BC, and CC as in Fig. 10. Initial conditions in patch 1 are $(I_1(\tau ),I_2(\tau ),I_3(\tau ))=(1,0,0)$ (solid black curve), in patch 2, $(I_1(\tau ),I_2(\tau ),I_3(\tau ))=(0,1,0)$ (red dashed curve) and in patch 3, $(I_1(\tau ),I_2(\tau ),I_3(\tau ))=(0,1,0)$ (blue dotted curve). Values of the recovery rate in rows (i) $\gamma _i=0.5$, (ii) $\gamma _i=1$, (iii) $\gamma _i=2$ and (iv) $\gamma _i=4$, $i=1,2,3$ with natural and disease-related death rates set to zero $\mu _i=0=\alpha _i$. All other parameters are in Table 3

Table 7 is a summary of the average probabilities of an outbreak and the values of ${\mathscr {R}}_0$ for FC, BC, and CC corresponding to Fig. 12. For comparison purposes, consider the case where the patches are isolated, not connected via dispersal, and there is no seasonal variation in transmission, $\beta _{j}(t)=\bar{\beta }_j$. In this case, the well-known result of Whittle (1955) can be applied: the probability of an outbreak in the low-risk patches equals zero, and the probability of an outbreak in the high-risk patch equals

$$\begin{aligned} 1-\dfrac{1}{{\mathscr {R}}_{01}}, \end{aligned}$$

where ${\mathscr {R}}_{01}=\bar{\beta }_1/\gamma _1$. With isolation and no seasonality, the probabilities of an outbreak in the high-risk patch equal 0.95, 0.9, 0.8, and 0.6 in cases (i), (ii), (iii), and (iv), respectively. With dispersal connecting the high- and low-risk patches and seasonality, it can be seen that the average probabilities in Table 7 decrease in the high-risk patch, from 0.6 to 0.28 in case FC (iv), but the average probabilities of an outbreak initiated from the low-risk patches increase significantly from 0 to as high as 0.74 in case FC (i) in patch 2.

Table 7 Average probability of an outbreak in three patches for FC, BC, and CC with synchronized dispersal and transmission, corresponding to Fig. 12

6 Summary and Conclusion

Seasonal changes that affect the pathogen life cycle or the within-host and between-host interactions result in seasonal outbreaks of many infectious diseases, such as seasonal influenza, AI, malaria, cholera, dengue, Ebola, and coronavirus diseases (Altizer et al. 2006; Endo and Nishiura 2018; Fisman 2007; Grassly and Fraser 2006; Kissler et al. 2020; Martinez 2018). In this investigation, we applied a stochastic time-nonhomogeneous, multi-patch epidemic model with seasonal and demographic variability to investigate how time and location affect the probability of an outbreak when the infection is introduced into the patch system. We applied a multi-type branching process approximation to the infected classes to obtain an analytical estimate for the probability of a disease outbreak. Examples with two and three patches were used to test the branching process approximation against the full nonlinear time-nonhomogeneous process. In particular, we investigated how the periodic probability of an outbreak changes with different assumptions regarding patch arrangement, connectivity, and relations between the periodic dispersal and transmission rates (cases (A)–(D) and FC, BC, and CC).

We found that seasonality in dispersal and transmission affects the time and location of the greatest risk for an outbreak. If the infection is introduced into a high-risk patch $({\mathscr {R}}_0>1)$ at a time when the transmission rate is large and increasing, then the probability of an outbreak is high. But if the infection is introduced at a time when the transmission rate is small and decreasing, or the dispersal rate to a low-risk patch is large, then the probability of an outbreak is low. Interestingly, seasonality in transmission and dispersal rates can, in some cases, result in a lower average risk of an outbreak than if the transmission and dispersal rates are constant (Tables 4, 5, 6). The shapes of the outbreak probabilities do not directly coincide with those of either the dispersal or transmission rates. In an ODE patch model without seasonality, developed for cholera, Kelly Jr. et al. (2016) investigated the optimal vaccination strategy. In a linear arrangement of patches, similar to BC, they found that after an outbreak occurs in a patch, the optimal vaccination strategy is to target neighboring or downstream patches. In our stochastic model, with dispersal and transmission rates changing during the season, the magnitude of these rates and whether they are increasing or decreasing at the time of the outbreak is important and makes the stochastic optimal control problem with seasonality an interesting and challenging problem.

As shown here and elsewhere, multi-type branching processes are often a good approximation method for the probability of an outbreak near the DFE, e.g., (Allen and van den Driessche 2013; Allen and Lahodny Jr 2012; Lahodny Jr and Allen 2013; Lahodny Jr et al. 2015; Milliken 2017; Nipa and Allen 2020). The branching process approximation may fail if ${\mathscr {R}}_0$ is too close to one, if demographic dynamics dominate the infection dynamics, or if population sizes are too small. The reasons for these failures are that the underlying assumptions of the multi-type branching process are no longer valid. The total population sizes must be sufficiently large and not deviate substantially from the disease-free state, and the initial infected population size must be small but grow to a sufficiently large size. Therefore, it is important to test the branching process approximation against the time-nonhomogeneous process.

There are many generalizations of these stochastic multi-patch epidemic models worthy of further investigation, such as additional stages or classes of infection, a mass action incidence rate, patch-dependent population densities, patch arrangements, and alternate movement and dispersal strategies. Realistic models that incorporate both demographic and seasonal variability in conjunction with case data and environmental data on specific diseases provide useful public health information on preventive and control measures such as isolation, quarantine, and travel restrictions. The impact of such measures has been evaluated in general models and in specific models applied to outbreaks of SARS, MERS, Ebola, and COVID-19, e.g., (Arino et al. 2007; Camitz and Liljeros 2006; Chinazzi et al. 2020; Dénes and Gumel 2019; Gao and Ruan 2012; Hsieh et al. 2007; Kwok et al. 2019; Parmet and Sinha 2020; Peak et al. 2020) and references therein. Application of our modeling framework and methods, coupled with information about travel patterns and seasonal trends on specific diseases (such as seasonal influenza, AI, dengue, malaria, cholera, Ebola, and coronavirus diseases), provide additional insight into the times and locations for quarantine and travel restrictions.

Appendices

ODE Model Assumptions

The following assumptions are taken from Wang and Zhao (2008) and applied to the ODE system (2). The system can be written as follows:

$$\begin{aligned} {\dot{x}}_i= {\mathscr {F}}_i(t, x) -{\mathscr {V}}_i (t, x)\equiv f_i(t, x), \ \ i =1,\ldots ,3n, \end{aligned}$$

(18)

where $x= (x_1,\ldots ,x_{3n})=(I_1,\ldots ,I_n,S_1,\ldots ,S_n,R_1,\ldots ,R_n)$ and ${\mathscr {V}}_i={\mathscr {V}}_i^+-{\mathscr {V}}_i^-$. In particular, linearization of system (18) about the DFE has the form

$$\begin{aligned} \dot{X}=\begin{pmatrix} F(t)-V(t) &{} O\\ -J(t) &{} M(t) \end{pmatrix}X. \end{aligned}$$

Matrices F(t) and V(t) are defined in Eqs. (5) and (6) and O is the $2n\times 2n$ zero matrix. Let $\dot{z}=M(t)z$ and $\dot{y}=-V(t)y$. The fundamental matrix solutions for these linear periodic systems are known as monodromy matrices. Let these monodromy matrices be denoted as $\phi _M(t)$ and $\phi _{-V}(t)$, respectively. The following assumptions guarantee there exists a basic reproduction number ${\mathscr {R}}_0>0$ (Theorem 2.1 p. 704, Wang and Zhao (2008)).

• (A1) The functions ${\mathscr {F}}_i(t,x)$, ${\mathscr {V}}_i^+(t,x)$, and ${\mathscr {V}}_i^-(t,x)$ are nonnegative and continuous on ${\mathbb {R}}\times {\mathbb {R}}^{3n}_+$ and continuously differential with respect to x.

• (A2) The functions ${\mathscr {F}}_i(t,x)$, ${\mathscr {V}}_i^+(t,x)$, and ${\mathscr {V}}_i^-(t,x)$ are $p-$periodic in t, $p>0$.

• (A3) If $x_i=0$ then ${\mathscr {V}}_i^-(t,x)=0$.

• (A4) ${\mathscr {F}}_i (t,x) = 0$ for $i=n+1,\ldots ,3n$.

• (A5) If $I=0$, then ${\mathscr {F}}_i (t,x) = V_i^+(t,x)=0$ for $i=1,\ldots ,n$.

• (A6) The DFE is stable if $I=0$, i.e., the spectral radius $\rho (\phi _M(p))<1.$

• (A7) The spectral radius $\rho (\phi _{-V}(p))<1$.

Assumptions (A1)–(A7) hold for the ODE system (2).

The following assumptions were applied by Bacaër and Ait Dads (2014) for the multi-type branching process approximation based on the linear system (4).

$$\begin{aligned} \dot{I}=[F(t)-V(t)]I, \end{aligned}$$

(19)

where matrices F(t) and V(t) are defined in (5) and (6) (Proposition, p. 36 Bacaër and Ait Dads (2014)).

• (H1) F(t) is nonnegative with at least one entry strictly positive for $t\ge 0.$

• (H2) $K(t) = F(t)- V(t)$ is irreducible for all $t\ge 0$.

• (H3) F(t) and V(t) are piecewise continuous and $p-$periodic for $t\ge 0$.

• (H4) $V(t)=(v_{ij}(t))$ has nonpositive off-diagonal elements, $v_{ij}(t)\le 0$, $i\ne j$, $t\ge 0$ and has positive diagonal elements, $v_{ii}(t)\ge A>0$, $t\ge 0$.

From these assumptions, the following results hold for the multi-type branching process. If ${\mathscr {R}}_0\le 1$, then the multi-type branching process with the same periodic rates (defined in Table 2) has an asymptotic probability of extinction ${\mathbb {P}}_{ext}(i_1,\ldots ,i_n,\tau )=1$ and if ${\mathscr {R}}_0>1$, then the asymptotic probability of disease extinction is a p-periodic function satisfying $0<{\mathbb {P}}_{ext}(i_1,\ldots ,i_n,\tau )<1.$

Derivation of Probability of Disease Extinction for Two Patches

Applying a multi-type branching process approximation for two patches, the detailed steps of the derivation of the probability of extinction are derived here using generating functions and the backward Kolmogorov differential equation. For $I_j(\tau )=1$ and $I_k(\tau )=0$, $j,k=1,2$ and $k\ne j$ the offspring pgf for patch j is

$$\begin{aligned} f_{j}(u_1,u_2,\tau )&=\frac{\beta _j(\tau )u_j^2+\mu _j+\alpha _j+\gamma _j+d^I_{jk}(\tau )u_k}{\beta _j(\tau )+\mu _j+\alpha _j+\gamma _j+d^I_{jk}(\tau )},\ j=1,2. \end{aligned}$$

The backward Kolmogorov differential equation in (9) for the branching process approximation of $I_1$ and $I_2$ is

$$\begin{aligned} \begin{aligned} - \frac{\partial p_{(i_1,i_2),(j,k)}(\tau ,t)}{\partial \tau }&=\beta _1(\tau )i_1p_{(i_1+1,i_2),(j,k)}(\tau ,t)\\&\quad +(\mu _1+\alpha _1+\gamma _1)i_1p_{(i_1-1,i_2),(j,k)}(\tau ,t)\\&\quad +d^I_{21}(\tau )i_2p_{(i_1+1,i_2-1),(j,k)}(\tau ,t)\\&\quad +\beta _2(\tau )i_2p_{(i_1,i_2+1),(j,k)}(\tau ,t)\\&\quad +(\mu _2+\alpha _2+\gamma _2)i_2p_{(i_1,i_2-1),(j,k)}(\tau ,t)\\&\quad +d^I_{12}(\tau )i_1p_{(i_1-1,i_2+1),(j,k)}(\tau ,t)\\&\quad -[\beta _1(\tau )i_1+(\mu _1+\alpha _1+\gamma _1)i_1+d^I_{21}(\tau )i_2\\&\quad +\beta _2(\tau )i_2+(\mu _2+\alpha _2+\gamma _2)i_2\\&\quad +d^I_{12}(\tau )i_1]p_{(i_1,i_2),(j,k)}(\tau ,t). \end{aligned} \end{aligned}$$

(20)

Also, the generating function $G_{(i_1,i_2)}(u_1,u_2,\tau ,t)$ for the two-patch model can be expressed in terms of the transition probabilities in (11):

$$\begin{aligned} G_{(i_1,i_2)}(u_1,u_2,\tau ,t)= & {} {\mathbb {E}}\left[ u_1 ^{I_1(t)} u_2^{I_2(t)}|(I_1(\tau ),I_2(\tau ))=(i_1,i_2)\right] \nonumber \\= & {} \sum _{j,k\ge 0}p_{(i_1,i_2),(j,k)}(\tau ,t)u_1^j u_2^k,\quad \tau <t. \end{aligned}$$

(21)

For $j=k=0$, $G_{(i_1,i_2)}(0,0,\tau ,t)=p_{(i_1,i_2),(0,0)}(\tau ,t)$ is the probability of disease extinction. From the independent assumptions of the random variables $I_1$ and $I_2$ in the branching process approximation, it follows that

$$\begin{aligned} G_{(i_1,i_2)}(u_1,u_2,\tau ,t)=[G_{e_1}(u_1,u_2,\tau ,t)]^{i_1}[G_{e_2}(u_1,u_2,\tau ,t)]^{i_2}, \end{aligned}$$

(22)

where $e_1=(1,0)$ and $e_2=(0,1).$

For initial data $(I_1(\tau ),I_2(\tau ))=(i_1,i_2)$, the probability of extinction at time $t>\tau$ is

$$\begin{aligned} p_{(i_1,i_2),(0,0)}(\tau ,t)=[p_{e_1,(0,0)}(\tau ,t)]^{i_1}[p_{e_2,(0,0)}(\tau ,t)]^{i_2}. \end{aligned}$$

(23)

For simplicity, let $G_{(i_1,i_2)}\equiv G_{(i_1,i_2)}(u_1,u_2,\tau ,t)$ and $p_{(i_1,i_2),(j,k)}\equiv p_{(i_1,i_2),(j,k)}(\tau ,t)$. By differentiating $G_{(i_1,i_2)}$ with respect to $\tau$ in Eq. (22) and applying the identities $G_{(i_1,0)}=G_{e_1}^{i_1}$ and $G_{(0,i_2)}=G_{e_2}^{i_2}$ yields

$$\begin{aligned} \frac{\partial G_{e_1}}{{\partial } \tau }&=\frac{1}{i_1[G_{(i_1-1,0)}]}\sum _{j,k}\frac{\partial p_{(i_1,0),(j,k)}}{\partial \tau }u_1^ju_2^k\\ \frac{\partial G_{e_2}}{{\partial }\tau }&=\frac{1}{i_2[G_{(0,i_2-1)}]}\sum _{j,k}\frac{\partial p_{(0,i_2),(j,k)}}{\partial \tau }u_1^ju_2^k. \end{aligned}$$

Substituting the backward Kolmogorov differential equation (20) into the right side, applying the identity (22), using offspring pgf $f_j$, and simplifying leads to

$$\begin{aligned} \frac{\partial G_{e_1}}{{\partial }\tau }&=-\frac{1}{G_{(i_1-1,0)}}\sum _{j,k}\Big \{\beta _1(\tau )p_{(i_1+1,0),(j,k)}(\tau ,t)\\&\quad +(\mu _1+\alpha _1+\gamma _1)p_{(i_1-1,0),(j,k)}(\tau ,t)\\&\quad +d^I_{12}(\tau )p_{(i_1-1,1),(j,k)}(\tau ,t)-[(\beta _1(\tau )\\&\quad +(\mu _1+\alpha _1+\gamma _1)+d^I_{12}(\tau )]p_{(i_1,0),(j,k)}(\tau ,t)\Big \}u_1^ju_2^k\\&=-\frac{1}{G_{(i_1-1,0)}}\Big \{\beta _1(\tau )G_{(i_1+1,0)}+(\mu _1+\alpha _1+\gamma _1)G_{(i_1-1,0)}+d^I_{12}(\tau )G_{(i_1-1,1)}\\&\quad -(\beta _1(\tau )+\mu _1+\alpha _1+\gamma _1+d^I_{12}(\tau ))G_{(i_1,0)}\Big \}u_1^ju_2^k\\&=-(\beta _1(\tau )+\mu _1+\alpha _1+\gamma _1+d^I_{12}(\tau ))\\&\quad [f_1(G_{e_1},G_{e_2},\tau )-G_{e_1}] \end{aligned}$$

and

$$\begin{aligned} \frac{\partial G_{e_2}}{{\partial }\tau }=-(\beta _2(\tau )+\mu _2+\alpha _2+\gamma _2+d^I_{21}(\tau ))[f_2(G_{e_1},G_{e_2},\tau )-G_{e_2}] \end{aligned}$$

Since the right side of the differential equation is independent of $u_1$ and $u_2$, the differential equation also applies to $G_{e_j}(0,0,\tau ,t)=p_{e_j,(0,0)}(\tau ,t)=p_{e_j,(0,0)}.$ That is,

$$\begin{aligned} \frac{d p_{e_1,(0,0)}}{d\tau }&=(\beta _1(\tau )+\mu _1+\alpha _1+\gamma _1+d^I_{12}(\tau ))[f_1(p_{e_1,(0,0)},p_{e_2,(0,0)},\tau )-p_{e_1,(0,0)}],\\ \frac{d p_{e_2,(0,0)}}{d\tau }&=(\beta _2(\tau )+\mu _2+\alpha _2+\gamma _2+d^I_{21}(\tau ))[f_2(p_{e_1,(0,0)},p_{e_2,(0,0)},\tau )-p_{e_2,(0,0)}]. \end{aligned}$$

Periodic Probability of an Outbreak for Three Patches with BC and CC

The periodic probabilities of an outbreak are computed from the branching process approximation and verified with the time-nonhomogeneous process (circles) for the three-patch models with bidirectional (BC) or circular connections (CC) (Figs. 13, 14). Parameter values are given in Table 3.

Fig. 13

(Color Figure Online) The periodic probabilities of an outbreak for the four cases of dispersal and transmission rates, (a)–(d) as in Fig. 5, with bidirectional connection (BC). The initial conditions are $(I_1(\tau ),I_2(\tau ),I_3(\tau ))=(1,0,0),(0,1,0)$, and (0, 0, 1) for patches 1, 2, and 3, respectively. Patch 1 is high-risk, ${\mathscr {R}}_{01}=5$, and patches 2 and 3 are low-risk, ${\mathscr {R}}_{02}=0.25$ and ${\mathscr {R}}_{03}=0.5$

Fig. 14

(Color Figure Online) The periodic probabilities of an outbreak for the four cases of dispersal and transmission rates, (a)–(d) as in Fig. 5, with circular connection (CC). The initial conditions are $(I_1(\tau ),I_2(\tau ),I_3(\tau ))=(1,0,0),(0,1,0)$ and (0, 0, 1) for patches 1, 2, and 3, respectively. Patch 1 is high-risk, ${\mathscr {R}}_{01}=5$, and patches 2 and 3 are low-risk, ${\mathscr {R}}_{02}=0.5$ and ${\mathscr {R}}_{03}=0.25$