25 Years of Self-Organized Criticality: Solar and Astrophysics

Abstract

Shortly after the seminal paper “Self-Organized Criticality: An explanation of 1/f noise” by Bak et al. (1987), the idea has been applied to solar physics, in “Avalanches and the Distribution of Solar Flares” by Lu and Hamilton (1991). In the following years, an inspiring cross-fertilization from complexity theory to solar and astrophysics took place, where the SOC concept was initially applied to solar flares, stellar flares, and magnetospheric substorms, and later extended to the radiation belt, the heliosphere, lunar craters, the asteroid belt, the Saturn ring, pulsar glitches, soft X-ray repeaters, blazars, black-hole objects, cosmic rays, and boson clouds. The application of SOC concepts has been performed by numerical cellular automaton simulations, by analytical calculations of statistical (powerlaw-like) distributions based on physical scaling laws, and by observational tests of theoretically predicted size distributions and waiting time distributions. Attempts have been undertaken to import physical models into the numerical SOC toy models, such as the discretization of magneto-hydrodynamics (MHD) processes. The novel applications stimulated also vigorous debates about the discrimination between SOC models, SOC-like, and non-SOC processes, such as phase transitions, turbulence, random-walk diffusion, percolation, branching processes, network theory, chaos theory, fractality, multi-scale, and other complexity phenomena. We review SOC studies from the last 25 years and highlight new trends, open questions, and future challenges, as discussed during two recent ISSI workshops on this theme.

1 Introduction

About 25 years ago, the concept of self-organized criticality (SOC) emerged (Bak et al. 1987), initially envisioned to explain the ubiquitous 1/f-power spectra, which can be characterized by a powerlaw function P(ν)∝ν ⁻¹. The term 1/f power spectra or flicker noise should actually be understood in broader terms, including power spectra with pink noise (P(ν)∝ν ⁻¹), red noise (P(ν)∝ν ⁻²), and black noise (P(ν)∝ν ⁻³), essentially everything except white noise (P(ν)∝ν ⁰). While white noise represents traditional random processes with uncorrelated fluctuations, 1/f power spectra are a synonym for time series with non-random structures that exhibit long-range correlations. These non-random time structures represent the avalanches in Bak’s paradigm of sandpiles. Consequently, Bak’s seminal paper in 1987 triggered a host of numerical simulations of sandpile avalanches, which all exhibit powerlaw-like size distributions of avalanche sizes and durations. These numerical simulations were, most commonly, cellular automata in the language of complexity theory, which are able to produce complex spatio-temporal patterns by iterative application of a simple mathematical redistribution rule. The numerical algorithms of cellular automata are extremely simple, basically a one-liner that defines the redistribution rule, with an iterative loop around it, but can produce the most complex dynamical patterns, similar to the beautiful geometric patterns created by Mandelbrot’s fractal algorithms (Mandelbrot 1977, 1983, 1985). An introduction and exhaustive description of cellular automaton models that simulate SOC systems is given in Pruessner (2012, 2013), and a review of cellular automaton models applied to solar physics is given in Charbonneau et al. (2001).

Four years after introduction, Bak’s SOC concept was applied to solar flares, which were known to exhibit similar powerlaw size distributions for hard X-ray peak fluxes, total fluxes, and durations as the cellular automaton simulations produced for avalanche sizes and durations (Lu and Hamilton 1991). This discovery enabled a host of new applications of the SOC concept to astrophysical phenomena, such as solar and stellar flare statistics, magnetospheric substorms, X-ray pulses from accretion disks, pulsar glitches, and so forth. A compilation of SOC applications to astrophysical phenomena is given in a recent textbook (Aschwanden 2011a), as well as in recent review articles (Aschwanden 2013; Crosby 2011). The successful spreading of the SOC concept in astrophysics mirrored the explosive trend in other scientific domains, such as the application of SOC in magnetospheric physics (auroras, substorms; see review by Sharma et al. 2014), in geophysics (earthquakes, mountain and rock slides, snow avalanches, forest fires; see Hergarten 2002 and review by Hergarten in this volume), in biophysics (evolution and extinctions, neuron firing, spread of diseases), in laboratory physics (Barkhausen effect, magnetic domain patterns, Ising model, tokamak plasmas; Jensen 1998), financial physics (stock market crashes; Sornette 2003), and social sciences (urban growth, traffic, global networks, internet) or sociophysics (Galam 2012). This wide range of applications elevated the SOC concept to a truly interdisciplinary research area, which inspired Bak’s vision to explain “how nature works” (Bak 1996). What is common to all these systems is the statistics of nonlinear processes, which often ends up in powerlaw-like size distributions. Other aspects that are in common among the diverse applications are complexity, contingency, and criticality (Bak and Paczuski 1995), which play a grand role in complexity theory and systems theory.

What became clear over the last 25 years of SOC applications is the duality of (1) a universal statistical aspect, and (2) a special physical system aspect. The universal aspect is a statistical argument that can be formulated in terms of the scale-free probability conjecture (Aschwanden 2012a), which explains the powerlaw function and the values of the powerlaw slopes of most occurrence frequency distributions of spatio-temporal parameters in avalanching systems. This statistical argument for the probability distributions of nonlinear systems is as common as the statistical argument for binomial or Gaussian distributions in linear or random systems. In this sense, solar flares, earthquakes, and stockmarket systems have a statistical commonality (e.g., De Arcangelis et al. 2006). On the other hand, each SOC system may be governed by different physical principles unique to each observed SOC phenomenon, such as plasma magnetic reconnection physics in solar flares, mechanical stressing of tectonic plates in earthquakes, or the networking of brokers in stock market crashes. So, one should always be aware of this duality of model components when creating a new SOC model. There is no need to re-invent the universal statistical aspects or powerlaw probability distributions each time, while the modeling of physical systems may be improved with more accurate measurements and model parameterizations in every new SOC application.

There is another duality in the application of SOC: the numerical world of lattice simulation toy models, and the real world of quantitative observations governed by physical laws. The world of lattice simulations has its own beauty in producing complexity with mathematical simplicity, but it cannot capture the physics of a SOC system. It can be easily designed, controlled, modified, and visualized. It allows us to perform Monte-Carlo simulations of SOC models and may give us insights about the universal statistical aspects of SOC. Real world phenomena, in contrast, need to be observed and measured with large statistics and reliable parameters that have been cleaned from systematic bias effects, incomplete sampling, and unresolved spatial and temporal scales, which is often hard to achieve. However, computer power has increased drastically over the last 25 years, exponentially according to Gordon Moore’s law, so that enormous databases with up to ≈10⁹ events have been gathered per data set from some SOC phenomena, such as from solar small-scale phenomena for instance (McIntosh and Gurman 2005).

We organize this review by describing first some basics of SOC systems (Sect. 2), concerning SOC definitions, elements of a SOC system, the probability concept, geometric scaling laws, transport process, derivation of occurrence frequency distributions, waiting time distributions, separation of time scales, and the application of cellular automata. Then we deliver an overview on astrophysical applications (Sect. 3), grouped by observational results and theoretical models in solar physics, magnetospheres, planets, stars, galaxies, and cosmology. In Sect. 4 we capture some discussions, open issues and challenges, critiques, limitations, and new trends on the SOC subject, including also discussions of SOC-related processes, such as turbulence and percolation. The latter section mostly results from discussions during two weeks of dedicated workshops on “Self-organized Criticality and Turbulence”, held at the International Space Science Institute (ISSI) Bern during 2012 and 2013, attended by participants who have contributed to this review.

2 Basics of Self-Organized Criticality Systems

2.1 SOC Definitions

The original definition of the term self-organized criticality (SOC) was inspired by a numerical lattice simulation of a dynamical system with spatially complex patterns, mimicking avalanches of a sandpile, which became the BTW model (Bak et al. 1987), and demonstrated that:

• Dynamical systems with extended spatial degrees of freedom naturally evolve into self-organized critical structures of states which are barely stable. Flicker noise, or 1/f noise, can be identified with the dynamics of the critical state. This picture also yields insight into the origin of fractal objects (Bak et al. 1987).

In this first seminal paper, the authors had already fractal structures like cosmic strings, mountain landscapes, and coastal lines as potential applications in mind and concluded: We believe that the new concept of self-organized criticality can be taken much further and might be the underlying concept of dissipative systems with extended degrees of freedom (Bak et al. 1987). In this spirit, the application of the SOC concept has been broadened substantially over the last 25 years.

If we read a recent definition of SOC, we find:

• Self-organized criticality is regarded as scale invariance without external tuning of a control parameter, but with all the features of the critical point of an ordinary phase transition, in particular long range (algebraic) spatiotemporal correlations (Pruessner 2012).

In the same vein, it is stated in the original paper of the SOC creators: The criticality in our theory is fundamentally different from the critical point at phase transitions in equilibrium statistical mechanics which can be reached by tuning of a parameter, for instance the temperature (Bak et al. 1987). The aspect of self-tuning in SOC systems is the most crucial difference to (second-order) phase transitions, where fine-tuning is necessary and is not automatically arranged by nature. The implications and theoretical details of this peculiar feature are discussed in Watkins et al. (2014). However, whenever there is a threshold for instabilities, the threshold value itself could be called a “critical point” that decides whether an instability, also called a nonlinear energy dissipation event, or avalanche, happens or not. Over the past 25 years, a lot of applications of the SOC concept have been made to slowly-driven systems with a critical threshold, especially in solar and astrophysics, as reviewed in this article. We therefore like to use a more pragmatic and physics-based definition of a SOC system:

• SOC is a critical state of a nonlinear energy dissipation system that is slowly and continuously driven towards a critical value of a system-wide instability threshold, producing scale-free, fractal-diffusive, and intermittent avalanches with powerlaw-like size distributions (Aschwanden 2014).

With this definition we broaden the meaning of the term “criticality” to a more general meaning of a “critical point”, which includes almost any nonlinear system with a (global) instability threshold (Fig. 1). In addition, a SOC system has to be self-organizing or self-tuning without external control parameter, which is accomplished by a slow and continuous driver, which brings the system back to the critical point after each avalanche. Thus, we can say that a SOC system has energy balance between the slowly-driven input and the (spontaneous) avalanching output, and thus energy is conserved in the system (in the time average).

Fig. 1

Left: The original sandpile SOC paradigm, consisting of the (input) driver, the self-organized criticality mechanism (self-tunig angle of repose), and the (output) avalanches. Right: In a physical SOC concept, the driver is a slow and continuous energy input rate, the criticality mechanism is replaced by a critical point in form of an instability threshold, where an avalanche is triggered, usually consisting of a nonlinear growth phase and a subsequent saturation phase

2.2 The Driver

The driver is the input part of a SOC system. Without a driver, avalanching would die out and the system becomes subcritical and static. On the other side, the driver must be slowly and continuous, so that the critical state is restored in the asymptotic limit, while a strong driver would lead the system into a catastrophic collapse and may destroy the system. In the classical BTW model, sand grains are dripped under the action of gravity at a slow rate, at random locations of the sandpile, which re-fill and restore dents from previous avalanches towards the critical angle of repose. In astrophysical systems, the driver or energy input of a SOC system may be gravity (in galaxy formation, star formation, black holes, planet formation, asteroid formation), gravitational disturbances (in Saturn ring), or creation and stressing of magnetic flux (in solar flares, stellar flares, neutron stars, pulsars). The driver must bring the system back to the critical point after each major avalanche, which means that the system is locally pushed towards the instability threshold again, so that further avalanching can occur. In the slowly-driven limit, the time duration of an avalanche is much longer than the (waiting) time intervals between two subsequent events, which warrants a separation of time scales. In some natural systems the driver may temporarily or permanently stop, such as the solar dynamo during the Maunder minimum that stopped solar flaring, or the final stage of the sweep-up of debris left over from the formation of the solar system 4.0 billion years ago that stopped lunar cratering.

2.3 Instability and Criticality

We broaden the meaning of “criticality” in the original BTW model to a system-wide “instability threshold”, which does not need to be tuned by external parameters, since an “instability threshold” is established by common physical conditions throughout a system. For instance, an earthquake is triggered at a critical stressing brake point that may have a similar threshold in different tectonic plates around the globe, due to similar geophysical conditions (i.e., the gravity force at the same distance from Earth center, similar continental drift rates, rock constitutions, and crust fracturing conditions). In analogy, a magnetic instability leading to magnetic reconnection is caused by similar physical threshold conditions in solar active regions (such as the kink instability, the torus instability, or the tearing mode instability), and thus solar or stellar flares occur whenever such global instability thresholds are exceeded locally. Such instabilities occur naturally because the driver continuously brings the system back to the instability threshold. In sandpiles, the dripping of additional sand grains rises the angle of repose wherever it is subcritical. In earthquakes, the continental drift is continuously driven by forces that are rooted deeper below the Earth crust. In solar flares, differential rotation, emergence of magnetic flux, and braiding of magnetic fields by random motion in the subphotospheric magneto-convection layer continuously build up nonpotential free magnetic energy that can be released in subsequent avalanches. The analogy of unstable coherent structures in a near-critical state in sandpiles and solar flares is visualized in Fig. 2.

Fig. 2

Left: A sandpile in a state in the vicinity of criticality is shown with a vertical cross-section z(x), with the slope (or repose angle) dz/dx (bottom), exhibiting short-range fluctuations due to noise and long-range correlations due to local deviations from the mean critical slope. Right: The solar analogy of a flaring region is visualized in terms of a loop arcade straddling along a neutral line in x-direction, consisting of loops with various shear angles that are proportional to the gradient of the field direction B _x /B _y , showing some local (non-potential) deviations from the potential magnetic field (bottom)

2.4 Avalanches

Avalanches are defined as nonlinear energy dissipation events, which occur in our generalized SOC definition whenever and wherever a local instability threshold is exceeded. Avalanches are the output part of a SOC system, which balance the energy input rate in the time average for conservative SOC systems. Avalanches are detectable events, which can be obtained in astrophysical observations with large statistics, such as length scales (L), time scales or durations (T), fluxes (F), fluences or energies (E). The occurrence frequency distributions of these observables tend to be powerlaw-like functions, a hallmark of SOC systems, but deviations from powerlaw functions can be explained by measurement bias effects (such as incomplete sampling, finite system-size effects, truncations of distributions), or could reflect multiple physical processes. Unnecessary to say that these observables and their size distributions and underlying scaling laws provide the most important evidence and tests of SOC models.

The time evolution of avalanches contain essential information on the underlying spatio-temporal transport process (i.e., diffusion, fractal diffusion, percolation, turbulence, etc.). A generic time evolution is an initially nonlinear (i.e., exponential) growth phase, followed by a quenching or saturation phase (as expressed in the popular saying “No trees grow to the sky!”). In solar flares, for instance, the initial growth phase is called “impulsive phase”, and the subsequent saturation phase is called “postflare phase”. In earthquakes, the terms “precursors” and “after shocks” are common.

2.5 Microscopic Structure and Complexity

SOC systems are a means to study complexity, systems with extended degrees of freedom. Ultimately, a real-world object consists of atoms that has as many degrees of freedom as the Avogadro number of atoms per mol quantifies, i.e., 6.0×10²³. Such large numbers prevent us from modeling complex nonlinear systems in a deterministic way. In order to deal with SOC systems, we have to resort to numerical simulations with far fewer degrees of freedom, and we have to approximate the complexity of microscopic structures by macroscopic parameters and statistical probability distributions. For example, the complex microscopic structure of the solar chromosphere (Fig. 3, left panel) can be rendered with a binary lattice on a much coarser scale (Fig. 3, right). The question is, whether the basic physics that governs the dynamics of a real-world system can also be adequately represented by numerical lattice simulations. In the example shown in Fig. 3, one binary node of a lattice corresponds to a cube with 1000 km length scale on the solar surface, where the complex plasma dynamics driven by magneto-hydrodynamic processes exceeds the information content of a binary lattice node by far, so that it appears to be hopeless to mimic the dynamics of a SOC system with numerical cellular automaton simulations. Interestingly however, numerical lattice simulations do reproduce the emergent complex behavior in physical systems to some extent, regardless of the vast discrepancy of spatial scales and information content. For instance, the statistical size distribution of solar flares can be reproduced with cellular automata for various physical parameters (spatial, temporal scales, flux, and energy), as demonstrated by Lu and Hamilton (1991). Therefore, SOC models have the powerful ability to give us insight into system dynamics in complex systems, regardless of the intricate details of real-world microscopic fine structure. On the other side, the mathematical world of numerical lattice simulations created a whole new cosmos of complex spatial patterns (i.e., Wolfram 2002) and cellular automaton toy models (i.e., Pruessner 2012), which appear to have nothing in common with real-world microscopic fine structure, except that they provide practical means to simulate the same dynamic behavior of complex nonlinear systems. Consequently, in this review on solar and astrophysical SOC applications, the emphasis is not on mathematical and numerical SOC models (except when they were specifically designed for astrophysical applications), although they make up for more than half of the extant SOC literature.

Fig. 3

Left: A high-resolution image (480×480 pixel) of chromospheric spiculae in solar active region 10380, observed on 2003 June 16 with the Swedish 1-m Solar Telescope (SST) on La Palma, Spain, using a tunable filter, tuned to the blue-shifted line wing of the Hα 6536 Å line (Courtesy of Bart DePontieu). Right: A digitized binary version of the left solar image, using a lattice grid with a size of 24×24 nodes. The left image shows the microscopic structure of real-world data, while the right image shows the rendering of numerical lattice simulations used in SOC models

2.6 The Scale-Free Probability Conjecture

Common characterizations of SOC systems are statistical distributions of SOC parameters (also called “size distributions”, “occurrence frequency distributions”, or “log(N)–log(S) plots”). How do we derive a statistical probability distribution function (PDF) for SOC systems? This question has been answered in the original SOC papers (Bak et al. 1987, 1988) in an empirical way, by performing numerical Monte-Carlo simulations of avalanches in Cartesian lattice grids, according to the well-known algorithm with next-neighbor interactions (BTW model). Several theoretical attempts have been made to derive statistical probabilities, by considering avalanches as a branching process (Harris 1963; Christensen and Olami 1993), by exact solutions of the Abelian sandpile (Dhar and Ramaswamy 1989; Dhar 1990, 1999; Dhar and Majumdar 1990), by considering the BTW cellular automaton as a discretized diffusion process using the Langevin equations (Wiesenfeld et al. 1989; Zhang 1989; Forster et al. 1977; Medina et al. 1989), or by renormalization group theory (Medina et al. 1989; Pietronero and Schneider 1991; Pietronero et al. 1994; Vespignani et al. 1995; Loreto et al. 1995, 1996). Most of these analytical theories represent special solutions to a particular set of mathematical redistribution rules, but predict different powerlaw exponents for the probability distribution functions obtained with each method, and thus lack the generality to interpret the ubiquitous and omnipresent SOC phenomena observed in nature.

A simple approach to estimate the size distributions of SOC avalanche sizes has recently been proposed by making a simple statistical probability argument, called the scale-free probability conjecture (Aschwanden 2012a, 2014), which predicts the functional form of powerlaws for most observable SOC parameters, and predicts specific values for their powerlaw slopes (or exponents). The derivation goes as follows. If we consider the derivation of a normal or Gaussian distribution function, we can toss a number of dice and enumerate all possible statistical outcomes, ending up with a binomial distribution function, which converges to a Gaussian distribution function for a large number of dice, and thus characterizes a maximum likelihood distribution. Similarly, we can enumerate all statistically possible sizes L of avalanches in a system bound by a finite size L _max , which is simply a number density that is reciprocal to the volume V=L ^d of avalanches with size L, i.e.,

$$ N(L) dL \propto L^{-d} dL \quad\mbox{for}\ L \le L_{max}, $$

(1)

where d is the Euclidean dimension of the SOC system. This distribution function is based on the principle of statistical maximum likelihood, which follows from braking up a finite system volume into smaller pieces. This distribution function is also related to packing rules (e.g., sphere packing) in geometric aggregation problems. A similar approach using geometric scaling laws was also applied to earthquakes (Main and Burton 1984). Of course, for slowly-driven SOC systems, only one avalanche happens at a time, and thus the whole SOC system is not fully “packed” with avalanches occurring at once, but the statistical likelihood probability for an avalanche of a given size is nevertheless proportional to the packing density, for a statistically representative subset of all possible avalanche sizes (in a system with L≤L _max ). This basic scale-free probability conjecture (Eq. (1)) straightforwardly predicts the size distribution of length scales of SOC avalanches, namely N(L)∝L ⁻³ in 3D space, and can be used to derive the size distributions of other geometric parameters.

2.7 Geometric Scaling Laws

Other geometric parameters are the Euclidean area A or the Euclidean volume V. The simplest definition of an area A as a function of a length scale L is the square-dependence,

$$ A \propto L^2 . $$

(2)

A direct consequence of this simple geometric scaling law is that the statistical probability distribution of avalanche areas is directly coupled to the scale-free probability distribution of length scales (Eq. (1)), and can be computed by substitution of L(A)∝A ^1/2 (Eq. (2)), into the distribution of Eq. (1), N(L)=N(L[A])=L[A]^−d=(A ^1/2)^−d=A ^−d/2, and by inserting the derivative dL/dA∝A ^−1/2,

$$ N(A) dA \propto N\bigl(L[A]\bigr) \biggl\vert {dL \over dA} \biggr\vert dA \propto A^{-(1+d)/2} dA . $$

(3)

Thus we expect an area distribution of N(A)∝A ⁻² in 3D-space.

Similarly to the area, we can derive the geometric scaling for volumes V, which simply scales with the cubic power in 3D space (d=3), or generally as,

$$ V \propto L^d . $$

(4)

Consequently, we can also derive the probability distribution N(V)dV of volumes V directly from the scale-free probability conjecture (Eq. (1)). Substituting L∝V ^1/d into N(L[V])∝L[V]^d∝V ⁻¹, and inserting the derivative dL/dV=V ^1/d−1, we obtain,

$$ N(V) dV \propto N\bigl(L[V]\bigr) \biggl\vert {dL \over dV} \biggr\vert dV \propto V^{-(2-1/d)} dV \propto V^{-\alpha_V} dV . $$

(5)

Thus, a powerlaw slope of α _V =2−1/d=5/3≈1.67 is predicted in 3D space (d=3). Since all the assumptions made so far are universal, such as the scale-free probability conjecture (Eq. (1)) and the geometric scaling laws A∝L ² (Eq. (2)) and V∝L ³ (Eq. (4)), the resulting predicted occurrence frequency distributions of N(A)∝A ⁻² (Eq. (3)) and N(V)∝V ^−5/3 (Eq. (5)) are universal too, and thus powerlaw functions are predicted from this derivation from first principles, which is consistent with the property of universality in theoretical SOC definitions.

2.8 Fractal Geometry

“Fractals in nature originate from self-organized critical dynamical processes” (Bak and Chen 1989). The fractal geometry has been postulated for SOC processes by the first proponents of SOC. However, the geometry of fractals has been explored at least a decade before the SOC concept existed (Mandelbrot 1977, 1983, 1985). An extensive discussion of measuring the fractal geometry in SOC systems associated with solar and planetary data is given in Aschwanden (2011a, Chap. 8) and McAteer (2013a).

The simplest fractal is the Hausdorff dimension D _d , which is a monofractal and depends on the Euclidean space dimension d=1,2,3. The Hausdorff dimension D ₃ for the 3D Euclidean space (d=3) is

$$ D_3 = {\log{V_f(t)} \over\log{(L)} } , $$

(6)

and analogously for the 2D Euclidean space (d=2),

$$ D_2 = {\log{A_f(t)} \over\log{(L)} } , $$

(7)

with A _f (t) and V _f (t) being the fractal area and volume of a SOC avalanche during an instant of time t. These fractal dimensions can be determined by a box-counting method, where the area fractal D ₂ can readily be obtained from images from the real world (e.g., for a solar flare as shown in Fig. 4), while the volume fractal D ₃ is generally not available (except in numerical simulations), unless one infers the corresponding 3D information from stereoscopic triangulation. A good approximation for the expected fractal dimension D _d of SOC avalanches is the mean value of the smallest likely fractal dimension D _d,min ≈1 and the largest possible fractal dimension D _d,max =d. The minimum possible fractal dimension is near the value of 1 for SOC systems, because the next-neighbor interactions in SOC avalanches require some contiguity between active nodes in a lattice simulation of a cellular automaton, while smaller fractal dimensions D _d <1 are too sparse to allow an avalanche to propagate via next-neighbor interactions. Thus, the mean value of the fractal dimension of SOC avalanches is expected to be (Aschwanden 2012a),

$$ D_d \approx{D_{d,min} + D_{d,max} \over2} = {(1+d) \over2} . $$

(8)

Thus, we expect a mean fractal dimension of D ₃≈(1+3)/2=2.0 for the 3D space, and D ₂≈(1+2)/2=1.5 for the 2D space. The example shown in Fig. 4 yielded a value of D ₂=1.55±0.03, which is close to the prediction of Eq. (8).

Fig. 4

Measurement of the fractal area of a solar flare, observed by TRACE 171 Å on 2000-Jul-14, 10:59:32 UT. The Hausdorff dimension is evaluated with a box-counting algorithm for pixels above a threshold of 20 % of the peak flux value, yielding a mean of D ₂=1.55±0.03 for the 7 different spatial scales (Δx=1,2,4,…,64 pixels) shown here (Aschwanden and Aschwanden 2008a)

Fractals are measurable from the spatial structure of an avalanche at a given instant of time. Therefore, they enter the statistics of time-evolving SOC parameters, such as the observed flux or intensity per time unit, which is proportional to the number of instantaneously active nodes in a lattice-based SOC avalanche simulation.

2.9 Spatio-Temporal Evolution and Transport Process

Let us consider some basic aspects in the time domain of SOC avalanches. The spatio-temporal evolution of SOC avalanches has been simulated with cellular automaton simulations (Bak et al. 1987, 1988; Lu and Hamilton 1991; Charbonneau et al. 2001), which produced statistics of the final avalanche sizes L and durations T, but there is virtually no statistics on the spatio-temporal evolution of the instantaneous avalanche size or radius r(t) as a function of time t, which would characterize the macroscopic transport process. Statistics on this spatio-temporal evolution is important to establish spatio-temporal correlations and scaling laws between L and T, which defines the macroscopic transport process.

Ignoring the complexity of the microscopic transport, which is quantified by an iterative redistribution rule in cellular automaton simulations, we can measure the radius $r(t)=\sqrt{A(t)/\pi}$ of a circular 2D area A(t) as a function of time t, which corresponds to the solid (Euclidean) area that is equivalent to the time-integrated fractal avalanche area. This has been performed for BTW cellular automaton simulations (Aschwanden 2012a), as well as for solar flare data (Aschwanden 2012b; Aschwanden and Shimizu 2013; Aschwanden et al. 2013a), and was found to fit a diffusion-type relationship,

$$ r(t) = \kappa(t - t_0)^{\beta/2} , $$

(9)

where t ₀ is the onset time of the instability, κ is the diffusion coefficient, and β is the diffusive spreading exponent: a value of β≲1 corresponds to sub-diffusion, β=1 to classical diffusion, β≳1 to hyper-diffusion or Lévy flight, and β=2 to linear expansion (Fig. 5). From this macroscopic evolution we expect a statistical scaling law of the form,

$$ L \propto\kappa T^{\beta/2} , $$

(10)

for the final sizes L and durations T of SOC avalanches. Substituting this scaling law L(T) into the PDF of length scales (Eq. (1)), we establish a powerlaw distribution function for time scales,

$$ N(T) dT = N\bigl(L[T]\bigr) {dL\over dT} dT = T^{-[1+(d-1)\beta/2]} dT = T^{-\alpha_T} dT , $$

(11)

with the powerlaw slope of α _T =1+(d−1)β/2, which has a value of α _T =1+β=2.0 for 3D-Euclidean space (d=3) and classical diffusion (β=1). This powerlaw slope for avalanche time scales is a prediction of universal validity, since it is only based on the scale-free probability conjecture (Eq. (1)), N(L)∝L ^−d, and the statistical property of random walk in the transport process.

Fig. 5

Comparison of spatio-temporal evolution models: Logistic growth with parameters t ₁=1.0, r _∞=1.0, τ _G =0.1, sub-diffusion (β=1/2), classical diffusion (β=1), Lévy flights or hyper-diffusion (β=3/2), and linear expansion (r∝t)

2.10 Flux and Energy Scaling

The original BTW model specified avalanche sizes by the total number of active nodes, which corresponds to the cluster area of an avalanche in a 2D lattice. If we want to characterize the area a(t) of an avalanche as a function of time, which is a highly fluctuating quantity in time, we can define also a time-integrated final area a(<t) that includes all nodes that have been gone unstable at least once during the course of an avalanche, which is a monotonically increasing quantity and quantifies the size of an avalanche with a single number A=a (t=T), which we simply call the time-integrated avalanche area.

In real-world data we observe a signal from a SOC avalanche in form of an intensity flux f(t) (e.g., seismic waves from earthquakes, hard X-ray flux from solar flares, or the amount of lost dollars per day in the stockmarket). Let us assume that this intensity flux is proportional to the volume of active nodes in the BTW model, which corresponds to the instantaneous fractal volume V _f (t) (Eq. (6)) in a macroscopic SOC model (Aschwanden 2012a, 2014),

$$ f(t) \propto V_f(t) \propto r(t)^{D_d} . $$

(12)

The flux time profile f(t) is expected to fluctuate substantially in real-world data as well as in lattice simulations, because the approximation of the instantaneous volume of a SOC avalanche implies a highly variable fractal dimension D _d (t), which can vary in the range of D _d,min ≈1 and D _d,max =d, with a mean value D _d =(1+d)/2 (Eq. (8)). Occasionally, the instantaneous fractal dimension may reach its maximum value, i.e., D _d (t)≲d, which defines an expected upper limit f _max (t) of

$$ f_{max}(t) \propto V(t) \propto r(t)^d . $$

(13)

This is an important quantity that corresponds to the peak flux of an avalanche, which is often measured in astrophysical observations.

Integrating the time-dependent flux f(t) over the time interval [0,t] yields the time-integrated avalanche volume e(t) up to time t, which is often associated with the total dissipated energy during an avalanche (tacitly assuming an equivalence between energy and avalanche volume), using Eq. (9),

$$\begin{aligned} e(t) \propto\int_{t_0}^t V_f(t) dt = \int_{t_0}^t r(t)^{D_d} dt =& \int _{t_0}^t \kappa^{D_d} (t-t_0)^{D_d \beta/2} dt \\ =& {\kappa^{D_d} \over D_d \beta/2+1} (t-t_0)^{D_d \beta/2 + 1}, \end{aligned}$$

(14)

which is a monotonically increasing quantity with time. We see that this total dissipated energy depends on the fractal dimension D _d and the diffusion spreading exponent β, within the framework of the fractal-diffusive transport model (Eq. (9)).

From this time-dependent evolution of a SOC avalanche we can characterize at the end time t a time duration T=(t−t ₀), a spatial scale L=r(t=t ₀+T), an expected flux or energy dissipation rate F=f(t=t ₀+T), an expected peak flux or peak energy dissipation rate P=f _max (t=t ₀+T), and a dissipated energy E=e(t=t ₀+T), which is identical to the avalanche size S in BTW models, i.e., E∝S, for which we expect the following scaling laws (using Eqs. (12)–(14)),

$$\begin{aligned} &F \propto L^{D_d} \propto T^{D_d \beta/2} , \end{aligned}$$

(15)

$$\begin{aligned} &P \propto L^d \propto T^{d \beta/2}, \end{aligned}$$

(16)

$$\begin{aligned} &E \propto S \propto L^{D_d+2/\beta} \propto T^{D_d \beta/2+1}. \end{aligned}$$

(17)

Finally we want to quantify the occurrence frequency distributions of the (smoothed) energy dissipation rate N(F), the peak flux N(P), and the dissipated energy N(E), which all can readily be obtained by substituting the scaling laws (Eqs. (15)–(17)) into the fundamental length scale distribution (Eq. (1)), yielding

$$\begin{aligned} N(F) dF =& N\bigl(L[F]\bigr) \biggl\vert {dL \over dF} \biggr\vert dF \propto F^{-[1+(d-1)/D_d]} dF , \end{aligned}$$

(18)

$$\begin{aligned} N(P) dP =& N\bigl(L[P]\bigr) \biggl\vert {dL \over dP} \biggr\vert dP \propto P^{-[2-1/d]} dP , \end{aligned}$$

(19)

$$\begin{aligned} N(E) dE =& N\bigl(L[E]\bigr) \biggl\vert {dL \over dE} \biggr\vert dE \propto E^{-[1+(d-1)/(D_d+2/\beta)]} dE . \end{aligned}$$

(20)

Thus this derivation from first principles predicts powerlaw functions for all parameters L, A, V, T, F, P, E, and S which are the hallmarks of SOC systems.

In summary, if we denote the occurrence frequency distributions N(x) of a parameter x with a powerlaw distribution with power law index α _x ,

$$ N(x) dx \propto x^{-\alpha_x} dx , $$

(21)

we have the following powerlaw coefficients α _x for the parameters x=L,A,V,T,F,P,E, and S,

$$ \begin{aligned} \alpha_L &= d \\ \alpha_A &= 1+(d-1)/2 \\ \alpha_V &= 1+(d-1)/d \\ \alpha_T &= 1+(d-1)\beta/2 \\ \alpha_F &= 1+(d-1)/D_d \\ \alpha_P &= 1+(d-1)/d \\ \alpha_E &= \alpha_S = 1+(d-1)/(D_d+2/\beta). \end{aligned} $$

(22)

If we restrict to the case to 3D Euclidean space (d=3), as it is almost always the case for real world data, the predicted powerlaw indexes are,

$$ \begin{aligned} \alpha_L &= 3 \\ \alpha_A &= 2 \\ \alpha_V &= 5/3 \\ \alpha_T &= 1+\beta\\ \alpha_F &= 1+2/D_3 \\ \alpha_P &= 5/3 \\ \alpha_E &= \alpha_S = 1+1/(D_3/2+1/\beta). \end{aligned} $$

(23)

Restricting to classical diffusion (β=1) and a mean fractal dimension of D _d ≈(1+d)/2 for d=3, we have the following absolute predictions of the FD-SOC model,

$$ \begin{aligned} \alpha_L &= 3 \\ \alpha_A &= 2 \\ \alpha_V &= 5/3 \\ \alpha_T &= 2 \\ \alpha_F &= 2 \\ \alpha_P &= 5/3 \\ \alpha_E &= \alpha_S = 3/2, \end{aligned} $$

(24)

to which we refer to as the standard FD-SOC model in this review. We will see that these powerlaw indices represent a good first estimate that applies to many astrophysical and other observations interpreted as SOC phenomena. In some cases, however, the measurements clearly do not agree with these standard values, which imposes interesting constraints for modified SOC models.

The scaling laws between SOC parameters E, P, and T (Eqs. (16)–(17)) imply the following correlations for standard parameters d=3, D ₃=2.0, and β=1,

$$\begin{aligned} &P \propto T^{3/2} , \qquad T \propto P^{2/3} , \end{aligned}$$

(25)

$$\begin{aligned} &E \propto S \propto T^{2} , \qquad T \propto E^{1/2} \propto S^{1/2} , \end{aligned}$$

(26)

$$\begin{aligned} &E \propto S \propto P^{4/3} , \qquad P \propto E^{3/4} \propto S^{3/4} , \end{aligned}$$

(27)

which are sometimes tested in observations and cellular automaton simulations.

2.11 Coherent and Incoherent Radiation

Self-organized criticality models can be diagnosed and tested by means of statistical distributions, e.g., by the omnipresent powerlaw or powerlaw-like size distributions, and by the underlying scaling laws that relate the powerlaw slopes of different observables to each other (see also McAteer et al. 2014 for a description of methods). The original paradigm of a SOC model, the BTW cellular automaton simulations (Bak et al. 1987, 1988), produced powerlaw distributions of two variables, the size S, and the time duration T. The size S is simply defined by the time-integrated area A of active nodes (pixels) in 2D lattice simulations, or by the time-integrated fractal volume V _f of active nodes (voxels) in 3D lattice simulations.

In astrophysical observations, however, the volume of an avalanche cannot be measured, but rather a flux intensity F _λ in some wavelength regime λ is observed, which is not necessarily proportional to the fractal volume V _f , depending on the emission mechanism that is dominant at wavelength λ. Therefore, for astrophysical observations in particular, we have to introduce a relationship between the observed flux F _λ and the emitting volume V _f that is fractal for a SOC avalanche process. For sake of simplicity we characterize this relationship with a power exponent γ (Aschwanden 2012b, 2013),

$$ F_{\lambda} \propto V_f^{\gamma}. $$

(28)

This definition allows us to distinguish two categories of physical processes: incoherent processes that have a linear relationship between the emitting flux and volume (γ=1), and coherent processes that have a nonlinear relationship,

$$ F_{\lambda} \propto V_f^\gamma, \qquad \left \{ \begin{array}{l@{\quad}l} \gamma> 1 & \mbox{(coherent process)} \\ \gamma= 1 & \mbox{(incoherent process)} \end{array} \right . $$

(29)

Incoherent processes are, for instance, free-free emission in optically thin media, bremsstrahlung, or gyrosynchrotron emission. Free-free emission is a common emission mechanism in soft X-rays and EUV, where the total flux scales with the emission measure EM integrated over the entire (fractal) source volume V _f . Coherent processes on the other hand, can occur by wave-particle interactions in collisionless plasmas, such as loss-cone instabilities, electron-beam instabilities, or electron cyclotron maser emission. The flux level of coherent waves amplifies exponentially or with a nonlinear power to the spatial scale of the source, and thus with a nonlinear power to the source volume.

What is the resulting modification in the size distribution of observed fluxes? Incoherent processes are expected to have the same size distribution as the size distribution of (fractal) avalanche volumes. For coherent processes, the size distributions that depend on the flux F will have a modified powerlaw slope, which we can calculate straightforwardly from the modified scaling laws (Eqs. (15)–(17)),

$$\begin{aligned} &F \propto V_f^\gamma\propto L^{\gamma D_d} \propto T^{\gamma D_d \beta/2} , \end{aligned}$$

(30)

$$\begin{aligned} &P \propto V^\gamma\propto L^{\gamma d} \propto T^{\gamma d \beta/2} , \end{aligned}$$

(31)

$$\begin{aligned} &E \propto L^{\gamma D_d+2/\beta} \propto T^{\gamma D_d \beta/2+1} , \end{aligned}$$

(32)

resulting into the frequency distributions,

$$\begin{aligned} N(F) dF =& N\bigl(L[F]\bigr) \biggl\vert {dL \over dF} \biggr\vert dF \propto F^{-[1+(d-1)/\gamma D_d]} dF , \end{aligned}$$

(33)

$$\begin{aligned} N(P) dP =& N\bigl(/[P]\bigr) \biggl\vert {dL \over dP} \biggr\vert dP \propto P^{-[1+(d-1)/\gamma d]} dP , \end{aligned}$$

(34)

$$\begin{aligned} N(E) dE =& N\bigl(L[E]\bigr) \biggl\vert {dL \over dE} \biggr\vert dE \propto E^{-[1+(d-1)/(\gamma D_d+2/\beta)]} dE . \end{aligned}$$

(35)

Consequently, the generalized powerlaw coefficients α _x for the parameters x=L, A, V, T, F, P, E and S are (Eq. (22)),

$$ \begin{aligned} \alpha_L &= d \\ \alpha_A &= 1+(d-1)/2 \\ \alpha_V &= 1+(d-1)/d \\ \alpha_T &= 1+(d-1)\beta/2 \\ \alpha_F &= 1+(d-1)/(\gamma D_d) \\ \alpha_P &= 1+(d-1)/(\gamma d) \\ \alpha_E &= 1+(d-1)/(\gamma D_d+2/\beta)\\ \alpha_S &= 1+(d-1)/(D_d+2/\beta), \end{aligned} $$

(36)

where we included also the time-integrated avalanche size S that is generally used in cellular automaton models, which corresponds in our definition to the time-integrated energy with γ=1. The modification with the coherence parameter γ predicts flatter powerlaw slopes (α _F ,α _P ,α _E ) for flux-related observables (F,P,E) of coherent processes. We will see that coherent emission processes in radio wavelengths (Sect. 3.1.4) indeed have been observed with flatter size distributions than incoherent emission processes.

2.12 Waiting Times and Memory

Waiting times, also called “elapsed times”, “inter-occurrence times”, “inter-burst times”, or “laminar times”, are defined by the time interval between two subsequent bursts. The distribution of waiting times requires to break a continuous time series down into discrete events, for instance by using a threshold criterion. Consequently, waiting time statistics requires a separation of time scales, which means that the burst durations have to be shorter than the waiting times, otherwise multiple bursts are counted as a single one and the waiting time between two closely following bursts is missing in the statistics.

2.12.1 Stationary Poisson Processes

If a process is purely random, also called a “Poisson process”, the waiting times Δt=t _i+1−t _i between subsequent bursts at times t _i and t _i+1 should be uncorrelated and follow a Poissonian probability distribution function, which can be approximated by an exponential function,

$$ P(\Delta t) = \lambda e^{-\lambda\Delta t}, $$

(37)

where λ is the mean burst rate or flare rate. If the flare rate λ is constant, we call this also a “stationary Poisson process”.

A waiting time distribution measured in a global system loses all timing information from individual local regions, so we can never conclude from the waiting times of a global system whether the waiting times in a local region is a random process or not. However, the opposite is true and can be mathematically proven, i.e., that the combination of time series with random time intervals produces a combined time series that has also random time intervals. This property is also called the superposition theorem of Palm and Khinchin (e.g., Cox and Isham 1980; Craig and Wheatland 2002) and is analogous to the central limit theorem (Rice 1995). An example that waiting times in local regions can be completely different from those of the global system was confirmed in earthquake statistics, where aftershocks (occurring in the same local region) exhibit an excess of short waiting times (Omori’s law; Omori 1895), compared with the overall statistics of (spatially) independent earthquakes.

2.12.2 Non-stationary Poisson Processes

Many SOC processes have variable drivers or spatial subsystems with different drivers. Consequently the burst rates or flare rates, and thus the waiting time statistics, may vary in time and/or space. If every spatial system is a random system with different flaring rates λ _i in individual local regions or during individual time epochs, a superposition of many random systems is called a “non-stationary Poisson process”, or “time-dependent Poisson process”. Let us consider non-stationarity in the time domain. A non-stationary Poisson process may be approximated by a subdivision into discretized time intervals with piecewise stationary processes with occurrence rates λ ₁,λ ₂,…,λ _n (Wheatland et al. 1998),

$$ P(\Delta t) = \left \{ \begin{array}{l@{\quad}l} \lambda_1 e^{-\lambda_1 \Delta t} & \mbox{for}\ t_1 \le t \le t_2 \\ \lambda_2 e^{-\lambda_2 \Delta t} & \mbox{for}\ t_2 \le t \le t_3 \\ \ldots&\ldots \\ \lambda_n e^{-\lambda_n \Delta t} & \mbox{for}\ t_n \le t \le t_{n+1} \end{array} \right . $$

(38)

where the occurrence rate λ _i is stationary during a time interval [t _i ,t _i+1], but has different values in subsequent time intervals. The time intervals [t _i ,t _i+1] where the occurrence rate is stationary are called Bayesian blocks, a special application of Bayesian statistics (e.g., see Scargle 1998 for astrophysical applications). If we make a transition to a continuous flaring rate λ(t) and use a time-dependent function f(λ) to describe the variation of the flaring rate λ(t), we obtain the following waiting time distribution (Wheatland et al. 1998, Wheatland 2003),

$$ P(\Delta t) = {\int_0^{\infty} f(\lambda) \lambda^2 e^{-\lambda\Delta t} d\lambda \over\int_0^{\infty} \lambda f(\lambda) d\lambda} , $$

(39)

where the denominator $\lambda_{0}=\int_{0}^{\infty}\lambda f(\lambda) d\lambda$ is the mean rate of flaring.

It is instructive to study the functional shape of waiting time distributions that result from non-stationary Poisson processes. In Fig. 6 we illustrate five cases, which each can be derived analytically: (1) a stationary Poisson process with a constant rate λ ₀; (2) a two-step process with two different occurrence rates λ ₁ and λ ₂; (3) a nonstationary Poisson process with a linearly increasing occurrence rate λ(t)=λ ₀ t/T, varying like a triangular function for each cycle, (4) a piecewise constant Poisson process with an exponentially varying rate distribution, and (5) a piecewise constant Poisson process with an exponentially varying rate distribution steepened by a reciprocal factor. For each case we show the time-dependent occurrence rate λ(t) and the resulting probability distribution P(Δt) of events. We see that a stationary Poisson process produces an exponential waiting-time distribution, while nonstationary Poisson processes with a discrete number of occurrence rates λ _i produce a superposition of exponential distributions, and continuous occurrence rate functions λ(t) generate powerlaw-like waiting-time distributions at the upper end. The analytical derivations of these five cases is given in Aschwanden (2011a).

Fig. 6

One case of a stationary Poisson process (top) and four cases of nonstationary Poisson processes with two-step, linear-increasing, exponentially varying, and δ-function like variations of the occurrence rate λ(t). The time-dependent occurrence rates λ(t) are shown on the left side, while the waiting-time distributions are shown in the right-hand panels, in the form of histograms sampled from Monte-Carlo simulations, as well as in the form of the analytical solutions. Powerlaw fits N(Δt)∝Δt ^−p are indicated with a dotted line and labeled with the slope p (Aschwanden and McTiernan 2010)

Thus we learn from the last four examples that most continuously changing occurrence rates produce powerlaw-like waiting-time distributions P(Δt)∝(Δt)^−p with slopes of p≲2,…,3 at large waiting times, despite the intrinsic exponential distribution that is characteristic to stationary Poisson processes. If the variability of the flare rate is gradual (third and fourth case in Fig. 6), the powerlaw slope of the waiting-time distribution is close to p≲3. However, if the variability of the flare rate shows spikes like δ-functions (Fig. 6, bottom), which is highly intermittent with short clusters of flares, the distribution of waiting times has a slope closer to p≈2. This phenomenon is also called clusterization and has analogs in earthquake statistics, where aftershocks appear in clusters after a main shock (Omori’s law; Omori 1895). Thus the powerlaw slope of waiting times contains essential information whether the flare rate is constant, varies gradually, or in form of intermittent clusters.

Powerlaw-like waiting time distributions can also be produced by standard BTW sandpile simulations, when correlations exist in the slowly-driven external driver, producing a “colored” power spectrum, especially when only avalanches above some threshold are included in the waiting-time distribution (Sanchez et al. 2002).

2.12.3 Waiting Time Probabilities in the Fractal-Diffusive SOC Model

The fractal-diffusive self-organized criticality (FD-SOC) model predicts a powerlaw distribution $N(T) \propto T^{-\alpha_{T}}$ of event durations T with a slope of α _T =[1+(d−1)β/2] (Eq. (11)) that derives directly from the scale-free probability conjecture N(L)∝L ^−d (Eq. (1)) and the random walk (diffusive) transport (L∝T ^β/2; Eq. (10)). For classical diffusion (β=1) and space dimension d=3 the predicted powerlaw is α _T =2. From this time scale distribution we can also predict the waiting time distribution with a simple probability argument. If we define a waiting time as the time interval between the start time of two subsequent events, so that no two events overlap with each other temporally, the waiting time cannot be shorter than the time duration of the intervening event, i.e., Δt _i ≥(t _i+1−t _i ). Let us consider the case of non-intermittent, contiguous flaring, but no time overlap between subsequent events. In this case the waiting times are identical with the event durations, and therefore their waiting time distributions are equal too, reflecting the same statistical probabilities,

$$ N(\Delta T) d\Delta t \propto N(T) dT \propto T^{-\alpha_T} dT \propto \Delta t^{-\alpha_{\Delta t}} d\Delta t , $$

(40)

with the powerlaw slope,

$$ \alpha_{\Delta t} = \alpha_T = 1 + (d-1)\beta/2 . $$

(41)

This statistical argument is true regardless what the order of subsequent event durations is, so it fulfills the Abelian property. Now we relax the contiguity condition and subdivide the time series into blocks with contiguous flaring, interrupted by arbitrarily long quiet periods when no event happens (Fig. 7). The contributions of waiting times from the subset of contiguous time blocks will still be identical to those of the event durations, while those time intervals from the intervening quiet periods add a few arbitrarily longer waiting times, which form an exponential drop-off in the case of random quiescent time intervals (Fig. 7). As long as the number of quiet time intervals is much smaller than the number of detected events, the modified waiting time distribution will still be similar to the one of contiguous flaring (Eq. (40)), which is α _Δt =2.0 for classical diffusion β=1 and space dimension d=3. Interestingly, this predicted slope is identical to that of nonstationary Poisson processes in the limit of intermittency (Fig. 6, bottom).

Fig. 7

The concept of a dual waiting time distribution is illustrated, consisting of active time intervals Δt≲T ₂ that contribute to a powerlaw distribution, which is equal to that of time durations, N(T), and random-like quiescent time intervals (Δt ^q) that contribute to an exponential cutoff. Vertical lines in the upper panel indicate the start times of events, between which the waiting times are measured (Aschwanden 2014)

We can define a mean waiting time 〈Δt〉 from the total duration of the observing period T _obs and the number of observed events n _obs ,

$$ \langle\Delta t \rangle= {T_{obs} \over n_{obs}} . $$

(42)

From the distribution of event durations T, we have an inertial range of time scales [T ₁,T ₂], over which we observe a powerlaw distribution, $N(T) \propto T^{-\alpha_{T}}$, with the corresponding number of events [N ₁,N ₂], so that we can define a nominal powerlaw slope of α _T =log(N ₂/N ₁)/log(T ₂/T ₁). If the mean waiting time of an observed time series becomes shorter than the upper limit of time scales, T ₂, we start to see time-overlapping events, a situation we call “event pile-up” or “pulse pile-up”. In such a case we expect that the waiting time distribution starts to be modified, because the time durations of the long events are underestimated (by some automated detection algorithm), so that the nominal powerlaw slope that is expected with no pulse pile-up, α _Δt =log(N ₂/N ₁)/log(T ₂/T ₁), has to be modified by replacing the upper time scale T ₂ by the mean waiting time 〈Δt〉,

$$ \alpha_{\Delta t}^{pileup} = \alpha_{\Delta t} \times \left \{ \begin{array}{l@{\quad}l} 1 & \mbox{for}\ \langle\Delta t \rangle > T_2 \\ \log(T_2)/\log{\langle\Delta t \rangle} & \mbox{for}\ \langle\Delta t \rangle \le T_2 \end{array} \right . $$

(43)

As a consequence, the measurements of event durations must suffer the same pile-up effect, and a similar correction is expected for the time duration distribution N(T),

$$ \alpha_T^{pileup} = \alpha_T \times \left \{ \begin{array}{l@{\quad}l} 1 & \mbox{for}\ \langle\Delta t \rangle > T_2 \\ \log(T_2)/\log{\langle\Delta t \rangle} & \mbox{for}\ \langle\Delta t \rangle \le T_2 \end{array} \right . $$

(44)

Thus the predicted waiting time distribution has a slope of α _T =2 in the slowly-driven limit, but can be steeper in the strongly-driven limit. We will see below that the waiting time distributions of solar flares correspond to the slowly-driven limit during the minima of the solar 11-year cycle, while their powerlaw slopes indeed steepen during the maxima of the solar cycle, when the flare density becomes so high that the slowly-driven limit, and thus the separation of time scales, is violated.

2.12.4 Weibull Distribution and Processes with Memory

As we stated in a previous section, we can never conclude from the waiting times of a global system whether the waiting times in a local region is a random process or not. Non-stationary Poisson processes may fit an observed waiting time distribution perfectly well, with an appropriate flaring rate function f(λ), but the best-fit solution is not unique. Local regions may have non-random statistics with clustering, memory, and persistence. Such non-Poissonian processes can, for instance, be characterized with the more general Weibull distribution, which originally has been used to describe particle size distributions (Weibull 1951). Here we outline the formalism according to an application to (solar) coronal mass ejections (Telloni et al. 2014).

Generalizing the Poissonian exponential function (Eq. (37)) we can define the waiting time distribution function P(Δt)

$$ P(\Delta t) = z(\Delta t) e^{-\int_0^{\Delta t} z(x) dx} , $$

(45)

where z(Δt) represents the local flaring rate,

$$ z(\Delta t) = { P(\Delta t) \over P(\Delta t \ge\Delta T)} , $$

(46)

defined by the ratio of the probability distribution function (PDF) P(Δt) and the Surviving Distribution Function (SDF) P(Δt≥ΔT). In a memory-less stochastic (Poisson) process, the probability of occurrence of an event is constant, e.g., z(Δt)=λ, producing the Poisson distribution (Eq. (37)). If the probability of occurrence changes with time, especially when the process has memory, z(Δt) can be expressed by Weibull (1951),

$$ z(\Delta t) = \lambda^k k (\Delta t)^{k-1} , $$

(47)

where k is the key parameter that describes whether the probability of occurrence decreases or increases with time (k<1 or k>1). Substituting Eq. (47) into Eq. (45) yields than the probability density function of a Weibull random variable Δt (Weibull 1951),

$$ P(\Delta t) = {k \over\beta} \biggl({\Delta t \over\beta} \biggr)^{k-1} e^{-(\Delta t / \beta)^k} , $$

(48)

where β=1/λ is the reciprocal of the occurrence rate of the events, k>0 is the shape parameter, and β>0 is the scale parameter of the distribution.

In Fig. 8 we display some forms of the Weibull distribution function for different shape parameters k=0.1,…,5. The distribution function turns into a powerlaw function for k↦0, into an exponential function for k=1, and into a Rayleigh distribution for k≫1, which is almost Gaussian-like. For k=1, the process is Poissonian or random and has no memory. For k<1 the flaring rate decreases over time, while for k>1 the flaring rate is increasing with time, indicating that the process has some memory and persistence, because a persistent driver with memory varies the flaring rate with a systematic trend, which causes also long correlation times among clusters of events. Thus, the Weibull distribution function allows to model random-like (Poissonian) processes as well as processes with memory and persistence.

Fig. 8

The Weibull probability density function (PDF) f(x;k,λ) for k=0.1,0.2,0.5,1.0,2.0,5.0 and λ=1, in a lin–lin display (left panel) and in a log–log display (right panel). Notice the asymptotic limit of a powerlaw function for k↦0

2.13 The Separation of Time Scales

Most of the original numerical simulations of SOC systems were performed in the slowly-driven limit, which warrants a strict separation of time scales. In lattice-type cellular automaton simulations, the separation of time scales is enforced by dropping only one single sand grain at a time, or disturbing only one single lattice node at a time. If nothing happens, the algorithm proceeds with the next input of a disturbance. In the alternative case, when a disturbance triggers an avalanche, the incremental input function is stopped until the avalanche process ends, after which another input step is continued. This asymptotic limit of strict time scale separation between the waiting time scale and durations of subsequent avalanches, is also called a “slowly-driven SOC system”. This ideal, but unnatural condition is, however, not necessarily always enforced in nature. Especially for SOC systems with time-variable drivers, the trigger rate can get so high that multiple avalanches are triggered near-simultaneously and small avalanches occur at various places while a previously triggered large avalanche is still evolving. If we encounter such a “multi-avalanching system”, or multi-avalanching behavior during some busy periods of time, we may call it a “fast-driven” or “strongly-driven” system. We can adopt the terminology of a slow or fast driver being a synonym for the existence or non-existence of time scale separation, which can be expressed by the ratio of the avalanche duration T to the waiting time Δt,

$$ \begin{aligned} {\mbox{Slow driver:}} & \mapsto \Delta t \gtrsim T \\ \mbox{Fast driver:} & \mapsto \Delta t \lesssim T. \end{aligned} $$

(49)

For a fast driver the question arises how this affects the observed (powerlaw-like) size distributions that we calculated in the slowly-driven limit. The answer depends very much on the event detection method. Ideally one would use imaging information so that the spatial locations of two temporally overlapping events can be separately determined and the time profiles of the two events can be properly disentangled. In practice, especially in the case of astrophysical observations, spatial sources of co-temporaneous events cannot be resolved and a time series analysis is the only available method. In that case, superimposed time profiles of different events can still be separated if they have a characteristic shape, for instance a rapid rise and an exponential decay, using a deconvolution method. If no proper deconvolution method is applied, which is unfortunately the case in almost all published studies with event statistics applied to SOC models, there will be a systematic bias of underestimating the time duration of long events, especially when the rule is applied that a previous event has to end before the next event is detected. This leads predictably to steeper powerlaw slopes in the time scale distribution N(T). We will see later on that an increase in the event rate (for instance the flaring rate during the maximum of the solar cycle) will lead to substantially steeper powerlaw slopes of the time scale duration (for solar flare events detected in soft X-rays), from a value of α _T ≈2 in the slowly-driven regime (during solar cycle minimum) to a large value of α _T ≲5 in the fast-driven regime (during solar cycle maximum, see Fig. 10). Interestingly, the size distribution of fluxes was not affected in the strongly-driven regime. In another study it was demonstrated that low resolution observations of a time profile causes an exponential cutoff at large values of the time scale distribution, which also leads to steeper powerlaw slopes (Isliker and Benz 2001). Thus, we generally expect steeper powerlaws or exponential distributions of time scales in the limit of strong driving with clustered events that violate the separation of time scales, although there are also reports with flatter powerlaw slopes during episodes of higher event rates (e.g., Bai 1993; Georgoulis and Vlahos 1996, 1998).

2.14 Cellular Automaton Models

Since the original BTW model has been a paradigm of SOC models for 25 years, we should evaluate its predictive potential, since every theory can only be validated when it is able to make quantitative predictions for future (or past) measurements. The original BTW model simulated a complex system by numerical lattice simulations of iterating a simple next-neighbor interaction redistribution rule (generally called a cellular automaton model, which produced a distribution with a powerlaw slope of α _E ≈0.98 for avalanche sizes in 2D space, or α _E ≈1.35 for avalanche sizes in 3D space Bak et al. 1987). These values are somewhat different from the predictions of the basic SOC model based on the scale-free probability conjecture (Sects. 2.6 and 2.7), which predicts α _E =9/7≈1.29 for avalanche sizes in 2D space, and α _E ≈1.50 for avalanche sizes in 3D space. Other extensive BTW simulations with a variety of grid sizes find α _E ≈1.42±0.01 for avalanche sizes in 2D space, and α _E ≈1.47±0.02 for avalanche sizes in 3D space (Charbonneau et al. 2001). The latter values are actually almost consistent with the value α _E =1.55 (in 2D space) obtained from a pre-Bak simulation as a model for propagating brittle failure in heterogeneous media (Katz 1986). From these few examples it is already clear that various cellular automaton models produce different powerlaw slopes, and thus the question arises whether the obtained powerlaw slopes depend on the numerical details of the setup of lattice simulations, or whether they have universal validity that is independent of numerical redistribution rules and may even apply to observations in nature.

In order to investigate the universality of cellular automaton models we compare the obtained powerlaw slope (α _S =α _E ) of avalanche sizes (which is the time-integrated volume of all active nodes at each time step of an avalanche) and the powerlaw slope (α _T ) of the avalanche durations T. An exhaustive collection of cellular automaton models are described in Pruessner (2012), from which we extract the powerlaw indices of the mentioned parameters (Table 1).

Table 1 Numerical simulations of SOC cellular automata: with spatial dimension d=1,2,3 and powerlaw exponents of avalanche sizes (α _E =α _S ) and durations (α _T ), adapted from Pruessner (2012), and theoretical predictions of the FD-SOC model (Eq. (22))

Based on the scale-free probability conjecture and the geometric scaling laws of the fractal-diffusive SOC model described in Sects. 2.6–2.10, we predict for classical diffusion (β=1) and a mean fractal dimension D _d =(1+d)/2 the following powerlaw slopes for avalanche size distributions (Eq. (22)): α _E =1 for 1D space, α _E =9/7≈1.29 for 2D space, and α _E =3/2=1.5 for 3D space, which agree with most of the measured slopes of avalanche sizes in cellular automaton simulations (Table 1). For event durations we predict: α _T =1 for 1D space, α _T =3/2=1.5 for 2D space, and α _T =2.0 for 3D space, which also roughly agrees with the simulations in Table 1.

Vice versa, the measured values listed in Table 1 can be used to invert the diffusive spreading exponent β and the fractal dimension D _d for cellular automata according to Eq. (22):

$$\begin{aligned} \beta =& { 2 (\alpha_T - 1) \over(d-1)} , \end{aligned}$$

(50)

$$\begin{aligned} D_d =& {(d - 1) \over(\alpha_E - 1)} - {2 \over\beta} . \end{aligned}$$

(51)

For instance, the 3D cellular automaton simulations listed in Table 1 exhibit a range of α _T ≈1.6–1.8 for the powerlaw slope of time durations, which is systematically below the prediction of the standard (FD-SOC) model with α _T =2.0. Application of Eq. (50) would then imply a diffusive spreading exponent of β≈0.6–0.8, which is the sub-diffusive regime. We will see later on that real-world data yield a powerlaw slope of α _T ≈2.0 (e.g., Table 2), which corresponds to classical diffusion or random walk (β=1). This tells us that the cellular automaton redistribution rules do not necessarily reflect the behavior of SOC processes found in the real world.

Table 2 Frequency distributions measured from solar flares in hard X-rays and γ-rays. The prediction is based on the FD-SOC model (Aschwanden 2012a)

The diffusion or spreading exponent β and the fractal dimension D _d are essentially macroscopic parameters to describe the average dynamics and inhomogeneous spatial structure of avalanches, which are microscopically defined in terms of an iterative mathematical redistribution rule. The diffusion exponent β characterizes the macroscopic transport process (subdiffusive, classical diffusion, hyper-diffusion), and the fractal dimension describes the spatial inhomogeneity of an avalanche, in the spirit of Bak and Chen (1989): Fractals in nature originate from self-organized critical dynamical processes. Cellular automata exhibit a range of fractal dimensions and diffusion exponents, as the values in Table 1 demonstrate, and thus may not have universal validity for SOC systems. If we find the same disparity among astrophysical observations, as we will survey in the following sections, nature operates in SOC systems with different spatial inhomogeneities and transport processes, which may be related to the underlying physical scaling laws in each SOC system. The cellular automaton world may have (slightly) different SOC parameters (β,D _d ) than the astrophysical world, but we are able to describe the nonlinear dynamics of complex systems with the same theoretical framework.

3 Astrophysical Applications

We subdivide the astrophysical phenomena that have been associated with SOC according to solar physics (Sects. 3.1, 3.2), the Earth’s magnetosphere and planets (Sect. 3.3), and stars and galaxies (Sect. 3.4). We tabulate the statistics of SOC parameters mostly in form of measured power law indices. In addition, we discuss briefly the theoretical interpretations in each case and summarize studies that contain modeling attempts of these SOC phenomena, often tailored to a specific astrophysical object.

3.1 Solar Physics: Observations

The applications of SOC theory to solar data outnumbers all other astrophysical applications. Therefore, we brake the subject down into observational statistics from different wavelengths (hard X-rays, soft X-rays, EUV, radio, etc.) in Sect. 3.1, and into various aspects of theoretical modeling (e.g., cellular automaton simulations, magnetic fields, magnetic reconnection, plasma magneto-hydrodynamics (MHD), coronal heating, particle acceleration, solar wind, Sun-Earth connection, etc.) in Sect. 3.2.

3.1.1 Statistics of Solar Flare Hard X-Rays

Solar flares provide the energy source for acceleration of nonthermal particles, which emit bremsstrahlung in hard X-ray wavelengths, once the non-thermal particles interact with a high-density plasma via Coulomb collisions. Most solar flares display an impulsive component in hard X-rays, produced by accelerated coronal electrons that precipitate towards the chromosphere and produce intense hard X-ray emission at the footpoints of flare loops. Therefore, hard X-ray pulses are a reliable signature of solar flares, often detected at energies ≳20 keV, but for smaller flares down to ≳8 keV.

Solar flare event catalogs containing the peak rate (P), fluences (E), and flare durations (T), have therefore been compiled from a number of spacecraft or balloon-borne hard X-ray detectors over the last three decades, such as from OSO-7 (Datlowe et al. 1974), a University of Berkeley balloon flight (Lin et al. 1984), HXRBS/SMM (Dennis 1985; Schwartz et al. 1992; Crosby et al. 1993), BATSE/CGRO (Schwartz et al. 1992; Biesecker et al. 1993, 1994; Biesecker 1994), WATCH/GRANAT (Crosby 1996; Georgoulis et al. 2001); ISEE-3 (Lu et al. 1993; Lee et al. 1993; Bromund et al. 1995); PHEBUS/GRANAT (Perez Enriquez and Miroshnichenko 1999). RHESSI (Su et al. 2006; Christe et al. 2008; Lin et al. 2001), and ULYSSES (Tranquille et al. 2009). Three examples of hard X-ray peak flux distributions are shown in Fig. 9. Note that the size distributions of peak counts have a sharp cutoff at the lower end due to a fixed count rate threshold that is generally used in the compilation of hard X-ray flare catalogs, and thus the powerlaw slope can be determined with the highest accuracy. Other parameters have generally a gradual rollover at the low end due to incomplete sampling and finite-resolution effects, which causes truncation effects in the histogram and hampers the accuracy of the powerlaw fit. The size distribution of solar flare hard X-ray counts, which has already been pointed out before the SOC concept came along (Dennis 1985), is still one of the “cleanest” powerlaw size distributions measured in astrophysics (Fig. 9).

Fig. 9

Occurrence frequency distributions of hard X-ray peak count rates P [cts s⁻¹] observed with HXRBS/SMM (1980–1989), BATSE (1991–2000), and RHESSI (2002–2010), with powerlaw fits. An average pre-flare background of 40 [cts s⁻¹] was subtracted from the HXRBS count rates. Note that BATSE/CGRO has larger detector areas, and thus records higher count rates (Aschwanden 2011b)

A compilation of occurrence frequency distribution powerlaw slopes of solar hard X-ray flare peak fluxes (α _P ), fluences or energies (α _E ), and flare durations (α _T ) is listed in Table 2. In this Table we combined both the powerlaw slopes α _E from the fluences (which is the time-integrated or total number of hard X-ray counts per flare) and nonthermal energies (which are computed from the hard X-ray energy spectrum assuming a low-energy cutoff at 10 or 25 keV), both representing a physical quantity in terms of energy. In Table 2 we indicate also the number of events, which constrains the accuracy of the fitted powerlaw slopes. Synthesizing the datasets with the largest statistics (HXRBS/SMM, BATSE/CGRO, RHESSI), the following means and standard deviations of the powerlaw slopes were found α _P =1.73±0.07 for the peak fluxes (Fig. 9), α _E =1.62±0.12 for the fluences or energies, and α _T =1.99±0.35 for the flare durations (Aschwanden 2011b). The uncertainties of the powerlaw slope quoted in literature generally include the formal fitting error only, while the standard deviations given here reflect methodical and systematic uncertainties also, since every dataset has been analyzed from different instruments and with different analysis methods. One of the largest systematic uncertainties results from the preflare background subtraction, because the preflare flux is often not specified in solar flare catalogs. Nevertheless, given these systematic uncertainties, the observed values are consistent with the theoretical predictions of the basic fractal-diffusive SOC model, based on an Euclidean space dimension of d=3, a mean fractal dimension of D ₃=2, and classical diffusion β=1, which yields α _P =1.67 for peak fluxes, α _E =1.50 for energies, and α _T =2.00 for durations (Eq. (24)). Thus, the basic fractal-diffusive SOC model predicts the correct powerlaw slopes within the uncertainties of hard X-ray measurements.

Frequency-size distributions of solar flares are generally sampled from the entire Sun, and thus from multiple active regions that are present on the visible hemisphere at a given time. This configuration corresponds to a multi-sandpile situation, and the resulting powerlaw distribution is composed of different individual active regions, which may have different physical conditions and sizes. In particular, different sizes may cause an exponential cut-off at the upper end of the size distribution due to finite system-size effects. A study of flare statistics on individual active regions, however, did not reveal significant differences in their size distributions, and thus the size distributions of individual active regions seem to follow the universal powerlaw slopes that are invariant, individually as well as in a superimposed ensemble (Wheatland 2000c), except for one particular active region (Wheatland 2010).

Instead of testing powerlaw slopes of size distributions, an equivalent test is a linear regression fit among SOC parameters. For instance, statistics of WATCH/GRANAT data exhibited correlations of P∝E ^0.60±0.01, T∝E ^0.53±0.02, and T∝P ^0.54±0.03 (Georgoulis et al. 2001), which are consistent with the predictions of the standard model (Sect. 2.10), i.e., P∝E ^0.75, T∝E ^0.50, and T∝P ^0.67, given the uncertainties of about ±0.15 due to data truncation effects that are not accounted for in the linear regression fits.

Time series analysis of solar hard X-ray bursts has been performed for a few flares with a variety of methods, such as wavelet analysis (Aschwanden et al. 1998a), search for quasi-periodic variations (Jakimiec and Tomczak 2010), search for sub-second time scales (Cheng et al. 2012), statistics of UV subbursts (used as proxies for the hard X-ray subbursts) during a flare that exhibit powerlaw distributions (Nishizuka et al. 2009a, 2009b), multi-fractal spectral analysis of a hard X-ray time profile (McAteer et al. 2007, McAteer 2013b), or wavelet and local intermittency measure (LIM) analysis (Dinkelaker and MacKinnon 2013a, 2013b). The size distributions N(t) of hard X-ray sub-burst durations during a flare were found to be mostly exponential (Aschwanden et al. 1998a), probably due to finite system-size effects in each flaring region. The LIM method can reveal scale-invariant time evolutions, such as the fragmentation of the energy release cascading from large to smaller structures (the “top-down” scenario), or a small flare event that is avalanching into a larger structure (the “bottom-up” scenario), but it was found that neither of the two extremes captures the totality of a flare time profile (Dinkelaker and MacKinnon 2013a, 2013b).

3.1.2 Statistics of Solar Flare Soft X-Rays

Solar flares display signatures of thermal emission in soft X-ray wavelengths, besides the non-thermal emission detected in hard X-rays. The emission in both wavelength regimes is produced by the same flare process, which is called the chromospheric evaporation scenario, but by different physical processes. While hard X-rays are mostly produced by bremsstrahlung of non-thermal particles precipitating down into the dense chromosphere, soft X-ray line and continuum emission is excited by impulsive heating of the chromospheric plasma. The precipitating electrons and ions essentially dictate the heating rate of the chromospheric plasma, while the energy emitted from the heated thermal plasma (typically to temperatures of T _e ≈10–35 MK) follows approximately the time integral of the hard X-ray-driven heating rate, a relationship that has been dubbed the Neupert effect. Because of this intimate relationship between soft X-rays and hard X-rays in solar flares, similar energy or size distributions are expected in both wavelength regimes, which is indeed the case, as the compilations in Tables 2 and 3 show.

Table 3 Frequency distributions measured from solar flares in soft X-rays. Measurements with no preflare background subtraction are marked with parentheses

Size distributions of soft X-ray peak fluxes, fluences, and durations were mostly obtained from flare detections with the OSO-3 spacecraft (Hudson et al. 1969), the Explorer (Drake 1971), Yohkoh/SXT (Shimizu 1995; Shimojo and Shibata 1999), the SMM/BCS (Lee et al. 1995), and the GOES spacecraft (Lee et al. 1995; Feldman et al. 1997; Veronig et al. 2002a, 2002b; Yashiro et al. 2006; Aschwanden and Freeland 2012). Interestingly, the size distribution of the peak count rates in the range of α _P =1.64–1.98 is similar to the hard X-rays, and thus implies a proportionality between the hard X-ray counts and the soft X-ray fluxes, which is different from what is expected from the Neupert effect. Since the Neupert effect predicts that the time profile of soft X-rays approximately follows the time integral of the impulsive hard X-rays, one would expect that the soft X-ray peak flux distribution should be equal to the hard X-ray fluences, which is however not the case (Lee et al. 1995). The different powerlaw slopes indicate a special scaling law between flare temperatures and densities, i.e., n _e ∝T ^−4/5 (Lee et al. 1995), while the Neupert effect must be considered as an oversimplified rule that neglects any temperature dependence.

Some of the size distributions of soft X-ray peak fluxes have been found to have values steeper than α _P ≥2.0 (Veronig et al. 2002a; Yashiro et al. 2006), which in hindsight we can understand to be a consequence of neglecting the subtraction of the preflare background flux, which makes up a substantial amount of the total flux for small flares.

Flare statistics from the GOES satellite could be sampled over a period of 37 years (1975–2011), which covers about three solar cycles. Since the soft X-ray flux from the Sun varies by about two orders of magnitude during each solar cycle, due to the variation of emerging magnetic fields and the resulting coronal plasma heating rate, which is driven by the solar magnetic dynamo, the Sun is an ideal system to study SOC systems with variable drivers. While the powerlaw of the soft X-ray peak rate was found to be invariant during different solar cycles, having a roughly constant value of α _F =1.98±0.11, the time durations were found to have a variable slope from α _T ≈2.0 during solar minima to α _T ≈2–5 during solar maxima (Fig. 10), which was explained in terms of a flare pile-up effect (Aschwanden and Freeland 2012). In other words, the separation of time scales, i.e., the waiting times and flare durations, is violated during the busy periods of the solar cycle maximum. In contrast, an opposite trend has been reported for a 158-day modulation of the flare rate (Bai 1993).

Fig. 10

Variation of the power-law slopes α _P (t) of the soft X-ray 1–8 Å peak flux (top panel) and the flare rise time α _T (t), detected with GOES (middle panel), and the annual variation of the sunspot number over 3 solar cycles (bottom panel). The sunspot number predicts the variation in the powerlaw slope α _T (t) of the flare time duration (smooth curve in middle panel) as a consequence of the violation of the separation of time scales (Aschwanden and Freeland 2012)

A power spectrum of a time series of the GOES 0.5–4 Å flux during a flare-rich episode of two weeks during 2000, containing about 100 GOES >C1.0 flares, has been found to follow a spectral slope of P(ν)∝ν ⁻¹ (Bershadskii and Sreenivasan 2003), which indeed confirms Bak’s original idea that the SOC concept provides an explanation for the 1/f-noise (Bak et al. 1987).

3.1.3 Statistics of Solar Flare EUV Fluxes

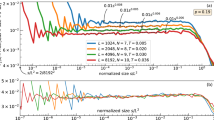
Large solar flares (with energies of E≈10³⁰–10³² erg) exhibit heated plasma with peak temperatures of T _e ≈10–35 MK, most conspicuously detected in soft X-rays, which cools down to temperatures of T _e ≈1–2 MK that is readily detected in the postflare phase in extreme ultra-violet (EUV) wavelengths. Also small flares, microflares, and nanoflares (with energies of E≈10²⁴–10²⁷ erg) radiate mostly in the EUV temperature range. Combining these wavelengths, one can obtain statistics of solar flare energies extending over up to 9 orders of magnitude (Fig. 11), hence the term “nanoflares”. Therefore, gathering flare statistics in EUV is expected to complement the lower end of the size distribution sampled in the upper end in soft X-rays and hard X-rays.

Fig. 11

Composite flare frequency distribution in a normalized scale in units of 10⁻⁵⁰ flares per time unit (s⁻¹), area unit (cm⁻²), and energy unit (erg⁻¹). The diagram includes EUV flares analyzed in Aschwanden et al. (2000b), from Krucker and Benz (1998), from Parnell and Jupp (2000), transient brightenings in (SXR) (Shimizu 1995), and hard X-ray flares (HXR) (Crosby et al. 1993). All distributions are specified in terms of thermal energy E _th =3n _e k _B T _e V, except for the case of HXR flares, which is specified in terms of nonthermal energies in >25 keV electrons. The slope of −1.8 is extended over the entire energy domain of 10²⁴–10³² erg (Aschwanden et al. 2000b)

A compilation of occurrence frequency distributions of flare samples observed in EUV is given in Table 4. The range of powerlaw slopes seems to vary over a much broader range, say within α _P ≈1.2–2.1 for EUV peak fluxes, α _E ≈1.3–2.6 for EUV-inferred energies, or α _T ≈1.4–2.3 for EUV event durations. The large scatter, which does not exist in flare statistics in hard X-ray wavelengths (Table 2), can be attributed to a number of methodical differences. The most important reason is incomplete temperature coverage when statistics of nanoflares is obtained in a single (narrowband) EUV filter, which results into relatively steep powerlaw slopes, while synthesized energy statistics combined from a broader range of EUV and soft X-ray filters combined yields the same powerlaw slope of α _P ≈1.8 in peak fluxes and α _E ≈1.5 in energies as obtained in soft X-rays and hard X-rays (Fig. 11; Aschwanden and Parnell 2002). Equally important is the scaling law used in the definition of flare energies. The classical approach is to estimate the thermal flare energy E _th =3k _B n _e T _e V from the peak electron density n _e , flare peak temperature T _e , and flare volume V. However, since the flare volume V cannot directly be measured, but only the flare area A instead, the scaling of the thermal energy depends crucially on the used geometric scaling law. Some authors used a “pill-box” model V=Ah with a constant height h, which corresponds to a geometric scaling law V∝L ², while a spherical volume scales as V∝L ³. In Sect. 2.7 we derived a distribution of N(A)∝A ⁻² for 2D areas, and a distribution of N(V)∝V ^−5/3 for 3D volumes, which explains part of the discrepancies among the powerlaw slopes compiled in Table 4. Other factors that play a role are the geometric scaling of fractal volumes, the flare selection, the flare detection algorithm, the detection thresholds, the synchrony in different temperature filters, the completeness of sampling, truncation effects in small samples, the powerlaw fitting method, etc. (e.g., Benz and Krucker 2002).

Table 4 Frequency distributions measured in small-scale events in EUV, UV, and Hα

Nonetheless, flare statistics from different wavelength regimes start to converge, as shown in Fig. 11. What is still needed is an unified identical detection method that uniformly samples events from the largest giant flare down to the smallest nanoflare.

3.1.4 Statistics of Solar Flare Radio Fluxes

Solar radio bursts are usually subdivided into incoherent (gyroemission, gyrosynchrotron emission, free-free emission) and coherent emission mechanisms (electron beam instability, loss-cone instability, maser emission). Since incoherent emission mechanisms scale with the volume of the emitting source, which could be a solar flare region, we expect some proportionality between the flare energy and the radio burst flux, such as for microwave bursts and type IV bursts (produced by gyrosynchrotron emission). Consequently we expect powerlaw slopes of their size distributions that are similar to other incoherent emission mechanisms of flares (e.g., bremsstrahlung in hard X-rays or soft X-rays). On the other hand, since coherent emission mechanisms produce a highly nonlinear response to some wave-particle instability, their emitted intensity flux is expected to scale nonlinearly with the flare volume, and thus may produce quite different size distributions.

We present a compilation of size distributions gathered from solar radio bursts in Table 5. Microwave bursts (MW), which are typically observed in frequencies of ν≈1–15 GHz, have been found to exhibit size distributions with powerlaw slopes within a range of α _P ≈1.7–1.9 (Akabane 1956; Kundu 1965; Kakinuma et al. 1969; Song et al. 2011, 2013; Das et al. 1997; Nita et al. 2002), similar to the size distributions observed in solar hard X-ray and soft X-ray bursts, which implies a near-proportionality between the flare energy and the radio peak flux.

Table 5 Frequency distributions measured from solar radio bursts, classified as type I storms (I), type III bursts (III), decimetric pulsation types (DCIM-P), decimetric millisecond spikes (DCIM-S), microwave bursts (MW), and microwave spikes (MW-S)

Type III bursts, which are believed to be produced by plasma emission excited by an electron beam-driven instability, display flatter size distributions in the order of α _P ≈1.2–1.5 (Fitzenreiter et al. 1976; Das et al. 1997; Aschwanden et al. 1995, 1998b), which can be explained by a nonlinear scaling F∝E ^γ between radio peak flux P and flare energy E. For the radio peak flux distribution $N(P) \propto P^{-\alpha_{P}}$, and assuming the standard volume scaling N(V)∝V ^−5/3 (Eq. (5)), we expect then, say for a nonlinear exponent γ=2, a powerlaw slope of α _P =(1+1/2γ)≈1.25. The fact that relatively flat powerlaw slopes have also been observed for other coherent radio bursts, such as α _P ≈1.3 for decimetric pulsations (DCIM-P; Aschwanden et al. 1998b), may also indicate a nonlinear scaling to the flare volume.

On the other hand, some very steep size distributions have been observed, such as α _P ≈3–5 for type I bursts (Mercier and Trottet 1997; Iwai et al. 2013), or α _P ≈3–7 for decimetric and microwave millisecond spike bursts (Aschwanden et al. 1998b; Ning et al. 2007), which implies either a strong quenching effect that inhibits high levels of radio fluxes, or a pulse-pileup problem that violates the separation of time scales (i.e., the inter-burst time intervals or waiting times are shorter than the burst durations). The latter effect is most likely to occur in the statistics of fine structure in complex patterns of radio dynamic spectra, where a multitude of small pulses occur in clusters. Such peculiar types of clustered radio emission are, for instance, type I bursts (Mercier and Trottet 1997; Iwai et al. 2013), or decimetric millisecond spikes (Aschwanden et al. 1998b). Low-resolution radio observations tend to cause an exponential cutoff at large radio flux values, even when the actual distribution has a powerlaw shape (Isliker and Benz 2001), and thus explains the trend of steeper powerlaw slopes. Also stochastic models of clustered solar type III bursts produce powerlaw-like size distributions with an exponential cutoff (Isliker et al. 1998b).

From the statistics of solar radio bursts we learn that we can discriminate between three diagnostic regimes (as grouped in Table 5): (1) the incoherent regime where the radio burst flux is essentially proportional to the flare volume (α _P ≈1.7–1.9); (2) the coherent regime that implies a nonlinear scaling between the radio peak flux and the flare volume P∝V ^γ with γ≈2 and α _P ≈1.2–1.5; and (3) the exponential regime with clustered bursts that violate the separation of time scales with steep slopes α _P ≈2–7 and have an exponential cutoff. Thus, the powerlaw slopes offer a useful diagnostic to quantify scaling laws between the radio flux (emissivity) and the flare volume.

3.1.5 Statistics of Solar Energetic Particle (SEP) Events

Solar energetic particle (SEP) events represent a subset of large solar flares that produce protons, electrons, and helium ions, with energies of ≳25 keV to 1 GeV. It was noted early on that the size distribution of peak counts of SEP events is flatter (α _E ≈1.2–1.4) than those of flare electromagnetic emission (Hudson 1978). Size distributions of the fluences of SEP events were gathered in a typical range of α _E ≈1.2–1.4 (Van Hollebeke et al. 1975; Belovsky and Ochelkov 1979; Cliver et al. 1991; Gabriel and Feynman 1996; Smart and Shea 1997; Perez Enriquez and Miroshnichenko 1999; Miroshnichenko et al. 2001; Gerontidou et al. 2002; Belov et al. 2007). The powerlaw slopes of the size distributions of peak fluxes and fluences are listed in Table 6, which clearly exhibit a much flatter range (α _P ≈α _E ≈1.2–1.4) than those measured in hard (Table 2) and soft X-rays (Table 3), as noted earlier (Hudson 1978). Cliver et al. (2012) interpreted this discrepancy as a selection effect of SEP events being preferentially associated with larger flares, and thus the SEP events are drawn from a subset of flares that do not form a statistically representative sample. This interpretation has been demonstrated by sampling subsets of flares that are associated with >10 MeV proton events, or with ≥1000 km s⁻¹ CMEs, which exhibited a similar flat powerlaw slope as the SEP events themselves (Fig. 12; Cliver et al. 2012). Note that a powerlaw function fits the size distribution of SEP fluences only in the low-fluence part, while the high-fluence part is better fitted by an exponential cutoff function, i.e., $N(E) \propto E^{-\alpha_{E}} \times\exp{(-E/E_{0})}$, based on SEP data from 41 solar cycles from 1561 to today (Miroshnichenko and Nymmik 2014).

Fig. 12

Size distributions for (1) peak 1–8 Å fluxes of all ≥M1.0 soft X-ray flares; (2) subset of flares associated with >10 MeV proton events; (3) subset of flares with ≥1000 km s⁻¹ CMEs; and (4) peak proton fluxes of >10 MeV SEP events. All SEP events were observed during 1996–2005 (adapted from Cliver et al. 2012)

Table 6 Frequency distributions of solar energetic particle (SEP) events

Alternatively, Kahler (2013) challenges the interpretation of a selection bias and suggests that the difference can be explained by the dimensionality of the SOC system. If we take the general expression of the powerlaw slope α _E for energy or fluences (Eq. (36)), we expect in the standard model, for classical diffusion (β=1) and incoherent processes (γ=1), and inserting the mean value of the fractal dimension D _d =(1+d)/2, a powerlaw slope of

$$ \alpha_E = 1+{2 (d-1) \over(d+5)} , $$

(52)

which yields α _E =3/2=1.5 in 3D space, but a flatter slope of α _E =9/7≈1.3 in 2D space (or even a limit of α _E =1 for d=1). This is conceivable if the avalanche spreads over a 2D surface only, such as a reconnection current sheet, or the surface of a shock wave. This would invalidate a close physical connection between flares and SEP events, and provide this way a diagnostics of the dimensionality of the particle acceleration process in flares and SEP events (Kahler 2013).

Because of the high energies of SEP events, which can harm astronauts or electronic equipment in space, statistical information that improves their predictability is highly desirable (Gabriel and Patrick 2003), but statistical studies demonstrate that it is not possible to predict the time of occurrence of SEP events within narrow limits (Xapsos et al. 2006).

3.1.6 Statistics of Solar Flare Waiting Times

In the simplest scenario we could envision that solar flares occur randomly in space and time. However, there are subsets of flares that occur simultaneously at different locations (called ”sympathetic flares”; Fritzova-Svestkova et al. 1976; Pearce and Harrison 1990; Wheatland 2006; Moon et al. 2002, 2003), as well as flare events that subsequently occur at the same location (called “homologous flares”; Fokker 1967), which indicates a spatial or temporal clustering that is not random. We outlined the concept of random processes in Sect. 2.12, which can produce an exponential waiting time distribution (for stationary Poisson processes), as well as powerlaw-like distributions of the waiting time (for non-stationary Poisson processes; Fig. 6). Moreover, both exponential and powerlaw distributions can be generated with the Weibull distribution (Sect. 2.12.3). The functional shape of the waiting time distribution depends moreover on the definition of events in a time series, where powerlaws are found more likely to occur when a threshold is used (Buchlin et al. 2005). Allowing an overlap of time scales between burst durations and quiet times, agreement was found between the waiting time distributions sampled with different thresholds (Paczuski et al. 2005; Baiesi et al. 2006). In summary, the finding of powerlaw-like waiting time distributions has no unique interpretation, because it can be consistent with both a random process without memory (in the case of a non-stationary Poisson process) or with a non-random process with memory (in the case of a Weibull distribution with k≠1). This dichotomy of stochasticity versus persistence or clustering has been noted in SOC processes before, for earthquakes that have aftershocks with an excess of short waiting times (Omori’s law; Omori 1895).

In Table 7 we compile studies on waiting times of solar flare phenomena, grouped into hard X-ray events, soft X-ray events, coronal mass ejections, radio bursts, and solar wind fluctuations. Statistics in hard X-rays were obtained from HXRBS/SMM (Pearce et al. 1993; Aschwanden and McTiernan 2010), BATSE/CGRO (Biesecker 1994; Grigolini et al. 2002; Aschwanden and McTiernan 2010), WATCH/GRANAT (Crosby 1996); ICE/ISEE-3 (Wheatland et al. 1998; Wheatland and Eddey 1998), and RHESSI (Aschwanden and McTiernan 2010).

Table 7 Waiting time distributions measured from solar flares hard X-ray events, soft X-ray events, coronal mass ejections, and radio bursts. The waiting time distribution (WTD) functions are abbreviated as: PL=powerlaw, E=exponential, PE=powerlaw with exponential rollover, DE=double exponential

All waiting time distributions observed for hard X-ray bursts have been reconciled with a single common model that represents a limit of intermittency,

$$ P(\Delta t) = \lambda_0 (1 + \lambda_0 \Delta t)^{-2} , $$

(53)

which has a powerlaw slope of α _Δt =2.0 for large waiting times (Δt≈1–1000 hrs) and flattens out for short waiting times Δt≲1/λ ₀, which is consistent with a highly intermittent flare productivity in short clusters with high rates, as it can be analytically derived (Aschwanden and McTiernan 2010), depicted in Fig. 6 (bottom panel). A similar functional form of the waiting time distribution is obtained with the diffusion entropy method (Grigolini et al. 2002).

In addition, the powerlaw slope of α _Δt =2 is also predicted by the fractal-diffusive model (Sect. 2.12.3) in the slowly-driven limit, while steeper observed slopes are consistent with the predicted modification for strongly-driven systems (Eq. (43)). The results compiled in Table 7 indeed yield higher values of α _Δt ≈3 during periods of high flare activity, as it occurs during the solar cycle maximum.

In soft X-rays, a similar powerlaw slope of α _Δt ≈2.1–2.4 was found, which could be fitted with a non-stationary Poisson process (Wheatland 2000a; Moon et al. 2001), with a shell model of turbulence (Boffetta et al. 1999), or with a Levy function (Lepreti et al. 2001). These different interpretations underscore the ambiguity of powerlaw distributions, which do not allow to discriminate between SOC and turbulence processes. Moreover, the powerlaw slope of waiting time distributions varies during the solar cycle, which implies a time-variable SOC driver (Wheatland and Litvinenko 2002). The flaring rate was found to vary among different active regions, as well as during the disk transit time of a single active region (Wheatland 2001). The variability in the flare rate was found to correlate with the sunspot number, however with a time lag of about 9 months, which reflects the hysteresis of the coronal response to the solar dynamo (Wheatland and Litvinenko 2001), a result that can be used for statistical flare forecasting (Wheatland 2004; Wheatland and Craig 2006). Additional tests whether the waiting time of solar flares is random (multi-Poissonian) or clumped in persistent clusters (with some memory) have been carried out with a Hurst analysis, finding a Hurst exponent of H=0.74±0.02 (compared with H=0.5 for a pure stochastic process) (Lepreti et al. 2000), or by fitting a Weibull distribution (Sect. 2.12.3), finding two statistical components for coronal mass ejections, a continuous random process during solar minima, and another component with temporary persistence and memory during solar maxima (Telloni et al. 2014), similar to the FD-SOC scenario (Fig. 7 and Sect. 2.12.3), or the aftershocks in earthquake statistics (Omori’s law).

Does the waiting time give us some information about the energy build-up in solar flares? Early studies suspected that the waiting time is the longer the more energy is built up, which predicts a correlation between the waiting time and the energy of the flare (Rosner and Vaiana 1978). However, several observational studies have shown that no such correlation exists (e.g., Lu 1995b; Crosby 1996; Wheatland 2000b; Georgoulis et al. 2001; Moon et al. 2001), not even between subsequent flares of the same active region (Crosby 1996; Wheatland 2000b). The original SOC model of BTW assumes that avalanches occur randomly in time and space without any correlation, and thus a waiting-time interval between two subsequent avalanches refers to two different independent locations (except for sympathetic flares), and thus bears no information on the amount of energy that is released in each spatially separated avalanche. In solar applications, flare events seem to deplete only a small amount of the available free energy, and thus no correlation between waiting times and flare magnitudes are expected to first order. In contrast, however, recent studies that analyze the probability differences of subsequent events from the GOES flare catalog, and compare them with randomly re-shuffled data, find non-trivial correlations between waiting times and dissipated energies. Flares that are close in time tend to have a second event with large energy. Moreover, the flaring rate as well as the probability of other large flares tends to increase after large flares (Lippiello et al. 2010), similar to the clustering of coronal mass ejections (CMEs) (Telloni et al. 2014), and aftershocks of earthquakes (Omori 1895).

3.1.7 Solar Fractal Measurements

“Fractals in nature originate from self-organized critical dynamical processes (Bak and Chen 1989). In principle, SOC avalanches could be non-fractal and encompass space-filling solid volumes, as the sandpile analogy suggests. However, using the BTW model as a paradigm for SOC avalanches, it is quite clear from inspecting numerical simulations that the next-neighbor interactions propagate in “tree-like” patterns that can indeed be quantified with a fractal dimension (e.g., Aschwanden 2012a). Also the EUV images of solar flares show highly fragmented postflare loops that can be characterized with a fractal dimension (Aschwanden and Aschwanden 2008a).

Interestingly, measurements of the area fractal dimension D ₂ in solar data have been published over the same 25-year era as SOC publications exist (Table 1). Reviews on fractal analysis of solar flare data can be found in Aschwanden (2011a, Chap. 8) and in McAteer (2013a). While cellular automaton simulations allow for various Euclidean space dimensions (d=1,2,3), solar observations are restricted to the 2D-case (d=2), for which the standard model predicts an mean area dimension of D ₂=(1+d)/2=1.5, with a lower limit of D _2,min ≳1.0 and an upper limit of D _2,max =2.0. The observed fractal dimensions listed in Table 8 indeed cover the full range of D ₂=[1.09,1.97] and have a median value of D _2,med =1.54, or a mean and standard deviation of D ₂=1.54±0.25. These fractal dimensions have been measured in a variety of solar phenomena: from granulation (Roudier and Muller 1987; Hirzberger et al. 1997; Bovelet and Wiehr 2001), super-granulation (Paniveni et al. 2005, 2010), active regions (Lawrence 1991; Cadavid et al. 1994; Lawrence et al. 1996; McAteer et al. 2005; Lawrence and Schrijver 1993; Meunier 1999, 2004), plages (Balke et al. 1993), quiet-Sun network (Lawrence et al. 1993; Gallagher et al. 1998), Ellerman bombs (Georgoulis et al. 2002), nanoflares (Aschwanden and Parnell 2002), to large flares (Aschwanden and Aschwanden 2008a; Aschwanden et al. 2013a). The lowest fractal dimensions D ₂≈1.1–1.3 are measured in granules and in the quiet-Sun network, which consist of elongated curvi-linear structures, while active region and flare areas have a higher fractal dimension of D ₂≈1.4–1.8, consisting of chains of coherent patchy areas, as expected for SOC avalanches with isotropic next-neighbor interactions. A lower threshold fractal dimension of D ₂≳1.2 (and 1.25) was found as a necessary condition for an active region to produce M-class (and X-class) flares (McAteer et al. 2005). In the overall, we can say that most solar observations are consistent with a predicted area fractal dimension of D ₂=(1+d)/2=1.5.

Table 8 Area fractal dimension D ₂ of scaling between length scale L and fractal area $A(L) \propto L^{D_{2}}$ measured from various solar phenomena observed in different wavelength regimes: WL=white light, H-α=visible spectral line in the Balmer series produced in hydrogen at 6562.8 Å, MG=magnetogram measured with Zeeman effect, e.g., from Fe XIV 5303 Å line; EUV=extreme ultra-violet, SXR=soft X-rays. The methods are: PA=perimeter vs. area, LA=linear size vs. area, and BC=box-counting

For the application of SOC models to solar flares, which have a 3D geometry, we cannot measure the volume fractal dimension D ₃ directly. If we rely on the simple mean-value theorem, D _d =(1+d)/2 (Eq. (8)), we expect a volume fractal dimension of D ₃=2.0. Attempts have been made to determine the 3D volume fractal dimension D ₃ from observations of 20 large-scale solar flares, using a fractal loop arcade model, which yielded a mean value of D ₃=2.06±0.48 (calculated from Table 1 in Aschwanden and Aschwanden 2008b). Thus, we can conclude that the solar flare observations are consistent with the volume fractal dimension predicted by the standard SOC model, i.e., D ₃=(1+d)/2=2.0 (for d=3).

This mean-value theorem predicts a scaling law between the fractal avalanche area $A_{f} \propto L^{D_{2}}$ and the fractal avalanche volume $V_{f} \propto L^{D_{3}}$,

$$ V_f \propto A_f^{\delta} , \qquad\delta= {D_3 \over D_2} = {1+3 \over1+2} = {4 \over3} \approx1.33 , $$

(54)

which is lower than the Euclidean scaling law, V∝A ^3/2=A ^1.5. Cellular automaton simulations yield an intermediate value for the exponent, δ=1.41±0.04 (Fig. 13; McIntosh and Charbonneau 2001).

Fig. 13

Relationship between the 3D fractal volume of a SOC avalanche (left panel) and the three 2D projections that show the 2D fractal areas (right panels), simulated in a 32³ lattice (McIntosh and Charbonneau 2001)

The volume fractal dimension is important to derive the correct scaling law between the length scale r(t) of a SOC avalanche at a given time t and the instantaneous fractal avalanche volume V _f (t) (Eq. (12)), being proportional to the observed flux f(t), as well as for the total time-integrated energy e(t) (Eq. (14)). It affects the powerlaw slopes of the size distributions of avalanche areas (α _A ), avalanche volumes (α _V ), flux (α _F ), and total energy (α _E ) (see Eqs. (22) and (36)).

The fractal dimension measured in magnetograms can diagnose both SOC behavior or turbulence, but cannot discriminate between the two interpretations because both processes have fractal-like structures. An alternative method to measure the fractal structure or intermittency of a turbulent magnetic field is the structure function (Frisch 1995; Abramenko et al. 2003),

$$ S_q(\mathbf{r})= \bigl\langle \bigl|{\mathbf{B}}_z (\mathbf{x} +\mathbf{r}) - \mathbf{B}_z(\mathbf{x}) \bigr| {\bigr\rangle }^q \propto(\mathbf{r})^{\zeta (q)} , $$

(55)

where q is an order of a statistical moment, r is a separation vector, x=(x,y) is a spatial location in a magnetogram, and B _z is the observed line-of-sight longitudinal magnetic field. This structure function essentially measures the level of long-range correlations, which are an intrinsic property of SOC avalanches. Analysis of magnetograms before solar flares have shown an increase in the degree of intermittency and in the maximum of the correlation length, which was interpreted in terms of enhanced turbulence as a precursor to a SOC avalanche of a solar flare (Abramenko et al. 2002, 2003; Abramenko and Yurchyshyn 2010). The presence of a topologically complex, asymmetrically fragmented magnetic network can trigger a magnetic instability acting as an energy source for a coronal dissipation event (Uritsky and Davila 2012).

A generalization to fractal areas, A _f ∝L ^D, is a multi-fractal system, which has a spectrum f(D) of fractal dimensions D,

$$ A_f \propto L^{f(D)} , $$

(56)

where D is called the strength or significance, and f(D) the singularity spectrum. This singularity spectrum has a peak at f(D) _max and a minimum of f(D) _min (Fig. 14), which is characterized by the terms contribution diversity C _div =D _max −D _min and dimensional diversity D _div =f(D) _max −f(D) _min , both being measures of the geometric complexity and richness of a fractal structure. Multi-fractal analysis of solar data has been carried out on magnetograms (Abramenko 2005; Conlon et al. 2008; Ioshpa et al. 2008; Hewett et al. 2008; Dimitropoulou et al. 2009). Flare-quiet active regions were found to have a lower degree of multi-fractality than flaring active regions (Abramenko 2005). Multi-fractality was also found to increase during magnetic flux emergence in active regions, while a decrease occurred when the active regions evolved to large-scale, coherent structures (Conlon et al. 2008; McAteer et al. 2010). While the exact energy scaling is not known, spatial complexity and flare productivity seem to be related, even when they have different fractal dimensions (Hewett et al. 2008). The 2D photospheric magnetic field contains the footprints of 3D magnetic structures in the solar corona, which explains numerous correlations between photospheric and coronal phenomena (e.g., Dimitropoulou et al. 2009; Uritsky et al. 2013). On the other side, solar active regions with major flares were not found to exhibit a higher level of fractality, multi-fractality, or non-Kolmogorov turbulence than non-flaring regions (Georgoulis 2012).

Fig. 14

A monofractal image of the Sierpinski carpet (left), a theoretical multifractal image (middle), and an observed multifractal solar magnetogram of active region NOAA 10030 (right), along with the singularity spectra f(α) (bottom panels) determined for these structures (Conlon et al. 2008)

While the previous discussion applies to fractal geometries in 2D space with two spatial dimensions, the concept of fractals has also been applied to a time series f(t), where a fractal dimension is measured in the 2D space of f versus t. We can easily imagine that a constant function f(t)=const represents a straight line in a 2D box [t,f], and thus has the fractal dimension of D ₂=1, while an erratically fluctuating noise time series renders a plotted box [t,f] almost black, and thus has an almost space-filling Euclidean dimension D ₂=2. So, a fractal (or multi-fractal) dimension of a time series is essentially a measure of the time variability, and has been applied to solar radio burst data (Higuchi 1988; Watari 1996), or daily flare indices (Watari 1995; Sen 2007). A multi-fractal spectrum of the hard X-ray time profile of a solar flare was used to discriminate thermal and non-thermal emission based on their different temporal signatures (McAteer 2013b). In principle, such a dimensional time variability analysis could also be applied to SOC simulations, and this way could characterize the predicted waiting time distribution, but we are not aware of such studies.

3.1.8 Flare Geometry Measurements

The most fundamental assumption in the SOC standard model is the scale-free probability conjecture, i.e., N(L)∝L ^−d (Eq. (1)), which should be easy to test with imaging solar observations, but there is surprisingly little statistics available. For solar flare observations we expect that SOC systems have an Euclidean dimension of d=3, and thus the prediction for the size distribution of flare length scales is N(L)∝L ⁻³. The directly measured quantity in solar flares is usually the Euclidean flare area A, which relates to the length scale by L∝A ^1/2 (Eq. (2)), and thus a size distribution of N(A)∝A ⁻² is expected.

In Table 9 we compile measurements of the flare geometry in terms of length scales L, flare areas A, or flare volumes V, which obey the expected geometric scaling laws of the SOC standard model within the uncertainties: α _L =3, α _A =2, α _V =5/3. The recent measurements in 7 different wavelengths using AIA/SDO have been derived from the time-integrated areas A(t<T) at the end time of the flares (at t=T), measured with five different thresholds and normalized (Aschwanden et al. 2013a). Note that the instantaneous flare areas a(t) at some given time 0<t<T are fractal, approximately following the scaling $a(t) \propto r(t)^{D_{2}}$ as a function of the instantaneous radius r(t) of the Euclidean flare area, while the time-integrated flare areas are nearly solidly filled and outline essentially the Euclidean area A∝L ² at the end time (t=T) of the flare when r(t=T)=L. These statistical measurements represent the most direct observational test of the scale-free probability conjecture, N(L)∝L ⁻³, and this way corroborate the standard SOC model.

Table 9 Measurements of powerlaw slopes of solar flare size distributions of geometric parameters: length scales (α _L ), flare areas (α _A ), and flare volumes (α _V ). The references are: B1998=Berghmans et al. (1998); A2000=Aletti et al. (2000); A2000b=Aschwanden et al. (2000b); AP02=Aschwanden and Parnell (2002); A2012b=Aschwanden (2012b); A2013=Aschwanden et al. (2013a); and A2012a=Aschwanden (2012a); L2010=Li et al. (2012)

Area measurements have also been carried out for supra-arcade downflows during flares, which were found not to be compatible with a powerlaw distribution (McKenzie and Savage 2011), a result that is not surprising given the small range of measured areas (covering about a half decade).

The geometric measurements are also of fundamental importance for deriving and testing physical scaling laws, which are generally expressed by a length scale (i.e., a coronal loop length), or by a volumetric emission measure (which is proportional to the total flare volume), or thermal energy (which is also proportional to the total flare volume). We will discuss such theoretical scaling laws in Sect. 3.2.7.

3.1.9 Solar Wind Measurements

The solar wind is a turbulent magneto-fluid, consisting of charged particles (electrons, protons, alpha particles, heavy ions) with typical energies of 1–10 keV, which escape the Sun’s gravity field because of their high kinetic (supra-thermal) energy and the high temperature of the solar corona. The solar wind has two different regimes, depending on its origin, namely a fast solar wind with a speed of v≲800 km s⁻¹ originating from open-field regions in coronal holes, and a slow solar wind with a speed of v≲400 km s⁻¹ originating from low latitudes in the surroundings of coronal streamers. The dynamics of the solar wind was originally explained by Parker (1958) as a supersonic outflow that can be derived from a steady-state solution of the hydrodynamic momentum equation. Later refinements take the super-radial expansion of the coronal magnetic field, the average macro-scale and fluctuating meso-scale electromagnetic field in interplanetary space, and the manifold micro-scale kinetic processes (such as Coulomb collisions and collective wave-particle interactions) into account. The properties of the solar wind that can be measured from the solar corona throughout the heliosphere are plasma flow speeds, densities, temperatures, magnetic fields, wave spectra, and particle composition, which all exhibit complex spatio-temporal fluctuations. Most of the observations of the solar wind were made in-situ (with the Mariner, Pioneer, Helios, ISEE-3, IMP, Voyager, ACE, WIND, Cluster, Ulysses, or STEREO spacecraft), complemented by remote-sensing imaging (with STEREO) and radio scintillation measurements.

The dynamics of the solar wind is often characterized by the MHD turbulent cascade model. The solar wind power spectrum exhibits fully developed turbulence of the Kolmogorov type, P(ν)∝ν ^−5/3, in interplanetary space and near Earth (Fig. 15), while the input spectrum in the lower corona is of the 1/f-noise type, P(ν)∝ν ⁻¹ (Matthaeus and Goldstein 1986; Nicol et al. 2009). The MHD turbulent cascade starts at the largest scales fed by MHD waves with a 1/f-noise spectrum in the lower corona, while turbulent interactions produce a cascade of energy through vortices and eddies to progressively smaller sizes with a spectrum of ν ^−5/3, and final energy dissipation at the smallest scales by heating of electrons, with a spectrum of ν ^−11/3 (Meyrand and Galtier 2010). The analysis of MHD turbulence in solar wind data includes determining power spectra and structure functions, waiting time distributions of solar-wind bursts, identifying the phenomenology or MHD turbulence (Kolmogorov 1941; Kraichnan 1974), characterizing self-similarity and intermittency, and identifying the most intermittent structures, such as shock waves, small random events, current cores, and 1D current sheets (e.g., Horbury and Balogh 1997; Veltri 1999).

Fig. 15

A spectrum of the solar wind is shown, based on CLUSTER observations from large scales (≈105 km) down to small scales (≈3 km) is shown, with the proton and electron gyroradius scale indicated. The solar wind spectrum is interpreted in terms of a turbulent MHD cascade, with the theoretically predicted slopes of f ^−5/3 and f ^−7/3 from gyro-kinetic theory. The plot proves that the energy continues cascading below the proton scale down to the electron scale, where it is converted to heat (via electron Landau damping resonance) causing the steepening of the B _z spectrum to f ⁻⁴ (Howes et al. 2008; Sahraoui et al. 2009; credit: ESA, CLUSTER)

Recent interpretations of the dynamics of the solar wind include self-organization and SOC systems. The strongest argument for a SOC interpretation is the fact that powerlaw size distributions were found for energy fluctuations (E _B ∝B ²), durations (T), and waiting times (Δt) in the solar wind (Table 10; Freeman et al. 2000a; Moloney and Davidsen 2011). Although the powerlaw shape of the waiting time distribution of solar wind bursts is not exponential, hence inconsistent with the original BTW model (Boffetta et al. 1999; Freeman et al. 2000a), it can be reproduced with a non-stationary Poisson process (Fig. 6; Wheatland et al. 1998; Aschwanden and McTiernan 2010). This was also demonstrated with MHD simulations (Watkins et al. 2001; Greco et al. 2009a, 2009b), and by cellular automaton simulations with correlations in the driver that produces a “colored” power spectrum (Sanchez et al. 2002).

Table 10 Powerlaw slopes measured in the size distributions of magnetic field fluctuations in the solar wind. The burst energy E is defined as the area-integrated and time-integrated Poynting flux, derived from the Akasofu parameter

SOC systems produce fractal spatio-temporal structures. The fractal nature of magnetic energy density fluctuations in the solar wind has been verified observationally (Hnat et al. 2007; Rypdal and Rypdal 2010a, 2010b). Moreover, solar wind turbulence is found to be multi-fractal, requiring a generalized model with multiple scaling parameters to analyze intermittent turbulence (Macek and Szczepaniak 2008; Macek and Wawrzaszek 2009; Macek 2010), although a single generalized scaling function is sometimes sufficient too (Chapman and Nicol 2009; Rypdal and Rypdal 2011). However, the fractal geometry of solar wind bursts seems not to be self-similar, since the ratio of kinetic (E _k ) to magnetic energy (E _B ∝B ²) is frequency-dependent, with a magnetic energy spectrum of $\propto E_{B}^{-5/3}$ and a kinetic energy spectrum of $\propto E_{k}^{3/2}$ (Podesta et al. 2006a, 2006b, 2007). It was suggested that the interplanetary magnetic field (IMF) is clustered (self-organized) by low-frequency magnetosonic waves, leading to a fractal structure with a Hausdorff dimension of D=4/3 and a turbulent power spectrum with ν ^−5/3 (Milovanov and Zelenyi 1999).

In the end, can we claim that the dynamics of the solar wind is consistent with a SOC system? Observationally we find that magnetic field and kinetic energy fluctuations measured in the solar wind exhibit powerlaw distributions, which is consistent with a SOC system. One argument against the SOC interpretation is the observed powerlaw distribution of waiting times (Boffetta et al. 1999), but this argument applies only with respect to the original BTW model, while it presents no obstacle for nonstationary Poisson processes. Another (Occam’s razor) argument was that a SOC interpretation is not needed when turbulence can already explain solar wind spectra (Watkins et al. 2001). Considering the spatial structure of the solar wind, a fractal (or multi-fractal) property was identified, another hallmark of SOC models. What about the driver, instability, and avalanches expected in a SOC system? The driver mechanism is the acceleration of the solar wind in the solar corona itself, a process that basically follows the hydrodynamic model of Parker (1958), and may be additionally complicated by the presence of nonlinear wave-particle interactions, such as ion-cyclotron resonance (e.g., for a recent review see Ofman 2010). Then, the instability threshold, triggering extreme bursts of magnetic field fluctuations, the avalanches of solar wind SOC events, can be caused by dissipation of Alvén waves, onset of turbulence, or by the ion-cyclotron instability. Thus, in principle the generalized SOC concept can be applied to the solar wind, if there is a system-wide threshold for an instability that causes extreme magnetic field fluctuations. On the other side, the MHD turbulent cascade model explains naturally two particular spatial scales with enhanced energy dissipation (i.e., the proton the electron gyroradii), which is in contrast with the scale-freeness of energy dissipation in classical SOC models. Nevertheless, the solar wind dynamics can be described by multiple models that do not exclude each other: (1) the MHD turbulent cascade model describes the power spectrum of the solar wind, (2) kinetic theory captures the microscopic physics of wave-particle interactions and the evolution of particle velocity distributions in the solar wind, and (3) SOC models quantify the statistics and macroscopic size distributions of extreme events in the solar wind.

3.1.10 Solar-Terrestrial Effects

A solar-terrestrial effect that has been modeled in terms of SOC models is the connection between solar flare occurrence and temperature anomalies on Earth. The scaling of the Earth’s short-term temperature fluctuations and solar flare intermittency was analyzed in terms of the spreading exponent and the entropy of diffusion, finding that both have a Lévy flight statistics with the same exponent α _Δt =2.1 in the waiting-time distribution (Scafetta and West 2003). The same data were re-analyzed by Rypdal and Rypdal (2010a), who found that only the integrated solar flare index is consistent with Levý flight, while the global temperature anomaly follows a persistent fractional Brownian motion. The persistence (long-range memory) of solar activity was investigated further and it was found that the sunspot number and the total solar irradiance are long-range persistent, while the solar flare index is very weakly persistent, with a Hurst exponent of H<0.6 (Rypdal and Rypdal 2012). A stochastic theory to model the temporal fluctuations in avalanching SOC systems has been developed to understand these solar-terrestrial observations (Rypdal and Rypdal 2008a, 2008b). Three other Earth climate factors (average daily temperature, vapor pressure, and relative humidity) were analyzed and found to exhibit power-law distributions and thus believed to constitute a SOC system (Liu et al. 2013).

The prediction of solar-terrestrial effects, such as geoeffective solar eruptions and SEP events, resulting in space-weather storms and magnetospheric disturbances, are of course of highest interest for our society. Statistics of the most extreme events need to be derived from the rarest events at the upper end of the size distributions, where a powerlaw extrapolation is often questionable, and thus has been modeled with different cutoff functions, often associated with finite-system size effects. The best relevant data we have at hand is the solar flare statistics from the last 40 years, while geological tracers (nitrate concentrations in polar ice cores or select radionuclides) extend over millenia, but are not reliable proxy records of solar flares or SEP events (Schrijver et al. 2012), because nitrate spikes in ice cores can also be caused by biomass burning plumes (Wolff et al. 2012). Theoretical studies focus on extreme value and record statistics in heavy-tailed processes with long-range memory (Schumann et al. 2012). The inclusion of memory and persistence is obviously very important, because the predicted number of extreme events during a clustered time interval can be much larger than predicted in a purely stochastic SOC model, such as in the original BTW model (Strugarek and Charbonneau 2014).

3.2 Solar Physics: Theoretical Models

3.2.1 Solar Cellular Automaton Models

One of the most ingenious simplifications of reducing complexity in nature to simplicity in theoretical modeling is the approach of numerical lattice simulations, also called cellular automaton models. In the case of simulating avalanches in a SOC system, Bak et al. (1987, 1988), slightly preceded by Katz (1986), just defined a discretized step in the evolution of an avalanche by a simple next-neighbor redistribution rule in a 3D lattice grid, the so-called BTW model,

$$ \begin{aligned} &z(i,j,k)=z(i,j,k)+1 \quad\mbox{initial input} \\ &z(i,j,k)=z(i,j,k)-6 \quad\mbox{if}\ z(i,j,k) \ge6 , \\ &z(i\pm1,j\pm1,k\pm1)=z(i\pm1,j\pm1,k\pm1)+1 \end{aligned} $$

(57)

which of coarse can also be generalized to a 2D avalanche with 4 neighbor nodes, or a 1D avalanche with 2 neighbor nodes. The crucial part is a critical threshold that decides whether an avalanche starts/continues, or stops, which is z _crit =6 in 3D, z _crit =4 in 2D, or z _crit =2 in 1D. Such cellular automaton simulations require millions of time steps until the system becomes critical, and another few millions to produce sufficient statistics of avalanche sizes. Then, the direct output of such numerical simulations are statistical distributions of avalanche sizes and durations. The size of an avalanche is generally defined as the time-integrated sum of all nodes that were active during any time step of an avalanche. Summarizing similar BTW-type lattice simulations, we compiled in Table 1 a list of powerlaw slopes that resulted from the avalanche sizes in 1D, 2D, and 3D lattice grids, which exhibit a dependence on the dimensionality of the system, as well as some scatter among the results from identical dimensions, due to slightly different definitions of the redistribution rules and different system sizes.

The first applications of BTW cellular automaton simulations to solar flares were made by Lu and Hamilton (1991), who interpreted the avalanches in terms of small magnetic reconnection events, where unstable magnetic energy is dissipated, and demonstrated that the powerlaw slopes of numerically simulated avalanche sizes, durations, and instantaneous peak sizes match the observed frequency distributions of hard X-ray fluences E, flare durations T, and peak fluxes P. The powerlaw slopes were found to be essentially invariant when the size of the system (i.e., the Cartesian lattice grid) was changed (Lu et al. 1993).

While the BTW model arranges an isotropic redistribution (in all next-neighbor directions), with the magnetic field strength B being the redistributed quantity, in the application to solar flares (Lu and Hamilton 1991), an anisotropic cellular automaton model with a one-directional redistribution along the direction with the largest magnetic field gradient was proposed by Vlahos et al. (1995), in order to mimic the inhomogeneity of active regions in general, and the directivity of the dominant magnetic field in the solar corona in particular. The anisotropic BTW model produced steeper powerlaw distributions than the isotropic standard model, a property that was utilized to construct a hybrid model with a steep powerlaw slope for nanoflares and a flatter slope for large flares (Vlahos et al. 1995; Georgoulis et al. 1995, 1998; Georgoulis and Vlahos 1996, 1998), which was believed to match the observations (Fig. 11). However, the anomalously steeper powerlaw slopes reported for nanoflares early on (Benz and Krucker 1998; Parnell and Jupp 2000), have been downward-corrected later on due to inadequate modeling effects (McIntosh and Charbonneau 2001; Benz and Krucker 2002; Aschwanden and Parnell 2002), and are now more consistent with the size distribution of larger flares (Fig. 11). Moreover, an anomalously steep powerlaw slope α _P >2 for the energy cannot be reconciled with the standard SOC model based on the scale-free probability conjecture and diffusive transport (Sects. 2.6–2.11).

The Sun often displays multiple sunspot groups or active regions at the same time, at least during the solar maximum. This implies, in Bak’s sandpile analogy, that solar flare statistics originates from multiple simultaneous sandpiles. Consequently the size distributions of active regions has to be folded into the event distributions, an effect that still produced size distributions close to a single powerlaw (Wheatland and Sturrock 1996; Wheatland 2000c).

Variants or alternatives to the BTW model that have been applied to simulate the size distributions of solar flares, to name a few, include 3D vector fields with periodic, constant, and symmetric boundaries (Galsgaard 1996), a BTW model with additional nonlocal (remote) triggering that accommodates sympathetic flaring (MacKinnon and MacPherson 1997; Macpherson and MacKinnon 1999), lattice models with non-stationary driving that reproduce the observed waiting time distributions (Norman et al. 2001), emergence of magnetic flux in evolving active regions (Vlahos et al. 2002), lattice models with deterministic drivers based on the BTW model (Strugarek et al. 2014) or on a finite driving rate version of the Olami–Feder–Christensen (OFC, Olami et al. 1992) model (Hamon et al. 2002), which usually is not in a SOC state but rather “on the edge of SOC”, prediction of solar flares by data assimilation to the BTW model (Belanger et al. 2007), a divergence-free field braiding cellular automaton model (Fig. 16; Morales and Charbonneau 2008a, 2008b, 2009), or drivers with diffusive characteristics that mimic a turbulent substrate (Baiesi et al. 2008). The 3D vector field simulations revealed two necessary criteria for the generation of powerlaws: a contiuous driver that produces large scale regions with coherent tension, and a partial (rather than a complete) release of the triggering quantity (Galsgaard 1996).

Fig. 16

Transformation of the flat 2-D lattice geometry of the divergence-free braiding BTW model onto a pseudo 3-D loop envelope and plane-of-sky for an arbitrary observer’s line-of-sight direction (left panel). The fractal area of the avalanche is projected into the observer’s plane (right panel) (Morales and Charbonneau 2009)

3.2.2 Analytical Microscopic Solar SOC Models

While cellular automaton models are most powerful in simulating SOC processes, the iterative numerical scheme is generally non-deterministic and unpredictable (with some exceptions, e.g., see Strugarek and Charbonneau (2014) for a discussion on prediction from numerical SOC models), while analytical models are deterministic and give us direct physical insights into the dynamics of a SOC system. Let us review a few of the analytical approaches that have been employed to model solar SOC processes.

A 1D cellular automaton model was constructed in terms of a branching probability p, which yields a probability of N(s)=sp ^s−1(1−p)² after s time steps, and this way leads to a size distribution of N(s)∝s ⁻² (MacKinnon et al. 1996). This branching-type model was extended to a 2D version by introducing some ad hoc functions that could produce powerlaw-like size distributions (Macpherson and MacKinnon 1999). This exercise demonstrated that the statistical redistribution rule of a cellular automaton model with higher dimensions (d≥2) cannot easily be formulated in terms of analytical branching probabilities. In an attempt to generalize this 1-D branching process to higher dimensions, Litvinenko (1998) points out a result from a tree branching process (Fig. 17), for which an asymptotic limit was found with the following analytical expression (Otter 1949),

$$ \bigl\langle N(s)\bigr\rangle \propto s^{-3/2} \exp{ \biggl(-{s \over s_0} \biggr)} , $$

(58)

that is close to observed frequency distributions of flare energies, if we identify the size s with the energy E of flares. A similar description of activation in a forest-fire model was adopted by Christensen et al. (1993).

Fig. 17

An avalanche represented by the tree generation of a branching process. Propagation to a site that is already activated by more than one neighbor (dashed lines) is ignored (Litvinenko 1998)

Size distributions of physical parameters and scaling laws can be derived from energy balance equations. Such an approach has been pursued by Wheatland and Glukhov (1998) using a probability balance equation or “master equation” (Gardiner 1983; Van Kampen 1992),

$$ {d \over dE} (e P) + P \int_0^E \alpha\bigl(E,E'\bigr) dE' - \int_E^\infty P\bigl(E'\bigr) \alpha\bigl(E', E\bigr) dE' = 0 , $$

(59)

where E is the flare energy, P(E) the probability distribution, α(E,E′)=α(E−E′) the probability for a transition from energy state E to E′, and e(E) is an arbitrary energy increase function of E in the active region. A general solution of this master equation was not found, but powerlaw distributions for the flare energy distribution N(E) were found for the special case when the energy supply rate e(E) does not depend on the free energy of the system (Wheatland and Glukhov 1998). The same energy balance equation was applied to quantify how the energy supply in the solar corona relates the flaring rate and free energy of the system, leading to a hysteresis of about 9 months during the 11-year solar cycle (Wheatland and Litvinenko 2001). Further semi-analytical work and Monte-Carlo simulations of this jump-transition model with a time-dependent driver (of the energy input rate) illustrated how the SOC system responds in form of modified flare energy and waiting time distributions (Wheatland 2008, 2009; Kanazir and Wheatland 2010).

The spatio-temporal transport process of a SOC avalanche can macroscopically be approximated by a fractal-diffusive relationship, r(t)=κ(t−t ₀)^β/2 (Eq. (9)), where β=1 corresponds to classical diffusion or random walk. The process of a random walk of particles through a fractal environment in 3D space was analytically described in Isliker and Vlahos (2003). Particles propagate freely in space not occupied by the fractal, but are scattered off into random directions when they hit a boundary of a fractal structure. This spatio-temporal transport process turns into a classical random walk in the limit of very sparse fractals, but produces enhanced diffusion (hyper-diffusion) with β>1 for fractal dimensions D _d >2. Since the diffusive spreading exponent β is a free parameter in the standard SOC model (Sect. 2.9), the analytical derivations of particle transport in fractal structures can give us physical insight into the nature of the diffusion process and the values of the spreading exponent β.

The redistribution rule that involves the next neighbors in a lattice grid during one time step of a SOC avalanche, has an extremely simple discretized form (Eq. (57)), but is hard to capture in the continuum limit, suitable for analytical models. Lu (1995c) envisions avalanches in a continuum-driven dissipative system, which is characterized by a coupled equation system of a one-dimensional diffusion process,

$$\begin{aligned} {\partial B(x,t) \over\partial t} =& {\partial\over\partial x} \biggl[ D(x,t) {\partial B \over\partial x} \biggr] + S(x,t) , \end{aligned}$$

(60)

$$\begin{aligned} {\partial D(x,t) \over\partial t} =& {Q(|\partial B/\partial x|) \over\tau} - {D(x,t) \over\tau} , \end{aligned}$$

(61)

where B(x,t) is a scalar field, D(x,t) is a spatially and temporally varying diffusion term, S(x,t) is a source term, Q(|∂B/∂x|) is a double-valued Heavyside function that has a low or high state and depends on the time history and an instability threshold. Isliker et al. (1998a) discretize the 3-D cellular automaton redistribution rule into a differential equation that represents a diffusion process,

$$ {\partial{\mathbf{B}}(\mathbf{x},t) \over\partial t} = \eta\nabla^2 {\mathbf{B}}(\mathbf{x},t) + \mathbf{S}(\mathbf{x},t) , $$

(62)

with a source term S(x,t) and a diffusion coefficient η=1/7(Δh ²/Δt). This differential equation contains a continuous function B(x,t) that behaves the same way as the nearest neighbors during one redistribution step, but a singularity occurs at the center location at Δh↦0, which requires a modification of the cellular automaton rule. Liu et al. (2002) and Charbonneau et al. (2001) transform the cellular automaton rule into a finite difference equation,

$$ {\partial B \over\partial t} = - {\partial^2 \over\partial x^2} \kappa \bigl(B_{xx}^2\bigr) {\partial^2 B \over\partial x^2} , $$

(63)

where $\kappa(B_{xx}^{2})$ is a diffusion coefficient that depends on the local curvature $B_{xx}^{2}$. This is a fourth-order nonlinear hyperdiffusion equation, which is interpreted as continuum limit of the cellular automaton rule, compatible with MHD in the regime of strong magnetic field and strong MHD turbulence (with high effective magnetic diffusity).

3.2.3 Analytical Macroscopic Solar SOC Models

Analytical descriptions of the macroscopic evolution of solar flares go back to Rosner and Vaiana (1978), who demonstrated that the two assumptions of (1) an exponentially growing energy storage, W(t)∝exp(τ/τ _G ), with growth time τ _G , and (2) a random-like interruption with an exponential distribution of saturation times, N(τ)∝exp(−τ/t _s ), leads directly to a powerlaw distribution of flare energies, $N(E) \propto E^{-\alpha_{E}}$, with a powerlaw index,

$$ \alpha_E = \biggl(1 + {\tau_G \over t_s}\biggr) . $$

(64)

However, observational data analysis did not confirm any correlation between waiting times (called energy storage times in Rosner and Vaiana 1978) and flare energies (Lu 1995b; Crosby 1996; Wheatland 2000b; Georgoulis et al. 2001; Moon et al. 2001). Also, flare time profiles show very rarely a simple exponential increase with an abrupt drop. Moreover, this model assumes an exponential distribution of waiting times, while observations exhibit powerlaw distributions with slopes of α _Δt ≈2–3 (Fig. 6).

Variations of this original model in terms of powerlaw-like growth (rather than exponential), or logistic growth (Aschwanden et al. 1998b), predict strong deviations from powerlaw distributions of flare energies and durations (Aschwanden 2011a, Chap. 3).

A better matching macroscopic description of SOC systems was developed in terms of a fractal-diffusive transport process (Aschwanden 2012a, 2012b), which can accommodate a fluctuating time profile of the energy dissipation rate or observed flux, a fractal spatial structure, diffusive transport (Fig. 18), and spatio-temporal scaling laws that predict powerlaw functions of all physical SOC variables. These scaling laws are in agreement with virtually all measurements made in solar flares. The time evolution of the avalanche radius r(t), the fractal dimension D _d (t) (in Euclidean space with dimension d), the average energy dissipation rate or flux f(t), the peak energy dissipation rate or peak flux p(t), and time-integrated energy or fluence e(t) are,

$$\begin{aligned} r(t) =& \kappa(t - t_0)^{\beta/2} , \end{aligned}$$

(65)

$$\begin{aligned} D_d(t) =& 1 + (d-1) \rho(t), \end{aligned}$$

(66)

$$\begin{aligned} f(t) =& f_0 t^{D_d(t) \beta/2}, \end{aligned}$$

(67)

$$\begin{aligned} p(t) =& p_0 t^{d \beta/2} , \end{aligned}$$

(68)

$$\begin{aligned} e(t) =& \int_{t_0}^t f(t) dt \approx f_0 t^{\langle D_d\rangle \beta/2} , \end{aligned}$$

(69)

where ρ(t) is a random function varying in the range of [0,1]. The fractal dimension D _d (t) and the flux time profile f(t) can fluctuate randomly, but the Euclidean radius r(t) and the total (time-integrated) energy e(t) are monotonically increasing quantities during an avalanche. The scaling laws between these parameters and the resulting size distributions are defined in terms of the fractal-diffusive transport and the scale-free probability conjecture (Sects. 2.6–2.11), and thus all powerlaw indices are predicted from first principles in this model. The same SOC model has been applied to a host of astrophysical phenomena (Aschwanden 2014).

Fig. 18

A cartoon that illustrates the concept of fractal-diffusive avalanche evolution. The Euclidean radius r(t) evolves like a diffusive random walk, such as r(t)∝t ^1/2 for classical diffusion, while the avalanche area is fractal (black substructures). The instantaneous fractal area $A_{f}(t) \propto r(t)^{D_{t}}$ consists of the number active nodes and is proportional to the energy dissipation rate dE(t)/dt or flux F(t) at a given time t (Aschwanden 2014)

3.2.4 Solar Magnetic Field Models and SOC

Since magnetic energy is believed to be the ultimate source of many phenomena in the solar corona, from sunspots, coronal loops, nanoflares, microflares, to large flares, eruptive filaments, and coronal mass ejections, magnetic processes clearly play a paramount role in solar SOC models. In cellular automaton models, the size of avalanches is measured by the number of all active nodes. In the original solar cellular automaton model, a magnetic field variable B _i,j is assigned to each node (x _i ,y _j ) in a 2D lattice grid, and an isotropic gradient ΔB, also called “field curvature”, is defined (Lu and Hamilton 1991; Charbonneau et al. 2001),

$$ \Delta B = B_{i,j} - {1 \over2d} \sum _{nn=1}^{2d} B_{nn} , \quad|\Delta B| > B_c , $$

(70)

where nn symbolizes the indices (i±1,j±1) of all next neighbors, while B _c is the critical threshold, and d the Euclidean space dimension. The next-neighbor redistribution rule is then (Charbonneau et al. 2001),

$$\begin{aligned} B_{i,j} \mapsto& B_{i,j} - {2d \over2d+1} B_c , \end{aligned}$$

(71)

$$\begin{aligned} B_{nn} \mapsto& B_{i,j} + {1 \over2d+1} B_c . \end{aligned}$$

(72)

Although the redistribution rule is locally conservative in the magnetic field strength (i.e., B _i,j +∑B _nn is constant), the magnetic energy is not conserved due to its quadratic dependence on the field strength (i.e., E _B =B ²/8π). For every redistribution step, the lattice energy decreases by an amount,

$$ \Delta E = {2d \over2d + 1} \biggl( 2 {|\Delta B| \over B_c} - 1 \biggr) B_c^2 , $$

(73)

which is slightly larger than the minimum “quantum” that can be released by the lattice,

$$ \Delta E_{min} = {2d \over2d + 1} B_c^2 . $$

(74)

Although the amount of dissipated energy per node is not exactly constant, because ΔE≳ΔE _min , it is in the spatial and temporal average sufficiently close to the constant ΔE _min so that we can assume an approximate proportionality between the time-integrated avalanche volume V and the time-integrated energy E, and thus can apply the flux and energy scaling for incoherent processes (Sects. 2.10–2.11).

While this concept of relating the magnetic energy to the avalanche volume provides a physical unit to a SOC avalanche, the immediate question arises whether such a SOC system is consistent with the physics of magnetohydrodynamics (MHD). Maxwell’s equations applied to a coronal plasma define an electric current density j,

$$ {\mathbf{j}} = {c \over4 \pi} (\nabla\times\mathbf{B}) , $$

(75)

yielding together with Ohm’s law (with electric conductivity σ) the so-called induction equation,

$$ {\partial{\mathbf{B}} \over\partial t} = \nabla\times(\mathbf{v} \times\mathbf{B}) + \eta \nabla^2 {\mathbf{B}} , $$

(76)

which contains a convective and a magnetic diffusion term (with magnetic diffusity η=c ²/4πσ), and fulfill the divergence-free condition for the magnetic field,

$$ \nabla\cdot{\mathbf{B}} = 0 . $$

(77)

Since the divergence-free condition is linear, it can easily be satisfied by a suitable choice of a redistribution rule, at least locally during each redistribution step, and globally within the threshold limit B<B _c .

The transformation of a cellular automaton redistribution rule into a discretized MHD differencing scheme started with Takalo et al. (1999a) for an application to a magnetotail field model, and with Vassiliadis et al. (1998) for an application to solar flares. The curl of the current j at the cell boundaries is defined in terms of the magnetic field vectors in each neighbor cell, as shown in Fig. 19 and defined by Ampère’s and Ohm’s law (Eqs. (75) and (76)). This way, a resistivity can be defined as a function of the current at the flux tube boundary, as expected from a current-driven instability. Anisotropic cellular automata correspond to a nonlinear resistivity, while isotropic ones can be associated with hyper-resistivity (Vassiliadis et al. 1998). In the continuum limit, however, singularities can arise (Isliker et al. 1998a), which largely disappear in 3D models (Isliker et al. 2000). For solar flare applications, a threshold of a critical current j _c was found to be physically more appropriate (Isliker et al. 2001), than a threshold of a critical magnetic field B _c as used in the original SOC models (Lu and Hamilton 1991).

Fig. 19

Cellular automaton model containing magnetic fluxtubes, each one characterized by a magnetic field B _z (x±1,y±1) and by four segments of currents $J(x,y\pm{1\over2})$ and $J(x\pm{1\over2},y)$ at the cell boundaries (Takalo et al. 1999a)

While the original SOC models have random drivers that incur little disturbances at random places, solar SOC models became more realistic by prescribing drivers that mimic the photospheric magneto-convection (at the lower boundary of the computation box) and drive MHD turbulence in 2D (Georgoulis et al. 1998), drivers that lead to collision of large-amplitude torsional Alfvén wave packets (Wheatland and Uchida 1999), drivers that conserve helicity (Chou 1999; 2001), by calculating linear force-free fields (Vlahos and Georgoulis 2004), by calculating an initial nonlinear force-free field from an observed magnetogram (Dimitropoulou et al. 2011), by using a sequence of observed vector magnetograms as an initial condition (Dimitropoulou et al. 2013), or by designing divergence-free (∇⋅B=0) redistribution rules (Fig. 16; Morales and Charbonneau 2008a, 2008b, 2009). Several of these SOC simulations were designed to mimic coronal heating according to the field line braiding scenario postulated by Parker (1988), where the SOC driver is represented by the photospheric convection-driven random motion of coronal loop footpoints, while SOC avalanches are triggered by magnetic reconnection above some critical threshold angle of magnetic field misalignments (Krasnoselskikh et al. 2002; Morales and Charbonneau 2008a, 2008b, 2009; Uritsky et al. 2013). In one recent study, the photospheric statistics of avalanches (measured from magnetograms) and coronal statistics (measured from extreme-ultraviolet images) was performed simultaneously and scaling relationships were found between these two types of events, i.e., $L_{cor} \propto L_{phot}^{1.39}$ and $T_{cor} \propto T_{phot}^{0.87}$, a correlation that implies a stochastic coupling between photospheric magnetic energy injection (into the corona) and coronal heating events (Uritsky et al. 2013). This stochasticity corroborates the findings of Dimitropoulou et al. (2009) on the lack of correlations between fractal properties of the photosphere and corona.

All these recent studies clearly demonstrate an advancement from the simple original cellular automaton algorithms to more sophisticated data-driven physical models. These physical models often are able to reproduce the standard size distributions and waiting time distributions that are predicted from the standard SOC model (Sects. 2.6–2.12). For instance, the dynamic data-driven integrated flare SOC model of Dimitropoulou et al. (2013) obtains the following powerlaw slopes: α _P =1.65±0.11 for peak energies, α _E =1.47±0.13 for energies, and α _T =2.15±0.15 for the duration of large flares, which agrees well with the standard model (α _P =1.67, α _E =1.5, α _T =2.0; Eq. (24)). It proves the robustness of the generic standard SOC model, regardless of the specific physics that is involved in a particular phenomenon. Vice versa, deviations from the predicted powerlaw size distributions of the standard model can reveal crucial hints which assumptions of the standard SOC model are violated, implying possible refinements to the model.

3.2.5 Magnetic Reconnection in Solar Flares and SOC

Once the interpretation of solar flares in terms of a SOC system was introduced (Lu and Hamilton 1991), physical scaling laws were envisioned that could explain the observed size distributions of time scales T, peak fluxes P, and (time-integrated) fluences or total energies E. A minimal magnetic reconnection model was formulated in terms of Alfvénic time scales ΔT, dissipated magnetic energy ΔE, and energy release rate ΔP=ΔE/ΔT (Lu et al. 1993; Nishizuka et al. 2009a, 2009b),

$$\begin{aligned} \Delta E =& (\Delta L)^3 \biggl\langle {B_{\perp}^2 \over8\pi} \biggr\rangle , \end{aligned}$$

(78)

$$\begin{aligned} \Delta T =& {\Delta L \over v_A} \zeta , \end{aligned}$$

(79)

$$\begin{aligned} \Delta P =& {\Delta E \over\Delta T} = (\Delta L)^2 \biggl\langle {B_{\perp}^2 \over8\pi} \biggr\rangle {v_A \over\zeta} , \end{aligned}$$

(80)

where v _A =B/(4πρ)^1/2 is the Alfvén velocity, ρ the plasma density, and ζ≈10¹,…,10² is a constant estimated from the reconnection scenario of Parker (1979). This equation system can be fitted to the observed correlations, i.e., E∝P ^1.82, E∝T ^1.77 and P∝T ^0.90 (Lu et al. 1993), using suitable scaling laws for the free variables B, ρ, and ζ. On the other side, the standard model (Eqs. (15)–(17)) predicts from first principles the relationships $E \propto P^{(D_{d}+2/\beta)/d} \approx P^{1.33}$, $E \propto T^{1+D_{d}\beta/2} \approx T^{2.00}$, and P∝T ^dβ/2∝T ^1.50 (with d=3, D _d =(1+d)/2, and β=1), which is not too far off from the measurements, given the large scatter in the correlations. Thus, an interpretation in terms of a magnetic reconnection model does not provide a unique fit to the observed size distributions or correlations of SOC parameters in solar flares, but it allows to test consistency between model and observations, and places physical units on the SOC parameters. Lu et al. (1993) predicted powerlaw behavior down to nanoflare events with energies of ΔE≈3×10²⁵ ergs, durations of ΔT≈0.3 s, and length scales of ΔL≈400 km.

An alternative SOC reconnection model applied to solar flares is the separator reconnection scenario (Longcope and Noonan 2000), where currents flowing along the network of magnetic field separators are sporadically dissipated. Scaling this system to solar length scales and inductances yields typical energies of E≈4×10²⁸ ergs, waiting times of Δt≈300 s, and a heat flux of F≈2×10⁶ ergs s⁻¹ cm⁻². The observed flare energy distribution N(E)∝E ^−3/2 requires a probability of P(L)∝L ⁻¹ for separator length scales L (Wheatland 2002; Wheatland and Craig 2003), which corresponds to a size distribution of N(L)dL∝L ⁻² dL. Generalizing the flare geometry to d=1,…,3 dimension depending on the reconnection topology (E∝L ^d), size distributions of 4/3≤α _E ≤2 were predicted (Craig 2001).

Solar flares produced by cascades of reconnecting magnetic loops were simulated in form of a SOC model by Hughes et al. (2003). This model produces a powerlaw distribution of flare energies with a slope of α _E =3.0±0.2. This prediction disagrees with most flare observations, which find α _E ≈1.5, but it corroborates anisotropic SOC models. Despite discrepancies, the model still gives us some insight into the topology of energy dissipation regions. The standard model predicts a probability distribution of N(L)∝L ⁻³ for length scales (Eq. (1)), and thus the model of Hughes et al. (2003) can be reconciled with the standard SOC model if the dissipated energy volume is proportional to the length scale, i.e., E∝L, which requires a 1D geometry of the dissipation region, such as separators of magnetic domains.

3.2.6 Particle Acceleration in Solar Flares and SOC

We can consider a hierarchy of SOC systems in our universe: our universe may be just one particular event in a multi-verse; galaxies are singular events in our universe; stars are singular events in a galactic system; planets are singular events in a solar system; solar flares are individual events in the solar corona; and accelerated particles are singular events of a solar flare hard X-ray burst. In the latter example we would consider the energy spectrum of accelerated particles as the energy distribution in a SOC system, while the acceleration process of each particle is an avalanche, driven by some electro-magnetic field in a magnetic reconnection region or shock structure. The threshold for particle acceleration is the run-away regime in a thermal plasma, which requires a velocity of a few times the thermal speed. Once the particle gets accelerated out of the thermal bulk distribution, either by a DC electric field, by wave-particle interactions, or by a quasi-parallel shock structure, it ends up with a final energy E≫E _th when it leaves the acceleration region, and the ensemble of all accelerated particles in a solar flare produce an energy spectrum that is often close to a powerlaw, $N(E) \propto E^{-\epsilon_{E}}$. What powerlaw slope does the standard SOC model predict? The scale-free probability conjecture, N(L)∝L ^−d (Eq. (1)), would still be applicable, since the probability to accelerate a particle in a subvolume with length scale L is reciprocal to the volume size. Also the fractal-diffusive transport process, L∝T ^β/2 (Eq. (9)), could still yield an appropriate model for any stochastic and diffusive (wave-particle or shock) acceleration process. However, the fractal dimension could vary from a straight trajectory with D _d ≳1 and β≈2 to a random path with D _d ≈(1+d)/2 and β≈1. Consequently, we predict powerlaw slopes for the energy spectrum in the range of ϵ _E =1+1/(γD ₃/2+1/β)≈1.5,…,1.67 (Eq. (36)), either for D ₃=1,…,2 or β=1,…,2. This is a relatively narrow range that should be testable. However, finite system-size effects are expected in relatively small magnetic reconnection regions, which will lead to a gradual cutoff at the upper end of the energy spectrum, with a steeper powerlaw slope if the energy spectrum is fitted with a double powerlaw function. Nevertheless, the standard SOC system predicts a lower limit of α _E ≥1.5 for all particle spectra.

Particle energy spectra in anomalous cosmic rays (Stone et al. 2008; Decker et al. 2010), super-Alfvénic ions in the solar wind (Fisk and Gloeckler 2006), and the hardest energetic electron spectra in solar flares (Holman 2003) exhibit all powerlaws of approximately N(E)∝E ^−1.5. A model of energetic particles accelerated during multi-island magnetic reconnection that reproduces this energy spectrum was derived by Drake et al. (2013). The omni-directional particle distribution f(v,t) was derived by including pitch-angle scattering, which yields a velocity dependence of v ⁻⁵ and corresponds to an energy flux of E ^−1.5 (Drake et al. 2013). Numerical simulations of electron acceleration by random DC electric fields constituting a SOC system were performed by Anastasiadis et al. (1997), yielding energy spectra with powerlaw slopes of α _E ≈1.58–1.64. Similar flat powerlaw spectra were simulated by Dauphin et al. (2007), although it was recognized that most observed X-ray spectra are steeper (probably due to finite system-size effects). Fermi acceleration in plasmoids interacting with fast shocks via fractal reconnection produces also similar energy spectra, which can be derived from the first-order Fermi process,

$$ N(E) \propto E^{-3/2} \exp{ \biggl( {{\sqrt{C} }\over {2 \pi\tau\sqrt{E}}} \biggr)} \approx E^{-3/2} , $$

(81)

where C is a constant of the scaling E(t)∝C/L ²=C/(L ₀−2ut)², u is the shock velocity, and τ is the escape time scale. The exponential cutoff in the energy spectrum (Eq. (81)) represents a deviation from an ideal powerlaw, but the superpositions of many such spectra produced in a fractal reconnection avalanche can naturally produce an ideal powerlaw spectrum (Nishizuka and Shibata 2013). Therefore, the observed powerlaw spectra can be produced by both, either by a first-order Fermi process, or by a fractal SOC model.

3.2.7 Hydrodynamic Flare Models and SOC

Measuring powerlaw slopes of different physical parameters in SOC systems provides a direct diagnostics or test of physical scaling laws. Hydrodynamic simulations or scaling laws were employed in a few studies in the context of SOC systems.

A shell model of MHD turbulence was used to demonstrate that chaotic dynamics with destabilization of the laminar phases and subsequent restabilization due to nonlinear dynamics can reproduce the observed waiting time distribution of N(Δt)∝(Δt)^−2.4, implying long correlation times, in contrast to classical SOC models that predict Poisson statistics of uncorrelated random events (Boffetta et al. 1999). A numerical simulation of a 1D MHD model of coronal loops was able to produce a similar waiting time distribution, N(Δt)∝(Δt)^−2.3, a result that was also used to underscore the existence of sympathetic flaring (Galtier 2001).

A frequently used hydrodynamic scaling law used in the study of the solar corona is the RTV law (Rosner et al. 1978), which can be derived from the energy balance between a constant heating rate and the conductive and radiative losses of a 1D coronal loop. This scaling law can be expressed by two equations,

$$\begin{aligned} T_e \propto&(p L)^{1/3} \propto n_e^{1/2} L^{1/2}, \end{aligned}$$

(82)

$$\begin{aligned} H \propto& T_e^{7/2} L^{-2} , \end{aligned}$$

(83)

where T _e is the maximum electron temperature at the loop apex, p=2n _e k _B T _e is the total (electron and ion) pressure, n _e is the electron density, L is the loop (half) length, and H is the constant heating rate. A consequence of the RTV scaling law is the scaling of the emission measure EM and thermal energy E _th for an ensemble of loops filling a volume V∝L ³,

$$\begin{aligned} EM \propto& n_e^2 V \propto n_e^2 L^3 , \end{aligned}$$

(84)

$$\begin{aligned} E_{th} =& 3 n_e k_B T_e V \propto T_e^3 L^2 . \end{aligned}$$

(85)

Conveniently, all these scaling laws can be expressed in terms of powerlaw functions, which makes it analytically straightforward to calculate the slopes of powerlaw distribution functions. Since all these scaling laws represent relationships between three physical parameters, two distribution functions need to be known to predict the distribution function of the third parameter. For instance, if we use the scale-free probability conjecture, N(L)∝L ⁻³ in 3D space (Eq. (1)), and a heating rate distribution,

$$ N(H) \propto H^{-\alpha_H} , $$

(86)

the distribution functions of all physical parameters (n _e ,T _e ,EM,E _th ) can be derived as a function of the variable α _H . In practice, there are additional corrections due to truncation effects, say a flux or emission measure threshold (EM>EM _thres ) due to the instrumental sensitivity limit in sampling of solar events. These truncation effects, however, can be either quantified by Monte-Carlo simulations or by analytical calculations (see Appendix A in Aschwanden and Shimizu 2013).

While the original RTV law was applied to a single coronal loop, supposedly to be in approximate energy balance between the heating rate (H) and the conductive loss rate (−E _cond ) and the radiative loss rate (−E _rad ),

$$ H - E_{cond} - E_{rad} = 0 , $$

(87)

the same scaling law can also be applied to the peak time t _peak of a flare, just at the turnover time between dominant heating and dominant cooling when energy balance occurs for a brief moment (Aschwanden and Shimizu 2013),

$$ \begin{aligned} H(t) - E_{cond}(t) - E_{rad}(t) &\ge0 \quad \mbox{for}\ t < t_{peak} \\ H(t) - E_{cond}(t) - E_{rad}(t) &= 0 \quad \mbox{for}\ t = t_{peak} \\ H(t) - E_{cond}(t) - E_{rad}(t) &\le0 \quad \mbox{for}\ t > t_{peak} \end{aligned} $$

(88)

Since the emission measure EM _p , peak temperature T _p , and length scale L _p can be directly measured with multi-wavelength imaging observations in solar flares, such as with AIA/SDO, the RTV law can then be tested and the resulting size distributions of the other physical parameters (n _p ,E _th ,H) can be predicted. An example is shown in Fig. 20, where the size distributions of the parameters L,T _p ,n _p ,H,EM _p ,E _th are shown, as log–log histograms of the observed and derived variables, and in form of scatterplots as a function of the length scale L to visualize the truncation effects caused by the flux threshold detection limit (EM≥EM _thresh ), and then compared with Monte-Carlo simulations of the size distributions (red curves in Fig. 20). A powerlaw index of α _H ≈1.8 is inferred for the unknown size distribution of heating rates H.

Fig. 20

Monte-Carlo simulations of size distributions (red curves) of flare parameters (diamonds) using the RTV relationships and a heating rate distribution $N(H) \propto H^{-\alpha_{H}}$ with a minimum value H ₀=0.4 erg cm⁻³ s⁻¹ and powerlaw slope α _H =1.8, an emission measure threshold of EM ₀≥10^48.5 cm⁻³. The size distributions derived from analytical calculations are overlaid with red curves (Aschwanden and Shimizu 2013)

The most interesting size distribution or scaling relationship concerns the heating rate H, which holds the secret of the coronal heating process and/or energy dissipation process of flares. From full-Sun simulations of the corona composed as an ensemble of myriads of individual 1D loops, a scaling law of the heating flux F _H ∝BL ⁻¹ was found (Schrijver et al. 2004), which corresponds to a volumetric heating rate of,

$$ H \propto{F_H \over L} \approx B L^{-2} . $$

(89)

A different scaling is obtained from a magnetic reconnection scenario in Petschek’s theory, by assuming that the loop apex temperature is balanced by conductive cooling, T _e ∝(2HL ²)^2/7 (Shibata and Yokoyama 1999, 2002),

$$ H \approx \biggl( {B^2 \over4 \pi} \biggr) {v_A \over L} . $$

(90)

A similar scaling law was derived for magnetic reconnection processes with the Sweet-Parker reconnection scenario (Sweet 1958; Parker 1957; Cassak et al. 2008). Obviously, statistics on the size distributions N(B) of the magnetic field are required in order to infer the heating rate distribution N(H). The flow chart in Fig. 21 summarizes how the observed distributions are related to the model assumptions and physical scaling laws for solar flare events or coronal heating events.

Fig. 21

Flow chart of input parameters (left), scaling laws (middle), and output distribution functions (right) of the fractal-diffusive SOC model applied to solar flares. The spatio-temporal parameters (L,A,V,τ) follow from universal probability statistics (top part of diagram), while the physical parameters and their scaling laws are specific to the hydrodynamics of solar flares (middle part of diagram), and the instrumental response functions as a function of temperature and wavelengths are specific to the observer (bottom part of diagram). The given powerlaw indices α _x are approximative values for dimensionality d=3 (Aschwanden and Shimizu 2013)

3.2.8 The Role of Nanoflares

It was pointed out early on that powerlaw distributions N(E)∝E ^−α of energies with a slope flatter than the critical value of α _E =2 imply that the energy integral diverges at the upper end, and thus the total energy of the distribution is dominated by the largest events (Hudson 1991),

$$ E_{tot} = \int_{E_{min}}^{E_{max}} E N(E) dE = \int_{E_{min}}^{E_{max}} (\alpha-1) E^{1-\alpha_E} dE = \biggl( {\alpha- 1 \over2-\alpha} \biggr) \bigl[ E_{max}^{2-\alpha} - E_{min}^{2-\alpha_e} \bigr] . $$

(91)

Therefore, in the opposite case, when the powerlaw distribution is steeper than the critical value, it will diverge at the lower end, and thus the total energy budget will be dominated by the smallest detected events, an argument that was used for dominant nanoflare heating in some cases with insufficient wavelength coverage of solar nanoflare statistics (e.g., Krucker and Benz 2000). The powerlaw slope α _E for energies depends sensitively on its definition (e.g., Benz and Krucker 2002), in particular on the assumptions of the flare volume scaling V(A) that has to be inferred from measured flare areas A in the case of thermal energies, E _th =3n _e k _B T _e V. Large flares (of M and X GOES class) were found to exhibit a powerlaw slope of α _Eth =1.66±0.13 for the thermal energies E _th (Fig. 20), which closely matches the powerlaw distributions of non-thermal energies determined from hard X-ray producing electrons, e.g., α _nth =1.53±0.02 for a much larger sample including smaller flares (Crosby et al. 1993). Thus, based on the statistics of large flares we do not see any evidence that would support nanoflare heating, at least not for flares with energies ≳10²⁹ erg. In contrast, recent flare area measurements based on RHESSI hard X-ray images yield a steeper distribution of flare areas, with α _A ≈2.7, and thus also a steeper distribution of total flare energies, with α _E ≈2.3 (Li et al. 2012). At this point it is not clear how the flare area statistics from high-resolution imaging in EUV compares with the coarse Fourier imaging in hard X-rays. We have also to be aware that synthesized flare energy statistics combined from all scales (Fig. 11) are composed of measurements with different event selection criteria, different detection methods, different energy definitions, and different activity levels of the solar cycle. What is needed in future studies is a homogeneous flare statistics from the largest to the smallest flare events, using the same method and identical time intervals (since the flaring rate varies orders of magnitude during the solar cycle) in order to obtain a self-consistent flare energy distribution on all scales.

3.3 Planets

Now we start our journey to review SOC interpretations in planetary atmospheres and solar system bodies, starting with the Earth’s magnetosphere (Sect. 3.3.1) and atmosphere (Sect. 3.3.2), and then continuing to lunar craters (Sect. 3.3.3), the asteroid belt (Sect. 3.3.4), Mars (Sect. 3.3.5), Saturn’s ring system (Sect. 3.3.6), Jovian and Neptunian Trojans (Sect. 3.3.7), Kuijper belt objects (Sect. 3.3.8), and extrasolar planets (Sect. 3.3.9).

3.3.1 The Earth’s Magnetosphere

In the Earth’s magnetosphere, a number of phenomena have been interpreted as features of a SOC system, such as geomagnetic substorms, current disruptions, magnetotail current disruptions and associated magnetic field fluctuations, bursty bulk flow events, and auroras seen in UV and optical wavelengths. Some of these are discussed briefly in the following, while a more detailed treatment is given in the review by Sharma et al. (2014). Magnetospheric SOC phenomena have also been reviewed previously (Aschwanden 2011a: Chaps. 1.6, 5.5, 7.2, 9.4, 10.5).

Most magnetospheric phenomena result from the interaction of the Earth’s (or some other planet’s) magnetic field with the ambient solar wind in the heliosphere, at the magnetopause, in the magneto-tail, and in the polar regions of the planet. The solar wind brings to Earth disturbances associated with solar flares, coronal mass ejections, shock waves and solar energetic particles, causing magnetospheric storms, substorms, and auroral activities. The solar wind is thus the driver of the processes in space weather. Substorms involve many processes, including magnetic reconnection, ballooning-mirror modes, current disruption, etc., which cause a fast unloading of the highly stressed geotail system (Papadopoulos et al. 1993; Baker et al. 1996, Horton and Doxas 1996). In addition, multi-scale intermittent turbulence of overlapping plasma resonances play an important role in substorms (Chang 1999a). Brief magnetospheric disturbances occur when the interplanetary magnetic field (IMF) flips southward, which triggers magnetic reconnection at the dayside magnetopause and transfers momentum and energy from the solar wind to the magnetosphere. Part of the transferred energy is stored in the magnetotail, where also magnetic reconnection and field relaxation events can occur during magnetospheric substorms. A magnetospheric substorm has three phases (Fig. 22): (1) the growth phase (when energy from the solar wind is transferred to the dayside magnetosphere), (2) the substorm expansion phase (when the energy stored in the magnetotail is released, the magnetosphere relaxes from the stretched tail, and the tail snaps into a more dipolar configuration and energizes particles in the plasma sheet), and (3) the recovery phase (during which the magnetosphere returns to its quiet state). The whole process causes changes in the auroral morphology (Fig. 22) and induces currents in the polar ionosphere, with the resultant heating leading to the auroral displays. The frequency of substorms is about 6 per day on average, but larger during geomagnetic storms.

Fig. 22

The three phases of a geomagnetic substorm are shown: the growth phase (top), the expansion phase (middle), and the recovery phase (bottom) (Baumjohann and Treuman 1996). The accompanying three auroral images were obtained with the IMAGE WIC instrument (credit: NASA)

How did the SOC concept came into play for magnetospheric processes? The bursty nature of magnetospheric phenomena, such as localized current disruptions in auroral blobs (Lui et al. 1988), bursty bulk flow events in the geotail (Angelopoulos et al. 1996, 1999), and the powerlaw magnetic field spectra in the magnetotail (Hoshino et al. 1994), have been interpreted in terms of an open, dissipative nonlinear system near a forced or self-organized critical state (Chang 1992, 1998a, 1998b, 1999a, 1999b; Klimas et al. 2000; Chang et al. 2003; Chapman and Watkins 2001; Consolini and Chang 2001; Consolini 2002). Probability or size distributions with a powerlaw shape (Table 11), the hallmark of SOC systems, have been measured from auroral blobs in UV (Lui et al. 2000; Uritsky et al. 2002, 2003, 2006) and optical light (Kozelov et al. 2004), from the auroral electron jet index (AE) (Takalo 1993; Consolini 1997, 2002), from magnetospheric substorm-related tail current disruptions (Consolini and Lui 1999), from geotail flow bursts (Angelopoulos et al. 1999), from ionospheric velocity fluctuations driven by the interplanetary magnetic field (Bristow 2008), and from electron bursts in the outer radiation belt (Crosby et al. 2005). A powerlaw slope of α _Δt ≈1.3 was also determined for waiting times in an AE index time series (Lepreti et al. 2004). Critical finite-size scaling and a fractal dimension of D ₂=1.54±0.02 was found for auroral blobs (Uritsky et al. 2006), which agrees with the mean-value estimate D ₂=(1+d)/2=1.5 (Eq. (8)) in the FD-SOC model. The powerlaw behavior, as observed in many magnetospheric phenomena (Table 11), provides the main basis for interpretation as SOC processes. The measurements listed in Table 11 were obtained from UVI onboard the POLAR spacecraft (Lui et al. 2000; Uritsky et al. 2002), from all-sky TV cameras at the Barentsburg Observatory (Kozelov et al. 2004), the GEOTAIL spacecraft (Angelopoulos et al. 1999), from the WIND spacecraft (Freeman et al. 2000b), with the SuperDARN radar network (Bristow 2008), and the STRV microsatellites (Crosby et al. 2005).

Table 11 Frequency distributions measured from magnetospheric phenomena. Values determined with non-standard methods are marked with parentheses. The data sets of Uritsky et al. (2002) refer to different observing periods, the data sets of Kozelov et al. (2004) to different luminosity threshold levels, and the data sets of Uritsky et al. (2008) to different latitude zones (HL=high latitude events, LLs=low-latitude small-scale events, and LLl=low-latitude large-scale events). The predictions (marked in boldface) are based on the FD-SOC model (Aschwanden 2012a)

The agreement between the statistics of large auroral events observed with POLAR/UVI (Uritsky et al. 2002) and small auroral events observed with a TV camera (Kozelov et al. 2004) is excellent (Fig. 23) and covers a combined (but not overlapping) range of 10 orders of magnitude in energy. However, we can see in Table 11 a glaring discrepancy between the measurements made by Lui et al. (2000) and by Uritsky et al. (2002), while the latter agree surprisingly well with the predictions of the standard fractal-diffusive SOC model (Aschwanden 2012a). The measurements by Lui et al. (2000) yield much flatter powerlaw slopes, close to unity. This discrepancy has been convincingly explained in terms of a different methodology and event definition: The statistics carried out by Lui et al. (2000) refers to equidistant time snapshots that count large avalanche events multiple times, while the analysis of Uritsky et al. (2002) determines the time-integrated avalanche areas and energies, consistent with standard definitions of SOC parameters (also used in the FD-SOC model: see Sect. 2.10 and Eqs. (14) and (20)). Another anomaly that was found is the latitude dependence of the size distribution of auroral events (see Uritsky et al. 2008 in Table 11), which indicates substantially different scaling regimes of bursty energy dissipation in the inner and outer portion of the geotail plasma sheet (Uritsky et al. 2008, 2009).

Fig. 23

Combined probability distributions of auroral blob parameters (top panel: event duration T; middle panel: maximum area A; bottom panel: time-integrated size S, approximately proportional to the or total energy E) measured with ground-based TV cameras (Kozelov et al. 2004) and with the UVI/POLAR spacecraft (Uritsky et al. 2002)

The SOC interpretation of magnetospheric phenomena has also stimulated cellular automaton simulations and alternative aspects of SOC modeling, such as finite system-size effects (Chapman et al. 1998, 1999; Chapman et al. 2001), powerlaw robustness under varying loading (Watkins et al. 1999), the discretization in terms of MHD equations (Takalo et al. 1999a, 1999b), renormalization group analysis (Tam et al. 2000; Chang et al. 2004), the scaling of the critical spreading exponents (Uritsky et al. 2001), phase transition-like behavior (Sitnov et al. 2000, 2001; Sharma et al. 2001), aspects of percolation and branching theory (Milovanov et al. 2001; Zelenyi and Milovanov 2004), chaotic turbulence models (Kovacs et al. 2001), forced SOC models (Consolini 2001; Chang et al. 2003), modeling of energetic particle spectra in magnetotail (Milovanov and Zelenyi 2002), MHD modeling of the plasma sheet dynamics near a SOC state (Klimas et al. 2004), aspects of complexity systems (Dendy et al. 2007), the framework of thermodynamics of rare events (Consolini and Kretzschmar 2007), kinetic theory of linear fractional stable motion (Watkins et al. 2009b), avalanching with an intermediate driving rate (Chapman and Watkins 2009; Chapman et al. 2009), and multi-fractal and fractional Lévy flight models (Zaslavsky et al. 2007, 2008; Rypdal and Rypdal 2010b).

The Earth’s magnetosphere is a large-scale natural system driven by the turbulent solar wind and exhibits non-equilibrium phenomena (Sharma and Kaw 2005), including SOC discussed here. In general the properties of such systems are characterized as a combination of global and multiscale features, and have been studied extensively using the techniques of nonlinear dynamics and complexity science (Sharma 1995; Klimas et al. 1996; Vassiliadis 2006). The first evidence of global coherence of the magnetosphere was obtained from time series data of AE index in the form of low-dimensional dynamics (Vassiliadis et al. 1990; Sharma et al. 1993). This result is consistent with the morphology of the magnetosphere derived from observations and theoretical understanding (Siscoe 1991), and simulations using global MHD models (Lyon 2000; Shao et al. 2003). The recognition of the low dimensional dynamics of the magnetosphere has stimulated a new direction in the studies of the solar wind-magnetosphere coupling and such systems in nature. Among these is the forecasting of the global conditions of space weather, viz. the AL and AE indices for substorms (Vassiliadis et al. 1995; Ukhorskiy et al. 2002, 2003, 2004; Chen and Sharma 2006) and the disturbance time index Dst for magnetic storms (Valdivia et al. 1996; Boynton et al. 2011). The forecasting of regional space weather requires data from the spatially distributed stations around the globe (Valdivia et al. 1999a, 1999b; Chen et al. 2008) and the predictability is largely determined by the availability of long time series data from the network of observing stations. The spatio-temporal dynamics of many systems are studied using such data, including the images obtained from satellite-borne imagers, by defining new variables computed from the data. For example, the fragmentation parameter (Rosa et al. 1998, 1999) represent the complexity of the spatial structure and has been used to model the dynamics of the solar atmosphere using the hard X-ray images from SOHO spacecraft. Further, the low-dimensionality of the magnetosphere has stimulated the development of models with a small number of equations (Vassiliadis et al. 1993, Horton and Doxas 1996).

The multiscale nature of the magnetosphere, expressed in many ways including the power law dependence of the scales, is a reflection of turbulence and plays an essential role in the accuracy of the forecasts. An early recognition of this was in the analogy of the dynamics of the magnetosphere to turbulence generated by a fluid flow past an obstacle (Rostoker 1984). The power law dependence of the AE index and of the solar wind provided quantitative measures of the power law indices and also the differences (Tsurutani et al. 1990). The scaling laws, which have been studies in detail using techniques such as the structure functions (Takalo et al. 1993), have many implications. The first is the characterization in terms of SOC, as discussed earlier in this section. The second is that the predictability of a multiscale system could not quantified readily in terms of the characteristic quantities such as the Lyapunov exponents (Vassiliadis et al. 1991) in a low-dimensional dynamical system. The presence of many scales as well as the non-equilibrium nature imply that predictions should be based on the statistical properties of the dynamical trajectories, e.g., using a mean-field approach (Ukhorskiy et al. 2004). Further, this approach is suitable for analyzing the predictability of extreme events (Sharma et al. 2012).

In summary, let us ask: What is the merit of the SOC concept in the context of magnetospheric phenomena? The standard fractal-diffusive SOC model (Sects. 2.6–2.11) predicts the probability distribution functions for each parameter as a function of the dimensionality (d), diffusive spreading exponent (β), fractal dimension (D _d ), and type of (coherent/incoherent) radiation process (γ). The waiting time distributions are predicted by the FD-SOC model to follow a powerlaw with a slope of α _Δt ≈2 during active and contiguously flaring episodes, while an exponential cutoff is predicted for the time intervals of quiescent periods. This dual regimes of the waiting time distribution predict both persistence and memory during the active periods, and stochasticity during the quiescent periods. All these predictions of the FD-SOC model provide useful constraints of the physical parameters and underlying scaling laws. Significant deviations from the size distributions predicted by the FD-SOC model could imply problems with the measurements or data analysis, such as indicated by the contradicting results of Lui et al. (2000) and Uritsky et al. (2002) in the case of auroral size distributions.

Let us emphasize again that the generic FD-SOC model is considered to have universal validity and explains the statistics and scaling between SOC parameters, but does not depend on the detailed physical mechanism that governs the instabilities and energy dissipation in a particular SOC process. The physical process may be well described by a number of established models, such as turbulence theory, kinetic theory, wave-particle interactions, and other branches of plasma physics. There was also a debate whether magnetospheric substorms are SOC or forced-SOC (FSOC) (e.g., Chang et al. 2003), an issue that largely disappears in our generalized FD-SOC concept, where a slow driver is required to bring the SOC system continuously near to the instability limit, but is does not matter whether the driver is internally, externally, or is globally organized.

3.3.2 Terrestrial Gamma-Ray Flashes

Terrestrial gamma-ray flashes (TGF) are gamma-ray bursts of terrestrial origin that have been discovered with the Burst and Transient Experiment (BATSE) onboard the Compton Gamma Ray Observatory (CGRO) and have been studied with RHESSI, Fermi, and AGILE since. These TGF bursts are produced by high-energy photons of energy >100 keV and last up to a few milliseconds. They have been associated with strong thunderstorms mostly concentrated in the Earth’s equatorial and tropical regions, at a typical height of 15–20 km (Fishman et al. 1994; Dwyer and Smith 2005; Smith et al. 2005). The physical interpretation is that the TGF bursts are produced by bremsstrahlung of high-energetic electrons that were accelerated in large electric potential drops within thunderstorms. However the gamma-rays produced in thunderstorms (at 5 km) can not readily propagate to higher altitudes due to atmospheric absorption. A mechanism for the generation of gamma rays that can reach the satellite-borne instruments is through the excitation of whistler waves by the relativistic electrons generated in the thunderstorms (Kaw et al. 2001; Milikh et al. 2005). The whistler waves form a channel by nonlinear self-focusing and the relativistic electrons propagate in this channel to higher altitudes (30 km). The gamma-ray generated at this altitude can escape the atmosphere and thus account for the BATSE/CGRO results.

A size distribution of the gamma-ray emission from TGF events needs to be corrected for the distance from the TGF-producing thunderstorm to the detecting spacecraft (in Earth orbit). In a combined analysis of TGF data from the RHESSI and Fermi satellites, corrected for their different orbits, different detection rates, and relative sensitivies, a true fluence distribution was derived, which was found to have a powerlaw shape of α _E =2.3±0.2 if a sharp cutoff was assumed, or a slope of α _E ≤1.3–1.7 when a more realistic roll-over of the RHESSI lower detection threshold is assumed (Ostgaard et al. 2012).

We can consider a part of the Earth’s atmosphere that contains a thunderstorm as a SOC system of finite size, where the electrostatic charging process represents the driver, the critical condition for electric discharging is given by an electric conductivity threshold, and the spontaneously triggered gamma-ray flashes or lightenings represent the avalanches. The PDF is then given by the scale-free probability conjecture (Eq. (1)), which together with the fractal-diffusive transport predicts an energy or fluence distribution with a powerlaw slope of α _E =1.5 in 3D space, which matches the observed and corrected fluence distribution with a slope of α _E ≈1.3–1.7. The agreement with the standard FD-SOC model is consistent with an incoherent process for gamma-ray production, where the gamma-ray flux is proportional to the emitting volume of a TGF.

3.3.3 Lunar Craters and Meteorites

An amazingly straight powerlaw size distribution has been found for the sizes of lunar craters (Fig. 25), with a cumulative powerlaw slope of $\alpha_{L}^{cum}=2.0$ over a size range of L=0.65–69,000 m, which covers 5 orders of magnitude (Cross 1966), derived from crater statistics measured in pictures of the lunar probes Ranger 7, 8, 9 combined with a lunar map of Wilkins (1946). Since a cumulative size distribution is flatter than a differential size distribution (by a value of one), this corresponds to a powerlaw slope of $\alpha_{L} = \alpha_{L}^{cum} + 1 = 3.0$. A similar powerlaw index of α _L =2.75 was found for the size distribution of meteorites and space debris from man-made rockets and satellites in the range of L=10 μm–10 cm (Fig. 3.11 in Sornette 2004).

Given the ubiquitous powerlaw shape of these size distributions, it is not far-fetched to consider the possibility of an interpretation in terms of a SOC model. Since lunar craters are believed to be produced by meteorite impacts, the directly observed meteorites and the lunar impact craters have the same origin in the solar system, although they cover different length scale ranges. We find that these observed powerlaw slopes of α _L ≈2.75–3.0 agree remarkably well with the scale-free probability conjecture, which predicts in 3D space a universal scaling exponent of α _L =3 (Eq. (1)). The reservoir of meteorites is the slow driver and small bodies that orbit in the solar system and provides projectiles for lunar or planetary impacts. The dissipated energy is essengially the kinetic energy of the projectiles, given by the relative velocity of the projectile (v _proj ) and the target (v _target ),

$$ E_{kin} = {1 \over2} m_{proj} (v_{proj} - v_{target} )^2 \ge {1 \over2} m_{proj} v_{inel}^2 , $$

(92)

which has to exceed the critical threshold v _inel that is given by the limit between elastic and inelastic collisions. If the projectile hits the target below this threshold, it will just bounce back by conservation of momentum, without producing an impact crater. If it hits the target with a larger velocity, the impact will produce a fractal-diffusive pattern of cracks on the projectile and target, similar to the rupture area during the energy release of an earthquake. In this analogy, lunar impact craters have much in common with earthquake “damage areas”, which is considered as a SOC process.

The size distribution of meteorites and planetesimals may also be generated by a SOC process in the first place. The slow driver that provides the trickling of sand grains is the gravity-driven formation process of the solar system itself, which clumps the local molecular cloud into meteorites and planets. The aspect of self-organized criticality, which is a balance between the gravity and the frictional force that controls the critical angle of repose in Bak’s sandpile, can be understood as a critical point between the condensation rate of planetesimals or meteorites (by self-gravity) and the diffusion rate (driven by thermal pressure and external gravitational disturbances). This critical threshold given by the balance of the condensation rate and the diffusion rate has to be exceeded in order to initiate the gravitational collapse that forms a solar system body. The gravitational collapse is the underlying instability in a physical SOC concept (Fig. 1, right frame).

Hence, from such a generalized point of view, we might consider the meteorite formation as a SOC pr ocess and the resulting lunar cratering as the imprint of this process. The main benefit of the FD-SOC framework is the direct prediction of the scale-free size distribution of crater sizes, i.e., N(L)∝L ⁻³ (Eq. (1)), which can also be used as a prediction for any other targets in the solar system, such as cratering on Earth, Mars, or Mercury. This allows us, for instance, to predict the collisional probability of an asteroid hitting our Earth, although we have to take into account the variability of the impact rate, which varied drastically during the lifetime of our solar system. Both the Moon and the Earth were subject of intense bombardment between 4.0 and 3.7 billion years ago, which was the final stage of the sweep-up of debris left over from the formation of the solar system (Bottke et al. 2012). The impact rate at that time was thousands of times higher than it is today.

3.3.4 The Asteroid Belt

The asteroid belt is a large accumulation of irregular small solar system bodies orbiting the Sun between the orbits of Mars and Jupiter. The largest of these small bodies is Ceres, with a diameter of 1020 km, followed by Pallas (538 km), Vesta (549 km), Juno (248 km), and extends down to the size of dust particles. While most planetesimals from the primordial solar nebula formed larger planets under the influence of self-gravity, the gravitational perturbations from the giant planets Jupiter and Saturn prevented a stable conglomeration of planetesimals in the zone between Mars and Jupiter. This fragmented soup of primordial planetesimals makes up the asteroid belt. The larger asteroids (≥120 km) are believed to be primordial, while the smaller ones are likely to be a byproduct of fragmentation events (Bottke et al. 2005).

Statistics of the sizes of asteroids has been carried out in the Palomar Leiden Survey (Van Houten et al. 1970), in the Spacewatch Surveys (Jedicke and Metcalfe 1998), in a Sloan Sky Survey (Ivezic et al. 2001), and in the Subaru Main-Belt Asteroid Survey (Yoshida et al. 2003; Yoshida and Nakamura 2007). Most of these statistics yield a powerlaw-like function for the cumulative size distribution (Fig. 25). From these values $\alpha_{L}^{cum}$ we can estimate the powerlaw slopes of the differential size distributions $\alpha_{L}=\alpha_{L}^{cum}+1$, which yield α _L =2.8 (Jedicke and Metcalfe 1998; Jedicke et al. 2002), a double powerlaw of α _L =2.3–4.0 (Ivezic et al. 2001), and α _L =2.3 (Yoshida et al. 2003; Yoshida and Nakamura 2007), see compilation in Table 12. Observational selection effects in asteroid surveys, of course, affect the reported powerlaw slopes, as discussed in Jedicke et al. (2002).

Table 12 Frequency distributions measured from planetary phenomena

If the small bodies in the asteroid belt are formed by a SOC process, the scale-free probability conjecture predicts a size distribution of N(L)∝L ⁻³, which is indeed close to what is observed (Fig. 25). However, there are slight deviations from a single powerlaw distribution for small and large bodies, which indicate some additional effects. Nevertheless, an almost scale-free behavior is observed for a range of L≈0.4–50 km, which makes it appropriate to consider the formation process in terms of a SOC system. As we discussed for the formation of meteorites above (Sect. 3.3.3), the aspect of self-organized criticality can be understood as a critical point between the condensation rate of planetesimals or meteorites by self-gravity, and the diffusion rate driven by external gravitational disturbances, mostly from the giant planets Jupiter and Saturn. If this critical threshold of the ratio of the condensation rate to the diffusion rate exceeds the value of unity, the self-gravity force takes over and forms a small solar system body, which represents an avalanche process with a well-defined instability threshold.

3.3.5 Mars

It has also been suggested to apply SOC dynamics to Martian fluvial systems (Rosenshein 2003). The motivation was that complexity theory provides powerful methods to analyze, interpret, and model terrestrial fluvial systems, including the fractal structure of meandering, sediment dynamics, bedrock incision, and braiding.

Another application of SOC systems to Mars is the statistics of dust storms, especially the interannual variability of Mars global dust storms (Pankine and Ingersoll 2004a, 2004b). Previously it was thought that the threshold for wind speed for starting saltation and lifting dust from the Martian surface was a finely tuned process. In the study of Pankine and Ingersoll (2004a, 2004b), however, it was shown that the fine-tuning of this parameter could be the result of a negative feeback mechanism that lowers the threshold of the wind speed. In this way, the Martian atmosphere/dust system could organize itself as a SOC system, and no fine-tuning of a critical threshold is required.

3.3.6 Saturn’s Ring System

Saturn and Jupiter are the most massive planets in our solar system with a gravity that is sufficiently strong to keep numerous moons, rings, and ringlets in their strong gravitational field. The Saturn ring extends from 7,000 km to 80,000 km above Saturn’s equator, consisting of particles ranging from 1 cm to 10 m, with a total mass of 3×10¹⁹ kg, which is comparable with the mass of its moon Mimas. Theories about the origin of Saturn’s ring range from nebular material left over from the formation of Saturn itself, collisional fragmentation (Greenberg et al. 1977), to the tidal disruption of a former moon.

When Voyager 1 passed the orbit of Saturn, it carried out radio occultation observations, which were analyzed with a scattering model and yielded the size distribution of ring particles in the range of L=0.01–10 m, being a powerlaw distribution of N(L)∝L ⁻³ (Fig. 25). The results of 8 size distributions obtained from 8 different locations in Ring A, C, and the Cassini division are shown in Fig. 24, which all are found to exhibit powerlaw indices in the range of α _L =2.74–3.11 (Zebker et al. 1985). Related to this is a wavelet transform analysis of the Encke gap ringlets in Saturn’s ring system (Bendjoya et al. 1993).

Fig. 24

Measurements of the particle size distribution functions for 8 Saturn ring regions with Voyager I radio occultation measurements (Ring C: C1.35, C1.51; Cassini division: CD2.01; Ring A: A2.12, A2.10, A2.14, A2.19, A2.24). The slopes of the fitted powerlaw functions in these 8 regions are: α _L =3.11, 3.05, 2.79, 2.74, 2.70, 2.75, 2.93, 3.03. The range of particle sizes is L=0.01–10 m (Zebker et al. 1985)

The coincidence of predicted and observed powerlaw distributions for meteorites, lunar craters, asteroids, and Saturn ring particles may have all the same explanation, namely SOC systems, although operating in different locations in our solar system, and in different ranges of length scales (Fig. 25). The critical threshold in all these systems is apparently given by the balance between the local self-gravity force and external gravity disturbances. All the gaps between the Saturn rings have been explained by mechanical resonances of Saturn’s moons, which orbit outside the ring and amplify gravitational disturbances whenever two moons have an integer ratio of their orbital periods. Thus, we have all parts of a physical SOC system: the driver, the instability, and the avalanches. Saturn’s moons are the driver of the system, because they provide random/periodic disturbances that lead to chaotic orbits of the ring particles. The instability is given by amplification of resonant orbits that leads to avalanches of particles, which clump in zones of non-resonant orbits. The appeal of SOC models is the simple way to predict the final size distribution of ringlets that result in the end, which cannot easily be predicted by celestial mechanics or chaos theory.

Fig. 25

Cumulative size distribution of Saturn ring particles (Zebker et al. 1985), near-Earth objects (McFadden and Binzel 2007), Jovian Trojans (Jewitt and Trujillo 2000), asteroids (Jedicke et al. 2002), Neptunian Trojans (Sheppard and Trujillo 2010), lunar craters (Cross 1966), Kuiper Belt objects (Fraser and Kavelaars 2008; Fuentes and Holman 2008), and Earth-sized extrasolar planets (Catanzarite and Shao 2011). The grey diagonal lines indicates the prediction of the FD-SOC model, with a powerlaw slope of $\alpha_{L}^{cum} = 2$ for the cumulative size distribution, corresponding to a powerlaw slope of $\alpha_{L} =\alpha_{L}^{cum}+1=3$ for the differential occurrence frequency distribution. A zone of paucity is indicated at a size range of L=30–45 km identified from Neptunian Trojans (Sheppard and Trujillo 2010)

3.3.7 Jovian and Neptunian Trojans

The Jovian Trojans are two swarms of asteroids, which lead or trail Jupiter by ±60^∘ on its orbit, known as the Lagrangian L4 and L5 point. The Jovian Trojans contain some 250 members. Their origin has been interpreted in terms of trapping of asteroidal fragments. A statistical analysis yielded a differential size distribution of N(L)∝L ^−3.0±0.3 in the size range of L=2–30 km, and N(L)∝L ^−5.5±0.9 in the size range of L=50–84 km (Jewitt and Trujillo 2000).

Similarly, Trojans have been detected in the L4 and L5 regions of the planet Neptune, with a size distribution that approaches a powerlaw slope of α _L =5±1 at the upper end (Sheppard and Trujillo 2010), while a flatter slope is found at the lower end. The scarcity of intermediate- and smaller-sized Neptune Trojans (≤45 km), which is also found for other objects in the Kuiper Belt, Jovian Trojans, and main belt asteroids, was interpreted in terms of a primordial origin, rather than a collisional or fragmentational origin, for which a size distribution of N(L)∝L ⁻³ is expected in the SOC model. However, the smaller bodies of the Neptunian Trojans in the range of L=2–30 km could still be consistent with a SOC origin, if they have the same distribution as Jovian Trojans (with N(L)∝L ^−3.0±0.3; Jewitt and Trujillo 2000). Their size range and distribution is close to that of asteroids (Fig. 25).

3.3.8 Kuijper Belt Objects

The Kuijper belt is a region of our solar system beyond the orbit of Neptune (at 30 AU) out to ≈50 AU, consisting of many small bodies. A size distribution of N(L)∝L ^−4.3 was found for objects with L≳100 km (Fraser et al. 2008; Fraser and Kavelaars 2008; Fuentes and Holman 2008). A comparison of the cumulative size distributions of Kuiper Belt objects, Neptunian Trojans, Jovian Trojans, and asteroids is shown in Fig. 25. Obviously, there is a paucity of objects in the zone of L≈30–45 km that shows up in the Neptunian Trojans and in the Kuiper belt objects (Fig. 25). The data seem to be consistent with the predicted powerlaw slope of α _L ≈3 only for small length scales of L≈1–30 km.

3.3.9 Extrasolar Planets

The oligarchic growth of protoplanets has been brought into the context of a self-organized protoplanet-planetesimal system (Kokubo and Ida 1998). The growth and orbital evolution of protoplanets embedded in a swarm of planetesimals has been simulated with a 3D N-body code, which shows the relative distribution of large planets that grow oligarchically, while most of the planetesimals remain small (Kokubo and Ida 1998).

Using the Kepler space telescope for search of Sun-like stars and (extrasolar) planets, a sample of over 150,000 stars was measured during the first 4 months of the mission. The Kepler science team determined sizes, surface temperatures, orbit sizes, and periods for over a thousand new planet candidates. From a size distribution of 1176 Earth-sized planet candidates within a range of L=2,…,20 Earth radii, a powerlaw distribution was found in the range of L≈2–10 Earth radii (Fig. 25), with a powerlaw slope of $\alpha_{L} = \alpha_{L}^{cum} + 1 = 1.48 + 1 = 2.48$, while the relatively narrow distribution falls of steeply between L≈10–20 Earth radii (Catanzarite and Shao 2011).

This sample from 1176 different stars can be considered as a galactic SOC system, in which case a size distribution of N(L)≈L ⁻³ is predicted by the FD-SOC model, which is close to the observed value of N(L)≈L ^−2.5 for a subset of Earth-like planets. The accretion of an Earth-like planet represents then an avalanche event, triggered by a gravitational instability in each stellar system.

3.4 Stars and Galaxies

We can obtain information on spatial scales and spatio-temporal scaling laws from SOC phenomena in our solar system (i.e., from the Sun, the planets, the magnetosphere), while such information from the rest of the universe is concealed by distance and cosmological time scales. Nevertheless, a number of stellar phenomena have been attributed to SOC phenomena. The observables are mostly time durations T, peak fluxes P, and fluences E of electromagnetic emission in some wavelength range, measured with some automated event detection algorithm from time series of a stellar object. We will compile such observations from stellar flares, pulsars, soft gamma-ray repeaters, blazars, and black-hole objects in the following, and compare them with the predictions of the FD-SOC model.

3.4.1 Stellar Flares

Time series with rapidly fluctuating emission in soft X-rays, EUV, and visible light from individual stars have been gathered with EXOSAT (Collura et al. 1988; Pallavicini et al. 1990), the Hubble Space Telescope (HST) (Robinson et al. 1999), the Extreme Ultraviolet Explorer (EUVE) (Osten and Brown 1999; Audard et al. 1999, 2000; Kashyap et al. 2002; Güdel et al. 2003; Arzner et al. 2007), the X-ray Multi-Mirror Mission (XMM) or Newton (Stelzer et al. 2007), and most recently with the surveys of the Kepler mission (Walkowicz et al. 2011; Maehara et al. 2012; Shibayama et al. 2013). Impulsive bursts detected in the time series in excess of the noise level have been interpreted as stellar flares, because they show similar temporal and wavelength characteristics as solar flares, except that they exceed solar flares in their luminosity by several orders of magnitude (Aschwanden et al. 2008c). Therefore, they should be considered as “giant flares” by solar standards. These stellar flares have been observed mostly in solar-like G-type stars (Notsu et al. 2013; Maehara et al. 2012; Shibayama et al. 2013), and in cool dwarf (dMe) stars (Robinson et al. 1999; Audard et al. 2000; Kashyap et al. 2002; Güdel et al. 2003; Arzner et al. 2007; Stelzer et al. 2007; Walkowicz et al. 2011; Maehara et al. 2012). From soft X-ray and EUV spectroscopy, flare temperatures of T _e ≈10–100 MK have been determined in some of the stellar flares, exceeding solar flare temperatures (T _e ≈5–35 MK). Consequently, the same physical interpretation in terms of magnetic reconnection with subsequent heating of chromospheric plasma has been proposed for stellar flares, in analogy to their solar analogs, although their total emission measure is a few orders of magnitude larger than for solar flares (Aschwanden et al. 2008c).

Let us have a look at the obtained size distributions of flare durations T, peak fluxes P, and fluences E that have been sampled from flares on individual stars, which are compiled in Table 13. Most powerlaw slopes of fluences are found in the range of α _E ≈1.9–2.3, which is significantly higher than measured in solar flares, where we found α _E ≈1.4–1.9 in soft X-rays (Table 3) and α _E ≈1.4–2.3 in EUV (Table 4), while the FD-SOC model predicts a value of α _E =1.5, which is matched indeed by solar flare observations in hard X-rays, i.e., α _E ≈1.4–1.7. However, several observations found powerlaw slopes of α _E ≈1.5–1.7 (Collura et al. 1988; Pallavicini et al. 1990; Osten and Brown 1999) that are consistent with the predictions of the FD-SOC model (α _E ≈1.5). Almost all size distributions of stellar flares have been characterized as powerlaw functions. The only exception (with an exponential size distribution) has been reported from optical flares of low-mass young stellar objects in the Orion nebula (Akopian 2012a) and from the region of ρ Ophiuchi (Akopian 2012b).

Table 13 Frequency distributions measured from stellar flares. The predictions (marked in boldface) are based on the FD-SOC model (Aschwanden 2012a)

This raises the question why most of the stellar (and a few solar) flare samples appear to have a different (steeper) size distribution than expected? Part of the explanation is probably the difference in luminosity, which puts the stellar flares at the upper end of the size distribution of solar flares, where size distributions tend to fall off steeper due to finite observing time and finite system-size effects. Moreover, cumulative size distributions, N ^cum(>x), as they generally are obtained in small samples of stellar flares (from inverse rank-order plots), show an exponential-like fall-off towards the largest event. This is a mathematical consequence of the integration of a powerlaw function that extends over a finite range [x ₁,x ₂], i.e., the differential frequency distribution,

$$ N(x) \propto(\alpha- 1) x^{-\alpha} , \quad x_1 \le x \le x_2 , $$

(93)

which yields the cumulative frequency distribution,

$$ N^{cum}(>x) = n {{\int_{x}^{x_2}} N(x') dx' \over {\int_{x_1}^{x_2} N(x') dx'}} = n {(x^{1-\alpha} - x_2^{1-\alpha}) \over (x_1^{1-\alpha} - x_2^{1-\alpha})}. $$

(94)

The powerlaw slope α ^cum of a cumulative size distribution needs to be fitted with this expression (Eq. (94)), in order to obtain the exact value of the powerlaw slope α=α ^cum+1 of the differential size distribution. Applying this method yields somewhat smaller slopes for stellar flare size distributions, in the order of α _E ≈1.8–2.1 (Table 7.7 in Aschwanden 2011a), but does not completely explain the difference between solar and stellar flares. The average of flare star observations with EUVE yields α _E =2.2±0.3, while the optical observations with Kepler exhibit a similar value (α _E =2.0±0.1), which are both steeper than predicted by the FD-SOC model.

Another explanation for the steeper powerlaw slopes of stellar flare distributions is the nonlinear scaling between the observed bolometric energy E _b and the soft X-ray peak flux P. From Kretzschmar (2011, Table 1 therein) we derive a scaling law between the bolometric fluence (total solar irradiance), which is equivalent to the bolometric energy E _b , and the soft X-ray GOES 1–8 Å peak flux P _x (Fig. 26, top),

$$ E_b \propto P_x^{0.78\pm0.13} . $$

(95)

Using this scaling law and the observed size distribution of bolometric energies measured with Kepler (Shibayama et al. 2013), i.e., $N(E_{b}) \propto E_{b}^{2.04\pm0.13}$, we can derive the distribution of equivalent GOES peak fluxes of stellar flares,

$$ N(P_x) dP_x \propto N\bigl(E_b[P_x] \bigr) {dE_b \over dP_x} dP_x \propto P_x^{-1.81\pm0.12} dP_x , $$

(96)

which is indeed more consistent with the size distribution of observed solar GOES peak fluxes, α _P =1.88±0.09 (Fig. 26 bottom and Table 3) and with the predictions of the FD-SOC model (α _P =1.67). The scaling law (Eq. (95)) and the size distributions of the bolometric flare energies and corresponding soft X-ray GOES peak fluxes obtained from 1538 stellar flares observed with Kepler (Shibayama et al. 2013) are shown in Fig. 26.

Fig. 26

Top: The scaling law of the total solar irradiance (TSI) and the GOES 1–8 Å flux based on a linear regression fit (solid line) to data from Kretzschmar (2011) is shown, i.e., $E_{b} \propto P_{x}^{0.78}$. A linear relationship is indicated with a dotted line. Middle: The bolometric flare energy of 1538 stellar flares observed with Kepler is histogrammed, yielding a size distribution with a powerlaw slope of α _E =2.04±0.13. Bottom: The size distribution of GOES fluxes inferred from the scaling law of Kretzschmar (2011) yields a powerlaw slope of α _P =1.88±0.09 (Aschwanden 2014)

Since solar flares show the trend of a steeper powerlaw slope α _E in the fluences measured in soft X-rays and EUV, compared to hard X-rays, we suspect also that the prolonged thermal emission in soft X-rays and EUV, due to plasma cooling, boosts the time-integrated fluence so that the total dissipated energy is overestimated, unlike the fluences in hard X-rays, where thermal emission is completely negligible at electron energies E≥25 keV. Unfortunately, current hard X-ray detectors are not sensitive enough to detect hard X-ray emission from stellar flares.

Thus, we conclude that hard X-rays provide the most accurate measurements of dissipated energies during flares, which are also consistent with the predictions of the FD-SOC model, while soft X-rays, EUV emission, and white-light (bolometric) emission exhibits a nonlinear scaling with the emitted energy. The fluence measured in soft X-rays and EUV emission are boosted due to plasma heating and cooling processes. The reconciliation of measurement methods of the total dissipated energy in hard X-rays, soft X-rays, and EUV is still an open problem, which could be resolved with multi-wavelength statistics of solar data, and by modeling the scaling laws between dissipated energies and the fluxes in different wavelengths. Apparently the bias in the soft X-ray and EUV wavelengths affects the energy distributions measured from (giant) stellar flares to a larger degree than those of solar flares.

3.4.2 Star Formation

The formation of stars is initiated by gravitational collapses of molecular clouds. Such a gravitational collapse can be triggered by collisions of two molecular clouds, by the explosion of a nearby supernova, which ejects shocked matter, or even by galactic collisions, which cause compression of matter and tidal forces. If there is a critical mass reached, which is quantified by the Jeans mass criterion, which mostly depends on the initial size of the unstable galactic fragment, the collapsing molecular cloud will build up a dense core by self-gravity, which forms a star with nuclear burning. Smaller sizes develop into non-radiating brown dwarfs.

Considering star formation as a SOC process, the situation is similar to the formation of planetesimals and planets, where a critical condition is given by the balance between the forces of self-gravity and diffusion. A collapsing molecular cloud gains kinetic energy from the gravitational potential according to the conservation of angular momentum. However, tidal forces, external gravitational disturbances, and thermal pressure represent forces that contribute to the local diffusion of the molecular cloud. Therefore there is a threshold for the instability of a gravitational collapse, which is self-organizing by the given balance between the opposing forces of contraction and diffusion. This process could possibly also be modeled in terms of a percolation model.

SOC avalanches have a fractal structure, and hence fractals are expected for star-forming regions also. Indeed, fractal and self-fimilar patterns have been observed in the Milky Way from dense cores to giant molecular clouds in a range of 0.1<L<100 pc (Elmegreen and Scale 2004; Bergin and Tafalla 2007), as well as in star-forming regions in the Andromeda nebula M33 (Sanchez et al. 2010). The fractal dimension in the interstellar medium has a value of D ₃≈2.3±0.3 (Elmegreen and Falgarone 1996), in bright young stars and molecular gas is D ₂≈1.9, and in fainter stars and HII regions is D ₃≈2.2–2.5. The predictions of the FD-SOC model is D ₃≈2.0. The fractal structure has generally been attributed to interstellar turbulence, which however does not exclude a generalized description in terms of a SOC process. It has been argued that the interstellar mass function (IMF) of starbursts is independent of local processes governing star formation and thus can be considered as a universal self-organized criticality process (Melnick and Selman 2000).

3.4.3 Pulsars

A pulsar is a highly magnetized, rapidly-rotating neutron star that emits a beam of electromagnetic radiation. Since the beamed emission is aligned with the magnetic axis, we observe rotationally modulated pulses whenever the beam axis points to the Earth (line-of-sight direction) during each period of its rapid rotation. Besides these regular periodic pulses on time scales of milliseconds, which are measured with high accuracy, there occur sporadic glitches in pulse amplitudes and frequency shifts, probably caused by sporadic unpinning of vortices that transfer momentum to the crust (Warszawski and Melatos 2008). Conservation of angular momentum produces then a tiny increase of the angular rotation rate, called “positive spin-ups” of the neutron star.

Statistics of these sporadic glitches (Table 14) exhibit powerlaw distributions of the pulsar peak fluxes or fluences, such as observed from the Crab pulsar and other pulsars in radio wavelengths (Argyle and Gower 1972; Lundgren et al. 1995; Cognard et al. 1996; Cairns (2004); Melatos et al. 2008), and thus were interpreted in terms of a SOC system (Young and Kenny 1996). While early measurements with extensive statistics exhibit powerlaw distributions with relatively steep slopes of α _P ≈3.0 (Argyle and Gower 1972; Lundgren et al. 1995; Cognard et al. 1996), more recent observations with smaller samples yield a large scatter of powerlaw slopes in the range of −0.13≤α _P ≤2.4 (Melatos et al. 2008) and α _E ≈4.6–9.0 (Cairns 2004). Other recent studies of giant micropulses from pulsars report a log-normal distribution of energies (Johnston and Romani 2002; Cairns et al. 2004), which is only consistent with a powerlaw function as an asymptotic limit in the tail of a log-normal function. Therefore, the distributions of giant pulses from pulsar glitches do not give rise to a narrow range of powerlaw slopes, and thus are not easy to explain in terms of a simple SOC model. Part of the large uncertainties of powerlaw slope measurements is clearly attributable to the small-number statistics in small samples (i.e., 6–30 pulses in the data sets of Melatos et al. 2008). The unusual steepness of reported powerlaw slopes may be associated with finite-size effects in a SOC system, which can cause an exponential-like cutoff at the upper end of the size distribution, as it is suspected for giant stellar flares (Sect. 3.4.1). Furthermore, the size distributions listed in Table 14, have been reported in different physical units (i.e., flux, pulse energy, electric field, frequency decrease ratios), and in form of both differential and cumulative size distributions, which need to be converted into the same energy units in order to make them directly comparable.

Table 14 Frequency distributions measured from giant pulses of pulsars (Crab, Vela, PSR), soft gamma-ray repeaters (SGR), black-hole objects (Cygnus X-1, Sgr A^∗), and a blazar (GC 0109+224). The size distributions were reported in units of (cumulative) pulse energies (Argyle and Gower 1972), in radio flux densities (Lundgren et al. 1995), (cumulative) pulse amplitudes (Cognard et al. 1996), electric fields (Cairns 2004), fractional increase of the spin frequency (Δν/ν) (Melatos et al. 2008), or peak fluxes (Ciprini et al. 2003). Powerlaw slopes of peak fluxes are marked with parentheses. Uncertainties (standard deviations) are quoted in brackets

A cellular automaton model has been developed for pulsar glitches, based on the superfluid vortex unpinning paradigm (Warszawski and Melatos 2008, 2012; Melatos and Warszawski 2008). The lattice grid in this model simulates the collective behavior of up to 10¹⁶ vortices in the interior of the pulsar. The cellular automaton generates scale-free avalanche distributions with powerlaw slopes of α _S =2.0–4.3 for avalanche sizes, and α _T =2.2–5.5 for avalanche durations. This numerical model produces size distributions that are not too far off the predictions of the FD-SOC model (α _E ≈1.5, α _T =2.0), but covers an intermediate range between the flatter slopes reported by Melatos et al. (2008) and the steeper slopes observed in radio wavelengths earlier. Larger observational statistics and a consistent definition of avalanche energies is needed to settle the pulsar SOC problem.

3.4.4 Soft Gamma Ray Repeaters

A class of gamma-ray bursts that were detected with the Compton Gamma Ray Observatory (CGRO), the Rossi X-ray Timing Explorer (RXTE), and International Cometary Explorer (ICE) in hard X-rays ≈20–40 keV (a wavelength regime that is also called soft gamma-rays), with repeated detections from the same source location, has been dubbed Soft Gamma Ray Repeaters (SGR). These gamma-ray bursts are believed to originate from slowly rotating, extremely magnetized neutron stars (magnetars) that are located in supernova remnants (Kouveliotou et al. 1998, 1999), where neutron star crust fractures occur, driven by the stress of an evolving, ultrastrong magnetic field in the order of B≳10¹⁴ G (Thompson and Duncan 1996). We should be aware that repeated bursts from the same source are the exception rather than the rule for gamma-ray bursts.

The size distributions of the fluences of sources SGR 1900+14 and SGR 1806-20 were found to exhibit powerlaw distributions with slopes of α _E =1.66 (Gogus et al. 1999) and α _E =1.43, 1.76, and 1.67 (Gogus et al. 2000), extending over a range of about 4 orders of magnitude in fluence. The waiting time distributions were found to be consistent with a log-normal distribution (which is approximately a powerlaw function in the upper tail). Based on these observational statistics, SGR bursts have been interpreted in terms of a SOC process (Gogus et al. 1999; 2000). Since the source location is identical for an object that produces SGR bursts, we can identify it with a single SOC system, an assumption that cannot be made for other gamma-ray bursts, which are non-repetitive and often do not have an unambiguous source identification with known distance. Moreover we find that the fluence or energy distribution of the bursts matches the prediction of the fractal-diffusive SOC model, with α _E =1.5. In the magnetar model, the triggering mechanism for SGR bursts is a hybrid of stress-induced starquakes and magnetically powered flares (Thompson and Duncan 1996), and thus has some similarity with the physical process of earthquakes.

A recent study was carried out with data from the Swift satellite, which has a rapid response, suitable for detecting afterglows of gamma-ray bursts. In a sample with 83 localized sources for which the redshift was known (and thus the distance), a size distribution of (distance-corrected) energies could be constructed, and a powerlaw distribution with slope of α _E =1.06±0.15 was found (Wang and Dai 2013). The size distribution of time duration was found to have a slope of α _T =1.10±0.15. These results were interpreted in terms of a 1D SOC system (Wang and Dai 2013), for which the FD-SOC model predicts α _E =1 and α _T =1. This 1D interpretation for gamma-ray bursts with afterglows appears to be different from soft gamma-ray repeaters, which are consistent with a 3D SOC system.

3.4.5 Blazars

Blazars are very compact objects associated with super-massive black holes in the center of active, giant elliptical galaxies. They represent a subgroup of active galactic nuclei (AGN), which emit a relativistic beam or jet that is aligned or nearly-aligned with the line-of-sight direction to Earth. Due to this particular geometry, blazars exhibit highly variable and highly polarized emission in radio and X-ray emission. Optically violent variable (OVV) quasars are a subclass of blazars.

The optical variability of blazar GC 0109+224 was monitored from 1994 onwards and the light curve exhibited a power spectrum P(ν)≈ν ^−p, with 1.57<p<2.05 (Ciprini et al. 2003), which is consistent with the 1/f or flicker noise characteristics of SOC avalanches in the BTW model (Bak et al. 1987; Hufnagel and Bregman 1992). The frequency distribution of radio peak fluxes of flaring events from blazar GC 0109+224 was found to be a powerlaw distribution (over about one order of magnitude), N(P)∝P ^−1.55 (Ciprini et al. 2003), which is consistent with the prediction of the FD-SOC model, i.e., N(P)∝P ^−1.67, within the uncertainties of the measurements. Interpreting blazars as a SOC phenomenon, the critical threshold for a pulse is given by the geometric coalignment condition between the emitted beam direction (of accelerated particles producing gyrosynchrotron emission) and the observer’s line-of-sight direction from Earth. The intermittency of blazar bursts observed on Earth is believed to be caused by sporadic bursts of energy releases, created by internal shocks that occur within AGN jets.

3.4.6 Black Holes and Accretion Disks

The first Galactic X-ray source that has been identified as a black-hole candidate, Cygnus X-1, emits hard X-ray pulses with a time variability down to 1 ms. These hard X-ray pulses are attributed to inverse Compton scattering of soft photons by hot electrons heading toward the event horizon within the black hole’s accretion disk.

Statistics of the fluctuations in the light curve from Cygnus X-1, observed in hard X-rays with Ginga and Chandra, exhibit complex 1/f noise spectra and size distributions of peak fluxes with very steep powerlaw slopes of α _P ≈7.1 (Negoro et al. 1995; Mineshige and Negoro 1999), which have been interpreted in terms of SOC models applied to accretion disks (Mineshige et al. 1994a, 1994b; Takeuchi et al. 1995; Mineshige and Negoro 1999). A SOC interpretation was also suggested for the VY Scl-type cataclysmic variable KR Aurigae (Kato et al. 2002; Dobrotka et al. 2012), UU Aqr (Dobrotka et al. 2012), and for the broad-line radio galaxy 3C-390.3 (Leighly and O’Brien 1997), for the Seyfert I MCG-6-30-15 (Sivron and Goralski 1998; Sivron 1998), or for the extreme narrow-line Seyfert 1 galaxy IRAS 13224-3909 (Gaskell 2004), which all exhibit a highly intermittent variability on top of a shot noise background like Cygnus X-1.

In contrast, a total of 39 X-ray flares observed with Chandra from Sgr A^∗, the 4×10⁶ M_⊙ black hole at the center of our Galaxy, revealed powerlaw distributions with slopes of α _P =1.9±0.4 for the peak luminosity (of the 2–8 keV flux) and α _E =1.5±0.2 for the fluence (Nielsen et al. 2013), which is perfectly consistent with the predictions of the FD-SOC model (α _P =1.67 and α _E =1.5).

Cellular automaton models were constructed to mimic mass accretion by avalanches that are triggered when the mass density of the disk exceeds some critical value, which could reproduce the 1/f power spectra N(ν)∝ν ^−1.6 and produced size distributions with powerlaw slopes of α _E =2.8 for energies and α _T =1.4 for durations (Mineshige et al. 1994a, 1994b; Yonehara et al. 1997). A BTW-related model produced an energy distribution of α _E =1.35 (Mineshige et al. 1994a, 1994b) that is closer to the FD-SOC prediction (α _E =1.5). Adding gradual diffusion to the SOC avalanches in the cellular automaton simulations produced a steeper (exponential) energy size distribution that was closer to the observations (Takeuchi et al. 1995). Further modified cellular automaton models were developed that include reservoirs of different capacities (Negoro et al. 1995), hydrodynamic models of advection-dominated accretion disks (Takeuchi and Mineshige 1997), relativistic effects (Xiong et al. 2000), non-local transport of angular momentum in terms of the kinematic viscosity of magnetic loops in the accretion disk corona (Pavlidou et al. 2001), and boson clouds around black holes (Mocanu and Grumiller 2012).

Most of the various cellular automaton models designed to mimic a physical mechanism operating in black-hole objects have difficulty to reproduce the observed steep size distributions, while most of them seem to produce 1/f power spectra without special assumptions. The observed steep size distributions may represent deviations of the accretion disk system from a pure SOC system. The notion of SOC may still be useful to understand the observations, but it cannot explain all properties of the fluctuations.

3.4.7 Galactic Structures

What physical mechanism produces galactic structures? A nonlinear theory was proposed in which the structure of spiral galaxies arises from percolation phase transition (Schulman and Seiden 1986a, 1986b; Seiden and Schulman 1990). The differential rotation of the galaxy triggers propagating patterns of star formation. This scenario is very similar to a SOC model, since it has a critical point at the second-order phase transition associated with the percolation threshold, which causes avalanches of star formations. Percolation processes, however, require fine-tuning, in contrast to SOC systems. The process of stochastic self-propagating star formation was simulated with a cellular automaton model that provides a representation of the percolation process operating in spiral galaxies (Seiden and Schulman 1990).

The formation of galaxies has been modeled with two opposite scenarios, the top-down scenario that starts with a monolithic collapse of a large cloud (Eggen et al. 1962; Zeldovich 1970), versus the now more widely accepted bottom-up scenario, where smaller objects merge and form larger structures that ultimately turn into galaxies (Searle and Zinn 1978; Peebles 1980). The second scenario is more widely accepted now and corresponds also closer to a SOC-driven avalanching scenario. In most models of galaxy formation, thin, rotating galactic disks result as a consequence of clustering of dark matter halos, gravitational forces and disturbances, and conservation of angular momentum. The fractal-like patterns of the universe from galactic down to solar system scales is thought to be a consequence of the gravitational self-organization of matter (Da Rocha and Nottale 2003). Fractal structures are observed throughout the universe (Baryshev and Teerikorpi 2002). It is conceivable that gravitational forces in an expanding universe lead to sporadic density fluctuations or waves that initiate a local instability of self-gravitating matter like an avalanche in a sandpile SOC model, in case a critical threshold exists without need of fine-tuning.

3.4.8 Cosmology

The spatial structure of the universe exhibits fractal structures of galaxy clusters out to a redshift of z=0.23 (Fig. 27), but becomes very homogeneous and isotropic at cosmological scales of the microwave background, with inhomogeneities of ≲10⁻⁴ according to the latest results of the COBE and WMAP missions. Self-organization and fractal scaling has been applied to some large-scale structures in our universe, such as to the galactic spiral structure (Nozakura and Ikeuchi 1988), the formation of the interstellar medium (Tainaka et al. 1993), the initial mass function of starbursts (Melnick and Selman 2000), the stellar dynamics in elliptical galaxy formation (Kalapotharakos et al. 2004), or to the gravitational structure formation in general on many scales (Da Rocha and Nottale 2003).

Fig. 27

The 2dF galaxy redshift survey (2dFGRS), conducted at the Anglo-Australian Observatory, shows a map of the galaxy distribution out to redshifts of z=0.23 or approximately 2 billion lightyears, which includes approximately 250,000 galaxies. Note the fractal large-scale structure of the universe that makes up the galaxy density (Colless et al. 2001)

The spatial flatness, homogeneity, and isotropy of the universe at cosmological scales can be considered as a critical point that would require an extreme fine-tuning, unless there is a self-organizing principle that creates such a special state in a natural way. Moffat (1997) proposes that the universe evolves as a SOC system (in the sense of a BTW model), where the Hubble expansion undergoes “punctuated equilibria” like the SOC scenario of intermittent evolution (Bak and Sneppen 1993). The inflationary scenario, which predicts a rapid expansion of the early universe to explain the flatness and the horizon problem, could be the manifestation of a major SOC avalanche, while a SOC scenario would predict many intermittent inflationary phases (Moffat 1997). The critical point of a cosmological system would be the critical density Ω=1 that discriminates between an open (Ω<1) and a closed (Ω>1) universe, independent of the initial conditions and without fine tuning of the parameters. A related SOC concept has also been applied to quantum gravity (Ansari and Smolin 2008). With the recent advent of string theory and multi-verses, we might even consider our universe being only one single avalanche episode in a multi-verse SOC scenario.

3.4.9 Cosmic Rays

Cosmic rays are high-energetic particles (protons, helium nuclei, or electrons) that originate from within our Milky Way, as well as from extragalactic space, and are detected when they hit the Earth’s atmosphere and produce a shower of high-energy particles (muons). The energy spectrum of cosmic rays extends over a large range of 10⁹ eV≲E≲10²¹ eV, with an approximate powerlaw slope of α _E ≈3.0 (Fig. 28). A closer inspection reveals a broken powerlaw with a “knee” at E _knee ≈10¹⁶ eV, which separates the cosmic rays accelerated inside our Milky Way (with a spectral slope of α _E1≈2.7) and in extragalactic space (with a slope of α _E2≈3.3). The sources of cosmic rays are believed to be supernova remnants, pulsars, pulsar-wind nebulae, and gamma-ray burst sources. The particles with higher energies (E≳E _knee ) have a uniform and isotropic distribution over the sky and are believed to originate mostly from active galactic nuclei (AGN).

Fig. 28

Cosmic ray spectrum in the energy range of E=10⁹–10²¹ eV, covering 12 orders of magnitude. There is a “knee” in the spectrum around E≈10¹⁶ eV, which separates cosmic rays originating within our galaxy (at lower energies) and those from outside the galaxy (at higher energies) (Credit: Simon Swordy, University of Chicago)

High-energy particles can be accelerated by a number of physical mechanisms, e.g., by electric fields, by shock waves, or by stochastic wave-particle interactions, such as by cyclotron resonance, which requires magnetic fields. In Sect. 3.2.6 we discussed how a first-order Fermi process as well as a fractal reconnection model can produce the observed powerlaw spectra of high-energy particles (Nishizuka and Shibata 2013). Cosmic rays, which travel through a large part of the universe, probably undergo many local acceleration processes, and thus their trajectories may look like a diffusive random walk. The acceleration process of cosmic rays has been interpreted in terms of a SOC process (Aschwanden 2014). The critical threshold is the “runaway regime” (e.g., Holman 1985) of a charged particle in a thermal distribution, which is a critical velocity, i.e., v _crit ≳4v _th , that is necessary to enable efficient acceleration out of the thermal distribution. Considering the subsequent acceleration process as a SOC avalanche, which can be achieved by an arbitrary number of localized acceleration steps, the particles are likely to undergo a diffusive random walk, as it is characterized by the fractal-diffusive SOC model. The FD-SOC model predicts than a powerlaw distribution for the energy spectrum of accelerated particles, which is approximately fulfilled for cosmic rays (as well as for nonthermal particles in solar flares). The FD-SOC model predicts an energy spectrum of N(E)≈E ^−1.5, which is however different from the observed cosmic ray spectrum with N(E)≈E ^−3.0. This discrepancy has been interpreted in terms of an incomplete sampling effect of cosmic-ray avalanches (Aschwanden 2014). Since cosmic rays are in-situ measurements in a very localized target region (i.e., the Earth surface), only a small 1-D cone of an isotropic cosmic-ray avalanche is sampled, leading to an energy gain that is proportional to the traveled length scale, i.e., L∝E, and thus to an energy spectrum N(E)∝N(L)∝L ⁻³∝E ⁻³. Solar flare observations, in contrast, provide remote-sensing of a complete SOC avalanche of accelerated particles, and thus are expected to have an energy spectrum of N(E)∝E ^−1.5, which is indeed an asymptotic limit for the hardest solar flare spectra (e.g., Dennis 1985; Miller et al. 1997).

4 Discussion: SOC Concepts, Critiques, New Trends, and Open Problems

4.1 A Dual Approach of Self-Organized Criticality Systems

A theory or a physical model is only useful (or acceptable) if it can make quantitative predictions, and if these predictions can be tested by observations, and hence the theory is falsifyable. What is the current status of a SOC theory or a SOC model? In this review we stress the dual nature of SOC models, in the sense that they include (i) universal statistical aspects that apply to all SOC systems, and (ii) special physical mechanisms that are idiosyncratic to a particular SOC phenomenon. There is a consensus that the powerlaw function of the size distribution of a SOC observable is a universal statistical aspect that is common to all SOC systems, regardless whether we sample statistics of solar flares or earthquakes, while the underlying physical mechanisms are completely different, such as magnetic reconnection in solar flares, or mechanical stressing in earthquakes. If we accept this dichotomy, we should be able to build a generalized SOC theory that predicts the universal statistical properties, which should be purely of “mathematical nature” and “physics-free”, while the nonlinear energy dissipation process of a SOC event still can be described with (single or multiple) specific physical SOC models that are different for every SOC manifestation. In this spirit we reviewed the basic elements of a generalized SOC theory in Sect. 2, while we touched on possible interpretations in terms of particular physical mechanisms that produce a SOC phenomenon in Sect. 3.

Let us review how the definition of a generalized SOC theory evolved over the last 25 years. The BTW model essentially defined a SOC process by simulating a cellular automaton, which demonstrated that a powerlaw size distribution resulted for avalanche sizes and durations. Since 1/f noise has a power spectrum in the form of a powerlaw function, the claim was made that both phenomena may be related. Many of the subsequent studies came up with different cellular automaton models, which produced a range of powerlaw slopes (see Table 1 and Pruessner 2012), some of them produced exact powerlaw size distributions over many orders of magnitudes (which demonstrated “universality” with regard to the scale-free size range, such as the Manna and Oslo model), while others exhibited significant deviations from exact powerlaw distributions (and thus cannot claim universality). The next important insight concerned the relationships between the powerlaw slopes of different SOC parameters, which depend on the nonlinear scaling laws between the SOC parameters. Further progress was made by predicting the statistical probability distributions of SOC parameters, using branching theory, percolation theory, discretized diffusion models, or renormalization group theory. A more detailed review on these theoretical and mathematical efforts is given in the article by Watkins et al. in this volume. A very simple theoretical framework that unifies many features of previous SOC models is the fractal-diffusive SOC model, based on the scale-free probability conjecture (Eq. (1)), which is able to predict probability distributions of observable SOC parameters and the underlying scaling laws between the SOC parameters. This basic SOC model has no free parameters for the most common case of 3D Euclidean space and classical diffusion transport, and offers a prediction for most of the astrophysical observations of SOC systems reviewed here. The model can also be adjusted to a different space dimension, fractal dimension, and type of diffusive transport. The FD-SOC model should be considered as a macroscopic approximation of the complex micro-dynamic processes in a SOC system.

Is this SOC theory complete? By no means, there is still a lot of statistics and data analysis required to pin down the scaling laws, statistical truncation bias, event selection bias, and other unknown effects for those SOC phenomena where the generic FD-SOC model yields a different prediction than what is observed. In addition, there are a number open questions in SOC models that try to reproduce real-world data, such as the time variability of the driver, effects that cause deviations from ideal powerlaw distributions, predictive capabilities, alternative SOC-related processes, which are discussed in the following sections.

4.2 Universal Aspects of SOC Systems

The universal aspects that are common to all SOC phenomena define a SOC theory. In Fig. 1 we sketched the basic characteristics of a SOC system: (i) a critical threshold for instabilities, (ii) a statistically slow driver that continuously nudges the system toward a critical point, and (iii) a nonlinear energy dissipation process when an avalanche is triggered. The most crucial and testable predictions of a SOC theory are the statistical probability distributions. The central key feature of the FD-SOC theory is the statistical probability argument for geometric length scales, the so-called scale-free probability conjecture, N(L)dL∝L ^−d dL. This statistical argument is derived by the same principle as a binomial distribution is derived for a stochastic process by enumerating all possible outcomes of dice combinations. This conjecture can easily be tested by extensive statistics of length scales, such as we demonstrated for lunar craters, asteroid sizes, Saturn ring particle sizes, magnetospheric aurora sizes, solar flare sizes, and can be done in the same way for other SOC processes, such as earthquake rupture areas, for instance. An additional assumption of the FD-SOC model is the fractal-diffusive transport, which involves random walk statistics for the avalanche transport, i.e., L∝T ^1/2 for classical diffusion, and a fractal geometry of the instantaneous avalanche size $V_{f} \propto L^{D_{d}}$, where the mean fractal dimension can be estimated from the mean-value dimension D _d ≈(1+d)/2. Integrating such a fractal-diffusive avalanche in time yields then the total size S of an avalanche. If energy dissipation of an avalanche is proportional to the time-integrated size of an avalanche, we obtain the total dissipated energy E∝S, the energy dissipation rate F∝V _f , and the peak energy dissipation rate P∝V. In astrophysical applications, the energy dissipation rate F is generally measured by the flux or intensity of electromagnetic radiation in some wavelength, but the universal meaning of the energy dissipation rate is simply the instantaneous avalanche size during a snapshot, while the total energy is the time-integrated avalanche volume. Thus this generalized SOC concept is still universally applicable to every SOC system, regardless if it is observed by an astronomical instrument, by a geophysical monitor, by financial statistics, or by computer lattice simulations.

4.3 Physical Aspects of SOC Systems

The physics comes in once we identify the avalanche, the threshold, and the dissipated energy with a particular instability in the real world (Table 16). For solar flares, for instance, the threshold may be given by a critical stressing angle between a potential and non-potential magnetic field line in an active region, the avalanche may be manifested by a solar flare emitting in all wavelengths, triggered by a magnetic reconnection process of the over-stressed magnetic field lines, and the dissipated energy can be measured by the change of magnetic energy before and after the flare, or by the thermal energy of the heated plasma, or by the total kinetic energy of accelerated particles. If we consider an earthquake, the threshold may be given by the limit of elastic stressing of tectonic plates, the instability is the slip-stick motion of the tectonic plates, the avalanche is the spatio-temporal pattern of the rupture area on the Earth’s surface, and the measured energy is the magnitude indicated by the vibrations detected by a seismometer. The advantage of separating the universal aspects from the physical aspects of a SOC system is that we can understand the statistics of SOC parameters independently of the physical model of a SOC phenomenon. For instance, we have very vague ideas about the exact physical process that occurs in pulsar glitches, in giant pulses from black-hole candidates, or in the bursts from soft gamma ray repeaters, but the FD-SOC model can predict the distributions and basic scaling laws between spatial and temporal parameters. In the case of imaging observations, where we can measure both spatial and temporal scales, the FD-SOC model can place absolute values on the diffusion coefficients, which may help to identify the physical transport process that occurs during an avalanche. We should also be aware that the universal FD-SOC model assumes a proportionality between the avalanche size S and total dissipated energy E, which may not always be the case, such as for coherent emission mechanisms (e.g., laser or maser emission), which requires a specific physical model.

4.4 Powerlaws and Deviations

The functional shape of size distributions of SOC parameters is generally expected to be a powerlaw function, i.e., N(x)dx∝x ^−α dx, which is a consequence of the scale-free nature of SOC processes. Numerical simulations of cellular automaton models were indeed capable to reproduce an exact powerlaw probability distribution function for avalanche sizes over many orders of magnitude, such as the Manna model (Manna 1991) or the Oslo model (Christensen et al. 1996), while substantial deviations from ideal powerlaw functions have been found in real-world observations, which raises the question how well the ideal powerlaw distributions predicted by standard SOC models characterizes real-world data. Taken to the extreme, sceptics doubt whether powerlaws have any relevance at all (Stumpf and Porter 2012).

Starting from first principles, a powerlaw function of length scales is predicted from the scale-free probability conjecture (Eq. (1)) in our generic standard model, which is fundamentally based on the principle of statistical maximum likelihood, and does not depend on any other assumption. However, this ideal distribution function is always limited within a finite range of spatial sizes [x ₁,x ₂], given by the spatial resolution limit or lower limit of complete sampling x ₁, and the finite system size or maximum avalanche size x ₂ that happened during the observed time interval x ₂. So, the powerlaw function is expected only over this limited range [x ₁,x ₂], while there is generally a rollover at the lower end and an exponential-like drop-off at the upper end. However, this range can be enlarged by lowering the lower limit x ₁ by more sensitive instruments, and by increasing the upper limit x ₂ by extending the total observing time (in case the largest avalanche does not exceed the finite system size).

Starting from the powerlaw function of the length scale distribution N(L)∝L ^−d, the FD-SOC model predicts powerlaw distribution functions for all other parameters, such as the area A, the volume V, the fractal area A _f , the fractal volume V _f , the flux F, the peak flux P, the fluence S, and energy E, because these SOC parameters are all related to each other by powerlaw relationships, such as by the definition of the Hausdorff dimension D _d , or the diffusive transport with spreading exponent β. Even the intermittent waiting times are predicted to be a powerlaw for contiguous flaring periods, with the only exception of quiescent time intervals, which may follow an exponential distribution (if they are produced randomly).

Then we should also be aware of the different predictions for a differential and for a cumulative size distribution. Even when a perfect powerlaw function exists for the differential size distribution over some range [x ₁,x ₂],

$$ N(x) \propto(\alpha- 1) x^{-\alpha} , \quad x_1 \le x \le x_2 , $$

(97)

the cumulative frequency distribution is not a perfect powerlaw function, with a slope that is flatter by one, but exhibits an exponential-like drop-off at the upper end, because the distribution goes to zero at the upper end x ₂ by definition,

$$ N^{cum}(>x) = n {{\int_{x}^{x_2}} N(x') dx' \over {\int_{x_1}^{x_2} N(x') dx'}} = n {(x^{1-\alpha} - x_2^{1-\alpha}) \over (x_1^{1-\alpha} - x_2^{1-\alpha})} , $$

(98)

where n is the total number of events. Therefore, cumulative size distributions show always a steeper distribution at the upper end x ₂ (i.e., the bin containing the largest event) than (1−α), for a differential size distributions with slope α, an effect that partially explains why (small) stellar flare samples have steeper powerlaw slopes than (large) solar flare samples (Sect. 3.4.1).

There are a number of additional effects that cause deviations from ideal powerlaw distribution functions. The most obvious deviations occur from the truncation of distribution functions. If we have statistics over many orders of magnitude, the truncation effects are less severe, but are crucial for small samples. Let us explain this with an example that is illustrated in Fig. 20. Solar flare statistics is usually limited by a peak count threshold, i.e., complete sampling is only achieved for P≥P _thresh . In this case we expect a perfect powerlaw for the differential size distribution of peak fluxes in the range of P _thresh ≤P≤P _max , where P _max is the count rate of the largest observed flare (for instance see Fig. 20e). However, if we sample the statistics of a related parameter, such as the thermal energy (Fig. 20f), the peak count threshold causes a truncation effect that extends over the lower half (logarithmic) range of energies, where sampling is not complete in energy and thus produces a broken powerlaw with a flatter slope in the lower half (logarithmic) range. The same truncation effect affects also linear regression fits. Nevertheless, these truncation effects can be numerically simulated or analytically calculated (e.g., see example in Aschwanden and Shimizu 2013, Appendix A), and this way can be taken into account in the prediction of the probability distribution functions of SOC parameters.

4.5 The Meaning of Self-Organized Criticality

After we have reviewed a large number of astrophysical observations (Sect. 3) with powerlaw behavior, the question arises whether all of these observed phenomena are SOC systems, and which are not consistent with a SOC interpretation. To answer this question we remind again our pragmatic generalized definition of a SOC system: SOC is a critical state of a nonlinear energy dissipation system that is slowly and continuously driven towards a critical value of a system-wide instability threshold, producing scale-free, fractal-diffusive, and intermittent avalanches with powerlaw-like size distributions (Aschwanden 2014). This definition is independent of any particular physical mechanism, but describes only some universal system behavior that is common to virtually all threshold-operated nonlinear energy dissipation processes, in the limit of slow driving. Given this much larger perspective of a SOC definition, we can ask whether the term “self-organized crtiticality” is still justified in this context, which includes also “critical points” now that define a threshold for an instability. The terms “self-organizing”, “self-tuning”, or “self-adjusting” mean in this context only that the system is continuously driven towards a critical threshold, without necessity of external control. If we have a self-sustaining slow driver, the continuous pushing of the system towards an instability threshold is automatically organized. In case the driver stops, the triggering of instabilities stops too, and the system becomes static. For instance, the cratering of the Moon has almost stopped, and thus the observed craters are only remnants of a dynamical state. However, during the times of heavy lunar meteorite bombardment, a SOC system with a critical (relative-velocity) threshold that triggered impacts on the Moon like earthquakes, or a scale-free distribution of meteorites could be an alternative source. The same is true for solar flares: there are quiescent static periods during the solar cycle minimum when nearly no magnetic flux is generated by the solar dynamo, while flaring during the maximum of the solar cycle constitutes a highly dynamic period of a continuously driven SOC system.

4.6 SOC and Turbulence

What is the relationship between a SOC system and a turbulent system? Because both systems exhibit powerlaw functions in the power spectrum, scale-free size distributions, and many degrees of freedom, there are commonalities that make their distinction difficult. Vortices are in turbulence what avalanches are in SOC. A first difference was noted in the predicted waiting time distribution. The original BTW model considered SOC avalanches as statistically independent and thus predicted an exponential waiting time distribution, while turbulent media exhibit long correlation times and predict powerlaw-like waiting time distributions (Boffetta et al. 1999; Giuliani et al. 1999; Freeman et al. 2000a). This argument, however, is alleviated by alternative SOC models (Sect. 2.12), such as non-stationary flaring rates (Wheatland et al. 1998), the fractal-diffusive SOC model (Aschwanden 2014), or models with persistence and memory as modeled with the Weibull distribution (Telloni et al. 2014).

How is SOC different from turbulence? Both processes may produce similar statistics for slow driving, but start to differ when we move from slow to intermediate driving, when the smallest avalanches are “swamped”, but the large avalanches persist, so that intermittent turbulence shows only finite-range powerlaw scaling (Chapman et al. 2009; Chapman and Watkins 2009; Chapman and Nicol 2009).

Instead of considering single vortices in fully developed turbulence as the equivalent of a SOC avalanche, a more satisfactory concept may be the notion of SOC in the state of near-critical turbulence, which is in the transition between the laminar state and the fully developed turbulence state. In this regime, the system profiles that store the free energy exciting the turbulence (i.e., pressure or temperature gradients, in a fusion plasma for instance) are very close to their local threshold values for the onset of instability. As a result, the local perturbations excited when these thresholds are overcome (giving rise to local eddies) may propagate to nearby locations (other eddies) as the former are relaxed, and the local profiles are brought back below critical. This is similar to the BTW sandpile. This regime is considered to be important in tokamak plasmas, because the local turbulent fluxes that bring the profiles back below a marginal state are strongest at higher temperatures. Thus, the equivalent to an avalanche is not a single eddy, but a chain of eddies at different locations connected in time, very much as a sand avalanche would happen in a sandpile. And the system is still in a turbulence-dominated regime, although turbulence is fully-developed only locally, not globally. These ideas were proposed in the mid-90s in the lab fusion community (Carreras et al. 1996; Newman et al. 1996; Mier et al. 2008; Sanchez et al. 2009), and have been given rise to a large body of work in the area of SOC, dealing with self-similarity, long-temporal correlations, and non-diffusive transport.

Intermittent turbulence (IT) and self-organized criticality (SOC) seem to co-exist in the magnetic field fluctuations of the solar wind at time scales of T=10–10³ s (Podesta et al. 2006a, 2006b, 2007), and in the solar corona (Uritsky et al. 2007). It was proposed that the coexistence of SOC and IT may be a generic feature of astrophysical plasmas, although the explicit complementarity between SOC and IT in astrophysical observations has not been demonstrated (Uritsky et al. 2007), IT phenomena can be explained without invoking SOC (Watkins et al. 2009a), and may need multi-fractal scaling (Macek and Wawrzaszek 2009), or three turbulence regimes (Meyrand and Galtier 2010).

The extent to which SOC and turbulence phenomena are really separable in complex systems is subject to a few conditions and topological constraints, also involving the ambient dimensionality. In two embedding dimensions, there is a theoretical possibility that SOC couples to turbulence via the inverse cascade of the energy, giving rise to large-amplitude events beyond the range of applicability of the conventional SOC (Milovanov and Rasmussen 2014). It has been discussed that the phenomenon occurs universally in two-dimensional fluid (as well as fluid-like, such as the drift-wave and drift-Alfven) turbulence and requires time scale separation in that the Rhines time of the vortical system must be small compared with the instability growth time. Then the typical avalanching behavior associable with SOC will be amplified by the inverse cascade, which acts as to fuel the SOC avalanches “on-the-fly” with the energy. The energy reservoir for this behavior is only limited to the finite size of the system. It has been suggested that this new complexity phenomenon, the SOC-turbulence coupling, has serious implications for operational stability of big fusion confinement devices such as for instance the future power plants, where it may trigger transport events of potentially a catastrophic character (Milovanov and Rasmussen 2014). In this regard, it was argued that SOC was not really an alternative to the notion of turbulence and that there is kind of SOC-turbulence duality instead, coming along with the condition for time scale separation. A hybrid SOC-turbulence model has also been developed based on statistical arguments, using nonlocal transport and the formalism of a space-fractional Fokker–Planck equation (Milovanov and Rasmussen 2014). According to the hybrid model, the processes of amplification taking place will manifest themselves in the form of algebraic tails on top of the typical log-normal behavior of the probability distribution function of the flux-surface averaged transport. This suggestion finds further justification in the general properties of log-normal behavior in hierarchical systems with subordination (Montroll and Shlesinger 1982). In the realm of solar physics, SOC predicts scale-free distributions for large avalanche events (e.g., in solar flaring active regions) down to the smallest avalanche events (e.g., in nano-flaring or non-flaring active regions), which implies also the same turbulence characteristics for flaring and non-flaring active regions, as it has been observationally verified (Georgoulis 2012). Related unifications of SOC processes, intermittent turbulence, and chaos theory include analysis of dynamical complexity via nonextensive Tsallis entropy (Milovanov and Zelenyi 2000; Balasis et al. 2011; Pavlos et al. 2012), fractional transport models (Zelenyi and Milovanov 2004; del Castillo-Negrete 2006), and the formalism of fractional Ginzburg–Landau equation (Milovanov and Rasmussen 2005; Milovanov 2013).

4.7 SOC and Percolation

A recent discussion of the SOC concept versus the percolation problem is given in Milovanov (2013). Both SOC and percolation systems share the implications of threshold behavior, the spatial self-similarity, and fractality. One essential difference is that percolation is a purely geometrical model, while SOC involves also the temporal fractality, i.e., the 1/f noise. Another difference is the role of fine-tuning, which needs an externally manipulated control parameter in a percolation system, while it is automatically self-organizing in a SOC system. However, some nonlinear phenomena have been modeled with both SOC and percolation models, such as the spread of diseases or forest fires, which indicates a strong commonality between the two models, as well as some ambiguity in the choice of the most suitable model for a given observed phenomenon (e.g., Grassberger and Zhang 1996). Regarding numerical simulations, both models can be represented with iterative lattice-grid simulations, using similar mathematical re-distribution rules in each iterative step. It has been discussed that SOC and percolation systems can be both represented with cellular automation models, but having different re-distribution rules. In the basic theoretical perspective, though, this lattice-grid approach seems to overly simplify the integral picture of the self-organization, as it tends to disregard the peculiar role of nonlinearity behind the phenomena of SOC. Generally, standard percolation processes can be made self-organized by including a feedback loop generating self-organization in a marginally stable state. Then marginal dynamical stability of systems with spatio-temporal coupling will also require marginal topological connectedness (Milovanov 2013), so that in the presence of many dynamical degrees of freedom the operation of nonlinear feedback will automatically lead the system into a state of critical percolation. This general theoretical framework has been demonstrated on a lattice model using random walks to represent the microscopic re-distribution rules and the idea of “holes” or missing occupied sites which by themselves could participate to the random walk and dynamically generate a feedback (Milovanov 2010; 2011).

From a practical (or observational) perspective, the question arises whether the percolation and SOC models predict the same, or different, size distributions, after adjustment of the optimum control parameters. However, since any automation model is only an idealized representation of microscopic physics in complex systems, none of the two models is expected to mimic microscopic transport to an accurate level, but may rather approximate the microscopic size distributions. In this regard, the advantage of the random walk approach once again lies in a theoretically consistent picture of the dynamics, making it possible to obtain non-Markovian kinetic equations at criticality in terms of fractional calculus (Milovanov 2009; 2011). The main idea here is that fractional generalizations of the diffusion and Fokker–Planck equations (e.g., Metzler and Klafter 2000 for review) incorporate via a Laplace convolution the key signatures of non-Gaussianity and long-time dependence characteristic of the dynamical systems at or near SOC. One by-product of the fractional model is the prediction that the relaxation of a super-critical system to SOC is of Mittag–Leffler type (similar to the Cole-Cole behavior in glassy systems and polymers: see Milovanov 2011). The Mittag–Leffler relaxation implies that the behavior is multi-scale with a broad distribution of durations of relaxation events consistently with a description in terms of fractional relaxation equation (e.g., Metzler and Klafter 2000; Sokolov et al. 2002) and at odds with a single-exponential relaxation dynamics of the Debye type (Coffey 2004 for an overview; references therein). We should stress that the notion of feedback plays a very important role in the phenomena of SOC, as it ensures a steady state, where the system is marginally stable against a disturbance (Kadanoff 1991). For instance, in sandpiles, the unstable sand slides off to decrease the slope and reinstall stability, thus providing a feedback of the particle loss process on the dynamical state of the pile. Following Sornette (1992), we also note that, using the idea of feedback, it is possible to convert the standard critical phenomena into self-organized criticality dynamics, thereby extending considerably the span of models exhibiting SOC. One example of this conversion is localization-delocalization transition on a separatrix system of nonlinear Schrödinger equation with disorder and self-adjusting nonlinearity, giving rise to a percolation structure in wave-number space, which is critical and self-organized (Milovanov and Iomin 2012; 2014).

In solar and astrophysics, percolation models have been applied to the formation of galaxies (Schulman and Seiden 1986a, 1986b; Seiden and Schulman 1990), to magnetotail current systems and the phenomena of tail current disruption (Milovanov et al. 1996; Milovanov et al. 2001; Milovanov 2013; Arzner et al. 2002), to the solar dynamo (Schatten 2007), to photospheric magnetic flux concentrations (Balke et al. 1993), and to the emergence of solar active regions (Wentzel and Seiden 1992; Seiden and Wentzel 1996). Each of these phenomena can also be modeled with a threshold-operated instability in a SOC system. Hence, the jury is still out which model describes the real-world observations better.

4.8 SOC and Branching Theory

A branching process is a Markov process (i.e., a memory-less process) that models a population with a random distribution at time step n to predict the number of individuals in the next generation or time step n+1 according to some probability distributions. To some degree, the branching process during a single time step has the same purpose as the re-distribution rule in a cellular automaton simulation. The question is whether the two processes have the same probability distributions for the spatio-temporal evolution of an avalanche event. The branching theory was mostly applied to the evolution of a population, which ended either in infinite growth or in global extinction. SOC avalanches end always after a finite time interval, and thus can only evolve as a branching process with final extinction. What is common to both processes is a critical threshold or critical probability for next-neighbor or next-generation propagation. Therefore, a self-organized branching process with critical probabilities (Zapperi et al. 1995; Corral and Font-Clos 2013) has much in common with a SOC system of the BTW-type. Again, for practical purposes to model observations, we may ask whether the two models predict equal or different size distributions, using some suitable critical probabilities.

In astrophysics, self-organizing branching theory has been applied to magnetotail current systems (Milovanov et al. 2001), to solar soft X-rays (Martin et al. 2010), and to solar flares (MacKinnon and MacPherson 1997; Macpherson and MacKinnon 1999; Litvinenko 1998). The branching theory applied to solar flares (MacKinnon and MacPherson 1997; Macpherson and MacKinnon 1999; Litvinenko 1998) as well as the self-organized branching process (SOBP) model (Zapperi et al. 1995; Hergarten 2012) predict both a size distribution of N(S)∝S ^−3/2, which is also predicted by the fractal-diffusive self-organized criticality (FD-SOC) model, and thus indicates an equivalent description of the multiplicative avalanche growth characteristics, and makes these two models indistinguishable with regard to their size distributions.

4.9 Challenges and Open Questions in Solar SOC Models

Attempting to connect the idealized analytical or numerical SOC models with real-world (astro)physical systems, one faces a host of questions that remain unanswered. We briefly touch on a few issues that arised from solar SOC models.

Evolving SOC Drivers:

The driver of a SOC system may naturally evolve in and out of a SOC state, vary cyclically or intermittently, or oscillate between low and high states. Well-known examples are the solar dynamo that cyclically modulates the solar flare rate, or the variability of low and high states in the black-hole object Cygnus X-1. Another example is a time-variable driver of solar active regions, as described in McAteer et al. (2014), which emulates how a dissipative, nonlinear dynamical system enters a SOC state. Standard SOC models, such as the BTW model, assume a steady driver and do not take into account the particular system behavior of variable SOC drivers. Real-world SOC systems are operated by time-variable drivers that are never exactly constant, which may alter the statistical distributions that are predicted from a constant driver. During the decay phase of a SOC driver, the dissipative properties of the system may possibly diffuse the available energy in a gradual (non-intermittent) fashion, and this way reduce the system’s control parameter to a value below the critical threshold, and this way inhibit intermittent instabilities (avalanches).

In a tectonic system, for example, earthquakes in an area would stop when inter-plate stresses are somehow mollified by repelling mantle motions below. While this is a hypothetical and hardly observable fact, at least within reasonable geological timescales, a solar active region, even a fiercely flaring/eruptive one, emerges, evolves, and disappears within weeks. If this system evolves into a SOC state, as amply argued in this review, then the discontinuation of magnetic-flux emergence from the solar interior signals the start of this active region’s demise. It is both, the time-dependent proper motions within the region (e.g., shear, sunspot rotation, outflows), as well as the overall solar differential rotation, which apparently quench the SOC-decaying driver in a gradual and non-intermittent manner by exhausting the region’s free magnetic energy. Flux emergence and related motions, on the other hand, become the realization of the classical SOC-building driver. The implementation of distinct SOC-building and SOC-decaying drivers, with the first being dominant during the SOC phase of the system, but weak or absent during the system’s decay, can characterize the finite lifetime of SOC states.

In the limit of a statistically slow SOC-building driver, another conceivable way for a system to exit SOC is by a “catastrophic” quenching of the SOC state by a single, system-wide instability that dissipates a substantial part of the system’s available energy. While this is in principle not prohibited in a SOC system and could occur when the entire system becomes a network of marginally stable configurations, observations suggests otherwise: earthquake clusters (e.g., Corral 2004) reveal that only a relatively small portion of the stress-accumulated free energy is released, regardless how powerful the earthquake is. In other words, a seismic fault does not disappear after any single earthquake. The same is qualitatively the case for solar active regions, where the total available free energy can be calculated or estimated (e.g., Tziotzou et al. 2013). This rule of thumb seems to indicate that SOC states fade away gradually only, rather than by a catastrophic event at once.

Hidden, Anisotropic, and Composite SOC States:

A potentially interesting finding on the evolution of a time-variable SOC driver was obtained from experiments with a static data-driven (S-IFM) and a dynamically driven (D-IFM) flare model of Dimitropoulou et al. (2011; 2013), described in McAteer et al. (2014). A given nonlinear force-free extrapolated magnetic field of an observed solar active region is first evolved into a SOC state, yielding a random but valid divergence-free magnetic configuration due to the S-IFM’s random driving. Next, the system is evolved back to the initial extrapolated state via D-IFM, while monitoring tests confirmed that the SOC state has not been destroyed. Therefore, one cannot rule out that the initial extrapolated-field state, despite being a force-free-equilibrium state, may in fact be a SOC state. The subject active region for the test happened to be an eruptive one; however, the eruptive property was not used in the test. Therefore, unless eruptive solar active regions have a topologically or otherwise distinct magnetic structure compared to non-eruptive ones, the same test might possibly work equally well with a non-eruptive active region. Should this be confirmed, it would be evidence that solar active regions, regardless of an eruptive or non-eruptive nature, may be in a SOC state. The question then arises, besides active regions, whether the quiet-Sun (or global stellar) magnetic field is in a SOC state also? This remains to be assessed. The lack of major flares and eruptions from non-eruptive active regions and the quiet Sun may be due to the lack of available free-energy density accumulation, a much weaker SOC-building driver, or a critical threshold of a different nature, heuristically proposed as an “anisotropic” SOC threshold by Vlahos et al. (1995) and subsequent works. It is now observed from exceptionally high-resolution solar observations that small-scale energy-release events resembling the hypothesized nanoflares occur in the active and the quiet solar corona (Cirtain et al. 2013; Winebarger et al. 2013). If the entire solar corona is in a “composite” SOC state, albeit with different critical thresholds and drivers in different regions, then there is a possibility to extend SOC validity over the global magnetic configurations of magnetically active, main-sequence stars.

Robustness of Power Laws:

Probability distributions of sizes and durations exhibit generally a powerlaw function with a specific slope for a given observable (such as the peak count rate, fluence, rise time, or decay time). The value of the powerlaw slope becomes the more robust, the larger the statistics is, gathered over sampling times as long as possible. Even for small statistics and short sampling times, the value of the powerlaw slope may be robust, as long as the driver is constant and the sample is statistically representative. However, this robustness is lost when subsets of data are histogrammed that contain some selection bias. This loss of robustness has been demonstrated in a study by Crosby et al. (1998), using a sample of some 1500 X-ray flares from the WATCH/GRANAT satellite, when subsets were selected by groups with different event durations: the power laws were found to be steeper for subsets with short duration, while they progressively flattened for longer events. A similar result was found for total-count distribution functions of these flares by Georgoulis et al. (2001), which was also used for a “statistical flare SOC cellular automaton model” (Georgoulis and Vlahos 1998).

The effect of a selection bias in time durations T on the size distribution function of an observable, such as the peak flux P, can easiest be understood from a scatterplot between the parameters P and T. If there would be an exact correlation with a correlation P∝T ^a, the distribution N(P;T=T _i ) of a subset with duration T _i would be a δ-function N(P=P _i ) at the value $P_{i} \propto T_{i}^{a}$. In reality, the correlations have a substantial scatter, which broadens the size distributions of each subset, but the trend that they are clustered around the value $P_{i} \propto T_{i}^{a}$ persists. A consequence of this scatter between correlated parameters is also that the threshold in an observable (say in the peak count rate, P≥P ₀), causes a truncation bias in the correlated parameter (say T≳T ₀). Therefore, even when the peak rate distribution N(P) exhibits an exact powerlaw down to the threshold value P ₀ of the sample, the correlated time duration distribution N(T) will have a smooth rollover, which is a significant deviation from an ideal powerlaw. At the upper end of size distributions, finite-size effects cause an additional fall-off, which is another deviation from an ideal powerlaw distribution. These well-understood effects should be taken into account in arguments countering power laws and their validity and interpretation, as expressed by Stumpf and Porter (2012).

Hybrid SOC Models and Multi-Fractal Effects:

There is also a controversy about the hypothesized “soft” nanoflare population (Parker 1988) that must be sufficiently steep (α _E >2) to allow the bulk of the dissipated energy to originate from the lower end of the distribution, via a mostly thermal energy release, thus balancing the coronal energy losses and maintaining a hot corona (Hudson 1991; see also Sect. 3.2.8). This review presents evidence that nanoflares share the same powerlaw distribution of energies as microflares and large flares do. Therefore, the bulk of the released energy stems from large flares in the upper end of the distribution, which is debated by some studies to be insufficient to maintain the corona at its observed temperature. Indeed, statistical properties of small-scale events have been revisited to correct for multiple selection biases and have been shown to obey flatter power laws than originally found. Given the ever-improving but always finite observational sensitivity, however, it is conceivable that such a soft population, if existing, may still be eluding observation or may be partially suppressed by the better sampled intermediate and large events, as it appears to be the case with the results of Crosby et al. (1998) and Georgoulis et al. (2001). In addition, the prediction of the statistical flare model (Georgoulis and Vlahos 1998) for a dual population of instabilities and a “knee” between them, moving from a steeper (softer) to a flatter (harder) power law (Georgoulis and Vlahos 1996), has yet to be confirmed or ruled out. The statistical flare model remains the only SOC model that produces double scaling owning to a double instability criterion featuring “isotropic” and “anisotropic”, directional relaxation (see, however, Fig. 4 of Hughes et al. (2003) and relevant discussion).

Hybrid models can explain broken-powerlaw distributions, which imply also multi-fractality, a property that has been measured in a number of solar active region studies on the magnetic flux distributions (Lawrence et al. 1993; Cadavid et al. 1994; Gallagher et al. 1998; McAteer et al. 2005; Abramenko 2005; Conlon et al. 2008, 2010; Hewett et al. 2008; Abramenko and Yurchyshyn 2010).

Predictability in a SOC System:

Are large events resulting from a SOC system predictable? This remains a widely open question with profound geophysical (i.e., earthquake prediction) and space-weather (i.e., solar-flare/eruption prediction) implications. The question can naturally be linked to the question of inter-event, or waiting times. Extensive discussion on waiting times and their distribution in this review (Sect. 2.12 and references therein) has established that the form of the SOC waiting-time distribution is not an invariant SOC property such as the power-law distribution functions of event size. The degree of memory, intrinsic and different in each SOC system, determines the form of the waiting-time distribution. The opposite is not true generally, because the form of the waiting-time distribution cannot uniquely specify the degree of memory of the SOC system that created it. In addition, an instability—regardless how intense—tends to release only a small fraction of the system’s available energy, hence always imposing a finite degree of stochasticity that is complementary to the finite memory of the system. In case of no memory, that gives rise to a classical BTW exponential waiting-time distribution, events are purely random and cannot be predicted. In particular cases—such as, e.g., deterministically driven models—Strugarek and Charbonneau 2014 showed that the memory of the SOC system could be raised up to a level where large events can be forecasted systematically. Though, it must be noted that predictions from a SOC system necessarily rely on different realizations of the stochastic process and by such are intrinsically probabilistic. Achieving the most significant prediction probabilities then depends on the memory level of the model and is a matter of the specific physics of the SOC system in question (discussion below).

Helicity Conservation in Solar SOC Models:

What physical quantity is conserved in a SOC system? Two of the telltale SOC features are metastability and marginal stability. Metastability typically involves a conservative property of the system in the course of driving as it occurs in the original BTW concept, while marginal stability reflects the mere result of an upper accumulation limit for the conserved parameter, hence defining the critical threshold. Perturbing a low-beta, magnetized environment of a solar active region, for instance, one builds electric currents while conserving magnetic flux. Using a flux critical threshold, however, would be misleading, as large, severely flux-imbalanced active regions (e.g., a single compact sunspot surrounded by scattered opposite-polarity flux) do not flare or erupt in general. Electric current density could constitute a critical threshold for magnetic reconnection and hence for an instability, but it is not a conserved quantity: when stopping the SOC-building driver, the free magnetic energy due to electric currents will be gradually dissipated via a SOC-decaying driver, returning the system to eruption-free stability reflected in a current-free, potential state (e.g., Contopoulos et al. 2011). Although a few non-conservative SOC models have been proposed (Vespignani and Zapperi 1998; Pruessner and Jensen 2002 and references therein), the greatly larger number of conservative SOC models implies that one should perhaps look into a conservative control parameter first to identify a critical threshold: an attractive concept is that of magnetic helicity, a physical quantity that is roughly conserved in high magnetic Reynolds-number plasmas even during reconnection (e.g., Berger 1999). Magnetic helicity could indeed provide a critical threshold, complemented by a minimum free magnetic energy necessary to keep in pace with the accumulated helicity (Tziotziou et al. 2012). This may lead to an unbiased interpretation of eruptions as instabilities occur not because of magnetic reconnection primarily, but because a part or the entire magnetic structure reached its limit in terms of accumulated helicity. Uncovering the crucial physical details of this and similar mechanisms, including how the control quantity of the system (magnetic helicity in this example) consistently accumulates until the system becomes unstable, may potentially achieve closure between physical models and statistical interpretations of complexity systems governed by SOC.

5 Summary and Conclusions

The literature on self-organized criticality (SOC) models counts over 3000 refereed publications at the time of writing, with about 500 papers dedicated to solar and astrophysics. Given the relatively short time interval of 25 years since the SOC concept was born (Bak et al. 1987), the productivity in this interdisciplinary and innovative field speaks for the generality, versatility, and inspirational power of this new scientific theory. Although there exist some previous similar concepts in complexity theory, such as phase transitions, turbulence, percolation, or branching theory, the SOC concept seems to have the broadest scope and the most general applicability to phenomena with nonlinear energy dissipation in complex systems with many degrees of freedom. Of course there is no such thing as a single “SOC theory”, but we rather deal with various SOC concepts (that are more qualitative rather than quantitative), which in some cases have been developed into more rigorous quantitative SOC models that can be tested with real-world data. Computer simulations of the BTW type provide toy models that can mimic complexity phenomena, but they generally lack the physics of real-world SOC phenomenona, because their discretized lattice grids do not reflect in any way the microscopic atomic or subatomic structure of real-world physical systems.

In this review we focus on the astrophysical applications only, including solar physics, magnetospheric, planetary, stellar, and galactic physics. We summarize first some basic concepts of a generalized SOC theory, covering different SOC definitions, the driver, instability and criticality, avalanches, microscopic structures, basic spatio-temporal scaling laws and derivations of basic occurrence frequency or size distributions, waiting time distributions, and a comparison of basic numerical cellular automaton simulations. Most of these aspects are the ingredients of a generalized fractal-diffusive self-organized criticality (FD-SOC) model (Aschwanden 2014), which we use as a standard model for the macroscopic description of a SOC system, bearing in mind that it represents only a first-order approximation to the statistics of the microphysics of SOC avalanches. This standard model is based on the scale-free probability conjecture, fractal geometry, and diffusive transport. This model can explain most of the astrophysical observations and enables us to discriminate which SOC-related observations can be explained with standard scaling laws, and which phenomena represent mavericks that need either a special model, an improved data analysis, or better statistical completeness. We summarize the major findings of this review in the following:

• 1. A general working definition of a SOC system that can be applied to the majority of the observed astrophysical phenomena interpreted as SOC phenomena can be formulated as: SOC is a critical state of a nonlinear energy dissipation system that is slowly and continuously driven towards a critical value of a system-wide instability threshold, producing scale-free, fractal-diffusive, and intermittent avalanches with powerlaw-like size distributions (Aschwanden 2014). This generalized definition expands the original meaning of self-organized “criticality” to a wider class of critical points and instability thresholds that have a similar (nonlinear) dynamical behavior and produce similar (powerlaw-like) statistical size distributions.

• 2. A generalized (macroscopic description of a) SOC model can be formulated as a function of the Euclidean space dimension d, the spatio-temporal spreading exponent β, a fractal dimension D _d , and a volume-flux scaling (or radiation coherency) exponent γ. For standard conditions [d=3, D _d ≈(1+d)/2, β=1, and γ=1], this SOC model predicts (with no free parameters) powerlaw distributions for all SOC parameters, namely α _L =3 for length scales, α _A =2 for areas, α _V =5/3 for volumes, α _F =2 for fluxes or energy dissipation rates, α _F =5/3 for peak fluxes or peak energy dissipation rates, and α _E =3/2 for time-integrated fluences or energies of SOC avalanches.

• 3. The underlying correlations or scaling laws are: A∝L ² for the maximum avalanche area, $A_{f} \propto L^{D_{d}}$ for the fractal avalanche area, V∝L ³ for the maximum avalanche volume, $V_{f} \propto L^{D_{d}}$ for the fractal avalanche volume, T∝L ^(2/β) for the avalanche duration, $F \propto L^{(\gamma D_{d})}$ for the flux or energy dissipation rate, P∝L ^(γd) for the peak flux or peak energy dissipation rate, $E \propto L^{(\gamma D_{d}+2/\beta)}$ for the fluence or total energy.

• 4. Moreover, the FD-SOC model predicts a waiting time distribution with a slope of α _Δt =2 for short waiting times, and an exponential drop-off for long waiting times, where the two waiting time regimes are attributed to intermittently active periods, and to randomly distributed quiescent periods. The contiguous activity periods are predicted to have persistence and memory.

• 5. Among the astrophysical applications we find agreement between the predicted and observed size distribution for 10 out of 14 reported phenomena, including lunar craters, meteorites, asteroid belts, Saturn ring particles, auroral events during magnetospheric substorms, outer radiation belt electron events, solar flares, soft gamma-ray repeaters, blazars, and black-hole objects.

• 6. Discrepancies between the predicted and observed size distributions are found for solar energetic particle (SEP) events, stellar flares, pulsar glitches, the Cygnus X-1 black hole, and cosmic rays, which require a modification of the standard FD-SOC model or improved data analysis. The disagreement for SEP events is believed to be due to a selection bias for large events, or could alternatively be modeled with a different dimensionality of the SOC system. For stellar flares we conclude that the bolometric fluence is not proportional to the dissipated energy and flaring volume. Pulsar glitches are subject to small-number statistics. Black hole pulses from Cygnus X-1 have an extremely steep size distribution that could be explained by a suppression of large pulses for a certain period after a large pulse. For cosmic rays, the energy distribution appears to be subject to incomplete uni-directional sampling by in-situ observations, rather than omni-directional sampling by remote-sensing methods.

• 7. Some of the SOC-associated phenomena have also been modeled with alternative models regarding their size or waiting time distributions and were found to be commensurable, such as in terms of turbulence, percolation, branching theory, or phase transitions. All these theories have some commonalities in their concept and can often not be discriminated based on their observed size distributions alone. Some of the physical processes may coexist and not exclude each other, such as SOC and turbulence in the solar wind.

A summary of theoretically predicted and observed powerlaw indices of selected astrophysical SOC phenomena is listed in Table 15, while more complete compilations for each phenomenon are given in Tables 2 to 14. The variation of powerlaw values among the same phenomena indicates incompatible data analysis methods or statistically irreconcilable samples. Improved data analysis, larger statistics, and more detailed complexity models are called for in future studies, which should reconcile existing discrepancies and answer the existing open questions and challenges. Besides the statistical improvements, also physical models (Table 16) that reproduce the underlying scaling laws are expected in future work. All these tasks present a rich and rewarding activity of future research in the field of complex systems. The SOC concept has clearly stimulated a new way of thinking and analyzing the dynamics and statistics of complex systems.

Table 15 Summary of theoretically predicted and observed powerlaw indices of size distributions in astrophysical systems

Table 16 Physical mechanisms operating in self-organized criticality systems