Abstract
In the seventeenth and eighteenth centuries, mathematicians and physical philosophers managed to study, via mathematics, various physical systems of the sublunar world through idealized and simplified models of these systems, constructed with the help of geometry. By analyzing these models, they were able to formulate new concepts, laws and theories of physics and then through models again, to apply these concepts and theories to new physical phenomena and check the results by means of experiment. Students’ difficulties with the mathematics of high school physics are well known. Science education research attributes them to inadequately deep understanding of mathematics and mainly to inadequate understanding of the meaning of symbolic mathematical expressions. There seem to be, however, more causes of these difficulties. One of them, not independent from the previous ones, is the complex meaning of the algebraic concepts used in school physics (e.g. variables, parameters, functions), as well as the complexities added by physics itself (e.g. that equations’ symbols represent magnitudes with empirical meaning and units instead of pure numbers). Another source of difficulties is that the theories and laws of physics are often applied, via mathematics, to simplified, and idealized physical models of the world and not to the world itself. This concerns not only the applications of basic theories but also all authentic end-of-the-chapter problems. Hence, students have to understand and participate in a complex interplay between physics concepts and theories, physical and mathematical models, and the real world, often without being aware that they are working with models and not directly with the real world.



From Galileo (1638)

From Newton (1687)

From d’ Alembert (1743)

From Carnot (1824)





Based on Figure 24, p. 110 in Dingrando et al. (2007)

Based on Figure 2.50, p. 41 in Hamper (2009)

Based on the figure of question 13, p. 269 in Johnston et al. (2015)
Similar content being viewed by others
Notes
The term ‘mathematics of high school physics’ refers to mathematics used in high school physics textbooks and high school physics classes, while the term ‘high school mathematics’ refers to mathematics presented in high school mathematics textbooks and taught in high school mathematics classes.
That is, physics that was formulated in the seventeenth and eighteenth centuries.
According to scholastics, these qualities determined the ‘form’ of a body, which was changeable, whereas its ‘substance’ was unchanging (Lewi 2006).
The same view had been stated some years earlier by the Aristotelian Jesuits Alesandro Picolomini and Benedict Pereira (Marshall 2011).
The idea that the world had a hidden mathematical structure had long been endorsed in Greek philosophy and science. Archimedes, however, used mathematics instrumentally (without metaphysical assertions) to analyze certain parts of the physical world in a systematic (and fruitful) way.
The figure is based on Heath’s translation of the Works of Archimedes (Archimedes 2010, p. 190). On the other hand, in Hiebert’s edition of the same Works (Archimedes 1913), which is based on an older manuscript, this figure contains triangles instead of rectangles. These manuscripts have been reproduced many times through the centuries, and the accuracy of their figures is questionable.
Mathematical procedures for the direct determination of ‘velocity’ as a quotient of space divided by time were at that time forbidden (Ravetz 1961).
It seems, however, that some experiments preceded theoretical analysis, guiding it (Mahoney 2012).
According to Cohen (2010), apart from the essentially Aristotelian agenda and the Aristotelian logical rigor, Galileo adopted one more Aristotelian characteristic: the continual trading between theoretical analysis and experience.
In his Principia, Newton redefined mechanics from a science of the manual arts and simple machines to ‘the science, expressed with exact propositions and demonstrations, of the motions that result from any forces whatever and of the forces that are required from any motions whatever’ (Newton 1999, p. 382).
The parallelogram rule for adding forces.
Newton uses the ‘method of first and ultimate ratios’ (i.e. elements of calculus) to show that the rectilinear figures coincide with the curvilinear ones, and their rectilinear perimeters with curvilinear lines (Newton 1999, pp. 433–434).
In fact, Varignon determined ‘force accélératrice’—force per unit mass, numerically equivalent to acceleration—as y = dv/dt = dx/dt 2 (Varignon 1700), whereas Euler wrote Newton’s second law (or his ‘new principle of mechanics’) in the form: 2Md2 x = ∓Pdt 2, where P was the net force and the coefficient ‘2’ was balancing his units (Euler 1752).
According to Gingras, quantification, which is related to measurements of properties through graduated instruments, has to be distinguished from mathematization, which concerns the formulation of abstract geometric or algebraic expressions, such as the law of refraction of light or the second Newton’s law (Gingras 2001).
Carnot gave the meaning of ‘motive power’ in a footnote:
We use here the expression motive power to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised (Carnot 1960, p. 5).
Caloric, according to the dominant theory of the era, was another name for heat, which was regarded as an imponderable and conserved fluid.
It is striking that in his Physics, Aristotle does not define ‘speed’ as an abstract concept, but only the swifter body in relation to the slower:
… if one thing is faster than another, it will cover a greater distance in an equal amount of time, and it will take less time to traverse an equal distance, and it will take less time to traverse a greater distance. Some people take these properties to define ‘faster’ (Aristotle 2008, 232a25–232a26).
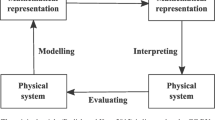
Only a small subset of the system’s properties is represented. Giere (2006) compares physical models with maps. Maps and models, he points out, represent partly and selectively only certain elements of the physical system they are referring to. There are geophysical maps that depict geophysical data, political maps that depict political divisions, cities, highways, etc. Maps and models represent parts of the world approximately (absolutely exact maps do not exist), using agreed design conventions.
It is a simple geometric figure on which many conventional imagistic elements are incorporated. These are the arrows denoting the forces’ vectors, the shading denoting the unshakable support, etc.
Contrary to what the figure shows, the suspending ball is regarded as a point mass.
Redish (2005) and Redish and Kuo (2015) argue, convincingly enough, that physicists are blending mathematics and physics when they are handling the mathematics of physics, loading physical meaning onto mathematics. Hence, the series of operations on models might be more complex, in reality, than what is presented here. Moreover, this might add one more difficulty to students’ understanding of high school physics mathematics.
Usually, in high school experiments, a lot of effort is made to reduce the complexity of the physical system, e.g. by minimizing disturbing factors like friction. So, the physical systems are modified to resemble their models as close as possible.
This is a second denotation of the term ‘mathematization’. In the second (‘historical’) part of this paper, the term was used, in a broader way, to denote all procedures to transform physics from a qualitative, philosophical study of nature to a quantitative and exact description and examination of it via mathematics.
Of course, teaching practice has always the problem of the limited time along with the amount of information students are asked to handle. Consequently, teachers cannot analyze every implicit assumption every time the class solves a problem. On the other hand, by organizing around a concept (‘model’) all these simplifying procedures (explicit or implicit) that are always used when a theory is applied probably will save time and effort, and students might better understand how physics works. This, however, is a matter of empirical research and instructional practice, not just a matter of theoretical contemplation.
Context-based physics approaches (Taasoobshirazi and Carr 2008; Löffler and Kauertz 2014), which also work with real world situations and authentic problems, have much in common with modeling instruction projects. Although they usually do not introduce their models explicitly, their focus is shifted from teaching and applying theoretical statements (given in the form of physics formulas) to explain certain key phenomena—a shift from content to context. Stinner’s Large Context Problems are designed with the same tenets (see for example Stinner 2007a, b).
The term parametric equation denotes here an equation with parameters, as it is usually used in high school algebra textbooks.
In his 1685 A treatise of Algebra, John Wallis tried to explain Viète’s terminology. According to Wallis, the term ‘species’ operates in a similar way with the particular names the English lawyers use to indicate indefinitely any person in any situation, e.g. John-on-Oaks and John-a-Dawn. So, Viète’s ‘species’ and symbols represent indefinitely any number and any quantity (Wallis 1685; Klein 1998).
In fact, Klein’s views were rather overlooked for many years, until the historian of mathematics Sabetai Unguru brought them to the fore as an additional argument against the case of geometric algebra (Unguru 1975). His article initiated a controversy between new and traditional historians of mathematics (van der Waerden 1976; Weil 1978; Unguru 1979; Rowe 1996), which, apart from geometric algebra, spread itself into the ontological status of mathematical concepts and propositions, as well as their connection to the symbolic systems used to represent and handle them. For example, it was discussed whether mathematical concepts were ‘eternal, unchanging, unaffected by the idiosyncratic features of the culture in which they appear’ (Unguru 1979, p. 555) or the products of historical processes, constructed by certain mathematicians within certain cultures, and shaped by the symbolic systems invented to represent them. The details of this controversy, however, are beyond the scope of this paper, and they will not be examined. For a philosophical analysis of these matters see Stenlund (2015).
Zetetics is one of the components of Viète’s analytic art (i.e. algebra), and consists in finding the equations or other mathematical relations to solve a problem (Viète 1983).
These empirical researches, however, were selected because they are related to the former theoretical statements. They are not, and could not be, a full survey of educational research on these mathematical concepts.
There is, however, no sharp distinction between them. When school mathematics is applied to an authentic situation of the real world, mathematical symbols stand for entities and procedures of this worldly situation, and acquire concrete meaning too. But in school physics, symbols in equations stand for physical magnitudes and have physical meaning from the very beginning.
References
Adúriz-Bravo, A. (2013). A ‘semantic’ view of scientific models for science education. Science & Education, 22(7), 1593–1612.
Angell, C., Guttersrud, O., Henriksen, E., & Isnes, A. (2004). Physics: Frightful, but fun. Pupils’ teachers’ views of physics and physics teaching. Science Education, 88, 683–706.
Angell, C., Kind, P. M., Henriksen, E., & Guttersrud, O. (2008). An empirical-mathematical modeling approach to upper secondary physics. Physics Education, 43(3), 256–264.
Archimedes. (1913). Archimedes Opera omnia (Vol. II, J. L. Heiberg, Ed.). Leipsig: Teubner.
Archimedes. (2010, 1st edition 1897). The works of Archimedes (T. Heath, Ed.). Cambridge: Cambridge University Press.
Aristotle. (1991). The complete works of aristotle (Vol. I, J. Barnes, Ed.). Oxford: Oxford University Press.
Aristotle. (2008). Physics (R. Waterfield, Trans.). Oxford: Oxford University Press.
Arseneault, M. (2014). The effects of modeling instruction in a high school physics classroom. Master Thesis, Louisiana State University.
Bagno, E., Berger, H., & Eylon, B. (2008). Meeting the challenge of students’ understanding of formula in high-school physics: A learning tool. Physics Education, 43(1), 75–82.
Bailer-Jones, D. (2009). Scientific models in philosophy of science. Pittsburgh: University of Pittsburgh Press.
Baltas, A. (1990). Once again on the meaning of physical concepts. In P. Nikolakopoulos (Ed.), Greek studies in the philosophy and history of science (pp. 293–313). Dordrecht: Kluwer.
Bardini, C., Radford, L., & Sabena, C. (2005). Struggling with variables, parameters, and indeterminate objects or how to go insane in mathematics. In H. Chick & J. Vincent (Eds.), Proceedings of the 29th conference of the international group for the psychology of mathematics education (Vol. 2, pp. 129–136). Australia: University of Melbourne.
Blay, M. (2002). La Science du Mouvement: de Galilée à Lagrange. Paris: Belin.
Blum, W., & Borromeo Ferri, R. (2009). Mathematical modeling: Can it be taught and learnt? Journal of Mathematical Modelling and Application, 1(1), 45–58.
Booth, L. R. (1988). Children’s difficulties in beginning algebra. In A. F. Coxford (Ed.), The ideas of algebra, K-12, 1988 yearbook (pp. 20–32). Reston, VA: National Council of Teachers of Mathematics.
Brewe, E. (2008). Modeling theory applied: Models in university physics classroom. American Journal of Physics, 76(12), 1155–1160.
Buty, C., & Mortimer, E. (2008). Dialogic/authoritative discourse and modeling in a high school teaching sequence on optics. International Journal of Science Education, 30(12), 1635–1660.
Capecchi, D. (2014). The problem of the motion of bodies: A historical view of the development of classical mechanics. Heidelberg: Springer.
Carnot, S. (1824). Réflexions sur la Puissance Motrice du Feu et sur les Machines Propres a Developer cette Puissance (p. 119). http://galica.bnf.fr.
Carnot, S. (1960). Reflections on the motive power of fire, and on machines fitted to develop that power (E. Mentoza, Ed., R. H. Thurston, Trans.). New York, Dover.
Castel, L. (1743). Vrai Système de Physique Générale de M. Isaac Newton. A la portée du Commun des Physiciens. Paris.
Christou, K., Vosniadou, S., & Vamvakousi, X. (2007). Students’ interpretations of literal symbols in algebra. In S. Vosniadou, A. Baltas, & X. Vamvakousi (Eds.), Reframing the conceptual change approach in learning and instruction. Amsterdam: Elsevier.
Cohen, F. (2010). How modern science came into the world: Four civilizations, one 17th-century breakthrough. Amsterdam: Amsterdam University Press.
Coll, R., & Lajium, D. (2011). Modeling and the future of science learning. In M. S. Khine & I. Saleh (Eds.), Models and modeling: Cognitive tools for scientific enquiry. Dordrecht: Springer.
Crawford, B., & Cullin, M. (2004). Supporting prospective teachers’ conceptions of modeling in science. International Journal of Science Education, 26(11), 1379–1401.
Crowe, Μ. (2007). Mechanics from Aristotle to Einstein. Santa Fe, New Mexico: Green Lion Press.
d’ Alembert J. R. (1743). Traite de Dynamique. Paris: Chez David, Libraire.
d’ Alembert J. R. (1749). Introduction aux Recherches sur la Precession des Equinoxes et sur la Nutation de l' Axe de la Terre dans le Systeme Newtonien, p. vii. Paris.
d’ Alembert, J. (1758). Traité de Dynamique, 2nd éd. Paris: David Libraire (Fac-sim par J. Gabey 1990).
de Fontenelle, B. B. (1752). Théorie des Tourbillions Cartésiens. Paris.
Dear, P. (1995). Discipline & experience: The mathematical way in the scientific revolution. Chicago: University of Chicago Press.
Dear, P. (2001). Revolutionizing the sciences: European knowledge and its ambitions, 1500–1700. Houndmills, Hampshire: Palgrave.
Dingrando, L., Fisher, D., Gonya, J., Haase, D., Klevickis, C., Turiel, I., et al. (2007). Focus on physical science. Colombus, OH: Glencoe/McGraw-Hill.
Ellermeijer, T., & Heck, A. (2002). Differences between the use of mathematical entities in mathematics and physics and the consequences for an integrated learning environment. In Proceedings of the first international GIREP seminar, September 2001, University of Udine, Italy (pp. 52–72).
Euler, L. (1752). Découverte d’ une Nouveau Principe de Mécanique. Mémoire de l’ Académie Royale des Sciences et Belles-Lettres de Berlin (Vol. 6, pp. 185–217).
Gabbey, A. (1992). Newton’s mathematical principles of natural philosophy: A treatise of ‘mechanics’? In P. M. Harman & A. Shapiro (Eds.), The investigation of difficult things: Essays on newton and the history of the exact sciences (pp. 303–320). Cambridge: Cambridge University Press.
Galileo, G. (1638). Discorsi e Dimostrazioni Matematiche, Intorno a Due Nuove Scienze (p. 171). http://galica.bnf.fr.
Galileo, G. (1978, 1st publ. 1638). Dialogues concerning the two new sciences (H. Grew & A. de Salvio, Trans.). In Great books of the western world: Gilbert, Galileo, Harvey (pp. 129–260). Chicago: Encyclopaedia Britannica.
Galileo, G. (2001, 1st publ. 1632). Dialogue concerning the two chief world systems (S. Drake, Trans.). New York: The Modern Library.
Galileo, G. (2010). Second letter from Galileo to Welser about the solar spots. In E. Reeves & A. van Helden (Eds. & Trans.), Galileo Galilei & Christoph Scheiner (pp. 107–130). Chicago: University of Chicago Press.
Giere, R. (1999). Science without laws. Chicago: University of Chicago Press.
Giere, R. (2006). Scientific perspectivism. Chicago: University of Chicago Press.
Gingras, Y. (2001). What did mathematics do to physics? History of Science, 39, 383–416.
Greca, I. M., & Moreira, M. A. (2001). Mental, physical, and mathematical models in the teaching and learning of physics. Science Education, 86(1), 106–121.
Grosslight, L., Unger, C., Jay, E., & Smith, C. (1991). Understanding models and their use in science: Conceptions of middle and high school students and experts. Journal of Research in Science Teaching, 28(9), 799–822.
Halloun, I. (1998). Interactive model-based education: An alternative to outcome-based education in physics. South African Journal of Science, 94, 313–318.
Halloun, I. (2006). Modeling theory in science education. Dordrecht: Springer.
Halloun, I. (2007). Mediated modeling in science education. Science & Education, 16(7), 653–697.
Hamper, C. (2009). Higher level physics for the I.B. diploma. Harlow, Essex: Pearson.
Hannam, J. (2010). God’s philosophers: How the medieval world laid the foundations of modern science. London: Icon Books.
Hansson, L., Hansson, Ö., Juter, K., & Redfors, A. (2015). Reality-theoretical models-mathematics: A ternary perspective on physics lessons in upper-secondary school. Science & Education, 24(5–6), 615–644.
Harper, E. (1987). Gosts of diofantus. Educational Studies in Mathematics, 18, 75–90.
Harrison, A. (2001). How do teachers and textbook writers model scientific ideas for students. Research in Science Education, 31, 401–435.
Hendry, R., & Psillos, S. (2007). How to do things with theories: An interactive view of language and models in science. In J. Brzeziński, A. Klawiter, T. Kuipers, K. Lastowski, K. Paprzycka, & P. Przybysz (Eds.), The courage of doing philosophy: Essays dedicated to Leszek Nowak (pp. 59–115). Amsterdam: Rodopi.
Hyslop, S. (2014). Algebraic collisions: Challenging descartes with cartesian tools. Foundations of Science, 19, 35–51.
Jackson, J., Dukerich, L., & Hestenes, D. (2008). Modeling instruction: An effective model for science education. Science Educator, 17(1), 10–17.
Johnston, K., Hewett, S., Holt, S., & Miller, J. (2015). Advanced physics for you. Oxford: Oxford University Press.
Jung, E. (2011). Intension and remission of forms. In H. Lagerlund (Ed.), Encyclopedia of medieval philosophy: Philosophy between 500 and 1500 (pp. 551–555). Springer: Dordrecht.
Justi, R., & Gilbert, J. (2003). Teachers’ views on the nature of models. International Journal of Science Education, 25(11), 1369–1386.
Karam, R., & Pietrocola, M. (2009). Recognizing the structural role of mathematics in physical thought. In M. Tasar & G. Cakmaki (Eds.), Contemporary science education research: International perspectives, a collection of Papers presented at ESERA 2009 conference, Istanbul (pp. 65–76).
Karam, R., Pospiech, G., & Pietrocola, M. (2010). Mathematics in physics lessons: Developing structural skills. In Symposium: addressing the role of mathematics in physics education, GIREP 2010, Reims.
Katz, V., & Parshall, K. H. (2014). Taming the unknown: A history of algebra from antiquity to the early twentieth century. Princeton: Princeton University Press.
Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics, 12, 317–326.
Klein, J. (1981, delivered as a lecture on the University of Marburg on February 3, 1932). The world of physics and the ‘natural’ world. The St. John’s Review, 33(1), 22–34.
Klein, M. (1990). Mathematical thought from ancient to modern times (Vol. II). Oxford: Oxford University Press.
Klein, J. (1998, 1st publ. 1968). Greek mathematical thought and the origin of algebra. New York: Dover.
Kuhn, T. S. (Ed.). (1977). Mathematical versus experimental traditions in the development of physical science. In The essential tension: Selected studies in scientific tradition and change (pp. 31–65). Chicago: University of Chicago Press.
Lemke, J. (1998). Multiplying meaning: Visual and verbal semiotics in scientific text. In J. Martin & R. Veel (Eds.), Reading science. London: Routledge.
Lewi, P. (2006). Speaking of graphics: An essay on graphicacy in science, technology and business. www.datascope.be/sog.htm.
Lindberg, D. (2008). The beginnings of western science: The European scientific tradition in philosophical, religious, and institutional context, prehistory to A.D. 1450. Chicago: Chicago University Press.
Löffler, P., & Kauertz, A. (2014). Applying physics models in context-based tasks in physics education. In C. Constantinou, N. Papadouris, & A. Hadjigeorgiou (Eds.), E-book proceedings of the ESERA 2013 conference: Science education research for evidence-based teaching and coherence in learning, strand 10 (pp. 171–179). Cyprus: Nicosia.
Macgregor, M., & Stacey, K. (1997). Students understanding of algebraic notation: 11–15. Educational Studies in Mathematics, 33, 1–19.
Mahoney, M. (1980). The beginnings of algebraic thought in the seventeenth century. In S. Gaukroger (Ed.), Descartes: Philosophy, mathematics and physics, chap. 5. Hassocks: The Harvester Press.
Mahoney, M. (2012). The mathematical realm of nature. In D. Garber & M. Ayers (Eds.), The cambridge history of seventeenth-century philosophy (pp. 702–756). Cambridge: Cambridge University Press.
Malone, K. (2008). Correlations among knowledge structures, force concept inventory, and problem-solving behaviors. Physical Review Physics Education Research, 4(2), 020107.
Marshall, D. B. (2011). Investigations into the applicability of geometry. Dissertation Thesis. Harvard University.
Matthews, M. (2005). Idealization and Galileo’s pendulum discoveries: Historical, philosophical and pedagogical considerations. In M. Matthews, C. Gauld, & A. Stinner (Eds.), The pendulum (pp. 209–235). Dortrecht: Springer.
McMullin, E. (1985). Galilean idealization. Studies in History and Philosophy of Science, 16(3), 247–273.
Murdoch, E., & Sylla, E. (1978). The science of motion. In D. Lindberg (Ed.), Science in the middle ages. Chicago: University of Chicago Press.
Newton, I. (1687). Philosophiae Naturalis Principia Mathematica (p. 37). http://galica.bnf.fr.
Newton, I. (1999). The principia (I. B. Cohen & A. Whitman, Trans.). Berkeley: University of California Press.
Petersen, O., & Pihl, M. (1974). Early physics and astronomy: A historical introduction. London: Macdonald & Janes.
Pietrocola, M. (2008). Mathematics as structural language of physical thought. In M. Vicentini & E. Sassi (Eds.), Connecting research in physics education with teacher education. International Commission on Physics Education. http://web.phys.ksu.edu/icpe/Publications/teach2/index.html.
Ravetz, J. (1961). The representation of physical quantities in eighteenth-century mathematical physics. Isis, 52(1), 7–20.
Redish, E. (2005). Problem solving and the use of math in physics courses. In Proceedings of the conference world view on physics education in 2005: Focusing on change, Delhi, August 2005.
Redish, E., & Kuo, K. (2015). Language of physics, language of math: Disciplinary culture and dynamic epistemology. Science & Education, 24(5–6), 561–590.
Rowe, D. (1996). New trends and old images in the history of mathematics. In R. Calinger (Ed.), Vita mathematica: Historical research and integration with teaching (pp. 3–16). Washington, DC: The Mathematical Association of America.
Schemmel, M. (2014). Medieval representations of change and their early modern application. Foundations of Science, 19, 11–34.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, 22, 1–36.
Sfard, A. (1995). The development of algebra: Confronting historical and psychological perspectives. Journal of Mathematical Behavior, 14, 15–39.
Skemp, R. (1976). Relational understanding and instrumental understanding. Mathematics Teaching, 77, 20–26.
Stenlund, S. (2015). On the origin of symbolic mathematics and its significance for Wittgenstein’s thought. Nordic Wittgenstein Review, 4(1), 7–92.
Stinner, A. (2007a). LCP 1: From intuitive physics to star trek. www.ArthurStinner.com.
Stinner, A. (2007b). LCP 2: Motion and the pendulum. www.ArthurStinner.com.
Suárez, M. (1999). The role of models in the application of scientific theories: Epistemological implications. In M. Morgan & M. Morrison (Eds.), Models as mediators: Perspectives on natural and social science (pp. 168–196). Cambridge: Cambridge University Press.
Taasoobshirazi, G., & Carr, M. (2008). A review and critique of context-based physics instruction and assessment. Educational Research Review, 3, 155–167.
Thompson, P. W. (1994). Students, functions, and the undergraduate curriculum. In E. Dubinsky, A. H. Schoenfeld, & J. J. Kaput (Eds.), Research in collegiate mathematics education I (pp. 21–44). Providence RI: American Mathematical Society.
Uhden, O., Karam, R., Pietrocola, M., & Pospiech, G. (2012). Modeling mathematical reasoning in physics education. Science & Education, 21, 485–506.
Uhden, O., & Pospiech, G. (2010). Translating between mathematics and physics: Analysis of student’s difficulties. In W. Kaminski & M. Kaminski (Eds.), GIREP 2010, teaching and learning physics today: Challenges? Benefits? (pp. 102–106). France: Reims.
Uhden, O., & Pospiech, G. (2012). Mathematics in physics: Analysis of students’ difficulties. In C. Bruguière, A. Tiberghien & P. Clément (Eds.), E-book proceedings of the ESERA conference 2011: Science learning and citizenship. Part 3 M. Michelini & R. Duit (co-eds) (pp. 218–222). Lyon, France: European Science Education Research Association.
Unguru, S. (1975). On the need to rewrite the history of greek mathematics. Archive for History of Exact Sciences, 15(1), 67–114.
Unguru, S. (1979). History of ancient mathematics: Some reflections on the state of the art. Isis, 70(4), 555–565.
Ursini, S., & Trigueros, M. (2004). How do high school students interpret parameters in algebra? In M. Johnsen Høines & A. B. Fuglestad (Eds.), Proceedings of the 28th conference of the international group for the psychology of mathematics education (Vol. 4, pp. 361–368).
Van der Waerden, B. L. (1976). Defence of a ‘shocking’ point of view. Archive for History of Exact Sciences, 15(3), 199–210.
Van Driel, J., & Verloop, N. (1999). Teachers’ knowledge of models and modeling in science. International Journal of Science Education, 21(11), 1141–1153.
Van Dyck, M., & Heeler, A. (2014). Script and symbolic writing in mathematics and natural philosophy. Foundations of Science, 19, 1–10.
Varignon, P. (1700). Manière générale de determiner les forces, les vitesses, les espaces, et les temps, une seule de ces quatre choses étant donnée dans toutes fortes de mouvements rectilignes variés à discrétion, Paris. Histoire de l’ Académie Royale des Sciences, année 1700 (pp. 22–27).
Viète, F. (1983, 1st publ. in Latin in 1591). The analytic art (R. Witmer, Trans.). New York: Dover.
Vosniadou, S. (2013). Model based reasoning and the learning of counter-intuitive science concepts. Infancia y Aprendizaje, 36(1), 5–33.
Wallis, J. (1685). A treatise of algebra. London: Richard Davis.
Weil, A. (1978). Who betrayed Euclid? (Extract from a letter to the editor). Archive for History of Exact Sciences, 19(2), 91–93.
Yoder, J. (1998). Unrolling time: Christiaan Huygens and the mathematization of nature. Cambridge: Cambridge University Press.
Zoupidis, A., Pnevmatikos, D., Spyrtou, A., & Kariotoglou, P. (2016). The impact of the acquisition of procedural and epistemological knowledge in conceptual understanding: The case of density and floating-sinking phenomena. Instructional Science. doi:10.1007/s11251-016-9375-z.
Conflict of interest
The authors declare that there is no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kanderakis, N. The Mathematics of High School Physics. Sci & Educ 25, 837–868 (2016). https://doi.org/10.1007/s11191-016-9851-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11191-016-9851-5