Skip to main content
SpringerLink
Log in

Bilinear form and soliton interactions for the modified Kadomtsev–Petviashvili equation in fluid dynamics and plasma physics

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

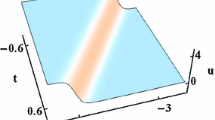
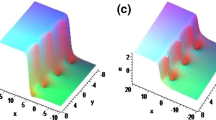
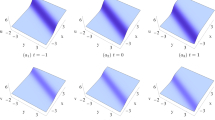
In this paper, we investigate the modified Kadomtsev–Petviashvili (mKP) equation for the nonlinear waves in fluid dynamics and plasma physics. By virtue of the rational transformation and auxiliary function, new bilinear form for the mKP equation is constructed, which is different from those in previous literatures. Based on the bilinear form, one- and two-soliton solutions are obtained with the Hirota method and symbolic computation. Propagation and interactions of shock and solitary waves are investigated analytically and graphically. Parametric conditions for the existence of the shock, elevation solitary, and depression solitary waves are given. From the two-soliton solutions, we find that the (i) parallel elastic interactions can exist between the (a) shock and solitary waves, and (b) two elevation/depression solitary waves; (ii) oblique elastic interactions can exist between the (a) shock and solitary waves, and (b) two solitary waves; (iii) oblique inelastic interactions can exist between the (a) two shock waves, (b) two elevation/depression solitary waves, and (c) shock and solitary waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. Oblique solitons mean that there exists a nonzero angle between the two solitons when they interact [15].

  2. Note that bilinear form (3a), (3b), (3c) is a new one, which is different from those obtained with the double logarithmic transformation in [28, 40].

References

  1. Zabusky, N.J., Kruskal, M.D.: Interaction of “ solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243 (1965)

    Article  MATH  Google Scholar 

  2. Ablowitz, M.J., Clarkson, P.A.: Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  Google Scholar 

  3. Agrawal, G.P.: Nonlinear Fiber Optics. Academic Press, San Diego (1995)

    Google Scholar 

  4. Belashov, V.Y., Vladimirov, S.V.: Solitary Waves in Dispersive Complex Media. Springer, Berlin (2005)

    MATH  Google Scholar 

  5. Qu, Q.X., Tian, B., Liu, W.J., Li, M., Sun, K.: Painlevé integrability and N-soliton solution for the variable-coefficient Zakharov–Kuznetsov equation from plasmas. Nonlinear Dyn. 62, 229–235 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  6. Anderson, M.H., Ensher, J.R., Matthews, M.R., Wieman, C.E., Cornell, E.A.: Observation of Bose–Einstein condensation in a dilute atomic vapor. Science 269, 198–201 (1995)

    Article  Google Scholar 

  7. Davis, K.B., Mewes, M.O., Andrews, M.R., van Druten, N.J., Durfee, D.S., Kurn, D.M., Ketterle, W.: Bose–Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 75, 3969–3973 (1995)

    Article  Google Scholar 

  8. Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Method for solving the Korteweg–de Vries equation. Phys. Rev. Lett. 19, 1095–1097 (1967)

    Article  MATH  Google Scholar 

  9. Steeb, W.H., Euler, N.: Nonlinear Evolution Equations and Painlevé Test. World Scientific, Singapore (1988)

    Book  MATH  Google Scholar 

  10. Rogers, C., Shadwick, W.F.: Bäcklund Transformations and Their Applications. Academic Press, New York (1982)

    MATH  Google Scholar 

  11. Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer, Berlin (1991)

    Book  MATH  Google Scholar 

  12. Hirota, R.: The Direct Method in Soliton Theory. Springer, Berlin (1980)

    Google Scholar 

  13. Wang, S., Tang, X.Y., Lou, S.Y.: Soliton fission and fusion: Burgers equation and Sharma–Tasso–Olver equation. Chaos Solitons Fractals 21, 231–239 (2004)

    Article  MathSciNet  Google Scholar 

  14. Zhang, C., Tian, B., Meng, X.H., Lü, X., Cai, K.J., Geng, T.: Painlevé integrability and N-soliton solution for the Whitham–Broer–Kaup shallow water model using symbolic computation. Z. Naturforsch. A 63, 253–260 (2008)

    Google Scholar 

  15. Zhang, H.Q., Meng, X.H., Li, J., Tian, B.: Soliton resonance of the (2+1)-dimensional Boussinesq equation for gravity water waves. Nonlinear Anal., Real World Appl. 9, 920–926 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Medina, E.: An N soliton resonance solution for the KP equation: interaction with change of form and velocity. Lett. Math. Phys. 62, 91–99 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  17. Jiang, Y., Tian, B., Liu, W.J., Li, M., Wang, P., Sun, K.: Solitons, Bäcklund transformation, and Lax pair for the (2+1)-dimensional Boiti–Leon–Pempinelli equation for the water waves. J. Math. Phys. 51, 093519 (2010)

    Article  MathSciNet  Google Scholar 

  18. Konopelchenko, B.G., Dubrovsky, V.G.: Some new integrable nonlinear evolution equations in 2+1 dimensions. Phys. Lett. A 102, 15–17 (1984)

    Article  MathSciNet  Google Scholar 

  19. Ren, B., Lin, J.: A new (2+1)-dimensional integrable equation. Commun. Theor. Phys. 51, 13–16 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Wazwaz, A.M.: Multi-front waves for extended form of modified Kadomtsev–Petviashvili equation. Appl. Math. Mech. 32, 875–880 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. O’Keir, I.S., Parkes, E.J.: The derivation of a modified Kadomtsev–Petviashvili equation and the stability of its solutions. Phys. Scr. 55, 135–142 (1997)

    Article  Google Scholar 

  22. Xu, T., Zhang, H.Q., Zhang, Y.X., Li, J., Feng, Q., Tian, B.: Two types of generalized integrable decompositions and new solitary-wave solutions for the modified Kadomtsev–Petviashvili equation with symbolic computation. J. Math. Phys. 49, 013501 (2008)

    Article  MathSciNet  Google Scholar 

  23. Hao, H.H., Zhang, D.J.: Soliton resonances for the modified Kadomtsev–Petviashvili equations in uniform and non-uniform media. Mod. Phys. Lett. B 24, 277–288 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  24. Veerakumar, V., Daniel, M.: Modified Kadomtsev–Petviashvili (MKP) equation and electromagnetic soliton. Math. Comput. Simul. 62, 163–169 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  25. Sun, Z.Y., Gao, Y.T., Yu, X., Meng, X.H., Liu, Y.: Inelastic interactions of the multiple-front waves for the modified Kadomtsev–Petviashvili equation in fluid dynamics, plasma physics and electrodynamics. Wave Motion 46, 511–521 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  26. Tsuji, H., Oikawa, M.: Two-dimensional interaction of solitary waves in a modified Kadomtsev–Petviashvili equation. J. Phys. Soc. Jpn. 73, 3034–3043 (2004)

    Article  MATH  Google Scholar 

  27. Das, G.C., Sarma, J.: Evolution of solitary waves in multicomponent plasmas. Chaos Solitons Fractals 9, 901–911 (1998)

    Article  MATH  Google Scholar 

  28. Hirota, R.: Classical Boussinesq equation is a reduction of the modified KP equation. J. Phys. Soc. Jpn. 54, 2409–2415 (1985)

    Article  MathSciNet  Google Scholar 

  29. Dubrovsky, V.G.: The construction of exact multiple pole solutions of some (2+1)-dimensional integrable nonlinear evolution equations via the \(\overline{\partial}\)-dressing method. J. Phys. A 32, 369–390 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  30. Dai, H.H., Geng, X.G.: On the decomposition of the modified Kadomtsev–Petviashvili equation and explicit solutions. J. Math. Phys. 41, 7501 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  31. Chen, A.H., Wang, F.F., Zhang, W.G.: Soliton solutions of Burgers’ equation and the modified Kadomtsev–Petviashvili equation. J. Phys. A 43, 365202 (2010)

    Article  MathSciNet  Google Scholar 

  32. Chen, J.B., Geng, X.G.: Algebro-geometric solution to the modified Kadomtsev–Petviashvili equation. J. Phys. Soc. Jpn. 74, 2217–2222 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  33. Chen, J.B., Geng, X.G.: Some quasi-periodic solutions to the Kadometsev–Petviashvili and modified Kadometsev–Petviashvili equations. Eur. Phys. J. B 50, 445–452 (2006)

    Article  MathSciNet  Google Scholar 

  34. Yan, Z.Y.: Jacobi elliptic function solutions of nonlinear wave equations via the new sinh-Gordon equation expansion method. J. Phys. A 36, 1961–1972 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  35. Deng, S.F.: Darboux transformations for the isospectral and nonisospectral mKP equation. Physica A 382, 487–493 (2007)

    Article  Google Scholar 

  36. Tian, B., Gao, Y.T.: Variable-coefficient higher-order nonlinear Schrödinger model in optical fibers: New transformation with burstons, brightons and symbolic computation. Phys. Lett. A 359, 241–248 (2006)

    Article  Google Scholar 

  37. Li, M., Bo, T., Liu, W.J., Zhang, H.Q., Meng, X.H., Xu, T.: Soliton-like solutions of a derivative nonlinear Schrödinger equation with variable coefficients in inhomogeneous optical fibers. Nonlinear Dyn. 62, 919–929 (2010)

    Article  MATH  Google Scholar 

  38. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Wronskian solutions and integrability for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Nonlinear Dyn. 67, 1023–1030 (2012)

    Article  MathSciNet  Google Scholar 

  39. Wang, L., Gao, Y.T., Meng, D.X., Gai, X.L., Xu, P.B.: Soliton-shape-preserving and soliton-complex interactions for a (1+1)-dimensional nonlinear dispersive-wave system in shallow water. Nonlinear Dyn. 66, 161–168 (2011)

    Article  MathSciNet  Google Scholar 

  40. Deng, S.F.: The multisoliton solutions for the mKPI equation with self-consistent sources. J. Phys. A 39, 14929–14945 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  41. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Wronskian solutions and integrability for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Nonlinear Dyn. 67, 1023–1030 (2012)

    Article  MathSciNet  Google Scholar 

  42. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Solitonic propagation and interaction for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Phys. Rev. E 83, 056601 (2011)

    Article  Google Scholar 

  43. Sun, Z.Y., Gao, Y.T., Yu, X., Liu, Y.: Amplification of nonautonomous solitons in the Bose–Einstein condensates and nonlinear optics. Europhys. Lett. 93, 40004 (2011)

    Article  Google Scholar 

  44. Sun, Z.Y., Gao, Y.T., Liu, Y., Yu, X.: Soliton management for a variable-coefficient modified Korteweg–de Vries equation. Phys. Rev. E 84, 026606 (2011)

    Article  Google Scholar 

  45. Meng, G.Q., Gao, Y.T., Yu, X., Shen, Y.J., Qin, Y.: Painleve analysis, Lax pair, Backlund transformation and multi-soliton solutions for a generalized variable-coefficient KdV–mKdV equation in fluids and plasmas. Phys. Scr. 85, 055010 (2012)

    Article  Google Scholar 

  46. Meng, G.Q., Gao, Y.T., Yu, X., Shen, Y.J., Qin, Y.: Multi-soliton solutions for the coupled nonlinear Schrodinger-type equations. Nonlinear Dyn. 70, 609 (2012)

    Article  MathSciNet  Google Scholar 

  47. Sun, Z.Y., Gao, Y.T., Yu, X., Liu, W.J., Liu, Y.: Bound vector solitons and soliton complexes for the coupled nonlinear Schrödinger equations. Phys. Rev. E 80, 066608 (2009)

    Article  Google Scholar 

Download references

Acknowledgements

This work has been supported by the National Natural Science Foundation of China under Grant No. 11272023, by the Fundamental Research Funds for the Central Universities of China under Grant No. 2011BUPTYB02, and by the Open Fund of State Key Laboratory of Information Photonics and Optical Communications (Beijing University of Posts and Telecommunications).

Author information

Authors and Affiliations

  1. State Key Laboratory of Information Photonics and Optical Communications, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yan Jiang, Bo Tian, Pan Wang & Min Li

  2. School of Science, Beijing University of Posts and Telecommunications, P.O. Box 122, Beijing, 100876, China

    Yan Jiang, Bo Tian, Pan Wang & Min Li

Authors
  1. Yan Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Min Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Tian.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jiang, Y., Tian, B., Wang, P. et al. Bilinear form and soliton interactions for the modified Kadomtsev–Petviashvili equation in fluid dynamics and plasma physics. Nonlinear Dyn 73, 1343–1352 (2013). https://doi.org/10.1007/s11071-013-0867-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-0867-y

Keywords

Search

Navigation