1 Introduction

In current research and industrial applications, there is a need for fast multibody (MBS) dynamics simulations. One can encounter applications like that in such areas as robotics, biomechanics, and automotive industry. The other places where one needs efficient MBS simulations can be found in various interdisciplinary applications like, e.g., molecular dynamics simulations [1, 2] or granular media physics [3]. The applications are more complex and demanding. They may come from different domains and more often require the exploitation of coupling techniques [4]. In this context, numerical formulations for MBS should provide stable, accurate and reliable results. This short literature review is mainly focused on efficient sequential and parallel algorithms for multi-rigid body dynamics. Also the Hamiltonian based formulations are recalled from the MBS simulations point of view.

Due to the advances in the robotics field, there has been a growing attention to the development of efficient, low order algorithms for the simulation of open-loop and closed-loop kinematic chain system dynamics [5–7]. It is especially worth noticing the analogies between the optimal filtering theory and robot dynamics [8] that gave foundations for various mass matrix factorizations of a manipulator. The idea of articulated body inertias (ABI) for solving the equations of motion for an \(n\)-link manipulator, originally introduced by Featherstone [9], expanded into various forms and flavors. A summary of ABI-like algorithms can be found in [10]. There are also recent advances in the field which can be found in different papers, e.g., [11–13]. The mature technology associated with recursive formulations gave basis for further development of efficient low order parallel algorithms.

With the advances in parallel computer architectures, researchers paid more attention to the development of parallel algorithms for multibody dynamics. This trend can be observed in early works in this field, e.g., [14–16]. In 1999, Featherstone [17] developed truly optimal-time, logarithmic order divide-and-conquer algorithm (DCA) for the dynamics of tree-like topologies as well as closed-loop multibody systems. Other authors [18] preferred the idea of a decomposition of multibody system into sub-chains. In [19], Critchley and Anderson explored the notion of recursive coordinate reduction. There are other works associated with parallel multibody dynamics simulations as well [3, 20, 21]. Recently, the divide-and-conquer based schemes [17] have attracted significant attention to the development of efficient parallel algorithms for large MBS, partially due to the fact that computationally powerful multicore processors or graphics processor units are cheaply available on the market. Various algorithms that are effectively based on the Featherstone’s DCA are elaborated with myriad of extensions to, e.g., humanoid robot simulations [22], molecular dynamics simulations, real-time applications, discontinuous changes in the system topology [23], sensitivity analysis, constraint enforcement [24–27], nonholonomic constraints, flexible multibody systems, or generalized constraint treatment. Advances in the application of the DCA approach to large multibody system simulations can be found in [28].

On the other hand, Hamilton’s canonical equations constitute an interesting alternative as a basis for elaborating low order formulations. As Hamilton’s canonical equations are expressed in terms of velocities and momenta of the system and the possible constraints are usually imposed at the velocity level, many sources indicate profitable characteristics of the Hamiltonian approach from the numerical point of view. Various authors exploited this approach for real-time simulations of vehicles [29], in the analyses of MBS subjected to intermittent motion [30], and in the development of penalty methods for constrained mechanical system dynamics [31]. Other interesting Hamiltonian based low order algorithms can be found in [32], where a recursive \(O(n)\) algorithm for multi-rigid-body dynamics has been presented. Initially, the formulations are elaborated for serial chains and subsequently extended to deal with closed-loop topologies. Nevertheless, the approach is purely sequential since it is based on the idea of ABI. Surprisingly, the literature review reveals that it is difficult to find a fully parallel approach for multi-rigid body dynamics simulations based on the Hamiltonian approach.

In previous papers [33, 34], the authors proposed a Hamiltonian based divide-and-conquer algorithm (HDCA) for open-loop multi-rigid body dynamics. In this paper, the HDCA algorithm is significantly extended and generalized to deal with systems possessing closed-loop and coupled-loops topologies. The method solves Hamilton’s canonical equations for constrained multi-rigid-body system in a divide-and-conquer manner. While the state of the mechanical system is described in terms of joint coordinates and joint momenta, the absolute coordinates are used as well to clearly present the underlying relationships between the variables. The HDCA recursive procedure for closed-loop multibody systems allows one to evaluate joint velocities and time derivatives of joint momenta with the aid of velocity level constraint equations in an efficient and parallelizable manner.

This paper is divided into four sections. Following the Introduction with brief literature review, Sect. 2 introduces basic concepts and definitions exploited in the paper and demonstrates novel Hamiltonian based parallel formulation for multi-rigid-body system dynamics possessing closed-loop chains. Section 3 describes and discusses the numerical results that were gathered to indicate the accuracy and efficiency of the proposed formulation. Original contributions of the paper are summarized in the last section.

2 Algorithm formulation

2.1 Hamilton’s canonical equations

This section provides a detailed formulation of the HDCA algorithm for the dynamics of complex multibody systems by utilizing the Hamilton’s approach. Before we begin with the algorithm development, Hamilton’s canonical equations for constrained multi-rigid body systems are recalled in a brief manner. At first, the classical equations of motion in dependent canonical coordinates are formulated. Subsequently, more elaborated form of Hamilton’s equations is demonstrated through the exploitation of the augmented momenta.

The state of the multibody system having \(n\) degrees of freedom can be described by a set of first-order Hamilton’s differential equations in the form [35, 36]

$$\begin{aligned} &\dot{\mathbf{q}}_{n} = \biggl( \frac{\partial \mathcal{H}(t,\mathbf {q} _{n},\mathbf {p}_{n})}{\partial \mathbf{p}_{n}} \biggr) ^{T} , \end{aligned}$$
(1)
$$\begin{aligned} &\dot{\mathbf{p}}_{n} = - \biggl( \frac{\partial \mathcal{H}(t,\mathbf {q} _{n},\mathbf {p}_{n})}{\partial \mathbf{q}_{n}} \biggr) ^{T}+ \mathbf{Q} _{n} -\boldsymbol {\Phi}^{T}_{\mathbf{q}} \boldsymbol{\lambda }_{m} , \end{aligned}$$
(2)
$$\begin{aligned} &\boldsymbol {\Phi} ( t,\mathbf{q}_{n} ) = \mathbf{0} \quad \Rightarrow \quad \dot{\boldsymbol {\Phi}}(t,\mathbf{q}_{n},\dot{ \mathbf{q}}_{n})= \boldsymbol {\Phi} _{\mathbf{q}}\dot{\mathbf{q}}_{n} + \boldsymbol {\Phi}_{t} = \mathbf {0}, \end{aligned}$$
(3)

where \(\mathbf{q}_{n}\), \(\mathbf{p}_{n}\) are system’s canonical coordinates and momenta, \(\mathbf{Q}_{n}\) are external, applied and centrifugal forces, and \(\boldsymbol {\Phi}\) are \(m\) algebraic constraint equations, which have to be fulfilled and which are associated with the unknown Lagrange multipliers \(\boldsymbol{\lambda }_{m}\). The terms \(\boldsymbol {\Phi}_{\mathbf{q}}\) and \(\boldsymbol {\Phi}_{t}\) represent the partial derivatives of the constraint equations with respect to the generalized coordinates and time, respectively. The Hamiltonian function is the Legendre transformation of the Lagrangian function, and it is defined as

$$ \mathcal{H}(t, \mathbf {q}_{n}, \mathbf {p}_{n}) = \dot{ \mathbf {q}}_{n}^{T} \mathbf {p} _{n} - \mathcal{L}(t, \mathbf {q}_{n}, \dot{\mathbf {q}}_{n}). $$
(4)

We consider mechanical systems subjected to holonomic constraints which are assumed to be independent. The motion of the system is analyzed with respect to the inertial reference frame. Since the total kinetic energy \(T\) is a quadratic function of the generalized velocities, it can be expressed with the use of canonical momenta

$$ T = \frac{1}{2} \dot{\mathbf {q}}_{n}^{T} \mathbf {M} \dot{\mathbf {q}}_{n} = \frac{1}{2} \dot{\mathbf {q}}_{n}^{T} \mathbf {p}_{n}, $$
(5)

where \(\mathbf {M}\) is the mass matrix of the system. As presented in [30], it is possible to reformulate Hamilton’s equations of motion to obtain a form which is more suitable for numerical implementations

$$\begin{aligned} \mathbf {P}_{n} & = \mathbf {M} \dot{\mathbf {q}}_{n} - \boldsymbol {\Phi}_{\mathbf{q}} ^{T} \boldsymbol {\sigma}_{m} , \end{aligned}$$
(6)
$$\begin{aligned} \dot{\mathbf {P}}_{n} &= \mathbf {Q}_{n} - \dot{\boldsymbol {\Phi}}_{\mathbf {q}}^{T} \boldsymbol {\sigma} _{m}, \end{aligned}$$
(7)

where \(\boldsymbol {\sigma}_{m}\) are the unknown constraint Lagrange multipliers impulses associated with the constraint equations at the velocity level, and \(\mathbf {P}_{n}\) are called augmented momenta vectors. One can combine (6) together with the velocity level constraint equations (3) to get a more concise matrix form

$$ \begin{bmatrix} \mathbf {M} & \boldsymbol {\Phi}_{\mathbf{q}}^{T} \\ \boldsymbol {\Phi}_{\mathbf{q}} & \mathbf {0} \end{bmatrix} \begin{bmatrix} \dot{\mathbf {q}}_{n} \\ -\boldsymbol {\sigma}_{m} \end{bmatrix} = \begin{bmatrix} \mathbf {P}_{n} \\ -\boldsymbol {\Phi}_{t} \end{bmatrix} . $$
(8)

Equations (7) and (8) describe the motion of a system through a set of \(2n+m\) equations, which have to be solved and integrated at each time-step to determine the state of the system in the next time-instant. To be able to solve the differential–algebraic equations, one has to specify initial conditions for positions and momenta at joints, which have to be consistent with the imposed constraint equations. It is easier to specify initial conditions for position of a system. The initial conditions for momenta \(\mathbf {p} _{n}\) can be calculated using (6). In order to do that, one has to assume that at the initial time-step all constraint force impulses are known to be zero (\(\boldsymbol {\sigma}_{m} = \mathbf {0}\)), and no momentum is absorbed at constrained directions (see [30] for a more detailed discussion).

2.2 Joint velocities and constraint force impulses

Articulated momentum definition and the integral form of the equations of motion

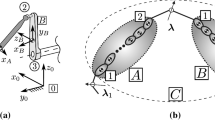
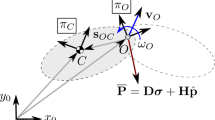
At an arbitrary point \(O\), which is not coincident with a body’s center of mass \(C\) (see Fig. 1b), the spatial momentum vector for a general body can be defined in a matrix form as \(\mathbf {P}_{O} \in {\mathcal{R}}^{6}\) [32]

$$ \mathbf {P}_{O} = \mathbf {M}_{O} \mathbf {V}_{O} = \begin{bmatrix} m\mathbf {I} & -m\widetilde{\mathbf {l}_{OC}} \\ m\widetilde{\mathbf {l}_{OC}} & \mathbf {J}_{O} \end{bmatrix} \begin{bmatrix} \mathbf {v}_{O} \\ \boldsymbol {\omega} \end{bmatrix} . $$
(9)

All expressions in (9) are derived with respect to the local coordinate frame with the origin at point \(O\) and then expressed in the global reference frame. The term \(\mathbf {M}_{O} \in {\mathcal{R}}^{6\times 6}\) denotes a mass matrix of the body for a given vector \(\mathbf {l}_{OC}\) between point \(O\) and point \(C\), while \(\mathbf {V} _{O}\) is a spatial velocity vector composed of translational \(\mathbf {v} _{O}\) and rotational \(\boldsymbol {\omega}\) components. The term \(m\) is the mass of that body and \(\mathbf {J}_{O}\) is the moment of inertia with respect to the axis of local reference frame defined at point \(O\) and expressed in the global reference frame. The identity matrix is defined as \(\mathbf {I}\in {\mathcal{R}}^{3}\) and the tilde symbol above a vector defines a skew-symmetric matrix associated with this vector. Let us consider a physical or compound rigid body \(A\) connected with the rest of the multibody system by arbitrary kinematic joints at the boundary points \(O_{1}\) and \(O_{2}\) as depicted in Fig. 1. From now on, let us consider such points as body’s interfaces called handles, by means of which the body communicates with the rest of the system using both active and constraint force components. Particularly, the spatial articulated momentum vector \(\overline{\mathbf {P}}\in {\mathcal{R}} ^{6}\) of linear and angular momenta related to a handle can be defined as

$$ \overline{\mathbf {P}} = \mathbf {D} \boldsymbol {\sigma} + \mathbf {H} \mathbf {p}, $$
(10)

where \(\mathbf {H}\in {\mathcal{R}}^{6\times n_{f}}\) represents the joint’s motion subspace (\(n_{f}\) – number of degrees of freedom for the joint) and \(\mathbf {D}\in {\mathcal{R}}^{6\times (6-n_{f})}\) is associated with the joint’s constrained directions [24, 26]. We assume that both matrices \(\mathbf {H}\) and \(\mathbf {D}\) consist of ones and zeros. The following identities hold in the formulation: \(\mathbf {H}^{T} \mathbf {H}=\mathbf {I}\), \(\mathbf {D}^{T} \mathbf {D}=\mathbf {I}\). The matrices \(\mathbf {H}\) and \(\mathbf {D}\) are orthogonal to each other, which yields the condition

$$ \mathbf {D}^{T} \mathbf {H} = \mathbf {0}. $$
(11)

Equation (10) assumes that the articulated momentum vector taken up from the system can be decomposed into the parts related to the active component \(\mathbf {H}\mathbf {p}\) and constraint component \(\mathbf {T}=\mathbf {D} \boldsymbol {\sigma}\). Vector \(\mathbf {p}\in {\mathcal{R}}^{n _{f}\times 1}\) denotes the joint canonical momenta, whereas vector \(\boldsymbol {\sigma}\in {\mathcal{R}}^{6-n_{f}}\) indicates constraint load impulses (Lagrange multipliers at the velocity level) at joints. The following condition holds for the Lagrange multipliers \(\dot{\boldsymbol {\sigma}}=\boldsymbol {\lambda}\) [30]. For an exemplary body \(A\) (see Fig. 1) with two handles at points \(O_{1}\) and \(O_{2}\), the integral form of the equations of motion can be formulated with the use of articulated momentum vectors as

$$\begin{aligned} &\mathbf {M}_{1}^{A} \mathbf {V}_{1}^{A} = \overline{\mathbf {P}_{1}^{A}} + \mathbf {S} _{12}^{A} \overline{\mathbf {P}_{2}^{A}} \end{aligned}$$
(12)
$$\begin{aligned} &\mathbf {M}_{2}^{A} \mathbf {V}_{2}^{A} = \mathbf {S}_{21}^{A} \overline{\mathbf {P} _{1}^{A}} + \overline{\mathbf {P}_{2}^{A}}, \end{aligned}$$
(13)

where the subscripts 1 or 2 indicate the handles \(O_{1}\) and \(O_{2}\). The above equations make use of the shift matrices \(\mathbf {S}_{12}^{A}\) and \(\mathbf {S}_{21}^{A}\), which are a handy tool for the transformation of six-dimensional momentum, force, and velocity vectors to other points of operation. If the position vector \(\mathbf {l}_{12}\) is measured from the point \(O_{1}\) to \(O_{2}\), the shift matrix takes the form

$$ \mathbf {S}_{12}^{A} = \begin{bmatrix} \mathbf {I} & \mathbf {0} \\ \widetilde{\mathbf {l}_{12}} & \mathbf {I} \end{bmatrix} _{6\times 6}, $$
(14)

where \(\mathbf {0}\in {\mathcal{R}}^{3\times 3}\) is the null matrix of appropriate size and \(\widetilde{\mathbf {l}_{12}}\) is a skew-symmetric matrix. By performing minor modifications, (12)–(13) can be rearranged (by using (10)) into the more favorable form

$$\begin{aligned} &\mathbf {V}_{1}^{A} = \boldsymbol {\xi}_{11}^{A} \mathbf {T}_{1}^{A} + \boldsymbol {\xi} _{12}^{A} \mathbf {T}_{2}^{A} + \boldsymbol {\xi}_{10}^{A} , \end{aligned}$$
(15)
$$\begin{aligned} &\mathbf {V}_{2}^{A} = \boldsymbol {\xi}_{21}^{A} \mathbf {T}_{1}^{A} + \boldsymbol {\xi} _{22}^{A} \mathbf {T}_{2}^{A} + \boldsymbol {\xi}_{20}^{A}. \end{aligned}$$
(16)

Equations (15)–(16) provide a direct relationship between the spatial velocity vectors \(\mathbf {V} _{1}^{A}\), \(\mathbf {V}_{2}^{A}\) of body \(A\) and constraint force impulses acting on the terminal bodies \(\mathbf {T}_{1}^{A}\), \(\mathbf {T}_{2}^{A}\). These equations form an integral form of the equations of motion for a general body \(A\) with two handles. The recursive assembly–disassembly procedure allows one to calculate all constraint force impulses and joint velocities in a divide-and-conquer manner. As a final remark, it is worth noticing that the matrix coefficients \(\boldsymbol {\xi}_{11}^{A}\), \(\boldsymbol {\xi}_{12}^{A}\), \(\boldsymbol {\xi}_{21}^{A}\), \(\boldsymbol {\xi}_{22}^{A}\) for the velocity level equations have the same form as the coefficients formulated in the original Featherstone’s paper (cp. [17]) for acceleration based equations. The coefficients include the system’s mass and inertia parameters. On the other hand, the quantities \(\boldsymbol {\xi}_{10}^{A}\), \(\boldsymbol {\xi}_{20}^{A}\) are associated with joint’s canonical momenta and joint positions.

Fig. 1
figure 1

A compound body \(A\) with two handles

Full size image

2.2.1 Assembly phase

This subsection formulates the integral form of the equations of motion for a compound body \(C\). Let us define a set of bodies \(A\) and \(B\) interconnected by a kinematic joint as shown in Fig. 2. The integral form of the equations of motion for body \(A\) and body \(B\) can be written as

$$\begin{aligned} &\mathbf {V}_{1}^{A} = \boldsymbol {\xi}_{11}^{A} \mathbf {T}_{1}^{A} + \boldsymbol {\xi} _{12}^{A} \mathbf {T}_{2}^{A} + \boldsymbol {\xi}_{10}^{A} , \end{aligned}$$
(17)
$$\begin{aligned} &\mathbf {V}_{2}^{A} = \boldsymbol {\xi}_{21}^{A} \mathbf {T}_{1}^{A} + \boldsymbol {\xi} _{22}^{A} \mathbf {T}_{2}^{A} + \boldsymbol {\xi}_{20}^{A} , \end{aligned}$$
(18)
$$\begin{aligned} &\mathbf {V}_{1}^{B} = \boldsymbol {\xi}_{11}^{B} \mathbf {T}_{1}^{B} + \boldsymbol {\xi} _{12}^{B} \mathbf {T}_{2}^{B} + \boldsymbol {\xi}_{10}^{B} , \end{aligned}$$
(19)
$$\begin{aligned} &\mathbf {V}_{2}^{B} = \boldsymbol {\xi}_{21}^{B} \mathbf {T}_{1}^{B} + \boldsymbol {\xi} _{22}^{B} \mathbf {T}_{2}^{B} + \boldsymbol {\xi}_{20}^{B}. \end{aligned}$$
(20)

The goal of the hierarchic assembly procedure is to construct the integral form of the equations of motion for body \(C\) in the analogous form as in the case of body \(A\) and \(B\), i.e.,

$$\begin{aligned} &\mathbf {V}_{1}^{C} = \boldsymbol {\xi}_{11}^{C} \mathbf {T}_{1}^{C} + \boldsymbol {\xi} _{12}^{C} \mathbf {T}_{2}^{C} + \boldsymbol {\xi}_{10}^{C} , \end{aligned}$$
(21)
$$\begin{aligned} &\mathbf {V}_{2}^{C} = \boldsymbol {\xi}_{21}^{C} \mathbf {T}_{1}^{C} + \boldsymbol {\xi} _{22}^{C} \mathbf {T}_{2}^{C} + \boldsymbol {\xi}_{20}^{C}, \end{aligned}$$
(22)

where the handles \(O_{1}\) and \(O_{2}\) of the compound body \(C\) are coincident with handle \(O_{1}\) of body \(A\) and handle \(O_{2}\) of body \(B\), respectively. The same form of the equations enables us to utilize the divide-and-conquer paradigm to assembly the whole system into one super-body, whose velocities depend on constraint force impulses at the terminal handles. In other words, the expressions \(\boldsymbol {\xi}_{11} ^{C}\), \(\boldsymbol {\xi}_{12}^{C}\), …, \(\boldsymbol {\xi}_{20}^{C}\) for body \(C\) have to be evaluated in terms of the known quantities for bodies \(A\) and \(B\). The procedure requires an intermediate calculations of the interbody force impulses \(\mathbf {T}_{1}^{B}\) and \(\mathbf {T}_{2}^{A}\) using the expressions for force impulses \(\mathbf {T}_{1}^{A}\) and \(\mathbf {T}_{2} ^{B}\). The presence of the interconnecting kinematic joint imposes the velocity level conditions given in the form

$$ \mathbf {V}_{1}^{B} - \mathbf {V}_{2}^{A} = \mathbf {H}\dot{\mathbf {q}}, $$
(23)

where \(\mathbf {H}\) is the joint motion subspace that maps joint velocity vectors \(\dot{\mathbf {q}}\) into the spatial velocity vectors. Let us substitute (18)–(19) into (23). By premultiplying the resulting conditions by \(\mathbf {D}^{T}\), we obtain

$$ \mathbf {D}^{T} \bigl( \boldsymbol {\xi}_{11}^{B} \mathbf {T}_{1}^{B} + \boldsymbol {\xi} _{12}^{B} \mathbf {T}_{2}^{B} + \boldsymbol {\xi}_{10}^{B} - \boldsymbol {\xi}_{21}^{A} \mathbf {T}_{1}^{A} - \boldsymbol {\xi}_{22}^{A} \mathbf {T}_{2}^{A} - \boldsymbol {\xi} _{20}^{A} \bigr) = \mathbf {0}. $$
(24)

Newton’s third law of motion has to be satisfied, thus the constraint force impulses have to satisfy the condition

$$ \mathbf {T}_{1}^{B} = -\mathbf {T}_{2}^{A} = \mathbf {D}\boldsymbol {\sigma}, $$
(25)

which enables us to use relation (25) in (24) to express the Lagrange multipliers \(\boldsymbol {\sigma}\) as a function of constraint force impulses \(\mathbf {T_{1}^{A}}\) and \(\mathbf {T_{2}^{B}}\) at the terminal bodies

$$ \boldsymbol {\sigma} = -{ \bigl[ \mathbf {D}^{T} \bigl( \boldsymbol { \xi}_{11}^{B} + \boldsymbol {\xi} _{22}^{A} \bigr) \mathbf {D} \bigr] }^{-1} \mathbf {D}^{T} \bigl( \boldsymbol {\xi} _{12}^{B} \mathbf {T}_{2}^{B} - \boldsymbol { \xi}_{21}^{A} \mathbf {T}_{1}^{A} + \boldsymbol { \xi} _{10}^{B} - \boldsymbol {\xi}_{20}^{A} \bigr) . $$
(26)

The inverse matrices appearing in (26) exist since both matrices \(\boldsymbol {\xi}_{11}^{B}\) and \(\boldsymbol {\xi}_{22}^{A}\) are symmetric and positive definite as long as the constraints imposed on the system are independent. To simplify the formulas, the following matrices are defined:

$$\begin{aligned} \mathbf {W} &= \mathbf {D} \mathbf {C} \mathbf {D}^{T} = -\mathbf {D} { \bigl[ \mathbf {D}^{T} \bigl( \boldsymbol {\xi}_{11}^{B} + \boldsymbol { \xi}_{22}^{A} \bigr) \mathbf {D} \bigr] } ^{-1} \mathbf {D}^{T} , \end{aligned}$$
(27)
$$\begin{aligned} \boldsymbol {\beta} &= \mathbf {D} \mathbf {C} \mathbf {b} = \mathbf {D} \mathbf {C} \mathbf {D} ^{T} \bigl( \boldsymbol {\xi}_{10}^{B} - \boldsymbol {\xi}_{20}^{A} \bigr) . \end{aligned}$$
(28)

Hence, (25) becomes

$$ \mathbf {T}_{1}^{B} = \mathbf {W} \boldsymbol { \xi}_{12}^{B} \mathbf {T}_{2}^{B} - \mathbf {W} \boldsymbol {\xi}_{21}^{A} \mathbf {T}_{1}^{A} + \boldsymbol {\beta} = -\mathbf {T}_{2}^{A}, $$
(29)

and enables us the calculation of constraint force impulses at the interconnecting joint using constraint force impulses at handle \(O _{1}\) of body \(A\) and handle \(O_{2}\) of body \(B\). The final step involves the substitution of (29) into (17) and (20)

$$\begin{aligned} \mathbf {V}_{1}^{A} &= \bigl[ \boldsymbol {\xi}_{11}^{A} + \boldsymbol {\xi}_{12}^{A} \mathbf {W} \boldsymbol {\xi}_{21}^{A} \bigr] \mathbf {T}_{1}^{A} + \bigl[ -\boldsymbol {\xi} _{12}^{A} \mathbf {W} \boldsymbol {\xi}_{12}^{B} \bigr] \mathbf {T}_{2}^{B} + \bigl[ \boldsymbol {\xi}_{10}^{A} - \boldsymbol {\xi}_{12}^{A} \boldsymbol {\beta} \bigr] , \end{aligned}$$
(30)
$$\begin{aligned} \mathbf {V}_{2}^{B} &= \bigl[ -\boldsymbol {\xi}_{21}^{B} \mathbf {W} \boldsymbol {\xi}_{21} ^{A} \bigr] \mathbf {T}_{1}^{A} + \bigl[ \boldsymbol {\xi}_{22}^{B} + \boldsymbol {\xi} _{21}^{B} \mathbf {W} \boldsymbol {\xi}_{12}^{B} \bigr] \mathbf {T}_{2}^{B} + \bigl[ \boldsymbol {\xi}_{20}^{B} + \boldsymbol {\xi}_{21}^{B} \boldsymbol {\beta} \bigr] . \end{aligned}$$
(31)

As the handles of the compound body \(C\) are coincident with the leftmost handle of body \(A\), and with the rightmost handle of body \(B\), respectively, the following equations are fulfilled:

$$\begin{aligned} \mathbf {V}_{1}^{C} = \mathbf {V}_{1}^{A} \quad \text{and} \quad \mathbf {T}_{1}^{C} = \mathbf {T}_{1}^{A} , \end{aligned}$$
(32)
$$\begin{aligned} \mathbf {V}_{2}^{C} = \mathbf {V}_{2}^{B} \quad \text{and} \quad \mathbf {T}_{2}^{C} = \mathbf {T}_{2}^{B}. \end{aligned}$$
(33)

The comparison of (30)–(31) with (21)–(22) leads to the following recursive expressions:

$$\begin{aligned} &\boldsymbol {\xi}_{11}^{C} = \boldsymbol { \xi}_{11}^{A} + \boldsymbol {\xi}_{12}^{A} \mathbf {W} \boldsymbol {\xi}_{21}^{A}, \qquad \boldsymbol {\xi}_{12}^{C} = -\boldsymbol {\xi}_{12}^{A} \mathbf {W} \boldsymbol {\xi}_{12}^{B} , \end{aligned}$$
(34)
$$\begin{aligned} &\boldsymbol {\xi}_{21}^{C} = -\boldsymbol {\xi}_{21}^{B} \mathbf {W} \boldsymbol {\xi}_{21}^{A} = \bigl( \boldsymbol { \xi}_{12}^{C} \bigr)^{T}, \qquad \boldsymbol { \xi}_{22}^{C} = \boldsymbol {\xi} _{22}^{B} + \boldsymbol {\xi}_{21}^{B} \mathbf {W} \boldsymbol {\xi}_{12}^{B} , \end{aligned}$$
(35)
$$\begin{aligned} &\boldsymbol {\xi}_{10}^{C} = \boldsymbol {\xi}_{10}^{A} - \boldsymbol {\xi}_{12}^{A} \mathbf {\beta}, \qquad \boldsymbol { \xi}_{20}^{C} = \boldsymbol {\xi}_{20}^{B} + \boldsymbol {\xi} _{21}^{B} \mathbf {\beta}. \end{aligned}$$
(36)

Equations (34)–(36) constitute the main formulas for the divide-and-conquer assembly–disassembly procedure, which enables us to construct the integral form of the equations of motion for the articulated body \(C\) consisting of bodies \(A\) and \(B\). At this point it is possible to perform the hierarchic assembly of the multibody system based on the binary tree decomposition (see Fig. 3). The efficient evaluation of the binary tree associated with the multibody system is a separate task and it will not be considered in this paper. The step finishes when the whole multibody system is assembled into one super-body. The assembly phase is summarized in Pseudo-algorithm 1.

Fig. 2
figure 2

The assembly of bodies \(A\) and \(B\) into body \(C\)

Full size image
Fig. 3
figure 3

Possible assembly–disassembly process for an exemplary multibody system with closed-loops. The process allows one to assemble the multibody system starting from individual bodies denoted by ellipses to build compound (or virtual) bodies. At the end of the assembly process, the whole MBS is constructed, which enables one to exploit the boundary conditions for the base body connections. In the disassembly phase, the process is reversed in order to decompose the system into individual bodies

Full size image
Algorithm 1
figure 4

Pseudo-algorithm for the assembly phase

Full size image

Base body connection

Let us define the integral form of the equations of motion for the whole system represented by one super-body as

$$\begin{aligned} &\mathbf {V}_{1}^{C} = \boldsymbol {\xi}_{11}^{C} \mathbf {T}_{1}^{C} + \boldsymbol {\xi}_{12} ^{C} \mathbf {T}_{2}^{C} + \boldsymbol {\xi}_{10}^{C} , \end{aligned}$$
(37)
$$\begin{aligned} &\mathbf {V}_{2}^{C} = \boldsymbol {\xi}_{21}^{C} \mathbf {T}_{1}^{C} + \boldsymbol {\xi} _{22}^{C} \mathbf {T}_{2}^{C} + \boldsymbol {\xi}_{20}^{C}. \end{aligned}$$
(38)

Constraint load impulses at point \(O_{1}\) and point \(O_{2}\) (provided that they exist) can be linked with the Lagrange multipliers \(\boldsymbol {\sigma}_{1}\) and \(\boldsymbol {\sigma}_{2}\) as

$$\begin{aligned} \mathbf {T}_{1}^{C} = \mathbf {D}_{1} \boldsymbol { \sigma}_{1}, \qquad -\mathbf {T}_{2}^{C} = \mathbf {D}_{2} \boldsymbol {\sigma}_{2}. \end{aligned}$$
(39)

On the other hand, the joint velocities can be expressed as

$$\begin{aligned} \dot{\mathbf {q}}_{1} = \mathbf {H}_{1}^{T} \mathbf {V}_{1}^{C}, \qquad -\dot{\mathbf {q}}_{2} = \mathbf {H}_{2}^{T} \mathbf {V}_{2}^{C}. \end{aligned}$$
(40)

At this point, three cases are possible:

  1. (a)

    The mechanism is free-floating. The boundary force impulses are equal to zero (\(\mathbf {T}_{1}^{C}=\mathbf {0}\), \(\mathbf {T}_{2}^{C}=\mathbf {0}\)), and the expressions for the spatial velocities of terminal bodies simplify to

    $$\begin{aligned} \mathbf {V}_{1}^{C} = \boldsymbol {\xi}_{10}^{C}, \qquad \mathbf {V}_{2}^{C} = \boldsymbol {\xi}_{20}^{C}. \end{aligned}$$
    (41)
  2. (b)

    The mechanism has an open-loop or tree-like topology. The handle \(O_{2}\) refers to the tip of the chain and the constraint force impulse \(\mathbf {T}_{2}^{C}\) is known to be zero. Thus, (37) can be reduced to the following form:

    $$ \mathbf {V}_{1}^{C} = \boldsymbol { \xi}_{11}^{C} \mathbf {T}_{1}^{C} + \boldsymbol { \xi}_{10} ^{C}. $$
    (42)

    Let us premultiply (42) by \(\mathbf {D}_{1}^{T}\). By using (39), one can resolve the relations for the unknown Lagrange multipliers \(\boldsymbol {\sigma}_{1}\) to get

    $$ \boldsymbol {\sigma}_{1} = - \bigl( \mathbf {D}_{1}^{T} \boldsymbol {\xi}_{11}^{C} \mathbf {D} _{1} \bigr) ^{-1} \mathbf {D}_{1}^{T} \boldsymbol {\xi}_{10}^{C} = \mathbf {C}_{1} \mathbf {D} _{1}^{T} \boldsymbol { \xi}_{10}^{C}. $$
    (43)

    Since \(\boldsymbol {\xi}_{11}^{C}\) remains symmetric and positive definite, there is no problem with finding the inverse. At this instant, the absolute velocity \(\mathbf {V}_{1}^{C}\) is determinable by using (42).

  3. (c)

    The mechanism has a closed-loop topology, and it is connected to the fixed base body by two kinematic joints at handle \(O_{1}\) and handle \(O _{2}\). By inserting (39) into relations (37)–(38), we obtain an intermediate formula that can be premultiplied by \(\mathbf {D}_{1}^{T}\) and \(\mathbf {D}_{2}^{T}\) to get

    $$ \begin{bmatrix} \mathbf {D}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {D}_{2} \end{bmatrix} ^{T} \begin{bmatrix} \boldsymbol {\xi}_{11}^{C} & \boldsymbol {\xi}_{12}^{C} \\ \boldsymbol {\xi}_{21}^{C} & \boldsymbol {\xi}_{22}^{C} \end{bmatrix} \begin{bmatrix} \mathbf {D}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {D}_{2} \end{bmatrix} \begin{bmatrix} \boldsymbol {\sigma}_{1} \\ -\boldsymbol {\sigma}_{2} \end{bmatrix} + \begin{bmatrix} \mathbf {D}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {D}_{2} \end{bmatrix} ^{T} \begin{bmatrix} \boldsymbol {\xi}_{10} \\ \boldsymbol {\xi}_{20} \end{bmatrix} = \mathbf {0}. $$
    (44)

    Equations (44) enable us to calculate the unknown boundary Lagrange multipliers

    $$ \begin{bmatrix} \boldsymbol {\sigma}_{1} \\ -\boldsymbol {\sigma}_{2} \end{bmatrix} = - \Biggl( \begin{bmatrix} \mathbf {D}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {D}_{2} \end{bmatrix} ^{T} \begin{bmatrix} \boldsymbol {\xi}_{11}^{C} & \boldsymbol {\xi}_{12}^{C} \\ \boldsymbol {\xi}_{21}^{C} & \boldsymbol {\xi}_{22}^{C} \end{bmatrix} \begin{bmatrix} \mathbf {D}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {D}_{2} \end{bmatrix} \Biggr) ^{-1} \begin{bmatrix} \mathbf {D}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {D}_{2} \end{bmatrix} ^{T} \begin{bmatrix} \boldsymbol {\xi}_{10} \\ \boldsymbol {\xi}_{20} \end{bmatrix} . $$
    (45)

    Usually, the inverse matrices in (45) exist. However, there are some circumstances, in which the calculation of constraint load impulses is not so straightforward. The problems with matrix inversions may arise when the system passes near or through the singular configuration or/and the system is redundantly constrained. The redundancy results in problems of joint reactions solvability [37, 38]. Nevertheless, let us assume that the boundary loads impulses have been successfully evaluated at this phase. With the boundary Lagrange multipliers \(\boldsymbol {\sigma} _{1}\), \(\boldsymbol {\sigma}_{2}\) known, the velocities that connect the assembly with the fixed base-body can be computed as

    $$ \begin{bmatrix} \dot{\mathbf {q}}_{1} \\ -\dot{\mathbf {q}}_{2} \end{bmatrix} = \begin{bmatrix} \mathbf {H}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {H}_{2} \end{bmatrix} ^{T} \begin{bmatrix} \boldsymbol {\xi}_{11}^{C} & \boldsymbol {\xi}_{12}^{C} \\ \boldsymbol {\xi}_{21}^{C} & \boldsymbol {\xi}_{22}^{C} \end{bmatrix} \begin{bmatrix} \mathbf {D}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {D}_{2} \end{bmatrix} \begin{bmatrix} \boldsymbol {\sigma}_{1} \\ -\boldsymbol {\sigma}_{2} \end{bmatrix} + \begin{bmatrix} \mathbf {H}_{1} & \mathbf {0} \\ \mathbf {0} & \mathbf {H}_{2} \end{bmatrix} ^{T} \begin{bmatrix} \boldsymbol {\xi}_{10} \\ \boldsymbol {\xi}_{20} \end{bmatrix} . $$
    (46)

    Analogously, the above scheme can be easily adapted to cope with more than two handles per body.

Disassembly phase

As soon as the constraint force impulses \(\mathbf {T}_{1}^{C}\) and \(\mathbf {T} _{2}^{C}\) are available, the disassembly phase is started (cf. Fig. 3). The values of \(\mathbf {T}_{1}^{C}\) and \(\mathbf {T}_{2} ^{C}\) can be transferred to the proceeding nodes of the binary tree to recursively compute all interconnecting constraint force impulses utilizing equation (29) and handles coincidence conditions (Eqs. (32)–(33)). When the interbody constraint force impulses are evaluated for all joints, the spatial velocities can be computed by using (15)–(16). Finally, it is possible to determine the joint velocities with the aid of projection onto the joints’ motion subspaces (see Eq. (23)). The disassembly phase is summarized in Pseudo-algorithm 2.

Algorithm 2
figure 5

Pseudo-algorithm for the disassembly phase

Full size image

The computational steps described above are equivalent to the evaluation of the first set of Hamilton’s canonical equations (1). The proposed method allows one to recursively calculate the derivatives of canonical coordinates without the need of determination of the system’s Hamiltonian and its partial derivatives \({\partial \mathcal{H}}/{\partial \mathbf{p}}\).

2.3 Derivatives of canonical momenta

This part of the paper is devoted to the calculation of time derivatives of canonical momenta. Initially, the equations of motion for MBS are formulated in terms of absolute momenta. Subsequently, the notion of articulated and accumulated momenta are exploited to form the equations of motion in a divide-and-conquer manner. Finally, the expressions for the time derivatives of canonical momenta are demonstrated.

Equations of motion for unconstrained body

According to Newton’s law of motion, the derivative of the absolute momenta vector of unconstrained body is equal to the sum of external load vectors. The following equations of motion, expressed with respect to the centroidal reference frame, are initially used:

$$ \dot{\mathbf {P}}_{C} = \mathbf {Q}_{C}. $$
(47)

To construct the equations of motion with respect to the local coordinate frame attached at point \(O \neq C\), one has to define the shift matrix \(\mathbf {S}_{CO}\) as

$$ \mathbf {P}_{C} = \mathbf {S}_{CO} \mathbf {P}_{O}, \qquad \mathbf {Q}_{C} = \mathbf {S}_{CO} \mathbf {Q}_{O}. $$
(48)

The shift matrix \(\mathbf {S}_{CO}\) is defined analogously to (14). Let us note that the spatial momentum vectors transform in the same way as spatial force vectors. The following identities [10] are useful in further derivations:

$$\begin{gathered} (\mathbf {S}_{CO})^{-1} = \begin{bmatrix} \mathbf {I} & \mathbf {0} \\ \widetilde{\mathbf {l}_{CO}} & \mathbf {I} \end{bmatrix} ^{-1} = \begin{bmatrix} \mathbf {I} & \mathbf {0} \\ -\widetilde{\mathbf {l}_{CO}} & \mathbf {I} \end{bmatrix} = \begin{bmatrix} \mathbf {I} & \mathbf {0} \\ \widetilde{\mathbf {l}_{OC}} & \mathbf {I} \end{bmatrix} = \mathbf {S}_{OC} , \end{gathered}$$
(49)
$$\begin{gathered} \mathbf {S}_{OC} \dot{\mathbf {S}}_{OC} = \begin{bmatrix} \mathbf {I} & \mathbf {0} \\ \widetilde{\mathbf {l}_{OC}} & \mathbf {I} \end{bmatrix} \begin{bmatrix} \mathbf {0} & \mathbf {0} \\ \dot{\widetilde{\mathbf {l}_{OC}}} & \mathbf {0} \end{bmatrix} = \begin{bmatrix} \mathbf {0} & \mathbf {0} \\ \dot{\widetilde{\mathbf {l}_{OC}}} & \mathbf {0} \end{bmatrix} = \dot{\mathbf {S}}_{OC} = \begin{bmatrix} \mathbf {0} & \mathbf {0} \\ \dot{\widetilde{\mathbf {l}_{OC}}} & \mathbf {0} \end{bmatrix} \begin{bmatrix} \mathbf {I} & \mathbf {0} \\ \widetilde{\mathbf {l}_{OC}} & \mathbf {I} \end{bmatrix} = \dot{ \mathbf {S}}_{OC} \mathbf {S}_{OC}. \end{gathered}$$
(50)

Equations (47) and (48) can be combined to obtain the equation of motion with respect to the local coordinate frame whose origin is attached at point \(O\)

$$ \dot{\mathbf {P}}_{O} + \dot{\mathbf {S}}_{CO} \mathbf {P}_{O} = \mathbf {Q}_{O}, $$
(51)

where \(\mathbf {Q}_{O}\) is a spatial external loads vector and \(\mathbf {P} _{O}\) is a spatial momentum vector related to the body at point O. A closer look at (51) reveals the fact that it is possible to conveniently simplify the expression \(\dot{\mathbf {S}}_{CO} \mathbf {P} _{O}\) and receive

$$ \dot{\mathbf {P}}_{O} + \dot{\mathbf {S}}_{O} \mathbf {P}_{O} = \mathbf {Q}_{O}, $$
(52)

where

$$ \dot{\mathbf {S}}_{O} = \begin{bmatrix} \mathbf {0} & \mathbf {0} \\ \widetilde{\mathbf {v}_{O}} & \mathbf {0} \end{bmatrix} _{6x6}, $$
(53)

and \(\dot{\mathbf {S}}_{O}\) consists of a skew-symmetric matrix of point \(O\)’s translational velocity vector in inertial reference frame.

Equations of motion for constrained body

Like in Sect. 2.2.1, let us consider two interacting bodies \(A\) and \(B\) (see Fig. 2). Let us assign again two handles per compound body by means of which the body interacts with other bodies in the system. The equations of motion for such system can be written in the form

$$\begin{aligned} \dot{\mathbf {P}}_{1}^{A} + \dot{\mathbf {S}}_{1}^{A} \mathbf {P}_{1}^{A} &= \mathbf {Q} _{1}^{A} + \mathbf {F}_{1}^{A} + \mathbf {S}_{12}^{A} \mathbf {F}_{2}^{A} , \end{aligned}$$
(54)
$$\begin{aligned} \dot{\mathbf {P}}_{1}^{B} + \dot{\mathbf {S}}_{1}^{B} \mathbf {P}_{1}^{B} &= \mathbf {Q} _{1}^{B} + \mathbf {F}_{1}^{B} + \mathbf {S}_{12}^{B} \mathbf {F}_{2}^{B}, \end{aligned}$$
(55)

where index 1 refers to the leftmost handle, and index 2 refers to the rightmost handle of a body. The matrices \(\dot{\mathbf {S}}_{1}^{A}\) and \(\dot{\mathbf {S}}_{1}^{B}\) contain absolute, translational velocities of body \(A\) and body \(B\) expressed at handle 1 of the first and second body, respectively. The terms \(\mathbf {F}_{1}\) and \(\mathbf {F}_{2}\) denote reaction forces, which have to satisfy Newton’s third law \(\mathbf {F} _{1}^{B} = -\mathbf {F}_{2}^{A}\). Newton’s third law of motion enables us to substitute \(\mathbf {F}_{1}^{B}\) from (55) into (54) to construct the expression for the coupled, articulated body

$$ \dot{\mathbf {P}}_{1}^{A} + \mathbf {S}_{12}^{A} \dot{\mathbf {P}}_{1}^{B} + \dot{\mathbf {S}}_{1}^{A} \mathbf {P}_{1}^{A} + \dot{\mathbf {S}}_{1}^{B} \mathbf {P} _{1}^{B} = \mathbf {Q}_{1}^{A} + \mathbf {S}_{12}^{A} \mathbf {Q}_{1}^{B} + \mathbf {F} _{1}^{A} + \mathbf {S}_{12}^{A} \mathbf {S}_{12}^{B} \mathbf {F}_{2}^{B}. $$
(56)

The equation can be reconstructed to a more suitable form using the simplifying transformation \(\dot{\mathbf {S}}_{1}^{B} = \dot{\mathbf {S}}_{1} ^{A} + \dot{\mathbf {S}}_{12}^{A}\) as

$$ \frac{d}{dt} \bigl( \mathbf {P}_{1}^{A} + \mathbf {S}_{12}^{A} \mathbf {P}_{1} ^{B} \bigr) + \dot{\mathbf {S}}_{1}^{A} \bigl( \mathbf {P}_{1}^{A} + \mathbf {S} _{12}^{A} \mathbf {P}_{1}^{B} \bigr) = \bigl( \mathbf {Q}_{1}^{A} + \mathbf {S} _{12}^{A} \mathbf {Q}_{1}^{B} \bigr) + \mathbf {F}_{1}^{A} + \mathbf {S}_{12} ^{A} \mathbf {S}_{12}^{B} \mathbf {F}_{2}^{B}. $$
(57)

Using the following substitutions

$$\begin{aligned} \mathbf {P}_{1}^{C} = \mathbf {P}_{1}^{A} + \mathbf {S}_{12}^{A} \mathbf {P}_{1}^{B}, \qquad \mathbf {Q}_{1}^{C} = \mathbf {Q}_{1}^{A} + \mathbf {S}_{12}^{A} \mathbf {Q} _{1}^{B}, \qquad \mathbf {S}_{12}^{C} = \mathbf {S}_{12}^{A} \mathbf {S}_{12}^{B}, \end{aligned}$$
(58)

and including the appropriate handles coincidence relations

$$\begin{aligned} \mathbf {F}_{1}^{C} = \mathbf {F}_{1}^{A}, \qquad \mathbf {F}_{2}^{C} = \mathbf {F} _{2}^{B}, \qquad \dot{\mathbf {S}}_{1}^{C} = \dot{\mathbf {S}}_{1}^{A}, \end{aligned}$$
(59)

(57) takes a more concise form, similar to the relations in (54)–(55)

$$ \dot{\mathbf {P}}_{1}^{C} + \dot{ \mathbf {S}}_{1}^{C} \mathbf {P}_{1}^{C} = \mathbf {Q} _{1}^{C} + \mathbf {F}_{1}^{C} + \mathbf {S}_{12}^{C} \mathbf {F}_{2}^{C}, $$
(60)

where \(\mathbf {P}_{1}^{C}\) and \(\mathbf {Q}_{1}^{C}\) are accumulated momenta and accumulated external loads. At this point it would be possible to perform the whole multibody system hierarchic assembly according to the binary tree decomposition. The purpose is to define the equation of motion of the whole system in terms of the boundary reaction forces. This step finishes when the base-body is reached.

Now, let us notice that the joint canonical momentum can be found as \(\mathbf {p}_{1} = \mathbf {H}_{1}^{T} \mathbf {P}_{1}^{C}\) [32]. Therefore, by exploiting (60), the time derivative of this expression yields

$$ \dot{\mathbf {p}}_{1} = \mathbf {H}_{1}^{T} \bigl( \mathbf {Q}_{1}^{C} - \dot{\mathbf {S}}_{1}^{C} \mathbf {P}_{1}^{C} + \mathbf {S}_{12}^{C} \mathbf {F}_{2} ^{C} \bigr) + \dot{\mathbf {H}}_{1}^{T} \mathbf {P}_{1}^{C}. $$
(61)

The drawback of (61) lies in the presence of the unknown reaction force \(\mathbf {F}_{2}^{C}\). Secondly, although (60) and (61) look promising, it would be more beneficial to express the equations of motion in terms of articulated momenta which at this stage are already available.

The common procedure in the modeling of constrained multibody systems possessing closed-loops is to virtually cut redundant joints to generate a tree-like system. This is done by introducing the unknown constraint forces at cut locations. The idea formally leads to an extended Lagrangian and extended Hamiltonian functions for the considered multibody system, derivation of which is presented in [30] and briefly recalled in Sect. 1. Let us assume that the compound body \(C\) is virtually cut at handle \(O_{2}\), which means that

$$ \overline{\mathbf {P}_{2}^{C}} = \mathbf {T}_{2}^{C}. $$
(62)

The comparison of the accumulated momenta definition (58) with the integral form of the equations of motion (compare (12)–(13)) yields

$$\begin{aligned} \mathbf {P}_{1}^{C} = \overline{\mathbf {P}_{1}^{C}} + \mathbf {S}_{12}^{C} \overline{\mathbf {P} _{2}^{C}} , \end{aligned}$$
(63)
$$\begin{aligned} \mathbf {P}_{2}^{C} = \mathbf {S}_{21}^{C} \overline{\mathbf {P}_{1}^{C}} + \overline{\mathbf {P} _{2}^{C}}. \end{aligned}$$
(64)

These expressions proclaim the fact that there is a clear dependency between accumulated and articulated momenta. Substituting (63) into (60) and exploiting (62) gives

$$ \frac{d}{dt} \overline{\mathbf {P}_{1}^{C}} + \dot{ \mathbf {S}}_{1}^{C} \overline{\mathbf {P} _{1}^{C}} + \bigl( \mathbf {S}_{1}^{C} \dot{\mathbf {S}}_{12}^{C} + \dot{\mathbf {S}}_{1}^{C} \mathbf {S}_{12}^{C} \bigr) \overline{\mathbf {P}_{2} ^{C}} - \mathbf {S}_{12}^{C} \dot{\mathbf {D}}_{2} \boldsymbol {\sigma}_{2} = \mathbf {Q} _{1}^{C} + \mathbf {F}_{1}^{C}, $$
(65)

which simplifies to

$$ \frac{d}{dt} \overline{\mathbf {P}_{1}^{C}} + \dot{\mathbf {S}}_{1}^{C} \overline{\mathbf {P} _{1}^{C}} + \dot{\mathbf {S}}_{2}^{C} \overline{\mathbf {P}_{2}^{C}} - \mathbf {S} _{12}^{C} \dot{\mathbf {D}}_{2} \boldsymbol {\sigma}_{2} = \mathbf {Q}_{1}^{C} + \mathbf {F} _{1}^{C}, $$
(66)

and allows eliminating reaction force \(\mathbf {F}_{2}^{C}\) with the derivative of (62). Let us premultiply (66) by the boundary joint’s motion subspace \(\mathbf {H}_{1} ^{T}\) to remove the dependence on the constraint force \(\mathbf {F}_{1} ^{C}=\mathbf {D}_{1}\dot{\boldsymbol {\sigma}}_{1}\), yielding

$$ \dot{\mathbf {p}}_{1} = \mathbf {H}_{1}^{T} \bigl( \mathbf {Q}_{1}^{C} - \dot{\mathbf {S}}_{1}^{C} \overline{\mathbf {P}_{1}^{C}} - \dot{\mathbf {S}}_{2} ^{C} \overline{\mathbf {P}_{2}^{C}} + \mathbf {S}_{12}^{C} \dot{\mathbf {D}}_{2} \boldsymbol {\sigma} _{2} \bigr) + \dot{\mathbf {H}}_{1}^{T} \overline{ \mathbf {P}_{1}^{C}}. $$
(67)

Please note that the quantity \(\dot{\mathbf {p}}_{1}\) is dependent on the known articulated momenta. Based on (62) and the assumption that there is a cut joint at handle \(O_{2}\), the value of the momentum’s derivative at handle \(O_{2}\) is equal to zero, i.e.,

$$ \dot{\mathbf {p}}_{2} = \mathbf {H}_{2}^{T} \frac{d}{dt} \overline{\mathbf {P} _{2}^{C}} + \dot{ \mathbf {H}}_{2}^{T} \overline{\mathbf {P}_{2}^{C}} = \mathbf {0}, $$
(68)

which is derived with the use of the identity in the form \(\mathbf {H} _{2}^{T} \dot{\mathbf {D}}_{2} = -\dot{\mathbf {H}}_{2} \mathbf {D}_{2}\). Any joint in the system that opens the loop(s) can be chosen as a cut joint. It is assumed that the time derivative of such joint’s canonical momenta are equal to zero.

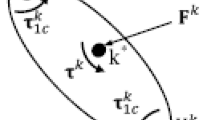
The above formalism can be extended to deal with any joint of constrained multibody system. The derivative of joint’s canonical momenta \(k\) related to any body \(K\) can be expressed in terms of already available articulated momenta as

$$ \dot{\mathbf {p}}_{k} = \mathbf {H}_{k}^{T} \bigl( \mathbf {Q}_{1}^{K} - \dot{\mathbf {S}}_{1}^{K} \overline{\mathbf {P}_{1}^{K}} - \dot{\mathbf {S}}_{c} \overline{\mathbf {P} _{c}} + \mathbf {S}_{kc} \dot{ \mathbf {D}}_{c} \boldsymbol {\sigma}_{c} \bigr) + \dot{ \mathbf {H}}_{k}^{T} \overline{\mathbf {P}_{1}^{K}}, $$
(69)

where subindex \(c\) designates a cut joint, \(\overline{\mathbf {P}_{1}^{K}}\) and \(\overline{\mathbf {P}_{c}}\) are the articulated momenta for joint \(k\) and cut joint \(c\), respectively. The derivatives of shift matrices \(\dot{\mathbf {S}}_{1}^{K}\) and \(\dot{\mathbf {S}}_{c}\) contain the translational velocities of handle \(k\) and handle \(c\) computed with respect to the global, inertial reference frame. The application of this form of equations of motion enables us to include unknown reaction force at cut location \(c\) within the definition of articulated momentum vector. Equation (69) allows us to calculate the time derivatives of canonical momenta, by having a vector of accumulated external loads \(\mathbf {Q}_{1}^{K}\), which is only unknown in this equation.

Articulated external loads.

The purpose of this section is to demonstrate how to calculate the articulated external loads by using a divide and conquer strategy.

Let us define articulated external loads vectors \(\overline{\mathbf {Q}}\) at handle \(O_{1}\) and handle \(O_{2}\) for bodies \(A\) and \(B\), respectively (cp. Fig. 2). Let us also construct the conditions describing the relation between external loads vectors as

$$\begin{aligned} &\mathbf {Q}_{1}^{A} = \overline{\mathbf {Q}_{1}^{A}} + \mathbf {S}_{12}^{A} \overline{\mathbf {Q} _{2}^{A}} , \end{aligned}$$
(70)
$$\begin{aligned} &\mathbf {Q}_{1}^{B} = \overline{\mathbf {Q}_{1}^{B}} + \mathbf {S}_{12}^{B} \overline{\mathbf {Q} _{2}^{B}}. \end{aligned}$$
(71)

Load vectors \(\mathbf {Q}_{1}^{A}\) and \(\mathbf {Q}_{1}^{B}\) represent the external forces acting on bodies \(A\) and \(B\), respectively, while \(\overline{\mathbf {Q}_{1}^{A}}, \dots , \overline{\mathbf {Q}_{2}^{B}}\) refer to resultant external loads. As the articulated load vectors \(\overline{\mathbf {Q}^{A}_{2}}\) and \(\overline{\mathbf {Q}^{B}_{1}}\) are associated with a single joint, the forces have to satisfy Newton’s law

$$ \overline{\mathbf {Q}^{B}_{1}} = - \overline{ \mathbf {Q}^{A}_{2}}. $$
(72)

One can substitute (71) into (70) and utilize (72) to algorithmically assemble the forces for body \(A\) and \(B\)

$$ \mathbf {Q}^{A}_{1} + \mathbf {S}^{A}_{12} \mathbf {Q}^{B}_{1} = \overline{\mathbf {Q} ^{A}_{1}} + \mathbf {S}^{A}_{12} \mathbf {S}^{B}_{12} \overline{\mathbf {Q}^{B} _{2}}. $$
(73)

By applying the relations (58) and handles’ coincidence conditions for compound body \(C\) (compare with (32)–(33)), one can obtain the following final form:

$$ \mathbf {Q}_{1}^{C} = \overline{ \mathbf {Q}_{1}^{C}} + \mathbf {S}_{12}^{C} \overline{\mathbf {Q} _{2}^{C}}. $$
(74)

Equation (74) presents the relation between the accumulated and articulated external loads vectors. Considering the whole multibody system assembled into one super-body \(C\), the articulated loads vector \(\overline{\mathbf {Q}^{C}_{2}}\) is equal to zero as we assume that it concerns the cut joint (see (62)) of a closed-loop system. Thus, the base-body connection conditions can be taken into account to receive

$$ \overline{\mathbf {Q}_{1}^{A}} = \mathbf {Q}_{1}^{C} = \mathbf {Q}_{1}^{A} + \mathbf {S} _{12}^{A} \mathbf {Q}_{1}^{B}. $$
(75)

By knowing the values of the articulated loads vectors for specified handles, by means of which the system \(C\) connects to the base-body, it is possible to perform a back-propagation phase by utilizing the equation

$$ \overline{\mathbf {Q}_{1}^{B}} = \mathbf {Q}_{1}^{B} - \mathbf {S}_{12}^{B} \overline{\mathbf {Q} _{2}^{C}} = - \overline{ \mathbf {Q}_{2}^{A}}. $$
(76)

The above procedure allows one to efficiently compute all necessary loads vectors in parallel achieving logarithmic \(O(\log_{2}{n})\) computational cost. If the external loads do not depend on the velocity terms, the method can be included in the phase of evaluation of joint velocities. Otherwise, it is unavoidable computing the loads separately, or expressing variables \(\mathbf {Q}_{1}\) and \(\mathbf {Q}_{2}\) for all bodies in terms of canonical momenta.

Derivatives of canonical momenta

By knowing all velocities, constraint force impulses, articulated momenta and articulated external loads, it is possible to compute the derivatives of canonical momenta for every joint \(k\) related to the body \(K\) using the following formula:

$$ \dot{\mathbf {p}}_{k} = \mathbf {H}_{k}^{T} \bigl( \overline{\mathbf {Q}_{1}^{K}} - \dot{ \mathbf {S}}_{1}^{K} \overline{\mathbf {P}_{1}^{K}} - \dot{\mathbf {S}} _{c} \overline{\mathbf {P}_{c}} + \mathbf {S}_{kc} \dot{\mathbf {D}}_{c} \boldsymbol {\sigma} _{c} \bigr) + \dot{\mathbf {H}}_{k}^{T} \overline{ \mathbf {P}_{1}^{K}}. $$
(77)

Equation (77) is equivalent to the second set of Hamilton’s canonical equations (2) for constrained multibody systems. There is no need to explicitly calculate the system’s Hamiltonian and its partial derivatives \({\partial \mathcal{H}}/{\partial \mathbf{q}}\).

3 Numerical examples

3.1 Illustrative examples

To verify the proposed HDCA algorithm, three examples of closed-loop mechanisms have been considered: single closed-loop with four bodies (case 1), single closed-loop with eight bodies (case 2), and double closed-loop with eight bodies (case 3). The mechanisms at their initial positions are illustrated in Fig. 4. The initial velocities are set to zero. Each body has a mass \(m=1\mbox{ kg}\), characteristic length of a body in the plane of motion \(l=1\mbox{ m}\), and a moment of inertia \(\mathbf {J}_{c} = \operatorname{diag}( [\begin{matrix} 1 & 1 & 1 \end{matrix}] )\) with respect to the centroidal reference frame of a body. The bodies are interconnected by revolute joints. The gravity forces act in the vertical direction, where \(g=9.81 \mbox{ m}/\mbox{s}^{2}\) is the acceleration due to gravity. The mechanisms should preserve the symmetry of the motion during the entire simulation. The results were competitively set against analogous DCA algorithm [17] that solves forward dynamics problem by using acceleration based Newton–Euler’s equations, and the closed-loops were enforced by the application of pseudo-inverses.

Fig. 4
figure 6

Numerical test cases at initial positions

Full size image

3.2 Accuracy results

The non-stiff Dormand–Prince one step solver implemented in MATLAB (\(\mathit{ode}45\)) was used with absolute and relative error tolerances set to \(\delta =10^{-6}\). Figure 5 presents the total energy preservation error as a function of the simulation time. It can be concluded from the plots that the HDCA algorithm preserves the energy better for all cases within the range of assumed integrator tolerances. Figures 6 and 7 demonstrate the vertical component of the position and translational velocity of point \(K\) for the first test case (see Fig. 4). The algorithm is able to reproduce the point’s trajectory correctly. The same conclusion may be drawn for other test cases. Figure 8 demonstrates a comparison of the constraint violation errors at the velocity level. The HDCA algorithm combines the equations of motion with the velocity level algebraic constraints. On the other hand, the DCA formulation makes use of algebraic constraints at the acceleration level. There is a huge discrepancy between the results in favor of the Hamilton’s divide-and-conquer method. In the case of HDCA, the constraint equations at the velocity level are satisfied within the numerical accuracy. This behavior has an impact on the constraints violation errors at the position level. The position constraint errors for the DCA approach diverge quadratically in terms of the simulation time. On the other hand, the drift made by the HDCA is negligible as indicated in Fig. 9.

Fig. 5
figure 7

Total energy error

Full size image
Fig. 6
figure 8

\(Y\) position of the point \(K\) for case 1

Full size image
Fig. 7
figure 9

\(Y\) velocity of the point \(K\) for case 1

Full size image
Fig. 8
figure 10

Constraint violation errors of kinematic loop closure at the velocity level

Full size image
Fig. 9
figure 11

Constraint violation errors of kinematic loop closure at the position level

Full size image

3.3 Efficiency results

Three MATLAB solvers are chosen to comparatively test the efficiency of the HDCA and the DCA algorithms, i.e., \(\mathit{ode}45\), \(\mathit{ode}113\), and \(\mathit{ode}23\). The Dormand–Prince one step solver (\(\mathit{ode}45\)) is suggested as a first try for most problems. The \(\mathit{ode}113\) method is a multistep and variable order Adams–Bashforth–Moulton PECE solver for non-stiff, but computationally intensive tasks. The \(\mathit{ode}23\) is an implementation of an explicit Runge–Kutta (2, 3) pair of Bogacki and Shampine. It may be more accurate than \(\mathit{ode}45\) in the presence of moderately stiff equations. The dynamics of the mechanisms (cases 1–3) presented in Fig. 4 are simulated for 10 seconds and various integration tolerances \(\delta =\{10^{-3}, 10^{-4}, \dots , 10^{-9}\}\). It is assumed that the relative integrator tolerance is equal to the absolute tolerance. A series of numerical experiments have been performed to measure the relative performance of HDCA and DCA formulations. Three numerical test cases are taken into account as described in Sect. 3.1.

The total wall-clock time of 10-second simulations and the number of right-hand side function evaluations taken by the integrators are recorded in order to build the comparisons. Figure 10 shows a ratio of the wall-clock time taken to execute DCA algorithm to the wall-clock time taken to process HDCA for a given test case. These measures are presented as a function of the integrators’ tolerances. On the other hand, Fig. 11 demonstrates the ratio of the right-hand side function evaluations associated with both algorithms in terms of the integrators’ tolerances. There are several remarks that can be made based on the plots. The performance of HDCA is in most cases worse than DCA when \(\mathit{ode}45\) integration routine is used for calculations. One case for which HDCA performs better than DCA can be observed for high integrator tolerances (\(10^{-9}\)). The situation changes when multi-step \(\mathit{ode}113\) integrator routine is exploited for calculations.

Fig. 10
figure 12

The wall-clock time of \(10\mbox{ s}\) simulation: DCA/HDCA

Full size image
Fig. 11
figure 13

Number of right-hand side function evaluations, DCA/HDCA

Full size image

This time HDCA has greater dominance over the acceleration based competitor measured either by using the wall-clock time or by counting the number of right-hand side function calls. It is worth noticing significant computational savings in terms of the wall-clock time for tight tolerances (i.e., \(10^{-9}\)). When \(\mathit{ode}23\) is exploited, one could take the performance advantages for the test case 1 and 2, while HDCA performs a little bit worse for the test case 3.

To complement the results, Table 1 demonstrates the mean wall-clock time taken for a single call of the right-hand side function. In our implementation, the HDCA approach requires less time to calculate the state variables for the test cases 1 and 2 than the analogous procedure for the DCA method. The mean time required to evaluate the right-hand side function is similar for both formulations when coupled-loop test case is considered. Table 2 presents the wall-clock time for the three test cases and three integrators used for the simulations. It turns out that \(\mathit{ode}23\) is much slower than other two integration methods. The fastest method solving Hamilton’s and Newton–Euler’s equations of motion was \(\mathit{ode}113\). Based on the results in Tables 1 and 2, one could estimate the total number of right-hand side function calls for each simulation.

Table 1 Mean right-hand side function evaluation time in milliseconds
Full size table
Table 2 The wall-clock time of 10 s simulation (in seconds)
Full size table

3.4 Discussion

The HDCA algorithm presented in this paper is the approach that enables one to simulate complex multi-rigid-body systems subjected to independent, holonomic constraints in an efficient and robust manner. Hamilton’s canonical equations are set and solved in a divide-and-conquer framework which enables a full exploitation of parallel computing. Pseudo-algorithm 3 presents a list of detailed algorithmic steps that one has to perform in order to calculate the time derivatives of joint canonical coordinates. The numerical cost of sequential calculations remains linear in terms of the number of bodies \(n\) in the system. The method exhibits near logarithmic complexity for \(n\) threads available for computations. The parallelizable assembly–disassembly procedure is exploited at several different levels of the algorithm. Velocities, Lagrange multipliers, and time derivatives of canonical momenta are evaluated in a recursive, divide-and-conquer manner. There are two general strategies that can be utilized to parallelize the computations. The recursive HDCA method is connected to the binary tree associated with the topology of a system. Inherently, one can assume that each node of this tree establishes an independent instance of calculation. At each level of the binary tree, one could perform embarrassingly parallel computations. On the other hand, the whole tree could be divided into well-balanced subtrees to equally spread the computational load over each thread.

Algorithm 3
figure 14

Pseudo-algorithm for HDCA

Full size image

There are several remarks that should be mentioned to properly analyze the numerical results gathered in Sect. 3. Firstly, the numerical examples examined in the paper are planar systems. Nevertheless, the HDCA algorithm can be successfully used to analyze the dynamics of spatial closed-loop systems. The method exploits spatial velocity as well as spatial momenta vectors. No simplifications have been made to limit the applicability of the formulation at any stage of the development. Moreover, the experience of the authors confirms that the HDCA method performs very well for fully three-dimensional multibody systems in terms of the total energy conservation and the constraint violation errors. Secondly, Sect. 3.2 shows that the HDCA algorithm is able to preserve the energy and constraint equations better than the DCA approach for considered closed-loop test cases. This property comes from the fact that HDCA takes the velocity level conditions as primary constraints. It is indicated that only the position constraints are violated, and the resulting errors are much smaller compared to the acceleration based DCA method. Thirdly, Sect. 3.3 demonstrates the performance of HDCA and the comparisons against DCA. The reader should be aware that the integrator absolute and relative tolerances are equal to each other in our implementations. The tolerances are equally assigned to the velocities vectors \(\dot{\mathbf {q}}\) as well as to the momenta vectors \(\mathbf {p}\). To compare both formulations more accurately, one should go into the details of the integration routines. This issue is beyond the scope of this paper.

In some applications, there is a need to calculate constraint forces. This issue is particularly important when design or control applications are considered. The HDCA algorithm presented in this paper allows one to calculate the constraint force impulses. The method needs some extensions to be able to determine the constraint forces. One method to calculate the constraint forces is to exploit the condition \(\dot{\boldsymbol {\sigma}}=\boldsymbol {\lambda}\). The finite difference method may be employed with its own advantages and disadvantages. The other way is to add a separate computational module for the calculation of reaction forces. It should be noted that the additional cost of such procedure is associated only with the evaluation of the matrices \(\boldsymbol {\xi}_{10}\) and \(\boldsymbol {\xi}_{20}\). The other coefficients are already available since they are calculated by the HDCA algorithm. The evaluation of constraint forces requires only a small fraction of the total cost of the assembly–disassembly procedure for the evaluation of velocities and constraint force impulses.

As the constraint forces are considered, one should mention additional property of the algorithm. The constraint force impulse multipliers \(\boldsymbol {\sigma}\) are the primary quantities evaluated by the HDCA method. In the case when a reaction force component \(\lambda_{i}\) never changes its sign during the motion, the Lagrange multiplier \(\sigma_{i}\) may eventually grow indefinitely with the simulation time (compare the condition \(\dot{\sigma _{i}}=\lambda_{i}\)). This may lead to numerical errors. Presumably, this issue could be circumvented by scaling the subspace of constrained directions \(\mathbf {D}_{i}\) that in turn would affect the value of the Lagrange multipliers \(\sigma_{i}\). Obviously, such a scaling should not have any effect on the value of the constraint force impulses \(\mathbf {T}_{i}\).

The HDCA algorithm is exploited for the dynamics simulation of systems possessing single kinematic loop and coupled kinematic loops. The idea demonstrated in the text can be generalized to cope with more complex topologies involving many coupled loops, especially when the number of handles per body is greater than two. The mentioned extensions require more detailed analysis of the topology of the system under consideration; however, the concept of the HDCA algorithm remains the same. Apart from the issues mentioned within this subsection, there are several other possibilities for the HDCA algorithm development. Undoubtedly, the adaptation of stabilization methods and symplectic integration procedures would further improve the HDCA algorithm’s efficiency and accuracy.

4 Conclusions

In this paper, a novel HDCA algorithm is presented for the simulation of constrained multi-rigid body system dynamics possessing closed-loop topologies. The HDCA approach utilizes Hamilton’s canonical equations of motion, which are recursively generated in a divide-and-conquer framework. The two- or multi-handle equations are formed for the spatial velocities of associated bodies and constraint load impulses at joints. Also the evaluation of the time derivatives of joint canonical momenta can be performed in a fully parallel manner. The comparison of the results with the analogous, acceleration-based divide-and-conquer formulation indicates the predominance of the HDCA method for the considered numerical examples in terms of the total energy conservation and constraint violation errors. Sample closed-loop test cases demonstrate excellent constraint satisfaction at the position and velocity level as well as marginal energy drift for various integration procedures used for calculations. The properties of the method makes the HDCA scheme worth considering in the applications to systems with more general topologies than those presented in the paper.