Abstract
Multibody system simulations are increasingly complex for various reasons, including structural complexity, the number of bodies and joints, and many phenomena modeled using specialized formulations. In this paper, an effort is pursued toward efficiently implementing the Hamiltonian-based divide-and-conquer algorithm (HDCA), a highly-parallel algorithm for multi-rigid-body dynamics simulations modeled in terms of canonical coordinates. The algorithm is implemented and executed on a system–on–chip platform which integrates a general-purpose CPU and FPGA. The details of the LDUP factorization, which is used in the HDCA approach and accounts for significant computational load, are presented. Simple planar multibody systems with open- and closed-loop topologies are analyzed to show the correctness of the implementation. Hardware implementation details are provided, especially in the context of inherent parallelism in the HDCA algorithm and linear algebra procedures employed for calculations. The computational performance of the implementation is investigated. The final results show that the FPGA–based multibody system simulations may be executed significantly faster than the analogous calculations performed on a general–purpose CPU. This conclusion is a good premise for various model-based applications, including real-time multibody simulation and control.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reliable and efficient robotic or multibody system (MBS) dynamics simulations might be challenging due to the complex interactions the systems are subjected to. At the moment, by and large, rigid-body models can be executed in real-time as long as the number of bodies is in the neighborhood of 10 to 15 and the number of collisions with friction and contact is sufficiently low [1]. The computational complexity increases as long as more bodies are added to the system or an additional type of physics is brought into the model (e.g., flexible bodies, MBS–ground interactions), which can severely limit the simulation speed. Additionally, multibody or robotic system models constitute an indispensable ingredient of a large class of model-based control strategies. For example, in model predictive control, one has to repeatedly (and in real-time) call an MBS model to evaluate a dynamically feasible state and control signals that satisfy a set of constraints that simultaneously optimize task objectives. Depending on the application (e.g., in large-scale optimal design of MBS), a multibody model often needs to be reduced or simplified to compromise the computational limitations. Simultaneously, one may observe an intensive development of parallel architectures with multicore processors, embedded multiprocessors, graphical processor units (GPUs), or field-programmable gate arrays (FPGAs) with a large emphasis on the development of parallel numerical methods and algorithms. The mentioned advancement in hardware and software does not transfer directly into the development of parallel solvers for multibody dynamics, and the topic requires further investigation.
1.1 Organization of text
The paper is organized into six sections. Section 1 discusses the scope of the paper, literature review, and objectives. Section 2 is concerned with the brief HDCA algorithm presentation, where both assembly and disassembly phases are exposed. Next, Sect. 3 demonstrates a method to calculate an inverse of a matrix that is exploited further in the implementations. Section 4 presents HDCA hardware implementation issues, including the discussion on the details of HDCA code design. Sample multibody systems used in the FPGA-based simulations are shown in Sect. 5. The performance of the implementations is also explored and discussed. Section 6 summarizes and concludes the text.
1.2 Literature review
Currently, multibody dynamics analysis of rigid-body systems is readily attainable by modern computational tools when the number of bodies is of moderate value. Nevertheless, the simulation of complex MBS possessing dozens of bodies for which the number of degrees of freedom (DOF) approaches several hundred (e.g., space systems, robotic tracked vehicles) or several thousand (e.g., bio-molecular systems) and even millions of DOFs (e.g., granular media), classical, sequential, state-of-the-art formulations may suffer from low computational efficiency and accuracy. Moreover, the analysis and simulation of interdisciplinary systems provide us with new scientific and engineering challenges [2].
Nowadays, hardware solutions (e.g., multicore CPUs, GPUs, FPGAs) have become common and relatively cheap. In that matter, there is an advance in numerical methods that exploit concurrent computations. The computational expenses spent by many existing multibody algorithms are high and usually do not exploit current computer hardware platforms to the extent possible [3]. The mentioned issues imply that researchers pay more and more attention to the development of parallel algorithms and formulations for modeling and analysis of MBS, including real-time simulations, e.g., [4], [5], [6], [7], [8], [9], [10].
Many different multibody dynamics formulations have been proposed over the years, presenting some advantages and drawbacks. One of the most critical difficulties in modeling MBS is the necessity to solve the systems of differential-algebraic equations (DAE). Consequently, a proper choice of a numerical integration procedure for solving DAEs that arise in MBS simulations is a difficult task and significantly impacts computational efficiency in practical applications [11], [12]. Most formulations exploit the Newton–Euler or Lagrange approach to generate the equations of motion. There is a limited number of Hamiltonian-based formulations for predicting the behavior of MBS in arbitrary topologies.
The availability of parallel computing architectures has encouraged researchers to develop parallel multibody dynamics algorithms. The well-known divide-and-conquer algorithm (DCA), originally developed by Featherstone [13], is among the most popular ones. The DCA constitutes a building block that lies the foundations for many methods and parallel codes for multibody dynamics [14]. Some of these deal with closed kinematic loops [15] and constraints [16]. Others extended the algorithm to enable the consideration of flexible bodies [17], discontinuities in system definition [18], and contacts [19]. Many improvements have been published to keep constraint drift under control, e.g., [20, 21]. There are also some extensions of the DCA combined with computed torque control methods to model and control fully-actuated multibody systems [22]. The practical applications of the DCA are multiple and range from the simulation of simple linkages and multibody chains to molecular dynamics [14, 23, 24].
A class of Hamiltonian-based divide-and-conquer algorithms for multibody system dynamics that exhibit near-optimal, logarithmic computational complexity have been recently proposed in [25], [26], [27]. The methods can be applied both for open- and closed-loop MBS and represent a unique suite of algorithms that attempts to parallelize constrained Hamilton’s equations practically. Its binary-tree structure allows distributing the computations among several processing cores in a scalable, logarithmic way. So far, several practical implementations of the divide-and-conquer algorithm have been developed on multicore CPUs [10] and GPUs [26].
1.3 Research outline
This paper presents an FPGA implementation of the Hamiltonian-based divide-and-conquer algorithm for forward dynamics simulation of multi-rigid-body systems. Initially, the HDCA algorithm is recalled as slightly modified as compared to the presentation in [26], [27]. Afterward, hardware implementation details are given, specifically tailored for HDCA purposes. Specifics of HDCA algorithm internal representation are demonstrated, emphasizing parts of the algorithm amenable for hardware acceleration. Further, the performance of the implementation is investigated based on two sample test cases, which mimic open- and closed-loop multibody system topologies. The final code is executed on Xilinx Z–7020 system on a chip (SoC) from Zynq–7000 (ZYNQ) family, which integrates a dual-core ARM Cortex-A9 based processing system (PS) with Artix–7 FPGA. Ultimately, the results show that hardware acceleration may enhance the efficiency of the HDCA algorithm. This may facilitate optimal design [28] or optimal control [29], [30] of multibody systems to be more performant.
2 HDCA algorithm formulation
This section discusses the HDCA algorithm for efficient forward dynamics simulations of mechanical systems. Constrained Hamilton’s equations are used to describe the motion of a multi-rigid-body system with the ultimate goal of calculating time derivatives of joint canonical coordinates. Conceptually, in the first step, the algorithm recursively evaluates joint velocities and constraint load impulse forces by systematically eliminating constraint loads between two physical or compound bodies under consideration. The results of the underlying assembly–disassembly procedure are subsequently used in the second step of the HDCA algorithm, the purpose of which is to recursively calculate the time derivatives of the joint articulated momenta before the time integration of the equations of motion.
The presentation described herein is detailed in a form that is slightly modified concerning the original exposition in [26], [27]. For simplicity, planar mechanisms containing only rotational joints are analyzed in the paper, but extensions to more complex systems are possible for the price of additional effort. The state of the mechanism is described by joint coordinates \(\mathbf{q}\) and joint canonical momenta \(\hat{\mathbf{p}}\), which gives \(2n\) equations of motion in \(n\) degrees-of-freedom. The HDCA algorithm is executed on a binary tree basis that corresponds to the topology of a multibody system, where nodes in the binary graph are associated with physical or compound bodies. The structure of the algorithm can be exploited to parallelize the computations, thus improving the numerical cost from linear \(O(n)\) for sequential computations to parallel logarithmic complexity \(O(\log _{2}(n))\) on \(n\) processing unit [26], [27]. Dense linear algebra sub-problems, such as matrix–matrix products or matrix inversions, inherently existent in the HDCA algorithm, can also be calculated in parallel to achieve even higher efficiency, as claimed in the paper.
2.1 Initialization
Before the assembly phase, the HDCA algorithm requires filling in the entries from which the hierarchic computations are started. The characteristic quantities, which are vectors and matrices (cf. \(\boldsymbol{\xi}\) symbol further in the text) correspond to rigid body physical properties.
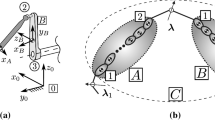
Specifically, Fig. 1 shows a rigid body subjected to planar translation and rotation with respect to inertial frame \(x_{0}y_{0}\). Two fixed frames attached to a body do not change the relative position and attitude. The \(3\times 3\)-dimensional rigid-body transformation matrix \(\mathbf{S}_{OC}\) (shift matrix) for a pair of frames \(\pi _{C}\) and \(\pi _{O}\) is defined as
where \(\mathbf{s}_{OC} = \begin{bmatrix} s_{OC_{x}}(\mathbf{q}) & s_{OC_{y}}(\mathbf{q}) \end{bmatrix} ^{\intercal}\) denotes a position vector measured from point \(O\) (handle of an articulated body, which denotes any selected point on a body or body-fixed frame used to model the interactions) to point \(C\) (center of mass or other handle, \(O \neq C\)) and
is an auxiliary matrix. The planar inertia matrix \(\mathbf{M}_{C}\) about the center of mass \(C\) has a simple diagonal from
where \(m\) is the mass of the body, \(J_{C}\) represents the inertia of the body about point \(C\). Planar shift matrix, as defined in Eq. (1), helps transform momentum, force, and velocity vectors to equivalent quantities expressed with respect to other frames (handles) on a body. Specifically, for a pair of handles attached at point \(C\) and \(O\) of a rigid body, the planar velocity transformation can be written as \(\mathbf{V}_{C}=\mathbf{S}_{OC}^{\intercal}\mathbf{V}_{O}\). The kinetic energy of a rigid body does not depend on the reference point (handle) chosen for its computation, as indicated in the following expression.
where \(\mathbf{V}_{C} = \begin{bmatrix} \mathbf{v}_{C}^{\intercal }& \omega _{C} \end{bmatrix} ^{\intercal}\) contains translational velocity of point \(C\) and angular velocity \(\omega _{C}\) of a frame \(\pi _{C}\) attached at point \(C\) with respect to the global frame. Likewise, \(\mathbf{V}_{O} = \begin{bmatrix} \mathbf{v}_{O}^{\intercal }& \omega _{O} \end{bmatrix} ^{\intercal}\) represents the stacked vector of the linear velocity of point \(O\) and angular velocity \(\omega _{O}\) of a frame \(\pi _{O}\) with respect to the global coordinate frame. With a slight abuse of notation, the expression \(\omega _{C} =\omega _{O}\) says that all frames on a rigid body move with the same angular velocity with respect to the global frame. The mass matrix about point \(O\) is given then by the formula
We now combine the linear and angular momentum to get a planar momentum vector of a rigid body
while the articulated momentum vector corresponding to a joint handle can be defined as
where \(\mathbf{T}=\mathbf{D}\boldsymbol{\sigma}\) is a joint impulse force (time-integral of joint constraint force), \(\boldsymbol{\sigma}\) denotes Lagrange multipliers that enforce velocity level constraint equations, and \(\hat{\mathbf{p}}\) represents joint (canonical) momentum, which is just a scalar value \(\hat{p}\) for planar revolute joint. Joint (canonical) momentum \(\hat{\mathbf{p}}\) is defined as a partial derivative of the Lagrangian function with respect to the joint velocities [31]. The quantities \(\mathbf{H}\) and \(\mathbf{D}\) represent the joint’s motion and constraint-force subspace, respectively. For planar revolute joints modeled in this paper, the matrices are defined as
and the sub-spaces are orthogonal to each other and fulfill the condition \(\mathbf{D}^{\intercal}\mathbf{H}=\mathbf{0}\). In the case of a rigid body with two handles located at points, \(O_{1}\) and \(O_{2}\) (joint locations are chosen for simplicity), the linear and angular momenta might be formulated as
which transform into
where
For a planar revolute joint both \(\mathbf{S}_{12}\mathbf{H}\) and \(\mathbf{S}_{21}\mathbf{H}\) simplify to \(\mathbf{H}\), which means that \(\boldsymbol{\xi}_{10}\) and \(\boldsymbol{\xi}_{20}\) can be expressed as
The matrix coefficients \(\boldsymbol{\xi}_{11}\), \(\boldsymbol{\xi}_{12}\), \(\boldsymbol{\xi}_{21}\), \(\boldsymbol{\xi}_{22}\) include the system’s mass and inertia parameters, whereas the vector coefficients \(\boldsymbol{\xi}_{10}\), \(\boldsymbol{\xi}_{20}\) take into account joint’s canonical momenta (among the other quantitites).
2.2 Assembly phase
In the assembly phase, a system of rigid bodies \(\mathcal{C}\) (Fig. 2) is formed as an assembly of a smaller set of articulated bodies \(\mathcal{A}\) and ℬ. The operation applies to all bodies in the system by taking into account a binary tree that corresponds to the topology of a multi-rigid-body system [13], [26], [27].
Technically, the assembly method in the HDCA eliminates a joint impulse force between two adjacent bodies \(\mathcal{A}\) and ℬ by considering constraints imposed by that joint. Ultimately, the equivalent coefficients \(\boldsymbol{\xi}\) for a larger articulated (compound) body \(\mathcal{C}\) can be evaluated. Thus, the assembly operation consumes the handle \(O_{2}^{\mathcal{A}}\) and \(O_{1}^{\mathcal{B}}\) by leaving the compound body \(\mathcal{C}\) equipped with the handle \(O_{1}^{\mathcal{A}}\) and \(O_{2}^{\mathcal{B}}\) only. The momentum equations for physical or compound body \(\mathcal{A}\) and ℬ before the assembly operation are
The joint between body \(\mathcal{A}\) and ℬ imposes the following constraints on handle \(O_{1}^{\mathcal{A}}\) and \(O_{2}^{\mathcal{B}}\)
that allows one to formulate the momentum equations within the compound body \(\mathcal{C}\)
In [26], [27], the recursive expressions have been derived to reflect the assembly operation. Thus, the formulae for the coefficients \(\boldsymbol{\xi}^{\mathcal{C}}_{ij}\) (\(i=1,2\), \(j=0,1,2\)) in Eq. (25) and (26) are
The characteristic vector-matrix quantities are collected in the following equations for convenience.
Equations (27)–(32) form major formulas that are used in the HDCA and let us assemble two physical or compound bodies to create a larger articulated body. This process is based on the binary tree corresponding to a multibody system’s physical topology.
2.3 Accumulated loads
To compute the derivatives of canonical momenta, it is still required to determine accumulated active load vectors. Because of this fact, the analogous divide-and-conquer assembly process can be devised to compute the necessary terms. First, let us define an external load vector at handle \(C\) (center of mass) to be \(\mathbf{Q}_{C}=[\mathbf{f}_{C}^{T}\quad \tau _{C}]^{T}\), where the \(\mathbf{f}_{C}\) vector denotes a linear force component, and \(\tau _{C}\) is a torque component. The relationship between forces/torques at a pair of handles defined at handle \(O_{1}\) and \(C\) belonging to an arbitrary rigid body can be written using a transformation matrix (1) as follows
This implies that the \(\mathbf{Q}_{1}\) load at a handle \(O_{1}\) of a rigid body is equivalent to a load at another handle \(C\) (center of mass). Let us note that momentum vectors, firstly introduced in Eq. (6), transform in the same way as load vectors.
The equivalent external (accumulated) load vectors for the compound body \(\mathcal{C}\) exploited in evaluating time derivatives of joint canonical momenta \(\dot{\hat{\mathbf{p}}}\) can also be calculated in the assembly phase. The accumulated loads provide the way to transform forces/torques between handles within subassembly and are given as [26], [27]
Subsequently, the quantities evaluated in (39) are used in the next stages of the HDCA algorithm.
2.4 Base body connection
The assembly step is completed when a whole multibody system is represented as a single articulated entity (compound body \(\mathcal{C}\)). By assuming that an open-loop chain is considered with a connection to a fixed base body via handle \(O_{1}^{\mathcal{C}}\), one can explicitly evaluate joint constraint force impulses and articulated external loads as
The quantities \(\overline{\mathbf{Q}_{1}^{\mathcal{C}}}\) and \(\overline{\mathbf{Q}_{2}^{\mathcal{C}}}\) are called articulated load vectors [26], [27] and are defined as resultant (equivalent) external loads acting on the assembly \(\mathcal{C}\). The situation for a closed-loop system topology is more involved and requires the evaluation of Lagrange multipliers \(\boldsymbol{\sigma}_{1}\), \(\boldsymbol{\sigma}_{2}\) to reflect the fixed base-body connection of two ends of a chain [27] to give
where
and then:
Articulated loads are the same as in the case of an open-loop topology.
2.5 Disassembly phase
Now, there is enough information to initiate the disassembly process, which works recursively from the root node of a binary tree to leaf-nodes. Constraint force impulses between adjacent compound body \(\mathcal{A}\) and ℬ are calculated in reverse order to the one performed in the assembly phase.
Starting from the quantities presented in (41), we can recursively calculate the intermediate articulated loads for each body in the system according to the following formulas [26], [27]
The hierarchic disassembly is continued, and the ultimate results are given in terms of absolute and joint velocities, constraint force impulses (together with the Lagrange multipliers \(\boldsymbol{\sigma}\)), and articulated loads \(\overline{\mathbf{Q}}\), which can be intuitively understood as net (equivalent) loads acting on a current body and its subtree with topological children [26], [27].
2.6 Time derivatives of canonical coordinates
If the adjacent bodies \(\mathcal{A}\) and ℬ are connected by a joint, then the joint velocity \(\dot{q}\) can be calculated with the use of Eq. (24) by taking the ortho-normality property of the joint’s motion subspace (\(\mathbf{H}^{\intercal}\mathbf{H}= \mathbf{I}\)) into account.
The second set of canonical equations, i.e., time derivatives of canonical momenta \(\dot{\hat{p}}\), are calculated based on the vectors of articulated loads and momentum vectors for particular body \(\mathcal{A}\) and yield
where
holds translational velocity \(\mathbf{v}_{\mathcal{B}}\) of joint under consideration.
2.7 HDCA summary
Ultimately the HDCA formulation leads to an efficient, recursive, and highly parallelizable method to generate a set of first-order Hamilton’s differential equations in the form
with the system Hamiltonian defined by \(\mathcal{H}=\dot{\mathbf{q}}^{T}\hat{\mathbf{p}}-\mathcal{L}\) (where ℒ is the Lagrangian for that system) and \(\boldsymbol{\tau}\) a vector of non-conservative generalized forces/torques. The HDCA algorithm calculates the forward dynamics of a kinematic chain and consists of several steps schematically detailed in Table 1.
The HDCA algorithm is executed on a binary tree basis that corresponds to the topology of a multibody system. An example of a tree associated with the flow of calculations is depicted in Fig. 3. The leaf nodes in the binary graph are related to physical bodies, whereas other nodes show the subassemblies generated in a hierarchic process. A root node of the binary tree shows the whole multibody system represented as a single entity. There are two main hierarchical passes over the binary tree: a pass from leaves to root node (assembly 2.2, 2.3) to calculate articulated–body and bias terms; and a second pass done in the reverse direction (disassembly 2.5) to calculate joint velocities and constraint impulse forces. The evaluation of time derivatives of canonical momenta (2.6) is the last step before the time integration of Hamilton’s equations to get the state of the system in the next time instant.
There are several extensions one could make to generalize the HDCA formulation proposed herein, including, e.g., various joint types, multiple joints to be connected to the same body, or closed-loop topologies analyzed in [27].
3 Matrix inversion
The HDCA formulation for open-loop system requires the calculation of matrix inverses. In the case of a single planar closed-loop system, the dimensions of a matrix to be inverted are \(4 \times 4\), and the inversion accounts for the significant computational load. When more complex systems are considered, the matrix inversions become expensive and may deteriorate potential performance benefits corresponding to the HDCA. Two algorithms are implemented on FPGA to deal with an inverse of a matrix: adjugate method and LDUP factorization, which might be generalized for matrix size increase.
3.1 Adjugate method
The adjugate method follows the standard equation for evaluating matrix inverses:
where \(adj(\mathbf{A})\) is the adjugate of a matrix \(\mathbf{A}\) and \(det(\mathbf{A})\) is its determinant. This method is used only for inverting the matrices of size \(2 \times 2\). The computational efficiency of the method for larger matrices would require much more addition and multiplication operations and consume much more FPGA resources. The significant factor causing this is the calculation of the determinant.
3.2 LDUP factorization
The LDUP factorization method [32] is much more complex than the previous method. Still, it does not require calculating the determinant and consumes much fewer FPGA resources than the previous method. The LDUP factorization is used for simulating the sample closed-loop system presented in the paper, and it is ready to be used in the spatial case.
The algorithm relies on decomposing a given non-singular, the square matrix \(\mathbf{A}\) in the following way
and then calculating its inverse as
where \(\boldsymbol{\mathcal{P}}\mathbf{A}\) is a permutation of rows of a matrix \(\mathbf{A}\), \(\boldsymbol{\mathcal{P}}\) is a permutation matrix, \(\mathbf{L}\) is a lower triangular matrix with all values on the diagonal equal 1, \(\boldsymbol{\mathcal{D}}\) is a diagonal matrix (different than \(\mathbf{D}\) introduced in Eq. (8)), and \(\mathbf{U}\) is an upper triangular matrix with all values on the diagonal equal 1. The LDUP algorithm consists of three main steps:
-
1.
 ,
, -
2.
 ,
, -
3.
 .
.
3.2.1 Gaussian elimination with partial pivoting
This iterative process transforms any square matrix into an upper triangular matrix. The role of partial pivoting and why it is needed in the elimination process is explained in [33]. It is convenient to define three auxiliary matrices. Row-switching matrix is obtained by swapping row i and row j of an identity matrix, to get
The quantity \(\mathbf{R}_{ij}\mathbf{A}\) switches i and j rows of \(\mathbf{A}\), whereas \(\mathbf{A}\mathbf{R}_{ij}\) switches columns analogically. Row-multiplying matrix is obtained by replacing a unit with the m number on ith position of an identity matrix
The expression \(\mathbf{E}_{i}(m)\mathbf{A}\) is obtained from \(\mathbf{A}\) by multiplying its row i by m, and \(\mathbf{A}\mathbf{E}_{i}(m)\) does the same thing for column i. Row-addition matrix is obtained from an identity matrix by replacing 0 in ith row and jth column (\(i \neq j\)) with m
Again, the matrix \(\mathbf{E}_{ij}(m)\mathbf{A}\) is taken from the original matrix \(\mathbf{A}\) by adding m times its row i to the row j. Simultaneously, the quantity \(\mathbf{A}\mathbf{E}_{ij}(m)\) is collected from \(\mathbf{A}\) by adding m times its column j to the column i.
Each iteration of the algorithm for a square matrix \(\mathbf{A}=\mathbf{A}_{n \times n}\) starts with partial pivoting. At iteration k the goal of partial pivoting is to diagonally place the largest out of the \(n-k+1\) main diagonal and subdiagonal entries of the column k. The process is symbolically stated as
where \(p_{k}\) is the row of the largest entry, and \(a_{ij}^{k-1}\) is the ith row, jth column entry of \(\mathbf{A}_{k-1}\), which is obtained from transforming \(\mathbf{A}\) after \(k-1\) iterations. Placing the largest value \(a_{p_{k}k}^{k-1}\) on the main diagonal is done by the above-mentioned row-switching matrix:
Gaussian elimination is performed with the use of the matrix \(\mathbf{M}_{k}(c_{k})\) defined as
where \(\psi _{ij}^{k}\) are the entries of \(\boldsymbol{\Psi}_{k}\). Inverse of \(\mathbf{M}_{k}\) is easily found by just changing the signs of all non-zero sub-diagonal entries, which is equivalent to:
The matrices for the next step are given as
where \(\mathbf{L}_{k}\) is a lower triangular matrix that can be obtained by just rearranging the values of \(\mathbf{L}_{k-1}\) and \(\mathbf{M}_{k}(-c_{k})\) without any calculations. Input matrices for the first step are: \(\mathbf{A}_{0}=\mathbf{A}\), \(\mathbf{L}_{0}=\mathbf{I}_{n \times n}\) and the final results after \(n-1\) iterations are:
where \(\mathbf{A}_{n-1}\) is an upper triangular matrix and:
3.2.2 Calculating inverses
The diagonal matrix \(\boldsymbol{\mathcal{D}}^{-1}\) can be taken directly from the Gaussian elimination process by calculating only the last \(c_{n}\) entry:
where \(c_{1}\),…, \(c_{n-1}\) were calculated in (62), and \(a_{nn}^{n-1}\) is taken from \(\mathbf{A}_{n-1}\). The upper-triangular matrix \(\mathbf{U}\) can now be calculated:
The lower-triangular matrix \(\mathbf{L}\) is simply \(\mathbf{L} = \mathbf{L}_{n-1}\). Each element of its inverse is calculated as:
where \(\hat{l}_{ij}\) are taken from \(\mathbf{L}^{-1}\), and \(l_{ij}\) are taken from \(\mathbf{L}\). The quantities for the case when \(i>j\) need to be calculated iteratively starting from \(\alpha =1\) and \(\alpha =n-1\) being the last iteration for all possible values of i and j that fulfill the condition \(i=j+\alpha \). The inverse of \(\mathbf{U}\) can be calculated analogically, but with the use of transposition:
3.2.3 UDLP product
First, an auxiliary \(\mathbf{B}\) matrix (which is upper triangular) is obtained as
The components of \(\mathbf{Y}=\mathbf{B}\mathbf{L}^{-1}\) can be calculated as
Finally, the inverse of \(\mathbf{A}\) is a permutation of columns of \(\mathbf{Y}\):
3.2.4 LDUP inversion summary
To implement the LDUP algorithm (e.g., on a CPU), it is usually more convenient to not calculate the permutation matrix \(\boldsymbol{\mathcal{P}}\) and perform all permutations based on the values of pivots \(p_{k}\) instead of explicit matrix multiplication.
Table 2 summarizes the algorithmic steps. In the first step, the matrices \(\mathbf{A}_{n-1}\), \(\mathbf{L}_{n-1}\) are calculated iteratively according to (68)-(69), \(c_{1}\),…, \(c_{n-1}\) coefficients and pivots \(p_{1}\),…, \(p_{n-1}\) are also needed in the next steps. In the second step, \(\boldsymbol{\mathcal{D}}^{-1}\) is calculated according to (75) and then \(\mathbf{U}\) according to (77). Triangular matrix inversions from the third step are completed with the use of (78). Fourth step is performed as shown in (80)–(81). Permutation (82) is performed based on the values of pivots \(p_{k}\) calculated in Sect. 3.2.1.
4 Hardware implementation
All design phases for the applied Artix–7 FPGA were written in a hardware description languages Verilog and System Verilog. Device drivers, as well as the parts of algorithms not implemented on FPGA, were written in C and fully executed on the SoC’s processing system.
4.1 Device overview
According to the datasheet, [34], the existing processing system memory and programmable logic (FPGA) are connected through a multilayered ARM AMBA AXI interconnect. Registers built on FPGA are visible for the processing system both for read and write operations. Communication with FPGA can be handled through a computer program written in C, C++, or Python. The program can be executed on a Linux-based operating system supplied by the vendor, but a bare-metal approach was chosen instead. It should be mentioned that the resources at the disposal are pretty limited. The frequency of onboard CPU without boost is \(667\text{ MHz}\), and FPGA contains 53200 hardware lookup tables (LUTs) and 220 digital signal processor (DSP) slices.
4.2 Floating–point arithmetic
Calculations on FPGA were performed in a single-precision floating-point format that occupies 32 bits. Single-precision floating-point numbers were implemented to closely conform with the IEEE 754 standard [35]. There were three types of operations developed:
-
addition,
-
multiplication,
-
inversion.
Subtraction is done by negating the subtrahend and then performing the addition. The floating-point number representation is based on the scientific notation given below.
where bias is always equal 1111111 (127 in decimal). For the example given above, fraction (usually called mantissa) is 1010101, and exponent is equal to 10000001 (129 in decimal). The whole value occupies 32 bits. Bit, representing a sign, is 0 for positive numbers and 1 otherwise. The number \(1.fraction\) is called normalized significand or simply significand. A short example is presented in Table 3.
Special cases such as de-normalized numbers are not handled since they are not required for multibody dynamics simulations. Treating those cases would also consume more resources. The only case in addition and multiplication operation is when one of the operands equals 0.
A fundamental addition operation is performed in the following steps:
-
1.
calculate the exponent difference \(\Delta exp\);
-
2.
shift the significand (of a smaller input number preserving the guard bits [36]) by \(\Delta exp\) bits to the right;
-
3.
perform addition of significands if input signs are equal and perform subtraction otherwise;
-
4.
shift the result to the left by \(n\) bits, where \(n\) is the position from the left of the first 1;
-
5.
round off the shifted result [36] and get the mantissa from it – set it as the output mantissa;
-
6.
calculate the output exponent as a difference of the exponent of a bigger input number and \(n\);
-
7.
set the output sign equal to the sign of a bigger input number.
When one of the input numbers is equal to 0, the result is set as the other number without performing any of the above-mentioned steps. One addition is executed using 339 LUTs and 0 DSP slices.
Multiplication is much simpler than addition. The output sign is a bitwise xor of input signs. The output significand is the product of input significands; if it is bigger or equals 2 (overflow), it needs to be shifted one bit to the right. The output exponent is the sum of input exponents reduced by bias (127) and, if an overflow happens, increased by 1. When one of the operands equals 0, the result is set to 0. The product of mantissas is calculated by 2 DSP slices, while the sign and the exponent are calculated using 47 LUTs.
In the case of inversion, the output significand is calculated by dividing 1 by the input significand and then shifting the final result one bit to the left. The division is done with the use of the long division algorithm. The output exponent is a bitwise not of the input exponent reduced by 2. Inversion consumes 1409 LUTs and 0 DSP slices.
4.3 HDCA design
The HDCA algorithm requires to call two main hierarchical steps: assembly and disassembly phase. All matrix multiplications involving the constrained motion subspace, i.e., \(\mathbf{D}\) matrix, are performed by just shifting the values, and no floating point operations are required. Because only one kinematic joint is analyzed, no multiplexers are needed as the values are always shifted similarly. The mentioned multiplications do not consume resources. Matrix inversion required to calculate \(\mathbf{C}\) matrix is performed with an adjugate method (as it is \(2 \times 2\) matrix for planar open–loop chain). Floating-point arithmetic (addition “+”, multiplication “\(\boldsymbol{\cdot}\)”, inversion “/”) resources needed for all sub-designs are gathered in Table 4. In all designs, the matrix-vector coefficients \(\xi \) and constraint force impulses related to body \(\mathcal{A}\) and ℬ are routed to the input, but they are not present in the table for clarity.
Due to the limited FPGA resources available, only 57 float additions and 75 float multiplications were synthesized. Moreover, 21 multiplications are always routed to subdesigns 1, 2 and 11 given in Table 4, and 12 additions are always routed to subdesign 11. Upon device reset all other float operations are connected to subdesigns 1, 2, 3, 7, 9, and 10. When all output values of those designs are already known, float operations are re-routed to subdesigns 4, 5, and 8. The design can be perceived as a simple state machine (Fig. 4) with two commands run/reset and two states: idle – for writing new input values and read – for reading the results.
4.4 Matrix inversion design
Float-point inversion consumes much more resources than addition because of the significand’s division part. This is the reason for performing Gaussian elimination described above by inverting the pivot (62) once and then multiplying (66) rather than dividing by it for all subdiagonal entries.
Let \(n\) be the size of a matrix to be inverted, and \(k\) be the iteration of Gaussian elimination starting from \(k=1\). Extracting (60) and pivoting in (61) are done with the use of multiplexers. Each step of Gaussian elimination requires exactly 1 inversion to get (62), \((n-k+1)(n-k)\) multiplications (\(n-k\) to calculate (66) and \((n-k)^{2}\) to obtain \(\mathbf{A}_{k}\) in (68)) and \((n-k)^{2}\) additions (\(\mathbf{A}_{k}\) in (68)). All iterations, in total, require
multiplications,
additions and \(n-1\) inversions. Evaluating \(\boldsymbol{\mathcal{D}}^{-1}\) matrix from (75) requires 1 inversion. Finding \(\mathbf{U}\) matrix from (77) requires \(n-i\) multiplications for each ith row, which gives in total:
Triangle inverse calculated as in (78) consumes \((n-i)(i-1)\) multiplications and additions for each \(i\)th diagonal below the main diagonal, which yields:
Calculating (80) requires \(i-1\) multiplications for each \(i\)th column, then totally, we get
Each element of \(\mathbf{Y}\) in (81) requires \(n-i+1\) multiplications and \(n-i\) additions for \(i>j\) and \(n-j\) multiplications and additions for \(i \leqslant j < n\), none resources for \(j=n\). This gives the following operation count in total:
multiplications and
additions. The last step, column permutation (82), is done by multiplexers. To reduce execution time, the sums in (81) and (78) are computed in a parallel manner with the use of binary tree reduction.
The number of multiplications required to perform the whole matrix inversion is a sum of operations that correspond to Eq. (86), (88), doubled (89), (90) and (91). This yields, in total, \((n-1)n(n+1)\) complexity. The number of additions is a sum of work related to evaluation of (87), doubled (89) and (92). In turn, this consumes \((n-1)^{2}n\) operations. Additionally, a \(4 \times 4\) matrix inversion case consumes 60 multiplications and 36 additions. The FPGA has enough resources to synthesize all operations along with multiplexers.
4.5 Coding
A convention has been used in the actual FPGA implementation to separate the algorithm from available resources. This approach makes rerouting some parts of the algorithm easier without interfering with the other parts. Another thing is that this order simplifies the change of the applied arithmetic from floating-point to fixed-point representations or even allows one to exploit some algorithms based on integers (where possible).
To exemplify the usage, a below-mentioned code snippet shows a few first lines of the module that contains the whole matrix inversion algorithm. Resources reserved for floating-point operations are linked externally in another module through  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ports.
ports.

5 Results
Two sample planar multibody systems were simulated on ZYNQ chip to investigate the feasibility and performance of the developed hardware designs. The analyzed systems are representatives of open- and closed-loop topologies (connectivities).
Figure 5 shows the sample mechanisms at their initial configurations. It is assumed that all joint velocities are initially equal to zero (\(\dot{\mathbf{q}}(t=0)=\mathbf{0}\)). All the bodies of the double pendulum and four-bar mechanism have the same shape, masses, and inertia properties demonstrated in Table 5. Revolute joints connect the parts. The only external forces applied to the bodies come from gravity (\(g=9.80665\) \(\frac{\mathrm{m}}{\mathrm{s}^{2}}\)).
Two types of simulations are performed in this study. The first corresponds to the program being executed solely on the onboard CPU. It is called a software (SW) version further in the text. On the other hand, in a hardware (HW) version, some steps are evaluated on the FPGA. General multibody procedures associated with, e.g., joint representation (see appendix A) are gathered in a prototype of a C library (called mbd library). Moreover, the explicit Euler method for forward integration in time was implemented with a constant time step \(\Delta t=0.0001\,s\)). The collected numerical results evaluated on the ZYNQ platform have been successfully verified against the simulation outcome recorded from the commercial multibody solver (MSC.ADAMS).
5.1 Double pendulum
This subsection presents the dynamic analysis results for a planar double pendulum modeled in joint canonical coordinates. Figure 6 shows positions and velocities for the joint between the body_1 and a base body. Figure 7 demonstrates the system’s total kinetic energy fluctuation. A plot of the difference in the system’s kinetic energy between HDCA and ADAMS results is also shown, which is at the level of single \(mJ\) for the single–precision arithmetic used herein and explicit integrator implemented to march forward in time.
Another aspect of this simulation study was to verify the performance of the hardware (HW) design of the  . Figure 8 presents a detailed sequence of operations, whereas Table 6 shows the relative and absolute measurements of the total execution time for 1-second simulation (10000 steps).
. Figure 8 presents a detailed sequence of operations, whereas Table 6 shows the relative and absolute measurements of the total execution time for 1-second simulation (10000 steps).
As the main procedure, the assembly phase works much faster in the hardware (HW) case. Other procedures that access FPGA registers consume much more time. The FPGA’s registers hold values for all inertial coefficients \(\boldsymbol{\xi}_{ij}\) (except for the quantity \(\boldsymbol{\xi}_{12}\), which fulfills the property \(\boldsymbol{\xi}_{21}=\boldsymbol{\xi}_{12}^{\intercal}\)) that correspond to body_1, body_2, and the compound body represent the entire multibody system modeled as a single assembly. With this design, time, in cycles, is wasted. However, a simple improvement can be made to make this approach more performant. The most significant change is observed in the update body routine. The procedure writes to 66 FPGA’s registers in total, which store all \(\boldsymbol{\xi}\) matrices related to body 1 and 2. The whole procedure can be moved to the FPGA. It is doable, as it is much simpler than the assembly step. Only six registers listed below are required to perform the update for one body.
-
1 for mass (\(m\)),
-
1 for moment of inertia (\(J_{C}\)),
-
2 for \(\mathbf{s}_{1C}\),
-
2 for \(\hat{p}_{1}\) and \(\hat{p}_{2}\).
Having this small modification in mind, an approximate execution time to perform the update would be \(\frac{12}{66}\cdot 190\,ms\approx 34.55\,ms\), and the total simulation time would be around \(60\,ms\) shorter than in the case of the software (SW) version.
5.2 Four–bar mechanism
The four-bar mechanism is considered here. The system is released from an initial position shown in Fig. 9 (\(\alpha _{0}= \frac{\pi}{4}\,rad\)), where all of the initial joint velocities are zero and fall under the gravity forces.
Planar four-bar mechanism. Loop closure constraint equations: \(\mathbf{r}(\mathbf{q}(t)) = \mathbf{r}_{0}(\mathbf{q}(t)) + \mathbf{r}_{1}(\mathbf{q}(t)) + \mathbf{r}_{2}(\mathbf{q}(t)) - \mathbf{r}_{3}\), and \(\alpha (\mathbf{q}(t)) = \alpha _{0} + \alpha _{1} + \alpha _{2} + \alpha _{3}\) (where \(\mathbf{r}_{3}\) is a constant vector such that \(\mathbf{r}_{3} = [400\,\mathrm{mm}\ \ 0 ]^{\intercal}\))
The system’s response is demonstrated in Fig. 10 and gives position \(\alpha _{0}\) and velocity \(\dot{\alpha}_{0}\) of joint of interest. The system kinetic energy and the difference in the kinetic energies are shown in Fig. 11.
Plots of errors made in loop-closure equations for position and orientation are demonstrated in Fig. 12 and 13. Even without additional stabilization terms, the errors are kept small. They are expected to accumulate when moving forward in time due to round-off errors associated with a single-precision arithmetic and simple explicit integrator used for simulations.
The last item analyzed here was to check the performance of the HW design of a matrix inversion required to calculate (42) from the  phase. A sequence of operations are given in Fig. 14.
phase. A sequence of operations are given in Fig. 14.
The purpose of the prepare inversion procedure is to evaluate the quantity given in equation (93), which is crucial to compute constraint impulse forces at the joints which connect the chain to the fixed base-body.
On the other hand, the routine, called get lagrange, evaluates the Lagrange multipliers \(\boldsymbol{\sigma}\), which enforce velocity-level constraint equations, as shown in equation (94).
where
Table 7 shows measurements of total execution time, taken from all 10000 integration time-steps related to crucial procedures presented in Fig. 14.
To perform a matrix inversion of \(\boldsymbol{\eta}\) on the FPGA, this matrix (and its inverse) has to reside in the memory space (registers) that can be accessed by the FPGA. Even though, from the programming perspective, access to this memory is the same as to the on-chip memory, it takes much more time. This is because the CPU accesses FPGA’s registers indirectly through the ARM AMBA AXI interface. This explains the time increase in procedures evaluating \(\boldsymbol{\eta}\) and using it for matrix product. A direct comparison between SW and HW versions reveals that in the latter case, the time spared in the entire simulation is very close to the time spared in matrix inversion step decreased by the total time wasted on prepare inversion and get lagrange routines. This prompts us that the reasoning is correct.
6 Summary and conclusions
This paper presents the Hamiltonian-based divide-and-conquer algorithm (HDCA) in a modified form to conform with the planar motion of mechanical systems. A unified structure of the formulation has been shown, which is tightly coupled with the implementations demonstrated in the text. Physically meaningful simulation results have been recorded even though single–precision arithmetic is used. A low-level solver prototype that exploits heterogeneous computations on CPU and FPGA is developed for efficient multibody dynamics simulations. Detailed performance analysis and operation count for individual computational steps in the HDCA algorithm have been presented and discussed. The results reveal that the computational savings on FPGA with respect to CPU-based versions depend on the phase of computations. Performance tests demonstrated that accelerating computations via FPGA in HDCA-based multibody simulations may give substantial improvements in some cases. Additionally, the matrix inversion algorithm is formulated and implemented on FPGA in a general way, and its application can be easily extended to three-dimensional systems.
There are at least a few detailed lessons learned from this research. Some of them could be potentially addressed as future development.
-
CPU access to FPGA’s registers must be rare to gain significant time savings.
-
In the assembly phase, the exploitation of \(\mathbf{W}_{\mathcal{A}}\), \(\mathbf{W}_{\mathcal{B}}\) and \(\hat{\boldsymbol{\beta}}\) is more preferred than the usage of \(\mathbf{W}\) and \(\boldsymbol{\beta}\) and lead to simpler equations with smaller matrices.
-
Assembly phase in the HDCA algorithm must be accelerated simultaneously with the initialization and disassembly phase.
-
The hardware used in this research is a resource-constrained board allowing for simple systems to be simulated. Applying the approach presented here to spatial, three-dimensional simulations would require a high-end FPGAs equipped with additional capabilities.
-
The implementation presented here is written directly in HDL. Translating the C/C++ code into HDL is worth trying.
References
Choi, H., Crump, C., Duriez, C., Elmquist, A., Hager, G., Han, D., Hearl, F., Hodgins, J., Jain, A., Leve, F., Li, C., Meier, F., Negrut, D., Righetti, L., Rodriguez, A., Tan, J., Trinkle, J.: On the use of simulation in robotics: opportunities, challenges, and suggestions for moving forward. Proc. Natl. Acad. Sci. 118(1), e1907856118 (2020). https://doi.org/10.1073/pnas.1907856118
Liu, C.K., Negrut, D.: The role of physics-based simulators in robotics. Annu. Rev. Control Robot. Auto. Syst. 4(1), 35–58 (2021). https://doi.org/10.1146/annurev-control-072220-093055
Negrut, D., Serban, R., Mazhar, H., Heyn, T.: Parallel computing in multibody system dynamics: why, when, and how. J. Comput. Nonlinear Dyn. 9(4), 041007 (2014). https://doi.org/10.1115/1.4027313
Negrut, D., Tasora, A., Anitescu, M., Mazhar, H., Heyn, T., Pazouki, A.: Chap. 20 – solving large multibody dynamics problems on the gpu. In: Hwu, W-m.W. (ed.) GPU Computing Gems Jade Edition. Applications of GPU Computing Series, pp. 269–280. Morgan Kaufmann, Boston (2012). https://doi.org/10.1016/B978-0-12-385963-1.00020-4. https://www.sciencedirect.com/science/article/pii/B9780123859631000204
Rodriguez, A.J., Pastorino, R., Luaces, A., Sanjurjo, E., Naya, M.A.: Implementation of state observers based on multibody dynamics on automotive platforms in real-time. In: The 5th Joint International Conference on Multibody System Dynamics, Lisbon, Portugal, pp. 24–28 (2018)
Rodriguez, A.J., Pastorino, R., Naya, M.A., Sanjurjo, E., Desmet, W.: Real-time estimation based on multibody dynamics for automotive embedded heterogeneous computing. In: ECCOMAS Thematic Conference on Multibody Dynamics, Prague, Czech Republic, June 19–22 2017
Pastorino, R., Cosco, F., Naets, F., Desmet, W., Cuadrado, J.: Hard real-time multibody simulations using arm-based embedded systems. Multibody Syst. Dyn. 37, 127–143 (2016). https://doi.org/10.1007/s11044-016-9504-0
Jung, J., Bae, D.: Accelerating implicit integration in multi-body dynamics using gpu computing. Multibody Syst. Dyn. 42, 169–195 (2018). https://doi.org/10.1007/s11044-017-9588-1
Rodriguez, A., Pastorino, R., Carro-Lagoa, A., Janssens, K., Naya, M.A.: Hardware acceleration of multibody simulations for real-time embedded applications. Multibody Syst. Dyn. 51, 455–473 (2021). https://doi.org/10.1007/s11044-020-09738-w
Malczyk, P., Frączek, J., González, F., Cuadrado, J.: Index-3 divide-and-conquer algorithm for efficient multibody system dynamics simulations: theory and parallel implementation. Nonlinear Dyn. 95(1), 727–747 (2019). https://doi.org/10.1007/s11071-018-4593-3
Laulusa, A., Bauchau, O.A.: Review of classical approaches for constraint enforcement in multibody systems. J. Comput. Nonlinear Dyn. 3(1), 011004 (2007). https://doi.org/10.1115/1.2803257. https://asmedigitalcollection.asme.org/computationalnonlinear/article-pdf/3/1/011004/5775955/011004_1.pdf
García de Jalón, J., Callejo, A., Hidalgo, A.F.: Efficient solution of Maggi’s equations. J. Comput. Nonlinear Dyn. 7(2), 021003 (2011). https://doi.org/10.1115/1.4005238. https://asmedigitalcollection.asme.org/computationalnonlinear/article-pdf/7/2/021003/5673205/021003_1.pdf
Featherstone, R.: A divide–and–conquer articulated–body algorithm for parallel O(log(n)) calculation of rigid–body dynamics. Int. J. Robot. Res. 18, 867–875 (1999). https://doi.org/10.1177/02783649922066619
Laflin, J.J., Anderson, K.S., Khan, I.M., Poursina, M.: Advances in the application of the dca algorithm to multibody system dynamics. J. Comput. Nonlinear Dyn. 9(4), 041003 (2014). https://doi.org/10.1115/1.4026072
Mukherjee, R.M., Anderson, K.S.: Orthogonal complement based divide–and–conquer algorithm for constrained multibody systems. Nonlinear Dyn. 48, 199–215 (2007). https://doi.org/10.1007/s11071-006-9083-3
Poursina, M., Anderson, K.S.: An extended divide-and-conquer algorithm for a generalized class of multibody constraints. Multibody Syst. Dyn. 29(3), 235–254 (2013). https://doi.org/10.1007/s11044-012-9324-9
Khan, I.M., Anderson, K.S.: A logarithmic complexity divide-and-conquer algorithm for multi-flexible-body dynamics including large deformations. Multibody Syst. Dyn. 34(1), 81–101 (2015). https://doi.org/10.1007/s11044-014-9435-6
Mukherjee, R.M., Anderson, K.S.: Efficient methodology for multibody simulations with discontinuous changes in system definition. Multibody Syst. Dyn. 18(2), 145–168 (2007). https://doi.org/10.1007/s11044-007-9075-1
Bhalerao, K.D., Anderson, K.S., Trinkle, J.C.: A recursive hybrid time-stepping scheme for intermittent contact in multi-rigid-body dynamics. J. Comput. Nonlinear Dyn. 4(4), 041010 (2009). https://doi.org/10.1115/1.3192132
Khan, I.M., Anderson, K.S.: Performance investigation and constraint stabilization approach for the orthogonal complement-based dca. Mech. Mach. Theory 67, 111–121 (2013). https://doi.org/10.1016/j.mechmachtheory.2013.04.009
Mukherjee, R., Malczyk, P.: Efficient approach for constraint enforcement in constrained multibody system dynamics. In: ASME 2013 IDETC/CIE Conferences, International Conference on Multibody Systems, Nonlinear Dynamics, and Control, Portland, Oregon, USA, pp. 1–8 (2013). https://doi.org/10.1115/DETC2013-13296
Kingsley, C., Poursina, M., Sabet, S., Dabiri, A.: Logarithmic complexity dynamics formulation for computed torque control of articulated multibody systems. Mech. Mach. Theory 116, 481–500 (2017). https://doi.org/10.1016/j.mechmachtheory.2017.05.004
Poursina, M., Bhalerao, K.D., Flores, S.C., Anderson, K.S., Laederach, A.: Strategies for articulated multibody-based adaptive coarse grain simulation of RNA. Methods Enzymol. 487, 73–98 (2011). https://doi.org/10.1016/B978-0-12-381270-4.00003-2
Malczyk, P., Frączek, J.: Molecular dynamics simulation of simple polymer chain formation using divide and conquer algorithm based on the augmented lagrangian method. Proc. Inst. Mech. Eng., Part K, J. Multi-Body Dyn. 2(229), 116–131 (2015). https://doi.org/10.1177/1464419314549875
Chadaj, K., Malczyk, P., Frączek, J.: Efficient parallel formulation for dynamics simulation of large articulated robotic systems. In: 2015 20th International Conference on Methods and Models in Automation and Robotics (MMAR), pp. 441–446 (2015). https://doi.org/10.1109/MMAR.2015.7283916
Chadaj, K., Malczyk, P., Frączek, J.: A parallel recursive hamiltonian algorithm for forward dynamics of serial kinematic chains. IEEE Trans. Robot. 33(3), 647–660 (2017). https://doi.org/10.1109/TRO.2017.2654507
Chadaj, K., Malczyk, P., Frączek, J.: A parallel hamiltonian formulation for forward dynamics of closed-loop multibody systems. Multibody Syst. Dyn. 39(1), 51–77 (2017). https://doi.org/10.1007/s11044-016-9531-x
Maciąg, P., Malczyk, P., Frączek, J.: Hamiltonian direct differentiation and adjoint approaches for multibody system sensitivity analysis. Int. J. Numer. Methods Eng. 121(22), 5082–5100 (2020). https://doi.org/10.1002/nme.6512. https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.6512
Pikuliński, M., Malczyk, P.: Adjoint method for optimal control of multibody systems in the hamiltonian setting. Mech. Mach. Theory 166, 104473 (2021). https://doi.org/10.1016/j.mechmachtheory.2021.104473
Maciąg, P., Malczyk, P., Frączek, J.: Joint-coordinate adjoint method for optimal control of multibody systems. Multibody Syst. Dyn. 56(4), 401–425 (2022). https://doi.org/10.1007/s11044-022-09851-y
Naudet, J., Lefeber, D., Daerden, F., Terze, Z.: Forward dynamics of open-loop multibody mechanisms using an efficient recursive algorithm based on canonical momenta. Multibody Syst. Dyn. 10(1), 45–59 (2003). https://doi.org/10.1023/A:1024509904612
Lay, D., Lay, S., McDonald, J.: Linear Algebra and Its Applications (2014)
Pivoting for LU Factorization. http://buzzard.ups.edu/courses/2014spring/420projects/math420-UPS-spring-2014-reid-LU-pivoting.pdf (2020)
Zynq-7000 SoC Data Sheet: Overview, DS190, Xilinx (2018)
Overton, M.L.: Numerical Computing with IEEE Floating Point Arithmetic. Society for Industrial and Applied Mathematics, USA (2001)
Castillo, A.B.: Design of Single Precision Float Adder (32-BIT Numbers) According to IEEE 754 Standard Using VHDL. Slovenská Technická Univerzita v Bratislave (MSc thesis) (2012)
Acknowledgements
This work has been supported by National Science Center under grant No. 2018/29/B/ST8/00374.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Prototype of joint library
Appendix A: Prototype of joint library
An approach to writing a general, three-dimensional solver in C language is to start the project by creating a library of joints. It should implement a minimum set of functions that can perform HDCA steps. Crucial matrices (\(\mathbf{W}_{\mathcal{A}}\), \(\mathbf{W}_{\mathcal{B}}\) and \(\hat{\boldsymbol{\beta}}\) instead of \(\mathbf{W}\) and \(\boldsymbol{\beta}\)) are created to complete the procedures.
There should be 10 functions, each implementing one product, where \(\mathbf{D}_{6 \times (6-n_{f})}\), \(\mathbf{H}_{6 \times n_{f}}\) and \(n_{f}\) (\(0 < n_{f} < 6\)) are passed as a single variable (joint’s ID). The required matrix products that should be implemented are listed below.
A sample code for \(\mathbf{D}^{\intercal}\boldsymbol{\xi}_{3 \times 3}\mathbf{D}\) (planar mechanism) is given below.

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Turno, S., Malczyk, P. FPGA acceleration of planar multibody dynamics simulations in the Hamiltonian–based divide–and–conquer framework. Multibody Syst Dyn 57, 25–53 (2023). https://doi.org/10.1007/s11044-022-09860-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-022-09860-x


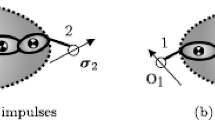




 ,
, ,
, .
.









