A Bioeconomic Model of a Multi-site Fishery with Nonlinear Demand Function: Number of Sites Optimizing the Total Catch

Abstract

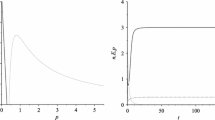
We present a mathematical model of a fishery on several sites with a variable price. The model takes into account the evolution during the time of the resource, fish and boat movement between the different sites, fishing effort and price that varies with respect to supply and demand. We suppose that the movements of the boats and resource as well as the variation of the price go on at a fast time scale. We use methods of aggregation of variables in order to reduce the number of variables and we derive a reduced model governing two global variables, respectively the biomass of the resource and the fishing effort of the whole fishery. We look for the existence of equilibria of the aggregated model and perform local stability analysis. Two main cases can occur. The first one corresponds to over-exploitation leading to fish extinction. At extinction, the fishing effort tends to a positive value. The second case corresponds to a durable fishery equilibrium which is globally asymptotically stable. In the later case, we show that there exists a number of fishing sites that optimizes the total catch of the fishery.

Appendices

Appendix 1: Calculation of the Fast Equilibria

We notice that $n(t)$ and $E(t)$, the global variables, are constants of motion of the fast process: migration and price variation. Fast equilibria are the solutions of the following system:

$$\begin{aligned} \displaystyle \sum _{i=1}^{\text {L}}m_{si}n_{i}- \sum _{i=1}^{\text {L}}m_{is}n_{s}&= 0\end{aligned}$$

(15)

$$\begin{aligned} m_{is}n_{s}- m_{si}n_{i}&= 0\end{aligned}$$

(16)

$$\begin{aligned} \beta _{i,i-1}E_{i-1}+\beta _{i,i+1}E_{i+1}-\left( \beta _{i-1,i}+ \beta _{i+1,i}\right) E_i&= 0\end{aligned}$$

(17)

$$\begin{aligned} D(p)-q\displaystyle \sum _{i=1}^{\text {L}}n_{i}^{*}E_{i}^{*}&= 0 \end{aligned}$$

(18)

Since $m_{is}=\frac{m_{0}}{k_{s}}$ and $m_{si}=\frac{m_{0}}{k_{i}}$ substituting $m_{is}$ and $m_{si}$ into the Eq. (16) leads to

$$\begin{aligned} n_{i}^{*} = \frac{k_i}{k_s}n_{s}^{*} \end{aligned}$$

(19)

Since $n=\displaystyle \sum _{i=1}^{\text {L}}n_{i}^{*}+n_{s}^{*}$ $\Rightarrow$ $n=\displaystyle \sum\nolimits _{i=1}^{\text {L}}\frac{k_i}{k_s}n_{s}^{*}+n_{s}^{*}$ $\Rightarrow$ $n=n_{s}^{*}\frac{\sum\nolimits _{i=1}^{\text {L}}k_{i}+k_{s}}{k_s}$ leads to:

$$\begin{aligned} n_{s}^{*} = \frac{k_s}{K}n \quad \text{ and } \quad n_{i}^{*} = \frac{k_i}{K}n \qquad \text{ for }\qquad i=1\ldots \text {L} \end{aligned}$$

Equation (17) states that $\beta _{1,2}E_{2}=\beta _{2,1}E_{1}$. As symmetric movement rates for boats were assumed, $\beta _{1,2}=\beta _{2,1}$ and therefore, $E_1 = E_2$ at equilibrium. Then a simple recurrence shows that $\forall i, E_i=E_{i+1}$. As a consequence, we obtain $\forall i \in \{1,\ldots ,\text {L}\}$ $E_{i}^{*}=E_{1}^{*}$. So, with $E=\displaystyle \sum _{i=1}^{\text {L}}E_{i}^{*}$ we obtain the following result

$$\begin{aligned} E_{i}^{*}=\frac{E}{\text {L}} \end{aligned}$$

From Eq. (18), we deduce that

$$\begin{aligned} D(p)&= q\displaystyle \sum _{i=1}^{\text {L}}\frac{k_{i}}{K}n \frac{E}{\text {L}}\end{aligned}$$

(20)

$$\begin{aligned}&= q(1-\alpha )n\frac{E}{\text {L}}\end{aligned}$$

(21)

$$\begin{aligned}&= QnE \end{aligned}$$

(22)

where $Q = q(1-\alpha )/\text {L}$. Because $D(p) = \frac{A}{p}$, at fast equilibrium, we have

$$\begin{aligned} p^* = p^*(n,E) = \frac{A}{QnE} \end{aligned}$$

(23)

Appendix 2: Derivation of the Aggregated Model

We substitute the fast equilibria computed in previous section and we obtain the following system:

$$\begin{aligned} \frac{dn_s}{d\tau }&= \varepsilon r_{s}n_{s}^{*}\left( 1-\frac{n_{s}^{*}}{k_s}\right) \\ \frac{dn_i}{d\tau }&= \varepsilon \left( r_{1}n_{i}^{*}\left( 1-\frac{n_{i}^{*}}{k_i} \right) -qn_{i}^{*}E_{i}^{*}\right) \\ \frac{dE_i}{d\tau }&= \varepsilon \left( -{\text {c}} + p^*qn_i^*\right) E_{i}^{*} \end{aligned}$$

Since $n=\sum _{i=1}^{\text {L}}n_{i}+ n_{s}$ we have $\frac{dn}{d\tau }=\sum _{i=1}^{\text {L}}\frac{dn_i}{d\tau }+\frac{dn_s}{d\tau }$. We perform a change of timescale $t=\varepsilon \tau$. At slow time scale, the equation governing total fish stock reads:

$$\begin{aligned} \frac{dn}{dt}&= r_{s}n_{s}^{*}\left( 1-\frac{n_{s}^{*}}{k_s} \right) +r_{1}\displaystyle \sum _{i=1}^{\text {L}}n_{i}^{*} \left( 1-\frac{n_{i}^{*}}{k_i}\right) -q\displaystyle \sum _{i=1}^{\text {L}}n_{i}^{*}E_{i}^{*} \\&= r_{s}\alpha n\left( 1-\frac{n}{K}\right) +r_{1}(1-\alpha )n \left( 1-\frac{n}{K}\right) -\frac{q(1-\alpha )}{\text {L}}nE \\&= n\left( 1-\frac{n}{K}\right) \left( \alpha r_{s}+ (1-\alpha )r_{1} \right) -\frac{q(1-\alpha )}{\text {L}}nE \end{aligned}$$

We denote $r= \alpha r_{s}+ (1-\alpha )r_{1}$ and $Q=\frac{q(1-\alpha )}{\text {L}}$. At slow time scale, the equation for fish stock finally reads:

$$\begin{aligned} \frac{dn}{dt}=rn\left( 1-\frac{n}{K}\right) -QnE. \end{aligned}$$

Equation governing total fishing efforts $E$ at slow time scale reads

$$\begin{aligned} \frac{dE}{dt}=\displaystyle \sum _{i=1}^{\text {L}} \frac{dE_i}{dt}&= \displaystyle \sum _{i=1}^{\text {L}}(-{ \text {c}}E_{i}^{*}+p^*qn_{i}^{*}E_{i}^{*}) \\&= -{\text {c}}\displaystyle \sum _{i=1}^{\text {L}}E_{i}^{*} +p^*q\displaystyle \sum _{i=1}^{\text {L}}n_{i}^{*}E_{i}^{*} \\&= \left( -{\text {c}}+p^*\frac{q(1-\alpha )}{\text {L}}n \right) E \\&= (-{\text {c}}+p^*Qn)E \end{aligned}$$

At slow scale time we finally have

$$\begin{aligned} \frac{dE}{dt}=(-{\text {c}}+p^*Qn)E \end{aligned}$$

where $p^*$ depends on $n$ and $E$ and is given by Eq. (23).