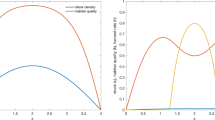
Abstract
The nature of fishing activities is such that marine habitats can be deteriorated when employing destructive fishing gear. This makes even more complex the determination of sustainable fishing policies and has led some authors to propose dynamic models which take into account this habitat degradation. In this work, we analyze in detail one of these models, an extension of the single-species Gordon–Schaefer model to two state interrelated variables: stock of fish and habitat. The model assumes that stock and carrying capacity are positively linked, and that the fishing activity has a direct and negative impact on the carrying capacity. We extend and characterize Clark’s most rapid approach optimal solution to this case.



Similar content being viewed by others
Data Availability
The data were produced by code written by the authors. The code and the data are available upon request.
Notes
A third way, appearing recently in [18], links directly habitat quality and fishing effort.
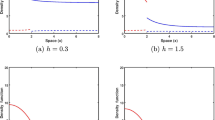
The value iteration algorithm was applied to a 256\(\times \)256 discretization of the state space with time increment \(h = 10^{-4}\) and iterations until the L1 distance between two successive functions was less than \(\varepsilon = 10^{-6}\). Running time was of the order of minutes on a 4-core Intel i7-6820HQ CPU@2.70GHz laptop.
We call “almost myopic” an agent that maximizes his instantaneous payoff plus a scrap value taking into account the environment; in our framework environment can be the stock of fish or the habitat or both.
When \(r=\rho \), a different formula applies.
References
Armstrong CW, Kahui V, Vondolia GK, Aanesen M, Czajkowski M (2017) Use and non-use values in an applied bioeconomic model of fisheries and habitat connections. Mar Resour Econ 32(4):351–369. https://doi.org/10.1086/693477
Auster PJ, Langton RW (1999) The effects of fishing on fish habitat, vol 22. American Fisheries Society Symposium, pp 150–187
Barbier E (2000) Valuing the environment as input: review of applications to mangrove-fishery linkages. Ecol Econ 35:47–61
Barbier E, Strand I (1998) Valuing mangrove-fishery linkages. A case study of Campeche, Mexico. Environ Resour Econ 12(2):151–166
Barbier E, Strand I, Sathirathai S (2002) Do open access conditions affect the valuation of externalities? Estimating the welfare effects of mangrove-fishery linkages in Thailand. Environ Resour Econ 21:343–367
Botsford LW, Castilla JC, Petersen CH (1997) The management of fisheries and marine ecosystems. Science 277(5325):509–515
Clark CW (1990) Mathematical bioeconomics: the optimal management of renewable resources, 2nd edn. Wiley, New York
Fluharty D (2000) Habitat protection, ecological issues, and implementation of the sustainable fisheries act. Ecol Appl 10:325–337
Foley NS, Armstrong CW, Kahul V, Mikkelsen E, Reithe S (2012) A review of bioeconomic modelling of habitat–fisheries interactions. Int J Ecol 2012(8):11
Holland D, Schnier KE (2006) Individual habitat quotas for fisheries. J Environ Econ Manag 51:72–92
Kahui V, Armstrong CW, Vondolia GK (2016) Bioeconomic analysis of habitat–fishery connections: fishing on cold water coral reefs. Land Econ 92(2):328–343. https://doi.org/10.3368/le.92.2.328
Kaiser MJ, de Groot S (2000) Effects of fishing on non-target species and habitats. Blackwell Science, Oxford, p 399
Kelly MRJ, Neubert MG, Lenhart S (2019) Marine reserves and optimal dynamic harvesting when fishing damages habitat. Theoretical Ecol 12:131–144. https://doi.org/10.1007/s12080-018-0399-7
Long NV, Tidball M, Zaccour G (2020) Optimal harvesting and taxation when accounting for marine environmental quality of the fishery. Nat Resour Model 33(3):e12244
Moeller HV, Neubert MG (2013) Habitat damage, marine reserves, and the value of spatial management. Ecol Appl 23(5):959–971
Nichols R, Yamazaki S, Jennings S (2018) The role of precaution in stock recovery plans in a fishery with habitat effect. Ecol Econ 146:359–369. https://doi.org/10.1016/j.ecolecon.2017.11.033
Nichols R, Yamazaki S, Jennings S (2018) Allocation of harvest between user groups in a fishery with habitat effect. Nat Resour Model 31(3):e12179. https://doi.org/10.1111/nrm.12179
Poulton AJ, Sethi SA, Ellner SP, Smeltz TS (2023) Optimal dynamic spatial closures can improve fishery yield and reduce fishing-induced habitat damage. Can J Fish Aquat Sci
Sainsbury K, Campbell R, Whitelaw A (1993) Effects of trawling on the marine habitat on the north west shelf of Australia and implications for sustainable fisheries management. In: Hancock D (ed) Sustainable fisheries through sustaining fish habitat, volume 17 of Bureau of resource sciences proceedings. Australian Society for Fish Biology Workshop, pp 137–145
Seierstad A, Sydsæter K (1987) Optimal control theory with economic applications. North-Holland, Amsterdam
Turner SJ, Thrush SF, Hewitt J, Cummings V, Funnell G (1999) Fishing impacts and the degradation or loss of habitat structure. Technical report. National Institute of Water and Atmospheric Research, Hamilton
Udumyan N (2012) Surexploitation des ressources halieutiques: habitat, récifs artificiels et apprentissage. PhD thesis, University of Marseilles
Vondolia GK, Chen W, Armstrong CW, Norling MD (2020) Bioeconomic modelling of coastal cod and kelp forest interactions: co-benefits of habitat services, fisheries and carbon sinks. Environ Resour Econ 75:25–48
Acknowledgements
The authors wish to acknowledge the advice of anonymous reviewers for the correction of errors in a first version of this paper, and for suggesting an extension of our analysis in the case \(c=0\).
Funding
This research did not receive funding.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to the research and to the writing of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.
Ethical Approval
This research does not involve human or animal studies.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection “Dynamic Games in Economics in Memory of Ngo Van Long” edited by Hassan Benchekroun and Gerhard Sorger.
Appendices
A Proofs of Propositions 2 and 3
It may be convenient in calculations to manipulate the following functions:
with which \(\chi \) can be written as:
Using (6) and (7), the first-order derivatives are given by:
Using (36) and (35) for the derivative of \(\chi \), one obtains:
This derivative does not depend, formally, on the control function E(t). Of course, the trajectories of X, K, \(\lambda _X\), and \(\lambda _K\) do depend on the control.
1.1 A.1 Proof of Proposition 2
If the trajectory is constrained to stay on the curve defined by \(\chi = 0\), then we must have, for all t, \(\chi (t) = \dot{\chi }(t) = 0\). With (37), this leads to the system of equations:
which is linear in the variables \(\lambda _X\) and \(\beta \lambda _K\). Solving this linear system, we obtain
For statement (b), we start from (37) but introduce the new functions \(F^{(1)}(X,K) = F(X,K) - X F_X(X,K) - \beta K F_K(X,K)\), \(G^{(1)}(K) = G(K) - K G'(K)\) and \(P^{(1)}(X,K) = F(X,K) P'(X)\). Accordingly:
Then, applying (2), (3), (6) and (7), separating the terms with E from the rest, we have:
If the trajectory is constrained to stay on the singular curve, then \(\ddot{\chi }(t) = 0\). We can also eliminate \(\lambda _X\) and \(\lambda _K\) using (38) and (39). The function \(\varphi (K,X)\) is defined as the term within braces, and the function \(\psi (K,X)\) is defined as the term within square brackets, after this substitution. Then, solving \(\ddot{\chi } = 0\), taking into account \(\dot{\chi } = 0\), implies \(0 = \varphi (K,X) - E \psi (K,X)\). This proves Proposition 2.
1.2 A. 2 Proof of Proposition 3
When \(\beta \) is set to 0 in (37), the expression of \(\dot{\chi }\) does not depend on \(\lambda _K\) anymore. Also, \(\chi = 0\) is equivalent to (9). Then, eliminating \(\lambda _X\) from (37) gives (10). This proves statement (a) of Proposition 3.
For the proof of statement (b), we first expose preliminary considerations. Assume we want the state to stay on a particular curve, given in general by the equation \(f(X,K) = 0\). Differentiating with respect to t, we have the identities:
The expression (42) gives the control as a feedback of the state. If one plugs (42) in the dynamics of the state, one gets the differential system:
and it is checked that this dynamics satisfies (41).
When \(\beta =0\), these expressions are simplified as:
which proves statement (b) of Proposition 3. In (43), the term F(X, K)/X is the extraction that would make the stock X constant. It is corrected with a term, proportional to G(K), taking into account the growth of the carrying capacity K.
B Logistic Growth Functions
In this section, we list the formulas obtained by specifying the general results of Sect. 2 to the logistic growth functions.
1.1 B.1 Dynamics and the Singular Control
Assume the control has the objective of keeping the function \(\chi \) equal to 0. Then, we have the following identities, in which we use the notation introduced in Section A.1.
1.1.1 B.1.1 Adjoint Variables
When using the logistic form of the growth functions, we obtain for the expressions (6) and (7):
1.1.2 B.1.2 The Function \(\chi (t)\)
The formulas for the first derivatives of \(\chi (t)\) are obtained from the generic formulas (37) and (40). Using the identities (44), we obtain:
1.1.3 B.1.3 Staying on the Curve \(\chi = 0\)
If the trajectory follows the curve \(\chi (t) \equiv 0\), then \(\chi = \dot{\chi } = 0\). Using (38) and (39) (or directly solving for \(\Theta _X\) and \(\Theta _K\) in (47) and (48)), we obtain the following values:
1.2 B. 2 Proof of Lemma 1
The proof consists in enumerating the solutions of the system of four Eqs. (15)–(18) with four unknowns. We exclude \(K = 0\) as a solution of (16) since in that case the dynamics (12) are not well defined. Then, the solution of (16) is
Next, \(X = 0\) is clearly a solution of (15). Replacing in (17) and (18), we find:
leading to \(\lambda _K = 0\) and the value of \(\lambda _X\) in (20). Assuming now that \(K \not = 0\) and \(X \not =0\), we have successively:
The two last equations are equivalent to (22) and (23) respectively. This concludes the proof of Lemma 1.
1.3 B. 3 Trajectories for E Constant
We investigate in this section the solutions to the differential systems when E is constant. To that end, it is convenient to perform the change of functions \(Z = K^{-1}\) and \(Y = X^{-1}\). This leads to the differential system:
Trajectories of the state. The solution of (13) is, classically, (26). This is obtained, for instance, using the function \(Z = K^{-1}\) and the linear differential equation (54), whose solution is:
The solution of (12) can be deduced as follows. Using the function \(Y = X^{-1}\) and (53), we have:
Consequently, the solution will be:
This equation directly leads to (27).
Alternative representations. Using the asymptotic quantities when \(t\rightarrow \infty \), derived in Sect. 3.1, the solution for E constant may be rewritten as:
Equations in the (K, X) plane. Provided \(K_0 \not = K^{\infty }\), the variable t can be eliminated from (57):
This is the amount of time needed to go from state \(K_0\) to state K. Then, replacing in (58), we have:
This is the equation of the trajectory in the (K, X) plane, parameterized by any point \((K_0,X_0)\) on the curve.
If \(K_0 = K^{\infty }\), the trajectory is included in the line \(\{ K = K^{\infty }\}\). If needed, the time variable may be eliminated from (58):
This is, in particular, the case in the standard model with K constant.
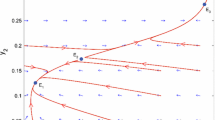
We now investigate the behaviors of trajectories in the (K, X) plane. From (59), and since with \(E=0\) we have \(X^{\infty }=K^{\infty }=\overline{K}\), these are the curves of equation
parameterized by any point \((K_0,X_0)\) on the curve.Footnote 4 These curves have the following property.
Lemma 3
Let f(K) be one of these curves, parameterized by \((K_0,X_0)\). There exists some \(K_1\in (0,\overline{K})\) such that \(\lim _{K\rightarrow K_1^+} f(K) = +\infty \) if:
-
(a)
\(\rho > r\), or
-
(b)
when and only when
$$\begin{aligned} X_0 ~ > ~ \frac{K_0 \overline{K}(r - \rho )}{r\overline{K}- \rho K_0} \end{aligned}$$(60)if \(\rho < r\).
The proof consists in analyzing the behavior of the curves when \(K\rightarrow 0\). If \(\rho > r\), we find that \(f(K) \sim K (r-\rho )/r < 0\): Then necessarily \(f(\cdot )\) changes sign between \(K=0\) and \(K=\overline{K}\), which can occur only by diverging to \(\pm \infty \). If \(\rho < r\), we find that \(f(K) \sim C(K_0,X_0) K^{r/\rho }\) for some value \(C(K_0,X_0)\). If this value is negative, which is equivalent to condition (60), this is the same situation as when \(\rho > r\) and there is a point \(K_1\) where \(f(\cdot )\) diverges. If this value is 0, the curve f has actually the equation
, and it does not diverge. If \(C(K_0,X_0) > 0\), the trajectory lies below the curve \(f_c(K)\) (solutions to the differential system cannot cross each other) so that it cannot diverge.
Adjoint variable trajectories with \(E=0\). In the specific case where \(E=0\), it is possible to obtain a formula for the adjoint variable \(\lambda _X\). Start with the differential equation for \(\Theta _X = X \lambda _X\)
and this last equation yields (28).
C Proof of Lemma 2
Proof
(a) Consider the polynomial in (24), that is,
Recall that we are looking for admissible roots of Pol(E), that is, such that \(0 \le E \le \min ( r, \rho /\beta )\). This polynomial has the following properties.
The existence part is proved by showing that \(Pol(\cdot )\) changes sign over the interval. The uniqueness follows from convexity.
Under the condition \(\overline{K}p> c > 0\), \(Pol(0) > 0\). Consider first the case \(r \le {\rho }/{\beta }\). This implies \(Pol(r) < 0\), and hence, \(Pol(E)=0\) for at least one \(E \in (0,r)\). Through tedious yet mechanical computations, using the assumption that \(\overline{K}p - c > 0\), one shows that \(Pol''(E) >0 \; \text{ if } \; E \in [0, r]\). Then, it is not possible to have three roots of \(Pol(\cdot )\) in the interval. When \(r > {\rho }/{\beta }\), then \(Pol({\rho }/{\beta }) < 0\), and the reasoning is similar. From this analysis, we conclude not only that \(Pol(\cdot )\) has a single root, but also that \(Pol'(E) <0\) in the region where E is admissible.
Moreover from (24), and for admissible E,
Then using total differentiation for the root \(E^\infty (c)\), we have:
(b) Now, we consider \(c=0\). In this case, with \(Pol_0(E) \equiv Pol(E)\vert _{c=0}\),
Let Q(E) denote the last polynomial of degree 2 in E. The discriminant of Q(E) is:
This quadratic polynomial of \(\beta \) has in turn as discriminant: \(48 (\delta + \rho )^2(\delta - r) (\delta + r)\). Then, if \(\delta < r\), this discriminant is negative and \(\Delta _\beta > 0\) for all values of \(\beta \). As a consequence, Q(E) has two real and positive roots \(E_1 < E_2\), where \(E_1\) is given explicitly by (25). We proceed with locating \(E_1\) with respect to the other roots of \(Pol_0(E)\): r and \(\rho /\beta \). We have:
If \(\delta < r\), this implies that \(0< E_1 < (\delta + r)/2\). If furthermore \(r \le \rho /\beta \), then \((\delta + r)/2 < \min ( r, \rho /\beta )\) and therefore \(E_1 = E_0^\infty \).
If \(\delta < r\) but \(r > \rho /\beta \), we just have \(E_0^\infty = \min ( E_1, \rho /\beta )\). \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Jean-Marie, A., Tidball, M. Dynamic Fishing with Endogenous Habitat Damage. Dyn Games Appl 14, 33–56 (2024). https://doi.org/10.1007/s13235-023-00511-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-023-00511-0