Complex Oscillations in the Delayed FitzHugh–Nagumo Equation

Abstract

Motivated by the dynamics of neuronal responses, we analyze the dynamics of the FitzHugh–Nagumo slow–fast system with delayed self-coupling. This system provides a canonical example of a canard explosion for sufficiently small delays. Beyond this regime, delays significantly enrich the dynamics, leading to mixed-mode oscillations, bursting and chaos. These behaviors emerge from a delay-induced subcritical Bogdanov–Takens instability arising at the fold points of the S-shaped critical manifold. Underlying the transition from canard-induced to delay-induced dynamics is an abrupt switch in the nature of the Hopf bifurcation.

Appendices

Appendix 1: Normal Form Reduction at Hopf Bifurcation

In Sects. 2.1 and 3, we have identified parameters for which the linearized equation at a fixed point, respectively of the full system (1) or of its fast subsystem, has a pair of purely imaginary eigenvalues. This provides us with the locus of possible Hopf bifurcations, and we show here aided by numerical evaluations that the system undergoes generic Hopf bifurcations. To this end one needs to reduce the system to normal form on the center manifold. This appendix is devoted to providing the outline of the method, in the context of the full system (slightly more complex than the fast one), and along the branch of Hopf bifurcations given by the first branch $\tau =\tau _1^0(J,\varepsilon ,a)$ for $a\in (1,\sqrt{1+2J})$, defined in Eq. (4). This curve corresponds to a change of stability of the fixed point $(a,a-a^3/3)$. We showed that as $\varepsilon \rightarrow 0$, the curve collapses to a nonsmooth curve made of a segment $\{J\tau <1, a=1\}$ and the curve of Hopf bifurcations of the fast system $\tau (a)$ given by Eq. (16). We further showed that for when $\varepsilon \rightarrow 0$, the Hopf bifurcation corresponding to $J\tau <1$ is supercritical, and otherwise subcritical.

We confirm this change of criticality of the Hopf bifurcation for $\varepsilon >0$ by reducing the system to normal form reduction along the Hopf bifurcation manifold. We follow a relatively standard tradition exposed for instance for delayed differential equations in Hale and Lunel (1993) and reviewed in Campbell (2009). We outline the method and calculations performed aided by the formal calculations software Maple®, before presenting the obtained coefficients and their shape as a function of the parameters.

This method is based on considering the delay differential Eq. (1) as a dynamical system in the Banach space X of continuous functions from $[-\tau ,0]$ to $\mathbb {R}^2$ endowed with the uniform norm.

$$\begin{aligned} \Vert z\Vert = \sup _{\theta \in [-\tau ,0]} \vert z(t)\vert \end{aligned}$$

where $\vert z(t)\vert$ is the Euclidian norm on $\mathbb {R}^2$ of the value of the function $z\in X$ at time $t\in [-\tau ,0]$. The delayed differential equation is expressed as a functional differential equation on this space. Indeed, defining now $z_t \in X$ as the portion of solution $(x(t),y(t),t\in [t-\tau ,t])$, with the definition

$$\begin{aligned} z_t(\theta )=z(t+\theta ), \quad -\tau \le \theta \le 0, \end{aligned}$$

we can rewrite Eq. (1) as:

$$\begin{aligned}\frac{d}{dt} x_t(\theta )={\left\{ \begin{array}{ll} \frac{\hbox {d}}{{\hbox {d}}\theta } x_t(\theta ) &{} -\tau \le \theta <0\\ \Big [y_t(0)+ x_t(0)+ J(x_t(0)-x_t(-\tau ))\Big ] -\frac{x_t(0)^3}{3} &{} \theta =0 \end{array}\right. }\end{aligned}$$

and similarly,

$$\begin{aligned}\frac{\hbox {d}}{{\hbox {d}}t} y_t(\theta )={\left\{ \begin{array}{ll} \frac{\hbox {d}}{{\hbox {d}}\theta } y_t(\theta ) &{} -\tau \le \theta <0\\ \Big [\varepsilon (a-x_t(0))\Big ] &{} \theta =0 \end{array}\right. }\end{aligned}$$

The terms within the brackets are the affine part of the flow, separated from the nonlinear cubic term in the equation on the first variable, which does not involve delays. Calculations are much simplified when changing variables so that the equilibrium is at the origin. This change of variable simply amounts changing the origin, i.e., consider the equation in terms of $\tilde{x}=x-x^*$. The equations now read:

$$\begin{aligned} \frac{\hbox {d}}{{\hbox {d}}t} \tilde{x}_t(\theta )=&{\left\{ \begin{array}{ll} \frac{\hbox {d}}{{\hbox {d}}\theta } \tilde{x}_t(\theta ) &{} -\tau \le \theta <0\\ \Big [(1-a^2)\tilde{x}_t(0)+ J(\tilde{x}_t(0)-\tilde{x}_t(-\tau ))\Big ] - a\tilde{x}_t(0)^2 - \frac{x_t(0)^3}{3} &{} \theta =0 \end{array}\right. },\\ \frac{\hbox {d}}{{\hbox {d}}t} \tilde{y}_t(\theta )=&{\left\{ \begin{array}{ll} \frac{\hbox {d}}{{\hbox {d}}\theta } \tilde{y}_t(\theta ) &{} -\tau \le \theta <0\\ -\varepsilon \tilde{x}_t(0) &{} \theta =0 \end{array}\right. }. \end{aligned}$$

The linear operator decomposes into a part only depending on $\tilde{z}_t(0)$:

$$\begin{aligned} A_0=\left( \begin{array}{cc} 1-a^2+J &{} 1 \\ -\varepsilon &{} 0 \end{array}\right) , \end{aligned}$$

and an operator depending on $\tilde{x}_t(-\tau )$:

$$\begin{aligned} A_1=\left( \begin{array}{cc} -J &{} 0 \\ 0 &{} 0 \end{array}\right) . \end{aligned}$$

At Hopf bifurcation points, i.e., when the characteristic equation

$$\begin{aligned} {\hbox {det}}(\lambda I_2 -A_0 - e^{-\lambda \tau }A_1)=0 \end{aligned}$$

has a complex solution $\lambda =\pm \mathbf {i}\omega$, a complex right eigenvector is:

$$\begin{aligned} v=\left( \begin{array}{cc} 1 \\ \frac{\mathbf {i}\varepsilon }{\omega } \end{array}\right) , \end{aligned}$$

which corresponds to a two-dimensional center eigenspace N:

$$\begin{aligned} \left( \begin{array}{cc} \cos (\omega \theta ) &{} \sin (\omega \theta ) \\ \displaystyle {-\frac{\sin (\omega \theta )\varepsilon }{\omega }} &{} \displaystyle {\frac{\cos (\omega \theta )\varepsilon }{\omega }} \end{array}\right) \end{aligned}$$

and an infinite-dimensional stable eigenspace S. The corresponding center manifold is given by:

$$\begin{aligned} \mathcal {M} = \{\phi \in X, \; \phi = \Phi u + h(u)\} \end{aligned}$$

where $u=(u_1,u_2)^t$ are the coordinates on the nullspace N and $h(u)\in S$. Classically, we project the solutions to the delay differential equation on $\mathcal {M}$ and obtain:

$$\begin{aligned} z_t(\sigma )= & {} \left( \begin{array}{cc} \cos (\omega \sigma )u_1(t) + \sin (\omega \sigma )u_2(t) \\ \displaystyle {-\frac{\sin (\omega \theta )\varepsilon }{\omega }u_1(t)+\frac{\cos (\omega \theta )\varepsilon }{\omega }u_2(t)} \end{array}\right) \\&+ \,\left( \begin{array}{cc} \displaystyle {h_{11}^1 (\sigma ) u_1(t)^2+h_{12}^1 (\sigma ) u_1(t)u_2(t)+h_{22}^1 (\sigma ) u_2(t)^2} \\ \displaystyle {h_{11}^2 (\sigma ) u_1(t)^2+h_{12}^2 (\sigma ) u_1(t)u_2(t)+h_{22}^2 (\sigma ) u_2(t)^2} \end{array}\right) + {\mathcal {O}} (\Vert x\Vert ^3) \end{aligned}$$

where the $h_{jk}^i$ characterize the Taylor expansion of the solution on the center manifold. These coefficients satisfy a system of affine ODEs, in which the affine term depends on the orthogonal basis of the nullspace, denoted $\psi (\theta )$ (which is straightforward to calculate) arising from the projection of the original equation on N. These are now classical methods, introduced and used in Campbell (2009), Stone and Campbell (2004), Faria and Magalhães (1995). In our case, the solution to the linear ordinary differential equation of $h_{jk}^i$ yields relatively complex expressions, in terms of six constants $C_1\cdots C_6$ that are then solved in order to match boundary values (and solve the original DDE on the center manifold). One finds:

$$\begin{aligned} h_{11}^1= & {} \frac{a}{3\omega } \big (\cos (\omega \theta )\Psi _{21}-\sin (\omega \theta )\Psi _{11}(0)\big ) + C_2 \\&-\, C_5 \sin (\omega \theta )\cos (\omega \theta ) + C_6 \left( \cos (\omega \theta )^2-\frac{1}{2}\right) \end{aligned}$$

and similar expressions for the other terms, and it is not hard to determine the constants. From these expressions, we obtain a system of ODEs describing the evolution in time of u:

$$\begin{aligned}{\left\{ \begin{array}{ll} \dot{u_1}=\omega u_2 + \Psi _{12}(0) (G_1(u_1,u_2) ) + {\mathcal {O}} (\Vert u\Vert ^4)\\ \dot{u_2}=\omega u_1 + \Psi _{22}(0) (G_1(u_1,u_2) ) + {\mathcal {O}} (\Vert u\Vert ^4) \end{array}\right. } \end{aligned}$$

with G a cubic polynomial, whose coefficients can be deduced from the evaluation of $h_{jk}^i$ and $C_i$, and the first Lyapunov coefficient, characterizing the type of the Hopf bifurcation, is a simple function of these coefficients. With the help of the formal calculations software Maple®, we compute all these coefficients analytically. It happens that, as of quadratic terms, only the coefficients of $u_1^2$ in $G_1$ and $G_2$ are nonzero, and cubic coefficients involved in the computation of the Lyapunov coefficients enjoy a relatively simple form. These coefficients are given by:

$$\begin{aligned}{\left\{ \begin{array}{ll} G_1(u_1,u_2)=-a \Psi _{11}(0) u_1^2 + u_1^3 \Psi _{11}(0)\left( -\frac{1}{3} -2 h^1_{11}(0)a\right) - 2\Psi _{11}(0) a h_{22}^1(0) + \cdots \\ G_1(u_1,u_2)=-a \Psi _{21}(0) u_1^2 -2 a h_{12}^1(0) u_1^2 u_2 + \cdots \\ \end{array}\right. } \end{aligned}$$

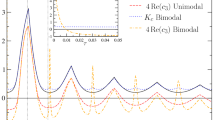
where the dots correspond to terms that are not necessary to compute the first Lyapunov coefficient. From this expression, classical formulae (see, e.g., Kuznetsov 1995) yield a very complex expression for the first Lyapunov coefficient as a function of the parameters (Fig. 13). This expression is, however, exact and allows direct numerical computation of the Lyapunov coefficient that we presented in Sect. 2.2.

Fig. 13

Self-coupled delayed FitzHugh–Nagumo system for $\tau >1/J$ and $\varepsilon =0.05$. a $\tau =0.6$, b $\tau =0.7$, (c)$\tau =0.9$. The system transitions from MMOs to bursting through a period of chaos, arising for similar parameter values as in the delayed FhN system

Appendix 2: The FitzHugh–Nagumo System with $\gamma \ne 0$

In this appendix, we provide one numerical example of delayed self-coupled FitzHugh–Nagumo system (8) with $\gamma \ne 0$ that has similar dynamics as the ones studied in the main text, i.e., for $\gamma$ small enough.

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}=x-\frac{x^3}{3}+y + J(x(t)-x(t-\tau ))\\ \dot{y}=\varepsilon (a-x+\gamma y) \end{array}\right. } \end{aligned}$$

(20)

The fixed points of the system are given by $y=(x-a)/\gamma$, where x is the solution of the cubic polynomial:

$$\begin{aligned} \frac{\gamma +1}{\gamma } x -\frac{x^3}{3} -\frac{a}{\gamma } = 0. \end{aligned}$$

This equation can be solved using Cardano method, exactly as we solve the cubic equation of the fast system. In detail, the Cardano discriminant of the equation writes:

$$\begin{aligned} \Delta = \frac{27}{b^2} \left( 9 a^2 -\frac{b+1}{b}\right) . \end{aligned}$$

when $\Delta >0$, the system has a unique solution:

$$\begin{aligned} x_0=\left( -\frac{3a}{2b} + \sqrt{\Delta }\right) ^{1/3} - \left( \frac{3a}{2b} + \sqrt{\Delta }\right) ^{1/3}, \end{aligned}$$

and when $\Delta <0$, we find 3 roots:

$$\begin{aligned} x_k = 2\left( \frac{b+1}{b}\right) ^{1/3} \cos \left( \frac{1}{3} \arccos \left( -\frac{3a\sqrt{b}}{2 \sqrt{(b+1)^3}}\right) + \frac{2 k \pi }{3}\right) . \end{aligned}$$

The stability of the fixed points can be analyzed in a similar fashion as done before. In that case, denoting by $x_*$ one of the equilibria found, the dispersion relationship corresponds to the determinant of the matrix:

$$\begin{aligned} \xi \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array}\right) - \left( \begin{array}{cc} A &{} 1 \\ -\varepsilon &{} \varepsilon \gamma \end{array}\right) \end{aligned}$$

with $A=1-(x_*)^2 +J (1-e^{-\xi \tau })$, and the dispersion relationship therefore reads:

$$\begin{aligned} \xi ^2- (A+\gamma \varepsilon )\xi +\varepsilon =0, \end{aligned}$$

or:

$$\begin{aligned} e^{-\xi \tau }=\frac{\xi ^2-\xi (1-(x_*)^2 +J+\gamma \varepsilon )+\varepsilon (\gamma (1-(x_*)^2 +J)+1)}{J\xi +\gamma \varepsilon J}. \end{aligned}$$

This appears much more complex to solve in closed form.

The fast dynamics is identical as that of the delayed FhN system, and therefore, the analysis of Sect. 3 applies. This allows to account for most of the behaviors of the FhN system. The only phenomenon requiring some more work is the presence of canard explosion and their type. Similar to the nondelayed case, the details of the slow dynamics matter for the demonstration of the presence of canard explosions. Here, we provide numerical evidences for canard explosion and show that similar phenomena of emergence of mixed-mode oscillations and bursting appear, for the same values of parameters, in the parameter regime where FhN system has a unique fixed point. Let us for instance consider the FhN model for $b=-1$ and $\gamma =-0.3$. We set $a=0.85$ (which leads the system to a similar situation as studied in the FhN system with $a=1.01$). For $\tau >1/J$, we have seen that geometric analysis of the fast system accounted for most phenomena arising in the FhN system. This property persists for the FitzHugh–Nagumo system, and we therefore observe the very same behaviors and transitions at similar delays.