Abstract
Model uncertainty makes it difficult to draw clear inference about mutual fund performance persistence. I propose a new performance measure, Bayesian model averaged (BMA) alpha, which explicitly accounts for model uncertainty. Using BMA alphas, I find evidence of performance persistence in a large sample of US funds. There is a positive and asymmetric relation between flows and past BMA alphas, suggesting that fund investors respond to the information in BMA alphas. My findings are robust to various sensitivity analyses, including alternative measures of post-ranking performance, flows and total net assets, and alternative econometric model specifications.
Similar content being viewed by others
Notes
Investors’ concerns about model uncertainty result in an additional risk premium in security prices (Hansen et al. 1999, 2002; Anderson et al. 2003; Hansen and Sargent 2006). In asset allocation, ignoring model uncertainty leads to perceived utility loss as high as 4.8% per year (Avramov 2002). Fama and French (1997) point out that model uncertainty is one of the problems in calculating industry costs of equity and show that the CAPM of Sharpe (1964) and the three-factor model of Fama and French (1993) can produce industry costs of equity estimates that differ by 2% or more. Pastor and Stambaugh (1999) find that model uncertainty also contributes to the difficulty in estimating individual firms’ costs of equity.
A number of papers apply Bayesian econometric techniques to study topics such as performance evaluation, portfolio choice and performance persistence in the mutual fund industry (e.g., Baks et al. 2001; Pastor and Stambaugh 2002a, b; Avramov and Wermers 2006; Busse and Irvine 2006; Jones and Shanken 2005; Friesen 2004; Huij and Verbeek 2007). These papers focus on parameter uncertainty, while my paper focuses on model uncertainty.
Berk and Green (2004) demonstrate that skilled managers may not have consistently good performance and fund returns need not be predictable if the supply of capital by investors is competitive and managers experience decreasing returns to scale.
Investment Company Fact Book 2007, Table 1 (http://www.ici.org/pdf/07fb_datasec_1.pdf).
In my sample that spans the period 1980–2003, I find that the average expense ratio of actively managed equity funds is 1.42% per year, while the average expense ratio of equity index funds is 0.64% per year. Actively managed bond and balanced funds also have higher average expense ratios than their passively managed counterparts.
The existence of skilled fund managers is consistent with semi-strong form efficiency if such managers possess private information.
These results are based on BMA alphas estimated with a skeptical prior belief in managerial skill and a 36-month estimation window. Using an alternative prior belief or a longer estimation window does not change my conclusions qualitatively.
Gruber (1996) also reports outflows from poorly performing funds. To sort funds into deciles, he uses a model that attributes fund return to the equity market, the bond market, a size factor and a growth factor.
Using exact monthly fund flow data of UK mutual funds between 1992 and 2000, Keswani and Stolin (2008) document the smart money effect in the UK, which is attributed to the buying decisions of both retail and institutional fund investors. The authors also document the smart money effect in the US using monthly mutual fund data available from 1991. Their results suggest that data frequency and sample period selection can affect tests of the smart money effect.
Christopherson et al. (1998) propose using net of benchmark returns as a solution to the problem of persistent estimation error in alphas.
Jones and Shanken (2005) and Friesen (2004) relax the prior independence assumption by specifying a hierarchical prior for fund alphas. A complete relaxation of the prior independence assumption requires the specification of hierarchical priors for both the fund alpha and regression coefficients. Such priors result in analytically intractable posterior distributions and require the use of Markov Chain Monte Carlo simulation techniques (see e.g., Koop 2003).
In Sect. 8.6, I explore the impact of using the more extreme prior belief of no skill.
In the CRSP Database, not all funds switched to monthly reporting of total net assets starting from 1991. In my own sample, two funds only reported quarterly total net assets in 1991—Seligman Frontier Fund and Lazards Funds: Equity Portfolio.
I use two estimation windows: 36 and 60 months.
“Appendix A” lists the variables in each model.
When I repeat the analysis of Table 1 using model probabilities estimated with a less skeptical prior belief or a 60-month estimation window, I obtain similar results. Identities of the top three models are the same in all robustness checks.
For example, if model j is the CAPM, then \( x_{i,j,t} \) is the market portfolio return in January 1983, and \( \overline{{b_{i,j} }} \) is the posterior mean of fund i’s market beta estimated from the previous 36 months.
Throughout the paper, I use Newey and West (1987) heteroskedasticity-and-autocorrelation consistent (HAC) standard errors to compute p values. The lag length is set to 6 months for computing the HAC covariance matrix. I also experiment with lag lengths of 3, 9, and 12 months and obtain qualitatively similar inferences. Hamilton (1994, pp. 282–283) describes the computation of the HAC covariance matrix and standard errors.
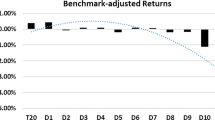
Besides model averaging risk-adjusted returns, I also measure future fund returns in two different ways. For each decile and the 10–1 portfolio, I calculate the average excess return (in excess of the risk-free rate) and a risk-adjusted return (alpha) defined with respect to a specific return generating model. For equity funds, the risk-adjusted return is Carhart’s (1997) four-factor alpha. For bonds funds, the risk-adjusted return is the alpha defined with respect to the model in Blake et al. (1993). For balanced funds, the risk-adjusted return must account for the fact that such funds can invest in both equities and bonds. Therefore, I employ the model in Elton et al. (1996a) and Gruber (1996) because it accounts for risks in these two asset classes (see “Appendix A”). Using these alternative measures of future fund returns, I find evidence of return predictability for balanced, equity and bond funds. These results are available from the author upon request. In Sect. 8.3, I examine the robustness of my results using net of benchmark returns to measure post-ranking performance.
Results of the intermediate portfolios are available from the author upon request.
Findings based on dollar cash flow are available from the author upon request.
As mentioned in Sect. 4, I assign equity funds to one of six investment objectives: small company growth, other aggressive growth, growth, income, growth, growth and income and maximum capital gain. Bond funds fall into one of three investment objectives: government bonds, mortgage-backed securities, and corporate bonds. Balanced funds represent a single investment objective.
I compute standard deviation only if a fund has a complete record of 12 monthly returns in a year.
Since I create the fractional and quintile performance ranks separately for each investment objective, it is never the case that I compare funds from different objective groups in constructing these ranks.
All alpha measures are estimated using data from the previous 36 months and come from the output of the Bayesian estimation (see Sect. 3.2). I estimate Sharpe ratio using monthly returns from the previous 12 months.
I obtain similar findings when I (1) estimate a bivariate VAR with three lags, and (2) use funds with continuous returns and flows for at least 12 months.
This is equivalent to computing the return in excess of the benchmark return for each fund in decile i and then averaging the funds’ excess returns to obtain the decile’s equally weighted alpha.
I continue to find evidence of persistence when funds are ranked using BMA alphas estimated with a less skeptical prior belief and a 36-month estimation window. I do not find evidence of persistence using the longer 60-month estimation window, regardless of the prior belief in skill. I do not compute Spearman correlation for Panel D because there are only two portfolios; the Best–Worst spread conveys the same information as the Spearman correlation in this case.
As an additional robustness check, I replace the CRSP index with the S&P 500 index to compute post-ranking alphas for equity and balanced funds. Making this change does not affect my findings. To ensure that results for balanced funds are robust to the benchmark’s allocation between stocks and bonds, I repeat my analyses using two alternative benchmarks. The first allocates equal weight (50%) to both the CRSP and Lehman indexes, the second allocates 70% weight to the CRSP index and 30% weight to the Lehman index. I obtain similar results using these alternative benchmarks.
The ten industry-sorted stock portfolios are from Ken French’s website. I thank him for generously providing the data. The ten industries are: (1) consumer nondurables, (2) consumer durables, (3) manufacturing, (4) energy, (5) business equipment, (6) telephone and television transmission, (7) wholesale, retail and some services, (8) healthcare, medical equipment and drugs, (9) utilities, and (10) other. The first three bond portfolios are portfolios of long-term, intermediate-term and short-term government bonds. The fourth portfolio is a portfolio of low-grade corporate bond. The long- and intermediate-term government bond portfolios are from Ibbotson Associates. The short-term government bond portfolio is the Merrill Lynch 1-to-3 year Treasury index (from Datastream). The low-grade corporate bond portfolio is the Merrill Lynch High Yield index (from Datastream).
Term premium for long-term Treasury securities is 10-year Treasury bond yield minus 3-month Treasury bill yield, term premium for 1-year Treasury securities is 1-year Treasury bill yield minus 3-month Treasury bill yield, default premium for corporate bonds is BAA corporate bond yield minus AAA corporate bond yield, default premium for commercial paper is 3-month commercial paper yield minus 3-month T-bill yield, 12-month production growth is calculated using the total Industrial Production index (G.17 supplement). All yields and the total Industrial Production index are obtained from the Federal Reserve Board. The CPI series is from the Bureau of Labor Statistics.
Throughout Sect. 8, whenever I estimate flow-performance regressions, I also examine the flows to deciles sorted by past BMA alphas. The decile-based analyses produce results similar to those of the flow-performance regressions. In addition, all flow-performance regression results are robust to the use of HIGHPERF, MIDPERF and LOWPERF as performance measures.
The assumption here is that flows occur at the end of the quarter (or year).
The alternative approach of estimating missing total net assets increases the sample slightly from 26,342 to 26,352 fund-years.
In Bayesian econometrics, precision is the inverse of variance. A prior standard deviation of 0.00001 translates into a precision of 1/(0.00001)2 = 1e10.
Results based on BMA alphas estimated with a 60-month estimation window are qualitatively similar.
Nanda et al. (2004) study funds that offer three classes: A, B and C. Class A charges a front-end load, while Class B and C do not. However, classes B and C charge a contingent deferred sales load (CDSL) when investors sell out of the fund. Class B’s CDSL typically starts at 5% in the first year and declines over time. Class C’s CDSL is at 1% in the first year and is usually waived thereafter. Class B shares are typically converted into Class A shares after 6–8 years, but not Class C shares. All three classes have to pay an annual 12b-1 fee, with class A incurring a lower 12b-1 fee than classes B and C.
I use pooled OLS instead of Fama–MacBeth regression because SPVOL is the same for all funds for any given year. In the Fama–MacBeth framework, adding market volatility to the annual cross-section regression causes the intercept and market volatility to be collinear, rendering estimation infeasible. Thus, I use pooled OLS regression for testing the market volatility hypothesis.
See Carlin and Louis (2000) for a detailed discussion of the empirical Bayes approach.
In Sect. 4, I provide details of the mutual fund investment objectives. The reader should note that I use all funds having at least 60 months of data only for specifying the values of the prior hyperparameters. For the empirical analyses, I retain funds with at least 37 months of data (see Sect. 4).
Poirier (1995, p. 543).
References
Anderson EW, Hansen LP, Thomas JS (2003) A quartet of semigroups for model specification, robustness, prices of risk, and model detection. J Eur Econ Assoc 1:68–123
Aragon GO, Ferson WE (2007) Portfolio performance evaluation. Found Trends Finance 2:83–190
Avramov D (2002) Stock return predictability and model uncertainty. J Financ Econ 64:423–458
Avramov D, Wermers R (2006) Investing in mutual funds when returns are predictable. J Financ Econ 81:339–377
Baks KP, Metrick A, Wachter J (2001) Should investors avoid all actively managed mutual funds? A study in bayesian performance evaluation. J Finance 56:45–85
Berk JB, Green RC (2004) Mutual fund flows and performance in rational markets. J Polit Econ 112:1269–1306
Blake CR, Elton EJ, Gruber MJ (1993) The performance of bond mutual funds. J Bus 66:371–403
Bollen NPB, Busse JA (2005) Short-term persistence in mutual fund performance. Rev Financ Stud 18:569–597
Brown SJ, Goetzmann WN (1995) Performance persistence. J Finance 50:679–698
Brown SJ, Goetzmann WN, Ibbotson RG, Ross SA (1992) Survivorship bias in performance studies. Rev Financ Stud 5:553–580
Busse JA (1999) Volatility timing in mutual funds: evidence from daily returns. Rev Financ Stud 12:1009–1041
Busse JA, Irvine PJ (2006) Bayesian alphas and mutual fund persistence. J Finance 61:2255–2288
Carhart MM (1997) On persistence in mutual fund performance. J Finance 52:57–82
Carlin BP, Louis TA (2000) Bayes and empirical Bayes methods for data analysis. Chapman & Hall, London
Chevalier J, Ellison G (1997) Risk taking by mutual funds as a response to incentives. J Polit Econ 105:1167–1200
Christopherson JA, Ferson WE, Glassman DA (1998) Conditioning manager alphas on economic information: another look at the persistence of performance. Rev Financ Stud 11:111–142
Christopherson JA, Ferson WE, Turner AL (1999) Performance evaluation using conditional alphas and betas. J Portf Manag 26:59–72
Cohen R, Coval J, Pastor L (2005) Judging fund managers by the company they keep. J Finance 60:1057–1096
Comer G, Larrymore N, Rodriguez J (2009) Controlling for fixed-income exposure in portfolio evaluation: evidence from hybrid mutual funds. Rev Financ Stud 22:481–507
Cremers KJ (2002) Stock return predictability: a Bayesian model selection perspective. Rev Financ Stud 15:1223–1249
Cremers M, Petajisto A (2006) How active is your fund manager? A new measure that predicts performance. Working Paper
Del Guercio D, Tkac PA (2002) The determinants of the flow of funds of managed portfolios: mutual funds vs. pension funds. J Financ Quant Anal 37:523–557
Del Guercio D, Tkac PA (2008) Star power: the effect of Morningstar ratings on mutual fund flow. J Financ Quant Anal 43:907–936
Elton EJ, Gruber MJ, Das S, Hlavka M (1993) Efficiency with costly information: a reinterpretation of evidence from managed portfolio. Rev Financ Stud 6:1–22
Elton EJ, Gruber MJ, Blake CR (1995) Fundamental economic variables, expected returns, and bond fund performance. J Finance 50:1229–1256
Elton EJ, Gruber MJ, Blake CR (1996a) The persistence of risk-adjusted mutual fund performance. J Bus 69:133–157
Elton EJ, Gruber MJ, Blake CR (1996b) Survivorship Bias and mutual fund performance. Rev Financ Stud 9:1097–1120
Fama EF, French KR (1993) Common risk factors in the returns on stocks and bonds. J Financ Econ 33:3–56
Fama EF, French KR (1997) Industry costs of equity. J Financ Econ 43:153–193
Fama EF, MacBeth JD (1973) Risk, return, and equilibrium: empirical tests. J Polit Econ 81:607–636
Ferson W, Schadt RW (1996) Measuring fund strategy and performance in changing economic conditions. J Finance 51:425–461
Friesen GC (2004) A new method for estimating mutual fund alphas. Working Paper
Frohlich CJ (1991) A performance measure for mutual funds using the Connor-Korajczyk methodology: an empirical study. Rev Quant Financ Acc 1:427–434
Goetzmann WN, Ibbotson RG (1994) Do winners repeat? Patterns in mutual fund performance. J Portf Manag 20:9–18
Goetzmann WN, Ingersoll J, Ivkovic Z (2000) Monthly measurement of daily timers. J Financ Quant Anal 35:257–290
Grinblatt M, Titman S (1992) The persistence of mutual fund performance. J Finance 47:1977–1984
Gruber MJ (1996) Another puzzle: the growth in actively managed mutual funds. J Finance 51:783–810
Hamilton JD (1994) Time series analysis. Princeton University Press, New Jersey
Hansen LP, Sargent TJ (2006) Fragile beliefs and the price of model uncertainty. Working Paper
Hansen LP, Sargent TJ, Tallarini TD Jr (1999) Robust permanent income and pricing. Rev Econ Stud 66:873–907
Hansen LP, Sargent TJ, Wang NE (2002) Robust permanent income and pricing with filtering. Macroecon Dyn 6:40–84
Hendricks D, Patel J, Zeckhauser R (1993) Hot hands in mutual funds: short-run persistence of relative performance. 1974–1988. J Finance 48:93–130
Henriksson RD, Merton RC (1981) On market timing and investment performance. II. Statistical procedures for evaluating forecasting skills. J Bus 54:513–533
Hoeting JA, Madigan D, Raftery AE, Volinsky CT (1999) Bayesian model averaging: a tutorial. Stat Sci 14:382–417
Huang J, Wei KD, Yan H (2007) Participation costs and the sensitivity of fund flows to past performance. J Finance 62:1273–1311
Huij J, Verbeek M (2007) Cross-sectional learning and short-run persistence in mutual fund performance. J Bank Finance 31:973–997
Jegadeesh N, Titman S (1993) Returns to buying winners and selling losers: implications for stock market efficiency. J Finance 48:65–91
Jensen MC (1968) The performance of mutual funds in the period 1945–1964. J Finance 23:389–416
Jones CS, Shanken J (2005) Mutual fund performance with learning across funds. J Financ Econ 78:507–552
Kacperczyk M, Sialm C, Zheng L (2006) Unobserved actions of mutual funds. Rev Financ Stud (forthcoming)
Keswani A, Stolin D (2008) Which money is smart? Mutual fund buys and sells of individual and institutional investors. J Finance 63:85–118
Khorana A (2001) Performance changes following top management turnover: evidence from open-end mutual funds. J Financ Quant Anal 36:371–394
Koop G (2003) Bayesian econometrics. Wiley, Chichester
Koski JL, Pontiff J (1999) How are derivatives used? Evidence from the mutual fund industry. J Finance 54:791–816
Kosowski R, Naik NY, Teo M (2007) Do Hedge funds deliver alpha? A Bayesian and bootstrap analysis. J Financ Econ 84:229–264
Lamont OA (2001) Economic tracking portfolios. J Econ 105:161–184
Lintner J (1965) The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Rev Econ Stat 47:13–37
Maher J, Brown R, Kumar R (2008) Firm valuation, abnormal earnings, and mutual funds flow. Rev Quant Financ Acc 31:167–189
Nanda V, Wang ZJ, Zheng L (2004) The ABCs of mutual funds: a natural experiment on fund flows and performance. Working Paper
Newey WK, West KD (1987) A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55:703–708
Pastor L, Stambaugh RF (1999) Costs of equity capital and model mispricing. J Finance 54:67–121
Pastor L, Stambaugh RF (2002a) Mutual fund performance and seemingly unrelated assets. J Financ Econ 63:315–349
Pastor L, Stambaugh RF (2002b) Investing in equity mutual funds. J Financ Econ 63:351–380
Petersen MA (2009) Estimating standard errors in finance panel data sets: comparing approaches. Rev Financ Stud 22:435–480
Poirier DJ (1995) Intermediate statistics and econometrics : a comparative approach. MIT Press, Cambridge
Reid BK, Rea JD (2003) Mutual fund distribution channels and distribution costs. Perspective. Investment Company Institute, Washington, DC
Ross SA (1976) The arbitrage theory of capital asset pricing. J Econ Theory 13:341–360
Sharpe WF (1964) Capital asset prices: a theory of market equilibrium under conditions of risk. J Finance 19:425–442
Shukla R, Trzcinka C (1994) Persistent performance in the mutual fund market: tests with funds and investment advisers. Rev Quant Financ Acc 4:115–135
Sirri ER, Tufano P (1998) Costly search and mutual fund flows. J Finance 53:1589–1622
Tang DY (2003) Asset return predictability and Bayesian model averaging. Working Paper
Treynor JL, Mazuy KK (1966) Can mutual funds outguess the market? Harv Bus Rev 66:131–136
Wermers R (2000) Mutual fund performance: an empirical decomposition into stock-picking talent, style, transactions costs, and expenses. J Finance 55:1655–1695
Zellner A (1971) An introduction to Bayesian inference in econometrics. Wiley, New York
Acknowledgments
This paper is based on my dissertation at Georgia State University. I am grateful to members of my dissertation committee, Vikas Agarwal (dissertation chair), Jason Greene, Jayant Kale, Stephen Smith, and Ajay Subramanian, for their valuable comments and suggestions. The paper has also benefited from the valuable and thoughtful comments of three anonymous referees, Dragon Tang and seminar participants at the 2007 FMA Annual Meetings, Fordham University and Georgia State University. All remaining errors are mine.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
See Table 15.
Appendix B
2.1 Prior distributions and specification of prior hyperparameters
To facilitate discussion in this and subsequent sections, I rewrite Eq. 1 as:
where r i is the S × 1 vector containing the S observations of r i,t (I assume the fund has monthly returns for S months); Z i = (l S , X i ) is the S × (K + 1) matrix containing l S , the S × 1 unit vector in the leftmost column and X i , the S × K matrix containing the explanatory variables specific to the jth model; \( \phi_{i} = (\alpha_{i} ,\beta_{i,1} , \ldots ,\beta_{i,K} )^{\prime} \), the (K + 1) × 1 coefficient vector and u i is the S × 1 vector containing the disturbance terms. To facilitate subsequent exposition, define the (K × 1) sub-vector, \( b_{i} = (\beta_{i,1} , \ldots ,\beta_{i,K} ) \). Following Pastor and Stambaugh (2002a), I employ the natural conjugate normal-inverted gamma prior for σ 2 u and ϕ i . Specifically, the prior for σ 2 u follows an inverted gamma distribution (Zellner 1971),
where “IG” stands for inverted gamma and \( \underline{\nu } \) and \( \underline{s}^{2} \) are parameters of the inverted gamma distribution. Conditional on σ 2 u , α i and b i are normally distributed
where \( \underline{{\alpha_{i} }} \) is the prior mean of α i , \( \underline{{b_{i} }} \) is the prior mean vector of b i , \( \underline{{\sigma_{\alpha }^{2} }} \) is the marginal prior variance of α i (“prior variance of alpha”) and \( \underline{{V_{b} }} \) is the marginal prior covariance matrix of b i . I assume α i and b i are independent of each other. Given this assumption, ϕ i is multivariate normal
where \( \phi_{i} = \left( {\underline{{\alpha_{i} }} ,\underline{{b^{\prime}_{i} }} } \right)^{\prime } \) and \( \underline{{V_{\phi } }} \) is defined as
The diagonal structure of \( \underline{{V_{b} }} \) stems from the assumed independence of α i and b i . To implement Bayesian estimation, I specify values for the prior hyperparameters \( \underline{{\alpha_{i} }} \), \( \underline{{\sigma_{\alpha }^{2} }} \), \( \underline{s}^{2} \), \( \underline{\nu } \), \( \underline{{b_{i} }} \), and \( \underline{{V_{b} }} \). I already discussed the specification of \( \underline{{\alpha_{i} }} \) and \( \underline{{\sigma_{\alpha }^{2} }} \) in Sect. 3.1. Thus, it only remains to describe specification of the remaining hyperparameters. Following Pastor and Stambaugh (2002a) and Busse and Irvine (2006), I employ an empirical Bayes approach in specifying values for \( \underline{s}^{2} \), \( \underline{\nu } \), \( \underline{{b_{i} }} \), and \( \underline{{V_{b} }} \).Footnote 43 Each fund is viewed as a draw from the cross section of funds with the same investment objective. Thus, prior uncertainty about a fund’s parameter is driven by the cross sectional variation in that parameter. For each investment objective, I select all funds having at least 60 months of data and compute the OLS estimate of b i for each fund.Footnote 44 Then I set \( \underline{{b_{i} }} \) equal to the sample mean of the OLS estimates and \( \underline{{V_{b} }} \) equal to the covariance matrix of the OLS estimates. Each OLS regression also yields \( \hat{\sigma }_{u}^{2} \), the estimate of σ 2 u . To explain how I specify \( \underline{s}^{2} \) and \( \underline{\nu } \), I introduce the first and second moments of σ 2 u . Based on Zellner (1971, pp. 371–372),
By substituting Eq. 17 into Eq. 18, I can express \( \underline{\nu } \) as
I insert the cross sectional mean and variance of \( \hat{\sigma }_{u}^{2} \) into the right-hand side of Eq. 19 and evaluate that expression. \( \underline{\nu } \) is set equal to the next largest integer of the resulting value on the right-hand side of Eq. 19. Once I have solved for \( \underline{\nu } \), I use that value, the cross sectional mean of \( \hat{\sigma }_{u}^{2} \) and Eq. 18 to solve for \( \underline{s}^{2} \).
2.2 Posterior distribution
I derive the posterior distributions of ϕ i and σ 2 u defined with respect to the jth model.Footnote 45 Given the distributional assumptions of u i,t , the likelihood function of r i is normal
The prior pdf of σ 2 u is
where \( \Upgamma (.) \) denotes the gamma function. Conditional on σ u , the prior pdf of ϕ i is
The product of Eqs. 20, 21 and 22 yields the joint posterior pdf of ϕ i and σ u
Rewriting \( (r_{i} - Z_{i} \phi_{i} )^{\prime}(r_{i} - Z_{i} \phi_{i} ) + \left( {\phi_{i} - \underline{{\phi_{i} }} } \right)^{\prime } \underline{{V_{\phi } }}^{ - 1} \left( {\phi_{i} - \underline{{\phi_{i} }} } \right) \) as
and rearranging the terms in the exponents gives us
where \( \overline{{V_{\phi } }} = \left( {\underline{{V_{\phi } }}^{ - 1} + Z^{\prime}_{i} Z_{i} } \right)^{ - 1} ,\overline{{\phi_{i} }} = \overline{{V_{\phi } }} \left( {\underline{{V_{\phi } }}^{ - 1} \underline{{\phi_{i} }} + Z^{\prime}_{i} r_{i} } \right),\bar{\nu } = S + \underline{\nu } , \) and \( \bar{\nu }\bar{s}^{2} = \underline{\nu } \underline{s}^{2} + r_{i}^{\prime } r_{i} + \underline{{\phi_{i} }}^{\prime } \underline{{V_{\phi } }}^{ - 1} \underline{{\phi_{i} }} - \overline{{\phi_{i} }}^{\prime } \left( {\underline{{V_{\phi } }}^{ - 1} + Z_{i}^{\prime } Z_{i} } \right)\overline{{\phi_{i} }} \). Conditional on σ u , the posterior pdf of ϕ i is multivariate normal and the posterior pdf of σ u is inverted gamma
In addition, the marginal posterior ϕ i follows a multivariate t distribution with mean and variance given by
For the jth model, the Bayesian estimate of alpha, \( E(\alpha_{i} |D,M_{j} ) \), is the (1,1) element of \( \bar{\phi }_{i} \).
2.3 Marginal likelihood and posterior model probability
The derivation of the posterior distribution leads us to the discussion of the marginal likelihood, \( p(D|M_{j} ) \), since it requires certain quantities from the prior and posterior distributions. Given the normal-inverted gamma natural conjugate prior, the marginal likelihood under the jth model has an analytical formFootnote 46
where \( \left| {\underline{{V_{{\phi_{j} }} }} } \right| \) and \( \left| {\overline{{V_{{\phi_{j} }} }} } \right| \) denote the determinants of \( \underline{{V_{{\phi_{j} }} }} \) and \( \overline{{V_{{\phi_{j} }} }} \) respectively. The subscript j reminds us that the various quantities in Eqs. 29 and 30 are computed under the jth model.
The jth model’s posterior model probability, \( p(M_{j} |D) \), is computed as (see, e.g., Hoeting et al. 1999)
where \( p(M_{j} ) \) is the prior model probability of the jth model. For this study, each model under consideration receives equal prior model probability, i.e., \( p(M_{j} ) = p(M_{k} )\,\,\forall \,j,k \). Thus, the jth model’s posterior probability simplifies to
Note that the denominator in Eq. 32 need not sum to 1. To the extent that models used by researchers do not capture all the models that can explain the data, the sum of the marginal likelihoods will not be 1. Posterior model probabilities are still well-defined in this instance. As long as a model’s marginal likelihood is the highest amongst all other models under consideration, it will receive the highest posterior model probability. Conversely, a model with the lowest marginal likelihood will receive the lowest posterior model probability.
Rights and permissions
About this article
Cite this article
Loon, Y.C. Model uncertainty, performance persistence and flows. Rev Quant Finan Acc 36, 153–205 (2011). https://doi.org/10.1007/s11156-010-0177-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11156-010-0177-0