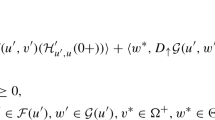Using ρ-cone arcwise connectedness on parametric set-valued optimization problems

Abstract

Within the inquiry about work, we explore a parametric set-valued optimization problem, where the objective as well as constraint maps are set-valued. A generalization of cone arcwise associated set-valued maps is presented named ρ-cone arcwise connectedness of set-valued maps. We set up adequate Karush–Kuhn–Tucker optimality conditions for the problem beneath contingent epiderivative and ρ-cone arcwise connectedness presumptions. Assist, Mond–Weir, Wolfe, and blended sorts duality models are examined. We demonstrate the related theorems between the primal and the comparing dual problems beneath the presumption.

1 Introduction

The class of parametric optimization problems ($\mathbb{POP}$s) is a special type of optimization problems ($\mathbb{OP}$s). It has applications in various fields of mathematical science, economics, and operational research. Many authors like Ioffe, Khanh, and Samei studied vector $\mathbb{OP}$s with parameters [1–14]. It has applications in inferring the Pontryagin maximum principle for control problems with state constraints. Khanh et al. [15–18] studied $\mathbb{POP}$s for set-valued case. They established the Fritz John and Kuhn–Tucker necessary optimality conditions of set-valued parametric optimization problems ($\mathbb{S}$-$\mathbb{VPOP}$s) under relaxed differentiability assumptions on the state variable and convexlikeness assumptions on the parameter. The $\mathbb{S}$-$\mathbb{VPOP}$s arise in such a situation where $\mathbb{OP}$s involve set-valued maps and the equality constraint represents equations, like differential equations and initial conditions. This class of $\mathbb{OP}s$ also arises in the case where the differential inclusions replace the differential equations to describe the system under consideration.

The arcwise connectedness is a generalization of convexity by replacing the line segment joining two points by a continuous arc which Avriel introduced in [19] in 1976. Later, in 2003, Fu et al. [20] and Lalitha et al. [21] introduced the concept of cone arcwise connected set-valued maps ($\mathbb{C}$A$\mathbb{CS}$-$\mathbb{VM}$) which is an extension of the class of convex set-valued maps. Lalitha et al. [21] established the sufficient optimality condition of $\mathbb{S}$-$\mathbb{VOP}s$ using contingent epiderivative and $\mathbb{C}$A$\mathbb{C}$ assumptions. In 2013, Yu [22] established the necessary and sufficient optimality conditions for the existence of global proper efficient points of vector $\mathbb{OP}s$ involving $\mathbb{C}$A$\mathbb{CS}$-$\mathbb{VM}$s. Yihong et al. [23] introduced the notion of α-order nearly $\mathbb{C}$A$\mathbb{CS}$-$\mathbb{VM}$s and derived the necessary and sufficient optimality conditions of $\mathbb{S}$-$\mathbb{VOP}$s.

In 2016, Yu [24] established the necessary and sufficient optimality conditions for the existence of global proper efficient elements of vector $\mathbb{OP}s$ involving $\mathbb{C}$A$\mathbb{CS}$-$\mathbb{VM}$s. In 2018, Peng et al. [25] introduced the notion of cone subarcwise connected set-valued maps ($\mathbb{CSCS}$-$\mathbb{VM}$) and established the second-order necessary optimality conditions for the existence of local global proper efficient elements of $\mathbb{S}$-$\mathbb{VOP}$s. For other different but connected points of view regarding this subject, the reader is directed to Ahmad et al. [26–28].

In this paper, we consider $\mathbb{S}$-$\mathbb{VPOP}$s

$$ \textstyle\begin{cases} \underset{(\mathrm{u}, a) \in W\times A}{\text{minimize}} & \mathfrak{F}(\mathrm{u}, \mathrm{a}) \\ \text{subject to} & \mathfrak{G}(\mathrm{u}, \mathrm{a})\cap (- \Omega _{2}) \neq \emptyset , \\ & \mathrm{p}(\mathrm{u}, \mathrm{a})=0. \end{cases} $$

(1)

Here, $W\neq \emptyset$ is a subset of normed space U, u is the state variable, and $\mathrm{a}\in A$ is the parameter, A is an arbitrary set,

$$ \mathfrak{F} : U\times A \to 2^{V_{1}}, \qquad \mathfrak{G} : U \times A \to 2^{V_{2}}$$

are set-valued maps, and $\mathrm{p} : U\times A \to V_{3}$ is a single-valued map with

$$ W \times A \subseteq \operatorname{dom}( \mathfrak{F}) \cap \operatorname{dom}( \mathfrak{G}),$$

$V_{j}$ ($j=1,2,3$) are real normed spaces and $\Omega _{2}$ is a solid pointed convex cone in $V_{1}$, where the objective function and functions attached to constraints are set-valued maps. We establish the sufficient Karush–Kuhan–Tucker (KKT) optimality conditions of problem (1) with the help of contingent epiderivative and ρ-cone arcwise connectedness (ρ-$\mathbb{C}$A$\mathbb{C}$) assumptions. Further, we formulate different types of duality relationships between the primal problem (1) and the corresponding dual problems.

This paper is organized as follows. Section 2 deals with some definitions and preliminary concepts of set-valued maps. In Sect. 3, a parametric $\mathbb{S}$-$\mathbb{VPOP}$ (1) is considered and the sufficient KKT optimality conditions are established for problem (1). Various types of duality theorems are studied under contingent epiderivative and ρ-$\mathbb{C}$A$\mathbb{C}$ assumptions.

2 Definitions and preliminaries

Let Ω be a nonempty subset of a real normed space V. Then Ω is called a cone if $\upeta v\in \Omega$, $\forall v\in \Omega$, $\upeta \geq 0$. Furthermore, Ω is called nontrivial if $\Omega \neq \{\theta _{V}\}$. Here, $\theta _{V}$ is the zero element of V, proper if $\Omega \neq V$, pointed if $\Omega \cap (-\Omega )= \{\theta _{V}\}$, solid whenever $\operatorname{int} ( \Omega )\neq \emptyset$, closed whenever $\overline{\Omega} = \Omega$, and convex whenever

$$ \upeta \Omega + (1-\upeta )\Omega \subseteq \Omega ,\quad \forall 0 \leq \upeta \leq 1, $$

where $\operatorname{int} (\Omega )$ and Ω̅ denote the interior and closure of Ω, respectively. We denote the space of all continuous linear functionals on V and Ω being a solid pointed convex cone in V by $V^{\ast}$. Then the dual cone $\Omega ^{+}$ to Ω and quasi-interior $\Omega ^{+i}$ of $\Omega ^{+}$ are defined as

$$\begin{aligned}& \Omega ^{+} = \bigl\{ \mathrm{v}^{\ast}\in V^{*} \mid \bigl\langle \mathrm{v}^{\ast}, \mathrm{v} \bigr\rangle \geq 0, \forall \mathrm{v} \in \Omega \bigr\} , \\& \Omega ^{+i} = \bigl\{ \mathrm{v}^{\ast}\in V^{\ast}: \bigl\langle \mathrm{v}^{\ast}, \mathrm{v}\bigr\rangle > 0, \forall \mathrm{v}\in \Omega \setminus \{ \theta _{V}\} \bigr\} , \end{aligned}$$

where $\langle \cdot , \cdot \rangle$ is the canonical bilinear form with respect to the duality between $V^{\ast}$ and V. Define a subset $\langle \mathrm{v}^{\ast}, W \rangle$ of $\mathbb{R}$ by

$$ \bigl\langle \mathrm{v}^{\ast}, W \bigr\rangle =\bigcup _{\mathrm{v} \in W} \bigl\{ \bigl\langle \mathrm{v}^{\ast}, \mathrm{v} \bigr\rangle \bigr\} $$

for any $W\subset V$. For any two nonempty subsets W, Ẃ of V and $\mathrm{v}^{\ast}\in V^{\ast}$, we also use the following notations:

$$ \bigl\langle \mathrm{v}^{\ast}, W\bigr\rangle \geq 0\ \bigl(\text{or, } 0 \leq \bigl\langle \mathrm{v}^{\ast}, W \bigr\rangle \bigr)\quad \Longleftrightarrow \quad \bigl\langle \mathrm{v}^{\ast}, \varpi \bigr\rangle \geq 0, \quad \forall \varpi \in W,$$

and

$$ \bigl\langle \mathrm{v}^{\ast}, W\bigr\rangle \geq \bigl\langle \mathrm{v}^{\ast}, \acute{W}\bigr\rangle \ \bigl(\text{or, } \bigl\langle \mathrm{v}^{\ast}, \acute{W}\bigr\rangle \leq \bigl\langle \mathrm{v}^{\ast}, W \bigr\rangle \bigr) \quad \Longleftrightarrow \quad \bigl\langle \mathrm{v}^{\ast}, \varpi \bigr\rangle \geq \bigl\langle \mathrm{v}^{\ast}, \acute{\varpi}\bigr\rangle ,$$

$\forall \varpi \in W$, $\forall \acute{\varpi}\in \acute{W}$. There are two types of cone-orderings in V with respect to a solid pointed convex cone Ω in V. For any two elements $\mathrm{v}_{1}, \mathrm{v}_{2} \in V$, we have $\mathrm{v}_{1}\leq \mathrm{v}_{2}$ iff $\mathrm{v}_{2} - \mathrm{v}_{1}\in \Omega$ and $\mathrm{v}_{1}< \mathrm{v}_{2}$ iff $\mathrm{v}_{2} - \mathrm{v}_{1}\in \operatorname{int}(\Omega )$. We say $\mathrm{v}_{2} \geq \mathrm{v}_{1}$ if $\mathrm{v}_{1}\leq \mathrm{v}_{2}$ and $\mathrm{v}_{2}> \mathrm{v}_{1}$ if $\mathrm{v}_{1}< \mathrm{v}_{2}$. For any two nonempty subsets W, Ẃ of V, we use the following notations: $W\leq \theta _{V}$ iff $\mathrm{v} \leq \theta _{V}$ ($\forall \mathrm{v}\in W$), $W < \theta _{V}$ iff $\mathrm{v} < \theta _{V}$ ($\forall v\in W$), $W\leq \acute{W}$ iff $\mathrm{v} \leq \acute{\mathrm{v}}$, $\forall \mathrm{v}\in W$, $\acute{\mathrm{v}}\in \acute{W}$, and $W< \acute{W}$ iff $\mathrm{v}< \acute{\mathrm{v}}$ for each $\mathrm{v}\in W$, $\acute{\mathrm{v}}\in \acute{W}$. Aubin [29, 30] introduced the notion of contingent cone to a nonempty subset of a real normed space. Also, Aubin [29, 30] and Cambini et al. [31] introduced the notion of second-order contingent set to a nonempty subset of a real normed space.

Definition 2.1

([29, 30])

Let $W\neq \emptyset$ be a subset of a real normed space V and $\acute{\mathrm{v}} \in \overline{W}$. The contingent cone to W at v́ is denoted by $\mathcal{T}(W, \acute{\mathrm{v}})$ and is defined as follows: an element $\mathrm{v} \in \mathcal{T}(W, \acute{\mathrm{v}})$ if there exist sequences $\{\upeta _{n}\}$ in $\mathbb{R}$ with $\upeta _{n} \to 0^{+}$ and $\{\mathrm{v}_{n}\}$ in V, with $\mathrm{v}_{n} \to \mathrm{v}$, such that $\acute{\mathrm{v}} + \upeta _{n} \mathrm{v}_{n} \in W$, $\forall n \in \mathbb{N}$ or there exist sequences $\{\mathrm{w}_{n} \}$ in $\mathbb{R}$ with $\mathrm{w}_{n}>0$ and $\{\acute{\mathrm{v}}_{n}\}$ in W, with $\acute{\mathrm{v}}_{n}\to \acute{\mathrm{v}}$, such that $\mathrm{w}_{n} ( \acute{\mathrm{v}}_{n} - \acute{\mathrm{v}} ) \to \mathrm{v}$, $\forall n \in \mathbb{N}$.

Let U, V be real normed spaces and $\mathfrak{F} : U\to 2^{V}$ be a set-valued map such that $\mathfrak{F}(\mathrm{u}) \subseteq V$ for all $\mathrm{u}\in U$; here, $2^{V}$ is the power set of V. The effective domain, image, graph, and epigraph of $\mathfrak{F}$ are defined respectively by

$$ \operatorname{dom}(\mathfrak{F}) = \bigl\{ \mathrm{u} \in U : \mathfrak{F}( \mathrm{u}) \neq \emptyset \bigr\} ,$$

$\mathfrak{F}(W) = \bigcup_{\mathrm{u}\in W} \mathfrak{F}(\mathrm{u})$ for any $\emptyset \neq W \subseteq U$,

$$ \operatorname{gr}(\mathfrak{F}) = \bigl\{ ( \mathrm{u}, \mathrm{v}) \in U \times V : \mathrm{v} \in \mathfrak{F}(\mathrm{u}) \bigr\} ,$$

and

$$ \operatorname{epi}(\mathfrak{F}) = \bigl\{ ( \mathrm{u}, \mathrm{v}) \in U \times V : \mathrm{v}\in \mathfrak{F}(\mathrm{u}) + \Omega \bigr\} .$$

Jahn and Rauh [32] introduced the notion of contingent epiderivative of set-valued maps which plays a vital role in various aspects of $\mathbb{S}$-$\mathbb{VPOP}s$.

Definition 2.2

([32])

A single-valued map ${\mathbb{D}}_{\uparrow }\mathfrak{F}(\acute{\mathrm{u}},\acute{\mathrm{v}}):U\to V$ whose epigraph coincides with the contingent cone to the epigraph of $\mathfrak{F}$ at $(\acute{\mathrm{u}}, \acute{\mathrm{v}})$, i.e.,

$$epi({\mathbb{D}}_{\uparrow }\mathfrak{F}(\acute{\mathrm{u}},\acute{\mathrm{v}}))=\mathcal{T}(epi(\acute{\mathrm{u}}),(\acute{\mathrm{u}},\acute{\mathrm{v}})),$$

is said to be the contingent epiderivative of $\mathfrak{F}$ at $(\acute{\mathrm{u}},\acute{\mathrm{v}})$.

We now turn our attention to the notion of cone convexity of set-valued maps, introduced by Borwein [33]. Let W be a nonempty convex subset of a real normed space U. A set-valued map $\mathfrak{F}: U \to 2^{V}$, with $W \subseteq \operatorname{dom}(\mathfrak{F})$, is called Ω-convex on W if $\forall \mathrm{u}_{1}, \mathrm{u}_{2} \in W$,

$$ \upeta \mathfrak{F}(\mathrm{u}_{1}) + (1 - \upeta ) \mathfrak{F}( \mathrm{u}_{2}) \subseteq \mathfrak{F}\bigl( \upeta \mathrm{u}_{1} + ( 1 - \upeta ) \mathrm{u}_{2}\bigr) + \Omega ,$$

here $\upeta \in [0, 1]$ [33]. Avriel [19] introduced the concept of arcwise connectedness as a generalization of convexity by replacing the line segment joining two points by a continuous arc. W is said to be an arcwise connected set if for all $\mathrm{u}_{1}, \mathrm{u}_{2} \in W$ there exists a continuous arc $\mathcal{H}_{\mathrm{u}_{1}, \mathrm{u}_{2}} (\upeta )$ defined on $[0, 1]$ with a value in W such that $\mathcal{H}_{\mathrm{u}_{1}, \mathrm{u}_{2}} (0)=\mathrm{u}_{1}$ and $\mathcal{H}_{\mathrm{u}_{1}, \mathrm{u}_{2}} (1) = \mathrm{u}_{2}$ [19]. Fu and Wang [20] and Lalitha et al. [21] introduced the notion of cone arcwise connected set-valued maps as an extension of the class of convex set-valued maps. Let W be an arcwise connected subset of a real normed space U and $\mathfrak{F}:U \to 2^{V}$ be a set-valued map with $W \subseteq \operatorname{dom}(\mathfrak{F})$. Then $\mathfrak{F}$ is said to be Ω-arcwise connected on W if

$$ (1-\upeta ) \mathfrak{F}(\mathrm{u}_{1}) + \upeta \mathfrak{F}( \mathrm{u}_{2}) \subseteq \mathfrak{F}\bigl(\mathcal{H}_{\mathrm{u}_{1}, \mathrm{u}_{2}} (\upeta )\bigr) + \Omega ,$$

$\forall \mathrm{u}_{1}, \mathrm{u}_{2}\in W$ and $\upeta \in [0, 1]$ [20, 21]. Peng and Xu [25] introduced the notion of cone subarcwise connected set-valued maps.

Let W be an arcwise connected subset of a real normed space U, $\mathrm{a} \in \operatorname{int}(\Omega )$, and $\mathfrak{F} : U \to 2^{V}$ be a set-valued map with $W \subseteq \operatorname{dom}(\mathfrak{F})$. Then $\mathfrak{F}$ is said to be Ω-subarcwise connected on W if

$$ (1 - \upeta ) \mathfrak{F}(\mathrm{u}_{1}) + \upeta \mathfrak{F}( \mathrm{u}_{2}) + \epsilon \mathrm{a} \subseteq \mathfrak{F}\bigl( \mathcal{H}_{\mathrm{u}_{1}, \mathrm{u}_{2}} (\upeta ) \bigr) + \Omega ,$$

$\forall \mathrm{u}_{1}, \mathrm{u}_{2}\in W$, for each $\epsilon > 0$, and $\forall \upeta \in [0, 1]$ [25].

3 Main results of the $\mathbb{S}$-$\mathbb{VPOP}$s

3.1 The ρ-$\mathbb{C}$A$\mathbb{C}$

We introduce the notion of ρ-$\mathbb{C}$A$\mathbb{C}$ of set-valued maps as a generalization of $\mathbb{C}$A$\mathbb{CS}$-$\mathbb{VM}$ which was introduced by Das et al. [34–42] and Treanţă et al. [43]. For $\rho =0$, we have the usual notion of cone convex set-valued maps introduced by Borwein [33].

Definition 3.1

Let U and V be real normed spaces, $W\subseteq U$ be an arcwise connected, $\mathrm{u}_{1}, \mathrm{u}_{2}\in W$, $e\in \operatorname{int}(\Omega )$, and $\mathfrak{F}: U \to 2^{V}$ be a set-valued map with $W \subseteq \operatorname{dom}(\mathfrak{F})$. Then $\mathfrak{F}$ is said to be ρ-Ω-arcwise connected (ρ-Ω-A$\mathbb{C}$) with respect to e on W for $\mathrm{u}_{1}$, $\mathrm{u}_{2}$ if there exists $\rho \in \mathbb{R}$ such that

$$ (1 - \upeta ) \mathfrak{F}(\mathrm{u}_{1}) + \mathrm{u} \mathcal{F}( \mathrm{u}_{2}) \subseteq \mathrm{u}\bigl( \mathcal{H}_{\mathrm{u}_{1}, \mathrm{u}_{2}} (\upeta )\bigr) + \rho \upeta ( 1 - \upeta ) \Vert \mathrm{u}_{1} - \mathrm{u}_{2} \Vert ^{2} e + \Omega , $$

(2)

$\forall \upeta \in [0, 1]$.

Remark 3.1

If $\rho > 0$, then $\mathfrak{F}$ is said to be strongly ρ-Ω-arcwise connected ($\mathbb{S}\rho$-Ω-A$\mathbb{C}$); if $\rho = 0$, we have the usual notion of Ω-arcwise connectedness; and if $\rho <0$, then $\mathfrak{F}$ is said to be weakly ρ-Ω-arcwise connected ($\mathbb{W}\rho$-Ω-A$\mathbb{C}$). Obviously, $\mathbb{S}\rho$-Ω-A$\mathbb{C}$ ⇒ Ω-arcwise connectedness ⇒ $\mathbb{W}\rho$-Ω-A$\mathbb{C}$.

Further, we construct an example of ρ-$\mathbb{C}$A$\mathbb{CS}$-$\mathbb{VM}$, which is not cone arcwise connected.

Example 3.1

Let $U =\mathbb{R}^{2}$, $V = \mathbb{R}$, $\Omega = \mathbb{R}_{+}$, and

$$ W = \biggl\lbrace \mathrm{u} = (\mathrm{u}_{1}, \mathrm{u}_{2}) : \mathrm{u}_{1} + \mathrm{u}_{2} \geq \frac{1}{4}, \mathrm{u}_{1} \geq 0, \mathrm{u}_{2}\geq 0 \biggr\rbrace \subseteq U.$$

Define

$$ \mathcal{H}_{\mathrm{u},\acute{\mathrm{u}}}(\upeta ) = \bigl(1 - \upeta ^{2}\bigr) \upeta + \upeta ^{2} \acute{\mathrm{u}},$$

where $\mathrm{u}=(\mathrm{u}_{1},\mathrm{u}_{2})$, $\acute{\mathrm{u}}=( \acute{\mathrm{u}}_{1}, \acute{\mathrm{u}}_{2})$, and $\upeta \in [0,1]$. Clearly, W is an arcwise connected set. Define a set-valued map $\mathfrak{F} : \mathbb{R}^{2} \to 2^{\mathbb{R}}$ as follows:

$$ \mathfrak{F}(\mathrm{u}) = \textstyle\begin{cases} [0,4], & \mathrm{u}_{1} + \mathrm{u}_{2} \geq \frac{1}{2}, \mathrm{u}_{1}\neq 3 \mathrm{u}_{2}, \mathrm{u}= ( \mathrm{u}_{1}, \mathrm{u}_{2}), \\ [5,9],& \text{otherwise}.\end{cases} $$

We choose $\mathrm{u}=(1,0)$, $\acute{\mathrm{u}}=(0,1)$, and $\upeta = \frac{1}{2}$. Then

$$ \mathcal{H}_{\mathrm{u},\acute{\mathrm{u}}} \biggl( \frac{1}{2} \biggr) = \biggl( \frac{3}{4}, \frac{1}{4} \biggr)$$

and

$$\begin{aligned} \frac{1}{2} \mathfrak{F}(1, 0)+\frac{1}{2} \mathfrak{F}(0, 1) & = \frac{1}{2} [0,4] + \frac{1}{2} [0,4] \\ & = [0,4] \nsubseteq [5,9] +\mathbb{R}_{+} \\ & = \mathfrak{F} \biggl( \frac{3}{4}, \frac{1}{4} \biggr) + \mathbb{R}_{+}. \end{aligned}$$

Hence $\mathfrak{F}$ is not $\mathbb{R}_{+}$-arcwise connected. On the other hand, by considering $\rho = -2$ and $e = 5$, we get that

$$ (1- \upeta ) \mathfrak{F} (1, 0)+\upeta \mathfrak{F}(0, 1) = (1- \upeta ) [0,4] + \upeta [0,4] = [0,4]$$

and

$$ \mathfrak{F}\bigl(\mathcal{H}_{\mathrm{u}, \acute{\mathrm{u}}} (\upeta )\bigr) + \rho \upeta ( 1 - \upeta ) \Vert \mathrm{u} - \acute{\mathrm{u}} \Vert ^{2} e = \mathfrak{F} \bigl( 1 - \upeta ^{2}, \upeta ^{2}\bigr)- 20 \upeta ( 1 - \upeta ).$$

For $\upeta \neq 0.5$, we have

$$ \mathfrak{F} \bigl(1 - \upeta ^{2}, \upeta ^{2}\bigr) = [0,4].$$

So,

$$\begin{aligned} ( 1 - \upeta ) \mathfrak{F}(1, 0)+\upeta \mathfrak{F}(0, 1) + 20 \upeta ( 1 - \upeta ) & = [0,4] + 20 \upeta ( 1 - \upeta ) \\ & \subseteq [0,4] + \mathbb{R}_{+} = \mathbb{R}_{+}. \end{aligned}$$

For $\upeta = \frac{1}{2}$, we have

$$ \mathfrak{F} \bigl(1-\upeta ^{2}, \upeta ^{2}\bigr) = \mathfrak{F} \biggl( \frac{3}{4}, \frac{1}{4} \biggr)= [3,5].$$

So,

$$\begin{aligned} ( 1 - \upeta ) \mathfrak{F}(1, 0)+\upeta \mathfrak{F}(0, 1) + 20 \upeta (1 - \upeta ) & = [0,4] + 5 \\ & = [5,9] \subseteq [5,9]+ \mathbb{R}_{+}. \end{aligned}$$

Consequently, $\mathfrak{F}$ is $(-2)$-$\mathbb{R}_{+}$-A$\mathbb{CS}$-$\mathbb{VM}$ with respect to 5 on W for $(1, 0)$, $(0, 1)$.

Theorem 3.2

Let U, V be real normed spaces, $W\subseteq U$ be arcwise connected, $e\in \operatorname{int}(\Omega )$, and $\mathfrak{F}: U \to 2^{V}$ be ρ-Ω-A$\mathbb{C}$ with respect to e on W. Let $\acute{\mathrm{u}}\in W$ and $\acute{\mathrm{v}}\in \mathfrak{F}(\acute{\mathrm{u}})$. Then

$$\mathfrak{F}(\mathrm{u})-\acute{\mathrm{v}}\subseteq {\mathbb{D}}_{\uparrow }\mathfrak{F}(\acute{\mathrm{u}},\acute{\mathrm{v}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\rho {\parallel \mathrm{u}-\acute{\mathrm{u}}\parallel }^{2}e+\mathrm{\Omega },\mathrm{\forall }\mathrm{u}\in W,$$

where

$$ \acute{\mathcal{H}}_{\acute{\mathrm{u}}, \mathrm{u}}(0+) = \lim_{ \upeta \to 0+} \frac{ \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}}( \upeta ) - \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}}(0)}{\upeta},$$

assuming that $\acute{\mathcal{H}}_{\acute{\mathrm{u}}, \mathrm{u}}(0+)$ exists for all $\mathrm{u}, \acute{\mathrm{u}}\in W$.

Proof

Let $\mathrm{u}\in W$. As $\mathfrak{F}$ is ρ-Ω-A$\mathbb{C}$ with respect to e on W, we have

$$ (1-\upeta ) \mathfrak{F}(\acute{\mathrm{u}}) + \upeta \mathfrak{F}( \mathrm{u}) \subseteq \mathfrak{F}\bigl( \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}}( \upeta )\bigr) + \rho \upeta (1 - \upeta ) \Vert \mathrm{u} - \acute{\mathrm{u}} \Vert ^{2} e + \Omega ,$$

$\forall \upeta \in [0, 1]$. Let $\mathrm{v}\in \mathfrak{F}(\mathrm{u})$. Consider a real sequence $\{\upeta _{n}\}$ with $\upeta _{n} \in (0, 1)$, $n \in \mathbb{N}$, such that $\upeta _{n}\to 0+$ when $n\to \infty$. Suppose $\mathrm{u}_{n} = \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}} ( \upeta _{n})$ and

$$ \mathrm{v}_{n} = (1 - \upeta _{n}) \acute{\mathrm{v}} + \upeta _{n} \mathrm{v} - \rho \upeta _{n} ( 1 - \upeta _{n}) \Vert \mathrm{u} - \acute{\mathrm{u}} \Vert ^{2} e.$$

Therefore, $\mathrm{v}_{n}\in \mathfrak{F}( \mathrm{u}_{n}) + \Omega$. It is clear that

$$ {\mathrm{u}_{n} = \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}} ( \mathrm{u}_{n}) \to \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}} (0) = \acute{ \mathrm{u}},}$$

$\mathrm{v}_{n}\to \acute{\mathrm{v}}$, when n tends to ∞,

$$ \frac{\mathrm{u}_{n} - \acute{\mathrm{u}}}{ \upeta _{n}} = \frac{ \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}} (\upeta _{n}) - \mathcal{H}_{\acute{\mathrm{u}}, \mathrm{u}} (0)}{ \upeta _{n}} \to \acute{\mathcal{H}}_{\acute{\mathrm{u}}, \mathrm{u}}(0+),$$

when n tends to ∞, and

$$ \frac{\mathrm{v}_{n} - \acute{\mathrm{v}}}{ \upeta _{n}} = \mathrm{v} - \acute{\mathrm{v}} - \rho ( 1 -\upeta _{n}) \Vert \mathrm{u} - \acute{\mathrm{u}} \Vert ^{2} e \to \mathrm{v} - \acute{\mathrm{v}} - \rho \Vert \mathrm{u} -\acute{\mathrm{u}} \Vert ^{2} e,$$

when $n\to \infty$. Therefore,

$$({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+),\mathrm{v}-\acute{\mathrm{v}}-\rho {\parallel \acute{\mathrm{u}}-\acute{\mathrm{u}}\parallel }^{2}e)\in \mathcal{T}(epi(\mathfrak{F}),(\acute{\mathrm{u}},\acute{\mathrm{v}}))=epi({\mathbb{D}}_{\uparrow }\mathfrak{F}(\acute{\mathrm{u}},\acute{\mathrm{v}})).$$

Consequently,

$$\mathrm{v}-\acute{\mathrm{v}}-\rho {\parallel \acute{\mathrm{u}}-\acute{\mathrm{u}}\parallel }^{2}e\in {\mathbb{D}}_{\uparrow }\mathfrak{F}(\acute{\mathrm{u}},\acute{\mathrm{v}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathrm{\Omega },$$

which is true for all $\mathrm{v}\in \mathfrak{F}(\mathrm{u})$. Hence,

$$\mathfrak{F}(\mathrm{u})-\acute{\mathrm{v}}\subseteq {\mathbb{D}}_{\uparrow }\mathfrak{F}(\acute{\mathrm{u}},\acute{\mathrm{v}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\rho {\parallel \mathrm{u}-\acute{\mathrm{u}}\parallel }^{2}e+\mathrm{\Omega },\mathrm{\forall }\mathrm{u}\in W.$$

Hence the theorem follows. □

3.2 Formulation of the main problem

Let U, $V_{1}$, $V_{2}$, and $V_{3}$ be real normed spaces and $\Omega _{1}$, $\Omega _{2}$, and $\Omega _{3}$ be solid pointed convex cones in $V_{1}$, $V_{2}$, and $V_{3}$, respectively. Let A be an arbitrary set and W be a nonempty subset of U. Suppose that

$$ \mathfrak{F} : U\times A \to 2^{V_{1}}, \qquad \mathfrak{G} : U \times A \to 2^{V_{2}}$$

are set-valued maps and $\mathrm{p} : U\times A \to V_{3}$ is a single-valued map with

$$ W \times A \subseteq \operatorname{dom}( \mathfrak{F} ) \cap \operatorname{dom}( \mathfrak{G}).$$

We consider a parametric $\mathbb{S}$-$\mathbb{VPOP}s$ (1), where u is the state variable and a is the parameter. The feasible set Š of problem (1) is defined by

$$ \check{S} = \bigl\{ ( \mathrm{u}, \mathrm{a}) \in W\times A : \mathfrak{G}( \mathrm{u}, \mathrm{a})\cap (-\Omega _{2}) \neq \emptyset \text{ and } \mathrm{p}(\mathrm{u}, \mathrm{a})=0 \bigr\} .$$

The minimizer and weak minimizer of problem (1) are defined in the following ways. A point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1})\in U \times A \times V_{1}$, with $(\acute{\mathrm{u}}, \acute{\mathrm{a}}) \in \check{S}$ and $\acute{\mathrm{v}}_{1} \in \mathfrak{F}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, is called a minimizer of problem (1) if there exists no point $(\mathrm{u}, \mathrm{a}, \mathrm{v}_{1}) \in U\times A \times V_{1}$, with $(\mathrm{u}, \mathrm{a}) \in \check{S}$ and $\mathrm{v}_{1}\in \mathfrak{F}(\mathrm{u}, \mathrm{a})$, such that

$$ \mathrm{v}_{1} - \acute{\mathrm{v}}_{1} \in - \Omega _{1} \setminus \{\theta _{V_{1}}\},$$

and is called a weak minimizer of problem (1) if there exists no point

$$ (\mathrm{u}, \mathrm{a}, \mathrm{v}) \in U\times A \times V_{1},$$

with $(\mathrm{u}, \mathrm{a}) \in \check{S}$ and $\mathrm{v}_{1} \in \mathfrak{F}(\mathrm{u}, \mathrm{a})$, such that $\mathrm{v}_{1} - \acute{\mathrm{v}}_{1} \in - \operatorname{int}(V_{1})$.

3.3 Sufficient optimality conditions

Let

$$ (\mathrm{u}, \mathrm{a}),(\acute{\mathrm{u}}, \mathrm{a}),( \mathrm{u}, \acute{ \mathrm{a}}),(\acute{\mathrm{u}}, \acute{\mathrm{a}}) \in U\times A, $$

$\acute{\mathrm{v}}_{1} \in \mathfrak{F}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, and $\acute{\mathrm{v}}_{2} \in \mathfrak{G}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$. Throughout the paper, we use the following assumptions:

$$\begin{aligned}& \mathfrak{F}(\mathrm{u}, \mathrm{a}) - \mathfrak{F}( \acute{ \mathrm{u}}, \mathrm{a}) \subseteq \Omega _{1}, \\& \mathfrak{G}(\mathrm{u}, \mathrm{a}) - \mathfrak{G}( \acute{\mathrm{u}}, \mathrm{a}) \subseteq \Omega _{2}, \\& \mathfrak{F}(\mathrm{u}, \acute{\mathrm{a}}) - \acute{\mathrm{v}}_{1} \subseteq -\Omega _{1}, \\& \mathfrak{G}(\mathrm{u}, \acute{\mathrm{a}}) - \acute{\mathrm{v}}_{2} \subseteq -\Omega _{1}, \\& \mathrm{p}(\mathrm{u}, \acute{\mathrm{a}}) + \mathrm{p}( \acute{\mathrm{u}}, \mathrm{a}) \in -\Omega _{3}. \end{aligned}$$

(3)

We now prove the following lemma which assists in establishing the sufficient KKT optimality conditions of the parametric $\mathbb{S}$-$\mathbb{VPOP}s$ (1).

Lemma 3.3

Let W be an arcwise connected subset of U and $(\acute{\mathrm{u}}, \acute{\mathrm{a}})\in U\times A$ with $\acute{\mathrm{v}}_{1} \in \mathfrak{F}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, $\acute{\mathrm{v}}_{2} \in \mathfrak{G}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, and $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}})\geq 0$. Let $e\in \operatorname{int}(\Omega _{1})$, $e^{\prime}\in \operatorname{int}(\Omega _{2})$, and $e^{\prime \prime}\in \operatorname{int}(\Omega _{3})$. Suppose that $\mathfrak{F}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{1}}$ is $\rho _{1}$-Ω-A$\mathbb{C}$ with respect to e, $\mathfrak{G}(\cdot, \acute{\mathrm{a}}) : U\to 2^{V_{2}}$ is $\rho _{2}$-Ω-A$\mathbb{C}$ with respect to $e^{\prime}$, and $\mathrm{p}(\cdot, \acute{\mathrm{a}}) : U \to V_{3}$ is $\rho _{3}$-Ω-A$\mathbb{C}$ with respect to $e^{\prime \prime}$ on W. Assume that the contingent epiderivatives ${\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)$ and ${\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)$ exist and the Gâteaux derivative $\mathrm{p}^{\prime}(\cdot, \acute{\mathrm{a}})(\acute{\mathrm{u}})$ exists. If equations in (3) are satisfied, then we have

$$\begin{array}{rl}& 〈{\mathrm{v}}_1^{\ast },\mathfrak{F}(\mathrm{u},\mathrm{a})-{\acute{\mathrm{v}}}_1〉+〈{\mathrm{v}}_2^{\ast },\mathfrak{G}(\mathrm{u},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & \ge 〈{\mathrm{v}}_1^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{a}}(0+))+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{G}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },{\mathrm{p}}^{\prime }(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\\ & +{\parallel \mathrm{u}-\acute{\mathrm{u}}\parallel }^2({\rho }_1〈{\mathrm{v}}_1^{\ast },e〉+{\rho }_2〈{\mathrm{v}}_2^{\ast },e^{\prime }〉+{\rho }_3〈{\mathrm{v}}_3^{\ast },e^{″}〉),\end{array}$$

(4)

$\forall (\mathrm{u}, \mathrm{A})\in W\times A$.

Proof

Let $(\mathrm{u}, \mathrm{a})\in W\times A$. As $\mathfrak{F}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{1}}$ is $\rho _{1}$-Ω-A$\mathbb{C}$ with respect to e on W and $\acute{\mathrm{v}}_{1}\in \mathfrak{F}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, we have

$$\mathfrak{F}(\mathrm{u},\acute{\mathrm{a}})-{\acute{\mathrm{v}}}_1\subseteq {\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{u}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+{\rho }_1{\parallel \mathrm{u}-\acute{\mathrm{u}}\parallel }^{2}e+{\mathrm{\Omega }}_1.$$

(5)

As $\mathfrak{G}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{2}}$ is $\rho _{2}$-Ω-A$\mathbb{C}$ with respect to $e^{\prime}$ on W and $\acute{\mathrm{v}}_{2}\in \mathfrak{G}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, we have

$$\mathfrak{G}(\mathrm{u},\acute{\mathrm{a}})-{\acute{\mathrm{v}}}_2\subseteq {\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+{\rho }_2{\parallel \mathrm{u}-\acute{\mathrm{u}}\parallel }^2{e}^{\prime }+{\mathrm{\Omega }}_2.$$

(6)

Again, as $\mathrm{p}(\cdot, \acute{\mathrm{a}}) : U \to V_{3}$ is $\rho _{3}$-Ω-A$\mathbb{C}$ with respect to $e^{\prime \prime}$ on W, we have

$$ \mathrm{p}(\mathrm{u}, \acute{\mathrm{a}}) - \mathrm{p}( \acute{\mathrm{u}}, \acute{\mathrm{a}}) \in \mathrm{p}^{\prime}(\cdot, \acute{\mathrm{a}}) (\acute{\mathrm{u}}) \bigl( \acute{\mathcal{H}}_{ \acute{\mathrm{u}}, \mathrm{u}}(0+) \bigr) + \rho _{3} \Vert \mathrm{u} - \acute{\mathrm{u}} \Vert ^{2} e^{\prime \prime}+ \Omega _{3}. $$

(7)

Hence, from Eq. (5), we have

$$\begin{array}{rl}& 〈{\mathrm{v}}_1^{\ast },\mathfrak{F}(\mathrm{u},\acute{\mathrm{a}})-{\acute{\mathrm{v}}}_1+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },\mathfrak{G}(\mathrm{u},\acute{\mathrm{a}})-{\acute{\mathrm{v}}}_2+\mathfrak{G}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },\mathrm{p}(\mathrm{u},\acute{\mathrm{a}})-\mathrm{p}(\acute{\mathrm{u}},\acute{\mathrm{a}})+\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\\ & \ge 〈{\mathrm{v}}_1^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },{\mathrm{p}}^{\prime }(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\\ & +{\parallel \mathrm{u}-\acute{\mathrm{u}}\parallel }^2({\rho }_1〈{\mathrm{v}}_1^{\ast },e〉+{\rho }_2〈{\mathrm{v}}_2^{\ast },e^{\prime }〉+{\rho }_3〈{\mathrm{v}}_3^{\ast },e^{″}〉).\end{array}$$

(8)

By Eq. (3), we have

$$\begin{aligned}& \bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F}( \mathrm{u}, \mathrm{a}) - \acute{\mathrm{v}}_{1} \bigr\rangle \geq \bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F}(\acute{ \mathrm{u}}, \mathrm{a}) - \acute{\mathrm{v}}_{1} \bigr\rangle , \\& \bigl\langle \mathrm{v}_{2}^{\ast},\mathfrak{G}( \mathrm{u}, \mathrm{a}) - \acute{\mathrm{v}}_{2} \bigr\rangle \geq \bigl\langle \mathrm{v}_{2}^{\ast}, \mathfrak{G}(\acute{ \mathrm{u}}, \mathrm{a}) - \acute{\mathrm{v}}_{2} \bigr\rangle , \\& \bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F}( \mathrm{u}, \acute{\mathrm{a}})-\acute{\mathrm{v}}_{1} \bigr\rangle \leq 0, \bigl\langle \mathrm{v}_{2}^{\ast}, \mathfrak{G}( \mathrm{u}, \acute{\mathrm{a}}) - \acute{\mathrm{v}}_{2} \bigr\rangle \leq 0, \end{aligned}$$

and $\langle \mathrm{v}_{3}^{\ast}, \mathrm{p}(\mathrm{u}, \acute{\mathrm{a}}) + \mathrm{p}(\acute{\mathrm{u}}, \mathrm{a}) \rangle \leq 0$. By assumption, we have $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}})\geq 0$. Therefore,

$$\begin{aligned} &\bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F}( \mathrm{u}, \mathrm{a}) - \acute{\mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathfrak{G}( \mathrm{u}, \mathrm{a}) - \acute{\mathrm{v}}_{2} \bigr\rangle \\ &\quad \geq \bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F} (\mathrm{u}, \acute{\mathrm{a}}) - \acute{\mathrm{v}}_{1} + \mathfrak{F}( \acute{\mathrm{u}}, \mathrm{a}) - \acute{\mathrm{v}}_{1} \bigr\rangle \\ &\qquad {} + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathfrak{G}( \mathrm{u}, \acute{\mathrm{a}}) - \acute{\mathrm{v}}_{2} + \mathfrak{G}( \acute{\mathrm{u}}, \acute{\mathrm{a}}) - \acute{ \mathrm{v}}_{2} \bigr\rangle \\ &\qquad {} + \bigl\langle \mathrm{v}_{3}^{\ast}, \mathrm{p}( \mathrm{u}, \acute{\mathrm{a}}) - \mathrm{p}(\acute{\mathrm{u}}, \acute{ \mathrm{a}}) + \mathrm{p}( \acute{\mathrm{u}}, \mathrm{a}) \bigr\rangle . \end{aligned}$$

(9)

Consequently,

$$\begin{array}{rl}& 〈{\mathrm{v}}_1^{\ast },\mathfrak{F}(\mathrm{u},\mathrm{a})-{\acute{\mathrm{v}}}_1〉+〈{\mathrm{v}}_2^{\ast },\mathfrak{G}(\mathrm{u},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & \ge 〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{G}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },{\mathrm{p}}^{\prime }(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\\ & +{\parallel \mathrm{u}-\acute{\mathrm{u}}\parallel }^2({\rho }_1〈{\mathrm{v}}_1^{\ast },e〉+{\rho }_2〈{\mathrm{v}}_2^{\ast },e^{\prime }〉+{\rho }_3〈{\mathrm{v}}_2^{\ast },e^{″}〉).\end{array}$$

(10)

It completes the proof of Lemma 3.3. □

We establish the sufficient KKT optimality conditions of the parametric $\mathbb{S}$-$\mathbb{VPOP}s$ (1) under contingent epiderivative and ρ-$\mathbb{C}$A$\mathbb{C}$ assumptions.

Theorem 3.4

(Sufficient optimality conditions)

Let W be an arcwise connected subset of U and $(\acute{\mathrm{u}}, \acute{\mathrm{a}})\in U\times A$, with $(\acute{\mathrm{u}}, \acute{\mathrm{a}})\in \check{S}$,

$$ \acute{\mathrm{v}}_{1} \in \mathfrak{F}(\acute{\mathrm{u}}, \acute{ \mathrm{u}}), \qquad \acute{\mathrm{v}}_{2} \in \mathfrak{G}( \acute{ \mathrm{u}}, \acute{\mathrm{a}}) \cap (-\Omega _{2}),$$

and $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}})\geq 0$. Let $e\in \operatorname{int}(\Omega _{1})$, $e^{\prime}\in \operatorname{int}(\Omega _{2})$, and $e^{\prime \prime}\in \operatorname{int}(\Omega _{3})$. Suppose that $\mathfrak{F}(\cdot, \acute{\mathrm{a}}): U \to 2^{V_{1}}$ is $\rho _{1}$-$\Omega _{1}$-A$\mathbb{C}$ with respect to e, $\mathfrak{G}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{2}}$ is $\rho _{2}$-$\Omega _{2}$-A$\mathbb{C}$ with respect to $e^{\prime}$, and $\mathrm{p}(\cdot, \acute{\mathrm{a}}) : U \to V_{3}$ is $\rho _{3}$-$\Omega _{3}$-A$\mathbb{C}$ with respect to $e^{\prime \prime}$ on W. Assume that the contingent epiderivatives ${\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)$ and ${\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)$ exist and the Gâteaux derivative $\mathrm{p}^{\prime}(\cdot, \acute{\mathrm{a}})(\acute{\mathrm{u}})$ exists. Suppose that the conditions of Lemma 3.3hold at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ for some

$$ \bigl(\mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast}\bigr) \in \Omega _{1}^{+} \times \Omega _{2}^{+} \times \Omega _{3}^{+},$$

with $\mathrm{v}_{1}^{\ast}\neq \theta _{V_{1}}$ and

$$ \rho _{1} \bigl\langle \mathrm{v}_{1}^{\ast}, e\bigr\rangle + \rho _{2} \bigl\langle \mathrm{v}_{2}^{\ast}, e^{\prime}\bigr\rangle + \rho _{3} \bigl\langle \mathrm{v}_{3}^{\ast}, e^{\prime \prime} \bigr\rangle \geq 0, $$

(11)

such that

$$\begin{array}{rl}& 〈{\mathrm{v}}_1^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathcal{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))\\ & +\mathfrak{G}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },{\mathrm{p}}^{\prime }(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\acute{\mathrm{u}}}(0+))+\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\\ & \ge 0,\end{array}$$

(12)

$\forall (\cdot, \mathrm{a}) \in W\times A$, and

$$ \bigl\langle \mathrm{v}_{3}^{\ast}, \acute{\mathrm{v}}_{2}\bigr\rangle =0, $$

(13)

then $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1})$ is a weak minimizer of problem (1).

Proof

Suppose that $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1})$ is not a weak minimizer of problem (1). Then there exist $(\mathrm{u}, \mathrm{a})\in \check{S}$ and $\mathrm{v}_{1}\in \mathfrak{F}(\mathrm{u}, \mathrm{a})$ such that $\mathrm{v}_{1} <\acute{\mathrm{v}}_{1}$. As

$$ \mathrm{v}_{1}^{\ast}\in \Omega _{1}^{+} \setminus \{\theta _{V_{1}}\},$$

$\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1} - \acute{\mathrm{v}}_{1} \rangle < 0$. As $(\mathrm{u}, \mathrm{a})\in \mathrm{a}$, there exists

$$ \mathrm{v}_{2} \in \mathfrak{G}( \mathrm{u}, \mathrm{a})\cap (- \Omega _{2}).$$

So, $\langle \mathrm{v}_{2}^{\ast},\mathrm{v}_{2} \rangle \leq 0$ as $\mathrm{v}_{2}^{\ast}\in \Omega _{2}^{+}$. Since $\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2} \rangle = 0$, we have

$$ \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} - \acute{\mathrm{v}}_{2} \bigr\rangle = \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} \bigr\rangle \leq 0.$$

Therefore,

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \acute{\mathrm{v}}_{1} - \acute{\mathrm{v}}_{2} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} - \acute{\mathrm{v}}_{2} \bigr\rangle < 0. $$

(14)

As the conditions of Lemma 3.3 hold at $(\acute{\mathrm{u}}, \acute{\mathrm{u}}, \acute{\mathrm{u}}, \acute{\mathrm{u}}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$, from Eqs. (4), (11), and (12), we have

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F}( \mathrm{u}, \mathrm{u})- \acute{\mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2}^{\ast}(\mathrm{u}, \mathrm{a}) - \acute{\mathrm{v}}_{2} \bigr\rangle \geq 0.$$

Hence,

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1}-\acute{\mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} - \acute{\mathrm{v}}_{2} \bigr\rangle \geq 0,$$

which contradicts (14). Consequently, $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1})$ is a weak minimizer of problem (1). □

3.4 Wolfe type dual

We consider a Wolfe type dual (15), where $\mathfrak{F}(\cdot, \acute{\mathrm{a}})$ and $\mathfrak{G}(\cdot, \acute{\mathrm{a}})$ are contingent epiderivable set-valued maps and $\mathrm{p}(\cdot, \acute{\mathrm{a}})$ is a Gâteaux derivable single-valued map, where $\acute{\mathrm{a}}\in A$.

$$\begin{array}{rl}\text{maximize}& {\acute{\mathrm{v}}}_1+〈{\mathrm{v}}_1^{\ast },{\acute{\mathrm{v}}}_2〉e,\\ \text{subject to}& \\ & 〈{\mathrm{v}}_1^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{G}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },{\mathrm{p}}^{\prime }(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\ge 0,\end{array}$$

(15)

$\forall (\mathrm{u}, \mathrm{a}) \in W\times A$, $\acute{\mathrm{u}}\in W$, $\acute{\mathrm{a}}\in A$, $\acute{\mathrm{v}}_{1}\in \mathfrak{F}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, $\acute{\mathrm{v}}_{2}\in \mathfrak{G}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}}) \geq 0$,

$$ \bigl(\mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast}\bigr) \in \Omega _{1}^{+} \times \Omega _{2}^{+} \times \Omega _{3}^{+},$$

and $\langle \mathrm{v}_{1}^{\ast}, e\rangle =1$.

Definition 3.5

A point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ satisfying all the constraints of (15) is called a feasible point of problem (15). The feasible point

$$ \bigl(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast}\bigr)$$

of problem (15) is called a weak maximizer of (15) if there exists no feasible point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \tilde{\mathrm{v}}_{1}^{\ast}, \tilde{\mathrm{v}}_{2}^{\ast}, \tilde{\mathrm{v}}_{3}^{\ast})$ of (15) such that

$$ \bigl(\mathrm{v}_{1} + \bigl\langle \tilde{\mathrm{v}}_{2}^{\ast}, \mathrm{v}_{2} \bigr\rangle e\bigr) - \bigl(\acute{ \mathrm{v}}_{1} + \bigl\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2} \bigr\rangle e\bigr)\in \operatorname{int}(\Omega _{1}).$$

We prove the duality results of Wolfe type of problem (1). The proofs are very similar to Theorems 3.10–3.12, and hence omitted.

Theorem 3.6

(Weak duality)

Let W be an arcwise connected subset of U, $(\acute{\mathrm{u}}_{0}, \acute{\mathrm{a}}_{0}) \in \check{S}$, $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ be a feasible point of problem (15), and $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}})\geq 0$. Let

$$ e\in \operatorname{int}(\Omega _{1}),\qquad e^{\prime}\in \operatorname{int}( \Omega _{2}), \qquad e^{\prime \prime}\in \operatorname{int}(\Omega _{3}).$$

Suppose that $\mathfrak{F} (\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{1}}$ is $\rho _{1}$-$\Omega _{1}$-A$\mathbb{C}$ with respect to e, $\mathfrak{G}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{2}}$ is $\rho _{2}$-$\Omega _{2}$-A$\mathbb{C}$ with respect to $e^{\prime}$, and $\acute{\mathrm{a}}(\cdot, \acute{\mathrm{a}}) : U \to V_{3}$ is $\rho _{3}$-$\Omega _{3}$-A$\mathbb{C}$ with respect to $e^{\prime \prime}$ on W. Assume that the contingent epiderivatives ${\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)$ and ${\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)$ exist and the Gâteaux derivative $\mathrm{p}^{\prime}(\cdot, \acute{\mathrm{a}})(\acute{\mathrm{u}})$ exists. Suppose that the conditions of Lemma 3.3hold at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ and (17) is satisfied. Then

$$ \mathfrak{F}(\mathrm{u}_{0}, \mathrm{a}_{0}) - \bigl( \acute{\mathrm{v}}_{1} + \bigl\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2}\bigr\rangle e\bigr) \subseteq V_{1} \setminus -\operatorname{int}(\Omega _{1}).$$

Theorem 3.7

(Strong duality)

Let $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1})$ be a weak minimizer of problem (1) and $\acute{\mathrm{v}}_{2}\in \mathfrak{G}(\acute{\mathrm{u}}, \acute{\mathrm{a}})\cap (-\Omega _{2})$. Assume that for some

$$ \bigl(\mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast}\bigr) \in \Omega _{1}^{+} \times \Omega _{2}^{+} \times \Omega _{3}^{+},$$

with $\langle \mathrm{v}_{1}^{\ast}, e\rangle =1$, Eqs. (12) and (13) are satisfied at the point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$. Then $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ is a feasible solution for problem (15). If the weak duality Theorem 3.6between (1) and (15) holds, then the point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ is a weak maximizer of problem (15).

Theorem 3.8

(Converse duality)

Let W be an arcwise connected subset of the space U and $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ be a feasible point of problem (15) with $\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2}\rangle \geq 0$ and $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}})\geq 0$. Let $e\in \operatorname{int}(\Omega _{1})$, $e^{\prime}\in \operatorname{int}(\Omega _{2})$, and $e^{\prime \prime} \in \operatorname{int}(\Omega _{3})$. Suppose that $\mathfrak{F} (\cdot, \acute{\mathrm{a}}) : U\to 2^{V_{1}}$ is $\rho _{1}$-$\Omega _{1}$-A$\mathbb{C}$ with respect to e, $\mathfrak{G}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{2}}$ is $\rho _{2}$-$\Omega _{2}$-A$\mathbb{C}$ with respect to $e^{\prime}$, and $\mathrm{p}(\cdot, \acute{\mathrm{a}} ) : U\to V_{3}$ is $\rho _{3}$-$\Omega _{3}$-A$\mathbb{C}$ with respect to $e^{\prime \prime}$ on W. Assume that the contingent epiderivatives

$${\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1),{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2),$$

exist and the Gâteaux derivative $\mathrm{p}^{\prime}(\cdot, \acute{\mathrm{a}})( \acute{\mathrm{u}})$ exists. Suppose that the conditions of Lemma 3.3hold at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ and (17) is satisfied. If $(\acute{\mathrm{u}}, \acute{\mathrm{a}})\in \check{S}$, then $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{2})$ is a weak minimizer of (1).

3.5 Mond–Weir type dual

We consider a Mond–Weir type dual (16), where $\mathfrak{F}(\cdot, \mathfrak{F})$ and $\mathfrak{G}(\cdot, \acute{\mathrm{a}})$ are contingent epiderivable and $\mathrm{p}(\cdot, \acute{\mathrm{a}})$ is a Gâteaux derivable single-valued map, where $\acute{\mathrm{a}}\in A$.

$$\begin{array}{rl}\text{maximize }& {\acute{\mathrm{v}}}_1,\\ \text{subject to}& \\ & 〈{\mathrm{v}}_1^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{a}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{G}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },{\mathrm{p}}^{\prime }(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\acute{\mathrm{u}}}(0+))+\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\ge 0,\end{array}$$

(16)

$\forall (\mathrm{u}, \mathrm{u}) \in W\times A$, $\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2} \rangle \geq 0$, $\acute{\mathrm{u}}\in W$, $\acute{\mathrm{a}}\in A$, $\acute{\mathrm{v}}_{1} \in \mathfrak{F}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, $\acute{\mathrm{a}}\in \mathfrak{G}(\acute{\mathrm{u}}, \acute{\mathrm{a}})$, $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}}) \geq 0$,

$$ \bigl(\mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast}\bigr) \in \Omega _{1}^{+} \times \Omega _{2}^{+} \times \Omega _{3}^{+},$$

with $\langle \mathrm{v}_{1}^{\ast}, e\rangle =1$.

Definition 3.9

A point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ satisfying all the constraints of problem (16) is called a feasible point of (16). The feasible point is called a weak maximizer of problem (16) if there exists no feasible point $(\mathrm{u}, \mathrm{a}, \mathrm{v}_{1}, \mathrm{v}_{2}, \tilde{\mathrm{v}}_{1}^{\ast}, \tilde{\mathrm{v}}_{2}^{\ast}, \tilde{\mathrm{v}}_{3}^{\ast})$ of (16) such that $\mathrm{v}_{1}- \acute{\mathrm{v}}_{1} \in \operatorname{int}(\Omega _{1})$.

Theorem 3.10

(Weak duality)

Let W be an arcwise connected subset of U, $(\mathrm{u}_{0}, \mathrm{a}_{0}) \in \check{S}$, $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ be a feasible point of problem (16), and $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}})\geq 0$. Let

$$ {e\in \operatorname{int}(\Omega _{1}), \qquad e^{\prime}\in \operatorname{int}(\Omega _{2}),\qquad e^{\prime \prime}\in \operatorname{int}( \Omega _{3}).}$$

Suppose that $\mathfrak{F}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{2}}$ is $\rho _{1}$-$\Omega _{1}$-A$\mathbb{C}$ with respect to e, $\mathfrak{G}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{2}}$ is $\rho _{2}$-$\Omega _{2}$-A$\mathbb{C}$ with respect to $e^{\prime}$, and $\mathrm{p}(\cdot, \acute{\mathrm{a}}) : U \to V_{3}$ is $\rho _{3}$-$\Omega _{3}$-A$\mathbb{C}$ with respect to $e^{\prime \prime}$ on W. Assume that the contingent epiderivatives ${\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{u}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)$ and ${\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)$ exist and the Gâteaux derivative $\mathrm{p}^{\prime}(\cdot, \acute{\mathrm{a}})(\acute{\mathrm{u}})$ exists. Suppose that the conditions of Lemma 3.3hold at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$. Assume that

$$ \rho _{1} +\rho _{2} \bigl\langle \mathrm{v}_{2}^{\ast}, e^{\prime}\bigr\rangle + \rho _{3} \bigl\langle \mathrm{v}_{3}^{\ast}, e^{\prime \prime} \bigr\rangle \geq 0. $$

(17)

Then $\mathfrak{F}(\mathrm{u}_{0}, \mathrm{a}_{0}) - \acute{\mathrm{v}}_{1} \subseteq V_{1} \setminus - \operatorname{int}(\Omega _{1})$.

Proof

We prove the theorem by the method of contradiction. Suppose that for some

$$ \mathrm{v}_{1}^{\circ}\in \mathfrak{F}( \mathrm{u}_{0}, \mathrm{a}_{0}), \qquad \mathrm{v}_{1}^{\circ}- \acute{\mathrm{v}}_{1} \in - \operatorname{int}(\Omega _{1}).$$

Therefore, $\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1}^{\circ}- \acute{\mathrm{v}}_{1} \rangle < 0$ as $\theta _{V_{1}} \neq \mathrm{v}_{1}^{\ast}\in \Omega _{1}^{+}$. Again, since $(\mathrm{u}_{0}, \mathrm{a}_{0})\in \check{S}$, we have

$$ \mathfrak{G} (\mathrm{u}_{0}, \mathrm{a}_{0})\cap (- \Omega _{2} ) \neq \emptyset ,$$

and $\mathrm{p}(\mathrm{u}_{0}, \mathrm{a}_{0}) =0$. We choose

$$ \mathrm{v}_{2}^{\circ}\in \mathfrak{G}( \mathrm{u}_{0}, \mathrm{a}_{0}) \cap (-\Omega _{2}).$$

So, $\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2}^{\circ}\rangle \leq 0$ as $\mathrm{v}_{2}^{\ast}\in \Omega _{2}^{+}$. Again, from the constraints of (16), we have $\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2} \rangle \geq 0$. Therefore,

$$ \bigl\langle \mathrm{v}_{2}^{\ast},\mathrm{v}_{2}^{\circ}- \acute{\mathrm{v}}_{2} \bigr\rangle = \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2}^{\circ}\bigr\rangle - \bigl\langle \mathrm{v}_{2}^{\ast}, \acute{ \mathrm{v}}_{2} \bigr\rangle \leq 0.$$

Hence,

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1}^{\circ}- \acute{\mathrm{v}}_{1} \bigr\rangle +\bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2}^{\circ}- \acute{\mathrm{v}}_{2} \bigr\rangle < 0. $$

(18)

As the conditions of Lemma 3.3 hold at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$, from Eqs. (4), (17) and the constraints of (16), we have

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F} \bigl( \mathrm{v}_{1}^{\circ}, \mathrm{a}\bigr) - \acute{ \mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathfrak{G}(\mathrm{u}_{0}, \mathrm{a}) - \acute{ \mathrm{v}}_{2} \bigr\rangle \geq 0.$$

Hence,

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1}^{\circ}- \acute{\mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2}^{\circ}- \acute{\mathrm{v}}_{2} \bigr\rangle \geq 0,$$

which contradicts (18). Therefore,

$$ \mathfrak{F}(\mathrm{u}_{0}, \mathrm{a}_{0}) - \acute{ \mathrm{v}}_{1} \subseteq V_{1}\setminus - \operatorname{int}(\Omega _{1}).$$

It completes the proof of the theorem. □

Theorem 3.11

(Strong duality)

Let $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1})$ be a weak minimizer of problem (1) and $\acute{\mathrm{v}}_{2}\in \mathfrak{G}(\acute{\mathrm{u}}, \acute{\mathrm{a}}) \cap (-\Omega _{2})$. Assume that for some

$$ \bigl(\mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast}\bigr) \in \Omega _{1}^{+} \times \Omega _{2}^{+} \times \Omega _{3}^{+},$$

with $\langle \mathrm{v}_{1}^{\ast}, e\rangle = 1$, Eqs. (12) and (13) are satisfied at the point

$$ \bigl(\acute{\mathrm{u}}, \acute{\mathrm{a}},\acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast}\bigr).$$

Then $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ is a feasible solution for problem (16). If the weak duality Theorem 3.10between (1) and (16) holds, then the point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ is a weak maximizer of (16).

Proof

As Eqs. (12) and (13) are satisfied at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$,

$$\begin{array}{rl}& 〈{\mathrm{v}}_1^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))+\mathfrak{F}(\acute{\mathrm{u}},\mathrm{a})-{\acute{\mathrm{v}}}_1〉\\ & +〈{\mathrm{v}}_2^{\ast },{\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))\\ & +\mathfrak{G}(\acute{\mathrm{u}},\mathrm{u})-{\acute{\mathrm{v}}}_2〉\\ & +〈{\mathrm{v}}_3^{\ast },{\mathrm{p}}^{\prime }(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}})({\acute{\mathcal{H}}}_{\acute{\mathrm{u}},\mathrm{u}}(0+))\\ & +\mathrm{p}(\acute{\mathrm{u}},\mathrm{a})〉\ge 0,\end{array}$$

(19)

$\forall (\mathrm{u}, \mathrm{a}) \in W\times A$, and $\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2} \rangle =0$. As $(\acute{\mathrm{u}}, \acute{\mathrm{a}})\in \check{S}$, $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}})=0$. Hence, $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ is a feasible solution for (16). Suppose that the weak duality Theorem 3.10 between problems (1) and (16) holds and the point $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ is not a weak maximizer of problem (16). Let

$$ \bigl(\mathrm{u}, \mathrm{a}, \mathrm{v}_{1}, \mathrm{v}_{2}, \tilde{\mathrm{v}}_{1}^{\ast}, \tilde{ \mathrm{v}}_{2}^{\ast}, \tilde{\mathrm{v}}_{3}^{\ast}\bigr)$$

be a feasible point for (16) such that $\acute{\mathrm{v}}_{1} - \mathrm{v}_{1} \in -\operatorname{int}( \Omega _{1})$. It contradicts the weak duality Theorem 3.10 between (1) and (16). Consequently, $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ is a weak maximizer for (16). □

Theorem 3.12

(Converse duality)

Let W be an arcwise connected subset of U, $\mathrm{p}(\acute{\mathrm{u}}, \acute{\mathrm{a}}) \geq 0$, and $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ be a feasible point of problem (16). Let

$$ e\in \operatorname{int}(\Omega _{1}),\qquad e^{\prime}\in \operatorname{int}(\Omega _{2}),\qquad e^{\prime \prime}\in \operatorname{int}(\Omega _{3}).$$

Suppose that $\mathfrak{F}(\cdot, \acute{\mathrm{a}}) : U \to 2^{V_{1}}$ is $\rho _{1}$-$\Omega _{1}$-A$\mathbb{C}$ with respect to e, $\acute{\mathrm{a}}(\cdot,\acute{\mathrm{a}}) : U \to 2^{V_{2}}$ is $\rho _{2}$-$\Omega _{2}$-A$\mathbb{C}$ with respect to $e^{\prime}$, and $\acute{\mathrm{a}}(\cdot, \acute{\mathrm{a}}) : U \to V_{3}$ is $\rho _{3}$-$\Omega _{3}$-A$\mathbb{C}$ with respect to $e^{\prime \prime}$ on W. Assume that the contingent epiderivatives ${\mathbb{D}}_{\uparrow }\mathfrak{F}(\cdot ,\mathfrak{F})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_1)$ and ${\mathbb{D}}_{\uparrow }\mathfrak{G}(\cdot ,\acute{\mathrm{a}})(\acute{\mathrm{u}},{\acute{\mathrm{v}}}_2)$ exist and the Gâteaux derivative $\mathrm{p}^{\prime}(\cdot, \acute{\mathrm{a}})(\acute{\mathrm{u}})$ exists. Suppose that the conditions of Lemma 3.3hold at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$ and (17) is satisfied. If $(\acute{\mathrm{u}}, \acute{\mathrm{a}})\in \check{S}$, then $(\acute{\mathrm{u}}, \acute{\mathrm{a}},\acute{\mathrm{v}}_{1})$ is a weak minimizer of (1).

Proof

Suppose that $(\acute{\mathrm{u}}, \acute{\mathrm{a}},\acute{\mathrm{v}}_{1})$ is not a weak minimizer of problem (1). Then there exist $(\mathrm{u}, \mathrm{a})\in \check{S}$ and $\mathrm{v}_{1} \in \mathfrak{F}(\mathrm{u}, \mathrm{a})$ such that $\mathrm{v}_{1} < \acute{\mathrm{v}}_{1}$. As $\mathrm{v}_{1}^{\ast}\in \Omega _{1}^{+} \setminus \{\theta _{V_{1}} \}$, $\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1} - \acute{\mathrm{v}}_{1} \rangle < 0$. As $(\mathrm{u}, \mathrm{a})\in \check{S}$, there exists

$$ \mathrm{v}_{2}\in \mathfrak{G}(\mathrm{u},\mathrm{a}) \cap (-\Omega _{2}).$$

So, $\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} \rangle \leq 0$ as $\mathrm{v}_{2}^{\ast}\in \Omega _{2}^{+}$. By the constraints of (16), we have $\langle \mathrm{v}_{2}^{\ast}, \acute{\mathrm{v}}_{2}\rangle \geq 0$. Therefore,

$$ \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} - \acute{\mathrm{v}}_{2} \bigr\rangle = \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} \bigr\rangle - \bigl\langle \mathrm{v}_{2}^{\ast}, \acute{ \mathrm{v}}_{2}\bigr\rangle \leq 0.$$

Indeed,

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1} - \acute{\mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} - \acute{\mathrm{v}}_{2} \bigr\rangle < 0. $$

(20)

As the conditions of Lemma 3.3 hold at $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1}, \acute{\mathrm{v}}_{2}, \mathrm{v}_{1}^{\ast}, \mathrm{v}_{2}^{\ast}, \mathrm{v}_{3}^{\ast})$, from Eqs. (4), (17) and the constraints of (16), we have

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathfrak{F}( \mathrm{u}, \mathrm{a}) - \acute{\mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathfrak{G}(\mathrm{u}, \mathrm{a}) - \acute{\mathrm{v}}_{2}\bigr\rangle \geq 0.$$

Hence,

$$ \bigl\langle \mathrm{v}_{1}^{\ast}, \mathrm{v}_{1} -\acute{\mathrm{v}}_{1} \bigr\rangle + \bigl\langle \mathrm{v}_{2}^{\ast}, \mathrm{v}_{2} - \acute{\mathrm{v}}_{2}\bigr\rangle \geq 0,$$

which contradicts (20). Consequently, $(\acute{\mathrm{u}}, \acute{\mathrm{a}}, \acute{\mathrm{v}}_{1})$ is a weak minimizer of problem (1). □

4 Conclusions

In this paper, we establish the sufficient KKT optimality conditions for the parametric $\mathbb{S}$-$\mathbb{VPOP}s$ (1) under ρ-Ω-A$\mathbb{C}$ and contingent epiderivative assumptions. We also construct the duals of Mond–Weir (16) and Wolfe (15) types and derive the duality results for weak minimizers between the primal problem (1) and corresponding dual problems.